The Federal Reserve Board eagle logo links to home page
Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]
Finance and Economics Discussion Series: 2009-27 Screen Reader version ♣

CONFIDENCE INTERVALS FOR LONG-HORIZON PREDICTIVE REGRESSIONS VIA REVERSE REGRESSIONS*

Min Wei**
Johnathan H. Wright

Keywords: Predictive regressions, long horizons, confidence intervals, small sample problems, persistence

Abstract:

Long-horizon predictive regressions in finance pose formidable econometric problems when estimated using the sample sizes that are typically available. A remedy that has been proposed by Hodrick (1992) is to run a reverse regression in which short-horizon returns are projected onto a long-run mean of some predictor. By covariance stationarity, the slope coefficient is zero in the reverse regression if and only if it is zero in the original regression, but testing the hypothesis in the reverse regression avoids small sample problems. Unfortunately this only allows the null of no predictability to be tested. In this paper, we show how to use the reverse regression to test other hypotheses about the slope coefficient in a long-horizon predictive regression, and hence to form confidence intervals for this coefficient. We show that this approach to inference works well in small samples, even when the predictors are highly persistent.

1 Introduction

Asset returns are widely thought to be somewhat forecastable, and perhaps more so at long than at short horizons. But inference in long-horizon predictive regressions is well known to be complicated by severe econometric problems in empirically relevant sample sizes. The problems arise because the predictors that are used are variables like the dividend yield or term spread that are highly persistent, while the regressor is an overlapping sum of short-term returns. This creates something akin to a spurious regression. This is compounded by the feedback effect, or absence of strict exogeneity--a shock to returns will in turn affect future values of the predictors. As a result, conventional t-statistics have rejection rates that are well above their nominal levels. The vast literature on the problems with long-horizon predictive regressions includes work such as Goetzmann and Jorion (1993), Elliott and Stock (1994), Stambaugh (1999), Valkanov (2003) and Campbell and Yogo (2006).

Hodrick (1992) proposed an approach to test the null hypothesis that a certain predictor does not help forecast long-horizon returns. His idea was instead of regressing the cumulative h-period returns onto the predictor at the start of the holding period, to regress the one-period return onto the average of the predictors over the previous h periods. Under stationarity, for the coefficient in the first projection to be equal to zero is necessary and sufficient for the coefficient in the second projection to be equal to zero. However, the second regression has a persistent right-hand-side variable, but not a persistent left-hand side variable. Intuitively, this might mean that the size distortions of a test based on the second regression are much smaller. Hodrick finds that this is indeed the case. This approach to inference has become fairly widely used.

However, many researchers believe that there is some time series predictability in asset returns, even after controlling for econometric problems (see for example Campbell (2000)). The contribution of this paper is to show that a methodology related to the reverse-regression can be used more widely, to test any hypothesis about the parameter vector in a long-horizon regression, not just that it is equal to zero. A confidence set for the parameter vector can then be formed by inverting the acceptance region of the test. The proposed confidence set is asymptotically equivalent to the conventional estimation of the predictive regression. However, we show that it has substantially better small-sample properties.

The approach to inference proposed here applies regardless of whether there is a single predictor or multiple predictors. That is an advantage of this approach to inference relative to some others that have been proposed, such as the method of Campbell and Yogo (2006) that applies only for a scalar predictor.

The plan for the remainder of the paper is as follows. Section 2 describes long-horizon regressions and the proposed approach to inference. Section 3 assesses the small sample performance of the methodology in a Monte-Carlo simulation. Section 4 contains an empirical application to forecasting excess stock and bond returns. Section 5 concludes.

2. The Methodology

Let r_{t+1} denote the continuously compounded return from t to t+1 and let r_{t+h}^{(h)} =(r_{t+1} +r_{t+2} ...r_{t+h} )/h denote the h-period return. Let x_t be some px1 vector of predictors. Assume that y_t =(r_t ,{x}'_t {)}' is covariance-stationary and that A(L)y_t =\varepsilon _t where A(L) is a lag polynomial with all roots outside the unit circle and \varepsilon _t is a martingale difference sequence with 2+\delta finite moments for some \delta >0. Consider the long-horizon predictive regression

\begin{displaymath} r_{t+h}^{(h)} =\alpha +{\beta }'x_t +\varepsilon _{t+h} \end{displaymath} (1)

Researchers commonly estimate this regression, using either Newey-West or Hansen-Hodrick standard errors (Newey and West (1987) and Hansen and Hodrick (1980)), to control for the serial correlation in the errors. Alternative standard errors in equation (1) are given by Hodrick standard errors 1B (Hodrick (1992)). This involves estimating the variance of (\alpha ,\beta ')'in the forward regression (equation (1)) as (\Sigma \tilde {x}_t \tilde {{x}'}_t )^{-1}\Sigma w_{t+1} {w}'_{t+1} (\Sigma \tilde {x}_t \tilde {{x}'}_t )^{-1} where w_{t+1} =(r_{t+1} -\bar {r})(\Sigma _{i=0}^{h-1} \tilde {x}_{t-i} ) where \tilde {x}_t =(1,{x}'_t )' and \bar {r} is the sample mean of returns. Hodrick standard errors 1B are valid only if \beta =0, because it is in this case alone that the sample variance of w_{t+1} is a consistent estimate of the zero-frequency spectral density of x_t \varepsilon _{t+h} .

Consider also the reverse regression of the one-period return on the h-period average of the regressor:

\begin{displaymath} r_{t+1} =\mu +{\gamma }'x_t^{(h)} +u_{t+1} \end{displaymath} (2)

where x_t^{(h)} =(x_t +x_{t-1} ...+x_{t-h+1} )/h. The coefficients in the forward and reverse regressions are related as
\begin{displaymath} \beta =V_{xx}^{-1} \mbox{Cov}(r_{t+h}^h ,x_t )=V_{xx}^{-1} \Sigma _{j=1}^h Cov(r_{t+j} ,x_t )/h=V_{xx}^{-1} \Sigma _{j=1}^h Cov(r_{t+1} ,x_{t-j} )/h \end{displaymath}


\begin{displaymath} =V_{xx}^{-1} Cov(r_{t+1} ,x_t^{(h)} )=V_{xx}^{-1} V_{xx} (h)V_{xx} (h)^{-1}Cov(r_{t+1} ,x_t^{(h)} )=V_{xx}^{-1} V_{xx} (h)\gamma \end{displaymath} (3)

where V_{xx} and V_{xx} (h) are the variance-covariance matrices of x_t and x_t^{(h)} , respectively, and the last equality on the first line uses the assumption of covariance-stationarity. A consequence of this is that \beta =0 if and only if \gamma =0. However, inference in the reverse regression is less prone to size distortions. Consequently, Hodrick (1992) also proposed testing the hypothesis that \beta =0 by testing the implication that \gamma =0 in the reverse regression, equation (2). Note that Hodrick proposed the reverse regression in addition to his standard errors 1B, where the latter are alternative standard errors for the forward regression. Both can only be used to test the hypothesis of no predictability, i.e. that \beta =0. However, the evidence for some predictability in asset returns at long horizons is quite strong, and we are instead perhaps more interested in testing other hypotheses about \beta , or forming a confidence set for it.

This paper proposes methods for inference on \beta beyond just testing that it is equal to zero. The proposed approach is asymptotically equivalent to Wald tests/confidence sets for \beta in equation (1), but turns out to have better small sample properties. The idea is that from equation (3), under covariance-stationarity, \beta =V_{xx}^{-1} V_{xx} (h)\gamma and so inference about \gamma from the reverse regression can be used for inference on \beta , taking account of the distribution of the x_t s. Since \gamma =V_{xx} (h)^{-1}Cov(r_{t+1} ,x_t^{(h)} ), we only need to adjust the numerator of the reverse regression, as

\beta =V_{xx}^{-1} Cov(r_{t+1} ,x_t^{(h)} ) (4).

We now describe concretely how to use (4) for inference on \beta . First let \theta _1 =\mbox{Cov}(r_{t+1} ,x_t^{(h)} ) and \theta _2 =V_{xx} . Also let \hat {\theta }_1 =(T-h)^{-1}\Sigma _{t=h+1}^T (r_{t+1} -\bar {r})(x_t^{(h)} -\bar {x}) and \hat {\theta }_2 =T^{-1}\Sigma _{t=1}^T (x_t -\bar {x})(x_t -\bar {x}{)}' be the sample counterparts where \bar {r}=T^{-1}\Sigma _{t=1}^T r_t and \bar {x}=T^{-1}\Sigma _{t=1}^T x_t . We have \beta =\theta _2^{-1} \theta _1 and assume that

\begin{displaymath} \sqrt T (\hat {\theta }-\theta )\to _d N(0,V) \end{displaymath} (5)

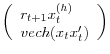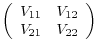where \theta =({\theta }'_{ & 1} ,vech(\theta _2 {)}'{)}', \hat {\theta }=(\hat {{\theta }'}_{ & 1} ,vech(\hat {\theta }_2 {)}'{)}' and V is the spectral density at frequency zero of \left( {{\begin{array}{*{20}c} {r_{t+1} x_t^{(h)} } \hfill \ {vech(x_t {x}'_t )} \hfill \ \end{array} }} \right), which can be partitioned conformably as \left( {{\begin{array}{*{20}c} {V_{11} } \hfill & {V_{12} } \hfill \ {V_{21} } \hfill & {V_{22} } \hfill \ \end{array} }} \right).

Two approaches to inference on \beta can be considered. The first uses the delta method as \beta is a nonlinear function of \theta that is itself root-T consistently estimable and asymptotically normal. Define an estimator of \beta as

\begin{displaymath} \tilde {\beta }=\hat {\theta }_2^{-1} \hat {\theta }_1 \end{displaymath} (6)

The distribution of this estimator can be obtained from (5) via the delta method. Concretely, because the derivatives of \beta with respect to \theta _1 and vech(\theta _2 )are \theta _2^{-1} and -(\theta _1 '\theta _2^{-1} \otimes \theta _2^{-1} )D_p , respectively, where D_p denotes the duplication matrix, it follows that:
\begin{displaymath} \sqrt T (\tilde {\beta }-\beta )\to _d N(0,[\left( {{\begin{array}{*{20}c} {\theta _2^{-1} } \hfill & {-(\theta _1 '\theta _2^{-1} \otimes \theta _2^{-1} )D_p } \hfill \ \end{array} }} \right)]\;V[\left( {{\begin{array}{*{20}c} {\theta _2^{-1} } \hfill & {-(\theta _1 '\theta _2^{-1} \otimes \theta _2^{-1} )D_p } \hfill \ \end{array} }} \right)]') \end{displaymath}

This accordingly implies that:
\begin{displaymath} \{\beta :T(\tilde {\beta }-\beta {)}'[\left( {{\begin{array}{*{20}c} {[\hat {\theta }_2^{-1} } \hfill & {-(\hat {\theta }_1 '\hat {\theta }_2^{-1} \otimes \hat {\theta }_2^{-1} )D_p } \hfill \ \end{array} }]} \right)\hat {V}\left( {{\begin{array}{*{20}c} {[\hat {\theta }_2^{-1} } \hfill & {-(\hat {\theta }_1 '\hat {\theta }_2^{-1} \otimes \hat {\theta }_2^{-1} )D_p } \hfill \ \end{array} }]} \right)']^{-1}(\tilde {\beta }-\beta {)}'\le F_p (\alpha )\} \end{displaymath}

is a 100-\alpha percent confidence set for \beta , where F_p (\alpha ) denotes the upper \alpha percentile of a \chi ^2(p)distribution and \hat {V} is a consistent estimator of V. We call this the delta-method variant of the proposed confidence interval.

However, the delta method can provide a poor approximation to the ratio of two random variables in small samples. This observation led Fieller (1954) to propose an alternative approach to inference on the ratio of two random variables. This method is based on inverting the acceptance region of a hypothesis test of a linear hypothesis that does not require any delta method approximation. This approach can be adapted here noting that

\begin{displaymath} \sqrt T (\hat {\theta }_2 \beta -\hat {\theta }_1 )\to _d N(0,\left( {{\begin{array}{*{20}c} {[-I_p } \hfill & {(\beta '\otimes I_p )} \hfill \ \end{array} }D_p ]} \right)V\left( {[{\begin{array}{*{20}c} {-I_p } \hfill & {(\beta '\otimes I_p )} \hfill \ \end{array} }D_p ]} \right)') \end{displaymath}


\begin{displaymath} T(\hat {\theta }_2 \beta -\hat {\theta }_1 {)}'[\left( {[{\begin{array}{*{20}c} {-I_p } \hfill & {(\beta '\otimes I_p )D_p } \hfill \ \end{array} }]} \right)\hat {V}\left( {[{\begin{array}{*{20}c} {-I_p } \hfill & {(\beta '\otimes I_p )} \hfill \ \end{array} }D_p ]} \right)']^{-1}(\hat {\theta }_2 \beta -\hat {\theta }_1 )\to _d \chi ^2(p) \end{displaymath}

This allows any hypothesis on \beta to be tested and means that
\begin{displaymath} \{\beta :T(\hat {\theta }_2 \beta -\hat {\theta }_1 {)}'[\left( {{\begin{array}{*{20}c} {[-I_p } \hfill & {(\beta '\otimes I_p )} \hfill \ \end{array} }D_p ]} \right)\hat {V}\left( {[{\begin{array}{*{20}c} {-I_p } \hfill & {(\beta '\otimes I_p )} \hfill \ \end{array} }D_p ]} \right)']^{-1}(\hat {\theta }_2 \beta -\hat {\theta }_1 )\le F_p (\alpha )\} \end{displaymath}

is a 100-\alpha percent confidence set for \beta . We call this proposed confidence interval, the Fieller variant of the proposed confidence set.

In the casep=1, the computation of this confidence interval does not require evaluating a test statistic at each point in a grid of values of \beta because the confidence set for \beta is

\begin{displaymath} \{\beta :\frac{T(\hat {\theta }_2 \beta -\hat {\theta }_1 )^2}{\left( {{\begin{array}{*{20}c} {[-1} \hfill & \beta \hfill \ \end{array} }]} \right)\hat {V}\left( {[{\begin{array}{*{20}c} {-1} \hfill & \beta \hfill \ \end{array} }]} \right)'}\le F_1 (\alpha )\} \end{displaymath}

which can be written as
\begin{displaymath} -\frac{b}{2a}\pm \sqrt {\frac{b^2-4ac}{4a^2}} \end{displaymath} (7)

where a=\hat {\theta }_2^2 -T^{-1}\hat {V}_{22} F_1 (\alpha ), b=2T^{-1}\hat {V}_{12} F_1 (\alpha )-2\hat {\theta }_1 \hat {\theta }_2 and c=\hat {\theta }_1^2 -T^{-1}\hat {V}_{11} F_1 (\alpha ), provided that a>0 and b^2>4ac, both of which occur with probability one asymptotically.3

Theorem 1 shows that the two proposed confidence sets are asymptotically equivalent to each other (for any p), which in turn means that they are both asymptotically equivalent to the conventional Wald confidence sets formed from estimating equation (1).

Theorem 1: The two proposed test statistics are asymptotically equivalent.

Proof. The delta-method tests the hypothesized value \beta using the test statistic:

\begin{displaymath} T(\tilde {\beta }-\beta {)}'[\left( {{\begin{array}{*{20}c} {[\hat {\theta }_2^{-1} } \hfill & {-(\hat {\theta }_1 '\hat {\theta }_2^{-1} \otimes \hat {\theta }_2^{-1} )D_p } \hfill \ \end{array} }]} \right)\hat {V}\left( {{\begin{array}{*{20}c} {[\hat {\theta }_2^{-1} } \hfill & {-(\hat {\theta }_1 '\hat {\theta }_2^{-1} \otimes \hat {\theta }_2^{-1} )D_p } \hfill \ \end{array} }]} \right)']^{-1}(\tilde {\beta }-\beta {)}' \end{displaymath}


\begin{displaymath} =T(\hat {\theta }_1 -\hat {\theta }_2 \beta {)}'[\left( {{\begin{array}{*{20}c} {[I_p } \hfill & {-(\tilde {\beta }'\otimes I_p )} \hfill \ \end{array} }D_p ]} \right)\hat {V}\left( {{\begin{array}{*{20}c} {[I_p } \hfill & {-(\tilde {\beta }'\otimes I_p )} \hfill \ \end{array} }D_p ]} \right)']^{-1}(\hat {\theta }_1 -\hat {\theta }_2 \beta ) \end{displaymath}

The Fieller method uses the test statistic
\begin{displaymath} T(\hat {\theta }_2 \beta -\hat {\theta }_1 {)}'[\left( {[{\begin{array}{*{20}c} {-I_p } \hfill & {(\beta '\otimes I_p )D_p } \hfill \ \end{array} }]} \right)V\left( {[{\begin{array}{*{20}c} {-I_p } \hfill & {(\beta '\otimes I_p )} \hfill \ \end{array} }D_p ]} \right)']^{-1}(\hat {\theta }_2 \beta -\hat {\theta }_1 ) \end{displaymath}


\begin{displaymath} =T(\hat {\theta }_1 -\hat {\theta }_2 \beta {)}'[\left( {[{\begin{array}{*{20}c} {I_p } \hfill & {-(\beta '\otimes I_p )D_p } \hfill \ \end{array} }]} \right)\hat {V}\left( {[{\begin{array}{*{20}c} {I_p } \hfill & {-(\beta '\otimes I_p )} \hfill \ \end{array} }D_p ]} \right)']^{-1}(\hat {\theta }_1 -\hat {\theta }_2 \beta ) \end{displaymath}

But since \tilde {\beta }\to & _p \beta , the difference between these two test statistics is o_p (1).

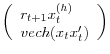Implementation of the proposed confidence intervals requires choosing a specific estimator of V, the spectral density matrix of \left( {{\begin{array}{*{20}c} {r_{t+1} x_t^{(h)} } \hfill \ {vech(x_t {x}'_t )} \hfill \ \end{array} }} \right). We use a Newey-West estimator with lag length equal to h.

We now turn to assessing how the proposed methods work in practice. The methods are referred to as "reverse regression" estimates even though they do not require explicit estimation of equation (2) because they are both based on assessing the covariance between one-period returns and the h-period mean of the predictor.

3. Monte-Carlo simulation.

The proposed approaches to inference are both asymptotically equivalent to conventional Wald tests and confidence intervals. The motivation for considering them is that they may work better in small samples. Like the conventional methods, their justification is based on an assumption of stationarity, and methods that assume stationarity often fare poorly in the presence of a unit root, or a near unit root, at least in empirically relevant sample sizes. But the proposed methods might in practice be quite robust to near non-stationarity. The intuition is that they back out the implied coefficient in the long-horizon regression from the correlation between one-period returns and a long-run average of the predictor. How well the proposed methods actually work in finite samples with nearly non-stationary predictors is the key practical question that we answer in a Monte-Carlo experiment.

In this experiment, returns and the predictor follow a VAR(1):

\begin{displaymath} \left( {{\begin{array}{*{20}c} {r_{t+1} } \hfill \ {x_{t+1} } \hfill \ \end{array} }} \right)=\mu +\Phi \left( {{\begin{array}{*{20}c} {r_t } \hfill \ {x_t } \hfill \ \end{array} }} \right)+\left( {{\begin{array}{*{20}c} {\varepsilon _{r,} _{t+1} } \hfill \ {\varepsilon _{x,} _{t+1} } \hfill \ \end{array} }} \right) \end{displaymath} (8)

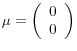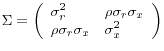where the errors are iid normal with mean zero and covariance matrix \Sigma . Following Campbell (2001), set \mu =\left( {{\begin{array}{*{20}c} 0 \hfill \ 0 \hfill \ \end{array} }} \right), \Phi =\left( {{\begin{array}{*{20}c} 0 \hfill & \alpha \hfill \ 0 \hfill & \varphi \hfill \ \end{array} }} \right) and \Sigma =\left( {{\begin{array}{*{20}c} {\sigma _r^2 } \hfill & {\rho \sigma _r \sigma _x } \hfill \ {\rho \sigma _r \sigma _x } \hfill & {\sigma _x^2 } \hfill \ \end{array} }} \right). As the units of measurement for returns and the predictors are arbitrary, we can normalize \sigma _r =\sigma _x =1 without loss of generality, leaving three free parameters: \alpha , \varphi and \rho .

After some algebra, the slope coefficient in the long-horizon regression is

\begin{displaymath} \beta =\{\frac{\omega _{21} }{\omega _{22} }{e}'_1 \Sigma _{i=1}^h \Phi ^ie_1 +{e}'_2 \Sigma _{i=1}^h \Phi ^ie_1 \}/h \end{displaymath}

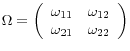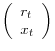where e_1 =(1,0{)}', e_2 =(0,1{)}' and \Omega =\left( {{\begin{array}{*{20}c} {\omega _{11} } \hfill & {\omega _{12} } \hfill \ {\omega _{21} } \hfill & {\omega _{22} } \hfill \ \end{array} }} \right) is the unconditional variance of \left( {{\begin{array}{*{20}c} {r_t } \hfill \ {x_t } \hfill \ \end{array} }} \right) so that vec(\Omega )=(I_4 -\Phi \otimes \Phi )^{-1}vec(\Sigma ). The population R-squared in this regression is
\begin{displaymath} \frac{\beta ^2\omega _{22} }{\beta ^2\omega _{22} +\Sigma _{i=1}^h {e}'_1 (\Sigma _{j=1}^i \Phi ^{j-1})\Sigma (\Sigma _{j=1}^i \Phi ^{j-1})'e_1 } \end{displaymath}

Table 1 shows the effective coverage of different confidence intervals for alternative horizons (h) and different combinations of \alpha , \varphi and \rho . The coverage rates of the confidence sets are of course 1 minus the sizes of the test that \beta is equal to its true value. The sample size is T=500, which corresponds to about 40 years of monthly data and the nominal coverage is 95 percent. The confidence intervals considered are the ordinary confidence intervals based on estimating equation (1), using Newey-West standard errors with a lag truncation parameter of h, the confidence interval based on estimating this equation using standard errors 1B of Hodrick (1992)--that are valid only under the null of no predictability--and the proposed confidence intervals based on either the delta or Fieller methods in the reverse regression. Confidence intervals based on Hansen-Hodrick standard errors were also constructed, but these have performance that is consistently very similar to those based on Newey-West standard errors, and so are not shown. In each case, the population R-squared is reported as an easily interpretable metric for the degree of predictability. At the horizon h=48, this ranges from 0 to 87 percent, indicating a wide variation in the degree of predictability.

The proposed confidence intervals are based on an assumption of stationarity, while the matrix \Phi has roots very close to unity. Nonetheless, while the Fieller confidence interval can have coverage that is somewhat below the nominal level, in no case is it less than 86 percent, and in most cases it is above 90 percent. The delta method consistently has modestly lower effective coverage, but it still always has effective coverage of at least 80 percent, and usually a good bit more. The comparison of the coverage rates leads us to prefer the Fieller interval, even though it is a little more complicated to compute and the improvement is small.

For the Newey-West confidence intervals, the effective coverage is much lower. It is generally around 80-85 percent at a horizon h=12, and falls as the horizon increases, and is around 70 percent at a horizon of 48 months. Using Hodrick standard errors 1B gives good coverage if \beta is small, but can work very poorly if \beta is large. This is not surprising given that these standard errors are only justified under the null of no predictability.

Table 2 repeats this exercise, with a sample size of T=1,000. All of the confidence intervals have coverage that is closer to the nominal level than in the smaller sample size; the relative coverage of the different methods is about the same. In this larger sample size, the proposed Fieller confidence intervals always have coverage over 90 percent, while the coverage rates of the delta method confidence intervals are just slightly lower. Meanwhile, confidence intervals based on estimating equation (1) with Newey-West standard errors or Hodrick standard errors 1B can have coverage rates below 80 and 60 percent, respectively.

Although in this Monte-Carlo simulation, we know the true value of \beta , in practice, of course, the researcher does not know the true value of this parameter and so it is important that the coverage of a confidence interval be as close as possible to the nominal level uniformly in \beta . In this regard, Tables 1 and 2 show that the proposed confidence intervals are more reliable than using either Newey-West standard errors or Hodrick standard errors 1B, because the coverage rates of intervals based on conventional standard errors are close to the nominal value only for some parts of the parameter space.

Coverage is of course not the only criterion for a confidence interval; precision matters too. The median width of the alternative confidence intervals is shown in Tables 3 and 4, for sample sizes of T=500 and T=1,000 respectively. The proposed confidence sets from the reverse regression are wider than those based on estimating equation (1) with Newey-West standard errors or Hodrick standard errors 1B. The Fieller confidence intervals are typically nearly twice as wide as those based on Newey-West standard errors and range from having the same width as Hodrick standard errors 1B to being more than twice as wide. The cases in which the proposed confidence intervals are particularly wide are, not surprisingly, also the cases in which the conventional confidence intervals have poor coverage. This is what one would expect, given that these are symmetric one-dimensional confidence intervals constructed around the parameter estimates.

4. Empirical Results.

We now apply this proposed methodology to two standard predictive regressions in finance; the prediction of excess stock returns using the dividend-yield and short-term interest rates and the prediction of excess bond returns using the term structure of interest rates.

4.1 Forecasting Excess Stock Returns

We first consider the regression of h-month cumulative excess returns for the value-weighted dividend-inclusive CRSP index on the log dividend yield at the start of the holding period. The sample period is December 1952-December 2007. The horizons are 12, 24, and 36 months.

Coefficient estimates are shown in Table 5, along with Newey-West standard errors and Hodrick standard errors 1B. Judging from the Newey-West standard errors, the estimates of \beta are significantly positive at all horizons, at least at the 10 percent level. Using the Hodrick standard errors, the estimate of \beta is significant only at the 10 percent level and only at the horizon of 12 months.

There is thus marginal evidence of predictability in returns, and of course even where we cannot reject the hypothesis that \beta =0, this does not rule out the possibility of some predictability of returns. This motivates testing a range of hypotheses, or equivalently forming a confidence interval for \beta that should have coverage close to the nominal level uniformly in the parameter space. Our simulation results earlier indicate that the confidence intervals proposed in this paper come close to doing this, while the use of existing standard errors (Newey-West or Hodrick standard errors 1B) does not. Accordingly, Table 5 also shows the 95 percent confidence intervals for \beta using both the delta method and Fieller variants of the proposed methodology. These are wider than one would get from conventional standard errors and also tend to be asymmetric around the OLS estimate of \beta . For example, at the three-year horizon, the OLS estimate of \beta is 0.55, the 95 percent confidence interval using Hodrick standard errors 1B would span from -0.37 to 1.47, but the Fieller confidence interval is from -0.95 to 1.39.

Following Ang and Bekaert (2007), we also considered the regression of h-month cumulative excess stock returns on both the log dividend yield and the one-month interest rate (using the Fama-Bliss riskfree rate) as they and other authors find that predictability is substantially greater in this bivariate regression. A useful property of the proposed approach to inference is that it can accommodate multiple predictors. Table 6 reports the coefficient estimates from estimating equation (1) with both Newey-West standard errors and Hodrick standard errors 1B. The coefficients on the dividend yield and short-term interest rate are significantly positive and negative, respectively, at the horizon of one year. The significance goes down at longer horizons, especially when using Hodrick standard errors 1B. All of this is consistent with Ang and Bekaert (2007).

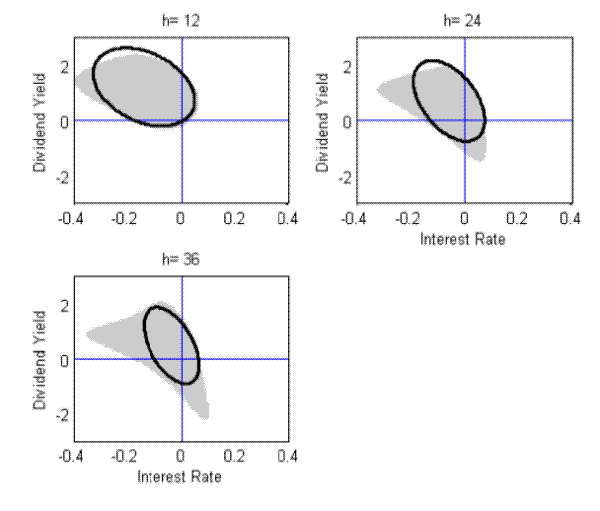
Figure 1 shows the confidence sets for \beta formed by the methods proposed in this paper. The confidence sets are quite large and include values of both elements of \beta that are far from zero. At the twelve-month horizon, the delta and Fieller variants of the proposed methods deliver very similar confidence sets. At longer horizons, they are notably different and the Fieller confidence set--that consistently gives the best coverage rates in the Monte-Carlo simulation--looks quite non-elliptical meaning that it cannot be close to any confidence set that is formed from a normal approximation to the distribution of any point estimate of \beta .

4.2 Forecasting Excess Bond Returns with the Slope of the Yield Curve

Let P_{n,t} be the price of an n-month zero-coupon bond in month t; the per annum continuously compounded yield on this bond is z_{n,t} =-\frac{12}{n}\log (P_{n,t} ). The excess return from buying this bond in month t and selling it in month t+1 is, over the one-month risk-free rate is

\begin{displaymath} r_{n,t+1} =\log (P_{n-1,t+1} )-\log (P_{n,t} )-z_{1,t} \end{displaymath}

where z_{1,t} is the one-month yield. We can then construct the h-period excess return r_{n,t+h}^{(h)} =\Sigma _{j=1}^h r_{n,t+j} . This is very close to--though not exactly the same as--the excess return on holding an n-month zero-coupon bond for h months over the return on holding the h-month bond for that same holding period, considered by Cochrane and Piazzesi (2005) and many others.

A basic premise of term structure analysis is that today's yield curve can be used to forecast future yield curves and the excess returns on long bonds. For example, when the yield curve is steep, long-term bonds have high expected returns (Fama and Bliss (1987)). Accordingly, researchers project excess returns onto the term structure of interest rates at the start of the holding period, running regressions of the form

\begin{displaymath} r_{n,t+h}^{(h)} =\alpha +{\beta }'x_t +\varepsilon _{t+h} \end{displaymath} (9)

where x_t is some vector of yields or spreads at time t.

We considered estimates of \beta formed from estimating equation (9) with the long-term bond maturity, n, ranging from 5 to 10 years and the holding period, h, being 1, 2 or 3 years. End-of-month data on zero-coupon yields from the dataset of Gürkaynak, Sack and Wright (2007) were used, except that for the one-month yield, the Fama-Bliss risk-free rate from CRSP was used instead.

We first used the spread between the ten-year and one-month yield as the sole predictor, x_t . Results are shown in Table 7, along with Newey-West standard errors and Hodrick standard errors 1B. Judging from these conventional standard errors, at the 12-month horizon, the estimates of \beta are all significantly positive, at least at the 5 percent level. At longer horizons, the estimate of \beta is not significant at the 5 percent level in the direct estimation of equation (9).

Table 7 also shows the proposed confidence intervals for \beta ; both the delta method and Fieller variants. At the 12-month horizon, these are a bit wider than would be obtained from Newey-West standard errors or Hodrick standard errors 1B. In the case n=60, the conventional confidence intervals do not span zero, while the proposed ones do. Judging from these results, there is virtually no evidence against the hypothesis that \beta =0 at longer horizons. However, there is no evidence against the hypothesis that \beta takes on many nonzero values either, as the proposed confidence intervals are very wide. The proposed confidence intervals are much wider than those based on either Newey-West standard errors or Hodrick standard errors 1B, but neither of these comes close to controlling coverage uniformly in \beta .

4.3 Forecasting Excess Bond Returns with the Term Structure of Forward Rates

In an influential paper, Cochrane and Piazzesi (2005) argued that while the slope of the yield curve has some predictive power for bond returns, using a combination of forward rates gives better forecasting performance, and that a "tent-shaped" function of forward rates has remarkable predictive ability for excess bond returns with R-squared values up to 44 percent.

Motivated by this finding, we estimated equation (9), using as the predictors the one-year yield, and the one-year forward rates ending in three and five years.4 Table 8 shows p-values from the conventional Wald test of the hypothesis that \beta =0 and using both the delta method and Fieller variants on the proposed approach to inference.

The Newey-West p-values indicate overwhelming significance at the shortest horizon of 12 months, and are also highly significant at the 24-month horizon. In contrast, Hodrick standard errors 1B and the proposed tests give p-values that are between 3 and 13 percent at the twelve-month horizon and are not significant at all at longer horizons. Thus, evidence for predictability of excess bond returns using forward rates is fairly marginal at the twelve month horizon and is nonexistent at longer horizons. This is based on just testing the hypothesis of no predictability and so does not require the use of the methods proposed in this paper, but it nonetheless is a finding of some interest, suggesting that the evidence that the tent-shaped factor helps forecast returns may not be nearly as strong as had been thought.5 What does require the methods proposed in this paper is testing other hypotheses about \beta or forming confidence sets.

Confidence sets for \beta when this vector contains more than two elements are hard to represent graphically. But for the delta method, the proposed point estimates for individual coefficients, given in equation (6), can be computed along with the associated delta-method standard errors. These are shown in Table 9 for n=120. The point estimates do indeed show the "tent-shaped" pattern, with a high coefficient on the one-year forward rate ending three years hence and lower coefficients on the other two forward rates. The proposed point estimates are almost identical to the conventional OLS point estimates, but the proposed standard errors are much larger than their conventional counterparts. Overall, the exercise indicates that the coefficients in the regression considered by Cochrane and Piazzesi (2005) are far less precisely estimated than one might suppose from conventional inference approaches and indeed even their significance is in doubt.

5. Conclusion

We have proposed two related methods for inference in a long-horizon predictive regression in this paper. Both methods are based on assessing the covariance between one-period returns and a long-term average of the predictor, and so have a motivation that is similar to the reverse regression of Hodrick (1992). However, our proposal for inference allows us to test any hypothesis on the slope coefficient in the long-horizon predictive regression; not just to test that it is zero, as in Hodrick's paper. The acceptance region of this test can be represented as a confidence set for this slope coefficient.

In Monte-Carlo simulations we have demonstrated that the proposed methods control the effective coverage of confidence intervals (equivalently control the size of tests) fairly well, uniformly in the parameter space. In empirical applications, we find that any evidence for predictability of excess stock and bond returns is marginal. However, using our methodology we are also unable to reject the hypothesis that the coefficient in the predictive regression takes on specific nonzero values. We are left with confidence sets for the coefficients in canonical predictive regressions in finance that include zero in some, but not all cases, and that are quite different from the conventional confidence sets as they are wider and sometimes asymmetric around the OLS point estimate of the predictive regression.

References

Andrews, Donald W.K. (1991): Heteroskedasticity and Autocorrelation Consistent Covariance Matrix Estimation, Econometrica, 59, pp.817-858.

Ang, Andrew and Geert Bekaert (2007): Stock Return Predictability: Is it There? Review of Financial Studies, 20, pp.651-707.

Bekaert, Geert, Robert J. Hodrick and David Marshall (2001): Peso Problem Explanations for Term Structure Anomalies, Journal of Monetary Economics, 48, pp.241-270.

Campbell, John Y. (2000): Asset Pricing at the Millennium, Journal of Finance, 55, pp.1515-1567.

Campbell, John Y. (2001): Why Long Horizons? A Study of Power Against Persistent Alternatives, Journal of Empirical Finance, 9, pp.459-491.

Campbell, John Y. and Motohiro Yogo (2006): Efficient Tests of Stock Return Predictability, Journal of Financial Economics, 81, pp.27-60.

Cochrane, John H. and Monika Piazzesi (2005): Bond Risk Premia, American Economic Review, 95, pp.138-160.

Cochrane, John H. and Monika Piazzesi (2008), "Decomposing the Yield Curve," manuscript, University of Chicago.

Elliott, Graham and James H. Stock (1994): Inference in Time Series Regression When the Order of Integration of a Regressor is Unknown, Econometric Theory, 10, pp.672-700.

Fama, Eugene F. and Robert R. Bliss (1987): The Information in Long-Maturity Forward Rates, American Economic Review, 77, pp.680-692.

Fieller, Edgar C. (1960): Some Problems in Interval Estimation, Journal of the Royal Statistical Society B, 16, pp.175-185.

Goetzmann, William and Philippe Jorion (1993): Testing the Predictive Power of Dividend Yields, Journal of Finance, 48, pp.663-679.

Gürkaynak, Refet S., Brian Sack and Jonathan H. Wright (2007): The U.S. Treasury Yield Curve: 1961 to the Present, Journal of Monetary Economics, 54, pp.2291-2304.

Hansen, Lars P. and Robert J. Hodrick (1980): Forward Exchange Rates as Optimal Predictors of Future Spot Rates: An Econometric Analysis, Journal of Political Economy, 88, pp.829-853.

Hodrick, Robert J. (1992): Dividend Yields and Expected Stock Returns: Alternative Procedures for Inference and Measurement, Review of Financial Studies, 5, pp.357-386.

Newey. Whitney K. and Kenneth D. West (1987): A Simple, Positive Definite, Heteroscedasticity and Autocorrelation Consistent Covariance Matrix, Econometrica, 55, pp.703-708.

Stambaugh, Robert (1999): Predictive Regressions, Journal of Financial Economics, 54, pp.375-421.

Valkanov, Rossen (2003): Long-Horizon Regressions: Theoretical Results and Applications, Journal of Financial Economics, 68, pp.201-232.

Table 1: Coverage of Alternative Confidence Intervals: Sample Size: 500
Panel A: \varphi =0.98


  \rho =-0.5 \beta =0 \rho =-0.5 \beta =0.02 \rho =-0.5 \beta =0.05 \rho =-0.5 \beta =0.1 \rho =0 \beta =0 \rho =0 \beta =0.02 \rho =0 \beta =0.05 \rho =0 \beta =0.1 \rho =0.5 \beta =0 \rho =0.5 \beta =0.02 \rho =0.5 \beta =0.05 \rho =0.5 \beta =0.1
h=12: Proposed: Fieller 0.93 0.94 0.97 0.99 0.95 0.95 0.96 0.98 0.93 0.93 0.94 0.96
h=12: Proposed: Delta 0.92 0.93 0.96 0.99 0.93 0.94 0.95 0.97 0.92 0.91 0.92 0.94
h=12: Newey-West 0.84 0.85 0.86 0.87 0.86 0.86 0.86 0.86 0.84 0.84 0.83 0.82
h=12: Hodrick 0.95 0.96 0.98 0.99 0.95 0.95 0.95 0.94 0.94 0.92 0.89 0.85
h=12: R^2 0.00 0.10 0.42 0.74 0.00 0.09 0.36 0.64 0.00 0.08 0.31 0.56
h=24: Proposed: Fieller 0.92 0.95 0.99 0.99 0.94 0.95 0.96 0.97 0.92 0.92 0.93 0.95
h=24: Proposed: Delta 0.90 0.94 0.98 0.98 0.92 0.93 0.94 0.95 0.90 0.88 0.89 0.91
h=24: Newey-West 0.80 0.82 0.84 0.83 0.82 0.83 0.81 0.80 0.81 0.79 0.78 0.77
h=24: Hodrick 0.94 0.97 0.98 0.95 0.95 0.95 0.92 0.83 0.94 0.91 0.83 0.72
h=24: R^2 0.00 0.15 0.54 0.75 0.00 0.13 0.42 0.63 0.00 0.11 0.35 0.54
h=36: Proposed: Fieller 0.91 0.96 0.98 0.98 0.93 0.93 0.95 0.95 0.91 0.89 0.90 0.92
h=36: Proposed: Delta 0.89 0.95 0.96 0.95 0.92 0.91 0.91 0.91 0.89 0.85 0.85 0.86
h=36: Newey-West 0.77 0.79 0.80 0.77 0.79 0.79 0.77 0.74 0.77 0.75 0.73 0.71
h=36: Hodrick 0.95 0.98 0.97 0.87 0.95 0.94 0.88 0.72 0.95 0.89 0.77 0.61
h=36: R^2 0.00 0.19 0.56 0.69 0.00 0.15 0.42 0.57 0.00 0.12 0.33 0.49
h=48: Proposed: Fieller 0.90 0.96 0.97 0.95 0.92 0.92 0.92 0.92 0.90 0.86 0.87 0.88
h=48: Proposed: Delta 0.88 0.95 0.94 0.91 0.91 0.89 0.87 0.86 0.88 0.82 0.80 0.81
h=48: Newey-West 0.73 0.77 0.75 0.71 0.77 0.75 0.72 0.68 0.73 0.71 0.68 0.67
h=48: Hodrick 0.95 0.98 0.95 0.76 0.96 0.93 0.83 0.62 0.94 0.87 0.71 0.53
h=48: R^2 0.00 0.20 0.54 0.62 0.00 0.15 0.39 0.51 0.00 0.12 0.31 0.43

Table 1: Coverage of Alternative Confidence Intervals: Sample Size: 500
Panel B: \varphi =0.99


  \rho =-0.5 \beta =0 \rho =-0.5 \beta =0.02 \rho =-0.5 \beta =0.05 \rho =-0.5 \beta =0.1 \rho =0 \beta =0 \rho =0 \beta =0.02 \rho =0 \beta =0.05 \rho =0 \beta =0.1 \rho =0.5 \beta =0 \rho =0.5 \beta =0.02 \rho =0.5 \beta =0.05 \rho =0.5 \beta =0.1
h=12: Proposed: Fieller 0.92 0.94 0.97 0.99 0.95 0.95 0.96 0.98 0.93 0.92 0.93 0.96
h=12: Proposed: Delta 0.90 0.92 0.96 0.99 0.93 0.94 0.95 0.97 0.90 0.90 0.91 0.93
h=12: Newey-West 0.83 0.84 0.85 0.87 0.86 0.86 0.86 0.84 0.83 0.82 0.81 0.79
h=12: Hodrick 0.93 0.96 0.98 0.99 0.95 0.95 0.95 0.93 0.94 0.91 0.88 0.83
h=12: R^2 0.00 0.19 0.62 0.86 0.00 0.18 0.55 0.80 0.00 0.16 0.50 0.74
h=24:Proposed: Fieller 0.91 0.96 0.99 0.99 0.94 0.95 0.96 0.98 0.92 0.91 0.92 0.95
h=24:Proposed: Delta 0.89 0.94 0.98 0.98 0.92 0.93 0.94 0.95 0.89 0.87 0.88 0.91
h=24:Newey-West 0.78 0.81 0.83 0.81 0.82 0.82 0.79 0.76 0.75 0.79 0.79 0.72
h=24:Hodrick 0.94 0.97 0.98 0.94 0.95 0.95 0.90 0.80 0.94 0.98 0.96 0.81
h=24:R^2 0.00 0.31 0.74 0.87 0.00 0.27 0.63 0.79 0.00 0.39 0.76 0.83
h=36: Proposed: Fieller 0.91 0.97 0.98 0.98 0.93 0.94 0.95 0.96 0.91 0.89 0.90 0.92
h=36: Proposed: Delta 0.87 0.96 0.97 0.95 0.91 0.91 0.91 0.91 0.87 0.83 0.83 0.86
h=36: Newey-West 0.75 0.79 0.79 0.72 0.79 0.78 0.73 0.69 0.75 0.71 0.68 0.65
h=36: Hodrick 0.94 0.98 0.96 0.81 0.95 0.94 0.84 0.64 0.94 0.86 0.70 0.53
h=36: R^2 0.00 0.39 0.76 0.83 0.00 0.31 0.64 0.75 0.00 0.26 0.55 0.69
h=48: Proposed: Fieller 0.90 0.97 0.97 0.96 0.92 0.92 0.93 0.93 0.89 0.86 0.87 0.89
h=48: Proposed: Delta 0.87 0.95 0.94 0.91 0.91 0.88 0.86 0.86 0.87 0.79 0.79 0.82
h=48: Newey-West 0.71 0.76 0.73 0.65 0.75 0.73 0.67 0.62 0.71 0.66 0.62 0.60
h=48: Hodrick 0.94 0.98 0.92 0.65 0.95 0.92 0.77 0.53 0.94 0.83 0.62 0.44
h=48: R^2 0.00 0.43 0.74 0.78 0.00 0.34 0.62 0.71 0.00 0.27 0.53 0.65

Notes: This Table shows the simulated coverage of alternative confidence intervals for the coefficient \beta in equation (1). The methods considered include confidence intervals from the reverse regression proposed in this paper. The delta-method and Fieller variants are labeled Proposed: Delta and Proposed: Fieller, respectively. Wald confidence intervals using the OLS estimates of equation (1) using Newey-West standard errors with a lag-truncation parameter of h and using Hodrick standard errors 1B (only valid if \beta =0) are also considered. These are Newey-West and Hodrick. The simulation design is described in section 3. The row labeled R2 gives the population R-squared in the regression. All confidence intervals have a 95 percent nominal coverage rate.

Table 2: Coverage of Alternative Confidence Intervals: Sample Size: 1000
Panel A: \varphi =0.98


  \rho =-0.5 \beta =0 \rho =-0.5 \beta =0.02 \rho =-0.5 \beta =0.05 \rho =-0.5 \beta =0.1 \rho =0 \beta =0 \rho =0 \beta =0.02 \rho =0 \beta =0.05 \rho =0 \beta =0.1 \rho =0.5 \beta =0 \rho =0.5 \beta =0.02 \rho =0.5 \beta =0.05 \rho =0.5 \beta =0.1
h=12: Proposed: Fieller 0.94 0.95 0.97 1.00 0.95 0.95 0.97 0.99 0.94 0.94 0.96 0.98
h=12: Proposed: Delta 0.93 0.94 0.97 0.99 0.94 0.94 0.96 0.98 0.93 0.93 0.95 0.97
h=12: Newey-West 0.87 0.87 0.88 0.89 0.88 0.88 0.87 0.87 0.87 0.86 0.86 0.86
h=12: Hodrick 0.95 0.96 0.98 0.99 0.95 0.95 0.95 0.95 0.94 0.93 0.91 0.88
h=12: R^2 0.00 0.10 0.42 0.74 0.00 0.09 0.36 0.64 0.00 0.08 0.31 0.56
h=24: Proposed: Fieller 0.94 0.96 0.99 1.00 0.94 0.95 0.97 0.99 0.93 0.94 0.95 0.97
h=24: Proposed: Delta 0.92 0.95 0.99 1.00 0.93 0.94 0.96 0.98 0.92 0.92 0.94 0.96
h=24: Newey-West 0.85 0.86 0.87 0.87 0.86 0.86 0.85 0.84 0.85 0.84 0.84 0.83
h=24: Hodrick 0.95 0.97 0.98 0.96 0.95 0.94 0.92 0.86 0.94 0.91 0.85 0.76
h=24: R^2 0.00 0.15 0.54 0.75 0.00 0.13 0.42 0.63 0.00 0.11 0.35 0.54
h=36: Proposed: Fieller 0.93 0.97 0.99 0.99 0.94 0.95 0.97 0.98 0.93 0.93 0.94 0.96
h=36: Proposed: Delta 0.92 0.96 0.98 0.99 0.93 0.94 0.95 0.97 0.92 0.91 0.92 0.94
h=36: Newey-West 0.83 0.84 0.86 0.84 0.84 0.84 0.83 0.82 0.83 0.82 0.81 0.81
h=36: Hodrick 0.95 0.97 0.97 0.89 0.95 0.94 0.89 0.76 0.95 0.89 0.80 0.66
h=36: R^2 0.00 0.19 0.56 0.69 0.00 0.15 0.42 0.57 0.00 0.12 0.33 0.49
h=48: Proposed: Fieller 0.93 0.97 0.99 0.98 0.94 0.95 0.96 0.97 0.93 0.92 0.93 0.95
h=48: Proposed: Delta 0.91 0.96 0.97 0.97 0.92 0.93 0.94 0.94 0.91 0.89 0.90 0.92
h=48: Newey-West 0.82 0.83 0.83 0.81 0.83 0.82 0.81 0.80 0.82 0.80 0.79 0.79
h=48: Hodrick 0.95 0.98 0.96 0.80 0.95 0.93 0.85 0.67 0.95 0.88 0.75 0.58
h=48: R^2 0.00 0.20 0.54 0.62 0.00 0.15 0.39 0.51 0.00 0.12 0.31 0.43

Table 2: Coverage of Alternative Confidence Intervals: Sample Size: 1000
Panel B: \varphi =0.99


  \rho =-0.5 \beta =0 \rho =-0.5 \beta =0.02 \rho =-0.5 \beta =0.05 \rho =-0.5 \beta =0.1 \rho =0 \beta =0 \rho =0 \beta =0.02 \rho =0 \beta =0.05 \rho =0 \beta =0.1 \rho =0.5 \beta =0 \rho =0.5 \beta =0.02 \rho =0.5 \beta =0.05 \rho =0.5 \beta =0.1
h=12: Proposed: Fieller 0.94 0.94 0.97 1.00 0.95 0.95 0.97 0.99 0.94 0.94 0.95 0.97
h=12: Proposed: Delta 0.93 0.94 0.97 1.00 0.94 0.94 0.96 0.98 0.93 0.93 0.94 0.97
h=12: Newey-West 0.86 0.87 0.88 0.89 0.88 0.88 0.87 0.87 0.86 0.85 0.85 0.84
h=12: Hodrick 0.95 0.96 0.98 0.99 0.95 0.95 0.95 0.96 0.94 0.92 0.90 0.88
h=12: R^2 0.00 0.19 0.62 0.86 0.00 0.18 0.55 0.80 0.00 0.16 0.50 0.74
h=24: Proposed: Fieller 0.93 0.96 0.99 1.00 0.94 0.95 0.98 0.99 0.93 0.94 0.96 0.98
h=24: Proposed: Delta 0.92 0.95 0.99 1.00 0.93 0.94 0.97 0.98 0.91 0.91 0.94 0.96
h=24: Newey-West 0.84 0.85 0.87 0.86 0.85 0.85 0.85 0.83 0.84 0.82 0.81 0.81
h=24: Hodrick 0.94 0.97 0.98 0.96 0.95 0.95 0.92 0.85 0.94 0.90 0.83 0.75
h=24: R^2 0.00 0.31 0.74 0.87 0.00 0.27 0.63 0.79 0.00 0.39 0.76 0.83
h=36: Proposed: Fieller 0.93 0.97 0.99 1.00 0.94 0.96 0.98 0.99 0.92 0.93 0.95 0.97
h=36: Proposed: Delta 0.91 0.96 0.99 0.99 0.92 0.94 0.96 0.97 0.90 0.90 0.93 0.95
h=36: Newey-West 0.82 0.84 0.85 0.82 0.84 0.84 0.82 0.80 0.82 0.80 0.79 0.78
h=36: Hodrick 0.95 0.98 0.97 0.86 0.95 0.94 0.87 0.73 0.94 0.88 0.76 0.63
h=36: R^2 0.00 0.39 0.76 0.83 0.00 0.31 0.64 0.75 0.00 0.26 0.55 0.69
h=48: Proposed: Fieller 0.92 0.98 0.99 0.99 0.94 0.95 0.97 0.97 0.92 0.92 0.94 0.96
h=48: Proposed: Delta 0.90 0.97 0.98 0.97 0.92 0.93 0.95 0.95 0.90 0.88 0.91 0.93
h=48: Newey-West 0.80 0.83 0.82 0.78 0.82 0.81 0.79 0.77 0.80 0.78 0.76 0.76
h=48: Hodrick 0.94 0.98 0.94 0.74 0.95 0.93 0.81 0.62 0.94 0.85 0.70 0.54
h=48: R^2 0.00 0.43 0.74 0.78 0.00 0.34 0.62 0.71 0.00 0.27 0.53 0.65

Notes: As for Table 1, except that the sample size is 1,000.

Table 3: Median Width of Alternative Confidence Intervals: Sample Size: 500
Panel A: \varphi =0.98


  \rho =-0.5\beta =0 \rho =-0.5\beta =0.02 \rho =-0.5\beta =0.05 \rho =-0.5\beta =0.1 \rho =0\beta =0 \rho =0\beta =0.02 \rho =0\beta =0.05 \rho =0\beta =0.1 \rho =0.5\beta =0 \rho =0.5\beta =0.02 \rho =0.5\beta =0.05 \rho =0.5\beta =0.1
h=12: Proposed: Fieller 0.040 0.038 0.041 0.053 0.040 0.041 0.046 0.061 0.040 0.043 0.051 0.068
h=12: Proposed: Delta 0.037 0.036 0.038 0.049 0.037 0.038 0.043 0.057 0.037 0.040 0.047 0.063
h=12: Newey-West 0.030 0.029 0.027 0.027 0.030 0.030 0.031 0.034 0.030 0.032 0.035 0.041
h=12: Hodrick 0.040 0.040 0.041 0.045 0.040 0.040 0.041 0.045 0.040 0.040 0.041 0.044
h=24: Proposed: Fieller 0.038 0.038 0.047 0.075 0.038 0.041 0.053 0.082 0.038 0.043 0.058 0.089
h=24: Proposed: Delta 0.034 0.034 0.042 0.067 0.034 0.037 0.047 0.074 0.034 0.039 0.052 0.079
h=24: Newey-West 0.026 0.024 0.024 0.029 0.027 0.027 0.030 0.039 0.026 0.029 0.035 0.047
h=24: Hodrick 0.038 0.039 0.040 0.043 0.038 0.038 0.039 0.042 0.038 0.038 0.039 0.042
h=36: Proposed: Fieller 0.036 0.037 0.051 0.087 0.036 0.040 0.056 0.094 0.036 0.043 0.061 0.099
h=36: Proposed: Delta 0.031 0.032 0.044 0.076 0.032 0.035 0.049 0.081 0.031 0.037 0.053 0.086
h=36: Newey-West 0.024 0.021 0.022 0.033 0.024 0.025 0.030 0.043 0.024 0.027 0.035 0.050
h=36: Hodrick 0.037 0.037 0.038 0.041 0.037 0.037 0.038 0.040 0.037 0.037 0.037 0.040
h=48: Proposed: Fieller 0.034 0.035 0.052 0.091 0.034 0.039 0.057 0.097 0.034 0.041 0.061 0.102
h=48: Proposed: Delta 0.029 0.030 0.044 0.078 0.029 0.033 0.049 0.083 0.029 0.035 0.052 0.087
h=48: Newey-West 0.021 0.019 0.022 0.035 0.021 0.023 0.029 0.045 0.021 0.025 0.034 0.052
h=48: Hodrick 0.035 0.035 0.036 0.039 0.035 0.035 0.036 0.038 0.035 0.035 0.036 0.038

Table 3: Median Width of Alternative Confidence Intervals: Sample Size: 500
Panel B: \varphi =0.99


  \rho =-0.5\beta =0 \rho =-0.5\beta =0.02 \rho =-0.5\beta =0.05 \rho =-0.5\beta =0.1 \rho =0\beta =0 \rho =0\beta =0.02 \rho =0\beta =0.05 \rho =0\beta =0.1 \rho =0.5\beta =0 \rho =0.5\beta =0.02 \rho =0.5\beta =0.05 \rho =0.5\beta =0.1
h=12: Proposed: Fieller 0.033 0.032 0.035 0.046 0.033 0.034 0.039 0.053 0.033 0.036 0.043 0.059
h=12: Proposed: Delta 0.031 0.030 0.032 0.043 0.031 0.032 0.037 0.050 0.031 0.034 0.040 0.055
h=12: Newey-West 0.025 0.024 0.023 0.022 0.025 0.025 0.026 0.029 0.025 0.026 0.029 0.034
h=12: Hodrick 0.033 0.034 0.035 0.040 0.033 0.033 0.035 0.039 0.033 0.033 0.034 0.038
h=24: Proposed: Fieller 0.032 0.033 0.044 0.073 0.033 0.036 0.049 0.079 0.032 0.038 0.052 0.083
h=24: Proposed: Delta 0.029 0.029 0.039 0.065 0.029 0.032 0.043 0.070 0.029 0.033 0.046 0.074
h=24: Newey-West 0.022 0.020 0.020 0.025 0.022 0.023 0.026 0.034 0.022 0.025 0.030 0.041
h=24: Hodrick 0.033 0.033 0.034 0.038 0.033 0.033 0.034 0.038 0.033 0.033 0.034 0.037
h=36: Proposed: Fieller 0.031 0.034 0.051 0.092 0.032 0.037 0.056 0.097 0.031 0.038 0.059 0.100
h=36: Proposed: Delta 0.027 0.029 0.044 0.079 0.027 0.031 0.048 0.083 0.027 0.033 0.050 0.086
h=36: Newey-West 0.020 0.018 0.020 0.031 0.020 0.021 0.026 0.039 0.020 0.024 0.031 0.046
h=36: Hodrick 0.032 0.032 0.034 0.037 0.032 0.032 0.033 0.036 0.032 0.032 0.033 0.036
h=48: Proposed: Fieller 0.030 0.034 0.056 0.104 0.031 0.037 0.060 0.107 0.030 0.038 0.063 0.111
h=48: Proposed: Delta 0.025 0.029 0.047 0.087 0.026 0.031 0.050 0.090 0.025 0.032 0.053 0.093
h=48: Newey-West 0.018 0.016 0.020 0.035 0.018 0.020 0.027 0.043 0.018 0.022 0.032 0.050
h=48: Hodrick 0.031 0.032 0.033 0.036 0.031 0.031 0.032 0.035 0.031 0.031 0.032 0.034

Notes: As for Table 1, except that here the median width of the confidence intervals is reported instead.

Table 4: Median Width of Alternative Confidence Intervals: Sample Size: 1000
Panel A: \varphi =0.98


  \rho =-0.5\beta =0 \rho =-0.5\beta =0.02 \rho =-0.5\beta =0.05 \rho =-0.5\beta =0.1 \rho =0\beta =0 \rho =0\beta =0.02 \rho =0\beta =0.05 \rho =0\beta =0.1 \rho =0.5\beta =0 \rho =0.5\beta =0.02 \rho =0.5\beta =0.05 \rho =0.5\beta =0.1
h=12: Proposed: Fieller 0.026 0.025 0.026 0.034 0.026 0.027 0.030 0.040 0.026 0.028 0.034 0.045
h=12: Proposed: Delta 0.025 0.024 0.025 0.033 0.025 0.026 0.029 0.039 0.025 0.027 0.032 0.044
h=12: Newey-West 0.021 0.020 0.019 0.018 0.021 0.021 0.021 0.024 0.021 0.022 0.024 0.028
h=12: Hodrick 0.026 0.026 0.027 0.030 0.026 0.026 0.027 0.030 0.026 0.026 0.027 0.030
h=24: Proposed: Fieller 0.025 0.024 0.030 0.050 0.025 0.027 0.035 0.056 0.025 0.029 0.039 0.061
h=24: Proposed: Delta 0.023 0.023 0.029 0.047 0.023 0.025 0.033 0.053 0.023 0.027 0.037 0.058
h=24: Newey-West 0.019 0.017 0.017 0.020 0.019 0.019 0.021 0.028 0.019 0.021 0.025 0.033
h=24: Hodrick 0.025 0.025 0.026 0.029 0.025 0.025 0.026 0.029 0.025 0.025 0.026 0.028
h=36: Proposed: Fieller 0.024 0.024 0.034 0.060 0.024 0.027 0.039 0.066 0.024 0.029 0.043 0.071
h=36: Proposed: Delta 0.022 0.022 0.031 0.055 0.022 0.025 0.036 0.061 0.022 0.027 0.040 0.065
h=36: Newey-West 0.018 0.016 0.016 0.024 0.018 0.018 0.022 0.032 0.017 0.020 0.026 0.038
h=36: Hodrick 0.024 0.024 0.025 0.027 0.024 0.024 0.025 0.027 0.024 0.024 0.025 0.027
h=48: Proposed: Fieller 0.023 0.023 0.036 0.065 0.023 0.027 0.041 0.071 0.023 0.029 0.045 0.076
h=48: Proposed: Delta 0.021 0.021 0.032 0.060 0.021 0.024 0.037 0.065 0.021 0.026 0.041 0.069
h=48: Newey-West 0.016 0.015 0.017 0.027 0.016 0.018 0.023 0.035 0.016 0.020 0.027 0.041
h=48: Hodrick 0.023 0.023 0.024 0.026 0.023 0.023 0.024 0.026 0.023 0.023 0.024 0.026

Table 4: Median Width of Alternative Confidence Intervals: Sample Size: 1000
Panel B: \varphi =0.99


  \rho =-0.5\beta =0 \rho =-0.5\beta =0.02 \rho =-0.5\beta =0.05 \rho =-0.5\beta =0.1 \rho =0\beta =0 \rho =0\beta =0.02 \rho =0\beta =0.05 \rho =0\beta =0.1 \rho =0.5\beta =0 \rho =0.5\beta =0.02 \rho =0.5\beta =0.05 \rho =0.5\beta =0.1
h=12: Proposed: Fieller 0.020 0.020 0.021 0.028 0.021 0.021 0.024 0.033 0.020 0.022 0.027 0.037
h=12: Proposed: Delta 0.020 0.019 0.020 0.027 0.020 0.020 0.023 0.032 0.020 0.022 0.026 0.036
h=12: Newey-West 0.016 0.015 0.015 0.014 0.016 0.016 0.017 0.019 0.016 0.017 0.019 0.022
h=12: Hodrick 0.020 0.021 0.022 0.026 0.020 0.021 0.022 0.025 0.020 0.020 0.022 0.025
h=24: Proposed: Fieller 0.020 0.020 0.027 0.046 0.020 0.022 0.031 0.051 0.020 0.024 0.034 0.055
h=24: Proposed: Delta 0.019 0.019 0.025 0.043 0.019 0.021 0.029 0.048 0.019 0.022 0.032 0.051
h=24: Newey-West 0.015 0.014 0.013 0.017 0.015 0.015 0.017 0.023 0.015 0.017 0.020 0.028
h=24: Hodrick 0.020 0.020 0.021 0.025 0.020 0.020 0.021 0.025 0.020 0.020 0.021 0.024
h=36: Proposed: Fieller 0.020 0.021 0.033 0.061 0.020 0.023 0.037 0.065 0.019 0.025 0.040 0.069
h=36: Proposed: Delta 0.018 0.019 0.030 0.056 0.018 0.021 0.034 0.060 0.018 0.023 0.037 0.063
h=36: Newey-West 0.014 0.013 0.014 0.021 0.014 0.015 0.018 0.028 0.014 0.017 0.022 0.033
h=36: Hodrick 0.020 0.020 0.021 0.024 0.020 0.020 0.021 0.024 0.020 0.020 0.021 0.024
h=48: Proposed: Fieller 0.019 0.022 0.038 0.072 0.019 0.024 0.041 0.076 0.019 0.026 0.045 0.079
h=48: Proposed: Delta 0.017 0.019 0.034 0.064 0.017 0.022 0.037 0.068 0.017 0.023 0.040 0.071
h=48: Newey-West 0.013 0.012 0.014 0.026 0.013 0.015 0.020 0.032 0.013 0.017 0.023 0.037
h=48: Hodrick 0.019 0.019 0.020 0.023 0.019 0.019 0.020 0.023 0.019 0.019 0.020 0.023

Notes: As for Table 3, except that the sample size is 1,000.

Table 5: Regression of h-month Excess Stock Returns on log Dividend yield


  h=12 h=24 h=36
Coefficient (SE) 0.826 0.683 0.548
Coefficient (SE) Newey-West Standard Error (0.403) (0.401) (0.323)
Coefficient (SE) Hodrick Standard Error [0.475] [0.470] [0.468]
Proposed CI: Fieller (-0.232,1.763) (-0.700,1.456) (-0.945,1.391)
Proposed CI: Delta (-0.083,1.775) (-0.392,1.464) (-0.566,1.303)

Notes: This table shows the estimated coefficients in regressions of excess h-month cumulative CRSP value-weighted stock returns (relative to the one month rate) on the log dividend yield (divided by 100). Newey-West standard errors with truncation parameter h are reported in round brackets and Hodrick standard errors 1B are given in square brackets. Both variants of the confidence intervals proposed in this paper (95 percent nominal coverage rate) are shown as well. The sample period is 1952:12-2007:12.

Table 6: Regression of Excess Stock Returns on Log Dividend Yield and One-Month Interest Rates


Twelve-month horizon (h=12): Dividend-Yield 1.14
Twelve-month horizon (h=12): Newey-West Standard Error (0.40)
Twelve-month horizon (h=12): Hodrick Standard Error [0.49]
Twelve-month horizon (h=12): Interest rate -0.14
Twelve-month horizon (h=12): Newey-West Standard Error (0.05)
Twelve-month horizon (h=12): Hodrick Standard Error [0.06]
Twelve-month horizon (h=12): Joint p-value: Newey-West 0.003
Twelve-month horizon (h=12): Hodrick 0.019
Two-year horizon (h=24): Dividend-Yield 0.88
Two-year horizon (h=24): Newey-West Standard Error (0.40)
Two-year horizon (h=24): Hodrick Standard Error [0.49]
Two-year horizon (h=24): Interest rate -0.08
Two-year horizon (h=24): Newey-West Standard Error (0.03)
Two-year horizon (h=24): Hodrick Standard Error [0.06]
Two-year horizon (h=24): Joint p-value: Newey-West 0.037
Two-year horizon (h=24): Hodrick 0.126
Three-year horizon (h=36): Dividend-Yield 0.70
Three-year horizon (h=36): Newey-West Standard Error (0.29)
Three-year horizon (h=36): Hodrick Standard Error [0.48]
Three-year horizon (h=36): Interest rate -0.07
Three-year horizon (h=36): Newey-West Standard Error (0.02)
Three-year horizon (h=36): Hodrick Standard Error [0.05]
Three-year horizon (h=36): Joint p-value: Newey-West 0.0009
Three-year horizon (h=36): Hodrick 0.232

Notes: As for Table 5, except that the predictive regressions are on both the log dividend yield and one-month interest rates. Point estimates for the long-horizon regression are shown, along with both Newey-West standard errors and Hodrick standard errors 1B, in round and square brackets respectively. The p-values testing the hypothesis that the coefficients on both predictors are jointly equal to zero are shown. The proposed confidence sets are shown graphically in Figure 1.

Table 7: Regression of Excess Bond Returns on the Yield Curve Slope:
Bond maturity of n months and holding period of h months


  n=60 n=72 n=84 n=96 n=108 n=120
Twelve-month holding period (h=12): \hat {\beta } (SE) 0.126 0.155 0.183 0.212 0.240 0.268
Twelve-month holding period (h=12): Newey-West Standard Error (0.045) (0.051) (0.058) (0.064) (0.070) (0.076)
Twelve-month holding period (h=12): Hodrick Standard Error [0.073] [0.083] [0.093] [0.103] [0.112] [0.122]
Twelve-month holding period (h=12): Proposed CI: Fieller (-0.007,0.254) (0.004,0.303) (0.015,0.351) (0.026,0.399) (0.037,0.448) (0.047,0.496)
Twelve-month holding period (h=12): Proposed CI: Delta (-0.008,0.241) (0.002,0.287) (0.013,0.334) (0.023,0.380) (0.034,0.426) (0.044,0.472)
Two-year holding period (h=24): \hat {\beta } (SE) 0.052 0.071 0.090 0.109 0.127 0.145
Two-year holding period (h=24): Newey-West Standard Error (0.052) (0.059) (0.066) (0.073) (0.079) (0.086)
Two-year holding period (h=24): Hodrick Standard Error [0.063] [0.072] [0.081] [0.090] [0.098] [0.107]
Two-year holding period (h=24): Proposed CI: Fieller (-0.080,0.196) (-0.079,0.240) (-0.077,0.284) (-0.075,0.329) (-0.072,0.373) (-0.070,0.418)
Two-year holding period (h=24): Proposed CI: Delta (-0.085,0.171) (-0.087,0.209) (-0.087,0.248) (-0.087,0.287) (-0.088,0.325) (-0.088,0.364)
Three-year holding period (h=36): \hat {\beta } (SE) 0.017 0.030 0.043 0.056 0.069 0.081
Three-year holding period (h=36): Newey-West Standard Error (0.033) (0.036) (0.039) (0.042) (0.045) (0.048)
Three-year holding period (h=36): Hodrick Standard Error [0.055] [0.063] [0.071] [0.080] [0.087] [0.095]
Three-year holding period (h=36): Proposed CI: Fieller (-0.086,0.112) (-0.086,0.141) (-0.084,0.170) (-0.082,0.199) (-0.079,0.228) (-0.077,0.258)
Three-year holding period (h=36): Proposed CI: Delta (-0.084,0.100) (-0.085,0.125) (-0.084,0.151) (-0.084,0.176) (-0.083,0.202) (-0.082,0.227)

Notes: This table shows the estimated coefficients in regressions of excess h-month cumulative n-year bond returns (relative to the one month rate) on the 10-year less 1-month slope of the term structure. Newey-West standard errors with truncation parameter h are reported in round brackets and Hodrick standard errors 1B are given in square brackets. Both variants of the confidence intervals proposed in this paper (95 percent nominal coverage) are shown as well.

Table 8: Regression of Excess Bond Returns on Forward Rates:
Bond maturity of n months and holding period of h months
(p-values testing the hypothesis that the slope coefficients are jointly zero)


  n=60 n=72 n=84 n=96 n=108 n=120
Twelve-month holding period (h=12): Newey-West 0.001 0.001 0.001 0.001 0.001 0.001
Twelve-month holding period (h=12): Hodrick 0.031 0.031 0.032 0.033 0.035 0.037
Twelve-month holding period (h=12): Proposed: Fieller 0.127 0.120 0.114 0.108 0.103 0.099
Twelve-month holding period (h=12): Delta 0.047 0.042 0.038 0.035 0.032 0.030
Two-year holding period (h=24): Newey-West 0.016 0.020 0.021 0.019 0.016 0.014
Two-year holding period (h=24): Hodrick 0.177 0.198 0.210 0.216 0.218 0.217
Two-year holding period (h=24): Proposed: Fieller 0.512 0.539 0.533 0.504 0.464 0.423
Two-year holding period (h=24): Delta 0.320 0.360 0.375 0.373 0.361 0.344
Three-year holding period (h=36): Newey-West 0.046 0.073 0.091 0.097 0.093 0.084
Three-year holding period (h=36): Hodrick 0.466 0.508 0.522 0.517 0.500 0.478
Three-year holding period (h=36): Proposed: Fieller 0.702 0.763 0.786 0.767 0.714 0.638
Three-year holding period (h=36): Delta 0.446 0.570 0.650 0.678 0.665 0.628

Notes: This table shows p-values from alternative tests of the hypothesis that the slope coefficients are jointly equal to zero in the estimation of the long-horizon regression (equation (9)) when the predictors are the one-year forward rates ending one, three and five years hence.

Table 9: Regression of Excess Bond Returns on Forward Rates:
Bond maturity of 120 months and holding period of h months
Conventional and Proposed Estimates and Standard Errors


  Long-Horizon Regression Proposed
Twelve-month holding period (h=12) \hat {\beta }_1 (SE) -0.504 -0.488
Twelve-month holding period (h=12) Newey-West Standard Error (0.133) (0.210)
Twelve-month holding period (h=12) Hodrick Standard Error [0.248]  
Twelve-month holding period (h=12) \hat {\beta }_2 (SE) 0.868 0.844
Twelve-month holding period (h=12) Newey-West Standard Error (0.344) (0.574)
Twelve-month holding period (h=12) Hodrick Standard Error [0.657]  
Twelve-month holding period (h=12) \hat {\beta }_3 (SE) -0.273 -0.273
Twelve-month holding period (h=12) Newey-West Standard Error (0.270) (0.460)
Twelve-month holding period (h=12) Hodrick Standard Error [0.574]  
Two-year holding period (h=24) \hat {\beta }_1 (SE)   -0.264
Two-year holding period (h=24) Newey-West Standard Error (0.150) (0.229)
Two-year holding period (h=24) Hodrick Standard Error [0.217]  
Two-year holding period (h=24) \hat {\beta }_2 (SE) 0.289 0.344
Two-year holding period (h=24) Newey-West Standard Error (0.360) (0.568)
Two-year holding period (h=24) Hodrick Standard Error [0.533]  
Two-year holding period (h=24) \hat {\beta }_3 (SE) 0.072 0.005
Two-year holding period (h=24) Newey-West Standard Error (0.254) (0.434)
Two-year holding period (h=24) Hodrick Standard Error [0.404]  
Three-year holding period (h=36) \hat {\beta }_1 (SE) -0.104 -0.116
Three-year holding period (h=36) Newey-West Standard Error (0.090) (0.165)
Three-year holding period (h=36) Hodrick Standard Error [0.191]  
Three-year holding period (h=36) \hat {\beta }_2 (SE) -0.026 0.076
Three-year holding period (h=36) Newey-West Standard Error (0.251) (0.367)
Three-year holding period (h=36) Hodrick Standard Error [0.465]  
Three-year holding period (h=36) \hat {\beta }_3 (SE) 0.229 0.119
Three-year holding period (h=36) Newey-West Standard Error (0.219) (0.271)
Three-year holding period (h=36) Hodrick Standard Error [0.361]  

Notes: This table gives the OLS estimate of equation (9) when the excess return is the return on holding a ten-year bond and the predictors are the one-year forward rates ending one, three and five years hence. Newey-West and Hodrick standard errors 1B are shown in round and square brackets, respectively. The table also shows the point estimates and standard errors associated with the delta-method variant of the approach to inference proposed in this paper.

Figure 1: Proposed Confidence Sets for the Coefficients in a Regression of Excess Stock Returns on Log Dividend Yield and One-Month Interest Rates at h month horizon
The three panels of this figure plots our proposed confidence sets for the coefficients in regressions of excess h-month cumulative CRSP value-weighted stock returns (relative to the one month rate) on the log dividend yield (divided by 100) and the short-term interest rate, for h=12, 24 and 36, respectively. The sample period is 1952:12-2007:12. The shaded region gives the Fieller variant of the proposed method; the black ellipses represent the delta method confidence sets.

Notes: This shows the proposed confidence sets for the coefficients in regressions of excess h-month cumulative CRSP value-weighted stock returns (relative to the one month rate) on the log dividend yield (divided by 100) and the short-term interest rate. The sample period is 1952:12-2007:12. The shaded region gives the Fieller variant of the proposed method; the black ellipses represent the delta method confidence sets.


Footnotes

1. * We are grateful to Bob Hodrick for helpful comments on an earlier draft of this manuscript. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other employee of the Federal Reserve System. Return to Text
2. ** Wei: Division of Monetary Affairs, Federal Reserve Board, Washington DC 20551; [email protected]; Wright: Department of Economics, Johns Hopkins University, Baltimore MD 21218; [email protected] Return to Text
3. Pathological cases for this confidence set are possible in finite samples. If b^2<4ac and a>0, then the confidence set is empty. If b^2<4ac and a<0, then it is the whole real line. If b^2>4ac and a<0, then it is the complement of the interval defined by equation (7). Return to Text
4. Here we are using three forward rates, not five as in Cochrane and Piazzesi (2005). The reason is that the Svensson yield curve used by Gürkaynak, Sack and Swanson (2007) is a function of only 6 parameters and the five forward rates will necessarily be extremely multicollinear. Cochrane and Piazzesi (2008) likewise use only three forward rates when forecasting excess bond returns using yields from this dataset. Return to Text
5. Bekaert, Hodrick and Marshall (2001) is a paper that casts doubt on the predictability of excess bond returns using the term structure, though it does not use the forward rates of Cochrane and Piazzesi (2005). Return to Text

♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text
Home | Economic Research and Data | Accessibility | Contact us
Last update: June 19, 2009