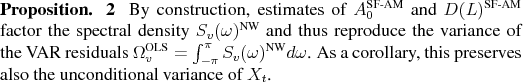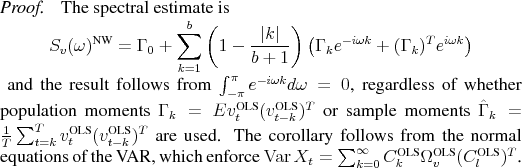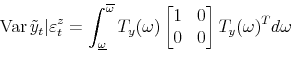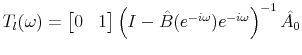Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2010-09 Screen Reader version ^♣

Are Spectral Estimators Useful for Implementing Long-Run Restrictions in SVARs?

Elmar Mertens*
Federal Reserve Board

July 2009

Keywords: Structural VAR, long-run identification, non-parametric estimation, spectral factorization

Abstract:

No, not really, since spectral estimators suffer from small sample and misspecification biases just as VARs do. Spectral estimators are no panacea for implementing long-run restrictions.

In addition, when combining VAR coefficients with non-parametric estimates of the spectral density, care needs to be taken to consistently account for information embedded in the non-parametric estimates about serial correlation in VAR residuals. This paper uses a spectral factorization to ensure a correct representation of the data's variance. But this cannot overcome the fundamental problems of estimating the long-run dynamics of macroeconomic data in samples of typical length.

JEL Classification: C32, C51, E17, E32

1 Introduction

VARs have been criticized for failures in estimating the responses to long-run shocks. A crucial element for long run identification is the spectral density at zero-frequency, also known as "long-run variance". But OLS estimates of VAR coefficients are concerned with minimizing forecast error variance, not estimating the long run variance. This has motivated Christiano, Eichenbaum, and Vigfusson (2006a; 2006b), henceforth "CEV", to propose a new way of estimating structural VARs using a combination of OLS and a non-parametric estimator. They argue that their estimator virtually eliminates the bias associated with the standard OLS estimator.

This paper shows that non-parametric estimates of the spectral density, henceforth called "spectral estimators", are no panacea for the implementation of long-run restrictions in finite sample. Macroeconomic time series display a fair amount of persistence, posing two serious challenges for long-run identification. First, an accurate representation of the true model typically requires a VAR with a high lag order, much higher than what is affordable in a sample of typical length and resulting in a sizable truncation bias (Chari, Kehoe, and McGrattan 2008, henceforth "CKM"). Second, there is the small sample bias in estimated coefficients known from Hurwicz (1950), which becomes ever more severe the smaller the sample, and the more persistent the data. As will be shown, both issues affect not only VARs in the time domain, but also spectral estimators in the frequency domain.

The conventional VAR technique as well as different combinations with spectral estimators are evaluated in the context of a simple two-shock RBC model, which has also been used by CEV and CKM. When using the various procedures to estimate the response of hours to technology, or to decompose the variance of fluctuations in output or hours, none of the procedures clearly dominates the others.

Furthermore, CEV do not consider some conceptual pitfalls in combining VAR coefficients with spectral estimates. Non-parametric estimates of the spectral density allow for non- residuals in the finite-order VAR, which is good since the underlying model is likely of infinite order. In what may be called "mixing and matching", the CEV approach plugs these estimates into the standard VAR formula alongside with coefficients from the finite-order VAR. This approach uses the extra information about omitted lags in the VAR to compute the long-run responses of variables to shocks--but not when mapping these back into impact responses. To retain a consistent representation of the data, that would however be necessary. Otherwise, the total variance of the data is misrepresented. In the simulations reported here, this misrepresentation is quantitatively relevant. As a related issue, when the relationship between forecast errors and structural shocks is inverted with the CEV coefficients, one obtains a time series which is identical to the shock estimates from OLS up to a scale factor. All in all, this is of concern for any researcher wanting to adopt the CEV strategy.

The CEV framework is amended here by recognizing that the non-parametric estimate contains information about omitted lags in the VAR. This misspecification has been stressed by CKM, Erceg, Guerrieri, and Gust (2005), Ravenna (2007) and Cooley and Dywer (1998). The adjusted procedure retains the OLS estimates and fills up the omitted lags with a spectral factorization of the spectral density's non-parametric estimate. By construction, this adjusted SVAR--in fact an SVARMA--matches the sample variance of the data just as OLS does. Overall, this corrected procedure suffers from the same basic problems as the other long-run identification methods: truncation and small sample bias.

The remainder of this paper is structured as follows: Section 2 describes the model economy against which the various estimation routines will be evaluated. Section 3 describes the various SVAR methods, including a new spectral factorization procedure. Section 4 presents the Monte Carlo results and Section 5 concludes the paper.

2 A Model Economy

This section describes a simple model economy, which will be used to illustrate and quantify the issues associated with various long-run identification schemes. None of the conceptual concerns related to spectral estimates raised in Section 3 will be specific to this model. The model is identical to the two-shock economy used by CKM and CEV.

The model is a common one-sector RBC economy driven by two shocks: First, a unit root shock to technology, . This is the permanent shock to be estimated by the VAR. Second, a transitory non-technology shock, $\tau_{lt}$ , which drives a wedge between private household's labor-consumption decision.

The representative household maximizes his lifetime utility over (per-capita) consumption, , and labor services,

$\begin{displaymath}E_0 \sum_{t=0}^\infty (\beta(1+\gamma))^t u(c_t,l_t) \end{displaymath}$

and faces the budget constraint $c_t + (1+\gamma) k_{t+1} - (1-\delta) k_t = (1-\tau_{lt}) w_t l_t + r_t k_t + T_t$ where

is the per-capita stock of capital,

the wage rate,

the rental rate of capital,

are lump sum taxes, $\gamma$ is the growth rate of population, $\delta$ the depreciation rate of capital ( $\gamma>0$ , $0\leq\delta\leq 1$ and $\beta<1$ ).

The non-technology shock $\tau_{lt}$ is an exogenous labor tax. As discussed by CKM, it need not be literally interpreted as a tax levy, but stands in for the effects of a variety of non-technology shocks introduced into second-generation RBC models. Mechanically, it distorts the first-order condition for consumption and labor. It works similar to a stochastic preference shock to the Frisch elasticity of labor supply. Chari, Kehoe, and McGrattan (2007) show how this labor "wedge" can be understood more generally as the reduced form process for more elaborate distortions, such as sticky wages.

The production function is constant returns to scale, where is labor-augmenting technological progress. Firms are static and maximize profits . Per-capita output equals production, , and the economy's resource constraint is $y_t = c_t + (1+\gamma) k_{t+1} - (1-\delta) k_t$ . The exogenous drivers follow linear stochastic processes:
$\begin{align*} \log{Z_t} &= \mu_z + \log{Z_{t-1}} + \sigma_z \varepsilon_t^Z \ \log{\tau_{l,t+1}} &= (1-\rho_l) \bar\tau_l+\rho_l\log{\tau_{l,t-1}} + \sigma_l \varepsilon_t^l \end{align*}$
where $\varepsilon_t^Z$ and $\varepsilon_t^l$ are standard-normal random variables. They are the technology shock, respectively labor shock. $\rho_l$ measures the persistence of the transitory labor tax. The scale factors $\sigma_z$ and $\sigma_l$ determine their relative importance in the model. ( $\mu_z$ is the drift in log-technology and $\bar\tau_t$ is the average tax rate.)

The calibration is identical to the baseline model of CEV, which uses parameter values familiar from the business cycle literature. Utility is specified as $u(c,l)=\log{c}+\psi\log{(1-l})$ (consistent with balanced growth) and the production function is Cobb-Douglas $F(k,l)=k^\theta l^{1-\theta}$ with a capital share of $\theta=0.33$ . The labor preference parameter is set to $\psi=2.5$ . On an annualized basis, the calibration sets the depreciation rate to 6%, the rate of time preferences to 2% and population growth to 1%.¹ Following CEV, the transitory shock is calibrated as an AR(1) with persistence $\rho_l=0.986$ . This calibration is identical to the values used by CKM except for their values of $\phi=1.6$ and $\rho_l=0.95$ .

The model economy is calibrated over different ratios in the variance of transitory to permanent shocks, $\sigma_l^2 / \sigma_z^2$ , which translate into different assumptions about the share of output fluctuations explained by technology shocks.² As a benchmark, maximum-likelihood estimates of CEV obtained from fitting the model to U.S. post-war data imply that around two-thirds of the bandpass-filtered variance in output can be attributed to technology shocks.³ The bandpass filter employed throughout this paper considers only fluctuations with durations between two-and-a-half and eight years, which is consistent with the NBER definitions of Burns and Mitchell (1946).

Data is simulated for samples of length , corresponding to 45 years of quarterly data; identical to the simulations of CKM and CEV. Following CEV and CKM, bivariate VARs are estimated using simulated data of the (log) growth rate of labor productivity and hours worked; $X_t = \begin{bmatrix}\Delta \log{(y_t/l_t)} & \log{l_t} \end{bmatrix}^T$ .⁴ For each simulated sample, the lag length of the VAR() is chosen by minimizing the Schwartz Information Criterion (SIC), typically picking small values close to one.⁵ When computing population moments, a VAR(1) is used. For each calibration, 1,000samples are simulated.

When looking at data simulated from this model, two statistics are of particular interest for this paper: How do hours worked respond to a technology shock? What is the share of fluctuations due to technology shocks? These questions are typically asked by empirical researchers trying to evaluate predictions from business cycle models with SVARs, such as Gali (1999) or Christiano, Eichenbaum, and Vigfusson (2004).

3 Long-Run Identification in VARs

The linearized solution to the model described in the previous section is only one example from a wider class of linear dynamic models to which the SVAR methods discussed here can be applied. None of the issues discussed in this section will be specific to the model described above. An economic model from this class is supposed to specify a VAR representation for a stationary vector of observable variables⁶ :
$\begin{align} X_t &= B(L) X_{t-1} + e_t \end{align}$
where is a polynomial in the lag-operator , $B(L) = \sum_{k=1}^{\infty} B_k L^{k-1}$ whose roots lie all outside the unit circle and the innovations are , $e_t \sim iid(0, \Omega)$ .

In principle, the model prescribes an infinite order VAR. When for this nests the case of a finite order VAR. But as noted by Cooley and Dywer (1998), many interesting models have only infinite order VAR representations. In the remainder of this paper the true VAR representation is always assumed to be of infinite order. The linearized solution to the model described in Section 2 has such an infinite order VAR representation; details are shown in Appendix B.

For the identification of structural shocks, there has to be an invertible one-to-one mapping from innovations to the structural shocks $\varepsilon_t$ driving the underlying model--such as technology, monetary policy errors, exogenous government spending etc.:
$\begin{align} e_t = & A_0 \varepsilon_t \end{align}$
where is square and $\vert A_0\vert \neq 0$ . Fernàndez-Villaverde et al. (2007) derive conditions when a linear dynamic model has an invertible VAR representation.⁷ (These are summarized in Appendix B.) This paper considers only cases where these conditions are satisfied, though possibly only in an infinite order VAR representation. The same applies to the situations studied by CKM, CEV as well as Erceg, Guerrieri, and Gust (2005). Excluding the complications arising from non-invertibilities allows to focus on problems owing to small sample bias and the finite order approximations of the VAR.⁸

It will be handy to introduce the notation
$\begin{align} C(L)&\equiv (I-B(L)L)^{-1} =\sum_{k=0}^\infty C_kL^k \qquad \text{where}\quad C_0=I \end{align}$
for the non-structural moving average (VMA) coefficients of . The structural moving average representation for is then $X_t = A(L) \varepsilon_t$ with .

In the spirit of CEV and CKM, only one of the structural shocks will be identified. For concreteness, let it be the first one, denoted $\varepsilon_t^z$ , and call it "technology shock". Think of the first element of as being a growth rate (a difference in logs), like the change in labor-productivity Gali (1999) or output growth Blanchard and Quah (1989). The identifying assumption is then that only the technology shock has a permanent effect on the level of the first element of . This restricts the matrix of long-run coefficients, $A(1)=\sum_{i=0}^\infty A_i$ :
$\begin{align} A(1) &= C(1) A_0 = \begin{bmatrix}\bar{a}_{11} & 0 & \ldots & 0 \ \char93 &\char93 & \ldots &\char93 \end{bmatrix} & \quad \text{and} \quad \bar{a}_{11}&>0 \end{align}$
This restriction holds exactly in the linearized solution to the model described in Section 2.

A key object for implementing this constraint is the spectral density of . The spectral density at frequency $\omega$ is defined as $S_X(\omega)\equiv \sum_{k=-\infty}^\infty E(X_tX_{t-k}^T) e^{-i\omega k} =C(e^{-i\omega}) \Omega C(e^{-i\omega})^T$ where is the imaginary unit.⁹ factors the spectral density of at frequency zero:
$\begin{align} A(1) A(1)^T & = C(1) \Omega C(1)^T = S_X(0) \end{align}$
One way to compute the first column of is by recovering from the Cholesky decomposition of . (This is the unique lower triangular factorization of a positive definite matrix.¹⁰):
$\begin{align*} A(1) &= \chol{\{S_X(0)\}} \notag \end{align*}$
CEV show that the restriction in (4) uniquely pins down the first column of and the Cholesky factorization is one possible implementation.¹¹

The long-run coefficients can then be mapped into the matrix of impact responses using the VAR dynamics encoded in the polynomial of lag coefficients :
$\begin{align} A_0 &= \left(I-B(1)\right) A(1) \end{align}$

3.1 OLS Implementation with Finite-Order VAR

Since the VAR innovations in (1) are assumed to be white noise, they satisfy the OLS normal equations $E X_{t-k} e_t^T = 0$ ( $\forall k$ ). And in principle, the coefficients could be estimated from least squares projections of on its infinite past. In practice, an empirical implementation can only work with a finite lag length. Henceforth $\ensuremath{B(L)^\text{OLS}\xspace}$ denotes a lag polynomial of finite order $p<\infty$ :
$\begin{align} \ensuremath{B(L)^\text{OLS}\xspace} &\equiv \sum_{k=1}^p \ensuremath{B_k^\text{OLS}\xspace} L^{k-1} \notag \ \ensuremath{v_t^\text{OLS}\xspace} &\equiv X_t - \ensuremath{B(L)^\text{OLS}\xspace} X_{t-1} \ \ensuremath{\Omega_v^\text{OLS}\xspace} &\equiv E\;[ \ensuremath{v_t^\text{OLS}\xspace} (\ensuremath{v_t^\text{OLS}\xspace})^T] \notag \ \intertext{where the normal equations are imposed for all lags $k\leq p$ } E X_{t-k} (\ensuremath{v_t^\text{OLS}\xspace})^T &= 0 \end{align}$
The associated VMA is $\ensuremath{C(L)^\text{OLS}\xspace} \equiv (I-\ensuremath{B(L)^\text{OLS}\xspace}L)^{-1}$ . Only stable VARs are considered, formally this requires all roots of $\ensuremath{C(L)^\text{OLS}\xspace}$ to be outside the unit-circle.

The standard procedure is to assume uncorrelated residuals, $\ensuremath{v_t^\text{OLS}\xspace}$ . Following Blanchardand Quah (1989), the long run restriction (4) is implemented based on an estimate of the spectral density at frequency zero constructed from the OLS estimates. Impact coefficients are computed by plugging these estimates into (6):
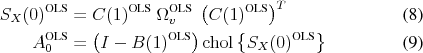
$\begin{align} \ensuremath{S_X(0)^\text{OLS}\xspace} &= \ensuremath{C(1)^\text{OLS}\xspace}\; \ensuremath{\Omega_v^\text{OLS}\xspace} \; \left(\ensuremath{C(1)^\text{OLS}\xspace}\right)^T \ \ensuremath{A_0^\text{OLS}\xspace} &= \left(I-\ensuremath{B(1)^\text{OLS}\xspace}\right) \chol{\left\{\ensuremath{S_X(0)^\text{OLS}\xspace} \right\}} \end{align}$

Using a finite-order VAR when the data has been generated from an infinite order process induces a truncation bias into the estimates. In this case, the OLS assumption of uncorrelated forecast errors $\ensuremath{v_t^\text{OLS}\xspace}$ is violated, which is an example of what Cooley and Dwyer criticized as an "auxiliary" (but not innocuous) assumption. This truncation bias arises even when the true population moments of the data generating process were known. Applied to data generated from a business cycle model the truncation bias in SVARs can be substantial, as shown by Cooley and Dwyer (1998), Erceg, Guerrieri, and Gust (2005), Ravenna (2007) or CKM. The truncation bias is also sizable for data from the model described Section 2 as will be seen in Figure 3 below.

3.2 CEV: Combining OLS with Spectral Estimate

CEV propose an alternative estimator for the matrix of impact coefficients. This new estimator uses a mixture of the OLS estimates of and a non-parametric estimator for . The procedure is motivated by observing that OLS projections construct $\ensuremath{B(L)^\text{OLS}\xspace}$ not necessarily with regard to but in order to minimize the forecast error variance $\ensuremath{\Omega_v^\text{OLS}\xspace}$ . Following Sims (1972), the least-squares objective seeks OLS coefficients which minimize the average distance between themselves and the true $B(e^{-i\omega})$ , weighted by the spectral density of , which may or may not be large at the zero frequency:¹²
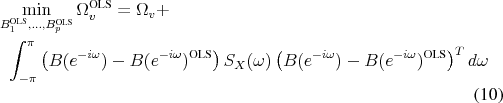
$\begin{multline} \min_{\ensuremath{B_1^\text{OLS}\xspace},\ldots, \ensuremath{B_p^\text{OLS}\xspace}} \ensuremath{\Omega_v^\text{OLS}\xspace} = \Omega_v + \int_{-\pi}^\pi \left(B(e^{-i\omega})-\ensuremath{B(e^{-i\omega})^\text{OLS}\xspace} \right) S_X({\omega}) \left(B(e^{-i\omega})-\ensuremath{B(e^{-i\omega})^\text{OLS}\xspace} \right)^T d\omega \end{multline}$
Accordingly, OLS will try to set $\ensuremath{B(1)^\text{OLS}\xspace}$ close to only if the data's spectrum is high at the zero frequency and $\ensuremath{S_X(0)^\text{OLS}\xspace}$ need not be the best possible estimate for the spectral density at frequency zero.

Instead of using $\ensuremath{S_x(0)^\text{OLS}\xspace}$ , CEV employ a spectral estimator of to construct . In Christiano, Eichenbaum, and Vigfusson (2006a), they consider two estimators, one based on Newey and West (1987) and the other on Andrews and Monahan (1992). Both are based on truncated sums of autocovariance matrices. To ensure positive definiteness, these are weighted by a Bartlett kernel. Where Newey-West sums over the (sample) autocovariances of ,
$\begin{align} \ensuremath{S_X(0)^\text{NW}\xspace} &= \sum_{k=-b}^{b} \left(1 - \frac{\vert k\vert}{b + 1}\right) E \left[{X_t X_{t-k}^T}\right] \end{align}$
Andrews-Monahan uses first the VAR to prewhiten the data and then sums over the residual autocovariances:
$\begin{align} \ensuremath{S_X(0)^\text{AM}\xspace} &= \ensuremath{C(1)^\text{OLS}\xspace} S_v^{NW}(0) \left(\ensuremath{C(1)^\text{OLS}\xspace}\right)^T \ \text{where}\quad \ensuremath{S_v(0)^\text{NW}\xspace} &= \sum_{k=-b}^{b} \left(1 - \frac{\vert k\vert}{b + 1}\right) E \left[{\ensuremath{v_t^\text{OLS}\xspace}(\ensuremath{v_{t-k}^\text{OLS}\xspace})^T}\right] \end{align}$
is a truncation parameter, also known as "bandwidth", which will be discussed in more detail below.¹³ The Andrews-Monahan estimator nests the OLS case when .

The new CEV estimator computes the long-run coefficients from the non-parametric density estimate. Combined with the OLS lag coefficients, CEV obtain their impact coefficients as
$\begin{align} \ensuremath{A_0^\text{CEV-AM}}\xspace &= \left(I-\ensuremath{B(1)^\text{OLS}\xspace}\right) \ensuremath{A(1)^\text{AM}\xspace} \text{where} \quad \ensuremath{A(1)^\text{AM}\xspace} &= \chol{\left\{\ensuremath{S_X(0)^\text{AM}\xspace}\right\}} \end{align}$
Impulse responses are $\ensuremath{A(L)^\text{CEV-AM}}\xspace = \ensuremath{C(L)^\text{OLS}\xspace}\ensuremath{A_0^\text{CEV-AM}}\xspace$ . Using the Newey-West estimator, impact coefficients are computed as $\ensuremath{A_0^\text{CEV-NW}}\xspace = \left(I-\ensuremath{B(1)^\text{OLS}\xspace}\right) \chol{\left\{\ensuremath{S_X(0)^\text{NW}\xspace}\right\}}$ . For brevity, the remainder of this section will mostly refer to the Andrews-Monahan estimator, with similar arguments holding for the Newey-West estimator. Section 4 presents simulations using both estimators.

The bandwidth choice is critical in estimating spectra, akin to choosing the lag order of a VAR. Bandwidth choice has been shown to be more important using other weighting schemes than the Bartlett kernel Newey and West (1994).¹⁴ For a consistent estimator, can grow with the sample size but at a smaller rate. CEV use a fixed and fairly large value of in a sample of observations.¹⁵

Theoretically, the prewhitening of Andrews-Monahan is appealing since it removes spikes from the spectral density of which make spectral estimation difficult (Priestley 1981, Chapter 7). Andrews and Monahan (1992) and Newey and West (1994) find the prewhitening to fare better in Monte Carlo studies than the original Newey-West estimator. Christiano, Eichenbaum, and Vigfusson (2006a) find no clearly superior choice between the two and Christiano, Eichenbaum, and Vigfusson (2006b) proceed to use only the Newey-West estimator.

To minimize the mean-squared error (MSE) of spectral estimates, the bandwidth selection schemes of Andrews (1991) and Newey and West (1994) can be used. However, constructing an MSE optimal estimator of the spectrum does not necessarily translate into an MSE optimal estimate of coefficients like $\ensuremath{A_0^\text{CEV-AM}}$ or $\ensuremath{A_0^\text{CEV-NW}}$ . Their MSE depends not solely on the MSE of $\ensuremath{S_X(0)^\text{AM}\xspace}$ but--amongst others--on bias and standard error of the spectrum in ways which are specific to the data generating process.¹⁶ Hence, the bandwidth selection scheme of Newey and West (1994) may serve as a useful starting point for bandwidth choice, but it is not necessarily optimal for the purpose of estimating impulse response or variance shares.

The simulations reported below use both the optimal bandwidth selection scheme of Newey and West (1994) and the large bandwidth choice of CEV. The former tend to pick fairly small bandwidths. For the various calibrations of the model economy considered here, the optimal bandwidth of the Newey-West estimator is typically close to ten, and the average for the Andrews-Monahan estimator is about four. In simulations not reported here, spectral estimates with intermediate bandwidth choices displayed performance characteristics which were intermediate between what is shown here for these two choices here.

3.3 Conceptual Problems with the CEV Procedure

The CEV procedure is motivated by dissatisfaction with $\ensuremath{B(1)^\text{OLS}\xspace}$ . In conventional SVAR implementations, this estimate is needed for two purposes: First, to construct the long run responses as in (9), and second in order to map back into impact responses as in (10). CEV replace $\ensuremath{B(1)^\text{OLS}\xspace}$ with a spectral estimate in the first step, but not in the second. This creates a non-negligible inconsistency in representing the overall dynamics of the VAR.

By plugging a spectral estimate into their SVAR computations, CEV have weakened the OLS assumption of uncorrelated residuals without fully accounting for its consequences. As a result, the impact coefficients of CEV will in general not reproduce the forecast error variance of the VAR, which is at the heart of variance computations. These and other consequences are illustrated here. The next sub-section shows how a spectral factorization could be used to incorporate spectral estimates into a VAR model while retaining an internally consistent model of the data.

The spectral estimates embody information about correlation in the VAR residuals $\ensuremath{v_t^\text{OLS}\xspace}$ . As can be seen from (14), the Andrews-Monahan estimator is constructed from autocovariances of the VAR residuals $\ensuremath{v_t^\text{OLS}\xspace}$ . Obviously, expresses a concern about serially correlated residuals. The Newey-West estimator $\ensuremath{S_X^\text{NW}\xspace}(\omega)$ also embodies concerns about serially correlated VAR residuals since it implies a spectrum for the VAR residuals, which is generally not constant across frequencies.¹⁷

Under the premise that the true model has only an infinite-order representation, it is indeed very plausible that the residuals from a VAR() will be correlated. In the spirit of Andrews and Monahan (1992), the VAR could then be viewed as having merely prewhitened the data. But typically, researchers fit the lag length of their VARs until the point where estimated residuals do not display any significant correlation. Employing a spectral estimate like (14) beyond this point implies a belief that there is still useful information to be gleaned from the estimated residuals--or in other words, it implies a distrust against the lag-selection criteria being chosen for the VAR. By allowing for residual dynamics poses, a researcher risks of overfitting the data, which may still reduce bias in the estimated spectra, but at the expense of a higher standard error.¹⁸ Against this backdrop, the assertion of Christiano, Eichenbaum, and Vigfusson (2006a) that the impulse responses computed from their procedure have "smaller bias, smaller means square error" appear even more striking--and as will be seen, these properties do neither extend to the wider set of calibrations studied below nor to other SVAR statistics like variance decompositions.

A researcher adopting the CEV strategy wants $\ensuremath{S_X(0)^\text{AM}\xspace}\neq\ensuremath{S_X(0)^\text{OLS}\xspace}$ and thus $\ensuremath{S_v(0)^\text{NW}\xspace}\neq\ensuremath{\Omega_v^\text{OLS}\xspace}$ .¹⁹ As a direct implication, the impact coefficients of CEV do not reproduce the forecast error variance of the VAR, $\ensuremath{A_0^\text{CEV-AM}}\xspace (\ensuremath{A_0^\text{CEV-AM}}\xspace )^T \neq \ensuremath{\Omega_v^\text{OLS}\xspace}$ . When computing the total variance of the data by summing over the conditional variations implied by the SVAR, the CEV procedure would not match the unconditional variance of the data either.²⁰ This mismatch in the unconditional variances of VAR what is implied by the impulse responses of CEV occurs both in population as well as in small sample. A similar argument applies to the Newey-West variant of the CEV procedure, where a researcher seeks $\ensuremath{S_X(0)^\text{NW}\xspace}\neq\ensuremath{S_X(0)^\text{OLS}\xspace}$ and thus $(I-\ensuremath{B(1)^\text{OLS}\xspace})\ensuremath{S_X(0)^\text{NW}\xspace}(I-\ensuremath{B(1)^\text{OLS}\xspace})^T\neq\ensuremath{\Omega_v^\text{OLS}\xspace}$ .

**Figure 1:** Percentage Errors in Variance of Output Growth Computed from CEV Procedure
Note: Percentage errors of variance in output growth, relative to true moments (left panel, "Population") or OLS sample moments (right panel, "Simulated"). Errors are computed for different calibrations of the importance of technology shocks in the data generating process. "Technology share" on the x-axis is the percentage of output variability due to technology shocks at business cycle frequencies (cycles with durations between two-and-a-half and eight years) in the data generating process.Variances denoted "CEV-NW" and "CEV-AM" are computed from the impulse responses of CEV's SVAR procedure using the Newey-West or Andrews-Monahan estimators respectively. The left panel, labeled "Population", uses variances computed from applying the SVAR procedures to the true population moments of the model. This panel documents mismatches arising from finite VAR order and spectral bandwidth. The right panel, labeled "Simulations", reports small means computed from 1,000simulations. (The variances are not bandpass-filtered.)

Figure 1 Data

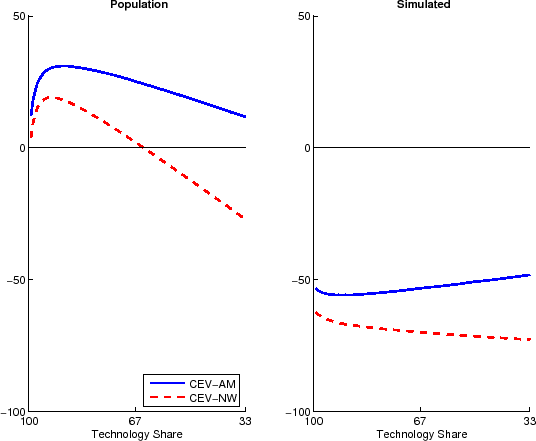For the model economy described in Section 2, Figure 1 illustrates the mismatch in the variance of output growth. In small sample, the variances implied by the CEV procedure are only about half as big as the OLS sample moments. As can be seen in the right panel of Figure 1, this occurs both when using the Newey-West or the Andrews-Monahan variant of the procedure and regardless of the share of fluctuations explained by technology shocks. As depicted in the left panel of the figure, the mismatch is qualitatively different, but also sizable when applying the procedure to the population moments of the model while using a lag length of and spectral bandwidth of .

The CEV procedure is motivated by concerns about the ability of OLS estimate to correctly capture the low-frequency dynamics of the data. But implicitly, differences between spectra estimated from OLS and the non-parametric methods are not attributed to misspecified dynamics, but rather to the VAR's forecast error variance. However, the accuracy of estimating $\ensuremath{\Omega_v^\text{OLS}\xspace}$ has so far not been doubted. In fact, getting a good estimate for forecast error variance is precisely the objective of OLS projections--see (11) above. Still, the CEV procedure deviates from previous contributions to the SVAR literature where identification is defined as a search over the space of matrices $\hat A_0$ satisfying $\hat A_0 \hat A_0^T=\ensuremath{\Omega_v^\text{OLS}\xspace}$ .²¹

Finally, a researcher might want to re-construct structural shocks based on (2) as $\ensuremath{\varepsilon_t^\text{CEV-AM}}\xspace = \left(\ensuremath{A_0^\text{CEV-AM}}\xspace \right)^{-1}\ensuremath{v_t^\text{OLS}\xspace}$ and compare them against $\ensuremath{\varepsilon_t^\text{OLS}\xspace} = \left(\ensuremath{A_0^\text{OLS}\xspace}\right)^{-1}\ensuremath{v_t^\text{OLS}\xspace}$ . She will be troubled noticing that the estimated technology shocks are perfectly correlated:²²

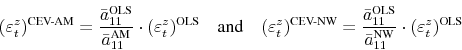
$\begin{displaymath}\ensuremath{(\varepsilon_t^z)^\text{CEV-AM}}\xspace = \frac{\ensuremath{\bar{a}_{11}^\text{OLS}\xspace}}{\ensuremath{\bar{a}_{11}^\text{AM}\xspace}} \cdot \ensuremath{(\varepsilon_t^z)^\text{OLS}\xspace} \quad\text{and}\quad \ensuremath{(\varepsilon_t^z)^\text{CEV-NW}}\xspace = \frac{\ensuremath{\bar{a}_{11}^\text{OLS}\xspace}}{\ensuremath{\bar{a}_{11}^\text{NW}\xspace}} \cdot \ensuremath{(\varepsilon_t^z)^\text{OLS}\xspace}\end{displaymath}$

This holds for any pair of matrices and constructed from (4) and (6) using $\ensuremath{B(1)^\text{OLS}\xspace}$ and a satisfying the zero restrictions (4). Under those conditions the top rows of $\ensuremath{\left(\ensuremath{A(1)^\text{OLS}\xspace}\right)^{-1}\xspace}$ , $\ensuremath{\left(\ensuremath{A(1)^\text{AM}\xspace}\right)^{-1}\xspace}$ and $\ensuremath{\left(\ensuremath{A(1)^\text{NW}\xspace}\right)^{-1}\xspace}$ are identical up to a scaling.²³

Since CEV were only concerned with impulses-responses and , the problem does not show up in their analysis. The construction of estimated shocks is however often used by researchers, for instance in order to plot historical decompositions or when identifying several shocks (see for example Altig et al. 2004).

3.4 Correct Identification with Spectral Factorization

To overcome the problems with the CEV procedure discussed above, it is necessary to parse out dynamics of $\ensuremath{v_t^\text{OLS}\xspace}$ implied by the spectral estimates. Also when the true model has an infinite order VAR representation, OLS projections of on a finite number of lags are well defined in the sense of satisfying the projection equations (8) for $k\leq p$ , but the residuals $\ensuremath{v_t^\text{OLS}\xspace}$ are not . In general, the residuals follow a moving average representation:
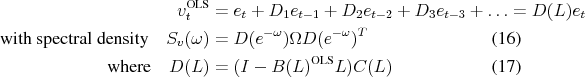
$\begin{align} \ensuremath{v_t^\text{OLS}\xspace} &= e_t + D_1 e_{t-1} + D_2 e_{t-2} + D_3 e_{t-3} + \ldots = D(L) e_t \notag \ \text{with spectral density} \quad S_v(\omega) &= D(e^{-\omega}) \Omega D(e^{-\omega})^T \ \text{where} \quad D(L) &= (I-\ensuremath{B(L)^\text{OLS}\xspace}L) C(L) \end{align}$

**Figure 2:** $D(1)\neq I$
Note: Each panel shows an element of $\sum_{k=0}^K D_k$ for different lags . is computed from population moments of a VAR(1) applied to the model economy of Section 2 for three different percentages of the bandpass-filtered variability in output explained by technology shocks. A technology share of 67.5% (solid line) corresponds to the maximum likelihood estimates of CEV.

Figure 2 Data

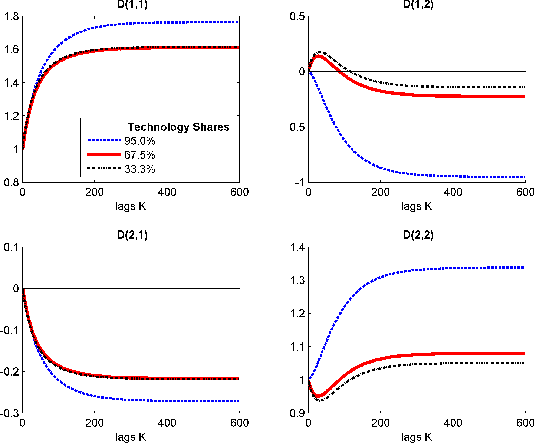CKM and CEV discuss a truncation bias which is hard to detect based on VAR lag-length selection procedures. In terms of the moving average , their results can be read as finding $D_i\approx 0$ but $D(1)\neq I$ . This can also be illustrated in the model economy described in Section 2. Figure 2 plots the population values of the cumulated sums $\sum_{k=0}^K D_k$ when for different calibrations of the share of fluctuations in output explained by technology shocks. (Results are similar for other values of .) At each lag, the increments are small and close to zero, but summing over many lags leads to $D(1)\neq I$ .

Many moving average representations can be consistent with a given spectrum. But only one of them is invertible. As will be shown next, is invertible and can be uniquely identified with a spectral factorization of $S_v(\omega)$ .

$\begin{prp} % latex2html id marker 680 [Invertibility of D(L)] When the underlying model has a fundamental VAR representation as in (\ref{GOPHER:eq:VARmodel}), and the OLS-VAR is stable, the moving average polynomial $D(L)$\ defined in (\ref{GOPHER:eq:DLdef}) has all its roots outside the unit-circle. \end{prp}$

$\begin{proof} The proof is straightforward since $(I-B(L))^{-1}=C(L)=(I-\ensuremath{B(L)^\text{OLS}\xspace})^{-1}D(L)$ has all roots outside the unit circle and the same has been assumed for the VMA of the VAR($p$), $\ensuremath{C(L)^\text{OLS}\xspace}=(I-\ensuremath{B(L)^\text{OLS}\xspace}L)^{-1}$. \end{proof}$

It is straightforward to recover from $S_v(\omega)$ with a spectral factorization. The "canonical spectral factorization" is a classic theorem in linear quadratic control, assuring existence and uniqueness of an invertible and a positive definite $\Omega$ consistent with (17).

$\begin{theorem}[Spectral Factorization, \cite{Hannan:1970:timeseriesbook}] Supp... ..._{k=1}^q D_k z^k$ which has all its roots outside the unit circle. \end{theorem}$

The theorem factors a spectrum constructed from a finite number of autocovariances into a finite-order MA. For an empirical application, a finite has of course to be chosen. But when applying the spectral factorization to the population objects of the true model (1), it remains to consider that is in general an MA( $\infty$ ). However, since the processes for and $\ensuremath{v_t^\text{OLS}\xspace}$ are stationary, their autocovariances and MA-coefficients vanish for large lags (Hamilton 1994, Chapter 3.A). Analogous to Sims (1972), a spectral factorization with an arbitrarily large but finite can arbitrarily well approximate the true spectrum and true . Alternatively the true can be thought of as being the limit of applying Theorem 3.4 to an ever increasing sequence of 's.

For a correct identification of the structural shocks, the true impact coefficients (6) can be written in terms $\ensuremath{B(L)^\text{OLS}\xspace}$ and as
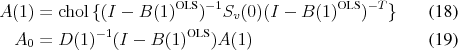
$\begin{align} A(1) &= \chol{\{(I-\ensuremath{B(1)^\text{OLS}\xspace})^{-1}S_v(0)(I-\ensuremath{B(1)^\text{OLS}\xspace})^{-T}\}} \ A_0 &= \ensuremath{D(1)^{-1}\xspace}(I-\ensuremath{B(1)^\text{OLS}\xspace}) A(1) \end{align}$

CEV construct $\ensuremath{A(1)^\text{AM}\xspace}$ according to (19) while using the spectral estimate $\ensuremath{S_v(0)^\text{NW}\xspace}$ . But they ignore the residual dynamics captured by in (20) when mapping $\ensuremath{A(1)^\text{AM}\xspace}$ back into the impact coefficients. As illustrated in Figure 2, is typically not a diagonal matrix in the model economy, far from equal to the identity matrix. Ignoring the residual captured by is the source of the variance misrepresentation discussed in the previous subsection.

To combine VAR coefficients and spectral estimates in an internally consistent fashion, a spectral factorization must be used. The spectral factorization of $\ensuremath{S_v(\omega)^\text{NW}\xspace}$ yields a unique and invertible MA(), denoted $\ensuremath{D(L)^\text{SF-AM}\xspace}$ , and an innovations variance matrix $\ensuremath{\Omega^\text{SF-AM}\xspace}$ . The superscript "SF-AM" indicates that these are calculated from the residual spectrum employed by the Andrews-Monahan estimator $\ensuremath{S_X(\omega)^\text{AM}\xspace}$ . Impact coefficients are then
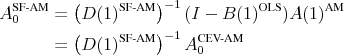
$\begin{align*} \ensuremath{A_0^\text{SF-AM}\xspace} &= \ensuremath{\left(\ensuremath{D(1)^\text{SF-AM}\xspace}\right)^{-1}\xspace} (I-\ensuremath{B(1)^\text{OLS}\xspace}) \ensuremath{A(1)^\text{AM}\xspace} &=\ensuremath{\left(\ensuremath{D(1)^\text{SF-AM}\xspace}\right)^{-1}\xspace} \ensuremath{A_0^\text{CEV-AM}}\xspace \end{align*}$

Sayed and Kailath (2001) survey a number of different algorithms for performing spectral factorizations. The computations reported here use a reliable and efficient algorithm from Li (2005), based on a state space representation of the moving average process of $\ensuremath{v_t^\text{OLS}\xspace}$ . (Details are given in Appendix A.)

In contrast to the CEV procedure, the spectral factorization is consistent with the variance of the data, in sample as well as in population.

$\begin{prp} By construction, estimates of \ensuremath{A_0^\text{SF-AM}\xspace} and \ensuremath{D(L)^\text{SF-AM}\xspace} factor the spectral density $\ensuremath{{S}_v(\omega)^\text{NW}\xspace}$ and thus reproduce the variance of the VAR residuals $\ensuremath{{\Omega}_v^\text{OLS}\xspace} = \int_{-\pi}^\pi \ensuremath{{S}_v(\omega)^\text{NW}\xspace} d\omega$. As a corollary, this preserves also the unconditional variance of $X_t$. \end{prp}$

$\begin{proof} The spectral estimate is \begin{displaymath}\ensuremath{S_v(\omega... ...mega_v^\text{OLS}\xspace} (\ensuremath{{C}_l^\text{OLS}\xspace})^T$. \end{proof}$

A spectral factorization can also be applied directly to the Newey-West estimate of the data's spectrum, $\ensuremath{S_X{\omega}^\text{NW}\xspace}$ , yielding coefficients for the VMA of , $\ensuremath{C(L)^\text{SF-NW}\xspace}$ and innovation variance $\ensuremath{\Omega^\text{SF-NW}\xspace}$ . Following (6), impact coefficients and impulse responses can then be computed as
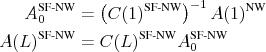
$\begin{align*} \ensuremath{A_0^\text{SF-NW}\xspace} &= \ensuremath{\left(\ensuremath{C(1)^\text{SF-NW}\xspace}\right)^{-1}\xspace} \ensuremath{A(1)^\text{NW}\xspace} \ensuremath{A(L)^\text{SF-NW}\xspace} &= \ensuremath{C(L)^\text{SF-NW}\xspace} \ensuremath{A_0^\text{SF-NW}\xspace} \end{align*}$
These impulse responses do not involve any VAR coefficients. Analogously to Proposition 3.4, their construction preserves the variance of the data.

4 SVARs applied to Data from Lab Economy

The previous section described several schemes for imposing the long-run restriction (4) on the data. The conventional method, going back to Blanchard and Quah (1989), uses OLS estimates of a VAR. The recently proposed procedure of CEV combines this with a non-parametric estimate of the spectral density at frequency zero. This procedure has been criticized above for its lack of internal consistency. Finally, this paper proposed a new method, combining OLS estimates and spectral estimators in an internally consistent way. This method relies on a spectral factorization ("SF") to uncover the dynamics implied by the non-parametric spectral estimators.

These procedures are applied here to data simulated from the model economy described in Section 2. The same data generating process has also been used by CEV and CKM.²⁴ For the CEV and SF methods, there are two variants depending on whether the spectral estimators of Newey and West (1987) or Andrews and Monahan (1992) are used. This section reports results for both.

Mimicking conditions faced by empirical researchers, "small" samples with 180 observations are simulated. In small sample, two distinct issues arise. First, there is truncation bias in VARs and spectral estimators arising from the need to specify a finite lag length , respectively a finite bandwidth . As discussed in Section 2, lag length is determined individually for each draw with an information criterion and spectral bandwidth is fixed at 150. In addition, alternative results are reported using the bandwidth selection procedure of Newey and West (1994) for Newey-West spectra. (See Section 3.2 for further discussion of bandwidth selection.)

Second, there is the small sample bias in estimated parameters known from Hurwicz (1950).²⁵ To isolate the pure truncation effects from the Hurwicz bias, the identification procedures are not only applied to simulated data, but also to VARs and spectral estimates constructed from the model's true population moments.²⁶

The procedures are evaluated in terms of of their capability to uncover two statistics typically of interest to applied researchers. Following CKM and CEV, estimates of the response of hours to a technology shock are computed. For brevity, the discussion is limited on impact coefficients , since all methods compute impulse responses from $\ensuremath{C(L)^\text{OLS}\xspace}$ and their estimates of (except when factorizing $\ensuremath{S_X(\omega)^\text{NW}\xspace}$ ). In addition, the share of fluctuations in output and hours due to technology shocks is estimated. As it is typical in the business cycle literature, these shares are computed after filtering out any fluctuations which do not correspond to cycles with a duration between two-and-a-half and eight years.²⁷ Two criteria are reported to assess the goodness of estimates: Bias and Root Mean Square Error (RMSE), both expressed as percentages relative to the true value known from the model.²⁸

The results show that all procedures are subject to substantial truncation and small biases and none works like a panacea. Different methods display different strengths and weaknesses. The claims by Christiano, Eichenbaum, and Vigfusson (2006a) of "smaller bias, smaller means square error" associated with their procedure do neither generalize to a wider range of model calibrations nor do they extend from the estimation of impact responses to variance shares.

**Figure 3:** Impact Response of Hours to Technology Shock
Note: Percentage points relative the model's true impact response of hours to a technology shock. Top row based on Andrews-Monahan estimator for CEV and SF, bottom row using Newey-West estimators; both with a fixed bandwidth of . "Technology share" on the x-axis is the percentage of output variability due to technology shocks at business cycle frequencies (cycles with durations between two-and-a-half and eight years) in the data generating process.

Figure 3 Data

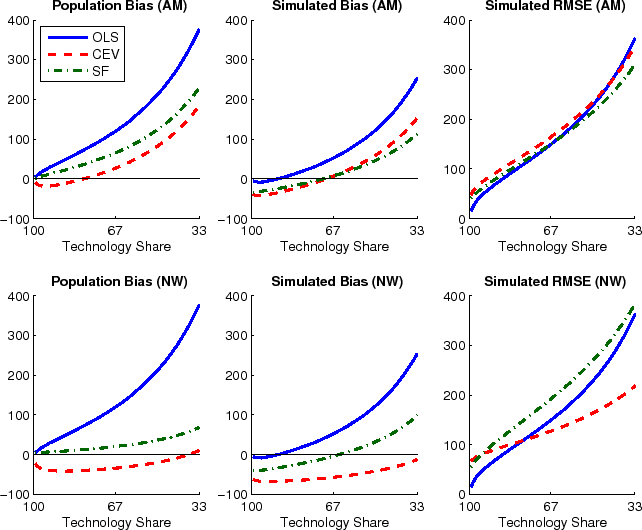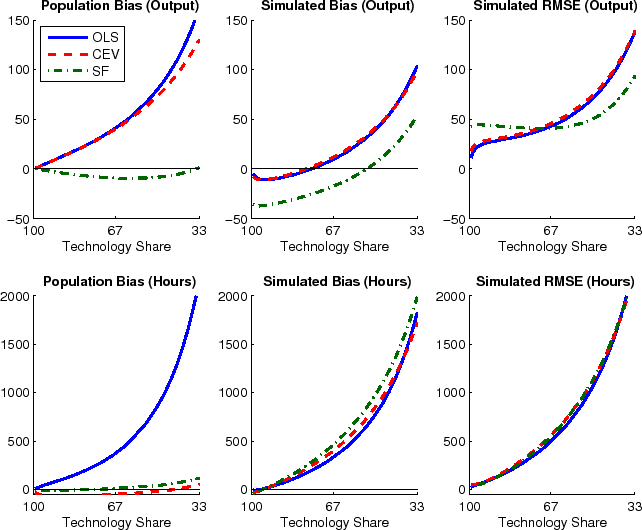
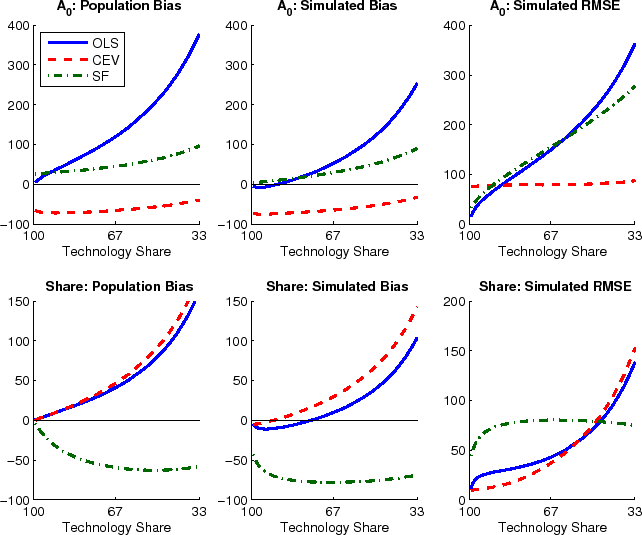
Effects from the truncation and the small sample bias can offset each other. This is the case when estimating the impact of technology on hours. The left column in Figure 3 shows how impact responses are overestimated in population whereas the simulated bias shown in the middle column of the figure is lower (more negative). This simulated bias displays the total effect from truncation and Hurwicz bias. The OLS method has the largest population bias and it is only partially offset by the Hurwicz bias. The two spectral methods suffer from substantially smaller truncation bias, and depending on the simulated importance of technology shocks, the total bias can be either negative or positive. Coincidentally, the upwards bias in SF-AM and SF-NW is exactly offset around technology shares of about two thirds, corresponding to the range of MLE estimates of CEV and CKM for U.S. data. (Similarly for CEV-AM, but not CEV-NW.) However, results are different for other calibrations of the technology share, which cautions strongly against extrapolating from a particular result to different data sets and different applications.

Unless the true share of technology shocks is very large, the RMSE of estimated impact coefficients are very large, often surpassing more than 100% of the true value. Interestingly, the RMSE do not differ much across the different methods, as can be seen in the right-most column of Figure 3. If anything, SF-NW is outperforming CEV-NW on bias, at the expense of a worse RMSE. This is likely due to an overfitting of the residual dynamics by SF-NW.

**Figure 4:** Technology Shares in Fluctuations of Output and Hours
Note: Percentage points relative the model's true technology share. Top row reports bias and RMSE for variance decomposition of output, bottom row for hours. Andrews-Monahan estimators of the spectral density used for CEV and SF with a fixed bandwidth of . (Similar results reported for Newey-West in Figure A.1). "Technology share" on the x-axis is the percentage of output variability due to technology shocks at business cycle frequencies (cycles with durations between two-and-a-half and eight years) in the data generating process.

Figure 4 Data

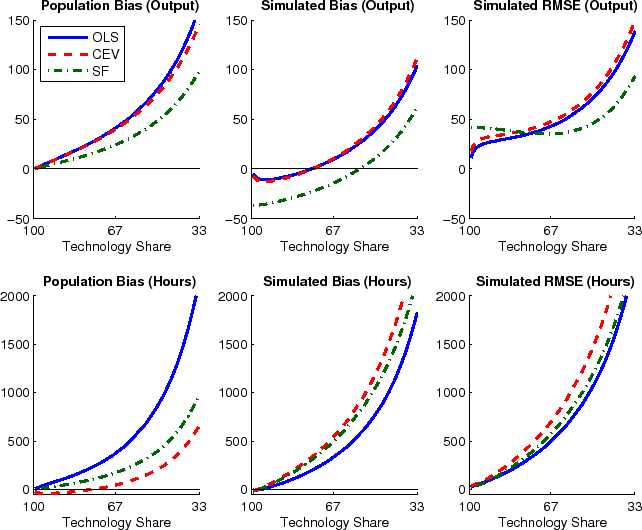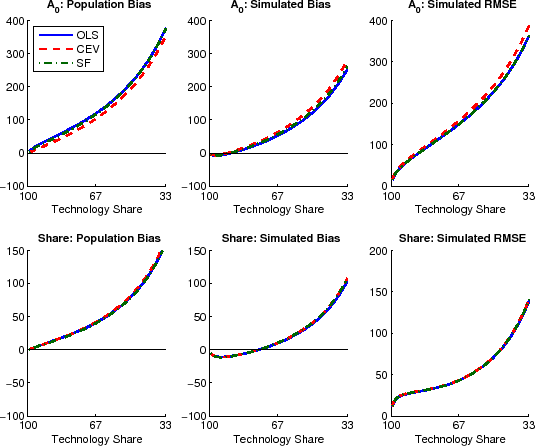
Turning to the estimated variance shares of output and hours shown in Figure 4, the relative performance of the various methods looks quite different. The panels in the top row of the figure show bias and RMSE for variance decompositions of output, the bottom row for variance decompositions of hours. For this figure, spectral densities have been estimated with the Andrews-Monahan estimator. Results are broadly similar when using the Newey-West estimator (see Figure A.1 in the separate appendix with additional results.)

Strikingly, for technology shares in output, bias and RMSE are very similar when using either OLS or CEV. The mismatch in total variance discussed in Section 3.3, does not seem to distort the computations of relative variance measures in this case. But, the two methods differ when decomposing the variance of hours. Bias and RMSE in the variance decomposition of hours are an order of magnitude larger than for output, cautioning very strongly against neglecting small sample issues when comparing SVAR estimates against model predictions. Moreover, the variance decompositions of hours provide a useful counterexample against disregarding OLS methods altogether, since OLS dominates the spectral methods both in terms of simulated bias and RMSE for all calibrations considered here. All in all, these results underline how truncation and Hurwicz bias interact with the different methods in ways which are hard to anticipate for an empirical researcher who does not know the true dynamics of the data.

The results presented in Figures 3 and 4 are based on a large and fixed spectral bandwidth of . A separate appendix with additional results shows that the results are similar for Newey-West spectra when their bandwidth has been chosen by the automatic bandwidth selection procedure of Newey and West (1994). Compared to the case of a large and fixed bandwidth, only two differences stand out. Estimating technology shares from a direct factorization of the Newey West spectrum perform worse compared to the large bandwidth case, both in terms of bias and RMSE, unless technology accounts for less than two thirds of business cycle fluctuations in output (see Figure A.1 in the appendix). Furthermore, the RMSE of impact coefficients estimated with CEV-NW is almost flat at around two thirds of the true value, independently of the true technology share (Figure A.2). Applying the automatic bandwidth selection for the residual spectra of the Andrews-Monahan estimator yields bandwidths close to zero, such that the results are mostly indistinguishable from the OLS estimates (Figure A.3).

5 Conclusions

In finite sample, truncation bias and Hurwicz bias pose fundamental problems when identifying structural shocks from restrictions on the long-run behavior of the data. These issues are present in the time domain when working with a VAR, as well as in the frequency domain when working with spectral estimators. Basically, the same estimates of the data's autocovariances are employed for constructing non-parametric estimates of the spectrum as well as for computing OLS coefficients. In both cases, truncation bias arises since there are only as many sample autocovariances as there are data points. And due to the Hurwicz bias, variance estimates tend to be biased downwards the smaller the sample and the larger the persistence of the data--again affecting both OLS estimates of VAR coefficients as well as non-parametric estimates of the spectral density.

Thus, spectral estimates offer no panacea against the truncation and small sample problems known from OLS. At best, by allowing for additional dynamics, they might improve upon OLS in terms of bias, but by overfitting the data, this comes at the expense of increasing RMSE.

The performance of different estimators appears to be very specific to the underlying model and its calibration, making it hard to predict, which procedure would do well in future applications using new data. Even for a given calibration, when a method performs better in terms of one model statistic, say impact coefficients, this does not necessarily translate into better performance for another statistic, like a variance share. Going forward, it would be more suitable to compare SVAR estimates (from any procedure), against the small sample predictions, not the true moments, of a specific model as in Cogley and Nason (1995), Kehoe (2006), Dupaigne, Feve, and Matheron (2007) and Dupaigne and Feve (2009).

Appendix

1 Spectral Factorization Method

Spectral factorization has a long tradition in the fields of linear quadratic control, robust estimation and control as surveyed for example by Whittle (1996).²⁹ Theorem 3.4 has been adapted from Hannan (1970, p. 66). The original theorem allows for unit roots in . The version stated above has been slightly strengthened by excluding the case of zero power in the spectral density at zero-frequency, to ensure the invertibility of the MA().³⁰

In the context of this paper, $S_v(\omega)$ will be the spectral density of $\ensuremath{v_t^\text{OLS}\xspace}=D(L)e_t$ where $E e_te_t^T = \Omega = A_0 A_0^T$ . We will be using non-parametric estimates of $S_v(\omega)$ based on weighted sums of the sample autocovariance function as described in Section 3.2.³¹

Theorem 3.4 requires $S_v(\omega)$ to be non-singular. This can be understood as requiring that the autocovariances need to decay sufficiently fast in relation to the number of MA lags. For example, in the scalar case and with , the first-order autocorrelation to be matched with a MA(1) cannot be larger than 0.5 in absolute value.³²

Algorithms for implementing the factorization go back to Whittle (1963) and have recently been surveyed by Sayed and Kailath (2001). The simulations reported here use the algorithm of Li (2005), which is based on a state space representation of and performed very reliably.³³ The remainder of this appendix describes the algorithm in more detail.

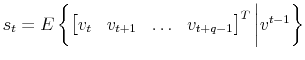Suppose follows an MA() as above. To represent it in a state space system, define the state vector $s_t = E\left\{\begin{bmatrix}v_t & v_{t+1} & \ldots & v_{t+q-1} \end{bmatrix}^T \bigg \vert v^{t-1}\right\}$ where $v^{t-1}$ is the entire history of realizations of up to time . Li then constructs the following state space system
$\begin{align*} s_{t+1} &= A s_t + D e_t \ v_t &= C s_t + e_t \end{align*}$

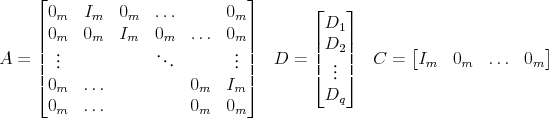
$\begin{align*} A &= \begin{bmatrix} 0_m & I_m & 0_m & \ldots & & 0_m \ 0_m & 0_m & I_m & 0_m & \ldots & 0_m \ \vdots & & & \ddots & & \vdots \ 0_m & \ldots & & & 0_m & I_m \ 0_m & \ldots & & & 0_m & 0_m \ \end{bmatrix}& D &= \begin{bmatrix} D_1 D_2 \vdots D_q \ \end{bmatrix} & C &= \begin{bmatrix} I_m & 0_m & \ldots & 0_m \end{bmatrix}\end{align*}$
where and are the $m\times m$ identity matrix, respectively the $n\times n$ zero matrix.

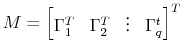
What is needed is a mapping from the autocovariances of , $\Gamma_k$ , to the state space objects. The objects of interest are the matrix containing the stacked MA coefficients as well as the variance $\Omega=E e_te_t^T$ of the innovations process. To obtain this mapping, it is useful to stack the autocovariances into a matrix $M = \begin{bmatrix}\Gamma_1^T & \Gamma_2^T & \vdots & \Gamma_q^t \end{bmatrix}^T$

Li (2005), Theorem 2 shows that the variance-covariance matrix of the states $\Psi \equiv E s_t s_t^T$ solves the Riccati equation $\Psi = A\Psi A^T + (M-A\Psi C^T) (\Gamma_0 - C\Psi C^T)^{-1}(M-A\Psi C^T)^T$ and that the MA() coefficients can be recovered as $D = (M-A\Psi C^T) (\Gamma_0 - C\Psi C^T)^{-1}$ and $\Omega = \Gamma_0 - C \Psi C^T$ . As shown by Li (2005), the above Riccati equation can be solved recursively, starting from $\Psi^{(0)} = 0$ and iterating over $\Psi^{(n+1)} = A\Psi^{(n)} A^T + (M-A\Psi^{(n)} C^T) (\Gamma_0 - C\Psi^{(n)} C^T)^{-1}(M-A\Psi^{(n)} C^T)^T$ since $\Psi=\lim_{n\to\infty}\Psi^{(n)}$ and $\Psi^{(n+1)}\geq\Psi^{(n)}$ .

At the end of each factorization computed for this paper, it has been verified that the factorization produces an invertible MA() polynomial, which matches the original spectral density. In all simulations, this held up to machine accuracy.

2 VARs Implied by Lab Economy

This section outlines how to derive the following: First, values from the lab economy for true VAR objects like , , , and the autocovariances of . Second, population coefficients of finite-order VARs implied by the lab economy.³⁴

The linearized solution to the lab economy described in Section 2 yields a state space model for labor productivity growth and hours

$\begin{align} X_t &= \begin{bmatrix}\Delta \log{(y_t/ l_t)} \log l_t \end{bmatrix} = \mathcal{C} Z_t & \text{with}\quad Z_t &= \mathcal{A} Z_{t-1} + \mathcal{B} \varepsilon_{t} \end{align}$
State vector and shock vector are:
$\begin{align} Z_t &= \begin{bmatrix} \hat k_t & \varepsilon_t^z & \tau_{l,t}^z & \hat k_{t-1} & \varepsilon_{t-1}^z & \tau_{l,t-1}^z \end{bmatrix}^{T} & \varepsilon_t &= \begin{bmatrix}\varepsilon_t^z & \varepsilon_t^l \end{bmatrix}^{T} \end{align}$
where $\hat k_t$ is the log-deviation of detrended capital from its steady state, $\tau_{l,t}$ and $\varepsilon_t^z$ are the labor wedge and the growth rate in technology. ( includes also lagged variables due to the presence of labor productivity growth in .)

The computation of the matrices $\mathcal{A}$ , $\mathcal{B}$ and $\mathcal{C}$ is straightforward, please see CKM for a detailed presentation.

True VAR objects The decomposition in section 4 uses the following objects of the true process: , , as well as the autocovariances of . Their computation from the state space is straightforward since true impulse responses and spectrum are given by $A(L)= \mathcal{C} \left(I-\mathcal{A}L\right)^{-1}\mathcal{B}$ and $S_X(\omega) = A(e^{-i\omega}) A(e^{-i\omega})^T$ . The impact coefficients $A_0 = \mathcal{C} \mathcal{B}$ are apparent from (21). Recalling equation (2), this also pins down the covariance matrix of the forecast errors $\Omega=\mathcal{C} \mathcal{B} \mathcal{B} \mathcal{C}^T$ .

In order to map forecast errors into structural shocks, must obviously be square and invertible. Furthermore, Fernandez-Villaverde, Rubio-Ramirez, and Sargent (2005) show that invertibility requires the eigenvalues of $\mathcal{A-B}(\mathcal{CB})^{-1}\mathcal{CA}$ to be strictly less than one in modulus, which is satisfied for all calibrations considered here.

The non-structural moving average representation of is $X_t = A(L)A_0^{-1} e_t = C(L)e_t$ . From (3), the coefficients of the non-structural VAR( $\infty$ ) representation of the model can be obtained by inverting this moving average, yielding $B(L)L=I-C(L)^{-1}$ .

The autocovariances $EX_tX_{t-k}^T$ can be directly computed from the state space model. The covariance matrix of the states $E Z_tZ_{t}^T\equiv \Omega$ is obtained as the solution to a discrete Lyapunov equation: $\Omega = \mathcal{A} \Omega \; \mathcal{A}^T + \mathcal{B}\mathcal{B}^T$ and the autocovariances of are $E X_tX_{t-k}^T = \mathcal{C} \mathcal{A}^k \Omega\; \mathcal{C}^T$ .

VAR() coefficients in population Finite-order VAR() can be computed as projections of on a finite number of its past values, $X_{t-1} \ldots X_{t-p}$ . In line with the notation of the main text, population coefficients of a VAR() are denoted with a superscript "".
$\begin{align*} X_t = \ensuremath{B(L)^\text{OLS}\xspace}X_{t-1} + \ensuremath{v_t^\text{OLS}\xspace} \end{align*}$
The coefficients of the lag polynomial $\ensuremath{B(L)^\text{OLS}\xspace}=\sum_{i=0}^{p-1}\ensuremath{B_i^\text{OLS}\xspace}L^i$ solve the OLS normal equations
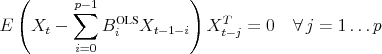
$\begin{align*} E \left( X_t - \sum_{i=0}^{p-1}\ensuremath{B_i^\text{OLS}\xspace}X_{t-1-i} \right) X_{t-j}^T &=0 \quad\forall j=1\ldots p \end{align*}$
which are evaluated using the autocovariance matrices of whose computations are described in the preceding paragraph. For instance if , $\ensuremath{B_1^\text{OLS}\xspace}=\left(E X_tX_{t-1}^T\right) \left(E X_tX_{t}^T \right)^{-1}$ . Detailed formulas for higher VARs can be found in Fernandez-Villaverde, Rubio-Ramirez, and Sargent (2005).

Chari, Kehoe, and McGrattan (2005), Proposition 1 show that the VAR representation of in the model is of infinite order and residuals from a VAR() will not be martingales. By construction, the projection residuals $\ensuremath{v_t^\text{OLS}\xspace}$ are orthogonal to $X_{t-1}$ , ..., $X_{t-p}$ , but they are not orthogonal to the complete history of . The moving average representation of the forecast errors $\ensuremath{v_t^\text{OLS}\xspace}=D(L)e_t$ is easily constructed from $D(L) = \left(I-\ensuremath{B(L)^\text{OLS}\xspace}L\right)\left(I-B(L)L\right)^{-1}$ .

Variance equation Even though the VAR() residuals $\ensuremath{v_t^\text{OLS}\xspace}$ are not , the usual variance equation is still applicable. For notational convenience, take the case of a VAR(1), $X_t = \ensuremath{B_1^\text{OLS}\xspace} X_{t-1} + \ensuremath{v_t^\text{OLS}\xspace}$ . The normal equations imply
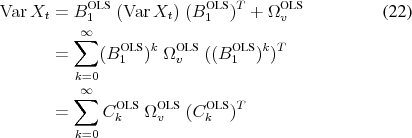
$\begin{align} \var{X_t} &= \ensuremath{B_1^\text{OLS}\xspace} \; (\var{X_t}) \; (\ensuremath{B_1^\text{OLS}\xspace})^T + \ensuremath{\Omega_v^\text{OLS}\xspace} \ &= \sum_{k=0}^\infty (\ensuremath{B_1^\text{OLS}\xspace})^k \; \ensuremath{\Omega_v^\text{OLS}\xspace} \; ((\ensuremath{B_1^\text{OLS}\xspace})^k)^T \notag \ &= \sum_{k=0}^\infty \ensuremath{C_k^\text{OLS}\xspace} \; \ensuremath{\Omega_v^\text{OLS}\xspace} \; (\ensuremath{C_k^\text{OLS}\xspace})^T \notag \end{align}$
The second line is obtained by recursive substitution of $\var{X_t}$ and the third line follows from the construction of moving-average coefficients of a VAR(1), $\ensuremath{C_k^\text{OLS}\xspace}=(\ensuremath{B_1^\text{OLS}\xspace})^k$ . The argument is easily extended to VARs with higher lag orders by using their companion form.

3 Bandpass-Filtered Variance Share from SVARs

This appendix describes how to compute the share of bandpass-filtered fluctuations attributed to technology shocks from a set of SVAR parameters, $\hat{B}(L)$ and $\hat{A_0}$ . The bandpass filter employed here considers only cycles with a duration between two-and-a-half and eight years. Denoting the bandpass-filtered level of (log) output $\tilde y_t$ , its variance can be easily computed from the transfer function

$\begin{displaymath}T_y(\omega) = \begin{bmatrix}(1-e^{-i\omega})^{-1} & 1 \end{bmatrix} \left(I-\hat{B}(e^{-i\omega})e^{-i\omega}\right)^{-1}\hat{A_0}\end{displaymath}$

Depending on the identification scheme, $\hat{A_0}$ corresponds to (true value) or $\ensuremath{A_0^\text{OLS}\xspace}$ , $\ensuremath{A_0^\text{CEV-AM}}$ , $\ensuremath{A_0^\text{CEV-NW}}$ , $\ensuremath{A_0^\text{SF-AM}\xspace}$ or $\ensuremath{A_0^\text{SF-NW}\xspace}$ and $\hat{B}(L)$ corresponds to the true (infinite order) polynomial or its finite-order counterpart $\ensuremath{B(L)^\text{OLS}\xspace}$ . When using the spectral factorization of $\ensuremath{S_X(\omega)^\text{NW}\xspace}$ , the inverse of $I-\hat{B}(e^{-i\omega})e^{-i\omega}$ is replaced by $\ensuremath{C^\text{SF-NW}\xspace}(e^{-i\omega})$ .

Using $\underline{\omega} = \frac{2 \pi}{8 \cdot 12}$ and $\overline{\omega}= \frac{2 \pi}{2.5 \cdot 12}$ the bandpass-filtered variance is

$\begin{displaymath}\var{\tilde y_t} = \int_{\underline{\omega}}^{\overline{\omega}} T_y(\omega) T_y(\omega)^T d\omega \end{displaymath}$

and the share of fluctuations attributed to technology shocks is the ratio $(\var{\tilde y_t\vert\varepsilon^z_t}) / (\var{\tilde y_t})$ , where $\var{\tilde y_t\vert\varepsilon^z_t}$ conditions only on fluctuations attributed to technology shocks.

$\begin{displaymath}\var{\tilde y_t\vert\varepsilon^z_t} = \int_{\underline{\omega}}^{\overline{\omega}} T_y(\omega) \begin{bmatrix}1 & 0 0 & 0 \end{bmatrix} T_y(\omega)^T d\omega \end{displaymath}$

Similar computations yield the variance shares for hours, when using the transfer function $T_l(\omega) = \begin{bmatrix}0 & 1 \end{bmatrix} \left(I-\hat{B}(e^{-i\omega})e^{-i\omega}\right)^{-1}\hat{A_0}$ .

Bibliography

Acemoglu, Daron, Kenneth Rogoff, and Michael Woodford, eds. 2006.

NBER Macroeconomics Annual 2006. Cambridge, MA: MIT Press.

Altig, David, Lawrence J. Christiano, Martin Eichenbaum, and Jesper Linde. 2004, December.

Firm-Specific Capital, Nominal Rigidities and the Business Cycle.
Northwestern University, mimeo.

Andrews, Donald W K. 1991.

Heteroskedasticity and Autocorrelation Consistent Covariance Matrix Estimation.
Econometrica 59 (3): 817-58 (May).

Andrews, Donald W K, and J Christopher Monahan. 1992.

An Improved Heteroskedasticity and Autocorrelation Consistent Covariance Matrix Estimator.
Econometrica 60 (4): 953-66 (July).

Blanchard, Olivier Jean, and Danny Quah. 1989.

The Dynamic Effects of Aggregate Demand and Supply Disturbances.
The American Economic Review 79 (4): 655-673 (September).

Burns, Arthur F., and Wesley C. Mitchell. 1946.

Measuring Business Cycles.
NBER.

Canova, Fabio, and Gianni de Nicolo. 2003.

On the sources of business cycles in the G-7.
Journal of International Economics 59 (1): 77-100 (January).

Chari, V. V., Patrick J. Kehoe, and Ellen R. McGrattan. 2005, July.

A critique of structural VARs using business cycle theory.
Staff Report 364, Federal Reserve Bank of Minneapolis.

Chari, V. V., Patrick J. Kehoe, and Ellen R. McGrattan. 2007.

Business Cycle Accounting.
Econometrica 75 (3): 781-836 (May).

Chari, V.V., Patrick J. Kehoe, and Ellen R. McGrattan. 2008.

Are structural VARs with long-run restrictions useful in developing business cycle theory?
Journal of Monetary Economics 55 (8): 1337-1352 (November).

Christiano, Lawrence J., Martin Eichenbaum, and Robert Vigfusson. 2003, July.

What Happens After a Technology Shock?
Working Paper 9819, NBER.

Christiano, Lawrence J., Martin Eichenbaum, and Robert Vigfusson. 2004.

The Response of Hours to a Technology Shock: Evidence based on a Direct Measure of Technology.
Journal of the European Economic Association 2 (2-3): 381-395 (April-May).

Christiano, Lawrence J., Martin Eichenbaum, and Robert Vigfusson. 2006a.

Alternative Procedures for Estimating Vector Autoregressions identified with Long-Run Restrictions.
Journal of the European Economic Association 2 (2-3): 475-483 (April-May).

Christiano, Lawrence J., Martin Eichenbaum, and Robert Vigfusson. 2006b.

Assessing Structural VARs.
Chapter 1 of NBER Macroeconomics Annual 2006.
MIT Press.

Cogley, Timothy, and James M Nason. 1995.

Output Dynamics in Real-Business-Cycle Models.
The American Economic Review 85 (3): 492-511.

Cooley, Thomas F., and Mark Dywer. 1998.

Business cycle analysis without much theory A look at structural VARs.
Journal of Econometrics 83 (1-2): 57-88 (March-April).

Dupaigne, Martial, and Patrick Feve. 2009.

Technology shocks around the world.
Review of Economic Dynamics, forthcoming.

Dupaigne, Martial, Patrick Feve, and Julien Matheron. 2007.

Avoiding pitfalls in using structural VARs to estimate economic models.
Review of Economic Dynamics 10 (2): 238-255 (April).

Erceg, Christopher J., Luca Guerrieri, and Christopher Gust. 2005.

Can Long-Run Restrictions Identify Technology Shocks?
Journal of the European Economic Association 3 (6): 1237-1278 (December).

Faust, Jon. 1998.

The robustness of identified VAR conclusions about money.
Carnegie-Rochester Conference Series on Public Policy 49 (December): 207-244.

Fernandez-Villaverde, Jesus, Juan Rubio-Ramirez, and Thomas J. Sargent. 2005, June.

A, B, C's (and D)'s for Understanding VARs.
Technical Working Paper 0308, NBER.

Fernàndez-Villaverde, Jesús, Juan F. Rubio-Ramirez, Thomas J. Sargent, and Mark W. Watson. 2007.

ABCs (and Ds) of Understanding VARs.
American Economic Review 97 (3): 1021-1026 (June).

Gali, Jordi. 1999.

Technology, Employment, and the Business Cycle: Do Technology Shocks explain Aggregate Fluctuations?
The American Economic Review 89 (1): 249-271.

Gali, Jordi, and Pau Rabanal. 2004, July.

Technology Shocks and Aggregate Fluctuations: How well does the RBC Model fit postwar U.S. data?
NBER Working Paper 10636.

Giannone, Domenico, and Lucrezia Reichlin. 2006.

Does information help recovering structural shocks from past observations?
Journal of the European Economic Association 4 (2-3): 455-465 (April-May).

Hamilton, James D. 1994.

Time-Series Analysis.
Princeton, NJ: Princeton University Press.

Hannan, E. J. 1970, June.

Multiple Time Series.
Wiley Series in Probability and Mathematical Statistics.
John Wiley & Sons.

Hansen, Lars P., and Thomas J. Sargent. 2005, September.

Recursive Models of Dynamic Linear Economies.
unpublished Manuscript.

Hansen, Lars P., and Thomas J. Sargent. 2007.

Robustness.
Princeton University Press.

Hurwicz, Leonid. 1950.

Least-Squares Bias in Time Series.
Chapter XV of Statistical Inference in Dynamic Economic Models, 365-383.
John Wiley & Sons, Inc.

Kehoe, Patrick J. 2006.

How to advance theory with structural VARs: use the Sims-Cogley-Nason approach.
Staff Report 379, Federal Reserve Bank of Minneapolis.

Li, Lei M. 2005.

Factorization of moving-average spectral densities by state-space representations and stacking.
Journal of Multivariate Analysis 96 (2): 425-438 (October).

Magnus, Jan R., and Heinz Neudecker. 1988.

Matrix Differential Calculus with Applications in Statistics and Econometrics.
Wiley Series in Probability and Statistics.
John Wiley & Sons.

Marcet, Albert. 2005.

Overdifferencing VAR's is OK.
mimeo.

McGrattan, Ellen. 2005, May.

Appendix: A Critique of Structural VARs Using Real Business Cycle Theory.
Federal Reserve Bank of Minneapolis, mimeo.

Newey, Whitney K, and Kenneth D West. 1994.

Automatic Lag Selection in Covariance Matrix Estimation.
Review of Economic Studies 61 (4): 631-53.

Newey, W.K., and K.D. West. 1987.

A simple positive semi-definite heteroskedasticity and autocorrelation consistent covariance matrix.
Econometrica 55:703-708.

Phillips, Peter C. B., Yixiao Sun, and Sainan Jin. 2006.

Spectral Density Estimation And Robust Hypothesis Testing Using Steep Origin Kernels Without Truncation.
International Economic Review 47 (3): 837-894 (August).

Priestley, M.B. 1981.

Spectral Analysis and Time Series.
Probability and Mathematical Statistics.
Amsterdam: Elsevier Academic Press.

Ravenna, Federico. 2007.

Vector autoregressions and reduced form representations of DSGE models.
Journal of Monetary Economics 54 (7): 2048-2064 (October).

Sayed, A.H., and T. Kailath. 2001.

A Survey of Spectral Factorization Methods.
Numerical Linear Algebra with Applications 8:467-496.

Sims, Christopher A. 1972.

The Role of Approximate Prior Restrictions in Distributed Lag Estimation.
Journal of the American Statistical Association 67 (337): 169-175 (March).

Sun, Yixiao, Peter C. B. Phillips, and Sainan Jin. 2008.

Optimal Bandwidth Selection in Heteroskedasticity-Autocorrelation Robust Testing.
Econometrica 76 (1): 175-194 (January).

Uhlig, Harald. 2005.

What are the effects of monetary policy on output? Results from an agnostic identification procedure.
Journal of Monetary Economics 52 (2): 381-419 (March).

Watson, Mark W. 2006.

Comment on Christiano, Eichenbaum, and Vigfusson's "Assessing Structural VARs".
Chapter 1 of NBER Macroeconomics Annual 2006.
MIT Press.

Whittle, P. 1963.

On the Fitting of Multivariate Autoregressions, and the Approximate Canonical Factorization of a Spectral Density Matrix.
Biometrika 50 (1/2): 129-134 (June).

Whittle, Peter. 1996.

Optimal Control, Basics and Beyond.
Wiley-Interscience Series in Systems and Optimization.
Chichester: John Wiley & Sons.

List of Figures

1. Percentage Errors in Variance of Output Growth Computed from CEV Procedure
2. D (1) ≠ I
3. Impact Response of Hours to Technology Shock
4. Technology Shares in Fluctuations of Output and Hours
A.1. Technology Shares in Fluctuations of Output and Hours (Newey-West)
A.2. Simulations with Automatic Bandwidth Selection (Newey-West)
A.3. Simulations with Automatic Bandwidth Selection (Andrews-Monahan)

ADDITIONAL RESULTS

**Figure A.1:** Technology Shares in Fluctuations of Output and Hours (Newey-West)
Note: Percentage points relative the model's true technology share. Top row reports bias and RMSE for variance decomposition of output, bottom row for hours. Newey-West estimators of the spectral density used for CEV and SF with a fixed bandwidth of . "Technology share" on the x-axis is the percentage of output variability due to technology shocks at business cycle frequencies (cycles with durations between two-and-a-half and eight years) in the data generating process.

Figure A1 Data

**Figure A.2:** Simulations with Automatic Bandwidth Selection (Newey-West)
Note: Estimated impact responses of hours to technology (top row) and technology share (bottom row) when using the Newey-West estimator with automatic bandwidth selection (Newey and West, 1994). "Technology share" on the x-axis is the percentage of output variability due to technology shocks at business cycle frequencies (cycles with durations between two-and-a-half and eight years) in the data generating process.

Figure A2 Data

**Figure A.3:** Simulations with Automatic Bandwidth Selection (Andrews-Monahan)
Note: Estimated impact responses of hours to technology (top row) and technology share (bottom row) when using the Andrews-Monahan estimator with automatic bandwidth selection (Newey and West, 1994). "Technology share" on the x-axis is the percentage of output variability due to technology shocks at business cycle frequencies (cycles with durations between two-and-a-half and eight years) in the data generating process.

Figure A3 Data

Footnotes

* For correspondence: Elmar Mertens, Board of Governors of the Federal Reserve System,Washington D.C. 20551. email [email protected]. Tel.: +(202) 452 2916. The views in this paper do not necessarily represent the views of the Federal Reserve Board, or any other person in the Federal Reserve System or the Federal Open Market Committee. Any errors or omissions should be regarded as those solely of the author Return to Text

1. The drift in technology is set to 0.4% and the average "labor tax" is set to 24.2% per quarter. Return to Text

2. CKM extensively document how different ratios in the variance of transitory to permanent shocks, $\sigma_l^2 / \sigma_z^2$ , affect the performance of standard VARs both in population and in small sample. McGrattan (2005) shows that in the limit, $\sigma_l / \sigma_z \to 0$ , a finite order VAR (even a

) in productivity growth and hours recovers the true responses--though the true system does not have a finite-order VAR representation. In this special case the model reduces to a standard, one-shock RBC model. Return to Text

3. To be precise, CEV estimate $\sigma_l =0.0056^2$ , $\sigma_z=0.00953$ corresponding to a technology share of 67.5%. Return to Text

4. In addition to this "LSVAR" specification, CKM run also VARs with quasi-differenced hours. This replaces the second VAR element

with $(1-\alpha L) \; l_t$ ( $\alpha \in \{0;0.999\}$ ). Depending on $\alpha$ , this captures popular (but also contested) specifications: On the one hand the "LSVAR" with hours in levels and $\alpha=0$ and on the other hand the "QDSVAR" with $\alpha=0.999$ , which approximates a VAR with differenced hours without introducing a unit MA root. The quasi-differencing is discussed in more detail by CKM as well as Marcet (2005), Gali and Rabanal (2004) and Christiano, Eichenbaum, and Vigfusson (2003). Return to Text

5. Results are insensitive to using other information criteria, such as the Akaike criterion (AIC). In general, AIC is known for picking higher values of

compared to SIC. For this lab economy, AIC has been found to pick lag lengths of up to

with an average of

. Return to Text

6. For notational convenience, but without loss of generality,

represents the demeaned variables, which is equivalent to including a constant in a VAR using the original data. Return to Text

7. Fernandez-Villaverde, Rubio-Ramirez, and Sargent (2005) give examples of interesting models where the conditions are satisfied and where not. For all calibrations considered, the model of Section 2 satisfies the condition of Fernàndez-Villaverde et al. (2007). Return to Text

8. See for example Giannone and Reichlin 2006 on the non-invertibility problem. Return to Text

9. Throughout this paper, transposes are complex conjugate. Return to Text

10. The spectral density $S_X(0)=C(1)\Omega C(1)^T$ is strictly positive definite when the variance covariance matrix of the forecast errors, $\Omega$ , is nonsingular.

inherits positive definiteness from $\Omega$ since

is nonsingular. $I-B(1)=C(1)^{-1}$ exists because of the assumed stationarity of the VAR process. Return to Text

11. Under the restrictions stated in (4),

can generally be described as

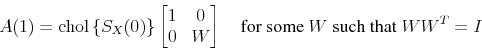
$\begin{displaymath}A(1) = \chol{\{S_X(0)\}} \begin{bmatrix}1 & 0 0 & W \end{bmatrix} \quad \text{for some } W\;\text{such that}\;WW^T=I \end{displaymath}$

In the lab economy described later, the VAR will be bivariate and the forecast errors

are a linear combination of only two shocks. Knowing the technology shock will then also identify the second shock up to its sign, $\vert W\vert=1$ . Return to Text

12. This can be derived by applying the definition of spectral density to $\ensuremath{v_t^\text{OLS}\xspace}=v_t+[B(L)-\ensuremath{B(L)^\text{OLS}\xspace}]X_{t-1}$ and computing the variance $\ensuremath{\Omega_v^\text{OLS}\xspace}$ as the integral over the spectral density. Return to Text

13. As elsewhere in this section, estimators have been written in terms of population moments, $E \left[{\ensuremath{v_t^\text{OLS}\xspace}(\ensuremath{v_{t-k}^\text{OLS}\xspace})^T}\right]$ . In empirical applications, the population moments are replaced by sample moments. For some variable

, the sample moment is $\ensuremath{E_T {Z} \xspace}_t\equiv 1/T \sum_{t=1}^T Z_t$ . Return to Text

14. Alternative weighting schemes are for example discussed by Priestley (1981) and Philips, Sun, and Jin (2006). Return to Text

15. The discussion of CEV suggests that this choice is supposed to be compatible with consistency--essentially promising that this bandwidth choice would barely grow as longer data samples become available. Watson (2006) regards it as a practically untruncated and inconsistent estimator. Return to Text

16. To be specific, $\ensuremath{A_0^\text{CEV-AM}}$ and $\ensuremath{A_0^\text{CEV-NW}}$ are functions of a spectral estimate and OLS estimates of the VAR. Analogously to arguments employed by Sun, Phillips, and Jin 2008 in the context of constructing confidence intervals, the MSEs of $\ensuremath{A_0^\text{CEV-AM}}$ and $\ensuremath{A_0^\text{CEV-NW}}$ could be approximated to a second order--holding the OLS estimates fixed--by a linear combination of bias and variance of the spectral estimate whose weights depend on the true values of the VAR. Furthermore, the MSEs of $\ensuremath{A_0^\text{CEV-AM}}$ and $\ensuremath{A_0^\text{CEV-NW}}$ will also depend on the covariance between $\ensuremath{S_X(0)^\text{AM}\xspace}$ , respectively $\ensuremath{S_X(0)^\text{NW}\xspace}$ , and the OLS estimates. Return to Text

17. $\ensuremath{S_X(\omega)^\text{NW}\xspace}$ generalizes (12) to the case of non-zero frequencies with $\Gamma_k \equiv E\left[ X_t X_{t-k}^T\right]$ :

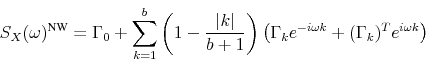
$\begin{displaymath}\ensuremath{S_X(\omega)^\text{NW}\xspace} = \Gamma_0 + \sum_{k=1}^b \left(1 - \frac{\vert k\vert}{b + 1} \right) \left( \Gamma_k e^{-i\omega k} + (\Gamma_k)^T e^{i\omega k} \right)\end{displaymath}$

and the implied spectrum of VAR residuals is $(I-\ensuremath{B(e^{-i\omega})^\text{OLS}\xspace}e^{-i\omega})) \ensuremath{S_X(\omega)^\text{NW}\xspace} (I-\ensuremath{B(e^{-i\omega})^\text{OLS}\xspace}e^{-i\omega}))^T$ Return to Text

18. In the simulations reported below, lag length is chosen separately for each sample based on the generally conservative Schwartz Information Criterion, typically choosing a lag length of one in the application presented here. Return to Text

19. This follows from comparing (15) and (16) with (9) and (10). Return to Text

20. The impulse-responses $\ensuremath{A(L)^\text{CEV-AM}}\xspace = \ensuremath{C(L)^\text{OLS}\xspace}\ensuremath{A_0^\text{CEV-AM}}\xspace$ imply the following variance measure

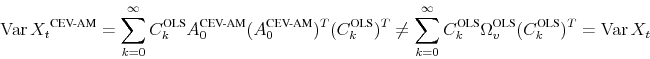
$\begin{displaymath}\ensuremath{\var{X_t}^\text{CEV-AM}}\xspace =\sum_{k=0}^\infty \ensuremath{C_k^\text{OLS}\xspace} \ensuremath{A_0^\text{CEV-AM}}\xspace (\ensuremath{A_0^\text{CEV-AM}}\xspace )^T (\ensuremath{C_k^\text{OLS}\xspace})^T \neq \sum_{k=0}^\infty \ensuremath{C_k^\text{OLS}\xspace} \ensuremath{\Omega_v^\text{OLS}\xspace} (\ensuremath{C_k^\text{OLS}\xspace})^T = \var{X_t} \end{displaymath}$

The last step holds because of the normal equations (8) regardless of whether $\ensuremath{v_t^\text{OLS}\xspace}$ is

or not. Return to Text

21. See for example Faust (1998), Canova and de Nicolo (2003) or Uhlig (2005). Return to Text

22. Recall from (4) that $\bar{a}_{11}$ is the top element of

. Return to Text

23. Both CEV and OLS use $\ensuremath{B(1)^\text{OLS}\xspace}$ in computing $\ensuremath{A_0^{-1}\xspace}=\ensuremath{A(1)^{-1}\xspace}\ensuremath{\left(I-B(1)\right)^{-1}\xspace}$ and except for the top left element, the first row of $\ensuremath{A(1)^{-1}\xspace}$ is full of zeros. Applying a standard result for inverting partitioned matrices (Magnus and Neudecker (1988), p. 11), the long run restriction (4) places the same zero restrictions on $\ensuremath{A(1)^{-1}\xspace}$ as it does on

. This applies equally to $\ensuremath{A(1)^\text{CEV-AM}}$ , $\ensuremath{A(1)^\text{CEV-NW}}$ and $\ensuremath{A(1)^\text{OLS}\xspace}$ . Finally, the top left element of $\ensuremath{A(1)^{-1}\xspace}$ equals $1/\bar{a}_{11}$ . Return to Text

24. As discussed in Section 2, the calibrations employed here are identical to the setting of CEV--except for considering a wider range of the technology share in output fluctuations. As discussed above as well, the CKM experiments differ slightly in their choice of $\psi$ and $\rho_l$ . Return to Text

25. This bias is particularly acute the smaller the sample and the higher the persistence of the data. It is pertinent in this example, since calibrating the model to match salient features of U.S. data requires a high degree of persistence in the non-technology shock, $\rho_l$ . Return to Text

26. In the case of the spectral estimators, this means evaluating (12) and (13) at true population moments, instead of sample autocovariances, while keeping the Bartlett weights and the truncation at the chosen bandwidth (here:

, respectively

when comparing against simulations using the bandwidth selection procedure of Newey and West (1994). The computation of VARs from population moments is equally straightforward, and details are described in Appendix B. Return to Text

27. The variance computations are explained in Appendix C. Return to Text

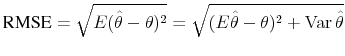28. Denoting the estimated parameter as $\theta$ and its estimate as $\hat\theta$ , relative bias is computed as $E(\hat\theta-\theta)/\theta\cdot 100\%$ . The RMSE is defined as $\text{RMSE}=\sqrt{E(\hat\theta-\theta)^2}=\sqrt{(E\hat\theta-\theta)^2 + \var{\hat\theta}}$ and it is converted into a percentage error using $\text{RMSE} /\theta\cdot 100\%$ . In both cases, expectations are computed from the arithmetic average over 1,000simulations. Return to Text

29. For a reference in the context of economics see Hansen and Sargent (2007; 2005). Return to Text

30. Suppose that $S(0)\neq 0$ . Since $\Omega$ is positive definite, it follows that $D(1) \neq 0$ . All roots of

are thus outside the unit circle and

is an invertible MA(

). Return to Text

31. The $\Gamma_k$ from Theorem 3.4 are a smoothed version of the sample autocovariance since they are the coefficients of an inverse Fourier transform of the Newey-West estimate of the spectral density. Return to Text

32. Given a covariance $\gamma_0$ and first-order autocovariance $\gamma_1$ , the spectrum equals $s(\omega)=\gamma_0 \cdot (1+2\gamma_1\cos{(\omega)})$ . And $\vert s(\omega)\vert\neq0$ requires $\vert\gamma_1/\gamma_0\vert<0.5$ . Return to Text

33. The paper of Li also shows how to reduce the number of iterations by stacking the MA(

) into first order form, however this comes at the cost of inverting larger matrices in the Riccati iterations which proved to be numerically less stable in the simulations computed for this paper. Return to Text

34. For this specific two-shock economy, details can also be found in McGrattan (2005). For general state space models details can be found in Fernandez-Villaverde, Rubio-Ramirez, and Sargent (2005). To simplify the VAR notation,

has been demeaned prior to the analysis. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text