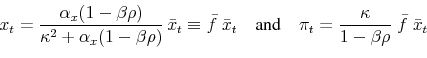Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2010-11 Screen Reader version ^♣

Managing Beliefs about
Monetary Policy under Discretion

Elmar Mertens

August 2009

Keywords: Optimal monetary policy, discretion, time-consistent policy, Markov-perfect equilibrium, incomplete information, Kalman filter

Abstract:

In models of monetary policy, discretionary policymaking often lacks the ability to manage public beliefs, which explains the theoretical appeal of policy rules and commitment strategies. But as shown in this paper, when a policymaker possesses private information, belief management becomes an integral part of optimal discretion policies and improves their performance.

Solving for optimal policy in a simple New Keynesian model, this paper shows how discretionary losses are reduced when the policymaker has private information. Furthermore, disinflations are pursued more vigorously, when the hidden information problem is larger, even when inflation is partly backward-looking.

JEL Classification: E31, E37, E47, E52, E58

1 Introduction

Starting with Kydland and Prescott (1977) and Barro and Gordon (1983b), the theoretical literature on rules versus discretion has documented clear benefits from commitment in monetary policy. Many economic decisions in the private sector are forward-looking and depend on policy expectations. In such an environment, policy rules and commitment strategies benefit from their ability to manage public beliefs about future policies. However, most of the rules-versus-discretion literature is based on models of perfect information, symmetrically shared between the central bank and the public.

Monetary policy is often conducted under imperfect information of various sorts. On the one hand, policymakers may face uncertainty about the state of the business cycle, the nature of structural relationships in the economy or a lack of access to timely data. The problems arising from this perspective have for example been analyzed by Sargent (1999) or Svensson and Woodford (2004) to name but a few. On the other hand, policymakers may also be privy to confidential information, for example arising from staff efforts in gathering and analyzing economic data or supervisory activities. Extending the work of Cukierman and Meltzer (1986), Faust and Svensson (2001); Faust and Svensson (2002), this paper focuses on the design of optimal monetary policy, when the policymaker has private information.¹

This paper shows how belief management becomes an integral part of discretionary policies, when the central bank has private information. In this case, the public will make inferences about the hidden information based on observed policy actions such that current policies directly affect inflation expectations.² The trade-offs faced by a discretionary policymaker resemble then those known from commitment problems.

Investigating the design of optimal policy when the central bank has private information also contributes to the literature on optimal transparency. Morris and Shin (2002) caution against providing the public with too much information. But Woodford (2005) doubts whether their conclusions will be relevant in a forward-looking model, where the economy is mostly affected by expectations of future policies. The model analyzed here provides an intriguing counterexample to this conjecture, in that policy losses are lower under hidden information when comparing discretionary policies in a New Keynesian model. Since hidden information gives scope for belief management under discretion, the result occurs precisely for reasons stressed by Woodford (2005).

Attention is limited here to Markov-perfect policies. In the spirit of "bygones are bygones", Markov-perfect state variables equilibrium must be relevant for current payoffs. When the public is imperfectly informed, its prior beliefs matter for public payoffs and they become a distinct, endogenous state variable of the policy problem, which is influenced by policy actions. By managing this state of (public) beliefs, the policymaker indirectly responds to past policies, even when reputational mechanisms via history-dependent strategies, known from Barro and Gordon (1983b) or Chari and Kehoe (1990), are excluded from the analysis.

In Markov-perfect models, a current decision-maker can influence a future decision-maker only via endogenous state variables, such as capital or government debt. In the model presented here, belief management leads to Markov perfect outcomes that share similarities with those from models with commitment respectively reputational mechanisms. Previous research has already recognized how discretionary outcomes can be improved by adding endogenous state variables to the policy problem. Usually, this is done by modifying the central bank's loss function, for example by adding concerns for interest rate smoothing Woodford (2003b) or by replacing inflation stabilization with price level targeting Vestin (2006).

What is novel about the present paper, is how beliefs naturally emerge as such an endogenous state variable, without the need for modifying the central bank's loss function or other aspects of the economy. To the extent that hidden information problems are an essential feature of interactions between policymakers and the public, this suggests that the importance of discretionary biases in practice might be different, and likely smaller than what is suggested by full information models.³

The problem of "public learns about central bank" studied here is distinct from settings of "bank learns about economy" studied for example by Sargent (1999), Aoki (2003) or Svensson and Woodford (2004). In the latter settings, atomistic individuals take policy as given without regard for inference problems faced by the policymaker. Policy constraints like the Phillips Curve are largely preserved. In the linear quadratic case studied by Svensson and Woodford (2004), certainty equivalence holds and optimal policies are identical to the full information case when actual values are replaced by policymakers' expectations. A key complication for my paper is that the central bank is a strategic, not an atomistic player, who takes the public's inference problem into account when devising its policy. This changes the policy constraints in non-trivial ways.

The framework adopted here exclusively assigns the policymaker, and not the public, with superior information. This is an extreme assumptions. Reality is best described by dispersed information, endowing different bits and pieces of hidden knowledge to the private sector and policymakers. The policy constraints change in dramatic ways when agents are learning about the policymaker, because of his strategic position in the economy. Those strategic effects are the main concern of the paper.

The effects of hidden information on optimal policy are illustrated with a simple New Keynesian model -- a model not chosen for its realism, but in order to document the differences with the symmetric information benchmark most clearly within a widely studied setting. The paper solves for the optimal discretion policy in a New Keynesian model where the output target of the policymaker is not directly observed by the public. The public only observes policy actions, but cannot disentangle whether the underlying shock to the output target is persistent or transitory. The policymaker faces a direct feedback from higher inflation expectations when choosing more expansionary policies cautioning him to temporarily boost aggregate activity at the expense of higher inflation. Compared to a full information model, a key difference is how optimal policy contracts the economy in response to inflationary beliefs. Moreover it does so more vigorously, the larger the credibility problems from hidden information. This result has important implications for the conduct of optimal disinflations.

To the best of my knowledge, my paper provides the first analysis of disinflations with an explicitly optimizing monetary policymaker and unknown policy targets.⁴ The results confirm conjectures by Sargent (1982) and Bordo et al. (2007) about the necessity to disinflate more quickly, when credibility is at stake. Other economists, for example Gordon (1982), have rather argued for prolonged and modest disinflation paths when inflation is persistent. Strikingly, my result is shown to carry over also to a setting with a hybrid Phillips Curve, where inflation persistence is partly exogenous. Evidently, disinflation costs are higher in such a setting. However, by bringing down inflation expectations early on a more aggressive disinflation policy still minimizes these costs, since it avoids inflation to persist based on ill-founded beliefs.

The information structure used here is similar to the models of Faust and Svensson (2001); Faust and Svensson (2002) and Cukierman and Meltzer (1986) who cast their models within similar linear-quadratic settings, but without providing a general framework capable of handling various models with endogenous state variables. Faust and Svensson (2001) focus on the welfare effects of credibility with a Lucas-supply curve. Using a forward-looking Phillips Curve, their results can be confirmed and extended here: Policy losses are reduced when output targets are unobservable, such that there is an explicit role for public beliefs. This disciplines the pursuit of persistent output targets, even when time-consistency is imposed on policy.

So far, problems of this kind have mostly been analyzed in highly stylized and often static settings.⁵ But the models used for policy analysis are typically dynamic and of larger scale. The technical appendix to this paper presents a flexible, yet tractable way to analyze optimal policy under hidden information, which is applicable to the kind of DSGE models used in policy analysis. The procedure remains tractable and transparent by relying on a linear-quadratic representation of the policy problem driven by Gaussian shocks. A key complication for models with imperfect information is to track the distribution of public beliefs. In a linear, homoscedastic setting, that collapses to tracking the evolution of means via the Kalman filter.

The remainder of this paper is structured as follows. Section 2 introduces hidden information in a textbook version of the New Keynesian model and shows how hidden information changes the policy problem. An extension incorporating belief shocks is shown in Section 3. Implications for disinflation strategies are analyzed in Section 4. The related literature is discussed in Section 5. Section 6 concludes the paper. A technical appendix extends the methods used here to a general class of linear quadratic policy problems.

2 A Simple Model of Hidden Information

This section illustrates the issues arising from hidden information with a simple textbook version of the New Keynesian model. The model model is purely forward-looking and the signal extraction problem is univariate. The next section extends this model to a setting where a hybrid Phillips Curve interacts with shocks from a richer information structure.

2.1 New Keynesian Economy

The model is largely identical to the textbook model of optimal policy in a New Keynesian model known from Clarida, Gali, and Gertler (1999), Walsh (2003) or Woodford (2003a). The only difference is a stochastic preference shock to the policymaker's objective function, which is unobservable to the public. Otherwise my model and its notation follow closely Gali (2003) where further details can be found. A key feature of the model is that inflation is determined purely by public expectations of current and future policies. This puts centerstage the concerns of the public about the policymaker's intentions.

Private Sector As in the textbook model, aggregate decisions of the private sector are represented by the New Keynesian Phillips and IS curves. In this simple model, IS curve and the short term interest rate are even redundant and the output gap can be used as policy control.

The private sector is populated by a continuum of identical firms and households, which trade goods and labor services. There is no capital accumulation and output equals consumption. Firms are monopolistically competitive and use staggered price-setting as in Calvo (1983). Optimal pricing decisions lead to the New Keynesian Phillips Curve as in Yun (1996) and King and Wolman (1996). The log-linearized Phillips Curve is
$\begin{align} \pi_t &= \beta \pi_{t+1\vert t} + \kappa x_t \end{align}$
where $\pi_t$ is inflation and is the output gap⁶. The parameter $\beta$ is the representative agent's discount factor and $\kappa$ is a reduced form parameter influenced amongst others by the frequency of price-setting.⁷ For any variable $z_{t+1}$ , $z_{t+1\vert t}$ denotes its private sector forecast. The underlying information set will be explained later.

The output gap measures the difference between actual output and its natural rate. The latter would be the output of the economy if there were no nominal frictions.⁸ My discussion will exclusively focus on monetary shocks that leave the natural rate unaffected. Conditional on those shocks, variations in the output gap are thus identical to variations in output and consumption.

Policy Objectives The policymaker seeks to minimize a present value of expected losses
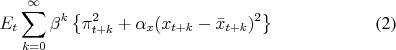
$\begin{align} E_t \sum_{k=0}^\infty \beta^k \left\{ \pi_{t+k}^2 + \alpha_x (x_{t+k}-\bar x_{t+k})^2 \right\} % \text{where}\quad L_t & = \pi_t^2 + \alpha_x (x_t-\bar x_t) \label{BURGUNDY:eq:loss201} \end{align}$
with $\alpha_x\geq 0$ . The expectations operator reflects the policymaker's information set, to be described later. The non-standard feature of the loss function is the time-varying target for the output gap, $\bar{x}_t$ , which will be specified as an exogenous stochastic process.

In principle, one could think of various ways to motivate the presence of $\bar{x}_t$ in the loss function⁹. However, the information structure used below will require that $\bar{x}_t$ is not observed by the private sector. To keep the model close to the NK benchmark, I maintain the assumption of a homogeneously informed private sector and follow Cukierman and Meltzer (1986) who interpret the output target as arising from time-varying preferences of the policymaker. Under this view, $\bar{x}_t$ represents the outcome of political influences on monetary policy to stimulate the economy. These preferences are assumed to vary exogenously with political representation in the government and the makeup of central banker's preferences.¹⁰ Such hidden pressures could arise even when the independence of the central bank is formally enshrined in law, since actual independence is a more fragile concept. For example Abrams (2006) gives a striking account of hidden but forceful policy influences. His study documents how U.S. President Nixon covertly pressured the then Chairman of the Federal Reserve, Arthur Burns to ease policy in the run-up to the Great Inflation.

Under either interpretation, the output target is capturing a form of heterogeneity otherwise not present in the model. In particular (2) does not necessarily represent a social welfare function. Faust and Svensson (2001) use a similar loss function for the policymaker. Their notion of representative welfare would then be to evaluate (2) at the average output target (here: zero)¹¹, $L^R_t=\pi^2_t + \alpha_x x^2_t$ . But without specifying the underlying heterogeneity and associated welfare weights this is at best an aggregation with unknown distributional consequences.

In reality, short-term interest rates are the typical instruments of monetary policy. But in this simple model, the short term interest rate can be perfectly substituted by the output gap as policy control. The IS curve is then redundant for determining equilibrium.

Discretionary Policy under Symmetric Information

Before turning to the informational structure of the model, it is helpful to study optimal policy when there is symmetric information. For the time being, let the output target follow a univariate AR(1) process $\begin{equation*} \bar{x}_{t+1} =\rho\; \bar x_t + e_{t+1} \quad\text{where}\quad e_{t+1} \sim N(0,\sigma_e^2) \quad\text{and}\quad \vert\rho\vert<1 \end{equation*}$ which is mutually observed by the policymaker and the public.¹² Under symmetric information, their expectations coincide such that $z_{t+1\vert t} = E_t z_{t+1}$ for any variable .

Lacking a commitment technology, the policymaker can always reoptimize his policies and for each optimization he takes his future choices as given. Sine there are only exogenous state variables, he takes the public's inflation expectations as given, too.¹³ Only Markov-perfect, discretionary equilibria are considered. This excludes for example trigger strategies to support commitment outcomes.

The solution to this problem is well known. The first order condition balances the inflation cost against the desire to attain the output target:
$\begin{align} \alpha_x (x_t - \bar{x}_t) + \kappa \pi_t &= 0 \end{align}$
(Section 2.3 below, will compare this optimality condition against its counterpart under hidden information.) Substitution of (3) into the Phillips Curve yields the following Markov-perfect policies:

$\begin{displaymath} x_t = \frac{\alpha_x (1 - \beta \rho)}{\kappa^2 + \alpha_x (1 - \beta \rho)} \bar x_t \equiv \bar{f} \; \bar x_t \quad\text{and}\quad \pi_t = \frac{\kappa}{1-\beta\rho} \;\bar{f}\;\bar x_t \end{displaymath}$

(1)

Inflation and output gap inherit the dynamic properties of the target process. A well known property of optimal policies in a linear quadratic framework is their certainty equivalence, which holds here, too, since $\bar{f}$ does not depend on the volatility $\sigma_e$ of the target shocks. Under hidden information, this will be different.

Sensibly, $\bar{f}$ is bounded between zero and one. In principle, the policymaker could always attain the output target by choosing $\bar{f}=1$ , but for $\alpha_x<\infty$ this has to be weighed against the inflation resulting from this policy. At the other extreme, there would be no inflation if $\bar{f}=0$ , but only at the cost of missing the target, which matters if $\alpha_x>0$ . Values outside the zero to one range would lead to further target deviations and be associated with unnecessary inflation. This will be useful to bear in mind when analyzing policies under hidden information.

Policies with $\bar{f}$ close to unity will be called "bold" and it is instructive to see how policy depends on the preference weight $\alpha_x$ and the persistence of the target process. Inspection of (4) reveals the intuitive property that policies get bolder the higher the preference weight on output, in fact $\bar{f}$ varies between zero and one when $\alpha_x$ is varied between zero and infinity.

Policies are less bold, when the target is persistent. Higher persistence of the target causes higher persistence in policy and thus higher inflation. This is a dynamic version of the inflation bias known from Kydland and Prescott (1977) and Barro and Gordon (1983a) and similar to the stabilization bias known from Svensson (1997).

Under hidden information there will be persistent and transitory shocks to the output target, neither of them being directly observable to the public. As in the full information case, what matters for the inflation response to a policy shock is its perceived persistence. The policymaker will then seek policies that are as bold as possible, while trying to keep perceived persistence as low as possible.

2.2 Hidden Information

Hidden information is introduced by assuming that the public can observe only policy, , but not shocks to the policy target. To make the public's signal extraction interesting, the target is henceforth driven by two components, one persistent, one transitory:
$\begin{align} \bar{x}_t &= \tau_t + \varepsilon_t && \varepsilon_t\sim N(0,\sigma_\varepsilon^2) \ \tau_{t+1} &= \rho\; \tau_t + \eta_{t+1} && \eta_t\sim N(0,\sigma_\eta^2) \quad\text{and}\quad 0<\vert\rho\vert<1 \end{align}$
The private sector has no structural uncertainty about the economy. All parameters are known, including the specification of the target process. The public must however infer the realizations of $\tau_t$ and $\varepsilon_t$ based on the observed history of policies, denoted .¹⁴

The policymaker observes the complete history of the target components and his expectations are typically different from those of the public. As before, for any variable , the policymaker's expectations are denoted $E_t z_{t+1} = E(z_{t+1} \vert \tau^t,\varepsilon^t)$ with the obvious property . Public expectations are $z_{t+1\vert t} = E(z_{t+1}\vert x^t)$ . By construction, $x_{t\vert t} = x_t$ and $\pi_{t\vert t} = \pi_t$ (since inflation is a choice variable of the private sector) but typically $\tau_{t\vert t} \neq \tau_t$ and $\varepsilon_{t\vert t} \neq \varepsilon_t$ .

Surprises in relative to the public's past information will be called "innovations". Formally, they are defined as
$\begin{align*} \tilde z_t &\equiv z_t - z_{t\vert t-1} \end{align*}$
Innovations provide an orthogonal decomposition of the public information set since $\tilde z_{t\vert t-1} =0$ . Even though they are unpredictable from the public's perspective, they may well be predictable based on the complete information set, and typically $E_{t-1}\tilde z_t$ will not be identical to zero.

Since the model is linear with Gaussian disturbances, rational expectations of the public can be computed recursively from the Kalman filter. Given prior beliefs $z_{t\vert t-1}$ and $x_{t\vert t-1}$ , the public observes a realization of policy and updates its beliefs according to
$\begin{align} z_{t\vert t} &= z_{t\vert t-1} + K_z \tilde x_t \quad \text{with Kalman gain}\quad K_z \equiv \frac{\cov{(z_t, \tilde x_t)}}{\var{\tilde x_t}} \end{align}$

A convenient property of the Kalman update is that it preserves the linearity of the model. The difference with adaptive expectations is that the gain coefficient is an endogenous parameter, identical to the least squares slope of projecting on $\tilde x_t$ . The present model is particularly simple since there is only one observable, , such that is a scalar. (A multivariate setting will be illustrated in Section 3.)

Signal Extraction for Given Policy

As will be verified below, the optimal policy is linear and has the form
$\begin{align} x_t &= f_\tau \tau_t + f_\varepsilon \varepsilon_t + f_b \tau_{t\vert t-1} \end{align}$
for some scalars $f_\tau$ , $f_\varepsilon$ and . Compared to the symmetric information case, the dependence on $\tau_{t\vert t-1}$ is novel. It captures policy responses to public beliefs. As will be shown shortly, it influences the persistence of policy shocks, which is a crucial factor in determining inflation.

The public belief system is a straightforward application of the Kalman filter with (6) as state equation and (8) as measurement equation. In the parlance of time-series econometrics, policy poses an unobserved components model to the public. Key for the Kalman filter is the ratio of policy loadings on the realized components of the output target, $f_\varepsilon /f_\tau$ . Only these loadings, and not , are relevant for the Kalman filter. (Details are given in Appendix B.) This "mixing ratio" $f_\varepsilon /f_\tau$ determines how much a policy innovation reveals about $\tau_t$ instead of $\varepsilon_t$ . It allows the policymaker to change the signal-to-noise ratio in the public's signal extraction problem.

From the perspective of the public, policy is driven by the innovations $\ensuremath{\tilde{x}_t}$ and it has an innovations representation in the form of an ARMA(1,1) process:
$\begin{align} x_t &= \rho x_{t-1} + \tilde x_t + \rho \psi \tilde x_{t-1} \ \text{with}\quad \psi & =(f_\tau + f_b) K_\tau - 1 \notag \end{align}$
For the public, the above innovations representation is observationally equivalent to the hidden components representation of policy (8). Both generate the same variances and autocovariances of policy, whilst implying different impulse responses as will be illustrated below. Via $\psi$ , the persistence of this ARMA depends on the policy coefficients $f_\tau$ , $f_\varepsilon$ and . For plausible assumptions of the policy coefficients, $\psi$ is bounded between zero and minus one. For $\psi=0$ , persistence is largest as policy follows an AR(1) with auto-correlation equal to $\rho$ . For $\psi=-1$ both roots of the ARMA(1,1) cancel and policy is . (Details can be found in Appendix A.)

Together with the Phillips curve (1), the innovations representation of policy is sufficient to determine inflation in a way which crucially depends on the "average persistence" of policy as captured by the ARMA roots $\rho$ and $\psi$ .
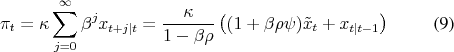
$\begin{align} \pi_t &= \kappa \sum_{j=0}^\infty \beta^j x_{t+j\vert t} = \frac{\kappa}{1-\beta\rho} \left((1 + \beta \rho\psi) \tilde x_t + x_{t\vert t-1} \right) \end{align}$
The policy function has two levers to affect the persistence of : First, there is the mixing ratio, which has been discussed above. If policy largely ignores the persistent target, i.e. if $f_\varepsilon /f_\tau$ is large such that $K_\tau$ is close to zero, the MA root gets close to cancel the AR root and policy is (correctly) perceived to be almost . In this case, inflation also approaches the solution (4) under symmetric information with $\rho=0$ .

But due to the second lever, , things need not collapse to the AR(1) case, when the mixing ratio tends to zero. In this case, $\psi$ converges to $\rho\cdot f_b$ , which is not necessarily zero.¹⁵ represents the marginal reaction to people's prior beliefs and affects the persistence of policy, too. A negative counteracts policy persistence induced by $\tau_t$ . The marginal reaction to beliefs is likely negative since beliefs $\tau_{t\vert t-1}$ will be inflationary; this conjecture will be verified in Section 2.4.

To keep inflation low, it is tempting to conclude that the policymaker should better ignore the persistent output target. Alternatively, a high mixing ratio could be chosen, with a higher responsiveness to transitory than persistent shocks, for example $f_\tau=1$ and $f_\varepsilon=100$ . But neither choice would likely be a sensible policy, since output plays not only an informational role. Attaining the output targets matters, too; calling for $f_\tau=f_\varepsilon=1$ and . For example, ignoring the persistent target by setting $f_\tau=f_b=0$ alleviates inflationary cost, but it also leads to persistent shortfalls from the $\tau$ -target. Neither would it appear sensible to overshoot the output target, for example by setting $f_\varepsilon=100$ . The optimal trade-off is the subject of the next sections. But an important restriction imposed by rational expectations has already become clear: at least on average actual policies must match public perceptions.

2.3 The Discretionary Policy Problem

This section sets up the discretionary policy problem for the simple, purely forward-looking New Keynesian model when there is the above structure of hidden information. Extensions of the model, including a hybrid Phillips Curve, will be analyzed in subsequent sections of this paper. The concepts and methods presented here are generalized to a wider class of linear quadratic models in the technical appendix of this paper.

Markov Perfect Equilibria Attention is limited here to Markov-perfect equilibria, which exclude reputational mechanisms via the kind of history-dependent strategies considered by Barro and Gordon (1983b) or Chari and Kehoe (1990) and avoids the associated multiplicity of equilibria. In the spirit of "bygones are bygones", state variables in a Markov-perfect equilibrium must be relevant for current payoffs.¹⁶ In the symmetric information setting shown above, these were the contemporaneous values $\tau_t$ and $\varepsilon_t$ (but not any elements of their history). Both of these state variables evolve in a purely exogenous fashion which accounts for the myopic behavior of discretionary policy under symmetric information: In Markov-perfect models, a current decision-maker can influence a future decision-maker only via endogenous state variables, like capital or government debt. This channel is however absent in the symmetric information version of the New Keynesian model.

Once hidden information is introduced, an additional state variable becomes relevant: Since the public observes only but neither $\tau_t$ not $\varepsilon_t$ , it is the public beliefs about the target components which are relevant for public payoffs. Precisely, it is the prior beliefs ( $\tau_{t\vert t-1}$ and $\varepsilon_{t\vert t-1}$ ) and not the posteriors ( $\tau_{t\vert t}$ and $\varepsilon_{t\vert t}$ ) which qualify as state variables for the time decision problem, since the latter are already influenced by time policies. In the present setting, $\varepsilon_t$ is and $\varepsilon_{t\vert t-1}=0$ so only $\tau_{t\vert t-1}$ needs to be tracked. The vector of Markov-perfect state variables is then
$\begin{align*} S_t &= \begin{bmatrix}\tau_t & \varepsilon_t & \tau_{t\vert t-1} \end{bmatrix}' \end{align*}$

The transition equation for the new state variable is given by the Kalman Filter. The response of beliefs to policy depends on the Kalman gain $K_\tau$ , which reflects how much policy reacts to $\tau_t$ .

$\begin{displaymath} \tau_{t+1\vert t} = \rho \tau_{t\vert t} \quad\text{and}\quad \tau_{t\vert t} = \tau_{t\vert t-1} + K_\tau \tilde x_t \end{displaymath}$

(2)

The discretionary policymaker retains the freedom to reoptimize his policies at each point in time. On the one hand, this allows a recursive representation of the policy problem as a dynamic program. On the other hand, he does not commit to future policies so these have to be taken as given in the decision problem. To be precise, what is taken as given is how the policymaker reacts to future state variables: Future policies are not given numbers but a given function of future state variables. This distinction is important here, since one of the state variables, $\tau_{t+1\vert t}$ , is under the influence of current policy so that future outcomes can be influenced. The continuation value of his dynamic program is a function of future states, denoted $V^0(S_{t+1})$ and the policy objective is to minimize
$\begin{align} \pi_t^2 + \alpha_x (x_t - \tau_t- \varepsilon_t)^2 + E_t V^0(S_{t+1}) \end{align}$
The linear quadratic nature of the model allows to guess (and verify) that the value function will be quadratic and policies linear in the state vector, which simplifies the analysis considerably:
$\begin{align*} V^0(S_{t+1}) &= S_{t+1} ' V^0 S_{t+1} + v^0 \ \Rightarrow \quad E_t V^0(S_{t+1}) &= 2 v_{13}^0 \rho \tau_t \tau_{t+1\vert t} + v_{33}^0 \tau_{t+1\vert t}^2 + t.i.p. \end{align*}$
for some positive definite matrix with elements $v_{13}^0$ , $v_{33}^0>0$ and a scalar . Throughout this paper, a zero superscript "" indicates coefficients embodying a guess about (future) policy and "" are terms independent of time policy.

The time-invariant solution to the discretionary policy problem has the linear form anticipated in (8). In principle, the policymaker is free to deviate from this "rule" at any time. He will just not find it optimal to do so.

An important constraint on the policy problem is the optimality of beliefs and decisions in the private sector. Optimality of beliefs are captured by the Kalman filter (7) and the the policymaker sees himself faced with a fixed Kalman gain $K_\tau^0$ when contemplating his policy problem. Optimal decisions of the private sector are represented by the Phillips Curve (1) where the policymaker takes as given how inflation expectations are related to future state variables; $\pi_{t+1\vert t} = g^0 \tau_{t+1\vert t}$ for some scalar . To sum up, the policy problem is to minimize
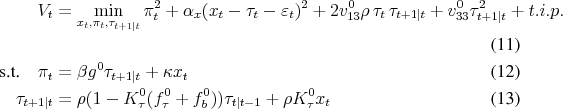
$\begin{align} V_t &= \min_{x_t,\pi_t,\tau_{t+1\vert t}} \pi_t^2 + \alpha_x (x_t - \tau_t- \varepsilon_t)^2 + 2 v_{13}^0 \rho \tau_t \tau_{t+1\vert t} + v_{33}^0 \tau_{t+1\vert t}^2 + t.i.p. \ \text{s.t.}\quad \pi_t &= \beta g^0 \tau_{t+1\vert t} + \kappa x_t %&= \beta g^0 \rho (1 - K_\tau^0(f_\tau^0+f_b^0)) \tau_{t\vert t-1} + (\kappa + \beta g^0 \rho K_\tau^0) x_t \ \tau_{t+1\vert t} &= \rho (1 - K_\tau^0(f_\tau^0+f_b^0)) \tau_{t\vert t-1} + \rho K_\tau^0 x_t \end{align}$
whose solution is indeed of the form anticipated in (8). Whilst beliefs embodied in , and $K_\tau^0$ are taken as given in the policy problem, in equilibrium they must be consistent with the solution to the policy problem. This poses an intricate fixed point problem. Fixed points between current expectations and future policy as in and are common in Markov-perfect models under symmetric information. What is new is the fixed point between current policy and beliefs about the systematic relationship between current policy and states contained in the Kalman gain $K_\tau^0$ .

Changed Policy Trade-Offs with Belief Management

The first-order conditions of (13) require optimal policy to satisfy
$\begin{align} \alpha_x (x_t - \bar{x}_t) + \kappa \pi_t + \rho K_\tau^0\mu_t &= 0 \end{align}$
where $\mu_t$ is the multiplier on the belief constraint (15). It is the term involving $\mu_t$ which distinguishes the optimality condition (16) from its counterpart under symmetric information (3) discussed above.

To shed some light on the fixed point considerations behind the solution to (13), suppose that the output target is positive and the policymaker must balance an increase in output against its inflationary costs. The marginal value of relaxing the belief constraint is likely positive, owing to the positive autocorrelation in the persistent component of the target. Likewise, the Kalman gain $K_\tau$ will be positive, since policy will co-move positively with the target. The new "belief term" $\rho K_\tau^0\mu_t$ in (16) will then caution the policymaker against pursuing the output target too aggressively. As will be seen in the numerical analysis below, optimal policy will be less bold under hidden information -- except when shocks to $\tau_t$ are so rare that the Kalman gain $K_\tau$ is very small.

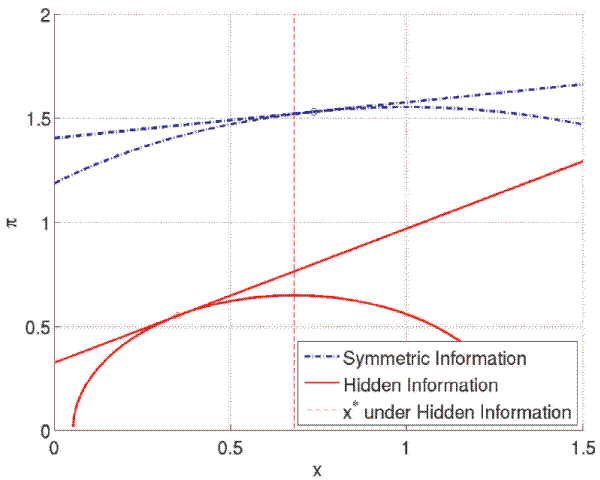
The change in policy trade-offs under hidden information can be nicely illustrated with a picture similar to Kydland and Prescott (1977). Under symmetric information, the policymaker's indifference curves over output and inflation are concentric around $\pi_t=0$ and $x_t=\bar{x}_t=\tau_t+\varepsilon_t$ . The optimality condition (3) seeks the tangency point between the indifference curves and the policy constraint. The latter being the Phillips Curve with intercept $\beta\pi_{t+1\vert t} = \beta \bar{g}^0 \rho \tau_t$ for some $\bar{g}^0$ . This is depicted by the dashed lines in Figure 1. In equilibrium, $\bar{g}^0$ must be identical to the optimal policy coefficient computed in (4), which is a positive number. That is, the larger policy responds to a given level of the persistent target, the higher the intercept it faces in equilibrium.

**Figure 1:** Policy Trade-Offs in the Simple Model
Figure 1 Data Note: Phillips Curve and indifference curves for policy problem in simple New Keynesian model. Computed for the case of a publicly anticipated, persistent target level: $\tau_t=1$ , $\tau_{t\vert t-1} =1$ and $\varepsilon_t=0$ . Dashed lines show symmetric information case with $\pi_{t+1\vert t} =\bar{g}\rho \tau_t$ and $\bar{g}$ computed from the equilibrium policy (4). Solid lines depict Phillips Curve (17) and indifference curves (18) under hidden information. Optima occur at the circled tangency points.

Under hidden information belief management comes into play and changes the picture. To reach some substantive conclusions, I am willing to make the following assumptions about the policy coefficients. Apart from being plausible, they will be verified to be true in the computations below for a wide range of calibrations. First, policy should react positively to target shocks, $f_\tau^0>0$ . Second, policy seeks to counteract belief . But third, it still seeks to accommodate a target, even when its realization coincides with public beliefs: $f_\tau^0+f_b^0>0$ .¹⁷ These imply that $K_\tau$ and are positive.

A key result is that hidden information steepens the slope of the Phillips Curve when compared against the symmetric information case. Substituting the belief dynamics (11), the Phillips Curve becomes
$\begin{align} \pi_t &= \beta g^0 \rho \left(1 - K_\tau^0(f_\tau^0+f_b^0)\right) \tau_{t\vert t-1} + \left(\kappa + \beta g^0 \rho K_\tau^0 \right) x_t \end{align}$
The steepening of the Phillips Curve worsens the policy trade-off and makes policies less bold with respect to both target components. Underlining the importance of beliefs, the intercept of the Phillips Curve depends now on the public's prior beliefs, $\tau_{t\vert t-1}$ , instead of the actual value of $\tau_t$ . Coming out of steady state with $\tau_{t\vert t-1}=0$ , this alone makes policies bolder than otherwise. An important aspect for the fixed point computations is that, via $K_\tau$ , the slope of the Phillips Curve becomes ever steeper the bolder policies are with respect to $\tau_t$ , which again tames the boldness of equilibrium policies.

Belief management changes the indifference curves as well. Most importantly, output acts as a signal about the persistence of policy targets which again influences the evaluation of future losses in the policy problem. This shifts output preferences, such that they are not centered around $\bar{x}_t=\tau_t+\varepsilon_t$ anymore. Substituting again the belief dynamics, the indifference curves can be computed from

$\begin{displaymath} \pi_t^2 + \alpha_x (x_t - \tau_t- \varepsilon_t)^2 + \gamma_0 x_t^2 + \gamma_1 \tau_t x_t + \gamma_2 \tau_{t\vert t-1} x_t \end{displaymath}$

(3)

where the scalars $\gamma_0>0$ , $\gamma_1\lessgtr 0$ and $\gamma_2>0$ depend on the coefficients of (18). ¹⁸ These indifference curves are centered around $\pi_t=0$ and
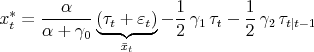
$\begin{align*} x_t^\ast &= \frac{\alpha}{\alpha+\gamma_0}\underbrace{(\tau_t + \varepsilon_t)}_{\bar{x}_t} - \frac{1}{2} \gamma_1 \tau_t - \frac{1}{2} \gamma_2 \tau_{t\vert t-1} \end{align*}$

Regardless of slope and intercept of the Phillips Curve, $x_t^\ast$ is the "maximally desirable" level of output. Apart from its dependence on the original target term $\bar{x}_t$ , it shifts both with the actual and perceived level of the persistent target component $\tau_t$ . But for starters consider a transitory shock to the output target, say $\varepsilon_t=1$ whilst $\tau_t=\tau_{t\vert t-1}=0$ : Any policy response will partly be attributed to a persistent shock and thus increase $\tau_{t+1\vert t}$ causing future inflation. The associated losses to the policymaker are captured by the $\gamma_0$ term of the indifference curves. Independently of the Phillips Curve, the policymaker does then not even desire to attain that transitory target but only a fraction $\alpha/(\alpha+\gamma_0)$ thereof.

Since $\gamma_2>0$ , public beliefs $\tau_{t\vert t-1}$ shift the indifference curves towards lower output levels. While $\gamma_1$ cannot be signed analytically, it happens to be positive over the range of calibrations considered below and this contributes to making policy less bold. All in all, prior beliefs of the public $\tau_{t\vert t-1} > 0$ caution policy in two ways: First they increase inflation immediately (the intercept of the Phillips Curve) and -- if not counteracted by current policy -- they herald future inflation and shrink the "maximally desirable" level of output, $x_t^\ast$ , towards zero.

2.4 Optimal Policy in the Simple Model

This section presents results for the optimal policy. Calibration values are taken from Gali (2003) with equally weighted policy preferences ( $\alpha_x=1$ ) and equal-probable shocks to the target components ( $\sigma_\eta=\sigma_\varepsilon=1$ ), see Table 1.¹⁹ The solution algorithm for the underlying fixed point problem is discussed in the technical appendix.

Table 1: Model Calibration

$\ensuremath{\beta}$	0.99
$\ensuremath{\sigma}$	1.00
$\ensuremath{\theta}$	0.75
$\ensuremath{\phi}$	1.00
$\ensuremath{\kappa}$	0.1717
Policy Preferences
$\ensuremath{\alpha_x}$	1.00
Driving Processes
$\ensuremath{\sigma_\varepsilon}$	1.00
$\ensuremath{\rho}$	0.90
$\ensuremath{\sigma_\eta}$	1.00
$\ensuremath{\sigma_{\bar x}}$	1.00
$\ensuremath{\sigma_n}$	1.00

Notes: Private-sector parameters taken from Gali (2003)'s calibration to quarterly U.S. data. Innovation variances are each normalized to unity and not intended to match the scale of any second moments. The sensitivity of results to $\rho$ and $\alpha_x$ is discussed in Section 2.4. As shown there, variations in $\alpha_x$ are isomorphic to varying $\kappa$ . As a measure of credibility, $\sigma_n$ is varied in Section 3.

Optimal Mixing Ratio and Belief Responses

Key statistics of the policy function are the mixing ratio $f_\varepsilon /f_\tau$ , which governs the Kalman gains, and via which policy responds to prior beliefs. As anticipated, is negative. The policy response to $\tau_{t\vert t-1}$ is synonymous with counteracting inflation expectations of the public formed in the past. There is a one-to-one correspondence between the public's prior beliefs of the hidden state and the public's inflation expectations in this simple model:

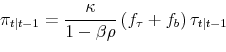
$\begin{displaymath}\pi_{t\vert t-1} = \frac{\kappa}{1-\beta\rho} (f_\tau + f_b) \tau_{t\vert t-1}\end{displaymath}$

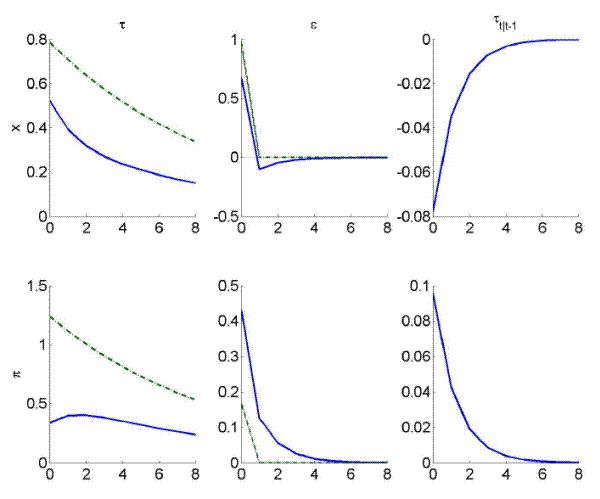
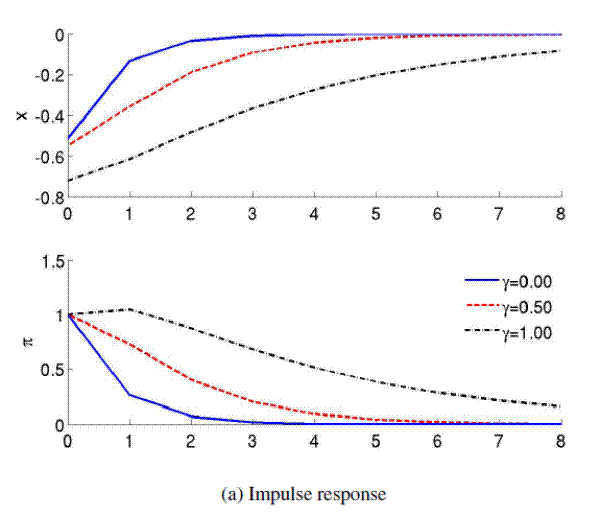
How optimal policy seeks to quell past beliefs can be seen from the impulse response shown in Figure 2. The first two columns show responses to shocks in $\tau_t$ and $\varepsilon_t$ . The third column documents responses to initial conditions $\tau_t=0, \varepsilon_t=0, \tau_{t\vert t-1}=1$ . This corresponds to a situation where the policymaker is faced with erroneous beliefs about his inflationary output preferences. The optimal response is a prolonged contraction until beliefs and outcomes have settled back in steady state after about four periods. Given that the New Keynesian model generally lacks endogenous persistence, the length of this learning process is a remarkable outcome echoing the results of Erceg and Levin (2003). Moreover, the effect of fighting past beliefs is also present in the other impulse responses. When the true target shock is , this leads to a contractionary policy one period after the shock. This pattern is similar (though not fully identical) to commitment policies under full information. In both cases, a credible promise to undo expansionary shocks in the future lowers inflation expectations; similar to the disciplinary channel emphasized by Walsh (2000), 2001 2001 and Gaspar, Smets, and Vestin (2006).

Figure 2: Optimal Policy in the Simple Model
Figure 2 Data Note: Impulse responses of output gap () and inflation ( $\pi_t$ ) under hidden (straight lines) and full information (dashed) to unit standard deviation shocks $\tau_t$ and $\varepsilon_t$ . The column labeled $\tau_{t\vert t-1}$ shows responses to initial conditions $\tau_t=0, \varepsilon_t=0, \tau_{t\vert t-1}=1$ .

The other lever of policy is the mixing ratio, which is higher compared to the full information case.²⁰ Under hidden information, policy is less bold in its pursuit of persistent output targets. This lowers the signal-to-noise ratio in the public's signal extraction problem and the public (correctly) places a lower probability on a policy innovation $\ensuremath{\tilde{x}_t}$ being caused by a persistent target shock.

Innovation Responses The model with hidden policy components is observationally equivalent to a symmetric information model where the policy target follows a univariate ARMA(1,1). Both yield the same second moments and have identical likelihoods. But there is an important difference: The hidden components model distinguishes different sets of impulses responses, which can be associated with different episodes in monetary policy.

Figure 3: Innovation Responses in the Simple Model
Figure 3 Data Note: This picture documents the updating of public beliefs about the evolution of output gap and inflation after a unit innovation in policy ( $\ensuremath{\tilde{x}_t}$ ) at time zero. Dashed lines are true impulses under the full information measure to structural shocks $\tau_t$ (top line on each graph, red) respectively $\varepsilon_t$ (bottom, green). These structural responses are scaled to yield a unit innovation in output. Dashed blue lines document update impulse responses formed by the public at times 1 (with square marker) respectively time 2 (circles). Top panel shows the output gap (), inflation ( $\pi_t$ ) is shown in the lower panel.

The differences between true impulse responses and public beliefs are illustrated in Figure 3. For output and inflation, the figure shows two sets of impulse response: First, the expected responses computed by the public, after observing a unit innovation in policy, $\ensuremath{\tilde{x}_t}$ , at time zero. After its initial upwards jump, output remains expanded at about half its impact value and decays persistently thereafter. The inflation path is equally equally elevated and persistent.

Secondly, the figure shows the true responses to the structural shocks $\tau_t$ and $\varepsilon_t$ , computed under the full information measure spanned by $(\tau^t, \varepsilon^t)$ . They are scaled such as to yield a unit innovation in output as well. After a shock to the persistent target, $\tau_t$ , policy is persistently more expansive than originally expected by the public. The difference between these two sets of impulse response represents the errors of public forecasts made in the initial period. As the structural responses unfold, the public learns about the true nature of the shock. The figure also shows how public beliefs are updated in subsequent periods, leading to persistent upwards, respectively downwards revisions of beliefs. The innovations responses are rational and on average correct. Persistently positive forecast errors to a shock in $\tau_t$ are offset by persistently negative forecast errors when a shock to $\varepsilon_t$ occurs.

When particular periods are supposed to have been dominated by one set of shocks rather than another, patterns of persistent forecast errors in public beliefs should be reflected in survey data. For example, Erceg and Levin (2003) use survey data to characterize the Volcker disinflation as a period of persistently excessive inflation forecasts. Their model uses a Gaussion information structure similar to mine, but for a fixed policy rule. The methods presented here can be used to derive the parameters of such a rule within an explicitly optimizing framework of monetary policy under hidden information.

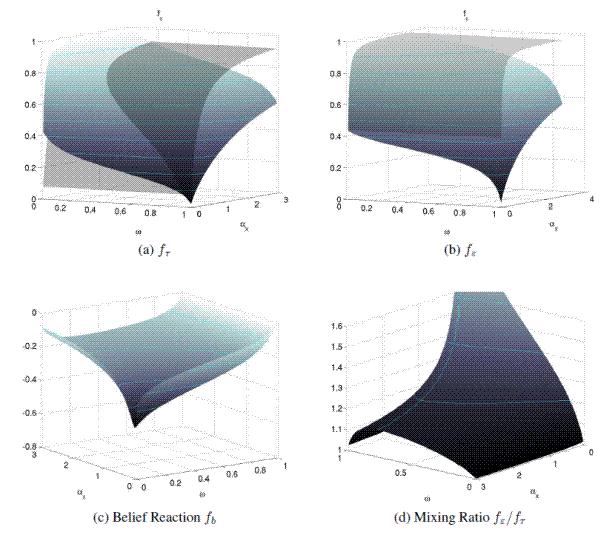
Sensitivity Analysis of Policy Coefficients

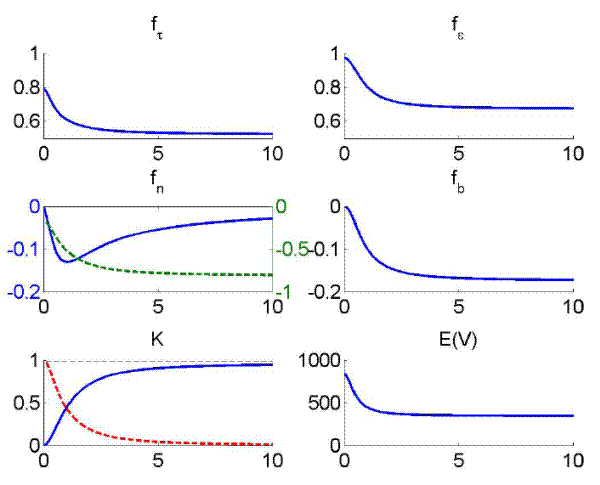
Policy trade-offs are particularly affected by two parameters: The relative variance of transitory to persistent target shocks and the preference weight $\alpha_x$ , whereas increases in the slope of the Phillips Curve, $\kappa$ , affect policy trade-offs similarly to decreases in $\alpha_x$ .²¹ When considering changes in the importance of the target components $\varepsilon_t$ and $\tau_t$ , the overall variance of the output target will be fixed at some level $\sigma^2_{\bar x}$ . Denoting the weight on $\tau_t$ by $\omega\in[0;1]$ this translates into

$\begin{displaymath}\sigma_\varepsilon^2 = (1-\omega) \sigma^2_{\bar x} \quad\text{and}\quad \sigma_\eta^2 = \omega (1-\rho^2)\sigma^2_{\bar x}\end{displaymath}$

Figure 4 documents changes in the policy coefficients $f_\tau$ , $f_\varepsilon$ , as well as the mixing ratio $f_\varepsilon /f_\tau$ due to variations in $\omega$ and $\alpha_x$ . The upper panels also show the corresponding values of $f_\tau$ and $f_\varepsilon$ under symmetric information. Because of certainty equivalence, their surfaces are flat along the $\omega$ -axis. When there is hidden information, $f_\varepsilon$ is uniformly smaller than under symmetric information. This is caused by the public's inability to distinguish between realizations in the two target components. Any innovation in will be partly attributed to have been caused by the persistent component $\tau_t$ . This has two adverse effects in the first-order condition (16): First, if the true shock was to the component $\varepsilon_t$ , inflation will be higher compared to the full information case. Second, since the public expects the target change to have some persistence, there will also be inflationary costs in the future, tracked by $\mu_t$ . Both effects caution the policymaker and lower $f_\varepsilon$ compared to the full information case.

Figure 4: Sensitivity Analysis
Figure 4a Data Figure 4b Data Figure 4c Data Figure 4d Data Note: Sensitivity of policy function due to variations in preference weight $\alpha_x$ and variance weight $\omega$ in the simple model of Section 2, keeping other parameters at their baseline values from Table 1. In order to provide the best perspective on each surface, axes are rotated differently in each panel. Transparent surfaces in Panels (a) and (b) depict corresponding variations in $f_\tau$ , respectively $f_\varepsilon$ in the symmetric information model.

Because of the second effect, $f_\tau$ is mostly smaller under hidden information as well. As the public underestimates the persistence of policy after a shock to $\tau_t$ (see Figure 3), inflation is lower than under full information. This would give the policymaker some slack in pursuing the output target, if it were not mostly outweighed by the marginal effect of policy on beliefs, which are represented by the term $\rho K_\tau \mu_t$ in the first-order condition (16). However, when the probability of a persistent shock is very small ( $\omega$ close to zero) or when the policymaker is known not to care much about attaining it ( $\alpha_x$ small), the Kalman gain $K_\tau$ will be small and public beliefs $\tau_{t\vert t}$ will be very insensitive to policy and their importance vanishes in (16). In those cases, persistent shocks are very hard to detect for the public. But when they occur, the policy response can be bolder than under symmetric information as is shown in Panel (a) of Figure 4.

It is worth recalling that a higher mixing ratio and a more negative reaction to prior beliefs increase the persistence of the policy process, causing higher inflation. Indeed, as can be seen from Panel (c) of the figure, is negative everywhere. The belief reaction is strongly negative, when there is more weight on inflation in the loss function (smaller values of $\alpha_x$ ) and when persistent shocks are more prevalent ( $\omega$ close to one). Both cases make it more important, respectively more likely, that inflationary beliefs are kept in check.

Under discretion, the policymaker takes the public's belief system as given, without actively seeking influence it, whereas commitment policymaker would have to consider the systematic effects of his actions on the Kalman gain for example. Still it is instructive to see how policy affects the public's signal-to-noise ratio via the mixing ratio. As shown in Panel (d), this ratio increases when policy preferences place more weight on output than inflation. As inflation becomes more and more costly for the policymaker, $f_\tau$ is decreasing faster than $f_\varepsilon$ , which makes it ever harder for the public to detect persistent policy changes. When changing $\omega$ , the mixing ratio is largest for intermediary values, typically above $\omega\geq 0.5$ . In this range, hidden information problem is most prevalent and a high mixing ratio helps to lessen the sensitivity of beliefs to policy. When $\omega$ approaches unity, the public can expect any policy to be caused by a persistent shock with near certainty and the mixing ratio drops to its full information level. When the target is almost exclusively driven by shocks ( $\omega\to 0$ ) expected future inflation drops towards zero and the mixing ratio drops to one as $f_\tau$ approaches $f_\varepsilon$ .

Policy Losses

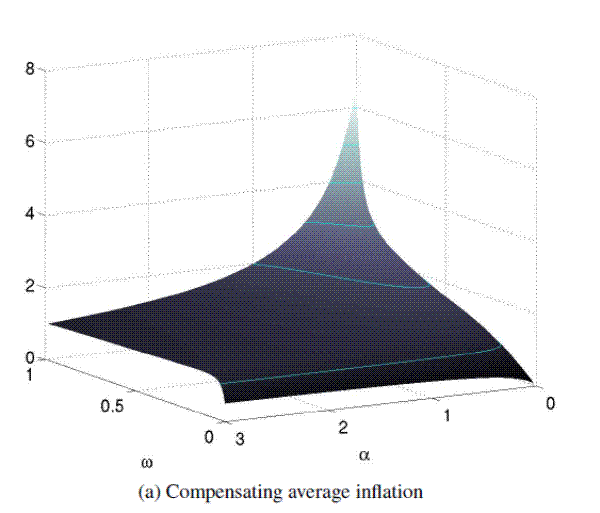
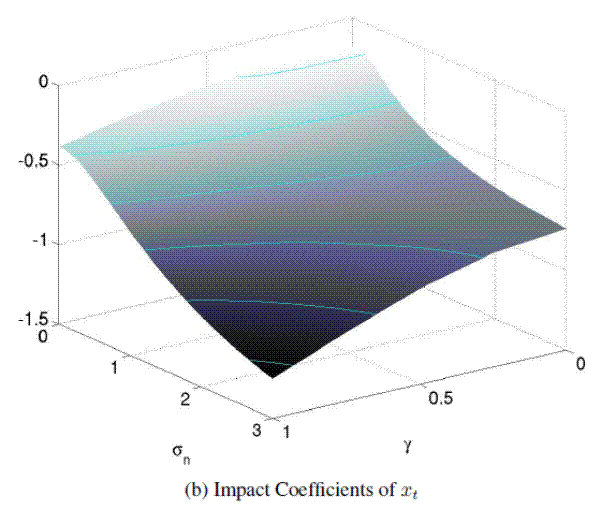
Comparing policies under hidden information against outcomes under full information begs the question what would be the preferred setting. Considering the loss function of the policymaker, it turns out that the ex-ante expectation of the policy loss, is improved under hidden information over the wide range of calibrations discussed above. Figure 5 reports how the improvement in policy losses under hidden information are large enough that an average inflation rate corresponding to about one-standard deviation unit would have to be added to inflation under hidden information for policy losses to be equal; the compensating inflation is somewhat smaller when the volatility weight on persistent shocks, $\omega$ , is very small; and it can be considerably larger when persistent shocks are very prevalent and the weight on inflation stabilization is large.²²

Figure 5: Improved Policy Losses under Hidden Information
Figure 5a Data Figure 5b Data Note: Panel (a) shows differences in expected policy losses between full and hidden information settings. A positive number means that policy losses are larger under full information, implying that hidden information outcomes are preferred. The difference in losses is expressed as a compensating increase in average inflation under hidden information, scaled in standard deviation units. Baseline calibration as shown in Table 1 wth variations in prefernce weight $\alpha_x$ and variance weight $\omega$ as indicated in the figure. Panel (b) shows impulse responses of output and inflation for different policies under under hidden information with. Straight lines show the optimal policy. Dash-dotted lines use the optimal coefficients $f_\varepsilon$ and $f_\tau$ but neglect prior beliefs (). Dashed lines correspond to using the symmetric information policy when there is hidden information. Compared with discretion under full information, the compensating rates of average inflation correspond to 0.37, 1.11 and 1.82 units of the standard deviation of inflation in each equilibrium.

Moreover, the same holds when considering the notion of "representative" loss discussed in Section 2.1. The reason is simply that the improvement in outcomes is due to the policymaker's restraint in pursuing the output targets. By lowering inflation and output gap, this is clearly beneficial for the "representative" loss, which would be minimized by keeping the output gap at zero anyway.

The benefits of reduced inflation also outweigh the policy losses from staying away from the targets, at least from an ex-ante perspective considering both persistent and transitory shocks as well as their respective likelihoods.²³ Conditional on the occurence of an shock $\varepsilon_t$ , inflation is of course higher, and the policymaker misses the target by more than he would under full information, see Figure 2. On average, this is however outweighed by the benefits incurred when a persistent shock occurs.

Considering the different levers present in the policy function (8) under hidden information, a quantitative decomposition of the reduction in policy loss looks as follows: First, there is the optimal policy under symmetric information. Feeding this same policy through the system but under the hidden information, losses drop by an amount, correspond to a compensating rate of average inflation of about one third of the standard deviation of inflation in the new equilibrium. The optimal policy under hidden information then seeks to improve upon this by changing the mixing ratio and by reacting to past beliefs. Using the optimal mixing ratio, but neglecting the response to prior beliefs () makes expected losses drop further; compared to full information the compensating average inflation amounts to about one standard deviation of inflation. In addition to this, the optimal policy reacts also negatively to prior beliefs and the average inflation compensating for the improvement in losses over full information equals almost two standard deviations of inflation. For comparison, the difference in full information losses of discretion and commitment corresponds to a compensating average inflation of about two-and-a-half standard deviations of inflation under discretion.

3 Belief Shocks

The simple New Keynesian model analyzed so far has only one communication channel between policymaker and public: Policy actions themselves. Since policy is driven by more shocks than there are communication channels, the public cannot perfectly infer the drivers of policy, not even in equilibrium. In reality, there are however other communication channels than the policy instrument itself. If these channels are informative, they will alleviate the public's inference problems and affect the scope of belief management for policy. This section extends the information structure of the simple model to a richer setting, nesting the cases of full and hidden information considered before.

In addition to observing policy, the public is now assumed to receive a noisy signal about the persistent output target. The target signal is contaminated by noise shocks , which will be called "belief shocks". They are and the public's measurement vector is $\begin{equation*} Z_t = \begin{bmatrix}x_t & (\tau_t + n_t) \end{bmatrix}' \quad\text{where}\quad n_t \sim N(0,\sigma_n^2) \end{equation*}$ and the notation for public beliefs of a variable is now adapted to $z_{t\vert t} \equiv E(z_t\vert Z^t)$ . The presence of two correlated observables in the public's inference problem requires to extend the univariate filtering methods discussed in the previous section. Also, the state vector needs to be augmented by . (Notice that $n_{t\vert t-1} = 0$ .) A detailed presentation of handling this and larger settings has been relegated to the technical appendix.

The belief shocks are uncorrelated with fundamentals (here: $\tau_t$ and $\varepsilon_t$ ) and play no role under symmetric information. But under asymmetric information they matter since they are correlated with an informative signal about fundamentals, giving rise to fluctuations driven by "non fundamental" shocks.²⁴ Inflation is affected by belief shocks via the forward-looking Phillips Curve (1), making it suboptimal for policy to ignore belief shocks. As with given prior beliefs about the output target ( $\tau_{t\vert t-1}$ ), they will raise inflation and optimal policy should want to fight their effects by contracting output. In the present model, economic responses to noise shocks will exhibit patterns similar to cost-push shocks, echoing results of Angeletos and La'O (2008b).

By changing the volatility of noise shocks, the extended model also nests the cases of hidden and full information analyzed in the previous section. The scope for hidden information increases with the volatility of belief shocks. For $\sigma_n=0$ , the model is identical to the full information model, since $\tau_t$ is perfectly observable. The opposite occurs when $\sigma_n$ is very large. In this case, the signal becomes useless and the model converges to the hidden information setting from the previous section where policy is the only observable.

Figure 6: Impulse Responses with Belief Shocks
Figure 6 Data Note: Straight lines are impulse responses to a unit belief shocks . For any variable , dashed lines (red) depict the evolution of prior beliefs $z_{t\vert t-1}$ . Calibration values from Table 1. Dash-dotted line in middle right panel, " $n_{t}$ ", depicts impulse response of the belief shock.

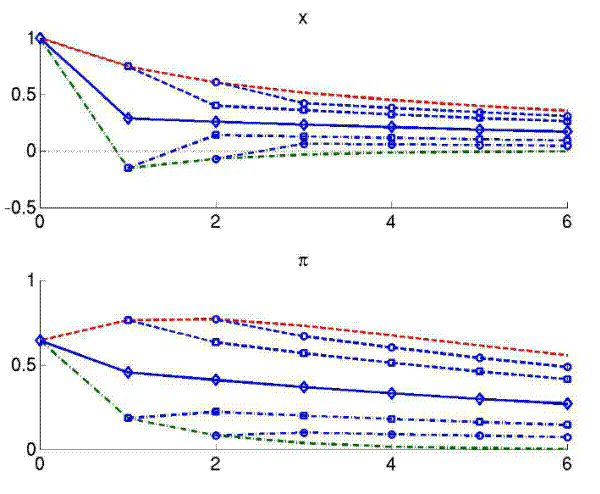
Impulse responses to a noise shock are shown in Figures 6, again using the baseline calibration from Table 1. Under this configuration, each of the three shocks in this model occurs with the same probability. When the target signal $\tau_t+n_t$ goes up because of a noise shock, this leads to ample confusion for the public. Current and expected inflation rise, since the public attributes part of the signal to the persistent target $\tau_t$ , To counteract these erroneous beliefs, policy contracts output. This is sensible in two ways: First it directly lowers inflation via the output term in (1). Second, it signals that the target $\tau_t$ may in fact not have gone up and thus reduces expected inflation. In the baseline calibration, it takes about four periods (one year) to fight these erroneous beliefs.

The resulting pattern of contracting output and elevated inflation is similar to the dynamics known from cost-push shocks. Figure 6 also documents that public beliefs of future output and inflation are both elevated during the entire episode, which distinguishes belief shock induced dynamics from cost-push behavior, since the latter would typically be accompanied by an expected recession as well.

Varying Transparency

How does policy change with the volatility of belief shocks? To answer this question, Figure 7 shows how policy coefficients and expected losses change when $\sigma_n$ is varied between zero and infinity. As discussed above, the limit points in this experiment are the symmetric information model, respectively the previously studied model with no target signal except for policy. The policy coefficients $f_\tau$ , $f_\varepsilon$ and vary smoothly and monotonically between the comparative statics of hidden vs full information studied before. They are all smaller and policy losses are reduced as the extent of hidden information increases with $\sigma_n$ .

Figure 7: Varying Transparency
Figure 7 Data Note: Change in policy coefficients, expected policy loss and Kalman gains while varying as the volatility of belief shocks, $\sigma_n$ is varied along the -axis. Computations are based on the belief shock model of Section 3. The middle left panel shows scaled response coefficients, , to a belief shock, since the size of belief is changed on the x-axis. The straight line shows responses to a belief shock with unit-standard deviation, $f_n\cdot\sigma_n$ . The dashed line scales the coefficient such that belief shock generates a unit increase in inflation on impact, $f_n /\pi_0$ (with units indicated on the right hand axis). (There is no inflation response to a belief shock when, $\sigma_n=0$ , and the plot shows no data for this point.) The bottom left panel shows Kalman gains (solid line) and (dashed line) from the public's updating equation (19). (Notice: The solid line, , converges to 0.94 not one as the variance of belief shocks grows to infinity.)

The policy response to noise shocks is always negative. The reasons are similar to what has been discussed in the previous section for the negative response to prior beliefs . A contraction lowers inflation directly via the Phillips Curve and indirectly via beliefs. For better comparison with the other coefficients, the middle left panel of Figure 7 shows how the policy reaction to one-standard deviation shock, $f_n\cdot\sigma_n$ changes with the shock variance. The noise response peaks at an intermediary level of the noise variance, where the public places roughly equal weight on policy and the target signal in its updating of beliefs. Formally, the public beliefs evolve as

$\begin{displaymath} \tau_{t\vert t} = \tau_{t\vert t-1} + K_x \ensuremath{\tilde{x}_t}\xspace + K_s (\ensuremath{\tilde{\tau}_t}\xspace + n_t) \end{displaymath}$

(4)

Changes in the Kalman gains

and

for various noise levels are shown in the bottom left panel of Figure 7. In the extremes the response of policy to noise shocks is zero, as either the size of the shock shrinks to zero (and there are no erroneous beliefs to fight) or the public pays no attention to a signal with infinite noise.

A natural interpretation of variations in noise variance is to view these as changes in transparency about the central bank's output target. The above results then document clear disadvantages from transparency. In a somewhat related model, Faust and Svensson (2001), Proposition 6.3 appear to establish the opposite: Namely that central bank losses were increasing, not decreasing, in transparency. The difference lies here in the definition of "transparency", and it is instructive to see how apparently innocuous differences in a model's setting can lead to different conclusions.

In the experiments of Faust and Svensson (2001), transparency means that targets can be perfectly inferred once policy is observed. In the experiments above, transparency ( $\sigma_n=0$ ) makes the target component $\tau_t$ directly observable, regardless of policy. Both imply the same information sets in equilibrium. But the constraints faced by the discretionary policymaker differ in profound ways. Under discretion, the policymaker takes the public beliefs system and its Kalman gains as given. When the target is perfectly observable, as is the case above, the current policymaker cannot influence beliefs, since the Kalman gain in (19) is zero.²⁵ In contrast, when targets are perfectly inferable from observed policies, this link is retained causing the difference in outcomes.

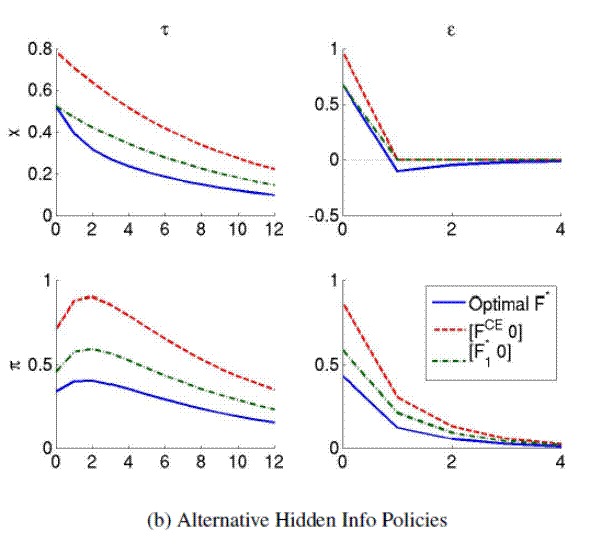
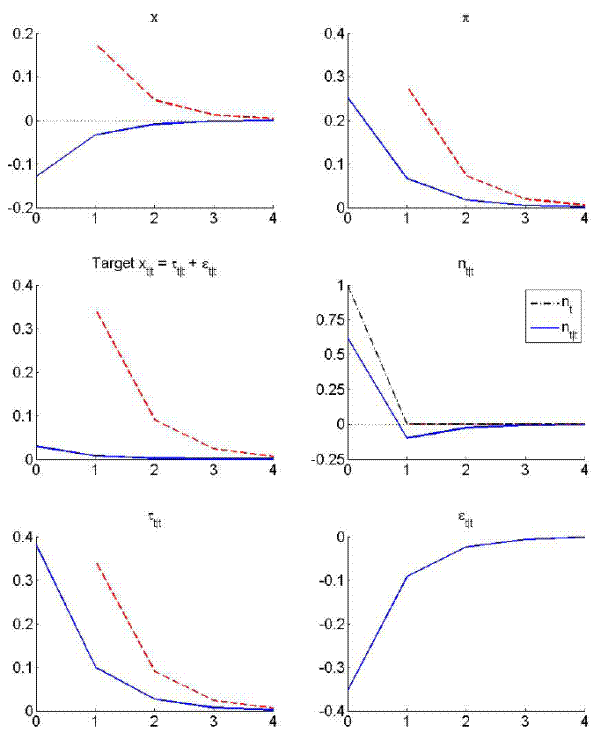
4 (In-)Credible Disinflations and Exogenous Persistence

A pertinent question in monetary policy is whether to conduct disinflations quickly or gradually. The answer involves a minimization of the economic costs incurred by the necessary output contractions along the disinflation path. These costs hinge on the persistence of inflation. If persistence is large, a larger or more protracted contraction might be necessary. A pertinent policy question is then whether to chose the "cold turkey" approach of a quick disinflation, involving a large initial contraction, or whether to chose a more gradual approach, implementing a longer sequence of smaller contractions.

Academic research has offered different advice on these issues, see for example the discussion between Gordon (1982) and Sargent (1982). Arguments for or against either approach differ in whether credibility is assumed to have an effect on inflation persistence or not. A quick disinflation could enhance the credibility of the policymaker's intention to disinflate and help reducing the inflation rate by itself. Taking this view, Sargent (1982) favors the "cold turkey" approach. Being more concerned with exogenous sources of inflation persistence makes Gordon (1982) lean towards advocating more gradual disinflation paths.

The framework presented in this paper allows to address these questions in a fully dynamic framework with an optimizing policymaker. The linear quadratic approach allows to handle multiple, endogenous state variables, including those arising from partially backward-looking inflation dynamics. To the best of my knowledge, this is the first explicitly optimizing analysis of disinflation strategies when policy goals are unobserved.²⁶

The following disinflation experiment is considered: How should policy react to a surge in inflation due to unfounded public beliefs? In an admittedly stylized way, this resembles the initial conditions of the Volcker disinflation as discussed by Erceg and Levin (2003) and Goodfriend and King (2005). Such inflation beliefs may be caused by a belief shock, , or inherited via $\pi_{t\vert t-1} = g^0 \tau_{t\vert t-1}$ . Qualitatively, results are similar in either case and the discussion below will focus on responses to belief shocks.

In the model of the previous sections, the cost of disinflation depends largely on the policymaker's capability to lower policy expectations quickly. In the belief shock model of the previous section, policy induces a stronger contraction of the economy in response to beliefs $\tau_{t\vert t-1}$ when credibility problems are larger, see the middle right panel of Figure 7.²⁷ While this suggests that disinflations should be more aggressive, it does not yet speak to concerns about the trade-offs under exogenous inflation persistence.

To see how policy changes in the presence of exogenous persistence, the Phillips Curve is augmented with a backward-looking term, representing price indexation at the rate $\gamma$ .²⁸
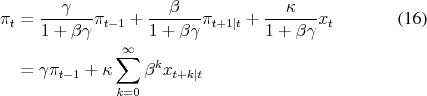
$\begin{align} \pi_t &= \frac{\gamma}{1+\beta\gamma} \pi_{t-1} + \frac{\beta}{1+\beta\gamma} \pi_{t+1\vert t} + \frac{\kappa}{1+\beta\gamma} x_t & = \gamma\pi_{t-1} + \kappa \sum_{k=0}^\infty\beta^k x_{t+k\vert t} \notag \end{align}$
In this hybrid Phillips Curve (20), inflation is not only determined by the expected path of future policies known from (1), but also by lagged inflation. Policy innovations are still the ultimate driver of inflation, but they carry less weight in changing current inflation.

Figure 8: Disinflation with Exogenous Persistence
Figure 8a Data Figure 8b Data Note: Panel (a): Impulse responses of output and inflation to a belief shock with varying degrees of price indexation ( $\gamma=\{0;0.5;1\}$ ) in the Phillips Curve (20). Belief shocks are normalized such that they produce a unit response in inflation on impact. Panel (b) reports the impact coefficients of output in response to such normalized belief shocks for different values of the indexation rate $\gamma$ and noise level $\sigma_n^2$ . (Other parameters calibrated as in Table 1.)

Figure 8 compares impulse responses to a belief shock when varying the indexation rate $\gamma \in \{0;0.5;1\}$ ; for $\gamma=0$ the model is identical to what has been studied above.²⁹ For better comparison of the disinflation policies, the belief shocks have been scaled such as to yield a unit innovation in inflation on impact. As higher indexation rates increase exogenous inflation persistence, optimal policy contracts the economy ever more aggressively to a belief shock -- bolstering the case for the "cold turkey" approach. The lower panel of Figure 8 confirms this also over a wider range of values for the noise variance $\sigma_n^2$ .

Even though policy contracts the economy more vigorously when exogenous persistence is larger, disinflations are not necessarily quicker. Due to the higher exogenous persistence in inflation it takes longer for inflation to fall when $\gamma$ is larger. Policy cannot avoid the higher degree of backward-lookingness in inflation. But this is precisely why an aggressive initial contraction is warranted. It does not only fight beliefs as in the previous section. By reducing current inflation, it reduces also the amount of future inflation caused by ill-founded beliefs to be carried forward via the backward-looking term in the Phillips Curve.

5 Related Literature

Since asymmetric information is such a pertinent issue in policymaking, it is no wonder, that there is a wide body of related literature. General surveys can be found in Rogoff (1989), Walsh (2003), Chapter 8 and Persson and Tabellini (2000), Chapter 15. The literature can roughly be classified by answering the following questions: Who learns about what and how? How is policy described, as an explicit optimization problems or by a behavioral policy rule? In this paper, policy is optimized while the public solves a signal extraction problem about hidden policy targets.

The tractability of the solution method presented here stems from the unobservable states following smooth, Gaussian processes as opposed to regime switches. Discrete regime switches are attractive for modeling central bank "types" like weak/soft or commitment/discretion as in Backus and Driffill (1985b), Cukierman and Liviatan (1991), Ball (1995), Walsh (2000) and King, Lu, and Pasten (2008). Unobserved regime switches lead to important non-linearities in the public's inference problem, which complicate the constraints in an optimal policy problem considerably. The aforementioned literature has correspondingly focused on very small state spaces and/or finite horizon problems, since unobserved regimes switches are hard to incorporate into the kind of general dynamic settings commonly used for policy analysis. Svensson and Williams (2006) discuss the resulting difficulties in more detail.

Learning about regime-switches does not pose such problem when it is the central bank who learns about economic conditions as in Sargent (1999). This is because of the strategic behavior of the policymaker when facing agents learning about, respectively from, him as opposed to the non-strategic behavior of atomistic private agents.

Svensson and Woodford (2003, 2004), Aoki (2006) study optimal policy with an imperfectly informed central bank in linear quadratic settings similar to mine. A convenient feature of this approach is that the public's "learning" reduces to a time-invariant signal extraction problem. This is different from the kind of evolutionary belief system studied in the learning literature represented for example by Evans and Honkapohja (2001). Adaptive learning leads to interesting dynamics where past data drives changes in regression coefficients, but is so far hard to capture in optimal policy problem. For fixed policy rules, the issue is analyzed by Orphanides and Williams (2006); 2005). An exception is the work of Gaspar, Smets, and Vestin (2006) who endow the public with a time-varying, adaptive learning rule. They derive a Markov-perfect policy with history dependence induced similarly as here via the reaction to people's beliefs. Their policies generate data with low inflation persistence to influence people's constant gain learning. Thanks to the lower complexity of the inference problem adopted here, their results can be corroborated in a very transparent way.

Hidden information is modeled here as a signal extraction problem where the private sector does not observe the realization of shocks, but where the structure of the economy and its parameter values are mutually known. In a rational expectations equilibrium, the private sector then knows the correct policy function but can only imperfectly infer the nature of shocks. This equilibrium notion is stronger than the self-confirming equilibria considered by Fudenberg and Levine (1993) and Sargent (1999) or the recursive learning schemes studied for example by Evans and Honkapohja (2001) or Orphanides and Williams (2005). In those cases, the public beliefs about structural relations may be erroneous as long as they are justified by the data generated from the model. In the rational expectations equilibrium pursued here, the public knows the true policy function -- but not the states driving it. This serves as a useful, non-trivial benchmark for evaluating the consequences of a superiorly informed policymaker in dynamic economies.

Closest to the simple model studied in Section 2 are the studies by Cukierman and Meltzer (1986) and Faust and Svensson (2001; 2002). This paper shares with them not only the linear framework and the Kalman filtering of the public, but also that it casts the policy problem around unobserved policy goals. New is the general framework capable of handling various models with endogenous state variables. Faust and Svensson (2001) focus on the welfare effects of credibility. Within a slightly different economic structure (forward-looking Phillips Curve instead of Lucas-supply curve),³⁰ their results are broadly confirmed here: Outcomes are improved when output targets are unobservable. (See also the discussion on varying transparency in Section 2.4.) The common force at work is that the updating of public beliefs depends directly on observed policy. Similar to mechanisms discussed by Walsh (2000), this disciplines policy while retaining Markov-perfect time-consistency.

6 Conclusions

This paper has solved for the optimal discretion policy in a New Keynesian model with unknown output targets and finds that the policy seeks to contract the economy in response to inflationary beliefs. In addition, the pursuit of output targets is scaled back, because of their inflationary effects on public beliefs. This policy, in particular its history dependence, shares some similarities with commitment policies. To the extent that hidden information is a realistic feature of actual policymaking, this suggests much smaller costs for real-world policymakers from retaining some degree of discretion as long as they keep public beliefs about their intentions in check.

The stylized model analyzed here implies that intransparency of policy targets is preferable -- at least under discretion. However, an important caveat is that public beliefs matter here only for linking economic activity to pricing decisions in the New Keynesian Phillips Curve. The welfare effects of transparency might be subject trade-offs, leading to more differentiated results, when expectations of future activity were to affect both investment and pricing decisions.

The model gives also rise to belief shocks as a source of business cycle fluctuations. Similar to the work of Lorenzoni (2006), such shocks shift public perceptions about economics fundamentals, whilst the actual fundamentals remain unchanged. Under imperfect information, these shifts in public beliefs are rational since the belief shocks are correlated with informative signals about fundamentals. The optimal discretion policy seeks to quell the erroneous beliefs arising from these shocks. In the New Keynesian model studied here, belief shocks induce dynamics similar to cost push shocks, which is similar to belief shock dynamics found by Angeletos and La'O (2008b) based on higher-order dynamics.

Apart from illustrating the optimal policy under imperfect information within a widely studied New Keynesian model, the technical appendix to this paper provides a general solution method which allows to extend the analysis to larger settings, relevant for practical policy analysis. By relying on linear quadratic approximations and Gaussian uncertainty, the optimal policy problem becomes tractable without losing its economic intricacy.

For the class of models considered here, public beliefs about the policymaker's hidden information become a distinct state variable of the policy problem, when a policymaker is better informed than the public. These public beliefs are shaped by observed policy actions, giving a scope for managing beliefs about future policies that is otherwise absent in a discretionary policy problem. Since public beliefs are a natural state variable under imperfect information, managing this state of beliefs is Markov-perfect and time consistent.³¹

A fruitful area for future research would be to extend the analysis to a policymaker's private information about economic fundamentals, for example determinants of potential output. Such information would be widely dispersed amongst different members of the public as well as the central bank, suggesting to combine the policy concepts studied here with the dispersed information settings studied for example by Lorenzoni (2006) or Angeletos and La'O (2008a).

Appendix

1 Innovation Representation in the Simple Model

This section derives the ARMA(1,1) innovations process (9) for policy in the simple model of Section 2. First, policy can be separated into innovation and public expectations
$\begin{align} x_t &= \underbrace{f_\tau\tilde\tau_t +f_\varepsilon\tilde\varepsilon_t}_{\tilde x_t} + \underbrace{(f_\tau+f_b)\tau_{t\vert t-1}}_{x_{t\vert t-1}} \end{align}$
The ARMA representation follows from using $\tau_{t+1\vert t} =\rho\;\tau_{t\vert t}$ and the Kalman filter to express the evolution of prior beliefs as
$\begin{align*} x_{t+1\vert t} = \rho x_t + \rho \left((f_\tau+f_b) K_\tau -1\right) \tilde{x}_{t} \end{align*}$

2 Kalman Filter in the Simple Model

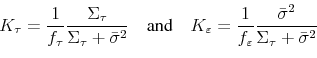In the simple model of Section 2, the signal extraction problem of the public uses the policy function (8) as measurement equation and the AR(1) transition of $\tau_t$ (6) as state equation. The Kalman gains are $\begin{equation*} K_\tau = \frac{1}{f_\tau} \frac{\Sigma_\tau}{\Sigma_\tau + \bar\sigma^2} \quad\text{and}\quad K_\varepsilon = \frac{1}{f_\varepsilon} \frac{\bar\sigma^2}{\Sigma_\tau + \bar\sigma^2} \end{equation*}$ where $\bar\sigma^2 \equiv f_\varepsilon^2 / f_\tau^2 \cdot \sigma_\varepsilon^2$ and $\Sigma_\tau$ solves the Riccati equation
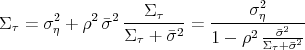
$\begin{align*} \Sigma_\tau &= \sigma_\eta^2 + \rho^2 \bar\sigma^2 \frac{\Sigma_\tau}{\Sigma_\tau + \bar\sigma^2} = \frac{\sigma_\eta^2}{1 - \rho^2 \frac{ \bar\sigma^2}{\Sigma_\tau + \bar\sigma^2}} \end{align*}$

As discussed on Section 2.3, it is plausible to assume that $0\leq f_\tau\leq 1$ , $0\leq f_\varepsilon \leq 1$ , $f_b\leq 0$ , and $f_\tau+f_b\geq 0$ . It is then straightforward to verify that $-1\leq \psi \leq 0$ , since the Kalman gains are positive and $f_\tau K_\tau + f_\varepsilon K_\varepsilon =1$ .

3 Compensating Rate of Average Inflation

Section 2.4 evaluates ex-ante policy losses based on the policymaker's objective function

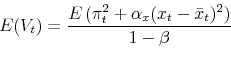
$\begin{displaymath}E(V_t) = \frac{E\left( \pi_t^2 + \alpha_x (x_t-\bar x_t)^2 \right)}{1-\beta} \end{displaymath}$

The difference in losses under hidden versus full information, can be expressed as a compensating rate of average inflation, $\bar\pi$ , which would equalize policy losses in both equilibria when added to the dynamics under hidden information.

$\begin{displaymath}E((1-\beta) V_t\vert\text{Full Info}) = E \left( (\pi_t+\bar\pi)^2 + \alpha_x (x_t-\bar x_t)^2 \vert\text{Hidden Info} \right)\end{displaymath}$

As an alternative measure of policy losses, this "compensating average inflation" abstracts from the validity of the linear quadratic framework for non-zero (or non-indexed) inflation rates in steady state.

Since this paper looks only at shocks to output targets, the calibration does not try to match a level of second moments observed in the data and the compensating rate of average inflation is scaled by the standard deviation of inflation under hidden information.

Bibliography

Abrams, Burton A. 2006.

How Richard Nixon Pressured Arthur Burns: Evidence from the Nixon Tapes.
Journal of Economic Perspectives 20 (4): 177-188 (Fall).

Angeletos, George-Marios, and Jennifer La'O. 2008a

October.
Dispersed Information over the Business Cycle: Optimal Fiscal and Monetary Policy.
mimeo, MIT.

Angeletos, George-Marios, and Jennifer La'O. 2008b

December.
Incomplete Information, Higher-Order Beliefs and Price Inertia.
mimeo, MIT.

Aoki, Kosuke. 2003.

On the optimal monetary policy response to noisy indicators.
Journal of Monetary Economics 50 (3): 501-523 (April).

Aoki, Kosuke. 2006.

Optimal commitment policy under noisy information.
Journal of Economic Dynamics and Control 30 (1): 81-109 (January).

Backus, David, and John Driffill. 1985a.

Inflation and Reputation.
The American Economic Review 75 (3): 530-538 (June).

Backus, David, and John Driffill. 1985b.

Rational Expectations and Policy Credibility Following a Change in Regime.
The Review of Economic Studies 52 (2): 211-221 (April).

Ball, Laurence. 1995.

Time-consistent policy and persistent changes in inflation.
Journal of Monetary Economics 36 (2): 329-350 (November).

Barro, Robert J., and David B. Gordon. 1983a.

A Positive Theory of Monetary Policy in a Natural Rate Model.
The Journal of Political Economy 91 (4): 589-610 (August).

Barro, Robert J., and David B. Gordon. 1983b.

Rules, Discretion and Reputation in a Model of Monetary Policy.
Journal of Monetary Economics 12 (July): 101-121.

Blinder, Alan S. 1998.

Central Banking in Theory and Practice.
1st MIT Press paperback edition, 1999.
The Lionel Robbins Lectures.
Cambridge, MA: The MIT Press.

Bordo, Michael D., Christopher Erceg, Andrew Levin, and Ryan Michaels. 2007

March.
Three Great American Disinflations.
NBER Working Papers 12982, National Bureau of Economic Research, Inc.

Calvo, G.A. 1983.

Staggerd Prices in a Utility-Maximizing Framework.
Journal of Monetary Economics 12 (3): 383-398.

Canzoneri, Matthew B. 1985.

Monetary Policy Games and the Role of Private Information.
The American Economic Review 75 (5): 1056-1070 (December).

Chari, V. V., and Patrick J. Kehoe. 1990.

Sustainable Plans.
The Journal of Political Economy 98 (4): 783-802 (August).

Christiano, Lawrence J., Martin Eichenbaum, and Charles L. Evans. 2005.

Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy.
Journal of Political Economy 113 (1): 1-45 (February).

Clarida, Richard, Jordi Gali, and Mark Gertler. 1999.

The Science of Monetary Policy: A New Keynesian Perspective.
Journal of Economic Literature 37 (December): 1661-1707.

Cukierman, Alex, and Nissan Liviatan. 1991.

Optimal accommodation by strong policymakers under incomplete information.
Journal of Monetary Economics 27 (1): 99-127 (February).

Cukierman, Alex, and Allan H. Meltzer. 1986.

A Theory of Ambiguity, Credibility, and Inflation under Discretion and Asymmetric Information.
Econometrica 54 (5): 1099-1128 (September).

Erceg, Christopher J., and Andrew T. Levin. 2003.

Imperfect credibility and inflation persistence.
Journal of Monetary Economics 50 (4): 915-944 (May).

Evans, George W., and Seppo Honkapohja. 2001.

Learning and Expectations in Marcoeconomics.
Princeton, NJ: Princeton University Press.

Faust, Jon, and Lars E O Svensson. 2001.

Transparency and Credibility: Monetary Policy with Unobservable Goals.
International Economic Review 42 (2): 369-97 (May).

Faust, Jon, and Lars E O Svensson. 2002.

The Equilibrium Degree of Transparency and Control in Monetary Policy.
Journal of Money, Credit and Banking 34 (2): 520-39 (May).

Fudenberg, Drew, and David K. Levine. 1993.

Self-Confirming Equilibrium.
Econometrica 61 (3): 523-545 (May).

Gali, Jordi. 2003.

New Perspectives on Monetary Policy, Inflation, and the Business Cycle.
Chapter 6 of Advances in Economics and Econometrics: Theory and Applications, edited by Mathias Dewatripont, Lars Peter Hansen, and Stephen J. Turnovsky, Eighth World Congress of the Econometric Society, 151-197.
Cambridge, UK: Cambridge University Press.

Gali, Jordi. 2008.

Monetary Policy, Inflation, and the Business Cycle: An Introduction to the New Keynesian Framework.
Princeton, New Jersey: Princeton University Press.

Gaspar, Vitor, Frank Smets, and David Vestin. 2006.

Adaptive Learning, Persistence, and Optimal Monetary Policy.
Journal of the European Economic Association 4 (2-3): 376-385 (04-05).

Goodfriend, Marvin, and Robert G. King. 2005.

The Incredible Volcker Disinflation.
Journal of Monetary Economics 52 (5): 981-1015 (July).

Gordon, Robert J. 1982.

Chapter 2 of Why Stopping Inflation May Be Costly: Evidence from Fourteen Historical Episodes, 11 - 40.
The University of Chicago Press.

Ireland, Peter N. 1995.

Optimal disinflationary paths.
Journal of Economic Dynamics and Control 19 (8): 1429-1448 (November).

Ireland, Peter N. 1997.

Stopping Inflations, Big and Small.
Journal of Money, Credit and Banking 29 (4): 759-775 (November).

King, Robert G., and Marvin Goodfriend. 1997.

The New Neoclassical Synthesis and the Role of Monetary Policy.
In NBER Macroeconomics Annual 1997, edited by Ben S. Bernanke and Julio J. Rotemberg, 231-283.
Cambridge (MA): The MIT Press.

King, Robert G., Yang K. Lu, and Ernesto S. Pasten. 2008.

Managing Expectations.
Journal of Money, Credit and Banking 40 (8): 1625-1666.

King, Robert G., and Alexander L. Wolman. 1996.

Inflation targeting in a St. Louis model of the 21st century.
Review 78 (3): 83-107 (May/June).

Kydland, Finn E., and Edward C. Prescott. 1977.

Rules Rather than Discretion: The Inconsistency of Optimal Plans.
The Journal of Political Economy 85 (3): 473-492 (June).

Lorenzoni, Guido. 2006

August.
A Theory of Demand Shocks.
NBER Working Papers 12477, National Bureau of Economic Research, Inc.
forthcoming in the American Economic Review.

Morris, Stephen, and Hyun Song Shin. 2002.

Social Value of Public Information.
American Economic Review 92 (5): 1521-1534 (December).

Orphanides, Athanasios, and John C. Williams. 2005.

Inflation scares and forecast-based monetary policy.
Review of Economic Dynamics 8 (2): 498-527 (April).

Orphanides, Athanasios, and John C. Williams. 2006.

Monetary Policy with Imperfect Knowledge.
Journal of the European Economic Association 4 (2-3): 366-375 (04-05).

Persson, Torsten, and Guido Tabellini. 2000.

Political Economics.
Zeuthen lecture book series.
Cambridge, MA: The MIT Press.

Rogoff, Kenneth. 1989.

Reputation, Coordination and Monetary Policy.
Chapter 6 of Modern Business Cycle Theory, edited by Robert J. Barro.
Cambridge, MA: Harvard University Press.

Sargent, Thomas J. 1982.

Chapter 3 of The End of Four Big Inflations, 41 - 97.
The University of Chicago Press.

Sargent, Thomas J.. 1999.

The Conquest of American Inflation.
Princeton (NJ): Princeton University Press.

Svensson, Lars E. O. 1997.

Optimal Inflation Targets, "Conservative" Central Banks, and Linear Inflation Contracts.
The American Economic Review 87 (1): 98-114.

Svensson, Lars E. O., and Michael Woodford. 2003.

Indicator variables for optimal policy.
Journal of Monetary Economics 50 (3): 691-720 (April).

Svensson, Lars E. O., and Michael Woodford. 2004.

Indicator variables for optimal policy under asymmetric information.
Journal of Economic Dynamics and Control 28 (4): 661-690 (January).

Svensson, Lars E.O., and Noah Williams. 2006

November.
Bayesian and Adaptive Optimal Policy under Model Uncertainty.
mimeo Princeton University.

Vestin, David. 2006.

Price-level versus inflation targeting.
Journal of Monetary Economics 53 (7): 1361-1376 (October).

Walsh, Carl E. 2000.

Market Discipline and Monetary Policy.
Oxford Economic Papers 52 (2): 249-271 (April).

Walsh, Carl E.. 2003.

Monetary Theory and Policy.
2nd edition.
Cambridge, MA: The MIT Press.

Woodford, Michael. 2003a.

Interest and Prices.
Princeton, NJ: Princeton University Press.

Woodford, Michael. 2003b.

Optimal Interest-Rate Smoothing.
Review of Economic Studies 70 (4): 861-886 (October).

Woodford, Michael. 2005

August.
Central bank communication and policy effectiveness.
The Greenspan Era: Lessons for the Future.
FRB Kansas City Symposium, Jackson Hole, Wyoming, 399-474.

Yun, Tack. 1996.

Nominal price rigidity, money supply endogeneity, and business cycles.
Journal of Monetary Economics 37 (2): 345-370 (April).

Footnotes

1. A complete literature review can be found in Section 5. Return to Text

2. Of course, in equilibrium inflation always depends on monetary policy. But in perfect information models of discretionary policy, this dependence occurs mostly indirectly and in ways beyond the control of a current period policymaker. Return to Text

3. See also 1998 1998, who downplays the relevance of time-inconsistency as a major distortion in real-world decisions at central banks. Return to Text

4. The closest counterpart to my analysis should be the work of Ireland (1995) who imposes a sluggish response of public beliefs to policy announcements. Return to Text

5. See for example the classic contributions by Backus and Driffill (1985a), Canzoneri (1985) and Cukierman and Liviatan (1991), where my definition of static includes also repeated play of one-period games. More recent work includes the papers by Ball (1995) and Walsh (2000). Fully dynamic, but limited in size, are the models of Gaspar, Smets, and Vestin (2006), Faust and Svensson (2001; 2002), Cukierman and Meltzer (1986). A more detailed discussion of the literature can be found in Section 5. Return to Text

6. Throughout the paper, all variables are in log-deviations from steady state, which implicitly assumes the existence and uniqueness of a steady state under discretionary policy. Return to Text

7. Details are given by Gali (2003), p. 159 from whom notation is adopted. Return to Text

8. King and Goodfriend (1997) explain how the New Keynesian model can be separated into a core real business-cycle model (RBC), which evolves as if there were no nominal frictions, and a set of "gap" variables that track the difference between the RBC core and the actual economy. This separation has been widely adopted for example in the textbooks of Walsh (2003), Woodford (2003a) and Gali (2008). Return to Text

9. For starters, time-variation in the output target could arise from variations in wedges between the frictionless and the efficient level of output. Time-varying markups would for example shrink distortions from monopolistic competition. There are non-monetary tools to fight such distortions, for example the kind of fiscal tools discussed by Gali (2003). $\bar{x}_t$ could then capture changes in the government's policy of handling these distortions. Return to Text

10. In the real world, pressures mounted on central bankers appear to be a recurring, though not necessarily permanent feature. For example, in the short history of the ECB there were the early attempts by German Finance Minister "Red" Oskar Lafontaine and later overtures from the French President Nicolas Sarkozy. Return to Text

11. In the results discussed below there will not be a conflict in ranking outcomes under this measure as opposed to the policymaker's objective. Return to Text

12. The process is mean zero and allows also for negative targets. But all variables are in deviation from steady state. By allowing for a (known) average target, this would lead to the classic inflation bias in steady state. (In the context of the present model, details can be found in Woodford (2003a).) To be consistent with non-zero inflation in steady state, the Phillips Curve is then viewed as allowing for indexation to the steady state rate of inflation as in Yun (1996). Return to Text

13. In general, the policymaker could not take inflation expectations as given numbers but as a given mapping from expected future state values, where the latter may be partly under his control. This will be the case under hidden information. Return to Text

14. In principle, this includes also the history of inflation rates $\pi^t$ . But as a choice variable of the private sector, inflation merely reflects the private sectors information set, without providing additional information beyond

. Return to Text

15. Since $x_t=x_{t\vert t}$ in this simple model, it follows that $f_\tau K_\tau + f_\varepsilon K_\varepsilon =1$ . When the mixing ratio goes to zero, this collapses to $f_\tau K_\tau =1$ . Return to Text

16. Persson and Tabellini (2000), Chapter 11 review applications of Markov-perfect equilibria to macroeconomic policy problems. Return to Text

17. This assumption implies that the public expects policies to be expansionary, $x_{t\vert t-1}>0$ , when $\tau_{t\vert t-1} > 0$ . Return to Text

18. It is straightforward to show that $\gamma_0>0$ follows from the positive definiteness of the value function, and $\gamma_2>0$ from the aforementioned assumptions on the policy coefficients. Analytically, $\gamma_1$ cannot be signed, but for the variety of calibrations considered in the numerical simulations below it turns out to be positive. Return to Text

19. Given the limited range of shocks considered, the calibration is not designed to match the level of variations observed in the data. Return to Text

20. For the baseline calibration, the mixing ratio is 1.2340 under symmetric information and 1.2866 under hidden information. Return to Text

21. The loss function can be written as $L_t=\kappa^2 \bar\pi_t^2 + \alpha_x(x_t-\bar{x}_t)^2$ , where $\bar\pi_t = \sum_{j=0}^\infty \beta^j x_{t+j\vert t}$ . Return to Text

22. Additional details are given in Appendix C. Return to Text

23. Expected loss,

, is the unconditional expectation of the policymaker's value function across states of nature. (See the Technical Appendix for computational details.) Optimal policy is of course defined on a state-by-state basis. Return to Text

24. The meaning of "fundamentals" is intended here in the sense of the full-information economy. Return to Text

25. This is similar to what Faust and Svensson (2001), p. 374 call the regime "OG: observable goal and intention", for which they find results corresponding to what has been found in this paper. Return to Text

26. Related is the work of Ireland (1995) who finds similar results when imposing a sluggish response of public beliefs on policy announcements. As an alternative, Ireland (1997) 1997 seeks to reconcile the conjectures of Sargent (1982) and Gordon (1982) by differentiating between disinflations at high or low levels of inflation. Return to Text

27. Similarly, the negative response to a belief shock is stronger for larger values of $\sigma_n$ , up to the point where the growing noise variance beliefs react less and less to these shocks as . Return to Text

28. As in Woodford (2003a) or Christiano, Eichenbaum, and Evans (2005) this can be derived from the optimizing behavior of Firms under Calvo pricing. Firms who do not optimize their prices are supposed to change prices at the rate $\Pi_{t-1}^\gamma$ where $\Pi_{t-1}$ is last period's level (not log) of inflation. As shown by Woodford (2003a), this changes also welfare functions such as (2) to be concerned with quasi-differenced inflation $\pi_t-\gamma \pi_{t-1}$ instead of inflation. The point of the experiment is here is however to consider how exogenous persistence changes policies whilst keeping the objective function constant. The policymaker's loss function is thus kept unchanged. Return to Text

29. Other parameters are calibrated at the values shown in Table 1. Return to Text

30. A further difference is that their analogue to the

shock $\varepsilon_t$ is not a target component but a control error of policy. Return to Text

31. This excludes the explicit reputational mechanisms based on history dependent strategies known from by Barro and Gordon (1983b) or Chari and Kehoe (1990) are excluded from the analysis. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Managing Beliefs aboutMonetary Policy under Discretion