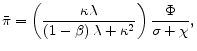Using a Projection Method to Analyze
Inflation Bias in a Micro-Founded Model*
Keywords: Inflation bias, discretionary monetary policy, projection methods
Abstract:
1 Introduction
Since Kydland and Prescott (1977) initiated the literature of rules versus discretion, improvement upon discretionary equilibria by reducing inflation bias has long been a research theme in policy circles as well as academia, including Barro and Gordon (1983), Clarida, Gali and Gertler (1999), M. King (1997) and Woodford (2003). In most of the existing papers on the inflation bias, the one-period loss function assigned to the central bank is quadratic in inflation and the level of output relative to its target. It is well known that Rotemberg and Woodford (1997) and Benigno and Woodford (2006) have provided a microfoundation for the use of such a loss function by showing that this simple quadratic function can be derived as the second-order approximation to the non-linear social welfare function in a Calvo model.
However, as discussed in Woodford (2003), such a derivation does not hold under discretion unless the steady-state level of output under flexible prices is sufficiently close to its efficient level; these papers approximate the model around the deterministic steady state with zero inflation, but the optimal allocation under discretion leads to an unknown positive inflation under monopolistic distortion. In light of this observation, this paper does not follow the conventional linear-quadratic approach to studying the inflation bias induced by discretion. Instead, we use a projection method to analyze the inflation bias in a microfounded non-linear model with a Calvo price-setting environment. In our model, since the optimal inflation rate under commitment is zero, the inflation bias is defined as the (optimal) discretionary inflation rate. To do so, we characterize a set of conditions for the optimal allocation under discretion without any approximations. We then use Chebyshev polynomials to approximate policy functions that link inflation and output to a set of state variables, thereby converting optimization conditions into a set of non-linear equations for the coefficients of Chebyshev polynomials. The results on inflation bias based on the global projection method are compared with those based on the linear-quadratic approximation method.
We would like to note that perturbation methods can be modified and used to analyze this problem. For example, Dotsey and Hornstein (2003) and Klein, Krusell and R
![]() os-Rull (2008) have employed a perturbation method, with an iterative procedure to compute numerical solutions: Dotsey and Hornstein (2003) solve an optimal discretion problem
with an iteration of the linear-quadratic approximation, while Klein, Krusell and R
os-Rull (2008) have employed a perturbation method, with an iterative procedure to compute numerical solutions: Dotsey and Hornstein (2003) solve an optimal discretion problem
with an iteration of the linear-quadratic approximation, while Klein, Krusell and R
![]() os-Rull (2008) apply a perturbation procedure to a nonlinear Generalized Euler Equation. These methods can be used to compute the optimal inflation rate at a deterministic
steady state. But we have chosen to use the projection method since this method can conveniently be extended to a stochastic setting with technology shocks.
os-Rull (2008) apply a perturbation procedure to a nonlinear Generalized Euler Equation. These methods can be used to compute the optimal inflation rate at a deterministic
steady state. But we have chosen to use the projection method since this method can conveniently be extended to a stochastic setting with technology shocks.
Our paper is not the only one to analyze the discretionary equilibrium in a nonlinear Calvo model. Wolman and Van Zandweghe (2008) use a fixed-point algorithm to solve for the optimal policy instrument and investigate whether multiple Markov Perfect Equilibria can arise in the Calvo model--as compared to the results of King and Wolman (2004) for the Taylor pricing contract. In addition, Adam and Billi (2007) work on optimal discretion in a model that is linear in every aspect except for the zero lower bound for the nominal interest rate.
The rest of this paper is organized as follows. In section 2, we describe a discretionary equilibrium in the Calvo (1983) pricing model where the planner is not allowed to make any commitment about his or her future behavior. Section 3 contains numerical results based on the projection method. In section 4, we conclude.
2 Economic Structure and Discretionary Equilibrium
This section describes the economic structure in our model and the discretionary equilibrium of the planner's problem.
2.1 Economic Structure
The economy is populated by households and firms.
2.1.1 Households
At period 0, the preference ordering of the representative household is summarized by
where
where
The parameter
The household's dynamic budget constraint at period ![]() is given by
is given by
where
The representative household maximizes (1) subject to the flow budget constraints (5) in each period. The first-order conditions are given by
and substitution of (8) into (6) yields the consumption Euler equation:
2.1.2 Firms
Each firm produces a differentiated good ![]() using a constant returns to scale production function:
using a constant returns to scale production function:
| (10) |
where
where
Furthermore, the Calvo type staggering transforms equation (4) into
Next, we will show that the profit maximization condition (12) can be rewritten in a recursive way. In order to see this, note that substituting (8) into (12) and then rearranging, we have
It is now useful to define two variables,
We then have the following recursive representations of the two variables
with two terminal conditions,
![\displaystyle \lim_{T\rightarrow \infty }\left( \alpha \beta \right) ^{T}E_{t}\left[ \left( \prod_{k=1}^{T}\Pi _{t+k}^{\epsilon -1}\right) F_{t+T}\right] =0,~~\lim_{T\rightarrow \infty }\left( \alpha \beta \right) ^{T}E_{t}\left[ \left( \prod_{k=1}^{T}\Pi _{t+k}^{\epsilon }\right) S_{t+T}\right] =0,](img57.gif)
|
where
In addition, substituting equation (18) into (13) leads to
We have thus expressed the profit maximization condition (14) and the price level definition (13) in terms of
2.1.3 Social Resource Constraint
In any model with staggered price setting, relative prices can differ across firms. Furthermore, if firms have different relative prices, there are distortions that create a wedge between the aggregate output measured in terms of production factor inputs and the aggregate demand measured in terms of the composite goods. In order to see the relative price distortions, let us aggregate individual outputs:
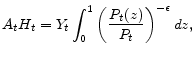 |
where
the aggregate production function can be written as follows:
In order to obtain a law of motion for the measure of relative price distortion described above, note that the Calvo-type staggering allows one to rewrite the measure of relative price distortions specified in equation (20) as
Then, substituting (13) into (22), one can derive an expression for how the measure of relative price distortions evolves over time:
Finally, the aggregate market clearing condition is given by
so the social resource constraint in period
2.2 The Planner's Problem under Discretion
In this section, following Woodford (2003), we interpret a planner's problem without commitment as an optimal planning problem. In his book (p. 465), the optimal allocation under discretion is defined as "a procedure under which at each time that an action is to be taken, the central bank evaluates the economy's current state and hence its possible future paths from now on, and chooses the optimal current actions in the light of this analysis, with no advance commitment about future actions, except that they will similarly be the ones that seem best in whatever state may be reached in the future."
Before proceeding, it is worth discussing implementability constraints, which restrict the feasible allocations of the social planner. First, the household budget constraint is not included as a constraint for the optimal allocation problem because of the lump-sum tax. Second, the size of the employment subsidy rate determines whether the profit maximization condition is binding or not as an implementability constraint in the optimal allocation problem.
In order to gain some insights about the role of the employment subsidy, we describe the equilibrium conditions for the flexible price model and then compare them with those for the first-best equilibrium. Since ![]() corresponds to the flexible-price model, it follows from (12) that the profit maximization condition for the flexible-price model turns out to be
corresponds to the flexible-price model, it follows from (12) that the profit maximization condition for the flexible-price model turns out to be
where
where
We can see from (27) that when we set
We now characterize the planner's problem under discretion, which is similar to the setup of Adam and Billi (2007) except for their imposition of the zero lower bound and our more disaggregated nonlinear constraints. The government at period 0 chooses a set of decision
rules for ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]() in order to maximize
in order to maximize
subject to the following equilibrium conditions in each period
Here, the absence of commitment leads us to express the values of period
3 Projection Methods and Numerical Results
This section starts with a description of a projection method to obtain numerical solutions for the discretionary equilibrium. We will also present our numerical results regarding the size of optimal inflation under discretion that are compared with those from a linear-quadratic approximation analysis (e.g. Woodford, 2003).
3.1 Projection Method with Homotopy Procedure: A Nontechnical Guide
We employ a projection method to compute numerical solutions that approximate the nonlinear dynamic system of implementablity conditions of the planner's problem and its first-order conditions. In order to deal with a feature of the generalized Euler equation that future variables should be expressed as functions of current variables, we approximate policy functions by a set of Chebyshev polynomials because functional forms of derivatives of Chebyshev polynomials are analytically known. We also adopt a homotopy procedure to improve on our initial guesses for the nonlinear solution. Our use of a homotopy procedure is motivated by our finding that in the course of obtaining valid solutions over the relevant range of state variables, it was important to have flexibility in setting and readjusting the range of these variables.2
In our computation, we begin by characterizing the full set of dynamic equilibrium conditions in a non-linear state-space representation. In order to do this, we define a new function ![]() in order to collect the policy functions of endogenous variables as follows:
in order to collect the policy functions of endogenous variables as follows:
where the realized values at period
where
Turning to the solution method, we adopt a projection method to approximate the functions. Furthermore, since we allow for random technology shocks, we express each of the functions,
![]() , as a linear combination of an outer product of orthogonal polynomials in
, as a linear combination of an outer product of orthogonal polynomials in
![]() and
and ![]() :
:
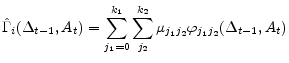 |
where
3.2 Some Implementation Issues
Initially, we investigated adapting existing code for solving the problem. We have located freely available FORTRAN code from Judd (1992) and MATLAB code from Gapen and Cosimano (2005). We found that the code was very useful for benchmarking and validation but difficult to modify to solve our particular problem.
For the problem at hand, we have found that--to obtain convergence for a given degree of approximation--it is important to start with a narrow range of values of
![]() in the definition of the Chebyshev polynomials, and then gradually extend the range. Thus, our code systematically adjusts the range of Chebyshev polynomials from narrow to
wide, for a given set of parameters and a given degree of approximation.
in the definition of the Chebyshev polynomials, and then gradually extend the range. Thus, our code systematically adjusts the range of Chebyshev polynomials from narrow to
wide, for a given set of parameters and a given degree of approximation.
We have implemented the projection method software in Java. The object oriented nature of Java and the availability of the open-source Eclipse IDE (Geer, 2005) for Java greatly facilitated developing the software.4 Furthermore, because of the notoriously slow "for" loops in MATLAB, the Java code runs much faster than it would have if we had used generic MATLAB routines.5 The Java code can run on both Linux and Windows machines. We currently use Mathematica as a user-interface to the Java Code. Both JBENDGE and JMulTi are based on the JStatCom which provides a standardized application interface which we hope to adopt in the future.6
There are a number of improvements in the code that could be addressed in the future. We envision developing a generic open source tool, but currently the code depends on Mathematica; we would like to develop a Dynare interface. The program uses a simple operator overloading while it would be preferable to use more efficient automatic differentiation techniques.
3.3 Numerical Results
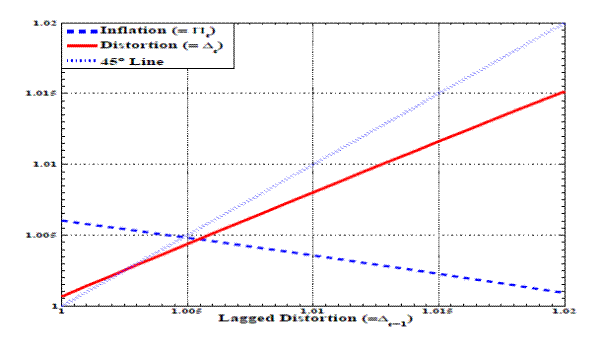
Note: This figure expresses the current level of relative price distortion as a function of its lagged level in order to demonstrate how the measure of the relative price distortion distortion converges to its steady-state level.To determine the optimal inflation rate under discretion, we must assign numerical values to the parameters. Although we experimented with many different values, the benchmark parameter values are taken from Yun (2005). For example, we assumed that utility is logarithmic in consumption
(![]() ) and quadratic in labor (
) and quadratic in labor (![]() ). We also set
). We also set
![]() ,
,
![]() , and
, and
![]() . We depart from Yun (2005) along one dimension: there is no subsidy nullifying the monopolistic distortion so the degree of monopolistic distortion is kept at
. We depart from Yun (2005) along one dimension: there is no subsidy nullifying the monopolistic distortion so the degree of monopolistic distortion is kept at
![]() in the benchmark. Table 1 summarizes our benchmark parameter values.
in the benchmark. Table 1 summarizes our benchmark parameter values.
Table 1: Calibration of Parameters
| Value | Definition | |
| 1 | Relative risk-aversion coefficient | |
| 1 | Inverse of labor supply elasticity | |
| 0.99 | Time-discount factor | |
| 11 | Demand elasticity | |
| 0.75 | Probability of fixing prices in each period | |
| 0.091 | Degree of distortion | |
| 0.95 | AR(1) coefficient of the logarithm of labor productivity | |
|
|
0.01 | Standard deviation of technology shock |
Using this benchmark specification, we solve the model via a projection method contemplating values for the relative price distortion in the range of
![]() . Figure 1 illustrates the solution of this discretionary equilibrium. The solid line represents the values of
. Figure 1 illustrates the solution of this discretionary equilibrium. The solid line represents the values of
![]() as a function of
as a function of
![]() , shown for a narrow range of
, shown for a narrow range of
![]() to focus on the area around the steady state. This line crosses the 45-degree line (dotted) at around 1.0026, which is the steady-state value for the dispersion measure.
At this steady state, the value of
to focus on the area around the steady state. This line crosses the 45-degree line (dotted) at around 1.0026, which is the steady-state value for the dispersion measure.
At this steady state, the value of ![]() is about 1.0054 (dashed line). In terms of the annualized rate for net inflation, this steady-state inflation rate corresponds to 2.2%.7
is about 1.0054 (dashed line). In terms of the annualized rate for net inflation, this steady-state inflation rate corresponds to 2.2%.7
Since the results in Figure 1 are based on a global solution method, it would be instructive to provide some measure of error in the approximation. As a heuristic measure, we compare two ways of computing the relative price distortion. One is the approximate solution for the
distortion as reported in Figure 1, and the other is the right-hand side of (32) with inflation set to the values reported in this figure. We then compute the relative difference between these two ways of computing the size of relative price distortion. Over the full
collocation range of distortion, ![]() , the maximum percentage difference is on the order of
, the maximum percentage difference is on the order of ![]() .
.
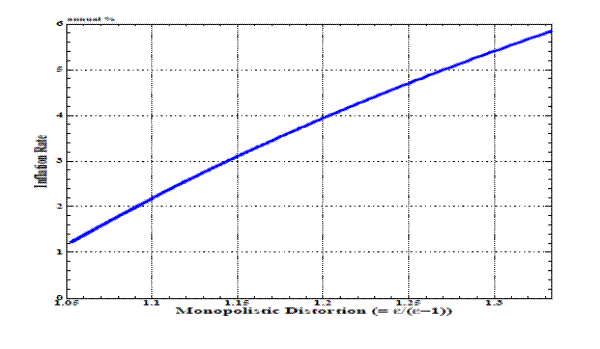
It is widely known that the size of the inflation bias depends on the degree of monopolistic competition, since imperfect competition makes equilibrium flexible-price output lower than the socially efficient output. In our benchmark specification used in Figure 1, the
elasticity of substitution (![]() ) determines how monopolistically competitive the economy is, and the size of distortion (
) determines how monopolistically competitive the economy is, and the size of distortion (![]() ) is equal to its reciprocal. Figure 2 shows the size of inflation bias changes as we change the markup by varying
) is equal to its reciprocal. Figure 2 shows the size of inflation bias changes as we change the markup by varying ![]() . Our benchmark of
. Our benchmark of
![]() corresponds to the markup of 1.1. As we decrease
corresponds to the markup of 1.1. As we decrease ![]() , the markup and inflation bias increase. When we choose
, the markup and inflation bias increase. When we choose ![]() , the markup is 1.33, and the inflation bias is about
, the markup is 1.33, and the inflation bias is about ![]() annually.
annually.
To bring out how other parameters affect the size of the inflation bias, we do some comparative statics with the model as shown in Table 2. First, according to the results based on the projection method using our benchmark parameter values, increasing ![]() increases the inflation bias for values of
increases the inflation bias for values of ![]() below 0.85. Increasing
below 0.85. Increasing ![]() decreases steady state inflation for values of
decreases steady state inflation for values of ![]() above 0.85.8 Second, the smaller the curvature parameters (
above 0.85.8 Second, the smaller the curvature parameters (![]() and
and
![]() ), the bigger the inflation bias. When the utility function moves closer to being linear in consumption and labor, the size of the inflation bias increases significantly.
), the bigger the inflation bias. When the utility function moves closer to being linear in consumption and labor, the size of the inflation bias increases significantly.
3.4 Comparison with the Linear-Quadratic Approximations
We now compare our results with those from the conventional linear-quadratic approach (e.g. Woodford, 2003). The inflation bias expression that emerges from this approach is
where
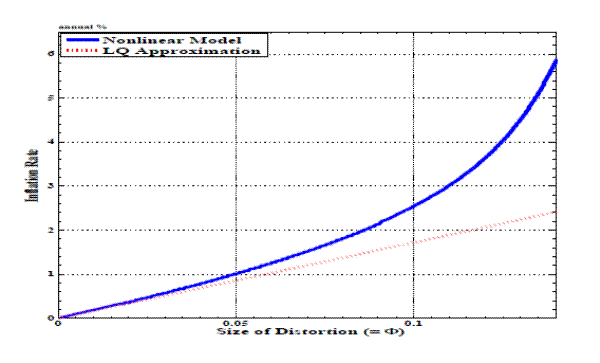
Figure 3 depicts how much the linear-approximation underestimates the inflation bias as we alter the value of ![]() by varying the value of
by varying the value of ![]() or
or ![]() . Note that the range of
. Note that the range of ![]() in this figure covers our benchmark parametrization of
in this figure covers our benchmark parametrization of
![]() . The solid line represents the size of inflation bias under our projection method. The magnitude of the inflation bias increases faster than linearly with respect to the amount
of monopolistic distortion. The dashed line represents the level of inflation bias under the linear-quadratic approximation and becomes tangent to the solid line as
. The solid line represents the size of inflation bias under our projection method. The magnitude of the inflation bias increases faster than linearly with respect to the amount
of monopolistic distortion. The dashed line represents the level of inflation bias under the linear-quadratic approximation and becomes tangent to the solid line as ![]() gets close to
0. The difference between the two lines increases as monopolistic distortion moves the economy farther away from the efficient outcome.
gets close to
0. The difference between the two lines increases as monopolistic distortion moves the economy farther away from the efficient outcome.
Finally, we compare the results of the sensitivity analysis that are obtained from the two approaches. In particular, equation (34) implies that since the discount factor is close to unity, we can approximate the inflation bias under the linear-quadratic approach by
using ![]()
![]()
![]() . According to this formula, the inflation bias is inversely related to
. According to this formula, the inflation bias is inversely related to ![]() ,
, ![]() , and
, and ![]() (given
the size of the total distortion), while the bias is approximately proportional to the size of monopolistic distortion (given the size of the markup). These predictions of the linear-quadratic approach on the sensitivity analysis are confirmed by numerical results in the final column of Table
2. Furthermore, as noted earlier, the nonlinear projection method indicates that the smaller the curvature parameters (
(given
the size of the total distortion), while the bias is approximately proportional to the size of monopolistic distortion (given the size of the markup). These predictions of the linear-quadratic approach on the sensitivity analysis are confirmed by numerical results in the final column of Table
2. Furthermore, as noted earlier, the nonlinear projection method indicates that the smaller the curvature parameters (![]() and
and ![]() ), the bigger the inflation bias. The linear-quadratic and nonlinear projection approaches therefore appear to produce a similar relationship between parameter values and the size of the inflation bias. Based on these
numerical results, one might argue that the simplicity and transparency of the linear-quadratic approach would be very helpful in relating the size of the inflation bias to the values for the parameters, though the linear-quadratic approach underestimates the size of inflation bias. But it should
be noted that such an interpretation could potentially be misleading. For example, when the discount factor is less than unity, the expression for
), the bigger the inflation bias. The linear-quadratic and nonlinear projection approaches therefore appear to produce a similar relationship between parameter values and the size of the inflation bias. Based on these
numerical results, one might argue that the simplicity and transparency of the linear-quadratic approach would be very helpful in relating the size of the inflation bias to the values for the parameters, though the linear-quadratic approach underestimates the size of inflation bias. But it should
be noted that such an interpretation could potentially be misleading. For example, when the discount factor is less than unity, the expression for ![]() indicates that an increase in
indicates that an increase in
![]() would imply a decrease in
would imply a decrease in ![]() . However, according to the results
based on the projection method using our benchmark parameter values, the size of inflation bias is not a monotone function of
. However, according to the results
based on the projection method using our benchmark parameter values, the size of inflation bias is not a monotone function of ![]() .
.
| Price Distortion Numberical Results | Nonlinear Solution Numberical Results | LQ Solution Numerical Results | |||||
| 0.5 | 1 | 1 | 11 | 1.001 | 1.004 | 1.004 | |
| 0.75 | 1 | 1 | 11 | 1.003 | 1.005 | 1.004 | |
| 0.95 | 1 | 1 | 11 | 1.093 | 1.003 | 1.003 | |
| 0.75 | 0.16 | 1 | 11 | 1.048 | 1.016 | 1.007 | |
| 0.75 | 1 | 1 | 11 | 1.003 | 1.005 | 1.004 | |
| 0.75 | 5 | 1 | 11 | 1.001 | 1.003 | 1.001 | |
| 0.75 | 1 | 0.25 | 11 | 1.027 | 1.013 | 1.008 | |
| 0.75 | 1 | 1 | 11 | 1.003 | 1.005 | 1.004 | |
| 0.75 | 1 | 4.75 | 11 | 1.001 | 1.002 | 1.001 | |
| 0.75 | 1 | 1 | 11 | 1.003 | 1.005 | 1.004 | |
| 0.75 | 1 | 1 | 21 | 1.001 | 1.001 | 1.001 |
| Note: The last two columns represent quarterly (gross) inflation for each set of parameter values. Specifically, the nonlinear solution corresponds to
|
4 Conclusion
We have demonstrated how a projection method can be used to compute the inflation bias in a full nonlinear version of the Calvo model. The annual inflation bias is between ![]() and
and
![]() under plausible parameter values.
under plausible parameter values.
In a recent paper, Schmitt-Grohe and Uribe (2009) report that the optimal inflation rate under commitment predicted by leading theories of monetary nonneutrality ranges from minus the real rate of interest to numbers insignificantly above zero. They also argue that the zero bound on nominal interest rates does not represent an impediment to setting inflation targets near or below zero. Meanwhile, our results indicate that the optimal inflation rate turns out to be substantially higher than zero in the absence of commitment.
In particular, we expect that the larger the "degree" of commitment, the smaller the size of the inflation bias. It would thus be interesting to see how the change in the "degree" of discretion affects the size of the inflation bias. In this vein, the format of Debortoli and Nunes (2007) provides an interesting starting point because they have modelled an imperfect commitment setting in which there is a continuum of loose commitment possibilities ranging from full commitment to full discretion.10 In addition, we note that it would be possible to use the same projection method to analyze the effects of loose commitment on the inflation bias.
Adam, K. and R. Billi (2007) "Discretionary Monetary Policy and the Zero Lower Bound on Nominal Interest Rates,"Journal of Monetary Economics, 54, 728-752.
Barro, R. and D. Gordon (1983) "A Positive Theory of Monetary Policy in a Natural Rate Model," Journal of Political Economy, 91, 589-610.
Benigno, P. and M. Woodford. (2006) "Optimal Taxation in an RBC Model: A Linear-Quadratic Approach,"Journal of Economic Dynamics and Control, 30, 1445-1489.
Calvo, G. (1983) "Staggered Prices in a Utility Maximizing Framework"Journal of Monetary Economics, 12, 383-398.
Clarida, R., J. Gali, and M. Gertler (1999) "The Science of Monetary Policy: A New Keynesian Perspective,"Journal of Economic Literature, 37, 1661-1707.
Debortoli, D. and R. Nunes. (2007) "Loose Commitment,"Federal Reserve Board, International Finance Discussion Paper 916.
Dotsey M. and A. Hornstein. (2003) "Should a Monetary Policy Maker Look at Money?"Journal of Monetary Economics, 50, 547-579.
Gapen, M. and T. Cosimano. (2005) "Solving Ramsey Problems with Nonlinear Projection Methods,"Studies in Nonlinear Dynamics & Econometrics 9.
Geer, D. (2005) "Eclipse Becomes the Dominant Java IDE."Computer, 38, 16-18.
Judd, K. (1992) "Projection Methods for Solving Aggregate Growth Models,"Journal of Economic Theory, 58, 410-452
Judd, K. (1998) Numerical Methods in Economics, MIT Press, Cambridge, MA.
Klein, P., P. Krushell, and J. V. R
![]() os-Rull. (2008) "Time-Consistent Public Policy," Review of Economic Studies, 75(3), 789-808.
os-Rull. (2008) "Time-Consistent Public Policy," Review of Economic Studies, 75(3), 789-808.
King, M. (1997) "Changes in UK Monetary Policy: Rules and Discretion in Practice,"Journal of Monetary Economics, 39, 81-97.
King, R. and A. Wolman (2004) "Monetary Discretion, Pricing Complementarity, and Dynamic Multiple Equilibria,"Quarterly Journal of Economics, 119, 1513-1553.
Kydland, F. and E. Prescott (1977) "Rules rather than Discretion: The Inconsistency of Optimal Plans," Journal of Political Economy, 85, 473-491.
Schaumburg, E. and A. Tambalotti (2007) "An investigation of the gains from commitment in monetary policy," Journal of Monetary Economics, 54, 302-324.
Schmitt-Grohe, S. and M. Uribe (2009) "The Optimal Rate of Inflation,"Forthcoming in Handbook of Monetary Economics.
Wolman, A. and W. Van Zandweghe (2008) "Discretionary Monetary Policy in the Calvo Model," Unpublished Manuscript.
Woodford, M. (2003) Interest and Prices, Princeton University Press, Princeton, NJ.
Yun, T. (2005) "Optimal Monetary Policy with Relative Price Distortions,"American Economic Review, 95, 89-108.
Appendices
This appendix provides additional detail about the model specification and our solution technique. Section A presents a full description of the Lagrangian of the government's planning problem when the planner cannot make commitment about his or her future behavior. Section B provides additional detail about our implementation of the residual function for the projection method. Section C describes how we use homotopy methods to obtain solutions.
A. Lagrangian
In the presence of technology shocks, the Lagrangian of this problem can be written as
![\displaystyle \frac{C_{t}^{1-\sigma }-1}{1-\sigma }-\frac{\upsilon H_{t}^{1+\chi }}{1+\chi}+\beta E_{t}\left[V\left( \Delta _{t}, A_{t+1}\right) \right]](img157.gif) |
|||
![\displaystyle + \phi_{1t} \left[\frac{A_{t} H_{t}}{\Delta _{t}} - C_{t}\right]](img158.gif) |
|||
![\displaystyle - \phi_{2t} \left[\left(1 - \tau_{P}\right) \frac{A_{t} H_{t}}{\Delta_{t}C_{t}^{\sigma}} + \alpha \beta E_{t}\left[L\left(\Delta _{t}, A_{t+1}\right)\right] - F_{t} \right]](img159.gif) |
|||
![\displaystyle - \phi_{3t} \left[\frac{\upsilon \left(1 - \tau_{P} \right) H_{t}^{1+\chi }}{\left(1 - \Phi\right) \Delta _{t}}+\alpha \beta E_{t}\left[ M\left( \Delta_{t}, A_{t+1}\right) \right] - S_{t} \right]](img160.gif) |
|||
![\displaystyle + \phi_{4t}\left[ \left( 1-\alpha \right) \left(\frac{1-\alpha \Pi_{t}^{\epsilon -1}}{1-\alpha }\right)^{\frac{\epsilon }{\epsilon -1}% }+\alpha \Pi _{t}^{\epsilon}\Delta _{t-1}-\Delta _{t}\right]](img161.gif) |
|||
![\displaystyle - \phi_{5t} \left[ F_{t} \left( \frac{1-\alpha \Pi _{t}^{\epsilon -1}}{% 1-\alpha }\right)^{\frac{1}{1-\epsilon}} - S_{t} \right].](img162.gif) |
where auxiliary functions
| (A.1) | |||
| (A.2) |
An noted earlier, the absence of commitment leads us to express the values of period
Having described the optimal policy problem under discretion, the first-order conditions can be summarized as follows:
| (A.3) |
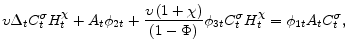 |
(A.4) |
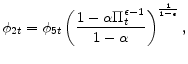 |
(A.5) |
| (A.6) |
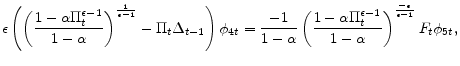 |
(A.7) |
![\begin{multline} \frac{A_{t}H_{t}}{\Delta _{t}^{2}C_{t}^{\sigma}}\phi _{2t}+\phi _{3t}\frac{\upsilon H_{t}^{1+\chi }}{\left(1 - \Phi \right) \Delta_{t}^{2}}-\phi _{4t}+\alpha \beta E_{t}\left[ \Pi _{t+1}(\Delta _{t},A_{t+1})^{\epsilon }\phi _{4t+1}\right] = \ \phi _{1t}\frac{A_{t}H_{t}}{\Delta _{t}^{2}}+\alpha \beta E_{t}\left[ \phi _{2t}L_{1}\left( \Delta _{t},A_{t+1}\right) +\phi _{3t}M_{1}\left( \Delta _{t},A_{t+1}\right) \right] , \end{multline}](img174.gif) |
(A.8) |
B. Projection Method with Collocation
We will approximate 11 policy functions by using Chebyshev polynomials as follows:
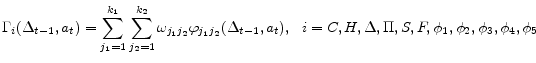
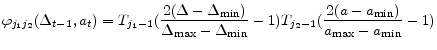
Having determined functional forms of approximate policy functions, we will determine a nonlinear system of equations for weights of 11 approximate policy functions. Specifically we use 11 equilibrium conditions to define 11 residual functions as follows. Each equilibrium condition generates a residual function as can be seen below:
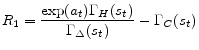
![\displaystyle R_{3} = \frac{\nu \Gamma_{H}(s_{t})^{1 + \chi} \Gamma_{\Delta}(s_{t}) }{1 - \Phi} + \alpha \beta E_{t}[M(s_{t+1})] - \Gamma_{S}(s_{t})](img188.gif)
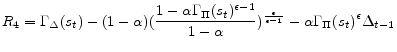
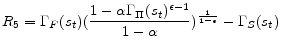
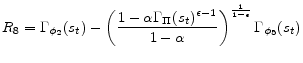
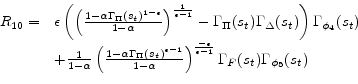
![\displaystyle \begin{array}{ll} R_{11} = & \frac{\Gamma_{C}(s_{t})^{1-\sigma}}{\Gamma_{\Delta}(s_{t})}\Gamma_{\phi_{2}}(s_{t})+ \Gamma_{\phi_{3}}(s_{t}) \frac{\nu (1+\chi)\Gamma_{H}(s_{t})^{1+\chi}}{(1 - \Phi)\Gamma_{\Delta}(s_{t})} - \Gamma_{\phi _{4}}(s_{t}) \ & + \alpha \beta E_{t}\left[\Gamma_{\Pi}(s_{t+1})^{\epsilon} \Gamma_{\phi _{4}}(s_{t+1})\right] - \Gamma_{\phi_{1}}(s_{t})\Gamma_{C}(s_{t}) - \Gamma_{\Delta}(s_{t}) \\ & - \alpha \beta E_{t}\left[\Gamma_{\phi _{2}}(s_{t}) L_{1}\left(s_{t+1}\right) + \Gamma_{\phi _{3}}(s_{t}) M_{1}\left(s_{t+1}\right) \right] \end{array}](img196.gif)
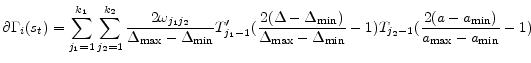
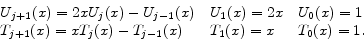
We now move onto the characterization of the integrals appearing in the residual functions. Fortunately, the expectation operator only involves three terms.
It is assumed in the paper that the technology shock follows a normal distribution with mean zero and standard deviation
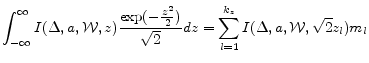
![\displaystyle E_{t}[M(s_{t+1})] = \sum_{l=1}^{k_{z}} {\hat M}(\Delta,a,\mathcal{W},\sqrt{2}z_{l}) m_{l}; E_{t}[L(s_{t+1})] = \sum_{l=1}^{k_{z}} {\hat L}(\Delta,a,\mathcal{W},\sqrt{2}z_{l}) m_{l}](img232.gif)
We will consider collocation. Under orthogonal collocation, we choose
![]() zeros of
zeros of
![]() and then substitute them into residual functions. Since all of 11 residual functions should become zero for each point of
and then substitute them into residual functions. Since all of 11 residual functions should become zero for each point of
![]() , it means that
, it means that
![]() =
=
![]() holds where
holds where
![]() represents a collocation point among
represents a collocation point among
![]() zeros of
zeros of
![]() and
and
![]() represents a vector function that contain residual functions:
represents a vector function that contain residual functions:
Finally we discuss how we choose ranges of the aggregate productivity and the relative price distortion. Following Judd (1992), the maximum of log productivity is set equal to the long-run value of ![]() that would occur if
that would occur if ![]() =
=
![]() for all
for all ![]() :
: ![]() =
=
![]() .11 The minimum of
log productivity is the negative of maximum of log productivity. The minimum value of the relative price distortion is 1. However, it is hard to make an appropriate choice of the maximum of the relative price distortion. In particular, this issue is closely related to our application of homotopy
method that will be explained in the next section.
.11 The minimum of
log productivity is the negative of maximum of log productivity. The minimum value of the relative price distortion is 1. However, it is hard to make an appropriate choice of the maximum of the relative price distortion. In particular, this issue is closely related to our application of homotopy
method that will be explained in the next section.
C. Projection Method with Homotopy Procedure
In the course of developing our model, we created routines for several heuristics for solving the nonlinear-equation system determining the collocation-polynomial weights. This section characterizes these heuristics using the homotopy formalism described in Judd (1998).
To summarize the basic idea, we begin by solving the model for a set of parameters that makes the model easy to solve. We use this solution to facilitate the solution of a "nearby" model that has parameters set closer to the parameter settings that we are really interested in. We repeat this process, solving a sequence of similar models en route to solving the model with our benchmark parametrization.
It might prove useful, in general, to use information provided by perturbation solutions as a basis for initial weights for the collocating polynomials. However, in our model we found the following heuristics easily implementable and capable of reliably producing accurate approximations with the appropriate dynamic properties. Although we did not do so, in the general case it seems likely to be worthwhile to investigate how to reliably exploit high order perturbation solutions to provide initial weights for projection calculations.
There are two distinct phases in this solution process. In the first phase, we solve the model using ![]() order polynomials, i.e. constant functions varying the parameters from the easy
values to the benchmark values.12 This phase employs the parameter homotopy described in Algorithm 1 below.13
order polynomials, i.e. constant functions varying the parameters from the easy
values to the benchmark values.12 This phase employs the parameter homotopy described in Algorithm 1 below.13
In the second phase, we increase the order of the Chebyshev polynomials. Prior to this phase, we are collocating with constant functions, and the range of the Chebyshev polynomials plays no role. In the second phase, the specific range of the Chebyshev polynomials can have a dramatic effect on the solvability of the system. Fortunately, experience with our model supports the following conjecture:
then
Thus, when the Chebyshev polynomial domain is small enough, the nonlinear system we must solve is similar to the system for
We express a projection method using the function ![]() where
where ![]() is the state at period
is the state at period ![]() ,
, ![]() is the set of parameters,
is the set of parameters, ![]() is the set of ranges for the Chebyshev polynomials, and
is the set of ranges for the Chebyshev polynomials, and ![]() is the set of orders for the Chebyshev polynomials. We use Newton's method to update the Chebyshev polynomials' weights in the following way:
is the set of orders for the Chebyshev polynomials. We use Newton's method to update the Chebyshev polynomials' weights in the following way:
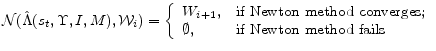
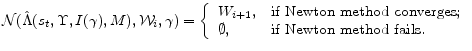
In applying a homotopy, we seek a
![]() and a sequence
and a sequence
![]() such that there is no failure of Newton's method for each value of
such that there is no failure of Newton's method for each value of
![]() . Thus, any algorithm applying a homotopy method must implement strategies for adjusting the value of
. Thus, any algorithm applying a homotopy method must implement strategies for adjusting the value of ![]() when Newton's method fails. In our code, we choose a recursive updating rule for the value of
when Newton's method fails. In our code, we choose a recursive updating rule for the value of ![]() . For example, suppose that we
failed the Newton's method at
. For example, suppose that we
failed the Newton's method at ![]() =
=
![]() . In this case, we shrink the value of
. In this case, we shrink the value of
![]() by setting a new value of
by setting a new value of
![]() as follows:
as follows:
![]() =
= ![]()
![]() , where
, where
![]() denotes the new trial value of
denotes the new trial value of ![]() ,
,
![]() is the old trial value of
is the old trial value of ![]() at the last round of Newton's
method and
at the last round of Newton's
method and ![]() is a shrink factor that is a positive constant between 0 and 1. If the Newton's method does not fail, we use the current value of
is a shrink factor that is a positive constant between 0 and 1. If the Newton's method does not fail, we use the current value of
![]() as a new value of
as a new value of
![]() . The following pseudo-code characterizes algorithms that work for our model.
. The following pseudo-code characterizes algorithms that work for our model.
Algorithm 1 Parameter Homotopy Procedures
Algorithm 2 Range Homotopy Procedures
![\displaystyle E_{0}\sum_{t=0}^{\infty }\beta ^{t}\left[ \frac{C_{t}^{1-\sigma }-1}{% 1-\sigma }-\frac{\upsilon H_{t}^{1+\chi }}{1+\chi }\right] ,](img4.gif)
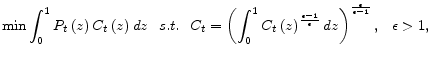
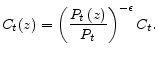
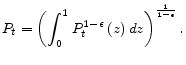
![\displaystyle C_{t}+E_{t}\left[ Q_{t,t+1}\frac{B_{t+1}}{P_{t+1}}\right] =\frac{B_{t}}{P_{t}% }+\left( 1-\tau _{W}\right) \frac{W_{t}}{P_{t}}H_{t}+\Xi _{t}-T_{t},](img20.gif)
![\displaystyle \frac{1}{R_{t}P_{t}}=E_{t}\left[ \frac{Q_{t,t+1}}{P_{t+1}}\right] .](img29.gif)
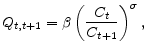
![\displaystyle \beta R_{t}E_{t}\left[ \left( \frac{C_{t}}{C_{t+1}}\right) ^{\sigma }\frac{% P_{t}}{P_{t+1}}\right] =1.](img32.gif)
![\displaystyle \sum_{k=0}^{\infty }\alpha ^{k}E_{t}\left[ Q_{t,t+k}\left( \left( 1-\tau _{P}\right) \frac{P_{t}^{\ast }}{P_{t+k}}-\frac{W_{t+k}}{A_{t+k}P_{t+k}}% \right) \left( \frac{P_{t}^{\ast }}{P_{t+k}}\right) ^{-\epsilon }Y_{t+k}% \right] ,](img40.gif)
![\displaystyle \sum_{k=0}^{\infty }\alpha ^{k}E_{t}\left[ Q_{t,t+k}\left( \left( 1-\tau _{P}\right) \frac{P_{t}^{\ast }}{P_{t+k}}-\frac{\epsilon }{\epsilon -1}\frac{% W_{t+k}}{A_{t+k}P_{t+k}}\right) P_{t+k}^{\epsilon }Y_{t+k}\right] =0.](img43.gif)
![\displaystyle P_{t}=\left[ \left( 1-\alpha \right) \left( P_{t}^{\ast }\right) ^{1-\epsilon }+\alpha P_{t-1}^{1-\epsilon }\right] ^{\frac{1}{1-\epsilon }}.](img44.gif)
![\displaystyle \left( 1-\tau _{P}\right) \sum_{k=0}^{\infty }\left( \alpha \beta \right) ^{k}E_{t}\left[ \left( \frac{Y_{t+k}}{C_{t+k}^{\sigma }}\right) \left( \frac{% P_{t+k}}{P_{t}}\right) ^{\epsilon -1}\right] \frac{P_{t}^{\ast }}{P_{t}}](img45.gif)
![\displaystyle \frac{\epsilon }{\epsilon -1}\sum_{k=0}^{\infty }\left( \alpha \beta \right) ^{k}E_{t}\left[ \left( \frac{W_{t+k}Y_{t+k}}{A_{t+k}P_{t+k}C_{t+k}^{% \sigma }}\right) \left( \frac{P_{t+k}}{P_{t}}\right) ^{\epsilon }\right] .](img47.gif)
![\displaystyle \left( 1-\tau _{P}\right) \sum_{k=0}^{\infty }\left( \alpha \beta \right) ^{k}E_{t}\left[ \left( \frac{Y_{t+k}}{C_{t+k}^{\sigma }}\right) \left( \frac{P_{t+k}}{P_{t}}\right) ^{\epsilon -1}\right] ,](img51.gif)
![\displaystyle \frac{\epsilon }{\epsilon -1}\sum_{k=0}^{\infty }\left( \alpha \beta \right) ^{k}E_{t}\left[ \left( \frac{W_{t+k}Y_{t+k}}{% A_{t+k}P_{t+k}C_{t+k}^{\sigma }}\right) \left( \frac{P_{t+k}}{P_{t}}\right) ^{\epsilon }\right] . \notag](img53.gif)
![\displaystyle S_{t}=\frac{\epsilon }{\epsilon -1}\left( \frac{W_{t}}{P_{t}A_{t}}\right) \left( \frac{Y_{t}}{C_{t}^{\sigma }}\right) +\alpha \beta E_{t}\left[ \Pi _{t+1}^{\epsilon }S_{t+1}\right] ,](img56.gif)
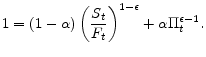
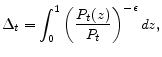
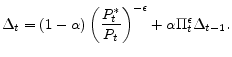
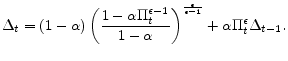
![\displaystyle V_{t}\left( \Delta _{t-1},A_{t}\right) =\max \left\{ \frac{C_{t}^{1-\sigma }-1}{1-\sigma }-\frac{\upsilon H_{t}^{1+\chi }}{1+\chi }+\beta E_{t}\left[ V_{t+1}\left( \Delta _{t},A_{t+1}\right) \right] \right\} ,](img83.gif)
![\displaystyle S_{t}=\frac{\upsilon H_{t}^{1+\chi }}{\left( 1-\tau _{W}\right) \left( 1-\epsilon ^{-1}\right) \Delta _{t}}+\alpha \beta E_{t}\left[ \Pi _{t+1}(\Delta _{t},A_{t+1})^{\epsilon }S_{t+1}(\Delta _{t},A_{t+1})\right] ,](img89.gif)