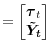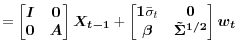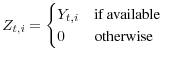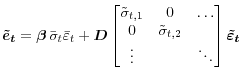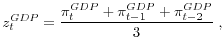Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2011-42 Screen Reader version ^♣

Measuring the Level and Uncertainty of Trend Inflation^*

Elmar Mertens†

Federal Reserve Board

September 28, 2011

Keywords: Trend cycle model, inflation target, stochastic volatility, surveys, bayesian econometrics

Abstract:

Firmly-anchored inflation expectations are widely viewed as playing a central role in the successful conduct of monetary policy. This paper presents estimates of trend inflation, based on information contained in survey expectations, the term structure of interest rates, and realized inflation rates. My application combines a variety of data sources at the monthly frequency and it can flexibly handle missing data arising from infrequent observations and limited data availability. In order to assess whether inflation expectations are anchored, uncertainty surrounding future changes in trend inflation -- measured by a time-varying volatility of trend shocks -- is estimated as well.

Not surprisingly, the estimates suggest that trend inflation in the U.S. rose and fell again over the 1970s and 1980s, accompanied by increases in uncertainty. Considering the recent crisis, full-sample estimates of trend inflation fell quite a bit, but not too dramatically. In contrast, real-time estimates recorded sizeable increases of trend uncertainty during the crisis of 2007/2008, which have abated since then.

JEL Classification: C53, E37, E47, E58

1 Introduction

Firmly-anchored inflation expectations are widely viewed as playing a central role in the successful conduct of monetary policy.¹ This paper presents estimates of trend inflation, based on a fairly broad information set, spanned by survey expectations, the term structure of interest rates, and realized inflation rates. In order to assess whether inflation expectations are anchored, I estimate not only the level of trend inflation, but also the uncertainty surrounding future changes in trend inflation.

While the task of monitoring inflation expectations is important, it is typically hampered by the lack of a comprehensive summary measure of inflation expectations. For example, a variety of survey measures exist, which often differ from one another in several aspects. Some indicators measure short term expectations, and some longer-term expectations of future inflation rates; some refer to changes in the CPI, others to the GDP or PCE deflators. In some cases, the forecast horizon may only vaguely be specified, in others the relevant price index may be left open. The series are often reported at different frequencies, and typically have different starting points. As an alternative data source, inflation expectations may also be extracted from financial market data, like the levels of nominal interest rates. While all these measures are potentially valuable, they are also likely subject to noise and measurement errors, and may at times convey conflicting signals.

This paper uses a time series model to condense information from a variety of data series -- inflation rates, survey responses about future inflation, and nominal interest rates -- into a common trend measure. Kalman filtering techniques and the Gibbs sampler allow to account for missing observations arising from the infrequent publication or limited availability of some series.

Adopting the trend concept of Beveridge and Nelson (1981), trend inflation is defined as the model's long-run forecast of PCE headline inflation. What makes this a common trend is the assumption that trend inflation moves in lock-step with the long-run forecasts for all other variables -- like levels of nominal yields, core inflation as well as survey responses. Equivalently, this assumption requires survey errors to be stationary, but allows them to have non-zero mean, and also requires that inflation differentials, say, between headline and core inflation are stationary, and that term premia and real yields are stationary. In addition, I will consider results from an extended version of the model, which allows for drift in real yields.

Uncertainty in the trend of inflation expectations is measured by the volatility of trend shocks, which is allowed to vary over time as in Stock and Watson (2007) and similar to Cogley et al.(2010). When the volatility of trend shocks is low, the trend behaves like a constant and we can speak of well-anchored inflation expectations. When the volatility of trend shocks is high, inflation expectations will likely become unmoored, and trend movements will start to become a major source of variations in actual inflation. By tracking time-variation in the uncertainty measure, the model can document whether and to what extent inflation expectations have become unanchored at times in the past, as well as providing an estimate of the current risk of changes in trend inflation.

The remainder of this paper is structured as follows. The next section offers a brief discussion of the Beveridge-Nelson trend with stochastic volatility before turning over to a description of my empirical model in Section 3. Section 4 presents trend estimates extracted from surveys and inflation, while Section 5 adds nominal yields to the conditioning set used for constructing the trend estimates. Section 6 discusses in more detail trend estimates for the most recent years and compares real-time estimates of trend inflation with the kind of in-sample estimates shown elsewhere in this paper. Section 7 presents estimates of trend inflation derived from models with smaller conditioning sets, which permits incorporation of richer time-varying dynamics in the persistence of the data and additional sources of stochastic volatility. A detailed review of the related literature is given in Section 8. Section 9 concludes the paper with a brief summary and an outlook on further research.

2 Trend Concept

Following Beveridge and Nelson (1981), this paper identifies trend inflation from long-term forecasts of inflation. This section provides a brief discussion of the trend concept, the role of stochastic volatility and the use of multivariate information in identifying the trend made in this paper. A description of the time-series model from which forecasts are generated in this paper will be deferred until Section 3. A more detailed discussion of the related literature is given in Section 8.

2.1 The Beveridge-Nelson Trend with Stochastic Volatility

An important motivation for monitoring inflation expectations is to detect shifts in people's belief about an economy's nominal anchor (or lack thereof). The Beveridge-Nelson trend is particularly suited for this task, since it is an expectation of future inflation conditional on some current information set. Formally, the Beveridge-Nelson trend ( $\tau_t$ ) of inflation ( $\pi_t$ ) is identified as the forecast of inflation at the infinite horizon:

$\displaystyle E_t \pi_{t+\infty} = \tau_t$

(1)

and actual inflation is assumed to be the sum of the trend and a stationary component, $\tilde\pi_t$ . Adopting the terminology of Cogley et al.(2010), $\tilde\pi_t$ will be called the "inflation gap".

$\displaystyle \pi_{t}$

$\displaystyle = \tau_t + \tilde\pi_t$

$\displaystyle \tilde\pi_t$

$\displaystyle \sim I(0)$

$\displaystyle E(\tilde\pi_t)$

$\displaystyle =0$

(2)

While the inflation gap has an unconditional mean equal to zero, it may have arbitrary serial correlation (withing the limits of stationarity).²

In this context it is important to notice that trend inflation is not a forecast of average inflation between now and some long-dated maturity, but rather the forecast of inflation at a long-dated point in time (namely the infinite horizon). As will be seen further below, focusing the trend on the infinite horizon turns out to be very convenient in order to derive a common trend restriction, which holds in a large class of model environments.³

As a simple example, consider first an economy with a well established and credible inflation target, where "credible" is understood such that policymakers will stabilize inflation around the target forever and that the public knows about this. In this economy the Beveridge-Nelson trend will be constant and identical to the target.⁴ As another example, suppose that an economy has just credibly adopted an inflation target, but that the target is different from average past inflation. In this case, the trend measure will crucially depend on the information set used to generate long-term inflation forecasts. When the information set contains knowledge about the new inflation target, the Beveridge-Nelson trend will instantaneously adjust to the new target rate -- even when the transition to the new target could be expected to take a while. If forecasts were however generated by extrapolating past inflation behavior, say with an autoregressive time-series model, trend estimates should converge only over time to the new target, where the rate of convergence would depend on the weight given by the forecast to more recent inflation behavior and on the length of the adjustment period to the new target regime.⁵ By using an estimated time-series model, this paper will invariably resort to generating forecasts by extrapolating from the past. But by using forward-looking information variables -- like surveys and financial market data -- the procedure should also be capable of detecting shifts in the inflation outlook not yet captured in realized inflation data.

Defining the trend measure as an expectation has immediate consequences for the implied dynamics of inflation itself. Differencing the trend definition in equation (1) yields a unit root process for the trend:

$\displaystyle \tau_t$	$\displaystyle = \tau_{t-1} + (E_t - E_{t-1}) \pi_{t+\infty}$	(3)
	$\displaystyle = \tau_{t-1} + \bar{e}_t \notag$

where the trend shocks,

, form a martingale-difference sequence under the conditioning set used to generate expectations; $E_{t-1} \bar{e}_t = 0$ . Unless trend shocks were always zero, the trend thus follows a random walk, which via (2) will be inherited by the process for actual inflation. As will be discussed next, a vital ingredient in my model is to assume a time-varying volatility of trend shocks,

$\displaystyle \bar{e}_t$

$\displaystyle \sim N(0, \bar\sigma_t)$

(4)

to allow for periods, when trend shocks are essentially zero and inflation is close to a stationary process, as well as to allow for situations when inflation expectations may become unanchored and trend shocks are sizable.

Taken at face value, the notion of a random walk component in the inflation process could seem troubling. Apart from statistical concerns, assuming a non-stationary inflation process would imply that monetary policy has failed in its task of keeping inflation rates stable. Ideally, the analysis should neither preclude the possibility of well anchored inflation expectations nor should such risks be ruled out.⁶

An inflation model with a Beveridge-Nelson decomposition as in (2), will always assign some weight to a non-stationary component in inflation. But as long as the weight is very small, the inflation process could arbitrarily well be represented by a stationary process; see for example Cochrane (1991). By estimating a time-varying volatility of trend shocks -- and thus a time-varying importance of the unit root component in inflation -- this paper will be able to capture episodes of stable as well as unanchored inflation expectations. As will be seen below, the model uses the same trend concept for inflation as Stock and Watson (2007) -- a Beveridge-Nelson trend with stochastic volatility -- which is also approximated by the model Cogley et al.(2010). But the model differs in its use of a multivariate dataset, combining information from surveys and the term structure of interest rates in estimating the trend.

2.2 Cointegration and the Multivariate Beveridge-Nelson Trend

A key aspect of this paper is the use of multivariate information, contained in various measures of realized inflation, survey responses as well as nominal interest rates, to identify changes in trend inflation. For concreteness, the analysis will always be concerned with identifying the trend in headline PCE inflation.⁷ As will be discussed next, a tight link will be imposed amongst the trend levels of different inflation measures, survey responses and nominal interest rates, requiring that all variables are subject to the same trend shocks.

Table 1: Data Description and Availability
Variable	Since	Frequency
Inflation Rates: PCE Deflator	02/1959	Monthly
Inflation Rates: Core PCE Deflator	02/1959	Monthly
Inflation Rates: Consumer Price Index	02/1947	Monthly
Inflation Rates: GDP Deflator	Q1/1947	Quarterly
Survey Expectations of Inflation: Blue Chip, CPI 4-quarter ahead	06/1980	Monthly
Survey Expectations of Inflation: Blue Chip, CPI Five-to-ten year	03/1987	March and October
Survey Expectations of Inflation: Livingston survey, CPI next 12 month	12/1946	June and December
Survey Expectations of Inflation: Michigan Survey $^\ast$ 1 year	01/1978	Monthly
Survey Expectations of Inflation: Michigan Survey $^\ast$ 5-to-10 year	02/1975	Monthly (since 1990)^**
Survey Expectations of Inflation: SPF, CPI 4-quarters ahead	08/1981	February, May, August and November
Survey Expectations of Inflation: SPF, CPI next 10 years	11/1991	February, May, August and November
Nominal Interest Rates: 10-year Treasury Yield	04/1953	Monthly (average)
Nominal Interest Rates: 30-year Treasury Yield	02/1977	Monthly $^{\ast\ast\ast}$ (average)
Nominal Interest Rates: Nine-to-ten year forward rate	08/1971	Monthly (first day of month)

Note: The model uses monthly observations from January 1960 through August 2011 of all data received by the end of August 2011. SPF denotes the Survey of Professional Forecasters.

$^{\ast}$ The Michigan survey does not specifically refer to any specific price statistic or consumption basket.

^** From February 1975 and April 1990, the Michigan 5-to-10-year survey was conducted only sporadically.

$^{\ast\ast\ast}$ From March 2001 to January 2006, data is unavailable for the 30-year Treasury Yield.

The data set used in this paper can broadly be classified in three groups of variables:

Realized inflation rates, like PCE headline and core inflation and CPI inflation.
Survey expectations of future inflation, like the Livingston Survey's CPI forecast for the next year the Michigan Survey's expected price change over the next 5-to-10 years.⁸
Nominal interest rates, like the yields on nominal Treasury securities at different maturities.

All variables are also listed in Table 1.⁹

Figure 1: Inflation and other Indicator Series

Note: Monthly data, where available, since 1960, expressed in annualized percentage points. Unless stated otherwise, inflation rates are shown as twelve-month trailing moving averages. (The model's information set uses monthly inflation rates -- as shown in Panel (a) for headline PCE inflation -- which span these moving averages.)

Figure 1 Data

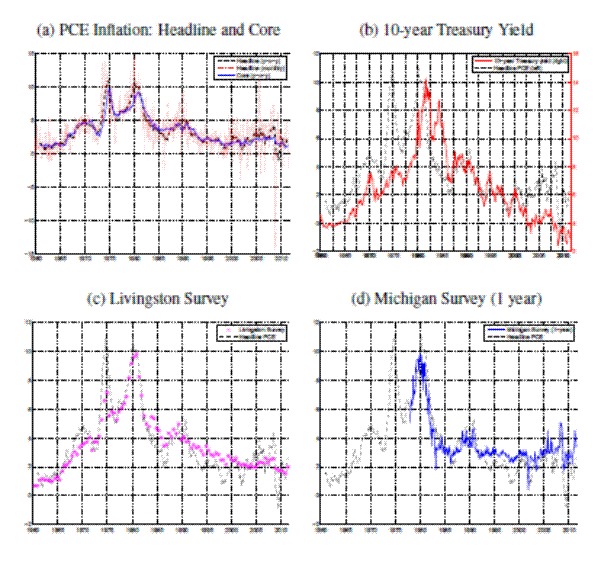
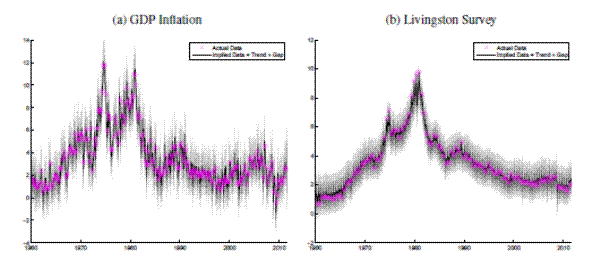
Some indicators measure short term expectations, and some longer term expectations of future inflation rates. Most surveys refer explicitly to changes in the CPI, while the price index relevant to bond investors cannot be observed. A basic tenet of this paper is the assumption that differences between the various indicators should not be expected to last forever. A visual inspection of Figure 1, which shows time series data for a few variables from this paper's data set in comparison with realized PCE inflation, suggests indeed some commonality in low frequency movements of inflation, survey and interest rates. However, it should also be noted that a closer inspection reveals that deviations between interest rates and inflation can be very persistent, and possibly non-stationary. Given the low power of formal tests for stationarity and cointegration, and a strong prior in favor of the cointegrating assumptions imposed by a vast body of theoretical models, I have chosen to impose the common trend assumption outlined below, trading off ease of interpretation against statistical flexibility. A further impediment to the application of formal cointegration tests is the regular occurrence of missing data values throughout the data set used here. There is however no problem of missing observations for PCE inflation and the 10-year Treasury yield - shown in Panel (b) of Figure 1 -- and augmented Dickey-Fuller Tests soundly reject a unit root in the difference between the 10-year Treasury yield and headline PCE inflation.¹⁰

Formally, I assume that a) differences between different inflation measures are stationary, b) survey errors are stationary, and c) real interest rates and risk premiums are stationary. (All variables are expressed in logs.) As a consequence of the Beveridge-Nelson decomposition (2), forecast errors of inflation at any horizon are stationary. Together with assumptions a) and b) it follows that differences between current headline PCE inflation, $\pi_t$ , and survey responses are stationary -- irregardless of the survey's inflation measure and forecast horizon. Based on the Fisher equation, nominal interest rates are the sum of a real rate, expected inflation and a residual, which I will refer to as a risk premium. Assumptions a) and c) ensure then that the difference between $\pi_t$ and the current nominal yield is stationary. Closer inspection of Panel (b) in Figure 1's suggests that deviations between nominal yields and inflation may at times be near permanent, contrary to assumption c), and Section 5 investigates the consequences of allowing for drift in the real rate of interest for estimates of trend inflation.¹¹

3 Empirical Model

This section lays out my basic time-series model. The model assumes that there is a common trend in inflation rates, surveys and nominal yields. Extensions will be considered in Section 5 (separate trend shocks affecting real rates) and Section 7 (time-varying gap dynamics). Initially, the presentation will assume that the entire data set can be observed without missing values. The handling of missing data will be described at the end of this section. Let $\vec{Y}_t$ denote a vector containing inflation rates, nominal yields and survey expectations.¹² Each variable is supposed to be integrated of order one and a multivariate Beveridge-Nelson decomposition holds:

$\displaystyle \vec{Y_t}$

$\displaystyle = \vec\tau_t + \vec{\tilde Y_t}$

$\displaystyle \lim_{k\to\infty} E_t \vec{Y_{t+k}}$

$\displaystyle = \vec\tau_t$

(5)

with stationary "gaps", which are unconditionally mean zero; formally $\vec{\tilde Y_t} \sim I(0)$ and $E(\vec{\tilde Y_t}) =\vec 0$ .

Reflecting the discussion of Section 2, it will be assumed that a common trend shock is driving each variables' trend level:

$\displaystyle \vec\tau_t$

$\displaystyle = \vec\tau_{t-1} + \vec 1 \, \bar{e}_t$

$\displaystyle \bar{e}_t$

$\displaystyle = \bar\sigma_t \bar\varepsilon_t$

$\displaystyle \bar\varepsilon_t$

$\displaystyle \sim N(0,1)$

(6)

The trend levels of individual variables may differ only in their initial values $\vec\tau_0$ . Changes in the trends of each variable are identical.¹³ The initial trend levels can differ, for example in reflection of average real yields, average term premiums or biases in survey expectations, which are all assumed to be stationary, but not necessarily mean zero.

As discussed in Section 2, the model accounts for time-variation in the importance of trend movements with stochastic volatility in the trend process. As in Stock and Watson (2007) it is assumed that the log-variance of trend shocks follows a driftless random walk.

$\displaystyle \log\bar\sigma^2_t$

$\displaystyle \equiv h_t$

$\displaystyle h_t$

$\displaystyle = h_{t-1} + \sigma_h \, \xi_t$

$\displaystyle \xi_t$

$\displaystyle \sim N(0,1)$

(7)

The gaps are stationary, but not necessarily . In order to handle a large cross-section of data with missing data, the dynamics of the gaps are required to follow a time-invariant VAR.

$\displaystyle \mat{A}(L) \vec{\tilde Y_t}$

$\displaystyle = \vec{\tilde e_t}$

(8)

where the roots of the lag-polynomial $\mat{A}(L)$ are restricted to be outside the unit circle. In the spirit of modern business cycle theory, the model allows for correlation between trend and gaps:¹⁴

$\displaystyle \vec{\tilde e_t}$

$\displaystyle = \vec\beta \,\bar\varepsilon_t + \vec{\tilde\varepsilon_t}$

$\displaystyle \vec{\tilde\varepsilon_t}$

$\displaystyle \sim N(\vec{0}, \mat{\tilde{\Sigma}})$

(9)

Please note that, this correlation is constant and pertains to the standardized trend shocks, $\bar\varepsilon_t$ instead of $\bar e_t$ . Allowing the gap shocks to load onto $\bar e_t$ would induce stochastic volatility in the gaps, but only via the trend shocks which is likely too restrictive.¹⁵

Choosing to model gap dynamics as being time-invariant enables the model to handle a larger set of variables with partly missing data, than what would be possible when gap dynamics were time-varying as in Cogley et al.(2010). For comparison, Section 7 will consider models estimated from smaller data sets, with drifting coefficients in the gap VAR and stochastic volatility in gap innovations.

Before describing the handling of missing data, it will be useful to summarize the model in its state space form. For a given realization of the stochastic volatility process, the state vector of the model consists of the trend vector $\vec\tau_t$ and the gaps $\vec{\tilde Y_t}$ as well as any lagged gaps needed for the companion form of (8). For the sake of exposition, it will be assumed below that the VAR in equation (8) has one lag, such that $\mat{A}(L) = \mat{I} - \mat{A}L$ . Denoting the state vector by $\vec{X_t}$ the state space system can then be written as

$\displaystyle \vec{X_t}$	$\displaystyle = \begin{bmatrix}\vec\tau_t \\ \vec{\tilde Y_t} \end{bmatrix}$	(10)
	$\displaystyle = \begin{bmatrix}\mat{I} & \vec{0} \\ \vec{0} & \mat{A} \end{bmatrix} \vec{X_{t-1}} + \begin{bmatrix}\vec{1} \bar\sigma_t & \vec{0} \\ \vec{\beta} & \mat{\tilde\Sigma^{1/2}} \end{bmatrix} \vec{w_t}$	(11)
$\displaystyle % & \vec{X_t} \vec{Y_t}$	$\displaystyle = \mat{C} \vec{X_t} %& \mat{C} &=\begin{bmatrix}\mat{I} & \mat{I} \end{bmatrix}$	(12)

where $\mat{C} = [\mat{I} \; \mat{I} ]$ , $\vec{w_t}\sim N(\vec{0},\vec{I})$ , and $\mat{\tilde\Sigma^{1/2}}$ denotes an arbitrary factorization of the variance covariance matrix of the gap residuals.

So far, it has been assumed that observations of $\vec{Y_t}$ are regularly available. In the case of missing data, the state space system (10) and (12) can be modified as follows. Denote the actual data as $\vec{Z_t}$ , with typical element $Z_{t,i}$ -- similarly, individual elements of $\vec{Y_t}$ will be denoted $Y_{t,i}$ -- and encode missing observations as

$\displaystyle Z_{t,i} = \begin{cases}Y_{t,i} \quad\text{if available} \\ 0 \quad\quad\text{otherwise} \end{cases}$

(13)

and replace the observer equation (12) with

$\displaystyle \vec{Z_t}$

$\displaystyle = \mat{C_t} \vec{X_t} % &$

(14)

where C_t is a deterministically varying measurement matrix. If data on $Y_{t,i}$ are available, the

th row of C_t is identical to the

th row of C and zero otherwise. The only variable with missing observations, which is treated differently than described above is the quarterly inflation series derived from the GDP deflator. As explained in Appendix B, each quarterly observation of GDP inflation is modeled as the three-month moving average of an unobservable monthly inflation rate.¹⁶

The model is estimated with a Gibbs sampling algorithm described in Appendix A. The algorithm yields not only estimates of the latent factors $\vec\tau_t$ and $\bar\sigma_t$ but also for the parameters of the gap VAR (8). In addition, the Gibbs sampler recovers the posterior distribution of missing data entries, conditional on the model and all observed data values. Examples of estimates for the posterior distribution of missing data values are shown Appendix B. The only fixed parameter is the volatility of shocks to the log-variances in (7), $\sigma_h$ , which has been set equal to $0.2 / \sqrt{3}$ , corresponding to the value of 0.2 used by [Stock and Watson (2007)] in their quarterly model.¹⁷

4 The Common Trend in Inflation and Surveys

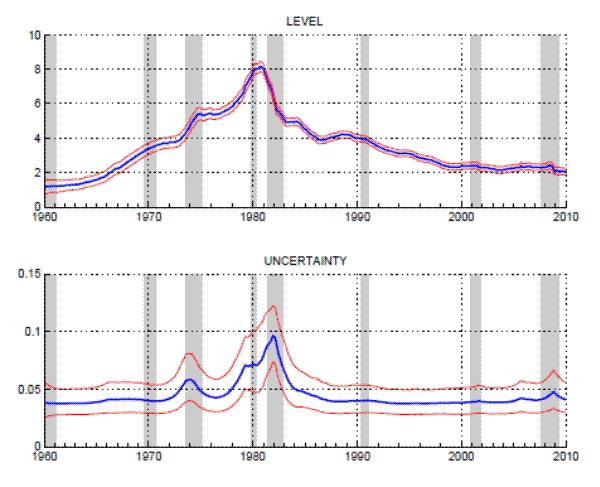
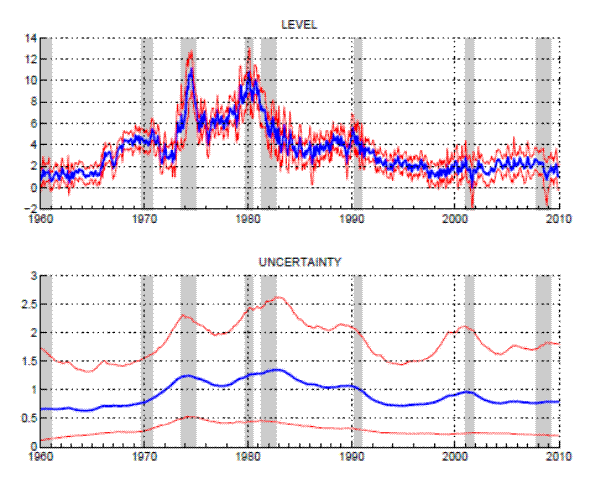
This section presents estimates about the level and uncertainty of trend inflation, extracted from the survey expectations and realized inflation rates listed in Table 1.¹⁸ The model described in Section 3 is estimated from monthly data since 1960, covering several complete cyclical episodes and different regimes for the conduct of monetary policy.

Data on inflation and nominal yields are taken from the FRED database, maintained by the Federal Reserve Bank of St. Louis, forward rate data from the Federal Reserve Board's website,¹⁹ and survey responses were obtained from the various survey providers. All variables have been transformed into annualized percentage rates using continuous compounding.²⁰ If available, all monthly observations since January 1960 are used and a detailed list of all variables as well as their availability is given in Table 1.

As shown in Figure 2, trend estimates based on surveys and inflation broadly track the "Great Inflation" of the 1970s and the subsequent disinflation under Federal Reserve Chairman Pal Volcker during the first half of the 1980s. Starting at about 1% in the early 1960s, the trend measure rises to a peak of about 8% percent in late 1980 from which it gradually descends until it reaches about $2\frac{1}{4}\%$ percent by 2000.

Figure 2: Inflation Trend based on Surveys and Inflation Rates ("SURV")

Note: The top panel shows the smoothed estimates of the trend and the bottom panel shows uncertainty about trend shocks. The estimates combine information from the surveys and inflation rate variables listed in Table 1. Red-dashed lines show 90% confidence intervals based on the model's posterior distribution conditional on all data. NBER recession dates are shaded.

Figure 2 Data

Very strikingly -- though not surprisingly -- large changes in trend inflation tend to be accompanied by increases in trend uncertainty, notably around 1974 and the late 1970s and early 1980s. Those were not only times when trend inflation was unacceptably high, but also when trend inflation has become unanchored. Interestingly, between 1974 and 1977, the measure of trend uncertainty decreased quite a bit, while the level estimate remained fairly stable at around $5\frac{1}{2}\%$ . Taken at face value, this result suggests that the unmooring of inflation expectations that had intensified around 1974 had temporarily abated -- albeit at a quite elevated level of trend inflation. However, it should be emphasized that the estimated volatilities will by design mostly mirror the size of changes in the estimated levels. Hence, the estimation is not likely to pick up pure inflation scares, i.e. periods in which an increase in trend uncertainty did not lead to an eventual change in the trend. While such events are possible under the model's data generating process, the kind of levels data used here cannot be very informative about their occurrence, at least not when using the model to construct retrospective estimates of uncertainty -- why estimate a high shock volatility for a date in the past when nothing seems to have happened after all? This consideration notwithstanding, stochastic volatility matters when estimating the model, since it helps to account for actual changes in inflation persistence, rather than its ability to detect mere changes in uncertainty which did not affect the level. As will be seen in Section 6, inflation scares, like in 1994 and some of the examples discussed by [Goodfriend (1993)], do affect the estimates in real-time.

The volatility of trend shocks -- labeled "uncertainty" in the lower panel of Figure 2 -- is measured by the standard deviation of a monthly trend shock, where the trend itself is expressed in units of annualized inflation rates. During "normal" times, like the 1960s or the Great Moderation period (1980s to 2007), the estimates of uncertainty typically stand at values close to 4 basis points. A monthly standard deviation of this size cumulates to a standard deviation of about 15 and 40 basis points over periods of one and ten years respectively-provided that the uncertainty of trend shocks remains at 4 basis points per month.²¹

Turning to the more recent years, the trend estimates have hovered just above 2 percent between 2000 and the onset of the recent crisis, accompanied by historically low values of uncertainty. (Figure 6 below depicts the trend estimates for the last decade in an enlarged picture.) The financial crisis has left a clear imprint on estimates of trend and uncertainty which will be discussed further in Section 6.

Figure 3: Data and the SURV Trend

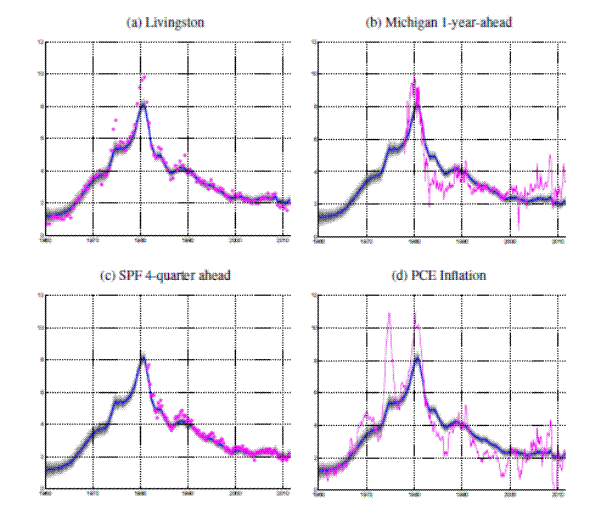
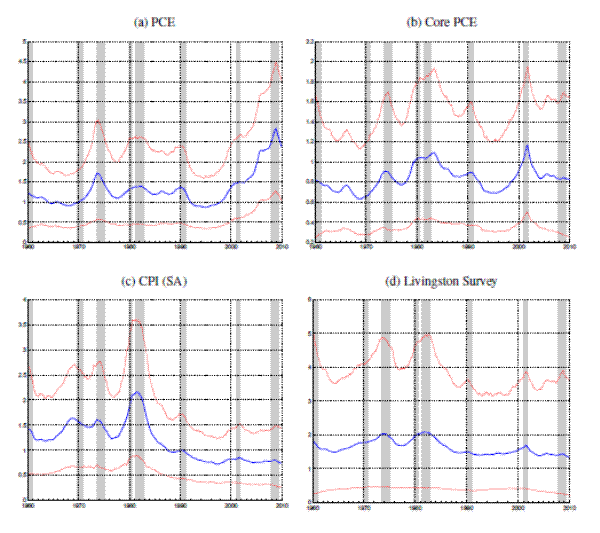
Note: Grey shaded bands and the solid blue line display the posterior distribution of SURV trend estimates, also shown in Figure 2.

Figure 3 Data

Figure 3 displays the SURV estimates of trend inflation alongside some select indicator variables, which are part of the underlying conditioning set. As expected, the estimated inflation trend broadly tracks low-frequency movements of inflation rates and survey responses. Interestingly, the trend measure follows more closely long-term survey expectations -- like the Livingston survey shown in Panel (a) of the figure -- than some short-term expectations. In particular, the one-year Michigan survey shown in Panel (b) is known to be a very noisy measure of inflation in the medium term, see van der Klaauw et al.( 2008) and Armantier et al. (2011), and the model's trend estimate do not take much signal from these survey responses. In contrast, the year-ahead expectations from the SPF appear to be tracked quite closely by the trend estimates. Interestingly, the SURV estimates interpret the bursts in realized inflation rates around 1974 only as part of a gradual rise n trend inflation, with the SURV trend peaking in 1980 but not 1974/75. As reported in Appendix C, a model conditioned on inflation rates attribute the inflation burst of 1974 much more strongly to a rise in the trend. The more gradual increase in the SURV trend is shaped by the responses to the Livingston survey -- the only survey for which observations are available for this period -- which rose only briefly above 6% during this period while annual inflation rates reached double digit levels.

5 Trend Inflation and Nominal Yields

5.1 Common Trend

The previous section presented estimates of trend inflation which were conditioned on survey responses and realized inflation rates. This section compares these results with model estimates conditioned on nominal yields and inflation rates. These conditioning sets will be referred to as "SURV" and "YLD" respectively. Table 2 in the appendix, describes the subsets of the data used throughout this paper to study the sensitivity of the trend measure to different conditioning sets. In each case, realized inflation rates are included in the information set as well, such that the trend level can be aligned with the model's long-term forecast of headline inflation in the PCE deflator. A detailed list of the variables used in each information set is given in Table 2. (Estimates based on all variables, which are close to the YLD estimates, are reported in Appendix C.)

Table 2: Model Information Sets
Information Set	Variables
ALL	all variables listed in Table 1
SURV	all surveys and inflation rates listed in Table 1
YLD	all nominal yields and inflation rates listed in Table 1
INF	all inflation rates listed in Table 1
SMALL	PCE Deflator (vintage data)
SMALL	Consumer Price Index (non-seasonally adjusted vintages)
SMALL	Nine-to-ten-year forward rate
SMALL	Livingston survey
TVP1	PCE Deflator
TVP1	Core PCE Deflator
TVP1	Consumer Price Index (seasonally adjusted)
TVP1	Livingston survey
TVP2	PCE Deflator
TVP2	Livingston survey
TVP2	10-year Treasury Yield

Note: Individual variables and the availability of each series is described in Table 1.

Considering the rise and fall of inflation in the 1970s and 1980s, the extent to which interest rates and inflation diverged over this period is notable, as can be seen from Panel (b) of Figure 1. The Fisher relation would suggest that both measures should strongly co-move, at least at intermediate horizons. In practice, inflation rates peaked twice, around 1975 and 1980, and came down fairly swiftly during the early 1980s, whereas interest rates rose only belatedly during the 1970s and stayed elevated at persistently higher levels well into the early 1990s, with the behavior of survey expectations roughly falling in between these two patterns.

Figure 4: Trend estimates "YLD" based on Nominal Yields and Inflation Rates

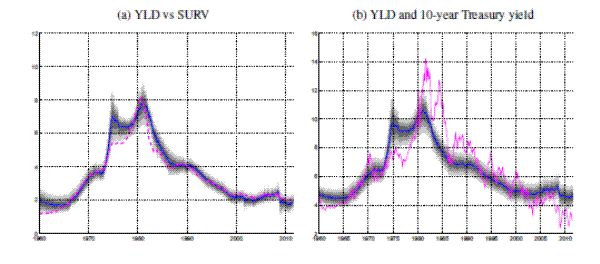
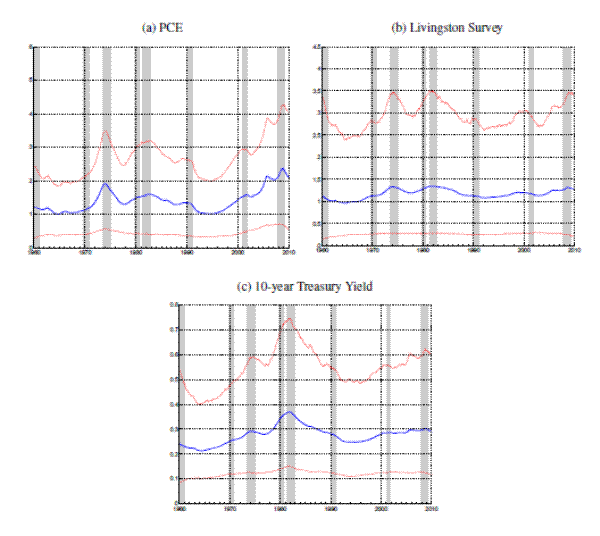
Note: The top panel shows the smoothed estimates of the trend and the bottom panel shows uncertainty about trend shocks. The estimates are derived from the nominal yields and inflation rates, denoted "YLD" in Table 1. Red-dashed lines show 90% confidence intervals based on the model's posterior distribution conditional on all data. NBER recession dates are shaded.

Figure 4 Data

Figure 4 compares trend estimates based on the YLD data set with the SURV trend and the 10-year Treasury yield. As can be seen in Panel (a) of the figure, trend estimates YLD and SURV peak in late 1980, at around 8%, and gradually decline until they reach about $2\frac{1}{4}\%$ by 2000. However, the persistently elevated level of long-term interest rates during the early 1980s is reflected in a somewhat slower decline in the YLD trend during the 1980s. These differences between the two trend estimates are consistent with the prolonged skepticisms of financial markets concerning the durability of the disinflation efforts of the Federal Reserve in the early 1980s, which led Goodfriend and King (2005) to refer to this episode as the "incredible Volcker disinflation." Notably, the YLD trend records also a marked peak in 1974/75, coinciding with the burst in inflation rates discussed at the end of the previous section. Estimates of trend and uncertainty based on the combined data of SURV and YLD, that is all variables listed in Table 1, are very similar to the YLD estimates (shown in Appendix C).

5.2 A Separate Yield Trend

The common-trend model for YLD depends on the assumed stationarity of real rates and risk premia; an assumption typically embodied in modern macroeconomic models, for example Smets and Wouters (2007) or Edge et al. (2008). However, it is open to question whether deviations between nominal yields, like the 10-year yield shown in Panel (b) of Figure 4, and the YLD trend are merely persistent (but stationary), or whether it might not be statistically more accurate to allow for deviations between trend inflation and yield trends.

This section considers an extended model, where long-term forecasts of yields are driven not only by changes in trend inflation, but also by a second shock, common only to yields. Nominal yields can be decomposed into the sum of expected inflation, real yield and a risk premium.²² The additional trend component could thus be related to shifts in real rates.²³ In many macro-economic models, long-term forecasts of the real yield depends on expected productivity growth. It is beyond the scope of this paper to assess the extent to which the estimates of $\tau_t^r$ are related to changes in perceived productivity growth. For the present purpose, it shall merely be stressed that $\tau_t^r$ is a measure of deviations between long-term forecasts of inflation and nominal yields, and thus a measure of the goodness of fit of the hitherto assumed cointegration between inflation and yields.

Based on the Fisher equation and the maintained assumption of stationary risk premia, the model assumes the following decomposition of the trend in nominal interest rates, denoted

$\displaystyle E_t i_{t+\infty}$

$\displaystyle = \tau_t^\pi + \tau_t^r$

(15)

where $\tau_t^\pi$ is trend inflation -- as defined above -- and $\tau_t^r$ is the long-term forecast for the real rate of interest, which follows a random walk, independent of shocks to trend inflation. As discussed in Section 2, the non-stationarity implied by the random walk is mitigated by specifying a stochastic volatility process for the trend shocks.

$\displaystyle \tau_t^r$

$\displaystyle =\tau_{t-1}^r + \bar{e}_t^r$

$\displaystyle \bar{e}_t^r$

$\displaystyle \sim N(0, (\bar\sigma_t^r)^2)$

$\displaystyle E(\bar{e}_t^r, \tau_{t+k}^\pi)$

$\displaystyle = 0 \quad \forall k$

(16)

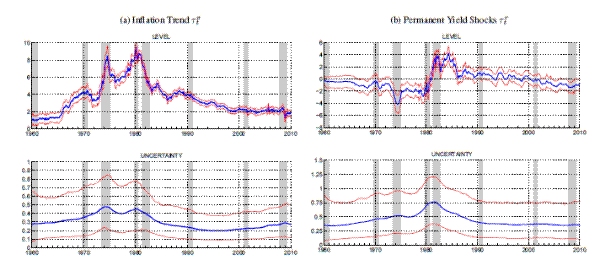
The model allows for stochastic volatility in both trends, while maintaining the assumption of time-invariant VAR dynamics for the gaps as in (8), allowing for arbitrary correlation between gap shocks and (standardized) trend shocks.

Figure 5: Trend Inflation and an Additional Trend Component in Yields

Note: Panel (a) shows estimated level and uncertainty of the inflation trend τ^π_t in the two-trend model described in Section 5.2 based on nominal yields and inflation rates (denoted ``YLD'' in Table 2). Panel (b) shows estimated level and uncertainty in the additional trend component of yields τ^π_t. The initial trend level in Panel (b) has been normalized to zero. Red-dashed lines show 90% confidence intervals based on the model's posterior distribution conditional on all data. NBER recession dates are shaded.

Figure 5 Data

Panels (a) and (b) of Figure 5 depict the estimated trend components, $\tau ^\pi _t$ and $\tau ^r_t$ , as well as estimates of their underlying volatilities from this extended model. The estimates are derived from nominal yields and inflation rates; the variable set denoted "YLD" in Table 2. The initial level of the separate yield trend has been normalized to zero, $\tau^r_0=0$ .

By and large, the estimated inflation trend shown in Panel (a) of the figure is very similar to the estimates from the common-trend model, discussed in Section 5.1. Notably, the volatility estimates shown in the lower half of Panel (a) display the protracted hump shape, extending over most of the 1970s and the early 1980s, which has also been found by Stock and Watson (2007), while the single-trend model discussed above documented more two distinct peaks during this period. The trend estimates from the two-trend model are slightly more volatile, with the "twin peaks" of 1974-75 and 1980 being a bit more pronounced than in Figure 4. The trend estimates for the recent crisis are discussed in Section 6.

Not surprisingly, given the choice of fitting separate trend shocks onto the yield process, the model chooses to do so. According to (15), deviations between the inflation trend and the common trend in yields are measured by $\tau ^r_t$ . As can be seen in Panel (b), these deviations are significantly negative for most of the 1970s, and significantly positive during the Volcker disinflation in the early 1980s. Loosely speaking, these estimates reflect the well known pattern of nominal interest rates having been "too low" relative to inflation, during the 1970s and having been "very high" during the 1980s; see, for example, Taylor (1999). According to the model estimates, these deviations from trend inflation have been so persistent, that the model prefers to interpret them as permanent effects driving $\tau_t^r$ . (As will be seen in Section 7, similar trend estimates are obtained when allowing for time-varying gap dynamics.)

As discussed in Section 2, my data set disregards TIPS-based measures of inflation compensation, since historical data is only available for about ten years, and at least during the initial years, the TIPS market was fraught with illiquid trading. For the model discussed in this section, which allows for an additional, common trend component in yields, estimates including TIPS data (not reported here) are however very close to what is shown in Figure 5.

6 Trend Estimates in Real-Time and the Recent Crisis

This section reviews the estimated trends derived from SURV data (Section 4) as well as YLD (Section 5) for the recent years. After discussing the full sample estimates -- already shown in the previous sections -- the section presents real-time simulations.

6.1 Full-sample Estimates for the Last Decade

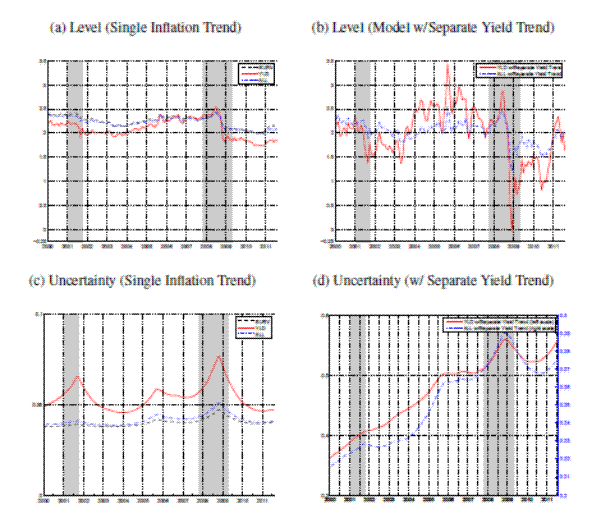
Panel (a) of Figure 6 compares estimates SURV, YLD and ALL for the last decade. The estimates are based on available data since 1960 and thus identical to what has been shown in the previous two sections. Estimates based on SURV and ALL are fairly similar, and as before, the discussion will mostly focus on SURV and YLD. The financial crisis has left a clear imprint on the various estimates of trend and uncertainty. Coincident with concerns about rising commodity prices during the first half of 2008, the trend estimates from SURV and YLD initially have edged higher before dropping by about 1/4 and 3/4 percentage points during the second half of 2008, when the crisis became more severe. Considering the historical estimates since 1960, shown in Panel (a) of Figure 4, such steep changes have occurred before, but they are not the norm either. Since 2009, the trend estimates from SURV and YLD have stayed at values close to 2%, a bit lower than before the crisis. Incidentally, Federal Reserve Chairman Bernanke has recently characterised the Federal Reserve's "mandate consistent" inflation rate to be "2 percent or a bit less" Board of Governors of the Federal Reserve System (2011).²⁴

Figure 6: Recent Inflation Trends

Note: Panels (a) and (b) depict estimates of the inflation trend $\tau_t^\pi$ and Panels (c) and (d) show the corresponding measures of trend shock volatility. All estimates are derived from available data since 1960. The conditioning sets are described in Table 2.

Figure 6 Data

Over the course of 2008, there is also a noticeable, though not dramatic, uptick in the uncertainty measure, in particular for YLD; shown in Panel (c) of the figure. Naturally, the model estimates see the highest volatility of trend shocks during the second half of 2008, when -- according to the level estimates -- the largest shocks to the trend occurred. Quantitatively, the uptick in uncertainty is modest. As can be seen from Figure 2 for the SURV estimates, it registers on a scale below the increase seen after the first oil shock in 1973/74, and with much less persistence. The uncertainty in the YLD measure rose quite a bit more, but remained below its estimates for the 1970s and 1980s (shown in Appendix C).

More importantly, any such risks of unanchored inflation expectations seem to have abated in the period since, as the volatility measures has come down over the course of 2009 and stands again at the historically low level of about 4 basis points.

Panel (b) of Figure 6 displays estimates of level and uncertainty of trend inflation estimated from YLD and ALL, while allowing for a separate yield trend, as described in Section 5.2. Both measures are more volatile than those derived from the model with a single, common trend in inflation and yields; and both dropped more vigorously in late 2008 than the single-trend estimates shown in Panel (a). However there is considerable uncertainty attending these estimates, in particular in the case of the YLD two-trend model whose estimates appear excessively volatile. Still, the posterior distributions of both estimates (not shown in the figure) place more than 90% of their mass on trend values below 2%, but not significantly below $1\frac{1}{2}\%$ , in late 2008. Both measures have recovered since then, at about 2%, slightly below their pre-crisis average.

6.2 Real-time Estimates

So far, this paper has presented full-sample estimates of level and uncertainty in the inflation trend based on data available through August 2011. Borrowing terminology from Kalman filtering, these results will be referred to as "smoothed" estimates. Smoothed trend measure for, say, December 2008 reflect all observations received through the end of the data sample in August 2011. Even when abstracting from data revisions, the hindsight knowledge contained in smoothed estimates may be substantial. To assess the issue, this section shows estimates based on a real-time simulation, where the model has been re-estimated for each month over the last decade.

Since the computational costs involved in re-estimating the model for each month are not negligible, the real-time simulations have been limited to a small subset of variables, which captures the salient features of the trend estimates seen so far. This "SMALL" conditioning set comprises two inflation rates (PCE and CPI), the Livingston survey and the nine-to-ten year forward rate (see also Table 2). In order to avoid hindsight bias from data revisions, the model uses vintage data for the PCE deflator and the non-seasonally adjusted CPI. All estimates use available data since 1960 and the first real-time estimation is simulated for January 1970.²⁵

Figure 7: Inflation Trend Estimates in Real-Time ("SMALL")

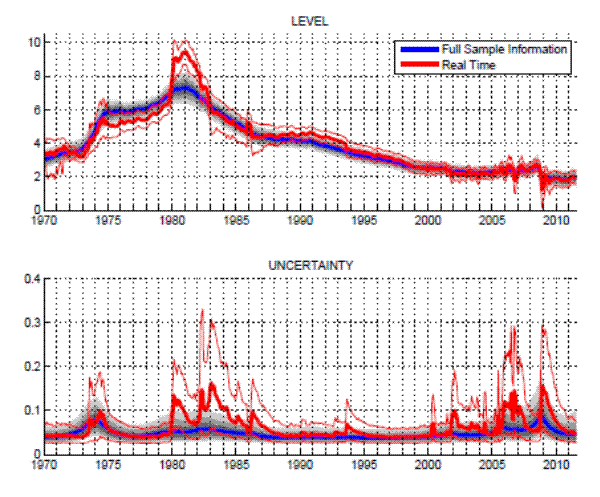
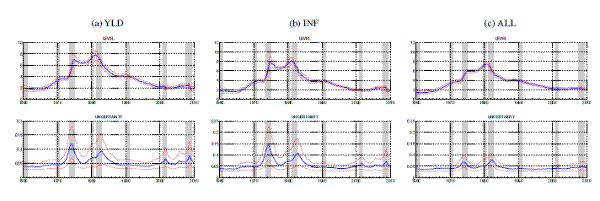
Note: Estimates are based on available real-time data for the for the SMALL data set described in Table 2, using vintage data since 1960 and until the end of any month. Grey shaded bands and the solid blue line display the posterior distribution of "smoothed" trend estimates conditional on all data received through August 2011. Red-solid lines denote posterior mean and 90% confidence intervals of real-time estimates.

Figure 7 Data

As shown in Figure 7, there are some marked differences between real-time and smoothed estimates of trend level and uncertainty. Both estimates see trend inflation hovering well anchored around 2 percent between 2001 and 2007, and both measures register a drop in trend inflation accompanied by an increase in uncertainty during late 2008. However, real-time estimates of level and uncertainty changed much stronger in late 2008 than the smoothed estimates, with the level of the real-time estimates dropping by almost 1 percentage point, whereas the smoothed estimated decreased only by about half as much. This difference reflects the mostly short-lived nature in the drop of real-time estimates of the trend level, leading the smoothed estimates to attribute a larger part of the decreases in the data around the crisis to the gaps instead of the trend. Also, the real-time estimate of trend uncertainty rises much stronger and more sharply in late 2008, than what is suggested by the smoothed estimates.

Another critical period occurred during the late 1970s, before the onset of the Volcker disinflation. In real-time, the trend estimates reacted more dramatically to incoming data-- this time overshooting the smoothed estimates by almost 2 percentage points over the course of 1979-82.²⁶ Both measures pick up marked increases in trend inflation between 1973 and 1975. However, for most of the 1970s, the real-time estimates are about 50 basis points lower than the smoothed trend measure, rendering the increase of the real-time trend in early 1980 even more pronounced. Strikingly, during the recent crisis the real-time measure of uncertainty reached about the same heights as during the early Volcker years and well into 1983/84, a period which Goodfriend (1993) also characterized as an inflation scare. Interestingly, the inflation scare of 1994 registers clearly in real-time estimates of trend and uncertainty. Since the bond market turmoil of 1994 proved short-lived, it barely shows up in the smoothed estimates.

7 Smaller Models with more Time-Varying Parameters

The empirical model described in Section 3 assumes time-invariant dynamics for gap variables. While this seems to be a practical choice given the size of the data set and the amount of missing values, which are modeled as latent factors, it stands in contrast to the lessons from Cogley and Sargent (2005a) and Cogley et al.(2010) who documented important variations, for example, in the persistence of the inflation gap. As a robustness check, this section extends the basic model to incorporate drifting coefficients in the gap VAR, as well as stochastic volatility in gap innovations. This extended model is then estimated with two smaller sets of variables.

In the the extended model the gap VAR (8) is replaced by

$\displaystyle \mat{A_t}(L) \vec{\tilde Y_t}$

$\displaystyle = \vec{\tilde e_t}$

(17)

where the coefficients of $\mat{A_t}(L)$ follow independent random walks, subject to a reflecting barrier, to ensure that each draw of $\mat{A_t}(L)$ has all roots outside the unit circle. The model is estimated with three lags and the volatility of changes in the VAR coefficients is estimated as well. To facilitate stability, only the volatility of changes in the VAR coefficients along the main diagonal of the first lag matrix is estimated with a vague prior.

The gap innovations have stochastic volatility, but constant correlations. As before, they are also correlated with the trend shocks.

$\displaystyle \vec{\tilde e_t} = \vec\beta \,\bar\sigma_t\bar\varepsilon _t + \mat{D} \begin{bmatrix}\tilde\sigma_{t,1} & 0 & \ldots \\ 0 & \tilde\sigma_{t,2} & \\ \vdots & & \ddots \end{bmatrix} \vec{\tilde\varepsilon_t}$

(18)

where D is a lower triangular matrix with ones on its main diagonal. In a manner analogous to the trend shock volatility (7), the logs of $\tilde\sigma_{t,i}$ follow independent random walks.

Figure 8: Time-varying Gap Persistence

Note: Posterior means and 90% confidence intervals for the maximum inverse root of the gap VAR's lag polynomial, denoted $\mat{A}_t(L)$ in (17). Panel (a) shows estimates for the common trend model TVP1. Panel (b) depicts estimates derived from the conditioning set TVP2, which includes the nominal yield on 10-year Treasuries. The TVP2 estimates allow for a separate yield trend as described in Section 5.2. The conditioning sets TVP1 and TVP2 are described in Table 2,

Figure 8 Data

Two sets of conditioning variables are considered. TVP1 comprises inflation rates (PCE headline and core as well CPI) and the Livingston survey, while TVP2 combines the 10-year yield with headline PCE inflation and the Livingston survey. In the case of TVP2, draws of the VAR coefficients frequently violated the stability requirement and a separate yield trend was allowed for, as discussed in Section 5.2.

The main results from the models with time-varying gap dynamics are twofold: First, the trend estimates -- shown in the Appendix -- are broadly similar to what has been reported above for the larger models with time-invariant gap dynamics. However, since the time-varying parameter models have additional flexibility in accounting for time-variation in the spectra for each variable, the estimated trends are more volatile than in the models with time-invariant gap dynamics, and surrounded by additional uncertainty.

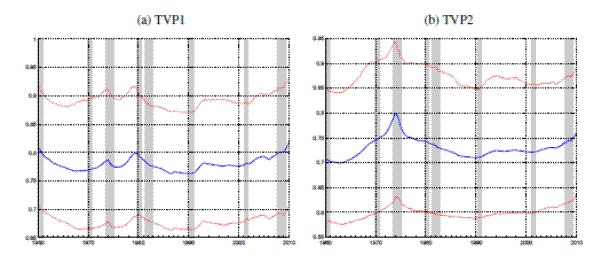
Second, time-variation in the persistence of the gaps appears to have been limited. Figure 8 plots the evolution of the maximum inverse root of $\mat{A_t}(L)$ for TVP1 and TVP2, which varied quite a bit, but not by very much either.

8 Related Literature

While my paper builds very closely on the studies by Stock and Watson (2007), Cogley and Sargent (2005b) and Cogley et al.(2010), it differs from these studies in using a much broader set of multivariate information variables to generate inflation forecasts. In order to handle such a larger data set, I have chosen to neglect some dimensions of the time-varying dynamics, which were embedded in these previous studies, while focusing my model on time-variation in the size of trend shocks. Compared with the quarterly models used by Stock and Watson (2007), Cogley and Sargent (2005b) and Cogley et al.(2010), the model used in this paper also handles missing observations, and combines monthly data series with less frequently sampled variables -- notably surveys, but also the inflation measure derived from the quarterly GDP deflator.

Stock and Watson (2007) use a univariate inflation model with time-varying inflation persistence to elucidate changing patterns in the forecastability of inflation in postwar data for the U.S., and document how time-varying volatility in trend shocks can be a very useful representation of the low frequency movements in U.S. inflation, which can already be discerned from Figure 1. To make their point, Stock and Watson (2007) use a simple representation of the inflation gap as a white noise process with time-varying volatility. In a similar spirit, Kiley (2008) estimates a bivariate trend-cycle model, with core inflation rates for PCE and CPI, where rolling estimates are used to uncover time-variation in the relative importance of shocks to trend and cycles.

Cogley and Sargent (2005b) and Cogley et al.(2010) extend this framework on two notable dimensions. First they use a trivariate system (with inflation, a nominal short rate and unemployment), imposing that inflation and the nominal short rate are cointegrated as described in Section 2 above. In addition, Cogley and Sargent (2005b) and Cogley et al.(2010) allow for persistent, but stationary, gap processes which are modeled as VARs with drifting transition coefficients and stochastic volatility in the VAR innovations. Both papers compute measures of trend inflation from time-varying parameter VARs, whose coefficients follow driftless random walks, and their trend estimates are derived from local "time " approximations of long-term inflation forecasts, in the spirit of the Beveridge-Nelson concept. While Cogley and Sargent (2005b) assume a constant variance of shocks to the VAR parameters, Cogley et al.(2010) estimate drifting volatilities for the parameter processes as well. Hence, innovations to the trend in Cogley and Sargent (2005b) have constant variance, while the model of Cogley et al.(2010) explicitly allows for a time-varying size of trend changes. In both models, the time-varying importance of trend movements is influenced by stochastic volatility in the VAR residuals. In contrast, my model tracks the time-varying importance of trend movements directly by estimating a stochastic volatility process for trend shocks, as in equations (3) and (4).

Cogley et al.(2010) emphasize non-negligible time-variation in the persistence of the inflation gap. Their approach is however very expensive to compute since the time-varying coefficients of the gaps' VAR process are latent variables themselves, thus adding $N^2 \times p$ latent variables to any model with variables and lags, which is feasible in the case of but less so when trying to use a more diverse data set, as it is done here with up to $N=14\xspace$ and infrequently sampled data.

Computational issues aside, the missing data in some of the series used here makes the data also less informative about the kind of time-varying persistence studied by Cogley and Sargent (2005b) and Cogley et al.(2010). To the extent that my paper is more concerned with characterizing movements in the common inflation trend -- which is identified from common low-frequency movements of my data panel -- and less with forecasting higher frequency dynamics of individual gap variables, the approach chosen in this paper offers a tractable and potentially useful approach for extracting trend information from diverse data sources. Section 7 compares my baseline results with a model using much less variables, but allowing for time-varying gap dynamics in the spirit of Cogley and Sargent (2005b) and Cogley et al.(2010).

The importance of low-frequency variations in U.S. inflation has been widely documented by previous studies, using at times very different methods. This evidence has motivated my choice to focus the model on time-variations in the low-frequency component of inflation. For example, Levin and Piger (2003) argue that changes in mean inflation -- which are closely related to the Beveridge-Nelson concept -- seem to account for a large part of the time-variation in inflation dynamics in the U.S. and other countries. Similarly, Faust and Wright (2011) document the importance of accounting for mean drift in forecasting inflation. Their simulated out-of-sample forecasts also suggest that the simple Stock and Watson (2007) model is a very competitive forecasting model, which despite its simplicity seems to capture a salient feature of the inflation process. Faust and Wright (2011) find that tracking drift in average inflation improves the performance of various other models as well. Kozicki and Tinsley (2001) document drifting means in nominal yields -- which they call "shifting endpoints" in the term structure of interest rates -- arguing that these shifting endpoints reflect the public's learning about long-term goals of monetary policy.²⁷

Another difference between between my work and the studies of Stock and Watson (2007), Cogley and Sargent (2005b) and Cogley et al.(2010) is to condition inflation forecasts on survey data. A variety of studies has found survey expectations of future inflation useful for constructing inflation forecasts, see for example Ang et al. (2007) and Gil-Alana et al. (2011). In evaluating the accuracy of survey expectations of inflation, Grant and Thomas (1999) argue that cointegration between survey responses and realized inflation is a weak requirement of rationality and find support for this hypothesis. While individual surveys may be biased and inefficient in that their forecast errors might be non-zero on average and predictable based on ex-ante information -- for example because of imperfect information processing or limited information of survey respondents -- survey responses should not permanently deviate from trend inflation. Clark and Davig (2011) have also investigated the relationship between realized inflation and survey expectations, emphasizing the role of time-varying dynamics in the spirit of Cogley et al.(2010). Their study identifies "long-term expectations" directly with a time series spliced together from the Survey of Professional Forecasters (SPF) 10-year forecast of inflation (since 1991) and a similar series from the Blue Chip surveys, based on which they document a marked decline in the volatility of long-term expectations.

Kozicki and Tinsley (2006) use survey data to model a "term structure of inflation expectations" with particular emphasis on long-term expectations. Their model imposes cross-equation restrictions on survey processes -- in the spirit of approximating survey expectations with autoregressive time-series forecasts -- which may help to the extent that such restrictions provide a good characterization of actual survey responses. Similarly, Haubrich et al. (2011) combine survey expectations with term structure data in a formal asset pricing model for Treasury securities -- imposing no-arbitrage restrictions on the estimated dynamics of the data -- from which they extract long-term inflation expectations. As will be seen in Section 3, my paper allows for arbitrary serial dependence and cross-correlations amongst trend deviations of individual input variables.

The implications of cointegration amongst nominal yields for tests of the expectations hypothesis of the term structure of interest rates has been studied by Campbell and Shiller (1987). More recently, their work has been updated by King and Kurmann (2002). The common yield trend considered by these studies arises presumably -- but not necessarily -- from trend inflation. Cogley (2005) has conducted a similar analysis using a VAR with time-varying parameters. While all of these studies have documented significant deviations from the expectations theory of the term structure, they have also found the assumed cointegration to be useful for modeling nominal yields in U.S. data. In adopting similar cointegrating assumptions, my paper will allow for deviations from the expectations hypothesis -- in the form of time-varying but stationary risk premia -- while interpreting the common trend in yields as arising from trend inflation. (Section 5 presents also results from an extended model, allowing for an additional trend component in yields.)

Finally, it might be worthwhile to relate the Beveridge-Nelson measure of trend inflation to structural shocks in theoretical business cycle models. Many popular workhorse models of monetary policy -- like Rotemberg and Woodford (1997), Christiano et al. (2005) or Smets and Wouters (2007) -- assume the existence of a constant inflation rate in steady-state, which corresponds to the special case of a constant trend with zero shocks. To account for the rise and fall of inflation in the U.S. during the 1970s and 1980s, Ireland (2007) augments a New-Keynesian DSGE model with a time-varying inflation target, driven by exogenous shocks with permanent effects.²⁸ The inflation target process in Ireland:2007:jmcb:InflationTarget's model is identical to a Beveridge-Nelson trend with constant-variance shocks. Similarly, Cogley and Sbordone (2008) estimate a New-Keynesian Phillips Curve model with trend inflation approximately equal to a homoscedastic Beveridge-Nelson trend.²⁹

Other studies, like Erceg and Levin (2003), Cogley and Sargent (2005a), Primiceri (2005) and Goodfriend and King (2005) have analyzed the consequences of opaque policy targets and the potential lack of credibility of monetary policy, and found these potentially useful in explaining U.S. inflation behavior of the 1970s and 1980s. Even though none of these models literally implies the existence of a (non-degenerate) unit root process for trend inflation as in Ireland (2007), they give rise to low-frequency comovements between inflation and nominal rates which -- as argued by Cogley and Sargent (2005b) -- are close to the kind of trend model discussed above. Viewed from this perspective, it should be noted that the trend shocks in (3) may not be structural shocks, but rather the outcome of evolving policy communications and learning dynamics in response to more fundamental economic disturbances.

9 Conclusions

This paper has presented estimates of the level and uncertainty of trend inflation, extracted from survey expectations, the term structure of interest rates and realized inflation rates since 1960. The application combines a variety of data sources at the monthly frequency and it can flexibly handle missing data arising from infrequent observations and limited data availability.

Estimates of trend uncertainty typically rise with estimates of trend inflation itself. This result confirms that episodes of high trend inflation tend to be periods in which inflation expectations have become unanchored, raising the risk of further drift in the trend's level. The result also underscores the need for detecting changes in level and uncertainty.

In the decade prior to the recent crisis, inflation expectations appear to have been well anchored at around 2 percent. But in late 2008, my estimates record a noticeable increase in trend uncertainty accompanied by a marked drop in the trend level. By historical standards, this increase in uncertainty was close to, but below, levels seen shortly after the oil crisis of 1973/74, and well below the peak in trend uncertainty witnessed during the early stages of the Volcker disinflation in 1980.

These results are based on "smoothed" estimates, which enjoy the benefit of hindsight knowledge about the full data sample (up to August 2011). In contrast, when derived from real-time forecasts, trend estimates have dropped quite vigorously during the recent crisis, accompanied by considerable increases in uncertainty. The smoothed estimates condition on the knowledge that a persistent deflation has eventually been averted -- presumably due to active monetary and fiscal policies -- explaining the smaller, though still noticeable, reaction in smoothed estimates of level and uncertainty to the crisis.

Appendix

A. The Gibbs Sampler

The model is estimated with a Gibbs sampler and Bayesian MCMC methods, using multiple chains as in Gelman et al. (2003). Convergence is assessed by the scale reduction test of Gelman et al. (2003). The only fixed parameter is the volatility of shocks to the log-variances, $\sigma_h$ in (7), which is set at a value consistent with the quarterly model of Stock and Watson (2007), $\sigma_h = 0.2 / \sqrt{3}$ . The VAR of the gaps -- see equation (8) -- is estimated with rejection sampling to ensure stability. The baseline results use three lags, similar results are also obtained when using one or six lags.

The following priors were used in the estimation:

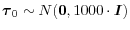A vague prior for the initial values of the trend vector $\vec\tau_0 \sim N(\vec{0}, 1000 \cdot \mat{I})$ .
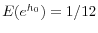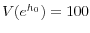A vague prior for the initial value of the trend's stochastic variance, which is log-normally distributed with $E(e^{h_0}) = 1 / 12$ , $V(e^{h_0}) = 100$ .
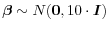The correlation between standardized trend shocks and innovations to the gaps have a fairly vague prior, centered on zero, $\vec{\beta} \sim N(\vec{0}, 10 \cdot \mat{I})$ .
Each coefficient of the lag polynomial in (8) has a normal prior, centered around zero, which is restricted such that the posterior draws are more likely to generate a stable transition matrix. The prior assumes zero correlation amongst the coefficients, and postulates that the diagonal elements of A have a standard deviation of 0.1 and all other elements have a prior standard deviation of 0.01. As can be seen from, Figure 9, the posterior distribution of the maximum root in the companion matrix of the gap VAR, is not severely restricted by this prior -- placing substantial mass on maximum roots of 0.9 and higher. If anything, this prior avoids too many draws of the maximum root to pile up at or near the unit root.
The variance-covariance matrix of the gaps has a completely vague prior, assuming an inverse Wishart distribution with 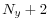degrees of freedom. Given 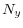gap variables, this is the minimum amount of degrees of freedom to ensure a well defined mean, but not a finite variance.

Figure 9: Persistence of Gap VARs

Note: Frequency of posterior draws of the maximum inverse root of $\mat{A}(L)$ , the lag polynomial of the gap VAR, equation (8), Conditioning sets are described in Table 2.

Figure 9 Data

The Gibbs sampler iterates over the following steps:

Draw 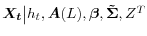$\vec{X_t} \big \vert h_t, \mat{A}(L), \vec\beta, \mat{\tilde\Sigma}, Z^T$ . This is simply a draw from the posterior distribution of a Kalman smoother, implemented as in Durbin and Koopman (2002).
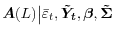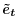Draw $\mat{A}(L) \big \vert \bar\varepsilon_t, \vec{\tilde Y_t}, \vec\beta, \mat{\tilde\Sigma}$ . This is a draw from the posterior distribution of a Bayesian regression with normal priors and known residual variances. The draw also implies a set of gap shocks $\vec{\tilde e_t}$ . As in Cogley and Sargent (2005b), rejection sampling is used to ensure stationarity of the VAR.
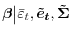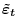Draw $\vec\beta \big \vert \bar\varepsilon_t, \vec{\tilde e_t}, \mat{\tilde\Sigma}$ . This is a draw from the posterior distribution of a Bayesian regression with normal priors and known residual variances. The draw implies a set of residuals $\vec{\tilde\varepsilon_t}$ .
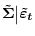Draw $\mat{\tilde\Sigma} \big \vert \vec{\tilde\varepsilon_t}$ . This is a draw from the posterior distribution of a Bayesian regression with normal priors and known residual variances.
Draw the log-variances 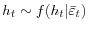$h_t \sim f(h_t \vert \bar\varepsilon_t )$ using the algorithm described by Kim et al. (1998).

For the models with time-varying gap dynamics, described in Section 7, the second step is replaced by a Kalman Filter, drawing the latent coefficient dynamics, conditional on the gaps, followed by a step drawing the innovation variances of each coefficient's random walk (which are assumed to be independent). Likewise, the stochastic volatility step is augmented by including the orthogonalized innovation variances of each gap. The innovation variances are orthogonalized by recursive application of draws from a Bayes regression as in Step 3 above.

The Gibbs sampler was run 8 times, with the number of draws depending on the size of each model. Each of the 8 independent runs was initialized at different starting values, which were drawn from the prior distribution of model parameters. In the case of the basic model with all variables, each run had draws, of which the first were discarded. Convergence of the draws was assessed using the scale reduction test of Gelman et al. (2003), and for each model parameter convergence was achieved at statistics below 1.1 (values close to 1 indicate good convergence).

B. Missing Data for the GDP deflator

This appendix describes how the model of Section 3 is augmented to handle missing data for the GDP deflator. The GDP deflator is available only at the quarterly frequency, whereas the model is monthly. What makes the GDP deflator different from, say, survey responses with missing observations, is that the GDP deflator measures price changes which accrue over the span of a quarter.

Suppose that the GDP deflator is observed in months etc. and denote the logarithm of the GDP deflator at the end of a quarter by $p^{\text{GDP}}_t$ and the implied quarterly inflation data by $z^{GDP}_t=400 \cdot (p^{\text{GDP}}_t - p^{\text{GDP}}_{t-3} )$ , and it becomes clear that it represents the trailing three-month moving average of a latent monthly series,

$\displaystyle z^{GDP}_t= \frac{\pi^{GDP}_t + \pi^{GDP}_{t-1} + \pi^{GDP}_{t-2}}{3} \; ,$

(19)

where the latent variable $\pi^{GDP}_t$ tracks annualized GDP inflation at the monthly frequency.

Figure 10: The Posterior Distribution of Monthly GDP Inflation and the Livingston Survey

Note: Posterior distribution of monthly values derived from the basic model described in Section 3 (using SURV data). Actual observations for GDP inflation and the Livingston survey -- which are respectively available on a quarterly and bi-annual basis -- are dotted. By construction, the posterior distribution collapses for the missing data values to the actual values, when available.

Figure 10 Data

Formally, this simply requires adding two lags of $\pi^{GDP}_t$ to the state vector,

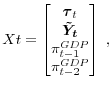
$\displaystyle Xt = \begin{bmatrix}\vec\tau_t \\ \vec{\tilde Y_t} \\ \pi^{GDP}_{t-1} \\ \pi^{GDP}_{t-2} \end{bmatrix}\; ,$

and to use (19) as measurement equation for GDP inflation in the months of March, July, October and December and $z^{GDP}_t=0$ otherwise. Based on the SURV model of Section 4, Figure 10 depicts the posterior distribution of the model estimates for $\pi_t^{GDP}$ . By construction, the distribution collapses to the actual observation for GDP inflation at the end of each quarter.

C. Additional Results

The results presented in this appendix are intended only for web publication.

C.1 Alternative conditioning sets

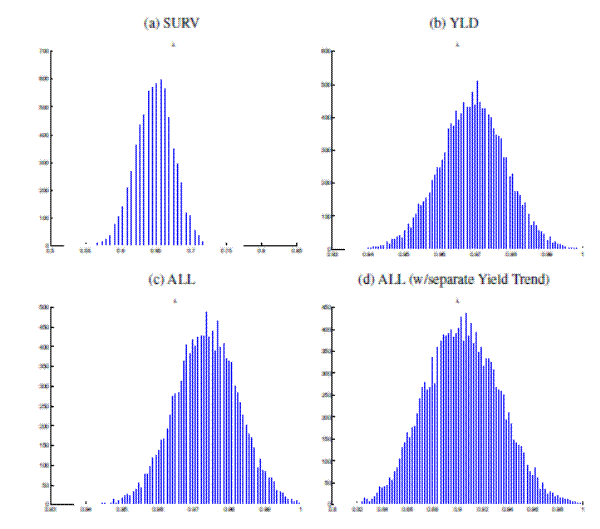
Panel (a) of Figure 11 shows estimates for YLD; the level estimates are also shown in Figure 4 of the main text. Panel (b) of Figure 11 shows the corresponding measures for INF, and Panel (c) displays estimates of trend level and uncertainty extracted from the joint data set of all variables listed in Table 1. These estimates are fairly close to the YLD estimates discussed in Section 5 of the main text.

Figure 11: Inflation Trend based on Alternative Conditioning Sets

Note: The top panel shows the smoothed estimates of the trend and the bottom panel shows uncertainty about trend shocks. The estimates are derived from the nominal yields and inflation rates listed in Table 1. Red-dashed lines show 90% confidence intervals based on the model's posterior distribution conditional on all data. NBER recession dates are shaded.

Figure 11 Data

C.2 Trend Estimates from Models with Time-varying Gap Dynamics

Figures 12 and 13 report estimates of level and uncertainty in trend inflation in the models with time-varying gap dynamics described in Section 7 of the main paper.

Figure 12: Inflation Trend from TVP1 model

Figure 12 Data

Figure 13: Trends in TVP2-Model with Separate Yield Trend

Note: The top panel shows the smoothed estimates of the trend and the bottom panel shows uncertainty about trend shocks. These estimates are derived from the extended model described in Section 7, allowing for time-varying gap dynamics, stochastic volatility in gap innovations, as well as an additional trend component in yields. The model is estimated from all available observations on headline PCE, the Livingston survey as well as the nominal yield on 10-year Treasuries -- the variable set denoted "TVP2" in Table 2. Panel (a) depicts level and uncertainty of the inflation trend τ^π_t, whereas Panel (b) shows estimates of level and uncertainty for the additional trend component, denoted τ^π_t in (15). Red-dashed lines show 90% confidence intervals based on the model's posterior distribution conditional on all data. NBER recession dates are shaded.

Figure 13 Data

C.3 Stochastic Volatility of Gaps in TVP Models

Figures 14 and Figures 15 report estimates of the stochastic volatility series for the gap variables in the time-varying parameter models (Section 7) for models TVP1 and TVP2 respectively.

Figure 14: Stochastic Volatility in Gaps of the TVP1 Model

Note: Posterior means and 90% confidence intervals for stochastic volatilities in the gap innovations, denoted $\sigma_{t,i}$ in (18). The estimates are derived from the time-varying parameter version of the common trend model described in Section 7, using available data since 1960 for headline PCE, core PCE, the seasonally adjusted CPI as well as the Livingston survey. This is the conditioning set called "TVP1" in Table 2.

Figure 14 Data

Figure 15: Stochastic Volatility in Gaps of the TVP2 Model

Note: Posterior means and 90% confidence intervals for stochastic volatilities in the gap innovations, denoted $\tilde\sigma_{t,i}$ in (18). The estimates are derived from the time-varying parameter version of the common trend model described in Section 7, when allowing for a separate yield trend as described in Section 5. The model is estimated from data since 1960 on headline PCE, the Livingston survey and nominal yields on 10-year Treasuries -- the conditioning set called "TVP2" in Table 2.

Figure 15 Data

Bibliography

Andrew Ang, Geert Bekaert, and Min Wei.

Do macro variables, asset markets, or surveys forecast inflation better?
Journal of Monetary Economics, 54(4):, 1163 - 1212, 2007.

Olivier Armantier, Wändi Bruine de Bruin, Wilbert van der Klaauw, Giorgio Topa, and Basit Zafar.

Inflation expectations and behavior: Do survey respondents act on their beliefs? mimeo Federal Reserve Bank of New York, 2011.

Meredith J. Beechey, Benjamin K. Johannsen, and Andrew T. Levin.

Are long-run inflation expectations anchored more firmly in the Euro area than in the United States? American Economic Journal: Macroeconomics, 3(2):104-29, 2011.

Stephen Beveridge and Charles R. Nelson.

A new approach to decomposition of economic time series into permanent and transitory components with particular attention to measurement of the "business cycle". Journal of Monetary Economics, 7(2):151-174, 1981.

Board of Governors of the Federal Reserve System.

Transcript of Chairman Bernanke's Press Conference, June 22, 2011.

John Y. Campbell and Robert J. Shiller.

Cointegration and tests of present value models. The Journal of Political Economy, 95(5):, 1062-1088, October 1987.

Lawrence J. Christiano, Martin Eichenbaum, and Charles L. Evans.

Nominal rigidities and the dynamic effects of a shock to monetary policy. Journal of Political Economy, 113(1):1-45, February, 2005.

Todd E. Clark and Troy Davig.

Decomposing the declining volatility of long-term inflation expectations. Journal of Economic Dynamics and Control, 35(7):981 - 999, 2011.

John H. Cochrane.

A critique of the application of unit root tests. Journal of Economic Dynamics and Control, 15(2):275 - 284, 1991.

Timothy Cogley.

Changing beliefs and the term structure of interest rates: Cross-equation restrictions with drifting parameters. Review of Economic Dynamics, 8(2):420-451, April, 2005.

Timothy Cogley and Thomas J. Sargent.

Drift and volatilities: Monetary policies and outcomes in the post WWII U.S. Review of Economic Dynamics, 8(2):262-302, April, 2005a

Timothy Cogley and Thomas J. Sargent.

The conquest of us inflation: Learning and robustness to model uncertainty. Review of Economic Dynamics, 8(2):528-563, April, 2005b

Timothy Cogley and Argia M. Sbordone.

Trend inflation, indexation, and inflation persistence in the new Keynesian phillips curve. The American Economic Review, 98(5):, 2101-26, 2008.

Timothy Cogley, Giorgio E. Primiceri, and Thomas J. Sargent.

Inflation-gap persistence in the U.S. American Economic Journal: Macroeconomics, 2(1):43-69, January, 2010.

J. Durbin and S. J. Koopman.

A simple and efficient simulation smoother for state space time series analysis. Biometrika, 89(3):603-615, September, 2002.

Rochelle M. Edge, Michael T. Kiley, and Jean-Philippe Laforte.

Natural rate measures in an estimated DSGE model of the U.S. economy. Journal of Economic Dynamics and Control, 32(8):, 2512-2535, August 2008.

Christopher J. Erceg and Andrew T. Levin.

Imperfect credibility and inflation persistence. Journal of Monetary Economics, 50(4):915-944, May, 2003.

Jon Faust and Jonathan H. Wright.

Forecasting inflation. mimeo, Department of Economics, Johns Hopkins University, May , 2011.

Martin Feldstein, Mervyn King, and Janet L. Yellen.

Innovations and issues in monetary policy: Panel discussion. The American Economic Review, 94(2):pp. 41-48, 2004. Papers and Proceedings of the One Hundred Sixteenth Annual Meeting of the American Economic Association San Diego, CA, January 3-5, 2004.

Andrew Gelman, John B. Carlin, Hal S. Stern, and Donald B. Rubin.

Bayesian Data Analysis. Chapman and Hall, 2nd edition, 2003.

Luis Gil-Alana, Antonio Moreno, and Fernando Pérez de Gracia.

Exploring survey-based inflation forecasts. Journal of Forecasting, (in press):n/a-n/a, 2011.

Marvin Goodfriend.

Interest rate policy and the inflation scare problem:, 1979-1992. Economic Quarterly, 79(1):1-24, Winter 1993.

Marvin Goodfriend and Robert G. King.

The incredible Volcker disinflation. Journal of Monetary Economics, 52(5):981-1015, July, 2005.

Alan P. Grant and Lloyd B. Thomas.

Inflationary expectations and rationality revisited. Economics Letters, 62(3):331 - 338, 1999.

Refet S Gürkaynak, Andrew T. Levin, and Eric Swanson.

Does inflation targeting anchor long-run inflation expectations? Evidence from the U.S., UK, and Sweden. Journal of the European Economic Association, 8(6):, 1208-1242, December 2010.

Joseph G. Haubrich, George Pennacchi, and Peter Ritchken.

Inflation expectations, real rates, and risk premia: evidence from inflation swaps. Working Paper, 1107, Federal Reserve Bank of Cleveland, March 2011.

Peter N. Ireland.

Changes in the Federal Reserve's inflation target: Causes and consequences. Journal of Money, Credit and Banking, 39(8):, 1851-1882, December 2007.

Michael T. Kiley.

Estimating the common trend rate of inflation for consumer prices and consumer prices excluding food and energy prices. Finance and Economics Discussion Series, 2008-38, Board of Governors of the Federal Reserve System (U.S.), July 2008.

Sangjoon Kim, Neil Shephard, and Siddhartha Chib.

Stochastic volatility: Likelihood inference and comparison with arch models. The Review of Economic Studies, 65(3):361-393, July, 1998.

Mervyn A. King.

Changes in UK monetary policy: Rules and discretion in practice. Journal of Monetary Economics, 39(1):81 - 97, 1997. Rules and Discretion in Monetary Policy.

Robert G. King and André Kurmann.

Expectations and the term structure of interest rates: Evidence and implications. Federal Reserve Bank of Richmond Economic Quarterly, (Fall):49-95, August, 2002.

Narayana Kocherlakota.

Communication, credibility and implementation -- some thoughts on current, past and future monetary policy. Speech at the National Association of State Treasurers, Bismarck, North Dakota., 30 August, 2011.

Sharon Kozicki and P. A. Tinsley.

Shifting endpoints in the term structure of interest rates. Journal of Monetary Economics, 47(3):613-652, June, 2001.

Sharon Kozicki and P.A. Tinsley.

Survey-based estimates of the term structure of expected U.S. inflation. Working Papers 06-46, Bank of Canada, December, 2006.

Andrew T. Levin and Jeremy M. Piger.

Is inflation persistence intrinsic in industrial economies? Working Papers, 2002-023, Federal Reserve Bank of St. Louis, 2003.

Clinton P. McCully, Brian C. Moyer, and Kenneth J. Stewart.

A reconciliation between the consumer price index and the personal consumption expenditure index. mimeo Bureau of Economic Analysis, September, 2007.

Frederic S. Mishkin.

Inflation dynamics. International Finance, 10:317-334, 2007.

Giorgio Primiceri.

Why inflation rose and fell: Policymakers' beliefs and U.S. postwar stabilization policy. NBER Working Papers, 11147, National Bureau of Economic Research, Inc, February 2005. Forthcoming in The Quarterly Journal of Economics.

Julio J. Rotemberg and Michael Woodford.

An optimization-based econometric framework for the evaluation of monetary policy. In Ben S. Bernanke and Julio J. Rotemberg, editors, NBER Macroeconomics Annual, 1997, pages 297-346. The MIT Press, Cambridge (MA), 1997.

Frank Smets and Rafael Wouters.

Shocks and frictions in U.S. business cycles: A Bayesian DSGE approach. The American Economic Review, 97(3):586-606, June, 2007.

James H. Stock and Mark W. Watson.

Why has U.S. inflation become harder to forecast? Journal of Money, Credit and Banking, 39(S1):3-33, February, 2007.

John B. Taylor, editor.

Monetary Policy Rules. The University of Chicago Press, Chicago, 1999. (Papers based on the National Bureau of Economic Research Conference on Research in Business Cycles, held at Stanford University 1998).

Jean Claude Trichet and Vítor Constancio.

Introductory statement to the press conference. European Central Bank, June 9, 2011.

Wilbert van der Klaauw, , Wändi Bruine de Bruin, Giorgio Topa, Simon Potter, and Michael Bryan.

Rethinking the measurement of household inflation expectations: Preliminary findings. Technical Report 359, Federal Reserve Bank of New York, December , 2008.

Michael Woodford.

Central bank communication and policy effectiveness. In The Greenspan Era: Lessons for the Future, pages 399-474, Jackson Hole, Wyoming, August, 2005. FRB Kansas City Symposium.

Janet L. Yellen.

Commodity prices, the economic outlook, and monetary policy. Remarks at the Economic Club of New York, April 11, 2011.

Footnotes

*I would like to thank Michiel DePooter, David López-Salido, Edward Nelson, Seth Pruitt, Jeremy Rudd, Mark Watson, Min Wei and Jonathan Wright for helpful conversations about this project. Excellent research assistance has been provided by Benjamin Brookins and Chrstine Garnier. Return to Text

†For correspondence: Elmar Mertens, Board of Governors of the Federal Reserve System, Washington D.C. 20551. email [email protected]. Tel.: +(202) 452 2916. The views in this paper do not necessarily represent the views of the Federal Reserve Board, or any other person in the Federal Reserve System or the Federal Open Market Committee. Any errors or omissions should be regarded as solely those of the author. Return to Text

1. For example, in testimony presenting the Monetary Policy Report of March 2011, Federal Reserve Chairman Bernanke emphasized that "[s]ustained rises in the prices of oil or other commodities would represent a threat both to economic growth and to overall price stability, particularly if they were to cause inflation expectations to become less well anchored. We will continue to monitor these developments closely and are prepared to respond as necessary to best support the ongoing recovery in a context of price stability." Similar views have been expressed by Federal Reserve Vice Chair Yellen (2011), Federal Reserve Bank President Kocherlakota (2011), ECB President Jean-Claude Trichet (Trichet and Constancio, 2011) and Bank of England Governor Mervyn King (Feldstein et al., 2004;, King, 1997) -- to name but a few. Further, Woodford (2005) provides a discussion of the interplay between inflation expectations and monetary policy in the context of theoretical models, and Mishkin(2007) reviews the channels through which changing behavior of trend inflation may have affected inflation dynamics. Return to Text

2. Setting the unconditional mean of the gap to zero is a normalization, since the mean gap cannot be identified independently from the initial trend level. Return to Text

3. In addition, Equation (3) below shows how the infinite horizon of allows to abstract from roll-over issues as time evolves, since changes in trend inflation merely reflect changes in information, but not changes in the forecast's target date -- which always remains equal to the infinite horizon. Return to Text

4. Such a setting would be consistent with DSGE models with credible monetary policies and a constant rate of inflation in steady state, as for example in Rotemberg and Woodford (1997), Christiano et al. (2005) or Smets and Wouters (2007). Return to Text

5. The relationship between the Beveridge-Nelson concept of trend inflation and theoretical models of monetary policy is further discussed in Section 8. Return to Text

6. For instance, Kozicki and Tinsley (2001), Gürkaynak et al.(2010) and Beechey et al. (2011) provide evidence -- based on the term structure of interest rates -- suggesting that long-term inflation expectations in the U.S. are time varying and far from constant. Return to Text

7. Amongst others, the Monetary Policy Report to the Congress from the Board of Governors of the Federal Reserve System describes the Board's outlook for inflation in terms of the PCE, since its construction better reflects the changing composition of spending than other measures, like the CPI. McCully et al.(2007) also provide a detailed comparison of the PCE and CPI price indices. Return to Text

8. The Michigan survey does ask respondents to refer to a specific price basket like the CPI or the PCE deflator. Return to Text

9. In principle, it is also straightforward to include TIPS-based measures of inflation compensation, also known as the break-even inflation rate of a TIPS security, in this framework. However, since data on inflation compensation is available only for roughly ten years, and at least initially, but also during the recent crisis, the underlying securities prices were heavily affected by liquidity premia, I have chosen not to include TIPS. Results not shown here suggest that these issues seem to have induced near-permanent effects on TIPS data, which distort the common trend extraction in significant ways. Allowing for a separate yield trend as discussed in Section 5.2 seems to prune these effects however quite well, and the inclusion of TIPS yields results similar to what is shown there. Return to Text

10. Using data from January 1960 until June 2011, augmented Dickey-Fuller tests (with and without intercept) reject the null hypothesis of a unit root in the difference between headline PCE inflation and the 10-year Treasury yield with

-values below 1%. Return to Text

11. In particular over the last ten years, deviations between the nominal yields of shorter dated Treasury securities -- like 5-year Treasuries -- have deviated quite substantially from inflation data and yields on longer-dated securities, which is why only longer dated Treasury yields and the nine-to-ten year forward rate is included in the data set. Return to Text

12. Throughout this paper, vector variables will be denoted with boldface letters, while scalars are printed in standard font. Return to Text

13. An alternative representation of the common trend assumption would be to write the multivariate Beveridge-Nelson decomposition in terms of a scalar trend, $\vec{Y_t} = \vec{1} \tau_t + \vec{\tilde{Y}_t}$ and to allow for non-zero means in the gaps instead of variable-specific initial trend levels. When it comes to estimating the model with a Gibbs sampler as discussed in Appendix A, the representation above turns out to be more efficient, since it allows to recover the initial trend levels jointly with the model's latent trend process. Return to Text

14. These correlations allow for transitory responses in the gaps to trend shocks. For example, if trend shocks were interpreted as exogenous shocks to the inflation target as in Ireland (2007), these gap responses would reflect the adjustments in sticky prices and wages to a new trend level. Return to Text

15. Estimates based on such a specification would display a poor ability to distinguish shocks which are permanent from shocks which are heteroscedastic but short-lived. For example, a few inflation measures contain large but transitory spikes around 9/11/11 due to distortions in non-market based price components, which could then erroneously be attributed to the trend. Return to Text

16. In terms if informational content, missing data for GDP inflation could also be modeled as in (14), which would however induce a slightly different pattern for the persistence of the latent monthly gap series implied by such a representation. Return to Text

17. Estimating the value from the data yields similar trend estimates, but considerably more volatile estimates of the log-variances

. Return to Text

18. Table 2 below, refers to this set of variables also as "SURV." Return to Text

19. http://www.federalreserve.gov/econresdata/researchdata/feds200628_1.html Return to Text

20. For example, using monthly observations of the PCE deflator

, PCE inflation is computed as $\pi_t = 1200 \cdot (\log{p_t} - \log{p_{t-1}})$ , and the annualized percentage yield on a nominal Treasury security,

, is transformed into $i_t = 100\cdot\log{(1+I_t/100)}$ . Return to Text

21. As the trend is modeled as a random walk, the standard deviation of cumulated changes grows with the square root of time. Return to Text

22. This decomposition is without loss of generality as long as the label "risk premium" is understood loosely as the residual between the nominal yield and the yield implied by the Fisher equation. Return to Text

23. In principle, shifts in term premia could also account for this additional trend component. Return to Text

24. Chairman Bernanke made this remark in the context of the release of the summary of economic projections by the FOMC, in which the projections for PCE inflation showed a central tendency between 1.7 and 2.0 percent. Return to Text

25. Between 1970 and December 1979, the vintage data provides only quarterly readings for the PCE deflator. Estimates simulated for this period are derived from a measurement equation, which interprets the quarterly PCE readings as the moving average of an unobserved monthly series. This is analogous to the treatment of the GDP deflator as described in Appendix B. Return to Text

26. The increase in the real-time measure of uncertainty also dwarfs movements in the smoothed estimates. Please notice as well, that for this dataset the smoothed estimated of uncertainty peaks more noticeably in 1974 instead of the late 1970s, as it has been the case for the larger model discussed in the previous sections. Return to Text

27. Kozicki and Tinsley (2001) also estimate a unit root model for nominal rates, called "moving average endpoint" specification, but with a constant variance of the unit root shocks, such that the model cannot match the time-varying importance of low-frequency movements in nominal yields, see for example Figure 1 above. Return to Text

28. In different versions of his model, Ireland (2007) considers the case in which target shocks are orthogonal to other fundamental shocks and the case of correlations between target shocks and other exogenous driving variables of the model. In each case, the inflation evolves as a random walk, driven by homoscedastic shocks. Return to Text

29. Cogley and Sbordone (2008) identify trend inflation from a VAR with drifting coefficients as in Cogley and Sargent (2005b), however without allowing for stochastic volatility. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Measuring the Level and Uncertainty of Trend Inflation*