
Habit formation heterogeneity:
Implications for aggregate asset pricing *
Keywords: Asset pricing, consumption-based asset pricing models, external habit, internal habit, heterogeneity, time-nonseparability, general equilibrium, computing equilibria, recursive solution
Abstract:
1 Introduction
The objective of this paper is to study the effect of habit heterogeneity on aggregate asset prices in a general equilibrium economy with two agents, which are heterogeneous with respect to their coefficients of relative risk aversion and habit preferences. Habit preferences are defined as external or internal habit formation. We consider a complete financial market where traded securities are a risky stock and a short-term discount bond. We study the effect of heterogeneity in habits on aggregate asset prices, namely, interest rate volatility, equity premium, equity return volatility, and Sharpe ratio.
There are two building blocks in our model, agents' heterogeneity and habit formation. On one hand, habit formation models became increasingly successful and important in explaining a number of dynamic asset pricing facts, such as the equity premium puzzle, (see, e.g. (Constantinides, 1990), (Campbell and Cochrane, 1999), and (Abel, 1990), (Abel, 1999)), as well as macroeconomic facts, such as output persistence, savings and growth, and response of consumption to monetary shocks (see, e.g., (Boldrin et al., 2001), (Carroll et al., 2000), and (Fuhrer, 2000)). However, different studies use different habit formation models without much guidance from the theory or empirical work about which preferences should be used. Although there are some empirical studies that explore whether different types of habit matter for matching conditional moment restrictions implied by the asset pricing theory ((Chen and Ludvigson, 2009), (Grishchenko, 2010), (Dai and Grishchenko, 2005)), the literature on computing explicit asset prices under different types of habits is virtually non-existent. In this paper we fill this gap.
On the other hand, various studies in the last decade have shown that heterogeneity among agents should be an important feature of the consumption-based equilibrium model. Heterogeneity can be modeled either with respect to preferences in a time-separable setting (see, e.g., (Dumas, 1989), (Wang, 1996), (Bhamra and Uppal, 2010)), idiosyncratic consumption and labor income risk (see, e.g., (Constantinides and Duffie, 1996), (Brav et al., 2002), (Jacobs and Wang, 2004), (Malloy et al., 2009), (Grishchenko and Rossi, 2011)), beliefs (see, e.g., (Detemple and Murthy, 1994), (Xiong and Yan, 2010)). Some studies solve models where heterogeneity (usually in risk aversion) is introduced in the models with habit formation (see, e.g. (Chan and Kogan, 2002), (Guvenen, 2005), (Pijoan-Mas, 2007), (Xiouros and Zapatero, 2010), (Ehling and Heyerdahl-Larson, 2010)). These studies consider only "catching up with Joneses" preferences, either multiplicative or additive. However, no one to date has explored the heterogeneity with respect to internal habit preferences. In the current study we fill this gap and model these two effects simultaneously. To our knowledge, our paper is the first to solve for equilibrium asset prices in the model that allow for (i) different type of habit in the preferences: namely, either external habit formation model (also known as "Catching up with Joneses") or internal habit formation; and (ii) heterogeneity in habit preferences' parameters between two agents. Namely, we ask the following two questions:
- Q1:
- Do internal habit (IH) formation models and their external counterparts (EH) obtain the same aggregate asset prices?
- Q2:
- Does heterogeneity with respect to parameters in the habit process helps to obtain aggregate asset pricing quantities consistent with historically observed asset prices?
The difference between two habit types, namely external habit and internal habit preferences, lies in the effect that current consumption has on future habit. (Abel, 1990), (Gali, 1994), and (Campbell and Cochrane, 1999) were among the first to study models with external habit formation and their implications for asset pricing (see also (Bekaert et al., 2010), (Wachter, 2006), (Menzly et al., 2004)).1 In these models past consumption enters into the habit process but has no effect on current consumption choice; that is, habit formation is an externality. On the other hand, (Abel, 1990), (Ryder and Heal, 1973), (Dunn and Singleton, 1986), (Sundaresan, 1989), (Constantinides, 1990), and (Detemple and Zapatero, 1991) study habit persistence, or internal habit formation, where past consumption choice enters into the habit process and affects current and future consumption choices. As a result, these two types of habits produce different pricing kernels and, consequently, lead to different asset pricing implications.
Empirical studies related to habit persistence are rather limited. Up to date, most of the habit formation models have been set and then calibrated to historical data to examine how well they fit unconditional and conditional moments of asset returns. Empirical exceptions in the literature represent (Ferson and Constantinides, 1991), (Heaton, 1995), (Dunn and Singleton, 1986), and (Dynan, 2000). (Ferson and Constantinides, 1991), for example, find empirical support for a one-lag internal habit in quarterly consumption data, while (Heaton, 1995) finds evidence for a multi-lag habit in the same data. On contrary, (Dynan, 2000) uses annual household food consumption data and finds no evidence for habit formation. Recently, (Chen and Ludvigson, 2009) and (Grishchenko, 2010) show, using quarterly consumption data and different econometric methods that preferences with internal habit formation are more consistent with observed aggregate asset prices than preferences with external habit. treat the habit functional form as unknown and find that the habit form is nonlinear albeit restricted to just a few consumption lags. (Grishchenko, 2010) estimates a flexible "mixture" habit formation model that includes both external and internal habit features with many consumption lags, but assumes linear functional form of habit. (Korniotis, 2010) finds support for external habit in annual consumption state-level data. Our approach is different from all papers mentioned above because we do not treat aggregate prices as given but explicitly compute them.
Although methods involving calibration, simulation, and econometric estimation of habit formation models present a step forward in learning about habit specification properties consistent with equilibrium prices, an ultimate solution for the equilibrium prices in the presence of various types of time-nonseparability is missing. Our paper fills this gap. Moreover, we contribute to the literature on heterogeneity in asset pricing by modeling agents' heterogeneity and habit formation in the fundamentally new way: the agents in our model differ with respect to the habit formation process, which might incorporate either internal or external habit specifications.
The general equilibrium quantities in a discrete time, finite horizon economy are determined by a recently developed recursive backward scheme in the paper of (Dumas and Lyasoff, 2011). The crucial features of their algorithm (designed for time-separable
preferences) that permits one to work only backwards in time instead of being stuck with a usual backward-forward procedure, are the time shift of the budget equation and the choice of the endogenous state variable (grid).2 With time-nonseparable preferences the problem is much more severe, since the pricing kernel at time ![]() is affected by the
whole future consumption stream. For our purposes, we are able to generalize their procedure to capture time-nonseparable preferences when allowing for one lag in the habit formation process. Our paper represents one of the first attempts that apply and extend the powerful algorithm of
Dumas-Lyasoff to study various asset pricing questions. The (Buss et al., 2011) paper is another example of the application of the Dumas-Lyasoff framework where the authors solve for asset pricing quantities in the general equilibrium set up with transaction costs
and recursive utility.
is affected by the
whole future consumption stream. For our purposes, we are able to generalize their procedure to capture time-nonseparable preferences when allowing for one lag in the habit formation process. Our paper represents one of the first attempts that apply and extend the powerful algorithm of
Dumas-Lyasoff to study various asset pricing questions. The (Buss et al., 2011) paper is another example of the application of the Dumas-Lyasoff framework where the authors solve for asset pricing quantities in the general equilibrium set up with transaction costs
and recursive utility.
There are several findings that emerge in our study. First, we answer the Q1 question positively, finding that internal habits present a considerable improvement over external habits. The reason is that the pricing kernel at every point in time is non-trivially affected by the consumption decisions made in the previous period, feature that is absent in the external habit formation models. Second, we match the equity premium, volatility of the stock market, and Sharpe ratio with the coefficient of relative risk aversion equal to 5 and internal habit strength parameter of a representative agent equal to 0.4. Third, we find that a combination of risk aversion coefficients 7 and 4 and habit coefficients 0.3 and 0.5 is able to match historically observed equity premium, volatility, and Sharpe ratio. The undesirable feature of our stylized model is that the model produces too high interest rate and interest rate volatility. However, we focus in our paper is on quantifying the difference between internal and external habits and do not attempt to resolve simultaneously both equity premium and risk-free rate puzzles. The answer to the Q2 question is negative. We do not find that heterogeneity in habit preferences produces substantially different results than a representative agent framework with habits. This result is possibly due to the complete market setting that we aim to relax in future research.
The rest of the paper is organized as follows. Section 2 presents the model, Section 3 describes the solution method, Section 4 reports results, and Section 5 concludes.
2.1 Information structure
We consider a (Lucas, 1978)-type exchange economy on the finite time span, discrete time space,
![]() , and discrete state space. Uncertainty is represented by a filtered probability space
, and discrete state space. Uncertainty is represented by a filtered probability space
![]() , where
, where
![]() represents the information flow or the tree structure, respectively, on which a one-dimensional Binomial process
represents the information flow or the tree structure, respectively, on which a one-dimensional Binomial process
![]() is defined.
is defined.
2.2 Agents' endowments and preferences
The economy is populated by two agents (or, two types of agents). At time ![]() , agent
, agent ![]() maximizes his life-time expected utility
maximizes his life-time expected utility
![]() :
:
where
CRRA time-separable case. Intratemporal utility function for agent ![]() is given by:
is given by:
Then marginal rate of substitution of agent ![]() at time
at time ![]() is:
is:
In all other cases intratemporal utility is defined over surplus consumption ![]() :
:
A surplus consumption is
![]() , where
, where ![]() is the habit function, that can take
two forms, external or internal:
is the habit function, that can take
two forms, external or internal:
where per-capita consumption is defined as
When habit preferences follow Definition 1, the marginal utility of consumption and pricing kernel are given by:
and
When habit preferences follow Definition 2, marginal utility of consumption and marginal rate of substitution are given by:
and
In all our models the marginal rate of substitution is identical to the pricing kernel.7 We allow for two sources of heterogeneity in the model: a relative
risk aversion coefficient ![]() and a habit parameter
and a habit parameter ![]() .8 We need to explore the main driving force of heterogeneity in the model solution. In sum, we consider three models: benchmark CRRA model and two habit models:
external and internal habits in the additive framework.
.8 We need to explore the main driving force of heterogeneity in the model solution. In sum, we consider three models: benchmark CRRA model and two habit models:
external and internal habits in the additive framework.
2.3 Description of the market
The economy is a standard (Lucas, 1978)-type economy. There is one risky asset, which produces a stream of dividends
![]() ,
, ![]() , in the form of a single perishable
consumption good. The dividend dynamics is captured by a simple binomial process:
, in the form of a single perishable
consumption good. The dividend dynamics is captured by a simple binomial process:
where
![]() ,
,
![]() . In the tradition of (Cox et al., 1979) we denote the nodes
. In the tradition of (Cox et al., 1979) we denote the nodes
![]() for "up" and "down" as the two successor nodes of a given node
for "up" and "down" as the two successor nodes of a given node ![]() at
time
at
time ![]() .9 The stock
.9 The stock ![]() ,
, ![]() , is a claim on dividends, defined in (11). Additionally, there exists a
locally risk-free (short-term) bond
, is a claim on dividends, defined in (11). Additionally, there exists a
locally risk-free (short-term) bond ![]() at
at
![]() :
:
where ![]() is a one-period interest rate.
is a one-period interest rate.
2.4 Equilibrium conditions
In this section we describe the equilibrium conditions and outline the solution algorithm. Denote ![]() and
and ![]() consumption and exiting wealth for agent
consumption and exiting wealth for agent ![]() at time
at time ![]() in state
in state ![]() , respectively;
, respectively; ![]() and
and ![]() - price and dividend of the risky asset at time
- price and dividend of the risky asset at time ![]() in state
in state ![]() , respectively;
, respectively; ![]() - an interest rate at time
- an interest rate at time ![]() and state
and state ![]() . Following (Dumas and Lyasoff, 2011), we define exiting wealth of agent
. Following (Dumas and Lyasoff, 2011), we define exiting wealth of agent
![]() as
as
![]() .10
In addition, we write the flow budget constraint and the kernel conditions at time
.10
In addition, we write the flow budget constraint and the kernel conditions at time ![]() , consistent with Dumas and Lyasoff's crucial time shift.
, consistent with Dumas and Lyasoff's crucial time shift.
Flow budget constraints:
The initial budget constraint is used to solve for time 0 consumption ![]() :
:
where
![]() and
and
![]() together with
together with
![]() and
and
![]() denote the initial endowment (prior to time 0) of both agents in the stock and in the riskless asset, respectively.11 The right-hand side of (13) is the entering wealth, which is used for consumption and a new portfolio composition on the left-hand side. We obtain the second agent's
budget equation via the aggregate resource constraint (16), given below.
denote the initial endowment (prior to time 0) of both agents in the stock and in the riskless asset, respectively.11 The right-hand side of (13) is the entering wealth, which is used for consumption and a new portfolio composition on the left-hand side. We obtain the second agent's
budget equation via the aggregate resource constraint (16), given below.
Kernel conditions: Agents agree on prices of traded assets, implying the following kernel conditions:12
The systems (13) and (15) are subject to terminal conditions at time
Aggregate resource constraint: An aggregate resource constraint holds at any point in time ![]() ,
,
![]() , and each state:
, and each state:
At time 0 the aggregate resource constraint is:
Market clearing conditions: for
![]() markets have to clear - while the stock is in positive net supply, the short-term bond is in zero net supply. We normalize the number of shares of the risky asset in the
economy to be in unit net supply, such that the terms portfolio holdings and weights are equivalent:
markets have to clear - while the stock is in positive net supply, the short-term bond is in zero net supply. We normalize the number of shares of the risky asset in the
economy to be in unit net supply, such that the terms portfolio holdings and weights are equivalent:
where
![]() and
and
![]() are agent
are agent ![]() 's portfolio holdings in a risky asset
's portfolio holdings in a risky asset
![]() and a short-term bond
and a short-term bond ![]() , respectively. We solve for the decision variables
, respectively. We solve for the decision variables
![]() ,
,
![]() ,
,
![]() and
and
![]() using the system of four equations (13) and (15), aggregate resource constraint (16),
and market clearing conditions (18).
using the system of four equations (13) and (15), aggregate resource constraint (16),
and market clearing conditions (18).
At every point in time
![]() and every node (Dumas and Lyasoff, 2011) solve the system of equations for time-separable preferences and find stock and bond prices
and every node (Dumas and Lyasoff, 2011) solve the system of equations for time-separable preferences and find stock and bond prices
![]() and
and ![]() , and the exiting wealth of the first agent,
, and the exiting wealth of the first agent,
![]() , for every value on the grid
, for every value on the grid
![]() . The next section provides more details on the interpolation and the backward induction procedure in case of time-nonseparable utility, induced by habit.
. The next section provides more details on the interpolation and the backward induction procedure in case of time-nonseparable utility, induced by habit.
3 Solution method
In this section we outline the (Dumas and Lyasoff, 2011) algorithm, compare it with other algorithms and discuss our modification which captures time-nonseparability, induced by habit. While attempts to solve heterogeneous agents models with external habit ((Chan and Kogan, 2002), (Xiouros and Zapatero, 2010), (Ehling and Heyerdahl-Larson, 2010) and (Heyerdahl-Larsen, 2010) among others) have already been successful, this paper is the first attempt to solve a model with heterogeneity in the habit formation process, especially internal habit. In order to understand the advantage of the Dumas-Lyasoff algorithm over the "traditional" approach and the global method we start with a review of both methods. We then describe the refinement of the Dumas-Lyasoff algorithm necessary for the model solutions with time-nonseparable preferences.
3.1 Global method
Global solution for the equilibrium results from all equilibrium conditions (kernel, budget, aggregate resource) for all points in time and all nodes being stacked together into one system of equations. Equilibrium consumption, portfolio holdings, and asset prices are the resulting (unique) solution (for given initial endowments), when the system converges.
The global system delivers reliable solutions for models with power preferences, with solutions being quite insensitive to starting values. However, it is not the case for time-nonseparable preferences. Theoretically, the global method is not limited to time-nonseparability in the utility function, in general, or the number of lags in the habit process, in particular. However, due to path dependency of the optimal consumption process, induced by habit formation, the corresponding consumption tree is not recombining. The resulting system incorporates a large number of equations and decision variables, such that the solution becomes sensitive to proper starting values.
The solution for a power utility model can be used as a starting value for a model with slightly increased habit strength and/or curvature parameter. Repeated use of such a procedure delivers a solution for fixed risk-aversion and habit strength parameters
![]() . Unfortunately our tests have shown that this technique is not powerful enough to solve a model with internal habit formation and an economy's life time of
more than
. Unfortunately our tests have shown that this technique is not powerful enough to solve a model with internal habit formation and an economy's life time of
more than ![]() , even with tiny steps. The reason is that the number of equations grows exponentially on a non-recombining tree.13
, even with tiny steps. The reason is that the number of equations grows exponentially on a non-recombining tree.13
Further, one often requires to plot equilibrium values against initial consumption share. The Dumas-Lyasoff algorithm provides these functions as an implicit outcome of the solution process, while one would need repeatedly to rerun the global method for various values of consumption share between zero and one. In view of the procedure for the iteration of proper starting values, this can be very time-consuming.
3.2 "Traditional" recursive approach
"Traditional" recursive approach can be viewed as an alternative to a global solution method. With this method, it is possible to solve a model recursively, state by state and period by period. The advantage is that the system of equation has a low dimensionality and, thus, is less sensitive to
a choice of starting values. Further, it is possible to exploit the recombining structure of the exogenous state variable. The system of equations is given through kernel conditions, a budget equation, and an aggregate resource constraint (which is necessary to determine consumption of agent 2)
associated with the node ![]() at time
at time ![]() :14
:14
Decision variables here are time-![]() consumption and portfolio weights. One could a priori think of using the entering wealth (RHS of (19)) as a grid
variable. But this choice is not very helpful because it is not clear how to set an upper bound for the wealth variable (see (Aiyagari, 1994) for a discussion). (Longstaff, 2009) addresses this problem by choosing "entering" portfolio weights
as endogenous state variables. However, lower and upper bounds of portfolio weights are only known under short-sale and borrowing constraints or when it is possible to argue that short-selling will not occur in equilibrium and the riskless security is absent, as in (Longstaff, 2009).15 Choosing portfolio weights as endogenous state variables would result in an
consumption and portfolio weights. One could a priori think of using the entering wealth (RHS of (19)) as a grid
variable. But this choice is not very helpful because it is not clear how to set an upper bound for the wealth variable (see (Aiyagari, 1994) for a discussion). (Longstaff, 2009) addresses this problem by choosing "entering" portfolio weights
as endogenous state variables. However, lower and upper bounds of portfolio weights are only known under short-sale and borrowing constraints or when it is possible to argue that short-selling will not occur in equilibrium and the riskless security is absent, as in (Longstaff, 2009).15 Choosing portfolio weights as endogenous state variables would result in an ![]() -dimensional grid in an economy with
-dimensional grid in an economy with ![]() agents and
agents and ![]() assets. A further curse of dimensionality will arise from time-
assets. A further curse of dimensionality will arise from time-![]() individual consumption for a one-lag internal habit, resulting in a
three-dimensional grid with
individual consumption for a one-lag internal habit, resulting in a
three-dimensional grid with ![]() and
and ![]() .
.
In general, a "traditional" method presents a backward-forward scheme, which is its most severe drawback, besides the difficulty of choosing appropriate endogenous state variables. The reason is that at time ![]() one solves for consumption
one solves for consumption ![]() , which also enters the pricing kernel at time
, which also enters the pricing kernel at time ![]() . However, using an idea of (Dumas and Lyasoff, 2011) for passing interpolated functions over to the next backward step, it is possible to avoid the forward step by interpolating time-
. However, using an idea of (Dumas and Lyasoff, 2011) for passing interpolated functions over to the next backward step, it is possible to avoid the forward step by interpolating time-![]() consumption on the grid of wealth/entering portfolio weights and pass it over to time
consumption on the grid of wealth/entering portfolio weights and pass it over to time ![]() . With internal habit, additionally
time-
. With internal habit, additionally
time-![]() consumption should be interpolated on the grid and passed over to the next backward step.
consumption should be interpolated on the grid and passed over to the next backward step.
3.3 Dumas-Lyasoff algorithm
(Dumas and Lyasoff, 2011) modify the "traditional" approach, by replacing the budget equation at time ![]() with budget equations of all successor nodes of the
state
with budget equations of all successor nodes of the
state ![]() . As in the "traditional" method one solves for
. As in the "traditional" method one solves for
![]() , but instead of solving for time-
, but instead of solving for time-![]() consumption, one solves for
the future consumption plans
consumption, one solves for
the future consumption plans
![]() . The idea behind this regrouping is that the portfolio holdings
. The idea behind this regrouping is that the portfolio holdings
![]() finance the future consumption plan
finance the future consumption plan
![]() . The remaining unknown in the system is time-
. The remaining unknown in the system is time-![]() consumption,
which forms the grid and has well-defined bounds provided by the aggregate resource constraint. This implies that in a market with
consumption,
which forms the grid and has well-defined bounds provided by the aggregate resource constraint. This implies that in a market with ![]() assets and
assets and ![]() agents the grid has a dimension of
agents the grid has a dimension of ![]() .16 17 In our case the system of equations is 4-dimensional (
.16 17 In our case the system of equations is 4-dimensional (![]() ,
, ![]() ), whereas the grid for power-, recursive-, and external habit preferences is one dimensional.
), whereas the grid for power-, recursive-, and external habit preferences is one dimensional.
(Buss et al., 2011) propose an extension of the Dumas-Lyasoff method to capture time-nonseparability induced by Epstein-Zin preferences and transaction costs.18 In the next section we show how to incorporate in the algorithm time-nonseparable preferences induced either by external or internal additive habits. The same algorithm can be also applied to multiplicative habit preferences.
3.4 Time-nonseparable preferences
Consider a binomial tree that has ![]() nodes at time
nodes at time ![]() . Pricing kernel dependence
on past consumption arises from introducing a one-lag habit in the utility function. Two paths lead to
. Pricing kernel dependence
on past consumption arises from introducing a one-lag habit in the utility function. Two paths lead to ![]() intermediate nodes at time
intermediate nodes at time ![]() , partially breaking down recombinicity and yielding
, partially breaking down recombinicity and yielding
![]() nodes. Nevertheless, for external habit one only has to care about path dependency because habit is modeled as per-capita consumption, which is given on the tree. However, for
internal habit agent's individual consumption forms the habit process,
nodes. Nevertheless, for external habit one only has to care about path dependency because habit is modeled as per-capita consumption, which is given on the tree. However, for
internal habit agent's individual consumption forms the habit process,
![]() , and enters the algorithm as another endogenous state variable.
, and enters the algorithm as another endogenous state variable.
External habit. The pricing kernels for agents 1 and 2 for external habit preferences given in Definition 1 are:
where initial habit is defined as
Internal habit. Internal habit preferences are defined in (2) and the pricing kernels for
![]() read
read
where
As pricing kernels in (21) indicate, past consumption ![]() enters as an additional endogenous state variable with domain
enters as an additional endogenous state variable with domain
![]() , as opposed to a simple externality in the external habit case. For the same reasons as above the second grid-dimension is
, as opposed to a simple externality in the external habit case. For the same reasons as above the second grid-dimension is
![]() . Unfortunately, these bounds are not tight enough, because they only guarantee positive surplus consumption but not the positivity of
marginal utility and of the pricing kernel. So, for a given
. Unfortunately, these bounds are not tight enough, because they only guarantee positive surplus consumption but not the positivity of
marginal utility and of the pricing kernel. So, for a given ![]() we search for the
we search for the ![]() -grid, such that the marginal utility and the pricing kernel of each agent remain positive. Since this grid is endogenous and its size is different for every
-grid, such that the marginal utility and the pricing kernel of each agent remain positive. Since this grid is endogenous and its size is different for every ![]() ,
a feasibility area (shown on Figure 1) over which we have to interpolate is not rectangular but is a set of scattered data points.
,
a feasibility area (shown on Figure 1) over which we have to interpolate is not rectangular but is a set of scattered data points.
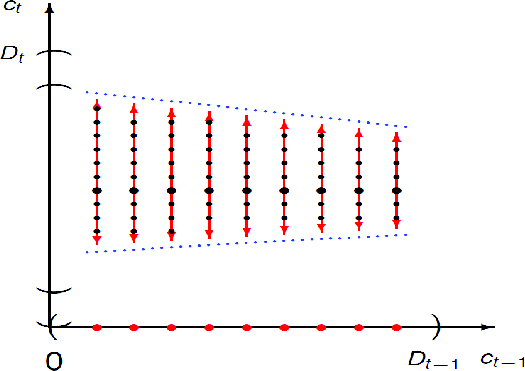 This figure represents the two-dimensional grid for a generic node, where the first grid dimension is
|
For interpolation we use the method of (Renka and Cline, 1984), which allows to interpolate over arbitrarily distributed points on the plane. In addition to the stock price and exiting wealth, as for time-separable preferences, next period consumption
![]() is interpolated on the specified two-dimensional grid to be used in the next backward step. The bounds of these decision variables can be tightened a priori as follows:
is interpolated on the specified two-dimensional grid to be used in the next backward step. The bounds of these decision variables can be tightened a priori as follows:
![]() ,
, ![]() .
.
There are two reasons why interpolation over an endogenous feasibility area is preferred to interpolation over a rectangular grid
4 Results
In this section we discuss the asset pricing implications of internal and external habit models outlined in Section 2. Table 1 provides calibration of the economy and utility function parameters used in the model solution.
Aggregate asset returns are computed as follows. At each time period between ![]() and
and ![]() and at each generic node
and at each generic node ![]() (at time
(at time ![]() ) with successive nodes
) with successive nodes
![]() (at time
(at time ![]() ) we compute a realized equity return
) we compute a realized equity return
![]() and a one period risk-free rate
and a one period risk-free rate ![]() :
:
Average equity return ![]() and average interest rate
and average interest rate ![]() are given by:
are given by:
and volatilities of equity return ![]() and interest rate
and interest rate ![]() are
given by:
are
given by:
We define equity premium as:
and Sharpe ratio as:
For each model specification we present the interest rate volatility, equity premium, volatility of equity return, Sharpe ratio, stock and bond holdings for agent 1 at time 0. Time-zero values are representative for the whole equilibrium and do not differ from averaged values over all paths. All
numbers are annualized. We report these results as functions of risk aversion parameters ![]() and
and ![]() of the two agents. We report results for
of the two agents. We report results for ![]() (following Dumas and Lyasoff) and for
(following Dumas and Lyasoff) and for ![]() to verify that our results are not driven by the time horizon issue. We provide historical asset prices in Table 2 as point of comparison to our model solutions.
to verify that our results are not driven by the time horizon issue. We provide historical asset prices in Table 2 as point of comparison to our model solutions.
4.1 Representative agent economy
Table 3 presents the model solution for a representative agent economy20 who has habit formation preferences with various
degrees of habit strength
![]() and 0.5. Naturally, the CRRA case is represented by the first row of the results in Panels A and B. We also vary risk aversion parameter
and 0.5. Naturally, the CRRA case is represented by the first row of the results in Panels A and B. We also vary risk aversion parameter
![]() . For each risk aversion parameter we report two sets of results, for internal habit (labeled IH) and external habit (labeled EH). Panels A and B present results for
. For each risk aversion parameter we report two sets of results, for internal habit (labeled IH) and external habit (labeled EH). Panels A and B present results for
![]() and
and ![]() , respectively. We find that internal habits have better ability
to match asset prices with reasonable
, respectively. We find that internal habits have better ability
to match asset prices with reasonable ![]() coefficients at all levels of
coefficients at all levels of ![]() . For
an example,
. For
an example,
![]() and
and ![]() an internal habit provides the equity premium equal to
3.14% per year while under external habit it is 2.24%. As Table 5 shows, equity premium has been close to
an internal habit provides the equity premium equal to
3.14% per year while under external habit it is 2.24%. As Table 5 shows, equity premium has been close to ![]() historically. The equity volatility in the IH case
is lower than historical too (11.29% vs. 15.06%), but overall this combination results in a reasonable Sharpe ratio of 0.28. At the same time, the model produces a well-known risk-free rate puzzle, the demonstration of the unrealistically high volatility of the interest rates compared with observed
levels. For instance,
historically. The equity volatility in the IH case
is lower than historical too (11.29% vs. 15.06%), but overall this combination results in a reasonable Sharpe ratio of 0.28. At the same time, the model produces a well-known risk-free rate puzzle, the demonstration of the unrealistically high volatility of the interest rates compared with observed
levels. For instance,
![]() and
and ![]() speciation produces the volatility of the risk-free rate
equal to 10.2%! With a higher risk aversion
speciation produces the volatility of the risk-free rate
equal to 10.2%! With a higher risk aversion
![]() and
and ![]() we definitely "over-shoot" the equity premium magnitudes,
but we keep these results to compare with the ones of a heterogeneous agents' economy. It is difficult to say what would be a correct level of habit strength in this setting. (Constantinides, 1990) estimates that
we definitely "over-shoot" the equity premium magnitudes,
but we keep these results to compare with the ones of a heterogeneous agents' economy. It is difficult to say what would be a correct level of habit strength in this setting. (Constantinides, 1990) estimates that ![]() is consistent with the historical first moments of the aggregate asset returns. (Grishchenko, 2010) estimates are slightly lower, around 0.7. However, both authors use an assumption of an infinitely-lived agent
with habit. Here, our time horizon is finite. We rerun the code for a longer time horizon
is consistent with the historical first moments of the aggregate asset returns. (Grishchenko, 2010) estimates are slightly lower, around 0.7. However, both authors use an assumption of an infinitely-lived agent
with habit. Here, our time horizon is finite. We rerun the code for a longer time horizon ![]() and show that our results are essentially the same (compare Panels A and Panel B in
Table 3).
and show that our results are essentially the same (compare Panels A and Panel B in
Table 3).
4.2 Economy with two agents
In this section we discuss results in the economy populated by two agents with various degrees of risk aversion and/or habit strength parameters. For each of Tables 4 through 9 we provide solutions for the following pairs of ![]() and
and ![]() : (4,2), (7,2), (7,4), and (5,5). As before, we vary the habit strength
parameters of both agents to be 0, 0.3, and 0.5. So, we have 9 combinations of habit strength parameters and 4 combinations of risk aversion parameters. For each such combination, we compute prices both for internal (IH) and external (EH) habit types.
: (4,2), (7,2), (7,4), and (5,5). As before, we vary the habit strength
parameters of both agents to be 0, 0.3, and 0.5. So, we have 9 combinations of habit strength parameters and 4 combinations of risk aversion parameters. For each such combination, we compute prices both for internal (IH) and external (EH) habit types.
4.2.1 Equity premium
The first observation from Table 4 is that one definitely needs some sort of nonseparability in the preferences for both agents. When either one or two agents have CRRA utility function, the model is unable to fit an equity premium at any reasonable level of risk aversion.
Second, the first combination of the risk aversion coefficients
![]() shows that it is not feasible to match equity premium for any combination of reported habit strength parameters
shows that it is not feasible to match equity premium for any combination of reported habit strength parameters
![]() . For example, when
. For example, when
![]() , IH produces 4.53% for the equity premium, while EH - 1.87%. For a longer horizon (
, IH produces 4.53% for the equity premium, while EH - 1.87%. For a longer horizon (![]() , Panel B) IH and EH produce 5.06% and 2.03%, respectively. When we move to
, Panel B) IH and EH produce 5.06% and 2.03%, respectively. When we move to ![]() combination for risk aversion, the equity premium is closer to observed, but
still low: IH gives 6.22% and 7.27% for
combination for risk aversion, the equity premium is closer to observed, but
still low: IH gives 6.22% and 7.27% for ![]() and 20, respectively. It is interesting to note that internal habit has a higher effect on raising the equity premium in the longer term
(
and 20, respectively. It is interesting to note that internal habit has a higher effect on raising the equity premium in the longer term
(![]() ), than external habit does: in the IH case, equity premium increases by more than 1%, while in the EH case, the equity premium increases by 47 basis points. It is to be expected
since internal habit has impact on future consumption choices by construction whereas external habit represents a mere externality. This relationship is true for every combination of risk aversion coefficients. Eventually, the combination of
), than external habit does: in the IH case, equity premium increases by more than 1%, while in the EH case, the equity premium increases by 47 basis points. It is to be expected
since internal habit has impact on future consumption choices by construction whereas external habit represents a mere externality. This relationship is true for every combination of risk aversion coefficients. Eventually, the combination of ![]() coefficients (7,4) and internal habit match the equity premium when habit strength parameters are set to
coefficients (7,4) and internal habit match the equity premium when habit strength parameters are set to ![]() and
and
![]() . At the same parameters, external habit produces only 4% equity premium. Overall, our results suggest that external habit would match the same moments with much higher levels of
habit strength coefficients than internal habit, which seems to be unreasonable given the empirical evidence.21 In sum, we conclude that internal habit is
a more promising type of nonseparability than external one for matching the equity premium.
. At the same parameters, external habit produces only 4% equity premium. Overall, our results suggest that external habit would match the same moments with much higher levels of
habit strength coefficients than internal habit, which seems to be unreasonable given the empirical evidence.21 In sum, we conclude that internal habit is
a more promising type of nonseparability than external one for matching the equity premium.
4.2.2 Equity volatility and Sharpe ratio
Table 5 reports the results for equity volatility solutions defined in Eq. (24). As in Table 4, Panel A shows that equity volatility increases with the habit strength of one or both agents and also with the risk
aversion parameters. For an example, internal habit obtains
![]() for
for
![]() with habit strength
with habit strength
![]() , and
, and
![]() for
for
![]() and the same habit parameters.
and the same habit parameters.
![]() combination matches the equity volatility (15.18% vs. 15.06% observed) for
combination matches the equity volatility (15.18% vs. 15.06% observed) for ![]() and
and ![]() . At the same time, external habit specification results in a considerably lower equity volatility. We observe similar solutions when
we increase our horizon to
. At the same time, external habit specification results in a considerably lower equity volatility. We observe similar solutions when
we increase our horizon to ![]() .
.
Equity volatility and equity premium solutions lead to the results in the Sharpe ratio consistent with the above results. Thus, for a combination of risk aversion parameters of 4 and 2 and equal habit strength parameters
![]() we obtain a Sharpe ratio of 26.85% for internal habit and 18.16% for external habit. A combination of parameters
we obtain a Sharpe ratio of 26.85% for internal habit and 18.16% for external habit. A combination of parameters
![]() and internal habit obtains a similar Sharpe ratio of 26.26%, while external habit produces a Sharpe ratio of 19.78% for this
combination. We conclude that this pattern is monotonic with respect to either increasing risk aversion parameter or increasing habit strength. Also, external habits fare much worse in terms of matching aggregate moments than internal habits do.
and internal habit obtains a similar Sharpe ratio of 26.26%, while external habit produces a Sharpe ratio of 19.78% for this
combination. We conclude that this pattern is monotonic with respect to either increasing risk aversion parameter or increasing habit strength. Also, external habits fare much worse in terms of matching aggregate moments than internal habits do.
4.2.3 Interest rate volatility
The interest rate volatility reported in Table 7 manifests the "achillean heel" present in many asset pricing models. While internal habit stochastic discount factor is more volatile than external one, this has a spillover effect on the interest rate volatility.
Thus, interest rate volatility is much higher in the internal habit case than in the external habit, both of them are unreasonably high. Only specifications with mild enough habit parameters produce reasonable levels of the interest rate volatility, but these levels are not enough to match other
moments, like equity premium. The example is the parameter combination
![]() , in which case internal habit produces interest rate volatility 2.17%, while external habit - 1.67%.
, in which case internal habit produces interest rate volatility 2.17%, while external habit - 1.67%.
4.2.4 Stock holdings
Table 8 reports stock holdings
![]() (in shares of unity) results for agent 1. Three findings emerge here. First, for a fixed level of risk aversion, the amount of risky holdings moderately increases, but remains
at a less than 50% level if the agent 1 has higher risk version than agent 2. Thus Panel A shows that for
(in shares of unity) results for agent 1. Three findings emerge here. First, for a fixed level of risk aversion, the amount of risky holdings moderately increases, but remains
at a less than 50% level if the agent 1 has higher risk version than agent 2. Thus Panel A shows that for
![]() and a fixed habit strength of agent 2
and a fixed habit strength of agent 2 ![]() the amount of risky holdings increases from 0.41 to 0.44 as habit strength of agent 1 increases from 0 to 0.5 in internal habit case. We obtain a similar effect for external habit case. Second, if we increase risk aversion of the agent 1 from 4 to 7, the amount of risky holdings is lower overall,
but it still increases with habit strength from 0.37 to 0.40. Third, increased risk aversion parameter of agent 2 (the combination of
the amount of risky holdings increases from 0.41 to 0.44 as habit strength of agent 1 increases from 0 to 0.5 in internal habit case. We obtain a similar effect for external habit case. Second, if we increase risk aversion of the agent 1 from 4 to 7, the amount of risky holdings is lower overall,
but it still increases with habit strength from 0.37 to 0.40. Third, increased risk aversion parameter of agent 2 (the combination of
![]() ), then the risky holdings of agent 1 increase compared with those of (4,2), because agent 2 becomes relatively more risk averse and gives up a share of his
consumption holdings to a agent 1. Again, this dynamics is very similar across internal and external habit cases. Also, Table 8 presents the case when two agents have identical risk attitude (
), then the risky holdings of agent 1 increase compared with those of (4,2), because agent 2 becomes relatively more risk averse and gives up a share of his
consumption holdings to a agent 1. Again, this dynamics is very similar across internal and external habit cases. Also, Table 8 presents the case when two agents have identical risk attitude (
![]() but might have different habit strength parameters. When
but might have different habit strength parameters. When ![]() we obtain that the risky asset share of agent 1 is higher than that of agent 2. Higher habit strength agents chose lower risky asset share in equilibrium because their current consumption choice has a higher effect on future consumption (in the internal case) and so they
aim to reduce exposure to risky assets and maintain (or increase) the level of consumption. Still, in this particular case, when the risk aversion parameters are the same, this effect is rather mild: agent 1 has only 2% higher risky asset share than agent 2. Naturally, when both agents have the
same risk aversion and same habit parameters, they share the risks equally and the economy becomes identical to a representative agent economy. The results are similar for
we obtain that the risky asset share of agent 1 is higher than that of agent 2. Higher habit strength agents chose lower risky asset share in equilibrium because their current consumption choice has a higher effect on future consumption (in the internal case) and so they
aim to reduce exposure to risky assets and maintain (or increase) the level of consumption. Still, in this particular case, when the risk aversion parameters are the same, this effect is rather mild: agent 1 has only 2% higher risky asset share than agent 2. Naturally, when both agents have the
same risk aversion and same habit parameters, they share the risks equally and the economy becomes identical to a representative agent economy. The results are similar for ![]() .
.
4.2.5 Bond holdings
Table 9 reports the bond holdings
![]() of agent 1. First, as a habit strength parameter
of agent 1. First, as a habit strength parameter ![]() increases,
agent 1 decreases his bond holdings
increases,
agent 1 decreases his bond holdings
![]() , which is a result of his increasing stock holdings
, which is a result of his increasing stock holdings
![]() . Since agent 1 is restricted in funds, he chooses to lend lower amount to agent 2 because he invests more in risk assets as shown in Table 8 and
discussed in Section 4.2.4. This effect is slightly lower under EH specification. Second, as the risk aversion of agent 1 increases from 4 to 7, and the risk aversion of agent 2 stays unchanged, agent 1 reduces his exposure to stocks (
. Since agent 1 is restricted in funds, he chooses to lend lower amount to agent 2 because he invests more in risk assets as shown in Table 8 and
discussed in Section 4.2.4. This effect is slightly lower under EH specification. Second, as the risk aversion of agent 1 increases from 4 to 7, and the risk aversion of agent 2 stays unchanged, agent 1 reduces his exposure to stocks (
![]() is lower) and invests more into bonds (
is lower) and invests more into bonds (
![]() is higher). Thus, for
is higher). Thus, for
![]() combination we obtain that bond holdings of agent 1 increase from 0.23 to 0.33 under IH specification. This effect is similar for EH preferences and this
combination of habit strength parameters. It is interesting that as we move to the case when agent 2 has a risk aversion of 4 (instead of 2), the bond holdings of agent 1 drop significantly (the stock holdings of agent 1 increase at the same time). External habit specification produces a similar
picture. Panel B reports the results for
combination we obtain that bond holdings of agent 1 increase from 0.23 to 0.33 under IH specification. This effect is similar for EH preferences and this
combination of habit strength parameters. It is interesting that as we move to the case when agent 2 has a risk aversion of 4 (instead of 2), the bond holdings of agent 1 drop significantly (the stock holdings of agent 1 increase at the same time). External habit specification produces a similar
picture. Panel B reports the results for ![]() case. When both risk aversion and habit strength of the agents are the same, we obtain a representative agent case and, naturally, obtain that
bond holdings are zero, because bonds are in a zero net supply when we aggregate.
case. When both risk aversion and habit strength of the agents are the same, we obtain a representative agent case and, naturally, obtain that
bond holdings are zero, because bonds are in a zero net supply when we aggregate.
The qualitative description of the results is similar in Panel B (![]() ), but the magnitude of these numbers is different. Consider the combination
), but the magnitude of these numbers is different. Consider the combination
![]() . Agent 1's bond holdings are 1.41 while his stock holdings are 0.41. In this case agent 2 holds more than a half of the stock than
agent 1. To survive in the longer period (
. Agent 1's bond holdings are 1.41 while his stock holdings are 0.41. In this case agent 2 holds more than a half of the stock than
agent 1. To survive in the longer period (![]() instead of
instead of ![]() ) he needs to
borrow from agent 1:
) he needs to
borrow from agent 1:
![]() because bond holdings are in the zero net supply. This effect is more or less severe but the overall level of debt holdings is higher in the longer-horizon economy.
because bond holdings are in the zero net supply. This effect is more or less severe but the overall level of debt holdings is higher in the longer-horizon economy.
When agents do not differ with respect to risk aversion (
![]() ), the effect of habits on bond holdings can be seen more clearly. If
), the effect of habits on bond holdings can be seen more clearly. If ![]() then agent 1 can afford to invest relatively more in the stock market because his current consumption choice has a lesser effect on future consumption. Indeed, his share of stock
then agent 1 can afford to invest relatively more in the stock market because his current consumption choice has a lesser effect on future consumption. Indeed, his share of stock
![]() in this case (see Table 5). To achieve this, agent 1 borrows from agent 2, which is manifested by
in this case (see Table 5). To achieve this, agent 1 borrows from agent 2, which is manifested by
![]() . This finding is similar for both shorter- and longer-horizon economies. The bond holdings results are largely unchanged across internal and external habit
specifications.
. This finding is similar for both shorter- and longer-horizon economies. The bond holdings results are largely unchanged across internal and external habit
specifications.
4.2.8 Habit with Epstein-Zin preferences
In addition to our internal and external habit preferences considered in the intertemporal power utility setting, we have also solved our model with both types of habits in the (Epstein and Zin, 1989) recursive preferences. Epstein and Zin (EZ) utility function differentiates between relative risk aversion coefficient and the elasticity of intertemporal substitution (EIS). It is easy to obtain that the EZ preferences imply the same form of the equity premium, as power utility. However, recursive preferences have different implications for the solution for the risk-free rate.22 At the same time (Kocherlakota, 1990) shows that if consumption growth follows a random walk process, Epstein-Zin utility converges to power utility and, thus, the EIS coefficient becomes essentially an inverse of RRA coefficient. (Yang, 2009) argues that habits can potentially account for this problem because habit formation generates persistent variations in the surplus consumption across time. In this setting, even though consumption growth is a random walk in the model, surplus consumption varies counter-cyclically. As a result, the model with habits and recursive preferences is not equivalent to power utility.
Our preliminary findings (not reported) indicate that EIS is an important driving force of the results. For example, a high enough EIS (around 1 and higher) helps to match the interest rate and interest rate volatility, but significantly decreases other economic variables, e.g., equity premium, compared to the habit-power utility case. It might be possible, that even with habits in recursive preferences, one might need some sort of incompleteness to pin down both, equity premium and risk-free rate puzzles. We leave this for future work a rigorous investigation of such preferences.
5 Conclusion
In this paper, we study the effect of alternative types of time-nonseparability (habit formation) on asset prices in a general equilibrium Lucas endowment economy with two heterogeneous agents with respect to their habit preferences and coefficients of relative risk aversion. We study asset pricing implications in a complete market setting and explore the improvement of introducing heterogeneity in habit formation over the representative agent framework. We also compute explicitly stock and bond holdings of two agents. We model nonseparability in preferences either as internal or external habits. We look how the model fares in terms of matching first and second moments of aggregate asset prices, namely, equity premium, volatility of equity return, Sharpe ratio, and interest rate volatility. Equilibrium quantities are determined by a recently developed algorithm of (Dumas and Lyasoff, 2011), which is refined to capture time-nonseparability.
There are several findings that emerge in our study. First, we answer question 1 set forth in the introduction of the paper positively by concluding that internal habit is a more promising type of nonseparability than external one. Second, we match the equity premium, volatility of the stock market, and Sharpe ratio with the coefficient of relative risk aversion equal to 5 and internal habit strength parameter of a representative agent equal to 0.4. Third, in the case when two agents differ with respect to risk aversion and habit strength parameters we find that a combination of risk aversion coefficients 7 and 4 and habit coefficients 0.3 and 0.5 is able to match historically observed equity premium, volatility, and Sharpe ratio. Fourth, in our stylized set up, we still face the risk-free rate puzzle, as neither of our specifications is able to match equity premium and interest rate volatility simultaneously. However, the purpose of the current study is not to explain both puzzles simultaneously, but to demonstrate that internal habit is preferred over external habit preferences in terms of matching some important moments with more reasonable coefficients of risk aversion and habit. Last but not the least, the answer to the second question is negative. In the current set up we did not find that habit heterogeneity helps with regard to replicating major features of the aggregate stock market. A possible explanation is that we considered our model in the complete market setting. A natural extension of this work is to consider our model with habits in an incomplete market set up with some frictions such as transaction costs, borrowing constraints, or other kinds of limited market participation. This represents the venue for our future research.
Bibliography
| Parameter | Description | Value |
| Economy parameterization: |
Economy's Life-time | 6, 20 |
| Economy parameterization: |
Time step | 1 |
| Economy parameterization: |
Initial dividend | 1 |
| Economy parameterization: |
Drift of diffusion | 0.0183 |
| Economy parameterization: |
Volatility of diffusion | 0.0357 |
| Economy parameterization: |
Initial stock endowment | 0.5 |
| Economy parameterization: |
Initial bond endowment | 0 |
| Preferences' parameters: |
Time discount factor | 0.999 |
| Preferences' parameters: |
RRA parameter | 2,4,5,7 |
| Preferences' parameters: |
Habit strength | 0.1,0.3,0.5 |
| Preferences' parameters: |
Initial habit (internal or external) |
This table presents the parametrization of the economy and utility-related (free) parameters.
This table reports historically observed equity premium, equity volatility, Sharpe ratio, and interest rate volatility. Real returns are measured annual, units are percent per year. The S&P500 premium is computed as the difference between the return on the S&P500 index and 30-day T-bill rate. The Sharpe ratio is computed as the mean of S&P500 premium divided by its standard deviation. A sample period is 1948 to 1996.
| IH
|
EH
|
IH
|
EH
|
IH
|
EH
|
||
| Equity premium | 0 | 0.0020 | 0.0056 | 0.0082 | |||
| Equity premium | 0.3 | 0.0066 | 0.0050 | 0.0314 | 0.0224 | 0.0588 | 0.0412 |
| Equity premium | 0.5 | 0.0263 | 0.0111 | 0.1521 | 0.0599 | 0.3086 | 0.1166 |
| Equity volatility | 0 | 0.0316 | 0.0331 | 0.0339 | |||
| Equity volatility | 0.3 | 0.0634 | 0.0540 | 0.1129 | 0.0904 | 0.1462 | 0.1150 |
| Equity volatility | 0.5 | 0.1337 | 0.0839 | 0.2907 | 0.1669 | 0.4107 | 0.2239 |
| Sharpe ratio | 0 | 0.0642 | 0.1682 | 0.2421 | |||
| Sharpe ratio | 0.3 | 0.1048 | 0.0930 | 0.2781 | 0.2475 | 0.4020 | 0.3585 |
| Sharpe ratio | 0.5 | 0.1966 | 0.1327 | 0.5231 | 0.3587 | 0.7513 | 0.5208 |
| Interest rate volatility | 0 | 0.0000 | 0.0000 | 0.0000 | |||
| Interest rate volatility | 0.3 | 0.0393 | 0.0279 | 0.1020 | 0.0736 | 0.1451 | 0.1057 |
| Interest rate volatility | 0.5 | 0.1282 | 0.0663 | 0.3294 | 0.1768 | 0.4621 | 0.2529 |
| IH
|
EH
|
IH
|
EH
|
IH
|
EH
|
||
| Equity premium | 0 | 0.0020 | 0.0056 | 0.0082 | |||
| Equity premium | 0.3 | 0.0071 | 0.0053 | 0.0341 | 0.0242 | 0.0640 | 0.0450 |
| Equity premium | 0.5 | 0.0285 | 0.0121 | 0.1664 | 0.0663 | 0.3378 | 0.1294 |
| Equity volatility | 0 | 0.0316 | 0.0331 | 0.0339 | |||
| Equity volatility | 0.3 | 0.0674 | 0.0571 | 0.1225 | 0.0980 | 0.1593 | 0.1254 |
| Equity volatility | 0.5 | 0.1450 | 0.0911 | 0.3182 | 0.1848 | 0.4495 | 0.2485 |
| Sharpe ratio | 0 | 0.0642 | 0.1682 | 0.2421 | |||
| Sharpe ratio | 0.3 | 0.1048 | 0.0930 | 0.2781 | 0.2475 | 0.4020 | 0.3585 |
| Sharpe ratio | 0.5 | 0.1966 | 0.1327 | 0.5231 | 0.3587 | 0.7513 | 0.5208 |
| Interest rate volatility | 0 | 0.0000 | 0.0000 | 0.0000 | |||
| Interest rate volatility | 0.3 | 0.0393 | 0.0279 | 0.1020 | 0.0736 | 0.1451 | 0.1057 |
| Interest rate volatility | 0.5 | 0.1282 | 0.0663 | 0.3294 | 0.1768 | 0.4621 | 0.2529 |
This table presents time 0 solutions for the asset pricing quantities equity premium, equity return volatility, Sharpe ratio and volatility of the interest rate. The agent can either form internal or external habit with a relative risk aversion (RRA) coefficient ![]() and habit strength
and habit strength ![]() . Panel A(B) presents the solutions for the economy with time horizon
. Panel A(B) presents the solutions for the economy with time horizon
![]() . Time discount factor
. Time discount factor
![]() . All numbers reported are in absolute values.
. All numbers reported are in absolute values.
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.0028 | 0.0034 | 0.0058 | 0.0056 | ||||
| 0.3 | 0.0060 | 0.0050 | 0.0094 | 0.0069 | 0.0156 | 0.0127 | 0.0118 | 0.0114 | |
| 0.5 | 0.0107 | 0.0079 | 0.0207 | 0.0120 | 0.0294 | 0.0218 | 0.0190 | 0.0178 | |
| 0.3 | 0 | 0.0039 | 0.0043 | 0.0043 | 0.0051 | 0.0098 | 0.0110 | 0.0118 | 0.0114 |
| 0.3 | 0.0107 | 0.0079 | 0.0142 | 0.0104 | 0.0327 | 0.0233 | 0.0314 | 0.0224 | |
| 0.5 | 0.0246 | 0.0131 | 0.0403 | 0.0188 | 0.0780 | 0.0408 | 0.0602 | 0.0358 | |
| 0.5 | 0 | 0.0048 | 0.0056 | 0.0053 | 0.0065 | 0.0159 | 0.0160 | 0.0190 | 0.0178 |
| 0.3 | 0.0154 | 0.0108 | 0.0181 | 0.0135 | 0.0516 | 0.0344 | 0.0602 | 0.0358 | |
| 0.5 | 0.0453 | 0.0187 | 0.0622 | 0.0253 | 0.1589 | 0.0625 | 0.1521 | 0.0599 |
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.0029 | 0.0038 | 0.0059 | 0.0056 | ||||
| 0.3 | 0.0065 | 0.0054 | 0.0109 | 0.0080 | 0.0171 | 0.0138 | 0.0127 | 0.0120 | |
| 0.5 | 0.0119 | 0.0086 | 0.0245 | 0.0143 | 0.0330 | 0.0240 | 0.0189 | 0.0192 | |
| 0.3 | 0 | 0.0042 | 0.0046 | 0.0049 | 0.0058 | 0.0107 | 0.0118 | 0.0127 | 0.0120 |
| 0.3 | 0.0118 | 0.0087 | 0.0166 | 0.0121 | 0.0361 | 0.0257 | 0.0341 | 0.0242 | |
| 0.5 | 0.0272 | 0.0146 | 0.0469 | 0.0224 | 0.0867 | 0.0455 | 0.0662 | 0.0393 | |
| 0.5 | 0 | 0.0053 | 0.0061 | 0.0106 | 0.0073 | 0.0127 | 0.0174 | 0.0189 | 0.0192 |
| 0.3 | 0.0174 | 0.0120 | 0.0212 | 0.0157 | 0.0575 | 0.0383 | 0.0662 | 0.0393 | |
| 0.5 | 0.0506 | 0.0210 | 0.0727 | 0.0300 | 0.1761 | 0.0702 | 0.1664 | 0.0663 |
This table presents time 0 solutions for the equity premium for the economy with two agents which differ by habit preference type (internal or external) and/or level of their relative risk aversion (RRA) coefficients. ![]() denotes the habit strength of the first(second) agent,
denotes the habit strength of the first(second) agent,
![]() denotes the RRA coefficient of the first(second) agent. Panels A and B present solutions for the economy with time horizon
denotes the RRA coefficient of the first(second) agent. Panels A and B present solutions for the economy with time horizon ![]() and
and ![]() , respectively. Time discount factor
, respectively. Time discount factor
![]() , initial endowments are equal for two agents:
, initial endowments are equal for two agents:
![]() . All numbers reported are in absolute values.
. All numbers reported are in absolute values.
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.0323 | 0.0333 | 0.0335 | 0.0331 | ||||
| 0.3 | 0.0529 | 0.0457 | 0.0650 | 0.0502 | 0.0700 | 0.0590 | 0.0580 | 0.0567 | |
| 0.5 | 0.0742 | 0.0591 | 0.1049 | 0.0686 | 0.1057 | 0.0839 | 0.0800 | 0.0776 | |
| 0.3 | 0 | 0.0399 | 0.0439 | 0.0386 | 0.0462 | 0.0501 | 0.0563 | 0.0580 | 0.0567 |
| 0.3 | 0.0751 | 0.0626 | 0.0838 | 0.0691 | 0.1151 | 0.0920 | 0.1129 | 0.0904 | |
| 0.5 | 0.1208 | 0.0823 | 0.1535 | 0.0952 | 0.1958 | 0.1291 | 0.1681 | 0.1222 | |
| 0.5 | 0 | 0.0449 | 0.0532 | 0.0457 | 0.0559 | 0.0750 | 0.0748 | 0.0800 | 0.0776 |
| 0.3 | 0.0923 | 0.0767 | 0.0959 | 0.0837 | 0.1518 | 0.1204 | 0.1681 | 0.1222 | |
| 0.5 | 0.1689 | 0.1029 | 0.1941 | 0.1168 | 0.2968 | 0.1702 | 0.2907 | 0.1669 |
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.0332 | 0.0362 | 0.0343 | 0.0331 | ||||
| 0.3 | 0.0571 | 0.0487 | 0.0742 | 0.0567 | 0.0768 | 0.0634 | 0.0620 | 0.0598 | |
| 0.5 | 0.0828 | 0.0641 | 0.1233 | 0.0789 | 0.1189 | 0.0917 | 0.0829 | 0.0835 | |
| 0.3 | 0 | 0.0424 | 0.0464 | 0.0425 | 0.0507 | 0.0538 | 0.0602 | 0.0620 | 0.0598 |
| 0.3 | 0.0818 | 0.0680 | 0.0945 | 0.0781 | 0.1261 | 0.1010 | 0.1225 | 0.0980 | |
| 0.5 | 0.1333 | 0.0908 | 0.1756 | 0.1095 | 0.2175 | 0.1432 | 0.1847 | 0.1341 | |
| 0.5 | 0 | 0.0486 | 0.0569 | 0.0320 | 0.0613 | 0.0579 | 0.0812 | 0.0829 | 0.0835 |
| 0.3 | 0.1019 | 0.0841 | 0.1082 | 0.0944 | 0.1674 | 0.1332 | 0.1847 | 0.1341 | |
| 0.5 | 0.1864 | 0.1144 | 0.2198 | 0.1339 | 0.3272 | 0.1900 | 0.3182 | 0.1848 |
This table presents time 0 solutions for the equity volatility for the economy with two agents which differ by habit preference type (internal or external) and/or level of their relative risk aversion (RRA) coefficients. ![]() denotes the habit strength of the first(second) agent,
denotes the habit strength of the first(second) agent,
![]() denotes the RRA coefficient of the first(second) agent. Panel A(B) presents the solutions for the economy with time horizon
denotes the RRA coefficient of the first(second) agent. Panel A(B) presents the solutions for the economy with time horizon
![]() . Time discount factor
. Time discount factor
![]() , initial endowments are equal for two agents:
, initial endowments are equal for two agents:
![]() . All numbers reported are in absolute values.
. All numbers reported are in absolute values.
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.0870 | 0.1032 | 0.1720 | 0.1682 | ||||
| 0.3 | 0.1137 | 0.1099 | 0.1440 | 0.1368 | 0.2227 | 0.2161 | 0.2038 | 0.2004 | |
| 0.5 | 0.1435 | 0.1332 | 0.1974 | 0.1744 | 0.2780 | 0.2603 | 0.2376 | 0.2296 | |
| 0.3 | 0 | 0.0978 | 0.0972 | 0.1115 | 0.1109 | 0.1966 | 0.1949 | 0.2038 | 0.2004 |
| 0.3 | 0.1427 | 0.1267 | 0.1699 | 0.1507 | 0.2846 | 0.2533 | 0.2781 | 0.2475 | |
| 0.5 | 0.2033 | 0.1586 | 0.2626 | 0.1978 | 0.3985 | 0.3157 | 0.3581 | 0.2932 | |
| 0.5 | 0 | 0.1064 | 0.1054 | 0.1155 | 0.1166 | 0.2127 | 0.2138 | 0.2376 | 0.2296 |
| 0.3 | 0.1671 | 0.1410 | 0.1883 | 0.1617 | 0.3398 | 0.2858 | 0.3581 | 0.2932 | |
| 0.5 | 0.2685 | 0.1816 | 0.3204 | 0.2170 | 0.5353 | 0.3672 | 0.5231 | 0.3587 |
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.0880 | 0.1064 | 0.1729 | 0.1682 | ||||
| 0.3 | 0.1142 | 0.1113 | 0.1468 | 0.1417 | 0.2230 | 0.2173 | 0.2040 | 0.2004 | |
| 0.5 | 0.1435 | 0.1348 | 0.1989 | 0.1810 | 0.2775 | 0.2617 | 0.2284 | 0.2296 | |
| 0.3 | 0 | 0.0996 | 0.0982 | 0.1156 | 0.1138 | 0.1985 | 0.1958 | 0.2040 | 0.2004 |
| 0.3 | 0.1444 | 0.1281 | 0.1753 | 0.1555 | 0.2861 | 0.2547 | 0.2781 | 0.2475 | |
| 0.5 | 0.2038 | 0.1606 | 0.2672 | 0.2049 | 0.3985 | 0.3175 | 0.3585 | 0.2932 | |
| 0.5 | 0 | 0.1095 | 0.1063 | 0.3312 | 0.1192 | 0.2186 | 0.2147 | 0.2284 | 0.2296 |
| 0.3 | 0.1707 | 0.1425 | 0.1960 | 0.1661 | 0.3436 | 0.2873 | 0.3585 | 0.2932 | |
| 0.5 | 0.2716 | 0.1838 | 0.3307 | 0.2241 | 0.5382 | 0.3692 | 0.5231 | 0.3587 |
This table presents time 0 solutions for the Sharpe ratio for the economy with two agents which differ by habit preference type (internal or external) and/or level of their relative risk aversion (RRA) coefficients. ![]() denotes the habit strength of the first(second) agent,
denotes the habit strength of the first(second) agent,
![]() denotes the RRA coefficient of the first(second) agent. Panel A(B) presents the solutions for the economy with time horizon
denotes the RRA coefficient of the first(second) agent. Panel A(B) presents the solutions for the economy with time horizon
![]() . Time discount factor
. Time discount factor
![]() , initial endowments are equal for two agents:
, initial endowments are equal for two agents:
![]() . All numbers reported are in absolute values.
. All numbers reported are in absolute values.
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.0001 | 0.0005 | 0.0002 | 0.0000 | ||||
| 0.3 | 0.0217 | 0.0167 | 0.0347 | 0.0211 | 0.0397 | 0.0324 | 0.0267 | 0.0299 | |
| 0.5 | 0.0371 | 0.0334 | 0.0674 | 0.0442 | 0.0663 | 0.0646 | 0.0405 | 0.0570 | |
| 0.3 | 0 | 0.0082 | 0.0147 | 0.0064 | 0.0170 | 0.0179 | 0.0292 | 0.0267 | 0.0299 |
| 0.3 | 0.0534 | 0.0381 | 0.0637 | 0.0457 | 0.1044 | 0.0755 | 0.1020 | 0.0736 | |
| 0.5 | 0.1064 | 0.0635 | 0.1463 | 0.0795 | 0.2006 | 0.1248 | 0.1678 | 0.1160 | |
| 0.5 | 0 | 0.0112 | 0.0264 | 0.0111 | 0.0294 | 0.0253 | 0.0532 | 0.0405 | 0.0570 |
| 0.3 | 0.0737 | 0.0565 | 0.0785 | 0.0650 | 0.1486 | 0.1133 | 0.1678 | 0.1160 | |
| 0.5 | 0.1738 | 0.0908 | 0.2065 | 0.1086 | 0.3367 | 0.1810 | 0.3294 | 0.1768 |
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.0001 | 0.0005 | 0.0002 | 0.0000 | ||||
| 0.3 | 0.0214 | 0.0169 | 0.0344 | 0.0219 | 0.0393 | 0.0325 | 0.0268 | 0.0299 | |
| 0.5 | 0.0367 | 0.0339 | 0.0667 | 0.0459 | 0.0664 | 0.0650 | 0.0406 | 0.0570 | |
| 0.3 | 0 | 0.0087 | 0.0149 | 0.0069 | 0.0175 | 0.0185 | 0.0294 | 0.0268 | 0.0299 |
| 0.3 | 0.0540 | 0.0386 | 0.0657 | 0.0471 | 0.1050 | 0.0759 | 0.1020 | 0.0736 | |
| 0.5 | 0.1065 | 0.0643 | 0.1487 | 0.0823 | 0.2008 | 0.1255 | 0.1681 | 0.1160 | |
| 0.5 | 0 | 0.0111 | 0.0267 | 0.0088 | 0.0301 | 0.0247 | 0.0535 | 0.0406 | 0.0570 |
| 0.3 | 0.0755 | 0.0571 | 0.0816 | 0.0667 | 0.1502 | 0.1139 | 0.1681 | 0.1160 | |
| 0.5 | 0.1758 | 0.0919 | 0.2129 | 0.1121 | 0.3384 | 0.1820 | 0.3294 | 0.1768 |
This table presents time 0 solutions for the interest volatility for the economy with two agents which differ by habit preference type (internal or external) and/or level of their relative risk aversion (RRA) coefficients. ![]() denotes the habit strength of the first(second) agent,
denotes the habit strength of the first(second) agent,
![]() denotes the RRA coefficient of the first(second) agent. Panel A(B) presents the solutions for the economy with time horizon
denotes the RRA coefficient of the first(second) agent. Panel A(B) presents the solutions for the economy with time horizon
![]() . Time discount factor
. Time discount factor
![]() , initial endowments are equal for two agents:
, initial endowments are equal for two agents:
![]() . All numbers reported are in absolute values.
. All numbers reported are in absolute values.
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.3362 | 0.2324 | 0.3658 | 0.5000 | ||||
| 0.3 | 0.4097 | 0.4061 | 0.3673 | 0.3419 | 0.4447 | 0.4411 | 0.5124 | 0.5102 | |
| 0.5 | 0.4456 | 0.4446 | 0.4219 | 0.4003 | 0.4719 | 0.4709 | 0.5184 | 0.5142 | |
| 0.3 | 0 | 0.3543 | 0.3915 | 0.2602 | 0.3395 | 0.3977 | 0.4247 | 0.4876 | 0.4898 |
| 0.3 | 0.4295 | 0.4357 | 0.3935 | 0.4017 | 0.4606 | 0.4624 | 0.5000 | 0.5000 | |
| 0.5 | 0.4622 | 0.4609 | 0.4447 | 0.4366 | 0.4812 | 0.4797 | 0.5059 | 0.5046 | |
| 0.5 | 0 | 0.3545 | 0.4183 | 0.3213 | 0.3870 | 0.4474 | 0.4461 | 0.4816 | 0.4858 |
| 0.3 | 0.4349 | 0.4504 | 0.4018 | 0.4295 | 0.4646 | 0.4713 | 0.4941 | 0.4954 | |
| 0.5 | 0.4686 | 0.4690 | 0.4536 | 0.4538 | 0.4841 | 0.4837 | 0.5000 | 0.5000 |
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.3402 | 0.2514 | 0.3685 | 0.5000 | ||||
| 0.3 | 0.4088 | 0.4068 | 0.3746 | 0.3552 | 0.4436 | 0.4409 | 0.5055 | 0.5043 | |
| 0.5 | 0.4404 | 0.4415 | 0.4234 | 0.4075 | 0.4679 | 0.4676 | 0.5118 | 0.5058 | |
| 0.3 | 0 | 0.3723 | 0.4059 | 0.2911 | 0.3614 | 0.4121 | 0.4357 | 0.4945 | 0.4957 |
| 0.3 | 0.4351 | 0.4433 | 0.4045 | 0.4160 | 0.4637 | 0.4669 | 0.5000 | 0.5000 | |
| 0.5 | 0.4620 | 0.4637 | 0.4477 | 0.4452 | 0.4805 | 0.4807 | 0.5028 | 0.5019 | |
| 0.5 | 0 | 0.3768 | 0.4364 | 0.1095 | 0.4095 | 0.3951 | 0.4589 | 0.4882 | 0.4942 |
| 0.3 | 0.4458 | 0.4611 | 0.4168 | 0.4441 | 0.4702 | 0.4776 | 0.4972 | 0.4981 | |
| 0.5 | 0.4714 | 0.4748 | 0.4586 | 0.4631 | 0.4853 | 0.4865 | 0.5000 | 0.5000 |
This table presents time 0 solutions for the stock holdings of agent 1 for the economy with two agents which differ by habit preference type (internal or external) and/or level of their relative risk aversion (RRA) coefficients. ![]() denotes the habit strength of the first(second) agent,
denotes the habit strength of the first(second) agent,
![]() denotes the RRA coefficient of the first(second) agent. Panel A(B) presents the solutions for the economy with time horizon
denotes the RRA coefficient of the first(second) agent. Panel A(B) presents the solutions for the economy with time horizon
![]() . Time discount factor
. Time discount factor
![]() , initial endowments are equal for two agents:
, initial endowments are equal for two agents:
![]() . All numbers reported are in absolute values.
. All numbers reported are in absolute values.
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 0.9219 | 1.4810 | 0.6931 | 0.0000 | ||||
| 0.3 | 0.5207 | 0.5228 | 0.7573 | 0.8602 | 0.2899 | 0.2997 | -0.0671 | -0.0520 | |
| 0.5 | 0.3181 | 0.3055 | 0.4546 | 0.5328 | 0.1474 | 0.1464 | -0.1016 | -0.0722 | |
| 0.3 | 0 | 0.8380 | 0.6110 | 1.3477 | 0.8932 | 0.5377 | 0.3887 | 0.0671 | 0.0520 |
| 0.3 | 0.4181 | 0.3581 | 0.6193 | 0.5376 | 0.2113 | 0.1909 | 0.0000 | 0.0000 | |
| 0.5 | 0.2282 | 0.2154 | 0.3296 | 0.3405 | 0.1012 | 0.1012 | -0.0339 | -0.0232 | |
| 0.5 | 0 | 0.8538 | 0.4606 | 1.0183 | 0.6312 | 0.2873 | 0.2784 | 0.1016 | 0.0722 |
| 0.3 | 0.3971 | 0.2762 | 0.5830 | 0.3877 | 0.1945 | 0.1455 | 0.0339 | 0.0232 | |
| 0.5 | 0.1976 | 0.1702 | 0.2847 | 0.2493 | 0.0889 | 0.0815 | 0.0000 | 0.0000 |
|
|
|
|
|
|
|
|
|
||
| 0 | 0 | 2.4718 | 3.6230 | 1.5285 | 0.0000 | ||||
| 0.3 | 1.4085 | 1.4024 | 1.8131 | 2.0095 | 0.6471 | 0.6640 | -0.0639 | -0.0492 | |
| 0.5 | 0.9066 | 0.8577 | 1.0732 | 1.2199 | 0.3600 | 0.3519 | -0.1372 | -0.0671 | |
| 0.3 | 0 | 1.9919 | 1.4789 | 3.0808 | 2.0828 | 1.0250 | 0.7579 | 0.0639 | 0.0492 |
| 0.3 | 1.0095 | 0.8661 | 1.3929 | 1.2059 | 0.4173 | 0.3759 | 0.0000 | 0.0000 | |
| 0.5 | 0.5831 | 0.5387 | 0.7409 | 0.7486 | 0.2185 | 0.2114 | -0.0322 | -0.0212 | |
| 0.5 | 0 | 1.9515 | 1.0116 | 6.1170 | 1.3920 | 1.0430 | 0.4907 | 0.1372 | 0.0671 |
| 0.3 | 0.8555 | 0.6029 | 1.2431 | 0.8255 | 0.3463 | 0.2575 | 0.0322 | 0.0212 | |
| 0.5 | 0.4448 | 0.3794 | 0.6024 | 0.5201 | 0.1663 | 0.1495 | 0.0000 | 0.0000 |
This table presents time 0 solutions for the bond holdings of agent 1 for the economy with two agents which differ by habit preference type (internal or external) and/or level of their relative risk aversion (RRA) coefficients. ![]() denotes the habit strength of the first(second) agent,
denotes the habit strength of the first(second) agent,
![]() denotes the RRA coefficient of the first(second) agent. Panel A(B) presents the solutions for the economy with time horizon
denotes the RRA coefficient of the first(second) agent. Panel A(B) presents the solutions for the economy with time horizon
![]() . Time discount factor
. Time discount factor
![]() , initial endowments are equal for two agents:
, initial endowments are equal for two agents:
![]() . All numbers reported are in absolute values.
. All numbers reported are in absolute values.
6 Appendix - Euler Equation
While (Abel, 1990) derives the pricing kernel of a time non-separable utility function from an indifference argument, we utilize the envelope theorem (known as the Benveniste-Scheinkman formula in Dynamic Programming) to derive the Euler equations and thus the stochastic
discount factor from the Bellman Equation, which can be derived from the agents' optimization problem (1) and is given through
| (A1) |
The corresponding budget equation is:
| (A2) |
and suppressing the index
| (A3) |
Saving notation and denoting a partial derivative with a subscript the F.O.C. of the Lagrangian are (skip the budget equation)
Plugging (A4) and (A5) into (A6) and rearranging, we can express prices in terms of the (derivatives of the) value function:
Differentiating the Bellman Equation w.r.t. the controls, yields
Plugging (A7) and (A8) into (A9), (A10) and (A11) and using the differentiated budget equation w.r.t. the right control gives:
Shifting (A12), (A13) and (A14) by one point in time ahead and substituting the resulting equations into (A7) and (A8) gives:
The pricing kernels of the two agents can be inferred from (A15) or (A16). If
![\begin{displaymath}\begin{array}{rll} MRS^1_{t,t+1} & = & \beta_1 \frac{(c_{1,t+1}-b_1c_{1,t})^{-\gamma_1} - \beta_1b_1\mathbb{E}_{t+1}\left[(c_{1,t+2}-b_1c_{1,t+1})^{-\gamma_1}\right]}{(c_{1,t}-b_1c_{1,t-1})^{-\gamma_1} - \beta_1b_1\mathbb{E}_t\left[(c_{1,t+1}-b_1c_{1,t})^{-\gamma_1}\right]} \\ MRS^2_{t,t+1} & = & \beta_2 \frac{(c_{2,t+1}-b_2 c_{2,t})^{-\gamma_2} - \beta_2b_2\mathbb{E}_{t+1}\left[(c_{2,t+2}-b_2 c_{2,t+1})^{-\gamma_2}\right]}{(c_{2,t}-b_2 c_{2,t-1})^{-\gamma_2} - \beta_2b_2\mathbb{E}_t\left[(c_{2,t+1}-b_2 c_{2,t} )^{-\gamma_2}\right]}. \end{array}\end{displaymath}](img231.gif)
|
(A17) |
where
Footnotes
Federal Reserve Board, Washington, DC 20551;
[email protected] Return to Text
![\displaystyle U_{i,t} = \mathbb{E}\left[ \sum_{j = 0}^T \beta^j u_i(c_{i,t+j},x_{i,t+j})\vert \mathcal{F}_t \right],](img10.gif)
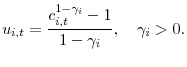
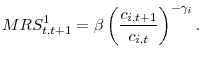
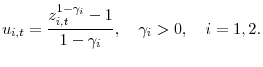
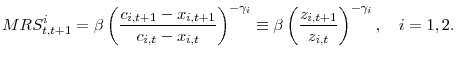
![\displaystyle MUC_{i,t} = \mathbb{E}_t\left[z_{i,t}^{-\gamma_i}\times \frac{\partial z_{i,t}}{\partial c_{i,t}} + \beta z_{i,t+1}^{-\gamma_i} \times \frac{\partial z_{i,t+1}}{\partial c_{i,t}}\right] = \mathbb{E}_t\left[z_{i,t}^{-\gamma_i} - \beta b z_{i,t+1}^{-\gamma_i}\right], \quad i=1,2](img30.gif)
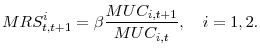
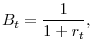
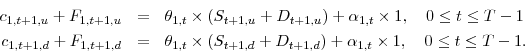
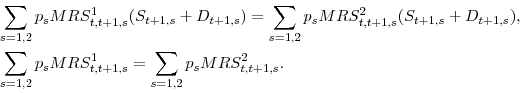
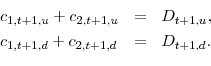
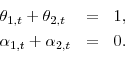

![\begin{displaymath}\begin{array}{rll} MRS^1_{t,t+1} & = & \beta \frac{(c_{1,t+1}-b_1c_{1,t})^{-\gamma_1} - \beta b_1\mathbb{E}_{t+1}\left[(c_{1,t+2}-b_1c_{1,t+1})^{-\gamma_1}\right]}{(c_{1,t}-b_1c_{1,t-1})^{-\gamma_1} - \beta b_1\mathbb{E}_t\left[(c_{1,t+1}-b_1c_{1,t})^{-\gamma_1}\right]} \\ MRS^2_{t,t+1} & = & \beta \frac{(c_{2,t+1}-b_2 c_{2,t})^{-\gamma_2} - \beta b_2\mathbb{E}_{t+1}\left[(c_{2,t+2}-b_2 c_{2,t+1})^{-\gamma_2}\right]}{(c_{2,t}-b_2 c_{2,t-1})^{-\gamma_2} - \beta b_2\mathbb{E}_t\left[(c_{2,t+1}-b_2 c_{2,t} )^{-\gamma_2}\right]}, \end{array}\end{displaymath}](img114.gif)
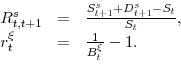
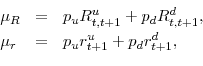
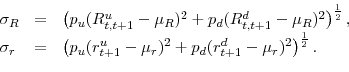
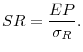
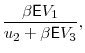
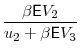
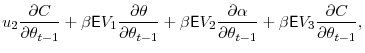
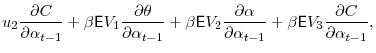

![\displaystyle \mathsf{E}_t\left[\beta\frac{ \frac{\partial}{\partial C_{t +1}} u (C_t, C_{t +1}) + \beta \mathsf{E}_{t +1} \left[ \frac{\partial}{\partial C_{t + 1}} u (C_{t + 1}, C_{t + 2}) \right] }{\frac{\partial}{\partial C_t} u (C_{t - 1}, C_t) + \beta \mathsf{E}_t \left[ \frac{\partial}{\partial C_t} u (C_t, C_{t +1}) \right]}(S_{t + 1} + \delta_{t +1})\right],](img226.gif)
![\displaystyle \mathsf{E}_t\left[\beta\frac{\frac{\partial}{\partial C_{t +1 }} u (C_t, C_{t +1}) + \beta \mathsf{E}_{t +1} \left[ \frac{\partial}{\partial C_{t + 1}} u (C_{t + 1}, C_{t + 2}) \right] }{\frac{\partial}{\partial C_t} u (C_{t -1}, C_t) + \beta \mathsf{E}_t \left[ \frac{\partial}{\partial C_t} u (C_t, C_{t + 1}) \right]} \right].](img228.gif)