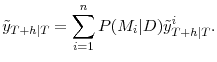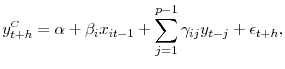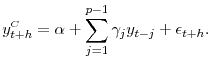Credit Spreads as Predictors of Real-Time Economic Activity:
A Bayesian Model-Averaging Approach*
Forthcoming in the Review and Economics and Statistics
Keywords: Forecasting, real-time data, Bayesian Model Averaging, credit spreads
Abstract:
1 Introduction
One area of agreement among economists at universities, central banks, and on Wall Street is that forecasting economic activity is hard. While the existing methods give us some ability to forecast economic developments for the current quarter and perhaps the quarter after that, their predictive power is modest at best and deteriorates rapidly as the forecast horizon extends beyond the very near term. Moreover, what little predictability there seems to be appears to be captured about as well by simple models--such as a univariate autoregression--as by the large number of complex statistical and DSGE forecasting methods that have been proposed in the literature; see, for example, Sims [2005]; Tulip [2005]; Faust & Wright [2009]; and Edge & Gürkaynak [2010].
Economists have long sought to improve on this record by using information from financial markets. Because they are inherently forward looking, the argument goes, financial market prices should impound information about investors' expectations of future economic outcomes.5 From a theoretical perspective, default-risk indicators such as credit spreads--the difference in yields between various corporate debt instruments and government securities of comparable maturity--are particularly well suited for forecasting economic activity. Philippon [2009], for example, presents a model in which the decline in investment fundamentals, owing to a reduction in the expected present-value of corporate cash flows, leads to a widening of credit spreads prior to a cyclical downturn. As emphasized by Bernanke et al. [1999] and Gilchrist & Zakrajšek [2012], increases in credit spreads can also signal disruptions in the supply of credit resulting from the worsening in the quality of corporate balance sheets or from the deterioration in the health of financial intermediaries that supply credit.6
The empirical success of default-risk indicators as predictors of economic activity is decidedly mixed, however, with results varying substantially across various credit spread indexes and different time periods. For example, the "paper-bill" spread--the difference between yields on nonfinancial commercial paper and comparable-maturity Treasury bills--had substantial forecasting power for economic activity during the 1970s and the 1980s, but its predictive ability vanished in the subsequent decade. In contrast, credit spreads based on indexes of speculative-grade (i.e., "junk") corporate bonds, which contain information from markets that were not in existence before the mid-1980s, did particularly well at forecasting output growth during the 1990s, according to Gertler & Lown [1999] and Mody & Taylor [2004]. Stock & Watson [2003], however, show that the forecasting ability of this default-risk indicator is quite uneven.
In a recent paper, Gilchrist et al. [2009] (GYZ hereafter) argue that these mixed results may be due to the fact that the credit spread indexes used by researchers tend to be based on aggregates of returns on a mishmash of bonds with different duration, credit risk, and other characteristics. In part to address these problems, GYZ constructed 20 monthly credit spread indexes for different maturity and credit risk categories using secondary market prices of individual senior unsecured corporate bonds.7 Their findings indicate that these credit spread indexes have substantial predictive power, at both short- and longer-term horizons, for the growth of payroll employment and industrial production. Moreover, they significantly outperform the predictive ability of the standard default-risk indicators, a result that suggests that using "cleaner" measures of credit spreads may, indeed, lead to more accurate forecasts of economic activity.
This paper extends the analysis of GYZ in several dimensions. Most importantly, we provide a thorough evaluation of the marginal information content of credit spreads in real-time economic forecasting. Given the extensive and ongoing search for consistent predictors of U.S. economic activity, the macroeconomics profession runs a substantial risk that results like those of GYZ are due to researchers stumbling on variables that just happen to fit the existing sample, but which, in reality, have no predictive power. The regular breakdown of new forecasting relationships soon after they are documented confirms that this risk is real. Thus, it is especially important that any such analysis takes into account model search and selection issues.
To guard against the problem of selecting financial indicators that just happen to fit our sample, we adopt a Bayesian Model Averaging (BMA) approach and evaluate it in a pseudo out-of-sample forecasting exercise. As explained more fully below, we add the new credit spread indexes to a predictor
set containing over 100 asset market indicators, as well as a large number of real variables, and begin with a prior that each predictor is equally likely to be useful in forecasting future economic activity. The posterior weight assigned to each predictor in period ![]() is then based on a Bayesian updating scheme that uses only the information available at time
is then based on a Bayesian updating scheme that uses only the information available at time ![]() . While our BMA scheme has, under certain conditions, a formal Bayesian justification, we follow a large and growing literature that takes a frequentist perspective and relies on the BMA framework as a pragmatic approach to data-based weighting of a large number of competing
prediction models8. The combination of the BMA framework and out-of-sample forecast evaluation mitigates--though does not completely eliminate--the problem of
data mining.
. While our BMA scheme has, under certain conditions, a formal Bayesian justification, we follow a large and growing literature that takes a frequentist perspective and relies on the BMA framework as a pragmatic approach to data-based weighting of a large number of competing
prediction models8. The combination of the BMA framework and out-of-sample forecast evaluation mitigates--though does not completely eliminate--the problem of
data mining.
While following GYZ's basic approach for constructing credit spread indexes, we also improve on their methodology by adjusting the underlying micro-level credit spreads for the call option embedded in many of the underlying securities. As pointed out by Duffee [1998] and Duca [1999], fluctuations in the value of embedded options--reflecting shifts in the term structure of risk-free rates--can substantially alter the information content of movements in corporate bond yields at business cycle frequencies.
Our results indicate that the new credit spread indexes have considerable marginal predictive power for real-time measures of economic activity, especially those of the cyclically sensitive nature. When using the entire predictor set to forecast a wide array of economic activity indicators, the gains in the root mean-square prediction error (RMSPE)--relative to a univariate autoregressive benchmark--are statistically significant and often substantial in economic terms. BMA forecasts consistently generate reductions in out-of-sample RMSPEs on the order of 10 percent when forecasting the cumulative growth of cyclically sensitive economic indicators four quarters into the future. Consumption growth is the main exception to this general result--there are no gains in predictive accuracy relative to our benchmark for this measure of economic activity.
When we omit the credit spread indexes from the predictor set and redo the analysis, we obtain the standard result, namely, that the predictive accuracy of the BMA method--like that of most other documented forecasting methods--is statistically indistinguishable from that of the univariate autoregressive benchmark. This result indicates that there is something different about the information content of credit spreads and that our BMA weighting scheme is able to pick out this difference in real-time from a large number of predictors, all of which were treated equally ex ante. Indeed, the analysis of the evolution of posterior weights that the BMA scheme assigns to various variables in the predictor set shows that it is economic downturns that lead to the majority of the posterior weight being placed on the credit spreads. This finding suggests that corporate bond spreads--when properly measured--may be one of the earliest and clearest aggregators of accumulating evidence of incipient recession.
The remainder of the paper is organized as follows. Section 2 describes our bond-level data and the construction of portfolios based on the option-adjusted credit spreads. In Section 3, we outline the econometric methodology used to combine forecasts by BMA. Section 4 contains our main empirical results. In Section 5, we compare the performance of BMA forecasts at different stages of the business cycle--that is, in economic recessions and expansions. And lastly, Section 6 concludes.
2.1 Credit Spreads
The key information for our analysis comes from a large sample of fixed income securities issued by U.S. corporations.9 Specifically, from the Lehman/Warga (LW) and Merrill Lynch (ML) databases, we extracted month-end prices of outstanding long-term corporate bonds traded in the secondary market between January 1986 and September 2011.10 To guarantee that we are measuring borrowing costs of different firms at the same point in their capital structure, we restricted our sample to senior unsecured issues with a fixed coupon schedule only. For such securities, we spliced the month-end prices across the two data sources.
We exploit the micro-level nature of our data to construct credit spreads that are not contaminated by the maturity/duration mismatch that is a bane of most commonly-used credit spread indexes. Specifically, for each individual bond issue in our sample, we construct a theoretical risk-free
security that replicates exactly the promised cash-flows of the corresponding corporate debt instrument. For example, consider a corporate bond ![]() issued by firm
issued by firm ![]() that at time
that at time ![]() is promising a sequence of cash-flows
is promising a sequence of cash-flows
![]() , which consists of the regular coupon payments and the repayment of the principle at maturity. The price of this bond in period
, which consists of the regular coupon payments and the repayment of the principle at maturity. The price of this bond in period ![]() is given by
is given by
![\displaystyle P_{it}[k] = \sum_{s=1}^{S} C_{s} D(t_{s}),](img7.gif) |
where
To ensure that our results are not driven by a small number of extreme observations, we eliminated all bond/month observations with credit spreads below 5 basis points and with spreads greater than 3,500 basis points.11 In addition, we dropped from our sample very small corporate issues--those with a par value of less than $1 million--and all observations with a remaining term-to-maturity of less than one year or more than 30 years.12 These selection criteria yielded a sample of 6,404 individual securities issued by firms in the nonfinancial sector and 942 securities issued by financial firms. We matched these corporate securities with their issuer's quarterly income and balance sheet data from Compustat and daily data on equity valuations from CRSP, yielding a matched sample of 1,156 nonfinancial firms and 202 financial firms.
| Bond Characteristic | Mean | StdDev | Min | Median | Max |
| No. of bonds per firm/month (Nonfinancial) | 3.14 | 3.89 | 1.00 | 2.00 | 76.0 |
| Mkt. value of issue ($mil.) (Nonfinancial) | 349.2 | 342.6 | 1.22 | 255.1 | 5,628 |
| Maturity at issue (years) (Nonfinancial) | 12.8 | 9.2 | 1.0 | 10.0 | 50.0 |
| Term to maturity (years) (Nonfinancial) | 10.4 | 8.3 | 1.0 | 7.4 | 30.0 |
| Duration (years) (Nonfinancial) | 6.28 | 3.30 | 0.91 | 5.72 | 17.1 |
| Credit rating (S&P) (Nonfinancial) | - | - | D | BBB1 | AAA |
| Coupon rate (pct.) (Nonfinancial) | 7.18 | 2.03 | 0.75 | 6.95 | 17.5 |
| Nominal yield to maturity (pct.) (Nonfinancial) | 7.07 | 3.08 | 0.42 | 6.79 | 44.3 |
| Credit spread (bps.) (Nonfinancial) | 222 | 290 | 5 | 132 | 3,499 |
| No. of bonds per firm/month (Financial) | 3.06 | 3.50 | 1.00 | 2.00 | 26.0 |
| Mkt. value of issue ($mil.) (Financial) | 486.8 | 566.9 | 9.11 | 274.4 | 4,351 |
| Maturity at issue (years) (Financial) | 10.4 | 8.0 | 2.0 | 10.0 | 40.0 |
| Term to maturity (years) (Financial) | 8.7 | 7.8 | 1.0 | 5.9 | 30.0 |
| Duration (years) (Financial) | 5.54 | 3.25 | 0.90 | 4.82 | 15.3 |
| Credit rating (S&P) (Financial) | - | - | C | A2 | AAA |
| Coupon rate (pct.) (Financial) | 6.80 | 1.94 | 2.00 | 6.60 | 15.8 |
| Nominal yield to maturity (pct.) (Financial) | 6.54 | 2.78 | 0.69 | 6.27 | 41.2 |
| Credit spread (bps.) (Financial) | 185 | 250 | 5 | 117 | 3,499 |
Note: Sample period: 1986:M1-2011:M9. No. of nonfinancial firms/bonds = 1,156/6,404 (Obs. = 334,685); No. of financial firms/bonds = 202/942 (Obs. = 46,135). The market value of the bond issues is deflated by the CPI (2000 = 100). Sample statistics are based on trimmed data; see text for details.
Table 1 contains summary statistics for the key characteristics of bonds in our sample by the type of firm (nonfinancial vs. financial). Note that a typical firm has only a few senior unsecured issues outstanding at any point in time--the median firm in both sectors, for example, has two such issues trading at any given month. The size of bond issues, measured by their market value, tend to be somewhat larger, on average, in the financial sector. Not surprisingly, the maturity of these debt instruments is fairly long, with the average maturity at issue of more than 10 years in both sectors. Because corporate bonds typically generate significant cash flow in the form of regular coupon payments, their effective duration is considerably shorter.
According to the S&P credit ratings, our sample spans the entire spectrum of credit quality, from "single D" to "triple A." At A2, the median bond/month observation in the financial sector is somewhat above that in the nonfinancial sector (i.e., BBB1), though they are both solidly in the investment-grade category. Turning to returns, the (nominal) coupon rate on the bonds issued by nonfinancial firms averaged 7.18 percent during our sample period, compared with 6.89 percent for bonds issued by their financial counterparts. The average expected total return was 7.29 percent per annum in the nonfinancial sector and 6.80 percent in the financial sector. Relative to Treasuries, an average bond issued by a nonfinancial firm has an expected return of about 222 basis points above the comparable risk-free rate. Reflecting their generally higher credit quality--at least as perceived by the ratings agencies--the average credit spread on a bond issued by a financial intermediary is 185 basis points.
2.2 Default Risk
The measurement of firm-specific default risk is the crucial input in the construction of our bond portfolios. To measure an issuer's probability of default at each point in time, we employ the contingent claims approach to corporate credit risk developed in the seminal work of Merton [1974,1973]. The key insight of this "distance-to-default" (DD) framework is that the equity of the firm can be viewed as a call option on the underlying value of the firm with a strike price equal to the face value of the firm's debt. Although neither the underlying value of the firm nor its volatility is directly observable, they can, under the assumptions of the model, be inferred from the value of the firm's equity, the volatility of its equity, and the firm's observed capital structure.
Formally, the distance-to-default--essentially, a volatility-adjusted measure of leverage--is given by
 |
where
The numerical procedure used to construct this market-based measure of default risk is based on Bharath & Shumway [2008]. Employing their methodology, we calculate the distance-to-default for all U.S. corporations covered by S&P's Compustat and CRSP over the 1986:M1-2011:M9 period. Figure 1 plots the cross-sectional median of the DDs for the 1,156 nonfinancial and 202 financial bond issuers in our sample. As a point of comparison, the figure also depicts the cross-sectional interquartile range (IQR) of the DDs for the entire Compustat-CRSP matched sample.14
According to this metric, the credit quality of the median nonfinancial bond issuer in our sample is, on average, appreciably higher than that of the median financial issuer, a result that is primarily due to the fact that financial firms tend to have higher leverage than their nonfinancial counterparts. More importantly, the median DD for both sets of firms is strongly procyclical, implying that equity market participants anticipate corporate defaults to increase during economic downturns. In addition, this indicator of default risk worsened significantly in periods of financial market stress, such as those associated with the stock market crash in October 1987 and the collapse of the Long-Term Capital Management hedge fund in the early autumn of 1998. In fact, during the height of the recent financial crisis in the latter part of 2008 and early 2009, the IQR of the distribution of the DDs across the entire U.S. corporate sector shifted noticeably lower, with the median DD of our sample of 202 financial firms falling to a historic low.
2.3 Call-Option Adjustment
Note: Sample period 1986:M1-2011:M9. The figure depicts the proportion of bonds in our sample that are callable. The shaded vertical bars represent the NBER-dated recessions.Figure 2 shows the proportion of bonds in our sample that are callable--that is, the issuer has, under certain pre-specified conditions, the right to "call" (i.e., redeem) the security prior to its maturity. The share of senior unsecured bonds with embedded call options is, on average, substantial in both sectors.15 Moreover, the proportion of callable debt has changed considerably over the course of our sample period, with almost all bonds being subject to a call provision at the start of our sample. In the late 1980s, however, the composition of debt began to shift noticeably toward noncallable debt, and by the mid-1990s, the majority of senior unsecured debt traded in the secondary market was in the form of noncallable securities. Over the past decade or so, this trend has been reversed, as firms resumed issuing large amounts of callable long-term debt.
As shown by Duffee [1998], if a firm's outstanding bonds are callable, movements in the risk-free rates--by changing the value of the embedded call option--will have an independent effect on bond prices, complicating the interpretation of the behavior of credit spreads. For example, as the general level of interest rates in the economy increases, the option to call becomes less valuable, which accentuates the price response of callable bonds relative to that of noncallable bonds. As a result, a rise in interest rates will, ceteris paribus, compress the credit spreads of callable bonds more than the credit spreads of their noncallable counterparts. In addition, prices of callable bonds are more sensitive to uncertainty regarding the future course of interest rates. On the other hand, to the extent that callable bonds are, in effect, of shorter duration, they may be less sensitive to changes in default risk.
To deal with this issue, we utilize the micro-level aspect of our bond data to adjust directly for the value of embedded options in callable bonds. Ideally, we would correct for the callability of each bond using option price theory. However, our bond-level data set does not contain any information regarding the terms of the underlying call provisions--it just indicates whether the bond is callable or not. Accordingly, we consider the following empirical credit-spread pricing model:
where
The distance-to-default and bond-specific controls are allowed to have differential effects on the credit spreads of callable and noncallable bonds. Because shifts in the Treasury term structure affect the value of the embedded call option, the spreads of callable bonds are also allowed to
depend separately on the level (
![]() ), slope (
), slope (
![]() ), and curvature (
), and curvature (
![]() ) of the Treasury yield curve.18
Note that movements in risk-free interest rates should, ceteris paribus, affect the credit spreads of noncallable bonds only insofar as they change firms' expected future cash flows and, as a result, their distance-to-default; thus, our specification does not allow these
term structure variables to directly affect the spreads of noncallable bonds. Likewise, the value of the embedded call option will change in response to fluctuations in interest rate uncertainty, so we allow the credit spreads on callable bonds to respond to the option-implied volatility on the
30-year Treasury bond futures (
) of the Treasury yield curve.18
Note that movements in risk-free interest rates should, ceteris paribus, affect the credit spreads of noncallable bonds only insofar as they change firms' expected future cash flows and, as a result, their distance-to-default; thus, our specification does not allow these
term structure variables to directly affect the spreads of noncallable bonds. Likewise, the value of the embedded call option will change in response to fluctuations in interest rate uncertainty, so we allow the credit spreads on callable bonds to respond to the option-implied volatility on the
30-year Treasury bond futures (
![]() )--again, this variable is not allowed to affect the spreads of noncallable bonds.
)--again, this variable is not allowed to affect the spreads of noncallable bonds.
We estimate the credit-spread regression (1) separately for the sample of securities issued by nonfinancial firms and those issued by financial firms. Assuming normally distributed pricing errors, the option-adjusted spread on a callable bond ![]() (i.e.,
(i.e.,
![]() )--denoted by
)--denoted by
![]() --is given by
--is given by
![\begin{displaymath}\begin{split}\tilde{S}_{it}[k] & = \exp \Bigg [ \ln S_{it}[k] - \big (\hat{\beta}_{0c}+\hat{\beta}_{1c} D\!D_{it} + \hat{\beta}_{2c} D\!D_{it}^{2} + \hat{\lambda}_{c}^{\prime} \mathbf{Z}_{it}[k] \big ) \\ & \quad - (\hat{\theta}_{1} L\!E\!V_{t} + \hat{\theta}_{2} S\!L\!P_{t} + \hat{\theta}_{3} C\!R\!V_{t} + \hat{\theta}_{4} V\!O\!L_{t}) - \frac{\hat{\sigma}_{t}^{2}}{2} \Bigg ], \end{split}\end{displaymath}](img35.gif)
|
where
| Marginal Effect |
|
|
|
|
| Distance-to-default: |
-0.209 | -0.136 | -0.125 | -0.133 |
| Distance-to-default: |
(0.011) | (0.008) | (0.028) | (0.015) |
| Term structure:
|
- | -0.473 | - | -0.421 |
| Term structure:
|
(0.041) | (0.081) | ||
| Term structure:
|
- | -0.288 | - | -0.218 |
| Term structure:
|
(0.037) | (0.047) | ||
| Term structure:
|
- | -0.074 | - | -0.123 |
| Term structure:
|
(0.038) | (0.034) | ||
| Term structure:
|
- | 0.144 | - | 0.147 |
| Term structure:
|
(0.013) | (0.017) | ||
| Adjusted |
0.746 | 0.746 | 0.615 | 0.615 |
|
|
0.000 | 0.000 | 0.000 | 0.000 |
Note: Sample period: 1986:M1-2011:M9. Entries in the table denote the estimated marginal effects of a one-unit change in the specified variable on the level of credit spreads (in percentage points) for noncallable (
Table 2 translates the selected coefficients from the estimated credit-spread pricing equation into the impact of variation in default risk (the sum of the linear and quadratic ![]() terms), the shape of the term structure, and interest rate uncertainty on the level of credit spreads. For callable bonds issued by nonfinancial firms, the effect of the distance-to-default on credit spreads is significantly attenuated
by the call-option mechanism: A one standard deviation increase in the distance-to-default--a signal of improving credit quality--implies a decrease of 21 basis points in the spreads of noncallable bonds, compared with a 14 basis points decline in the spreads of their callable
counterparts. The same call-option mechanism, however, does not seem to be as important for bonds issued by financial intermediaries. In that case, a one standard deviation increase in the distance-to-default implies a narrowing of spreads of about 13 basis points for both types of bonds.
terms), the shape of the term structure, and interest rate uncertainty on the level of credit spreads. For callable bonds issued by nonfinancial firms, the effect of the distance-to-default on credit spreads is significantly attenuated
by the call-option mechanism: A one standard deviation increase in the distance-to-default--a signal of improving credit quality--implies a decrease of 21 basis points in the spreads of noncallable bonds, compared with a 14 basis points decline in the spreads of their callable
counterparts. The same call-option mechanism, however, does not seem to be as important for bonds issued by financial intermediaries. In that case, a one standard deviation increase in the distance-to-default implies a narrowing of spreads of about 13 basis points for both types of bonds.
The estimates in Table 2 also indicate that movements in the shape of the Treasury term structure and interest rate uncertainty have first-order effects on the credit spreads of callable bonds, which are consistent with the theoretical predictions. For example, a one standard deviation increase in the level factor implies a narrowing of about 45 basis points in the credit spreads on callable bonds in both sectors. Similarly, an increase in the option-implied volatility on the long-term Treasury bond futures of one percentage point implies a widening of callable credit spreads of about 15 basis points because the rise in interest rate uncertainty lowers the prices of callable bonds by boosting the value of the embedded call option.
[Financial Firms]
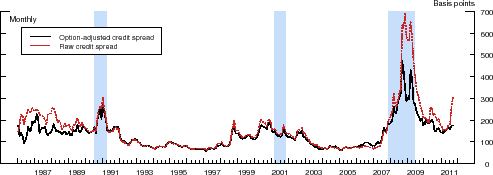
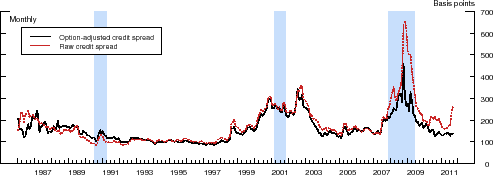
The importance of the option-adjustment procedure over the entire sample period is illustrated in Figure 3, which shows the time path of the average credit spread in our two data sets, calculated using both the raw and option-adjusted spreads. Although the two series
in each sector are clearly highly correlated (
![]() for nonfinancial issuers and
for nonfinancial issuers and
![]() for financial issuers) and are all strongly countercyclical, there are a number of noticeable differences. First, the option-adjusted credit spreads are, on average, lower than
their unadjusted counterparts, reflecting the positive value of the embedded call options. By eliminating, at least in part, fluctuations in the call option values, the option-adjusted credit spreads are also less volatile, on average, than the raw credit spreads. Lastly, the largest differences
between the two series occurred in the mid-1980s and during the recent financial crisis. The former period was characterized by a high general level of interest rates and relatively high uncertainty regarding the future course of long-term interest rates, whereas the difference during the latter
period owes primarily to the plunge in interest rates and the steepening of the term structure that began with the onset of the financial crisis in the summer of 2007, two factors that more than offset the spike in interest rate volatility that occurred during that period.
for financial issuers) and are all strongly countercyclical, there are a number of noticeable differences. First, the option-adjusted credit spreads are, on average, lower than
their unadjusted counterparts, reflecting the positive value of the embedded call options. By eliminating, at least in part, fluctuations in the call option values, the option-adjusted credit spreads are also less volatile, on average, than the raw credit spreads. Lastly, the largest differences
between the two series occurred in the mid-1980s and during the recent financial crisis. The former period was characterized by a high general level of interest rates and relatively high uncertainty regarding the future course of long-term interest rates, whereas the difference during the latter
period owes primarily to the plunge in interest rates and the steepening of the term structure that began with the onset of the financial crisis in the summer of 2007, two factors that more than offset the spike in interest rate volatility that occurred during that period.
2.4 Distance-to-Default Portfolios
We summarize the information contained in credit spreads, DDs, and excess equity returns for the sample of bond issuers by constructing portfolios based on expected default risk--as measured by our estimate of the distance-to-default--at the beginning of the period. These conditional DD-based
portfolios are constructed by sorting the three financial indicators in month ![]() into bins based on the percentiles of the distribution of the distance-to-default in month
into bins based on the percentiles of the distribution of the distance-to-default in month ![]() . Separate portfolios are formed for the financial and nonfinancial issuers.
. Separate portfolios are formed for the financial and nonfinancial issuers.
The distance-to-default portfolios are constructed by computing a weighted average of DDs in month ![]() for each bin, with the weights equal to the book value of the firm's liabilities at
the end of month
for each bin, with the weights equal to the book value of the firm's liabilities at
the end of month ![]() . Similarly, the stock portfolios are computed as a weighted average of excess equity returns in month
. Similarly, the stock portfolios are computed as a weighted average of excess equity returns in month ![]() for each bin, with the weights equal to the market value of the firm's equity at the end of month
for each bin, with the weights equal to the market value of the firm's equity at the end of month ![]() .20 Given the relatively large number of nonfinancial issuers, the bins for nonfinancial portfolios are based on the quartiles of the DD distribution, yielding
four credit-risk categories, denoted by NFIN-DD1, NFIN-DD2, NFIN-DD3, and NFIN-DD4. The financial bond issuers, by contrast, are sorted into two credit-risk categories--denoted by FIN-DD1 and FIN-DD2--based on the median of the DD distribution.
.20 Given the relatively large number of nonfinancial issuers, the bins for nonfinancial portfolios are based on the quartiles of the DD distribution, yielding
four credit-risk categories, denoted by NFIN-DD1, NFIN-DD2, NFIN-DD3, and NFIN-DD4. The financial bond issuers, by contrast, are sorted into two credit-risk categories--denoted by FIN-DD1 and FIN-DD2--based on the median of the DD distribution.
To control for maturity, we further split each DD-based bin of nonfinancial credit spreads into four maturity categories: (1) NFIN-MTY1: credit spreads of bonds with the remaining term-to-maturity of more than 1 year but less than (or equal) to 5 years; (2) NFIN-MTY2: credit
spreads of bonds with the remaining term-to-maturity of more than 5 years but less than (or equal) 10 years; (3) NFIN-MTY3: credit spreads of bonds with the remaining term-to-maturity of more than 10 years but less than (or equal) to 15 years; (4) NFIN-MTY4: credit
spreads of bonds with the remaining term-to-maturity of more than 15 years. Given the substantially smaller sample of bonds issued by firms in the financial sector, we split the two credit-risk categories in this sector into two maturity categories: (1) FIN-MTY1: credit spreads of bonds
with the remaining term-to-maturity of more than 1 year but less than (or equal) to 5 years; and (2) FIN-MTY2: credit spreads of bonds with the remaining term-to-maturity of more than 5 years. All told, this gives us a total of 16 nonfinancial and 4 financial
DD/maturity bond portfolios. Within each of these portfolios, we compute a weighted average of option-adjusted credit spreads in month ![]() , with the weights equal to the market value of the
outstanding issue.
, with the weights equal to the market value of the
outstanding issue.
The DD-based portfolios considered thus far were based on asset prices of a subset of U.S. corporations, namely firms with senior unsecured bonds that are traded in the secondary market. We also consider a broader set of DD-based financial indicators by constructing the same type of portfolios
using the distance-to-default estimates and excess equity returns for the entire matched CRSP-Compustat sample of U.S. corporations. Given the large number of firms in any given month, we increase the number of bins by sorting--for both nonfinancial and financial firms separately--the DDs and
excess equity returns in month ![]() into 10 deciles based on the distribution of the distance-to-default in month
into 10 deciles based on the distribution of the distance-to-default in month ![]() . As before, the conditional DD portfolios are constructed by computing a weighted average of DDs in month
. As before, the conditional DD portfolios are constructed by computing a weighted average of DDs in month ![]() for each DD decile,
whereas the stock portfolios are computed as a weighted average of excess equity returns in month
for each DD decile,
whereas the stock portfolios are computed as a weighted average of excess equity returns in month ![]() . This procedure yields a total of 20 additional DD-based portfolios for the
nonfinancial sector and another 20 portfolios for the financial sector.21
. This procedure yields a total of 20 additional DD-based portfolios for the
nonfinancial sector and another 20 portfolios for the financial sector.21
3 Econometric Methodology
We examine the predictive content of the DD-based portfolios, as well as a large number of other predictors, within the Bayesian Model Averaging (BMA) framework, an approach that is particularly well-suited to deal with model uncertainty. Initially proposed by Leamer [1978], BMA has been used extensively in the statistics literature; see, for example, Raftery et al. [1997] and Chipman et al. [2001]. The BMA approach to model uncertainty has also found numerous econometric applications, including the forecasting of output growth (Min & Zellner [1993] and Koop & Potter [2004]); the forecasting of recession risk (King et al. [2007]); cross-country growth regressions (Fernandez et al. [2001b] and Sala-i-Martin [2004]); exchange rate forecasting (Wright [2008]); and the predictability of stock returns (Avramov [2002] and Cremers [2002]).
3.1 Bayesian Model Averaging
We begin with a brief review of the formal Bayesian justification for our model-averaging approach. The researcher starts with a set of ![]() possible models, where the
possible models, where the ![]() -th model, denoted by
-th model, denoted by ![]() , is parametrized by
, is parametrized by
![]() . The researcher has prior beliefs about the probability that the
. The researcher has prior beliefs about the probability that the ![]() -th
model is true--denoted by
-th
model is true--denoted by ![]() --observes data
--observes data ![]() , and updates her beliefs to
compute the posterior probability that the
, and updates her beliefs to
compute the posterior probability that the ![]() -th model is the true model, according to
-th model is the true model, according to
where
is the marginal likelihood of the
Each model also implies a forecast. In the presence of model uncertainty, the BMA forecast weights each of the individual forecasts by their respective posterior probabilities. To operationalize a BMA forecasting scheme, the researcher needs only to specify the set of models, the model priors
![]() , and the parameter priors
, and the parameter priors
![]() . In this paper, we follow a growing literature that considers a large set of very simple models. Specifically, the models are all linear regression models, with each
model adding a single regressor to the baseline specification. More formally, the
. In this paper, we follow a growing literature that considers a large set of very simple models. Specifically, the models are all linear regression models, with each
model adding a single regressor to the baseline specification. More formally, the ![]() -th model in our framework is given by
-th model in our framework is given by
where
In setting the model priors, we assume that all models are equally likely--that is,
![]() . For the parameter priors, we follow the general trend of the BMA literature (e.g., Fernandez et al. [2001a]) in specifying that
the prior for
. For the parameter priors, we follow the general trend of the BMA literature (e.g., Fernandez et al. [2001a]) in specifying that
the prior for
![]() and
and
![]() , denoted by
, denoted by
![]() , is uninformative and is proportional to
, is uninformative and is proportional to
![]() , for all
, for all ![]() , while using the
, while using the ![]() -prior specification of Zellner [1986] for
-prior specification of Zellner [1986] for ![]() conditional on
conditional on
![]() . The
. The ![]() -prior is given by
-prior is given by
![]() , where the shrinkage hyperparameter
, where the shrinkage hyperparameter ![]() measures the strength of the prior--a smaller value of
measures the strength of the prior--a smaller value of ![]() corresponds to a more dogmatic prior.
corresponds to a more dogmatic prior.
Letting
![]() and
and
![]() denote the OLS estimates of the corresponding parameters in equation (4), the Bayesian
denote the OLS estimates of the corresponding parameters in equation (4), the Bayesian ![]() -period-ahead forecast made from model
-period-ahead forecast made from model ![]() at time
at time ![]() is given by
is given by
where
where
Clearly, the BMA forecast in equation (7) will depend on the value of the shrinkage hyperparameter ![]() . A low value of
. A low value of ![]() implies that the model likelihoods are roughly equal, and so the BMA forecast will resemble equal-weighted model averaging (Bates & Granger [1969]). In contrast, a high value of
implies that the model likelihoods are roughly equal, and so the BMA forecast will resemble equal-weighted model averaging (Bates & Granger [1969]). In contrast, a high value of
![]() amounts to weighting the models by their in-sample
amounts to weighting the models by their in-sample ![]() values, a procedure
that is well known to generate poor out-of-sample forecasting performance. Because the relationship between the out-of-sample root mean square prediction error and the parameter
values, a procedure
that is well known to generate poor out-of-sample forecasting performance. Because the relationship between the out-of-sample root mean square prediction error and the parameter ![]() is often
U-shaped, the best out-of-sample forecasts are obtained when
is often
U-shaped, the best out-of-sample forecasts are obtained when ![]() is neither too small nor too big. Our baseline results are based on a standard value (
is neither too small nor too big. Our baseline results are based on a standard value (![]() ) taken from the aforementioned literature, but we also conduct sensitivity analysis, which shows that our results are robust with respect to this choice.
) taken from the aforementioned literature, but we also conduct sensitivity analysis, which shows that our results are robust with respect to this choice.
We apply BMA to forecasting various indicators of economic activity using standard macroeconomic variables and asset market indicators as predictors. The common predictors ![]() in the
predictive regression (4) are a constant and lags of the dependent variable. It is worth emphasizing that we view the forecasting scheme proposed above as a pragmatic approach to data-based weighting of models and make no claim to its Bayesian optimality
properties.22
in the
predictive regression (4) are a constant and lags of the dependent variable. It is worth emphasizing that we view the forecasting scheme proposed above as a pragmatic approach to data-based weighting of models and make no claim to its Bayesian optimality
properties.22
3.2 The Forecasting Setup
We focus on forecasting real economic activity, as measured by real GDP, real personal consumption expenditures (PCE), real business fixed investment, industrial production, private payroll employment, the civilian unemployment rate, real exports, and real imports over the period from
1986:Q1 to 2011:Q3. All of these series are in quarter-over-quarter growth rates (actually 400 times log first-differences), except for the unemployment rate, which is simply in first differences. Our objective is to forecast the cumulative growth rate (or the cumulative change in the case of
the unemployment rate) for each of these economic indicators from quarter ![]() through quarter
through quarter ![]() .
.
Specifically, let ![]() denote the growth rate in the variable from quarter
denote the growth rate in the variable from quarter ![]() to quarter
to quarter ![]() . (In the case of the unemployment rate,
. (In the case of the unemployment rate, ![]() denotes the first difference.) The average value of
denotes the first difference.) The average value of ![]() over the forecast horizon
over the forecast horizon ![]() is denoted by
is denoted by
![]() . The
. The ![]() -th
forecasting model in our setup is given by:
-th
forecasting model in our setup is given by:
where
The set of possible predictors listed in Table 3 includes 15 different real-time macroeconomic series and 119 asset market indicators. Among the latter set are our 20 bond portfolios of option-adjusted credit spreads, as well as average DDs and
excess equity returns for different default-risk portfolios; in addition, we consider the predictive content of the three Fama-French risk factors (i.e., the excess market return and the SMB and HML factors), stock return on industry portfolios, a range of standard interest rates and interest rate
spreads, implied volatilities from options quotes, commodity prices, and commonly-used credit spreads.23 As noted above, the set of models considered also
includes a model in which we restrict
![]() . All told, our BMA forecasting scheme includes 135 different models.
. All told, our BMA forecasting scheme includes 135 different models.
The timing convention in the forecasting regression (8) is as follows. We think of forecasts as being made in the middle month of each quarter. For macroeconomic variables, we use the February, May, August, and November vintages of data from the real-time data set compiled and maintained by the Federal Reserve Bank of Philadelphia; this includes data through the previous quarter for all the macroeconomic series that we consider. All asset market indicators are as of the end of the month from the first month of the current quarter and would have been available to forecasters as of the middle month of the quarter.
Importantly, our empirical option-adjustment procedure is also implemented in real-time--that is, the parameters of the credit-spread regression (1) are estimated each month using only data available at that time. The resulting real-time coefficient estimates are used
to compute the option-adjusted credit spreads, which are then sorted into the DD-based bond portfolios.24 With these fully real-time data in hand, we then
use BMA to construct forecasts of the values of the dependent variable for the current and next four quarters (i.e.,
![]() . Thus, we are considering both "nowcasting" (i.e.,
. Thus, we are considering both "nowcasting" (i.e., ![]() ) and
prediction at horizons up to one year ahead.
) and
prediction at horizons up to one year ahead.
We evaluate the accuracy of these BMA forecasts in a recursive out-of-sample forecast evaluation exercise, starting with the forecasts made in 1992:Q1 and continuing through to the end of the sample period in 2011:Q3. The implementation of BMA in this recursive forecasting scheme uses the
![]() -prior (see the discussion above) with the same shrinkage hyperparameter
-prior (see the discussion above) with the same shrinkage hyperparameter ![]() for
each date. This means that the prior is tighter for the forecasts that are made later in the forecast period--the data,
for
each date. This means that the prior is tighter for the forecasts that are made later in the forecast period--the data,
| Predictor (No. of series) | Data Transformation |
| Macroeconomic Indicators: GDP | log difference |
| Macroeconomic Indicators: PCE | log difference |
| Macroeconomic Indicators: PCE (durable goods) | log difference |
| Macroeconomic Indicators: Residential investment | log difference |
| Macroeconomic Indicators: Business fixed investment | log difference |
| Macroeconomic Indicators: Government spending | log difference |
| Macroeconomic Indicators: Exports | log difference |
| Macroeconomic Indicators: Imports | log difference |
| Macroeconomic Indicators: Nonfarm private payrolls | log difference |
| Macroeconomic Indicators: Civilian unemployment rate | difference |
| Macroeconomic Indicators: Industrial production | log difference |
| Macroeconomic Indicators: Single-family housing starts | log difference |
| Macroeconomic Indicators: GDP price deflator | log difference |
| Macroeconomic Indicators: Consumer price index | log difference |
| Macroeconomic Indicators: M2 | log difference |
| Asset Market Indicators: Credit spreads in DD-based bond portfolios (nonfinancial) (16) | level |
| Asset Market Indicators: Credit spreads in DD-based bond portfolios (financial) (4) | level |
| Asset Market Indicators: Avg. DD by DD percentile (nonfinancial bond issuers) (4) | level |
| Asset Market Indicators: Avg. DD by DD percentile (nonfinancial firms) (10) | level |
| Asset Market Indicators: Excess stock returns by DD percentile (nonfinancial bond issuers) (4) | level |
| Asset Market Indicators: Excess stock returns by DD percentile (nonfinancial firms) (10) | level |
| Asset Market Indicators: Avg. DD by DD percentile (financial bond issuers) (2) | level |
| Asset Market Indicators: Avg. DD by DD percentile (financial firms) (10) | level |
| Asset Market Indicators: Excess stock returns by DD percentile (financial bond issuers) (2) | level |
| Asset Market Indicators: Excess stock returns by DD percentile (financial firms) (10) | level |
| Asset Market Indicators: 3-month nonfinancial commercial paper rate | level |
| Asset Market Indicators: 3-month nonfinancial commercial paper rate | less 3-month Tbill rate |
| Asset Market Indicators: 3-month Eurodollar rate | level |
| Asset Market Indicators: 3-month Eurodollar rate | less 3-month Tbill rate |
| Asset Market Indicators: 3-month Treasury bill rate | level |
| Asset Market Indicators: Federal funds rate | level |
| Asset Market Indicators: 1- to 10-year Treasury yields (10) |
level |
| Asset Market Indicators: 1- to 10-year Treasury yields (10) | less 3-month Tbill rate |
| Asset Market Indicators: Fama-French risk factors (3) | level |
| Asset Market Indicators: S&P 100 futures implied volatility (VXO) | level |
| Asset Market Indicators: Treasury futures implied volatility (10- and 30-year) | level |
| Asset Market Indicators: Gold price | 2nd difference of logs |
| Asset Market Indicators: Oil price | 2nd difference of logs |
| Asset Market Indicators: CRB commodity price index | 2nd difference of logs |
| Asset Market Indicators: S&P 500 dividend yield | log |
| Asset Market Indicators: Moody's Baa-Aaa credit spread | level |
| Asset Market Indicators: Returns on industry portfolios (10) | level |
Note: All macroeconomic series come from the real-time data set maintained by the Federal Reserve Bank of Philadelphia. The NIPA series are in real terms (c-w, $2000). [a] The nominal Treasury yields between maturities of 1- and 10-years are taken from the Treasury yield curve estimated by Gürkaynak et al. [2007].
of course, are also more informative at that point--a choice that is consistent with what a researcher would have done, if she was applying BMA as a shrinkage device at each point in time.
An important issue in this type of real-time forecasting exercise is the definition of what constitutes the "actual" values with which to compare our forecasts. The macroeconomic indicators that we are forecasting are subject to benchmark revisions, and some of the series are also subject to definitional and conceptual changes. None of these changes seem sensible to predict in a real-time forecasting exercise. Accordingly, we follow a standard convention (e.g., Tulip [2005] and Faust & Wright [2009]), which is to measure actual realized values from the data as recorded in the real-time data set of the Philadelphia Fed two quarters after the quarter to which the data refer. In general, this implies that we are comparing our forecasts to the "first final" vintage in series from the National Income and Product Accounts (NIPA).
3.3 Inference
The accuracy of the BMA forecasts is evaluated by comparing the RMSPE (root mean-square prediction error) of the BMA forecast to that obtained from a univariate autoregression:25
Unfortunately, evaluating the statistical significance of the difference in RMSPEs from BMA and the direct autoregression is complicated by the fact that the forecasts are generated by nested models. As shown by Clark & McCracken [2001], the distribution of the Diebold & Mariano [1995] test statistic under the null hypothesis of equal forecast accuracy has a nonstandard distribution in this case. Accordingly, we use a bootstrap to approximate the limiting distribution of the Diebold-Mariano statistic under the null hypothesis. In the bootstrap, the predictors are, by construction, irrelevant--nevertheless, they have time-series and cross-sectional dependence properties that are designed to mimic those of the underlying data. The resulting bootstrapped
The specific bootstrap re-sampling scheme used follows Gonçalves & Perron [2011] and Clark & McCracken [2012]. Specifically, we estimate two models: (1) a restricted model
that involves estimating an AR(4) process for ![]() ; and (2) an unrestricted model that consists of a regression of
; and (2) an unrestricted model that consists of a regression of ![]() on four lags of itself and the first three principal components of the entire predictor set. In each bootstrap replication, we then re-sample the residuals of the unrestricted model using a wild bootstrap and then construct a
bootstrap sample of
on four lags of itself and the first three principal components of the entire predictor set. In each bootstrap replication, we then re-sample the residuals of the unrestricted model using a wild bootstrap and then construct a
bootstrap sample of ![]() using these re-sampled residuals, together with the coefficients from the restricted model; see Clark & McCracken [2012]
for details. The predictor set meanwhile, is held fixed, implying that the predictors are, by construction, irrelevant for the forecasting of the dependent variable in all samples. As implemented, this bootstrap preserves any conditional heteroskedasticity in the data.26
using these re-sampled residuals, together with the coefficients from the restricted model; see Clark & McCracken [2012]
for details. The predictor set meanwhile, is held fixed, implying that the predictors are, by construction, irrelevant for the forecasting of the dependent variable in all samples. As implemented, this bootstrap preserves any conditional heteroskedasticity in the data.26
4 Results
Table 4 contains the relative out-of-sample RMSPEs of the BMA forecasts, based on the benchmark value of the shrinkage hyperparameter ![]() .
Bootstrapped
.
Bootstrapped ![]() -values testing the null hypothesis that the relative RMSPE is equal to one are shown in brackets. For real GDP growth, the RMSPEs from the BMA forecasts, relative to those from
the direct autoregression, are around 0.9 at all forecast horizons beyond the current quarter. As evidenced by the the associated
-values testing the null hypothesis that the relative RMSPE is equal to one are shown in brackets. For real GDP growth, the RMSPEs from the BMA forecasts, relative to those from
the direct autoregression, are around 0.9 at all forecast horizons beyond the current quarter. As evidenced by the the associated ![]() -values, these economically meaningful improvements in
forecast accuracy are all statistically significant, at least at the 5 percent level.
-values, these economically meaningful improvements in
forecast accuracy are all statistically significant, at least at the 5 percent level.
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 0.96 | 0.90 | 0.87 | 0.88 | 0.87 |
| GDP [p-value] | [0.03] | [0.01] | [0.01] | [0.02] | [0.02] |
| Personal consumption expenditures | 0.88 | 0.90 | 0.97 | 1.03 | 1.06 |
| Personal consumption expenditures [p-value] | [0.01] | [0.02] | [0.12] | [0.28] | [0.35] |
| Business fixed investment | 0.94 | 0.84 | 0.90 | 0.90 | 0.88 |
| Business fixed investment [p-value] | [0.01] | [0.00] | [0.01] | [0.02] | [0.01] |
| Industrial production | 0.96 | 0.92 | 0.93 | 0.92 | 0.91 |
| Industrial production [p-value] | [0.02] | [0.02] | [0.04] | [0.05] | [0.05] |
| Private employment | 0.92 | 0.86 | 0.90 | 0.90 | 0.88 |
| Private employment [p-value] | [0.00] | [0.00] | [0.02] | [0.02] | [0.01] |
| Unemployment rate | 0.95 | 0.87 | 0.86 | 0.87 | 0.88 |
| Unemployment rate [p-value] | [0.01] | [0.00] | [0.00] | [0.01] | [0.02] |
| Exports | 0.98 | 0.95 | 0.93 | 0.98 | 1.00 |
| Exports [p-value] | [0.00] | [0.00] | [0.00] | [0.03] | [0.10] |
| Imports | 0.94 | 0.92 | 0.93 | 0.93 | 0.94 |
| Imports [p-value] | [0.00] | [0.00] | [0.02] | [0.04] | [0.05] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a direct autoregression; the autoregressive benchmark is also included in the set of candidate models. Bootstrapped
The relative accuracy of BMA in forecasting output growth appears to reflect, in part, its ability to predict the growth of business fixed investment. In addition, BMA also does well in forecasting the external dimension of U.S. economic performance, namely the growth of both exports and imports. Personal consumption expenditures, in contrast, are considerably less predictable. Although BMA is noticeably more accurate than the direct autoregression in forecasting consumption growth over the very near term, the relative RMSPEs are statistically indistinguishable from one at the two- to four-quarter-ahead horizons. This result may reflect the fact that optimal consumption smoothing generally implies very little predictability of consumption growth, even if other more cyclical components of aggregate demand are forecastable.
Our BMA setup also implies economically and statistically significant gains in accuracy when predicting the growth of industrial production and changes in labor market conditions at both the near- and longer-term forecast horizons. In the case of industrial production, the relative RMSPEs lie between 0.9 and 0.96, improvements that are borderline statistically significant. The relative RMSPEs in the case of employment growth and changes in the unemployment rate are mostly around 0.88, values that are all significantly below one at a 5 percent significance level.27
Note that the benchmark to which we compared the accuracy of our BMA forecasts is a simple univariate autoregression. Another, even simpler, possible benchmark is given by a constant forecast, which is equal to the real-time sample average of the variable being predicted at all horizons. As it turns out, for sample periods dominated by the "Great Moderation," a constant forecast is a relatively good benchmark because the macroeconomic indicators considered in our exercise seem to have contained little forecastable variation during this period. The counterpart to Table 4 using this alternative benchmark is in Appendix D. The upshot of those results is that our BMA forecasts of cyclically-sensitive indicators of economic activity still deliver economically and statistically significant reductions in RMSPEs relative to the constant forecast benchmark.
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 |
| GDP [p-value] | [0.11] | [0.13] | [0.14] | [0.15] | [0.14] |
| Personal consumption expenditures | 0.97 | 0.96 | 0.99 | 1.03 | 1.06 |
| Personal consumption expenditures [p-value] | [0.14] | [0.11] | [0.21] | [0.32] | [0.40] |
| Business fixed investment | 0.95 | 0.95 | 0.95 | 0.97 | 0.94 |
| Business fixed investment [p-value] | [0.01] | [0.04] | [0.05] | [0.09] | [0.05] |
| Industrial production | 0.99 | 1.02 | 1.05 | 1.05 | 1.04 |
| Industrial production [p-value] | [0.09] | [0.52] | [0.67] | [0.53] | [0.33] |
| Private employment | 0.98 | 1.00 | 1.05 | 1.06 | 1.03 |
| Private employment [p-value] | [0.07] | [0.26] | [0.58] | [0.51] | [0.24] |
| Unemployment rate | 0.97 | 0.97 | 1.02 | 1.05 | 1.04 |
| Unemployment rate [p-value] | [0.01] | [0.03] | [0.36] | [0.51] | [0.31] |
| Exports | 0.97 | 1.02 | 1.02 | 1.02 | 1.01 |
| Exports [p-value] | [0.00] | [0.61] | [0.32] | [0.27] | [0.19] |
| Imports | 0.96 | 0.97 | 1.01 | 1.04 | 1.04 |
| Imports [p-value] | [0.00] | [0.04] | [0.16] | [0.28] | [0.26] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a direct autoregression; the autoregressive benchmark is also included in the set of candidate models. Bootstrapped
Overall, our first set of results indicates that for forecasting a range of real economic activity indicators, BMA--with (option-adjusted) portfolio credit spreads in the set of predictors--yields improvements relative to the univariate autoregressive benchmark that are both economically and statistically significant. The gains in forecasting accuracy are most pronounced for cyclically-sensitive indicators of economic activity, such as the growth of business fixed investment and industrial production, as well as for indicators measuring changes in labor market conditions.28
To gauge more precisely the information content of credit spreads in predicting economic activity, we repeat the above analysis, except that we exclude the 20 models that utilize the credit spreads in the DD-based bond portfolios from the pool of prediction models. As shown in Table 5, very few of the entries are less than 0.97, and, especially at longer forecast horizons, most relative RMSPEs are greater than one. This finding is consistent with the standard result that a majority of forecasting methods perform about as well as a univariate autoregression. These results also illustrate a sense of how the information content of our portfolio-based credit spread indexes differs from that of the other real and asset market indicators in the predictor set: When assigning the weight to a predictor using only information available at the time of the forecast, the BMA method singles out the portfolio-based credit spreads and is able to exploit their predictive ability for future economic activity to improve significantly upon the benchmark forecast.
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 0.94 | 0.91 | 0.90 | 0.94 | 0.97 |
| GDP [p-value] | [0.00] | [0.00] | [0.01] | [0.02] | [0.06] |
| Personal consumption expenditures | 0.87 | 0.86 | 0.95 | 0.98 | 1.04 |
| Personal consumption expenditures [p-value] | [0.00] | [0.00] | [0.07] | [0.13] | [0.30] |
| Business fixed investment | 0.92 | 0.83 | 0.90 | 0.90 | 0.91 |
| Business fixed investment [p-value] | [0.00] | [0.00] | [0.01] | [0.02] | [0.02] |
| Industrial production | 0.94 | 0.91 | 0.94 | 0.94 | 0.92 |
| Industrial production [p-value] | [0.01] | [0.01] | [0.05] | [0.07] | [0.07] |
| Private employment | 0.91 | 0.86 | 0.90 | 0.89 | 0.86 |
| Private employment [p-value] | [0.00] | [0.00] | [0.00] | [0.01] | [0.01] |
| Unemployment rate | 0.91 | 0.86 | 0.85 | 0.86 | 0.87 |
| Unemployment rate [p-value] | [0.00] | [0.00] | [0.00] | [0.00] | [0.00] |
| Exports | 0.98 | 0.97 | 0.99 | 1.05 | 1.10 |
| Exports [p-value] | [0.00] | [0.00] | [0.02] | [0.36] | [0.56] |
| Imports | 0.93 | 0.89 | 0.90 | 0.92 | 0.93 |
| Imports [p-value] | [0.00] | [0.00] | [0.01] | [0.05] | [0.08] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a direct autoregression; the autoregressive benchmark is also included in the set of candidate models. Bootstrapped
Another way to highlight the predictive ability of credit spreads is shown in Table 6, which contains the results of the forecasting exercise based only on models that include portfolio credit spreads as predictors. These results are very similar to those reported in Table 4, which utilize the information content of the entire predictor set. Although restricting the predictor set to only DD-based portfolios of credit spreads leads to some loss of predictive accuracy for real GDP growth, it actually improves the accuracy of the BMA forecasts for labor market indicators and business fixed investment. Because the autoregressive benchmark is embedded in all of these forecasting exercises, the results in Tables 5-6 together imply that any forecasting gains over the univariate autoregression are due predominantly to the information content of credit spreads in our DD-based portfolios.
4.1 Which Predictors are the Most Informative?
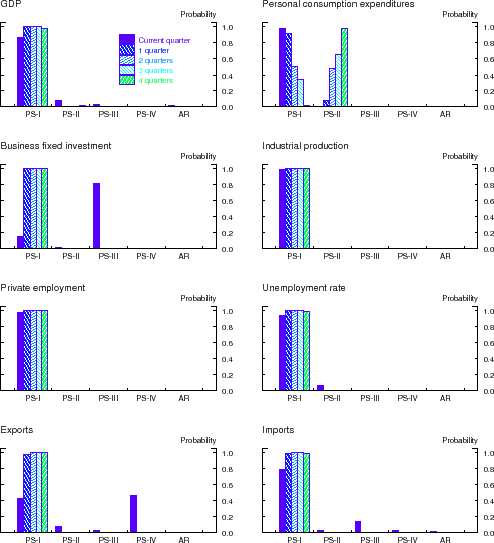
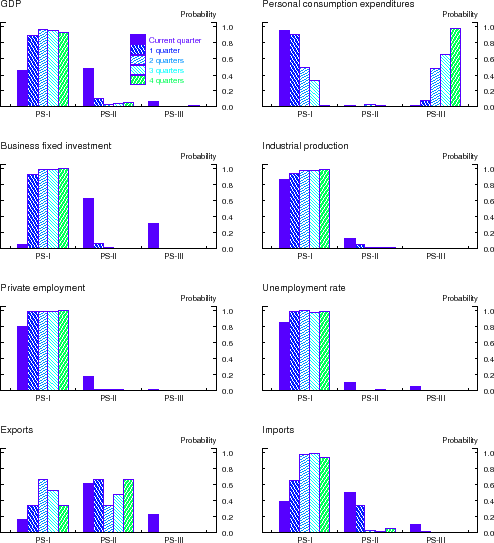
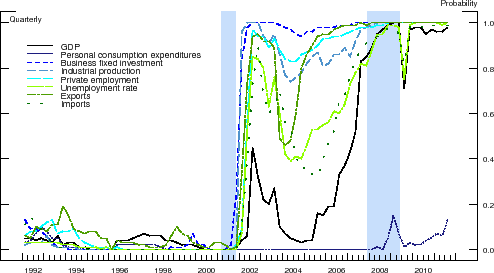
The vertical bars in the panels of Figure 4 depict the final total weights--that is, the sum of posterior probabilities--that BMA assigns to variables in the following predictor subsets: PS-I = option-adjusted credit spreads in the 20 DD-based bond portfolios; PS-II = macroeconomic variables; PS-III = other interest rates and interest rate spreads; and PS-IV = all other asset market indicators. Lastly, the AR bucket in each panel represent the final posterior probabilities that BMA assigned to the autoregressive benchmark. Results are shown for all the forecast horizons considered and for each of the eight different indicators of economic activity. Note that, by construction, these probabilities sum up to one at each forecast horizon.
These results provide a visual confirmation of the information content of the option-adjusted credit spreads in our DD-based bond portfolios. With the exception of consumption growth, BMA assigns the vast majority of the posterior weight to credit spreads in the DD-based portfolios. But even in
that case, most of the posterior weight for the near-term forecasts of the growth in real PCE (i.e., ![]() ) is assigned to the portfolio credit spreads; at longer horizons (i.e.,
) is assigned to the portfolio credit spreads; at longer horizons (i.e.,
![]() ), BMA forecasts of consumption growth assign some weight to the macroeconomic variables, but the accuracy of these forecasts is, according to Table 4, statistically indistinguishable from those made by the benchmark autoregression.
), BMA forecasts of consumption growth assign some weight to the macroeconomic variables, but the accuracy of these forecasts is, according to Table 4, statistically indistinguishable from those made by the benchmark autoregression.
It should be emphasized, however, that Figure 4 shows the posterior probabilities for the different subsets of predictors as of 2011:Q3, that is, at the end of our sample period. In our real-time forecasting exercise, these posterior probabilities were updated each time a new forecast was made and thus, in principle, could have changed over time. Figure 5 illustrates how these probabilities evolved over time. Specifically, for each indicator of economic activity, the figure plots the total posterior weight attributed to the option-adjusted credit spreads in the 20 DD-based portfolios against the time that the forecast was made. (To conserve space, we show the posterior probabilities for the four-quarter-ahead forecast horizon only.)
In line with the specified prior, forecasts made in the 1990s assigned very little weight to the portfolio credit spreads. The macroeconomic outcomes during the 2000-01 cyclical downturn led BMA to significantly increase--relative to other predictors--the posterior weight on the portfolio credit spreads, a pattern that was further reinforced by the 2007-09 financial crisis. In fact, by the end of our sample period, BMA assigns the vast majority of the posterior weight to the information content of credit spreads in the DD-based portfolios, a result consistent with those shown in Figure 4. However, it is important to note that during the 1990s--a portion of the sample sample period that is included in the forecast evaluation--the real-time BMA forecasts of economic activity based on the entire predictor set would have differed markedly from those based only on the credit spreads.
Note: The figure depicts the sum of final (as of 2011:Q3) posterior probabilities that BMA assigns to variables in the following predictor subsets: PS-I = option-adjusted credit spreads in the 20 DD-based bond portfolios; PS-II = macroeconomic variables; PS-III = other interest rates and interest rate spreads; and PS-IV = all other asset market indicators; the bars in the AR bucket represent the final posterior probabilities that BMA assigned to the autoregressive benchmark.The time-series evolution of posterior weights is important because the prediction of cyclical turning points is of special interest in many forecasting applications. As emphasized by Philippon [2009], the anticipation of rising defaults associated with economic downturns may make corporate bond spreads a particularly timely indicator of an incipient recession. The result is also consistent with the recent work by Gertler & Kiyotaki [2010], Gertler & Karadi [2011], Brunnermeier & Sannikov [2011], and He & Krishnamurthy [2012], who introduce macroeconomic models in which shocks to the value of assets held by financial intermediaries--by reducing the supply of credit--have independent effects on the real economy.
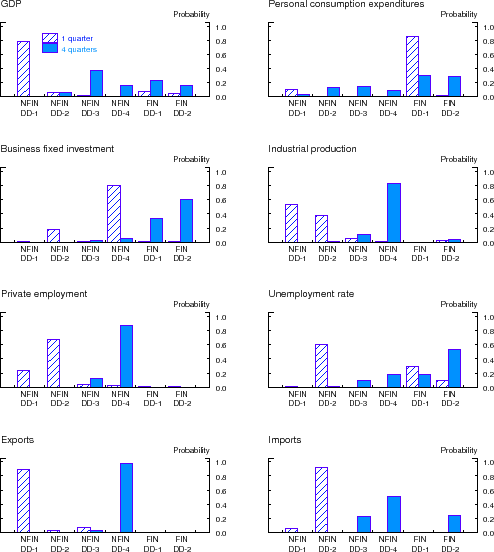
Next, we examine the posterior weights implied by the forecasting exercise shown in Table 5, a case in which the predictor set includes only the option-adjusted credit spreads in the 20 DD-based bond portfolios. Figure 6 depicts the total final posterior probabilities that BMA assigns to nonfinancial portfolios in each DD quartile (NFIN-DD1, NFIN-DD2, NFIN-DD3, and NFIN-DD4) and the posterior probabilities assigned to the financial portfolios in the two halves of the DD distribution (FIN-DD1 and FIN-DD2). Results are shown for the one-quarter-ahead and four-
Note: The figure depicts the sum of final (as of 2011:Q3) posterior probabilities that BMA assigns to the option-adjusted credit spreads in the DD-based bond portfolios. The results shown are for the case in which the predictor set includes only the option-adjusted credit spreads in the 20 DD-based bond portfolios (see Table 6). The posterior probabilities for maturity categories within each DD bin--four in the case of nonfinancial portfolios and two in the case of financial portfolios--have been added together.quarter-ahead forecast horizons only. For the ease of presentation, we also summed up the posterior probabilities across the maturity categories within each DD-based portfolio--by construction, therefore, these six posterior probabilities must sum to one.
In forecasting economic activity over the subsequent quarter (i.e., ![]() ), BMA tends to place most posterior weight on credit spreads based on portfolios that contain bonds issued by
nonfinancial firms. At the four-quarter-ahead forecast horizon, in contrast, the posterior probabilities are concentrated on credit spreads based on portfolios that contain bonds issued by financial firms in the lower half of the credit-quality spectrum; though not reported, most of that posterior
probability is assigned to portfolios that contain longer maturity bonds (i.e., FIN-DD1-MTY2).
), BMA tends to place most posterior weight on credit spreads based on portfolios that contain bonds issued by
nonfinancial firms. At the four-quarter-ahead forecast horizon, in contrast, the posterior probabilities are concentrated on credit spreads based on portfolios that contain bonds issued by financial firms in the lower half of the credit-quality spectrum; though not reported, most of that posterior
probability is assigned to portfolios that contain longer maturity bonds (i.e., FIN-DD1-MTY2).
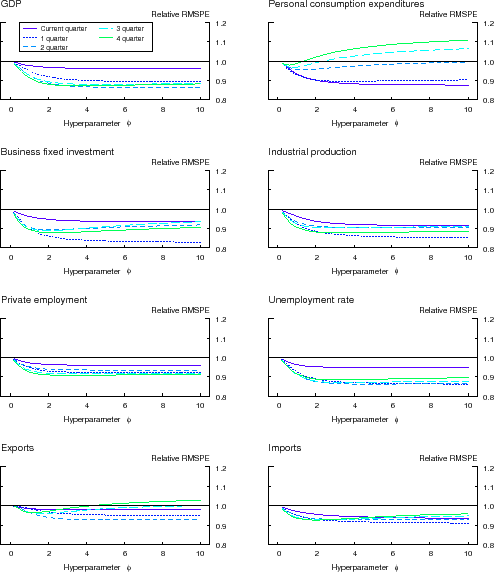
4.2 Robustness Checks
The appendixes at the end of the paper contain a number of robustness checks. The results reported thus far have been based on the value of the shrinkage hyperparameter ![]() . In
Appendix H, we show that our BMA forecasts generate relative RMSPEs that are less than one for a wide range of choices of
. In
Appendix H, we show that our BMA forecasts generate relative RMSPEs that are less than one for a wide range of choices of ![]() .
.
Appendix A reports BMA forecasting results that rely on different forms of empirical option-adjustment techniques when constructing DD-based portfolios, as well as for the case when we construct the portfolios using raw (i.e., unadjusted) credit spreads. In general, we find that the BMA forecasts that use raw credit spreads continue to be more accurate--at least at shorter horizons--than the forecasts obtained from direct autoregressions. However, the gains in predictive accuracy are neither as large nor as consistent as those based on the option-adjusted credit spreads.
These results suggest that the information content of credit spreads on corporate bonds is significantly influenced by fluctuations in the values of embedded options. Given that the widely-used credit spread indexes (e.g., the Baa-Aaa and the "high-yield" spreads) are constructed using prices on both callable and non-callable bonds and that the portion of callable corporate debt is changing over time, this may also help explain the uneven forecasting performance of standard credit spread indexes for future economic activity.
5 When Do Credit Spreads Forecast Best?
Predictive relationships between economic variables may be episodic, performing better at some times than at others; see, for example, Stock & Watson [2009] and Rossi [2012]. Therefore, it seems natural to ask if the ability of credit spreads to forecast economic activity owes its performance to recessions, expansions, or both. To formally examine this question, we consider the relative RMSPEs of the BMA forecasts over two different subsamples: (1) forecasts made for quarters that turned out to fall into NBER-dated contractions; and (2) forecasts made for quarters that turned out to fall into NBER-dated expansions. When creating these two subsamples, we use the standard
| Economic Activity Indicator | 0 quarter forecast horizon (NBER-Dated Expansions) | 1 quarter forecast horizon (NBER-Dated Expansions) | 2 quarter forecast horizon (NBER-Dated Expansions) | 3 quarter forecast horizon (NBER-Dated Expansions) | 4 quarter forecast horizon (NBER-Dated Expansions) | 0 quarter forecast horizon NBER-Dated Contractions | 1 quarter forecast horizon NBER-Dated Contractions | 2 quarter forecast horizon NBER-Dated Contractions | 3 quarter forecast horizon NBER-Dated Contractions | 4 quarter forecast horizon NBER-Dated Contractions |
| GDP | 1.03 | 1.05 | 1.03 | 0.91 | 0.87 | 0.88 | 0.74 | 0.71 | 0.85 | 0.92 |
| GDP [p-value] | [0.93] | [0.80] | [0.34] | [0.02] | [0.01] | [0.16] | [0.09] | [0.11] | [0.28] | [0.35] |
| Personal consumption expenditures | 0.97 | 0.99 | 0.92 | 0.94 | 1.03 | 0.73 | 0.80 | 1.01 | 1.12 | 1.11 |
| Personal consumption expenditures [p-value] | [0.13] | [0.24] | [0.05] | [0.08] | [0.26] | [0.06] | [0.19] | [0.48] | [0.60] | [0.59] |
| Business fixed investment | 0.94 | 0.87 | 0.97 | 0.87 | 0.88 | 0.94 | 0.76 | 0.78 | 0.84 | 0.83 |
| Business fixed investment [p-value] | [0.01] | [0.01] | [0.08] | [0.02] | [0.02] | [0.20] | [0.12] | [0.12] | [0.24] | [0.26] |
| Industrial production | 1.00 | 1.03 | 1.09 | 1.02 | 0.97 | 0.92 | 0.84 | 0.85 | 0.87 | 0.89 |
| Industrial production [p-value] | [0.19] | [0.54] | [0.82] | [0.26] | [0.11] | [0.07] | [0.10] | [0.15] | [0.24] | [0.28] |
| Private employment | 0.98 | 1.02 | 1.07 | 1.01 | 0.93 | 0.88 | 0.70 | 0.75 | 0.77 | 0.82 |
| Private employment [p-value] | [0.08] | [0.41] | [0.59] | [0.14] | [0.05] | [0.02] | [0.02] | [0.13] | [0.24] | [0.28] |
| Unemployment rate | 1.02 | 1.03 | 1.06 | 0.98 | 0.90 | 0.87 | 0.77 | 0.73 | 0.77 | 0.86 |
| Unemployment rate [p-value] | [0.88] | [0.61] | [0.64] | [0.08] | [0.03] | [0.02] | [0.03] | [0.05] | [0.09] | [0.20] |
| Exports | 1.01 | 1.04 | 1.03 | 1.05 | 1.06 | 0.95 | 0.88 | 0.84 | 0.86 | 0.85 |
| Exports [p-value] | [0.54] | [0.78] | [0.29] | [0.39] | [0.37] | [0.09] | [0.07] | [0.12] | [0.20] | [0.22] |
| Imports | 0.95 | 0.97 | 1.02 | 0.97 | 0.98 | 0.95 | 0.89 | 0.87 | 0.91 | 0.92 |
| Imports [p-value] | [0.00] | [0.03] | [0.24] | [0.08] | [0.11] | [0.20] | [0.19] | [0.25] | [0.30] | [0.35] |
Note: Overall sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. The table breaks out the forecasts into two subsamples--forecasts made for quarters that turned out to fall into NBER-dated expansions (left panel) and forecasts made for quarters that turned out to fall into NBER-dated recessions (right panel). The quarters corresponding to peaks and troughs are both coded as being part of the recession. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a direct autoregression for the two subsamples. The autoregression is also included in the set of candidate models. Bootstrapped
NBER business cycle dates and code quarters corresponding to peaks and troughs as being part of the recession.
Clearly, this exercise is of no use to real-time economic forecasting--no forecaster ever knows whether the quarter for which the prediction is being made will turn out to be a recession or an expansion. Nevertheless, it is still useful as a diagnostic to understand, ex post of course, when the predictability of credit spreads in the DD-based portfolios arose.29 The results of this exercise are summarized in Table 7.
Depending on the measure of economic activity being predicted and the forecast horizon, the BMA forecast may be more accurate than the autoregressive benchmark during economic expansions alone. For example, the relative RMSPE of the BMA forecast is significantly below one when predicting real GDP growth and business fixed investment during economic expansions at the three- and four-quarter-ahead horizons; a similar result holds for the year-ahead change in the unemployment rate.
In economic terms, however, the estimated gains in predictive accuracy from our BMA forecasts appear to be greatest during economic downturns. During the two NBER-dated recessions in our sample, the relative RMSPEs are below one for all indicators and all horizons, with the sole exception being the growth of real PCE at longer horizons. At the same time, the recessions typically span such a short period of time that the gains in forecast accuracy during economic contractions alone are statistically significant only at shorter horizons. All told, the documented improvements in overall predictive accuracy from BMA forecasts based on credit spreads in our DD-based portfolios appear to accrue mainly, though not exclusively, in recessionary periods.
6 Conclusion
This paper has revisited the forecasting of real-time economic activity using a large number of macroeconomic and asset market indicators. Our contribution involved expanding the set of asset market indicators with credit spreads based on corporate bond portfolios sorted by the instrument's maturity and credit risk as measured by the issuer's distance-to-default. These portfolio credit spreads were constructed directly from the secondary market prices of a large number of senior unsecured bonds issued by U.S. financial and nonfinancial corporations. Using a flexible empirical credit-spread pricing framework, the micro-level credit spreads were adjusted for the callability of the underlying issue, a pervasive feature of the corporate cash market and one that significantly influences the information content of credit spreads for future economic activity.
To take explicitly into account model selection issues, we employed Bayesian model averaging techniques. Our results indicate that the accuracy of the BMA forecasts significantly exceeds--both economically and statistically--the accuracy of the forecasts obtained from a univariate direct autoregression, a benchmark that has proven to be quite difficult to beat when forecasting real-time economic activity.
The gains in forecasting accuracy stem almost exclusively from the inclusion of the option-adjusted portfolio credit spreads in the set of predictors--Bayesian model averaging consistently assigns very high posterior probabilities to models that include these asset market indicators. In contrast, if the portfolio credit spreads are omitted from the predictor set, the BMA forecasts of future economic activity are generally statistically indistinguishable from the forecasts obtained from a direct autoregression. This finding highlights the rich amount of information contained in corporate bond spreads, information, as argued by Gilchrist & Zakrajšek [2012], that may be particularly useful for identifying the importance of credit supply shocks in the determination of macroeconomic outcomes.
Although the combination of BMA and out-of-sample forecasting appreciably mitigates concerns about data mining, the sample period used in the analysis contains only three distinct recessions. Economic downturns in the United States have different causes, with factors such as monetary tightenings, oil price shocks, and bursting of asset price bubbles all having played varying roles in our historical sample. Time alone will tell how our BMA forecasts do in predicting future recessions. However, to the extent that significant disruptions in credit supply may also accompany future recessions, BMA forecasts utilizing the information content of credit spreads in our DD-based bond portfolios will likely provide a timely and informative signal regarding the evolution of cyclically-sensitive indicators of real economic activity, such as growth of business fixed investment and industrial output, as well as of changes in labor market conditions.
Bibliography
Journal of Econometrics 131(1-2):359-403.
Journal of Financial Economics 64(3):423-458.
Operational Research Quarterly 20(4):451-468.
New England Economic Review November:51-68.
In J. B. Taylor & M. Woodford (eds.), The Handbook of Macroeconomics, pp. 1341-1393. Elsevier Science B.V, Amsterdam.
Review of Financial Studies 21(3):1339-1369.
Working Paper, Dept.Economics, Princeton University.
Journal of Business and Economic Statistics 29(2):238-249.
In P. Lahiri (ed.), Model Selection, pp. 65-116. IMS Lecture Notes-Monograph Series, No.8, Beachwood, OH.
Journal of Econometrics 105(1):85-110.
Journal of Business and Economic Statistics 30(1):53-66.
Review of Financial Studies 15(4):1223-1249.
Forthcoming, Handbook of Economic Forecasting.
Journal of Business and Economic Statistics 13(3):253-263.
Economic and Financial Review, Federal Reserve Bank of Dallas Third Quarter:2-13.
Journal of Finance 53(6):225-241.
Brookings Papers on Economic Activity 41(2):209-259.
Journal of Finance 62(3):1421-1451.
Journal of Business and Economic Statistics 48(1):1-10.
Journal of Finance 46(2):555-576.
Review of Economics and Statistics 80(1):45-61.
American Economic Review 71(4):545-565.
Journal of Business and Economic Statistics 27(4):486-479.
Journal of Econometrics 100(2):381-427.
Journal of Applied Econometrics 16(5):563-576.
American Economic Review 82(3):472-492.
Review of Economics and Statistics 80(1):34-44.
Journal of Monetary Economics 58(1):17-34.
In B. M. Friedman & M. Woodford (eds.), Handbook of Macroeconomics, vol. 3, pp. 547-599. North-Holland, Elsevier, Amsterdam.
Oxford Review of Economic Policy 15(3):132-150.
Journal of Monetary Economics 56(4):471-493.
American Economic Review 102(4):1692-1720.
Working Paper, University of Montreal.
Journal of Monetary Economics 54(8):2291-2304.
Journal of Money, Credit, and Banking 34(2):340-360.
Journal of Financial Economics 22(2):305-322.
Financial Analysts Journal 45(5):38-45.
Forthcoming, American Economic Review.
Finance and Economics Discussion Series Paper 2007-57, Federal Reserve Board.
The Econometrics Journal 7(2):550-565.
John Wiley & Sons, Inc., New York, NY.
Finance and Economics Discussion Series Paper 2004-70, Federal Reserve Board.
Journal of Banking and Finance 28(3):695-720.
Journal of Fixed Income 17(1):38-47.
Bell Journal of Economics and Management Science 4(1):141-183.
Journal of Finance 29(2):449-470.
Journal of Econometrics 56(1-2):89-118.
Economic Letters 82(2):167-172.
Working Paper, London School of Economics.
Quarterly Journal of Economics 124(3):1011-1056.
Journal of the American Statistical Association 92(437):179-191.
Forthcoming, Handbook of Economic Forecasting.
American Economic Review 94(4):813-835.
In B. S. Bernanke & M. Woodford (eds.), The Inflation-Targeting Debate, vol. 32, pp. 283-310. NBER Studies in Business Cycles, Cambridge, MA.
Federal Reserve Bank of Richmond Economic Quarterly 89(3):71-90.
NBER Working Paper No.1467.
In J. Fuhrer, Y. Kodrycki, J. Little, & G. Olivei (eds.), Understanding Inflation and the Implications for Monetary Policy, pp. 99-202. The MIT Press, Cambridge.
Finance and Economics Discussion Series Paper 2005-31, Federal Reserve Board.
Working Paper, University of Houston.
Journal of Econometrics 146(2):329-341.
In P. K. Goel & A. Zellner (eds.), Bayesian Inference and Decision Techniques, pp. 233-243. North-Holland, Amsterdam, The Netherlands.
A. Different Option-Adjustment Procedures
This section reports the relative RMSPEs of BMA forecasts (as in Table 4 of the paper) using different forms of the call-option adjustment:
- (1)
- Table A-1 reports results with no option-adjustment--that is, the DD-based portfolios are constructed using raw credit spreads.
- (2)
- Table A-2 reports results without any Jensen's inequality correction--the
 term is deleted from the option adjustment.
term is deleted from the option adjustment. - (3)
- Table A-3 reports results with a time-invariant Jensen's inequality correction--the
 term in the option adjustment is replaced by
term in the option adjustment is replaced by
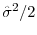 , where
, where
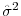 is the sample variance of the errors over all bonds and all time periods.
is the sample variance of the errors over all bonds and all time periods.
According to entries in Table A-1, BMA forecasts that use raw credit spreads continue to be more accurate than the forecasts obtained from direct autoregressions, at least at shorter horizons. Although gains in forecast accuracy are economically and statistically significant in some cases, they are neither as large nor as consistent--both across economic indicators and horizons--as those that relied on the option-adjusted credit spreads. The BMA forecasts that use option-adjusted spreads with the alternative option adjustments (Tables A-2 and A-3) have virtually identical predictive accuracy, compared with the baseline option adjustment (Table 4 of the paper). In summary, the option adjustment is important for the predictive content of credit spreads. However, how one treats the Jensen's inequality term in our regression-based option-adjustment procedure is inconsequential.
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 0.97 | 0.97 | 0.94 | 0.96 | 0.92 |
| GDP [p-value] | [0.05] | [0.06] | [0.05] | [0.07] | [0.04] |
| Personal consumption expenditures | 0.96 | 0.97 | 1.00 | 1.05 | 1.09 |
| Personal consumption expenditures [p-value] | [0.07] | [0.15] | [0.22] | [0.33] | [0.45] |
| Business fixed investment | 0.93 | 0.89 | 0.96 | 0.95 | 0.94 |
| Business fixed investment [p-value] | [0.01] | [0.01] | [0.06] | [0.05] | [0.05] |
| Industrial production | 0.97 | 0.98 | 1.05 | 1.05 | 1.05 |
| Industrial production [p-value] | [0.03] | [0.08] | [0.60] | [0.42] | [0.35] |
| Private employment | 0.96 | 0.97 | 1.04 | 1.09 | 1.06 |
| Private employment [p-value] | [0.03] | [0.07] | [0.37] | [0.49] | [0.30] |
| Unemployment rate | 0.96 | 0.97 | 1.05 | 1.09 | 1.07 |
| Unemployment rate [p-value] | [0.00] | [0.04] | [0.46] | [0.55] | [0.34] |
| Exports | 0.98 | 0.96 | 0.99 | 1.00 | 0.96 |
| Exports [p-value] | [0.00] | [0.00] | [0.02] | [0.07] | [0.03] |
| Imports | 0.95 | 0.95 | 1.00 | 1.01 | 0.99 |
| Imports [p-value] | [0.00] | [0.01] | [0.11] | [0.15] | [0.13] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a direct autoregression; the autoregressive benchmark is also included in the set of candidate models. Bootstrapped
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 0.96 | 0.90 | 0.86 | 0.88 | 0.89 |
| GDP [p-value] | [0.03] | [0.01] | [0.01] | [0.02] | [0.03] |
| Personal consumption expenditures | 0.89 | 0.91 | 0.97 | 1.02 | 1.06 |
| Personal consumption expenditures [p-value] | [0.01] | [0.03] | [0.11] | [0.27] | [0.35] |
| Business fixed investment | 0.94 | 0.82 | 0.88 | 0.86 | 0.86 |
| Business fixed investment [p-value] | [0.01] | [0.00] | [0.01] | [0.01] | [0.01] |
| Industrial production | 0.97 | 0.93 | 0.94 | 0.92 | 0.91 |
| Industrial production [p-value] | [0.03] | [0.02] | [0.04] | [0.05] | [0.06] |
| Private employment | 0.93 | 0.87 | 0.90 | 0.90 | 0.89 |
| Private employment [p-value] | [0.00] | [0.00] | [0.01] | [0.02] | [0.02] |
| Unemployment rate | 0.96 | 0.88 | 0.87 | 0.87 | 0.88 |
| Unemployment rate [p-value] | [0.01] | [0.00] | [0.00] | [0.01] | [0.02] |
| Exports | 0.98 | 0.95 | 0.92 | 0.96 | 0.98 |
| Exports [p-value] | [0.00] | [0.00] | [0.00] | [0.01] | [0.06] |
| Imports | 0.95 | 0.93 | 0.94 | 0.94 | 0.95 |
| Imports [p-value] | [0.00] | [0.00] | [0.03] | [0.05] | [0.08] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a direct autoregression; the autoregressive benchmark is also included in the set of candidate models. Bootstrapped
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 0.96 | 0.90 | 0.86 | 0.86 | 0.86 |
| GDP [p-value] | [0.03] | [0.01] | [0.01] | [0.02] | [0.02] |
| Personal consumption expenditures | 0.88 | 0.88 | 0.94 | 1.01 | 1.06 |
| Personal consumption expenditures [p-value] | [0.01] | [0.02] | [0.08] | [0.22] | [0.35] |
| Business fixed investment | 0.94 | 0.82 | 0.87 | 0.87 | 0.87 |
| Business fixed investment [p-value] | [0.01] | [0.00] | [0.00] | [0.01] | [0.01] |
| Industrial production | 0.96 | 0.93 | 0.91 | 0.90 | 0.90 |
| Industrial production [p-value] | [0.03] | [0.02] | [0.03] | [0.04] | [0.06] |
| Private employment | 0.93 | 0.87 | 0.90 | 0.90 | 0.88 |
| Private employment [p-value] | [0.00] | [0.00] | [0.01] | [0.02] | [0.01] |
| Unemployment rate | 0.96 | 0.88 | 0.86 | 0.85 | 0.87 |
| Unemployment rate [p-value] | [0.01] | [0.00] | [0.00] | [0.00] | [0.01] |
| Exports | 0.98 | 0.95 | 0.93 | 0.97 | 0.99 |
| Exports [p-value] | [0.00] | [0.00] | [0.00] | [0.02] | [0.06] |
| Imports | 0.95 | 0.93 | 0.92 | 0.92 | 0.93 |
| Imports [p-value] | [0.00] | [0.00] | [0.02] | [0.03] | [0.05] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a direct autoregression; the autoregressive benchmark is also included in the set of candidate models. Bootstrapped
B. Raw vs. Option-Adjusted Credit Spreads
One of the aims of the paper was to demonstrate that by using "cleaner" measures of credit spreads, one is able to improve on real-time forecasts of economic activity, as well as to point out that the well-documented uneven forecasting performance of standard credit spread indexes (i.e., the Baa-Aaa and the "junk" spreads) might reflect contamination induced by swings in the values of embedded options. This appendix compares the information content of raw credit spreads with that of their option-adjusted counterparts. In particular, the vertical bars in the panels of Figure B-1 depict the final total weights--that is, the sum of posterior probabilities--that BMA assigns to variables in the following predictor subsets: PS-I = option-adjusted credit spreads in the 20 DD-based bond portfolios; PS-II = raw credit spreads in the 20 DD-based bond portfolios; and PS-III = all other predictors (this subset of models also includes the autoregressive benchmark). Results are shown for all the forecast horizons considered and for each of the eight different indicators of economic activity. Note that, by construction, these probabilities sum up to one at each forecast horizon.
These results provide a visual confirmation of the fact that information content of the option-adjusted credit spreads consistently exceeds that of raw credit spreads, especially for cyclically-sensitive indicators of economic activity and at horizons extending beyond the very near term.
Note: The figure depicts the sum of final (as of 2011:Q3) posterior probabilities that BMA assigns to variables in the following predictor subsets: PS-I = option-adjusted credit spreads in the 20 DD-based bond portfolios; PS-II = raw credit spreads in the 20 DD-based bond portfolios; and PS-III = all other predictors (this subset of models also includes the autoregressive benchmark).C. BMA Forecasts With the Median Credit Spread
This appendix reports the relative RMSPEs of BMA forecasts (as in Table 4 of the paper) that use only the median credit spread of our 24 DD-based bond portfolios, rather than all the 24 credit spreads. According to the entries in Table C-1, the resulting BMA forecasts continue to be more accurate than the forecasts obtained from direct autoregressions. The predictive gains, however, are smaller than those from the corresponding forecasts that included all the portfolio-based credit spreads.
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 0.98 | 0.96 | 0.94 | 0.95 | 0.95 |
| GDP [p-value] | [0.10] | [0.06] | [0.07] | [0.08] | [0.10] |
| Personal consumption expenditures | 0.95 | 0.96 | 0.99 | 1.03 | 1.06 |
| Personal consumption expenditures [p-value] | [0.05] | [0.09] | [0.21] | [0.31] | [0.38] |
| Business fixed investment | 0.95 | 0.85 | 0.85 | 0.86 | 0.86 |
| Business fixed investment [p-value] | [0.01] | [0.00] | [0.00] | [0.01] | [0.01] |
| Industrial production | 0.97 | 0.93 | 0.92 | 0.91 | 0.92 |
| Industrial production [p-value] | [0.03] | [0.02] | [0.03] | [0.04] | [0.06] |
| Private employment | 0.98 | 0.94 | 1.01 | 1.06 | 1.04 |
| Private employment [p-value] | [0.03] | [0.02] | [0.24] | [0.44] | [0.26] |
| Unemployment rate | 0.96 | 0.94 | 0.99 | 1.02 | 1.03 |
| Unemployment rate [p-value] | [0.01] | [0.00] | [0.10] | [0.27] | [0.26] |
| Exports | 0.98 | 1.05 | 1.05 | 1.03 | 1.02 |
| Exports [p-value] | [0.00] | [0.93] | [0.73] | [0.35] | [0.23] |
| Imports | 0.95 | 0.93 | 0.93 | 0.90 | 0.92 |
| Imports [p-value] | [0.00] | [0.00] | [0.02] | [0.02] | [0.04] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a direct autoregression; the autoregressive benchmark is also included in the set of candidate models. Bootstrapped
D. Alternative Benchmark
This appendix reports the RMSPEs of BMA forecasts (as in Table 4 of the paper), relative to the benchmark of a constant forecast, which is equal to the real-time sample average of the variable being predicted at all horizons. According to the entries in Table D-1, the BMA forecasts incorporating the information content of option-adjusted credit spreads in the DD-based portfolios again generally do better than this very simple benchmark.
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 0.89 | 0.85 | 0.83 | 0.85 | 0.85 |
| GDP [p-value] | [0.00] | [0.01] | [0.01] | [0.03] | [0.02] |
| Personal consumption expenditures | 0.85 | 0.85 | 0.89 | 0.98 | 1.03 |
| Personal consumption expenditures [p-value] | [0.08] | [0.17] | [0.27] | [0.38] | [0.44] |
| Business fixed investment | 0.81 | 0.72 | 0.79 | 0.82 | 0.84 |
| Business fixed investment [p-value] | [0.00] | [0.00] | [0.00] | [0.02] | [0.02] |
| Industrial production | 0.90 | 0.90 | 0.93 | 0.92 | 0.90 |
| Industrial production [p-value] | [0.00] | [0.02] | [0.05] | [0.06] | [0.05] |
| Private employment | 0.48 | 0.53 | 0.62 | 0.66 | 0.68 |
| Private employment [p-value] | [0.03] | [0.03] | [0.05] | [0.05] | [0.05] |
| Unemployment rate | 0.80 | 0.74 | 0.77 | 0.80 | 0.82 |
| Unemployment rate [p-value] | [0.00] | [0.00] | [0.00] | [0.00] | [0.01] |
| Exports | 0.94 | 0.95 | 0.94 | 0.99 | 1.01 |
| Exports [p-value] | [0.03] | [0.00] | [0.00] | [0.20] | [0.29] |
| Imports | 0.92 | 0.96 | 0.94 | 0.97 | 0.99 |
| Imports [p-value] | [0.44] | [0.22] | [0.03] | [0.07] | [0.10] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a constant forecast (i.e., a forecast that is set equal to the recursively estimated real-time sample mean at all horizons); the constant forecast is also included in the set of candidate models. Bootstrapped
E. Alternative Bootstrap
This appendix reports the relative RMSPEs of BMA forecasts (as in Table 4 of the paper), except that the ![]() -values of the null hypothesis of equal predictive accuracy use a different
bootstrap procedure.
-values of the null hypothesis of equal predictive accuracy use a different
bootstrap procedure.
This alternative bootstrap involves fitting an AR(4) process to ![]() and separately estimating a dynamic factor model using the set of all predictors
and separately estimating a dynamic factor model using the set of all predictors ![]() :
:
and
where the elements of the vector
Entries in Table E-1 shows the relative RMSPEs of our BMA forecasts, exactly as in Table 4, except using these alternative ![]() -values; these alternative
-values; these alternative
![]() -values are quite similar to those reported in the paper.
-values are quite similar to those reported in the paper.
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 0.96 | 0.90 | 0.87 | 0.88 | 0.87 |
| GDP [p-value] | [0.01] | [0.00] | [0.00] | [0.01] | [0.01] |
| Personal consumption expenditures | 0.88 | 0.90 | 0.97 | 1.03 | 1.06 |
| Personal consumption expenditures [p-value] | [0.00] | [0.01] | [0.11] | [0.49] | [0.70] |
| Business fixed investment | 0.94 | 0.84 | 0.90 | 0.90 | 0.88 |
| Business fixed investment [p-value] | [0.00] | [0.00] | [0.00] | [0.01] | [0.01] |
| Industrial production | 0.96 | 0.92 | 0.93 | 0.92 | 0.91 |
| Industrial production [p-value] | [0.00] | [0.00] | [0.02] | [0.02] | [0.02] |
| Private employment | 0.92 | 0.86 | 0.90 | 0.90 | 0.88 |
| Private employment [p-value] | [0.00] | [0.00] | [0.00] | [0.01] | [0.01] |
| Unemployment rate | 0.95 | 0.87 | 0.86 | 0.87 | 0.88 |
| Unemployment rate [p-value] | [0.00] | [0.00] | [0.00] | [0.00] | [0.00] |
| Exports | 0.98 | 0.95 | 0.93 | 0.98 | 1.00 |
| Exports [p-value] | [0.02] | [0.00] | [0.00] | [0.07] | [0.16] |
| Imports | 0.94 | 0.92 | 0.93 | 0.93 | 0.94 |
| Imports [p-value] | [0.00] | [0.00] | [0.02] | [0.03] | [0.04] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a direct autoregression; the autoregressive benchmark is also included in the set of candidate models. Bootstrapped
F. Forecasting With the Term Spread and the Paper-Bill Spread
This appendix reports the relative RMSPEs of forecasts that use--in addition to the lags of the variable being forecasted--either the 10y/3m term spread or the paper-bill spread as predictor. Table F-1 reports the results using the term spread, while Table 15 reports the results using the paper-bill spread.
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 |
| GDP [p-value] | [0.44] | [0.24] | [0.21] | [0.21] | [0.21] |
| Personal consumption expenditures | 1.00 | 1.01 | 1.02 | 1.03 | 1.03 |
| Personal consumption expenditures [p-value] | [0.39] | [0.52] | [0.48] | [0.54] | [0.52] |
| Business fixed investment | 0.99 | 0.99 | 0.98 | 0.98 | 0.97 |
| Business fixed investment [p-value] | [0.19] | [0.16] | [0.13] | [0.12] | [0.11] |
| Industrial production | 0.99 | 1.00 | 1.00 | 0.99 | 0.98 |
| Industrial production [p-value] | [0.09] | [0.15] | [0.15] | [0.09] | [0.08] |
| Private employment | 1.00 | 1.00 | 1.01 | 1.00 | 0.99 |
| Private employment [p-value] | [0.26] | [0.22] | [0.24] | [0.19] | [0.13] |
| Unemployment rate | 1.01 | 1.01 | 1.01 | 1.00 | 0.98 |
| Unemployment rate [p-value] | [0.71] | [0.49] | [0.27] | [0.18] | [0.11] |
| Exports | 1.02 | 1.03 | 1.04 | 1.05 | 1.07 |
| Exports [p-value] | [0.98] | [0.91] | [0.88] | [0.88] | [0.86] |
| Imports | 0.99 | 0.99 | 0.99 | 0.98 | 0.96 |
| Imports [p-value] | [0.07] | [0.12] | [0.12] | [0.10] | [0.07] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the forecast using a direct autoregression augmented with the term spread (10-year less 3-month Treasury yield) to the forecast using the unaugmented direct autoregression. Bootstrapped
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP | 1.05 | 1.04 | 1.09 | 1.08 | 1.09 |
| GDP [p-value] | [1.00] | [0.98] | [1.00] | [0.99] | [0.99] |
| Personal consumption expenditures | 0.97 | 1.03 | 1.04 | 1.05 | 1.05 |
| Personal consumption expenditures [p-value] | [0.04] | [0.92] | [0.92] | [0.91] | [0.88] |
| Business fixed investment | 0.95 | 1.00 | 1.01 | 1.02 | 1.02 |
| Business fixed investment [p-value] | [0.0] | [0.32] | [0.49] | [0.61] | [0.60] |
| Industrial production | 1.00 | 0.97 | 1.01 | 1.02 | 1.02 |
| Industrial production [p-value] | [0.18] | [0.11] | [0.61] | [0.60] | [0.51] |
| Private employment | 0.98 | 0.99 | 1.03 | 1.05 | 1.05 |
| Private employment [p-value] | [0.06] | [0.14] | [0.72] | [0.83] | [0.80] |
| Unemployment rate | 0.98 | 0.98 | 1.00 | 1.02 | 1.02 |
| Unemployment rate [p-value] | [0.03] | [0.06] | [0.48] | [0.67] | [0.72] |
| Exports | 1.01 | 1.07 | 1.07 | 1.08 | 1.07 |
| Exports [p-value] | [0.50] | [0.97] | [0.98] | [1.00] | [0.99] |
| Imports | 0.95 | 0.94 | 0.97 | 0.99 | 0.99 |
| Imports [p-value] | [0.00] | [0.01] | [0.09] | [0.22] | [0.26] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate (or change in the case of unemployment rate) of each economic activity indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the forecast using a direct autoregression augmented with the 3-month paper-bill spread to the forecast using the unaugmented direct autoregression. Bootstrapped
G. BMA Forecasts of Inflation
This appendix reports the relative RMSPEs of our BMA forecasts (as in Table 4 of the paper), but where the variable being forecasted is inflation, measured either by the GDP price deflator or the CPI. According to the entries in Table G-1, our BMA forecasts do not improve on the autoregressive benchmark.
| Economic Activity Indicator | 0 quarter forecast horizon | 1 quarter forecast horizon | 2 quarter forecast horizon | 3 quarter forecast horizon | 4 quarter forecast horizon |
| GDP price deflator | 1.00 | 1.00 | 1.01 | 1.01 | 1.02 |
| GDP price deflator [p-value] | [0.53] | [0.52] | [0.44] | [0.37] | [0.36] |
| CPI | 1.00 | 1.02 | 1.02 | 1.01 | 1.02 |
| CPI [p-value] | [0.40] | [0.66] | [0.35] | [0.27] | [0.26] |
Note: Sample period: 1986:Q1-2011:Q3. The jump-off date for the out-of-sample recursive forecasts is 1992:Q1. The forecasted variable is the cumulative growth rate of each inflation indicator over the specified forecast horizon. Entries in the table denote the ratio of the RMSPE from the BMA forecast to the RMSPE from a direct autoregression; the autoregressive benchmark is also included in the set of candidate models. Bootstrapped
H. Varying the Hyperparameter 
The results reported in the paper were based on the value of the shrinkage hyperparameter ![]() . This appendix examines the robustness of our results to different values of
. This appendix examines the robustness of our results to different values of ![]() , the parameter governing the strength of the
, the parameter governing the strength of the ![]() -prior. Figure H-1
plots the out-of-sample RMSPE of the BMA forecast--relative to the RMSPE from a direct autoregression--as a function of
-prior. Figure H-1
plots the out-of-sample RMSPE of the BMA forecast--relative to the RMSPE from a direct autoregression--as a function of ![]() for all six economic indicators and all five forecast horizons.
Our BMA forecasting setup delivers substantial gains in forecast accuracy relative to the direct autoregression for a wide range of values of
for all six economic indicators and all five forecast horizons.
Our BMA forecasting setup delivers substantial gains in forecast accuracy relative to the direct autoregression for a wide range of values of ![]() ; in fact, the qualitative nature of our
results appears to be fairly insensitive to the choice of the shrinkage parameter. In some cases, the relative RMSPE decreases monotonically in
; in fact, the qualitative nature of our
results appears to be fairly insensitive to the choice of the shrinkage parameter. In some cases, the relative RMSPE decreases monotonically in ![]() (at least over the range of values of
(at least over the range of values of
![]() considered). In others, the relationship between the RMSPE and
considered). In others, the relationship between the RMSPE and ![]() is
U-shaped, and the best forecasts are consequently obtained with a small or intermediate value of
is
U-shaped, and the best forecasts are consequently obtained with a small or intermediate value of ![]() .
.
With a sufficiently small value of ![]() --implying a very informative prior--BMA outperforms the univariate time-series benchmark in all cases considered in this paper. This is an
attractive feature of BMA with a sufficiently informative prior, at least in this data set. Overall, setting
--implying a very informative prior--BMA outperforms the univariate time-series benchmark in all cases considered in this paper. This is an
attractive feature of BMA with a sufficiently informative prior, at least in this data set. Overall, setting ![]() as a benchmark seems to be a good choice because it yields relative
RMSPEs that are less than one in nearly all cases, and it often yields substantial gains in forecast accuracy.
as a benchmark seems to be a good choice because it yields relative
RMSPEs that are less than one in nearly all cases, and it often yields substantial gains in forecast accuracy.
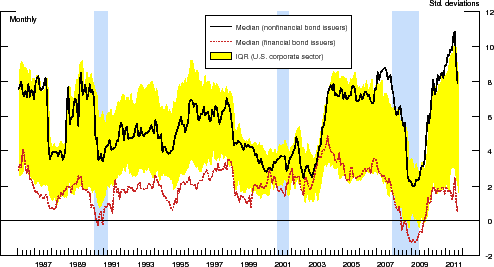
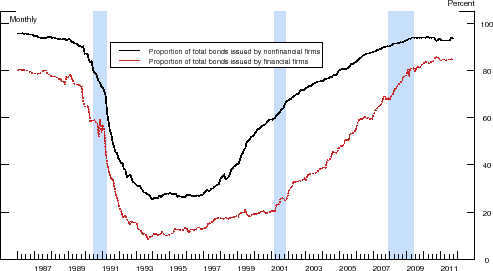
![\begin{displaymath}\begin{split}\ln S_{it}[k] & = C\!A\!L\!L_{i}[k] \times \big( \beta_{0c} + \beta_{1c} D\!D_{it} + \beta_{2c} D\!D_{it}^{2} + \lambda^{\prime}_{c} \mathbf{Z}_{it}[k]) \\ & \quad + (1 - C\!A\!L\!L_{i}[k]) \times ( \beta_{0n} + \beta_{1n} D\!D_{it} + \beta_{2n} D\!D_{it}^{2} + \lambda^{\prime}_{n} \mathbf{Z}_{it}[k] ) \\ & \quad + C\!A\!L\!L_{i}[k] \times \big( \theta_{1} L\!E\!V_{t} + \theta_{2} S\!L\!P_{t} + \theta_{3} C\!R\!V_{t} + \theta_{4} V\!O\!L_{t} \big) + R\!T\!G_{it}[k] + \epsilon_{it}[k], \end{split}\end{displaymath}](img23.gif)
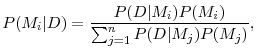
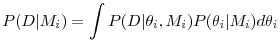
![\displaystyle P(D\vert M_{i}) \propto \left[ \frac{1}{1+\phi} \right]^{-\frac{1}{2}} \times \left[ \frac{1}{1+\phi}S\!S\!R_{i} + \frac{\phi}{1+\phi}S\!S\!E_{i} \right]^{-\frac{(T-p)}{2}},](img87.gif)