
Expectations of functions of stochastic time
with application to credit risk modeling*
Keywords: Time change, default intensity, credit risk, CDS options
Abstract:
1 Introduction
Stochastic time-change offers a parsimonious and economically well-grounded device for introducing stochastic volatility to simpler constant volatility models. The constant volatility model is assumed to apply in a latent "business time." The speed of business time with respect to calendar time is stochastic, and reflects the varying rate of arrival of news to the markets. Most applications of stochastic time-change in the finance literature have focused on the pricing of stock options. Log stock prices are naturally modeled as Lévy processes, and it is well known that any Lévy process subordinated by a Lévy time-change is also a Lévy process. The variance gamma (Madan and Seneta, 1990; Madan et al., 1998) and normal inverse Gaussian (Barndorff-Nielsen, 1998) models are well-known early examples. To allow for volatility clustering, Carr, Geman, Madan, and Yor (2003) introduce a class of models in which the background Lévy process is subordinated by the time-integral of a mean-reverting CIR activity-rate process, and solve for the Laplace transform of the time-changed process. Carr and Wu (2004) extend this framework to accommodate dependence of a general form between the activity rate and background processes, as well as a wider class of activity rate processes.
In this paper, we generalize the basic model in complementary directions. We discard the assumption that the background process is Lévy, and assume instead that the background process (![]() ) has a known Laplace transform,
) has a known Laplace transform,
![]() . Maintaining the requirement that the business clock (
. Maintaining the requirement that the business clock (![]() ) and the background process are independent, we develop two different series solutions for the Laplace transform of the time-changed process
) and the background process are independent, we develop two different series solutions for the Laplace transform of the time-changed process
![]() given by
given by
![]() . In fact, our methods apply generically
to a very wide class of smooth functions of time, and in no way require
. In fact, our methods apply generically
to a very wide class of smooth functions of time, and in no way require ![]() to be the Laplace transform of a stochastic process. Henceforth, for notational parsimony, we drop the auxilliary
parameter
to be the Laplace transform of a stochastic process. Henceforth, for notational parsimony, we drop the auxilliary
parameter ![]() from
from ![]() .
.
Our two series solution are complementary to one another in the sense that the restrictions imposed by the two methods on ![]() and on
and on ![]() differ substantively. The first method requires that
differ substantively. The first method requires that ![]() be a Lévy process, but imposes fairly mild restrictions on
be a Lévy process, but imposes fairly mild restrictions on
![]() . The second method imposes fairly stringent restrictions on
. The second method imposes fairly stringent restrictions on ![]() , but very
weak restrictions on
, but very
weak restrictions on ![]() . In particular, the second method allows for volatility clustering through serial dependence in the activity rate. Thus, the two methods may be useful in different
sorts of applications.
. In particular, the second method allows for volatility clustering through serial dependence in the activity rate. Thus, the two methods may be useful in different
sorts of applications.
Our application is to modeling credit risk. Despite the extensive literature on stochastic volatility in stock returns, the theoretical and empirical literature on stochastic volatility in credit risk models is sparse. Empirical evidence of stochastic volatility in models of corporate bond and credit default swap spreads is provided by Jacobs and Li (2008), Alexander and Kaeck (2008), Zhang et al. (2009) and Gordy and Willemann (2012). To introduce stochastic volatility to the class of default intensity models pioneered by Jarrow and Turnbull (1995) and Duffie and Singleton (1999), Jacobs and Li (2008) replace the widely-used single-factor CIR specification for the intensity with a two-factor specification in which a second CIR process controls the volatility of the intensity process. The model is formally equivalent to the Fong and Vasicek (1991) model of stochastic volatility in interest rates. An important limitation of this two-factor model is that there is no region of the parameter space for which the default intensity is bounded nonnegative (unless the volatility of volatility is zero).4
In this paper, we introduce stochastic volatility to the default intensity framework by time-changing the firm's default time. Let
![]() denote the calendar default time, and let
denote the calendar default time, and let
![]() be the corresponding time under the business clock. Define the background process
be the corresponding time under the business clock. Define the background process ![]() as the time-integral (or "compensator") of the default intensity and
as the time-integral (or "compensator") of the default intensity and ![]() as the business-time survival probability function
as the business-time survival probability function
![]() . If we impose independence between
. If we impose independence between ![]() and
and ![]() , as we do throughout this paper, then time-changing the default time is equivalent to time-changing
, as we do throughout this paper, then time-changing the default time is equivalent to time-changing ![]() , and the calendar-time survival probability function is
, and the calendar-time survival probability function is
The idea of time-changing default times appears to have first been used by Joshi and Stacey (2006). Their model is intended for pricing collateralized debt obligations, so makes the simplifying assumption that firm default intensities are deterministic.6 Mendoza-Arriaga et al. (2010) apply time-change to a credit-equity hybrid model. If we strip out the equity component of their model, the credit component is essentially a time-changed default intensity model. Unlike our model, however, their model does not nest the CIR specification of the default intensity, which is by far the most widely used specification in the literature and in practice. Most closely related to our paper is the time-changed intensity model of Mendoza-Arriaga and Linetsky (2012).7 They obtain a spectral decomposition of the subordinate semigroups, and from this obtain a series solution to the survival probability function. As in our paper, the primary application in their paper is to the evolution of survival probabilities in a model with a CIR intensity in business time and a tempered stable subordinator. When that CIR process is stationary, their solution coincides with that of our second solution method. However, our method can be applied in the non-stationary case as well and generalizes easily when the CIR process is replaced by a basic affine process. Empirically, the default intensity process is indeed non-stationary under the risk-neutral measure for the typical firm (Jacobs and Li, 2008; Duffee, 1999).
Our two expansion methods are developed for a general function ![]() and wide classes of time-change processes in Sections 2 and 3. An application to credit risk modeling is presented in Section 4. The properties of the resulting model are explored with numerical examples in Section 5. In Section 6, we show that
stochastic time-change has a very large effect on the pricing of deep out-of-the-money options on credit default swaps. In Section 7, we demonstrate that our expansion methods can be extended to a much wider class of multi-factor affine jump-diffusion business time
models.
and wide classes of time-change processes in Sections 2 and 3. An application to credit risk modeling is presented in Section 4. The properties of the resulting model are explored with numerical examples in Section 5. In Section 6, we show that
stochastic time-change has a very large effect on the pricing of deep out-of-the-money options on credit default swaps. In Section 7, we demonstrate that our expansion methods can be extended to a much wider class of multi-factor affine jump-diffusion business time
models.
2 Expansion in derivatives
The method of this section imposes weak regularity conditions on ![]() , but places somewhat strong restrictions on
, but places somewhat strong restrictions on ![]() . Throughout this section, we assume
. Throughout this section, we assume
The
where
We assume that ![]() is a smooth function of time. Imposing Assumption 1, we expand
is a smooth function of time. Imposing Assumption 1, we expand ![]() as a formal series and integrate:
as a formal series and integrate:
From equation (A.1) and the recurrence rule (A.3), it follows immediately that where
Defining the constants
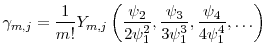
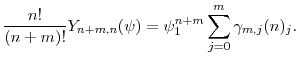
Observing that
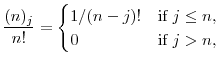
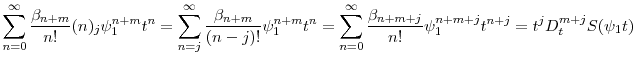
To obtain a generating function for the constants
![]() , we substitute
, we substitute
![]() for
for ![]() and then divide each side by
and then divide each side by
![]() .
.
By Assumption 1(ii),
To guarantee that the series expansion in equation (2.5) is convergent, we would require rather strong conditions. The function ![]() must be entire, the
coefficients
must be entire, the
coefficients
![]() in equation (2.3) must decay faster than geometrically, and the coefficients
in equation (2.3) must decay faster than geometrically, and the coefficients
![]() must vanish at a geometric rate in
must vanish at a geometric rate in ![]() . In application, it may be that
none of these assumptions hold. If
. In application, it may be that
none of these assumptions hold. If ![]() is analytic but non-entire, then
is analytic but non-entire, then
![]() , so geometric behavior in the
, so geometric behavior in the
![]() would not be sufficient for convergence. Furthermore, we will provide a practically relevant specification below in which the
would not be sufficient for convergence. Furthermore, we will provide a practically relevant specification below in which the
![]() are increasing in
are increasing in ![]() for fixed
for fixed ![]() . Even if the series expansion in equation (2.5) is, in general, divergent, we will see that it may nonetheless be computationally effective.
. Even if the series expansion in equation (2.5) is, in general, divergent, we will see that it may nonetheless be computationally effective.
We now provide an alternative justification for equation (2.5) to clarify the convergence behavior of our expansion. We introduce a regularity condition on ![]() :
:
Assumption 2 implies
so
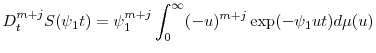
Let ![]() be the remainder function from the generating equation (2.6), that is,
be the remainder function from the generating equation (2.6), that is,
and let
The following proposition formalizes our approximation:
where Assumption 2 guarantees the change of the order of integration and the last equality follows from the fact that
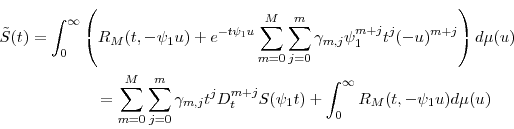
which implies the conclusion.
Since ![]() can be arbitrarily large, Proposition 1 provides a rigorous meaning for equation (2.5). However, it does not by itself
explain why we should expect
can be arbitrarily large, Proposition 1 provides a rigorous meaning for equation (2.5). However, it does not by itself
explain why we should expect
![]() to provide a good approximation to
to provide a good approximation to
![]() . Equation (2.8) shows that the divergent sum (2.5) comes from the Laplace transform of the locally convergent sum in (2.6) (with
. Equation (2.8) shows that the divergent sum (2.5) comes from the Laplace transform of the locally convergent sum in (2.6) (with ![]() replaced by
replaced by
![]() ). It has been known for a long time that a divergent power series obtained by Laplace transforming a locally convergent sum is computationally very effective when
truncated close to the numerically least term. In recent years, this classical method of "summation to the least term" has been justified rigorously in quite some generality for various classes of problems.10 The analysis of Costin and Kruskal (1999) is in the setting of differential equations, but their method of proof extends to much more general problems. Although the series in our analysis is not a
usual power series, the procedure is conceptually similar and therefore expected to yield comparably good results.
). It has been known for a long time that a divergent power series obtained by Laplace transforming a locally convergent sum is computationally very effective when
truncated close to the numerically least term. In recent years, this classical method of "summation to the least term" has been justified rigorously in quite some generality for various classes of problems.10 The analysis of Costin and Kruskal (1999) is in the setting of differential equations, but their method of proof extends to much more general problems. Although the series in our analysis is not a
usual power series, the procedure is conceptually similar and therefore expected to yield comparably good results.
For an interesting class of processes for ![]() , the sequence
, the sequence
![]() takes a convenient form. Let
takes a convenient form. Let
![]() be the scaling parameter of the process, and let
be the scaling parameter of the process, and let
![]() be the precision parameter. We introduce the assumption
be the precision parameter. We introduce the assumption
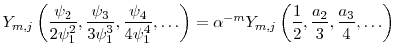
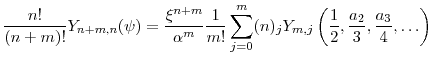 |
(2.12) |
Define a new set of constants
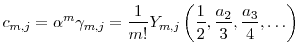
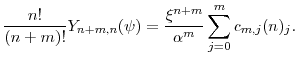
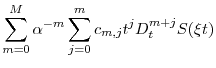 |
(2.13) | ||
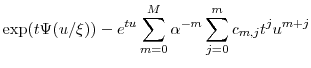 |
(2.14) |
This solution is especially convenient for two reasons. First, when the precision parameter
![]() is large, the expansion will yield accurate results in few terms. The variance
is large, the expansion will yield accurate results in few terms. The variance
![]() is inversely proportional to
is inversely proportional to
![]() , so
, so ![]() converges in probability to
converges in probability to
![]() as
as
![]() . This implies that
. This implies that
![]() for large
for large
![]() . Since the expansion constructs
. Since the expansion constructs
![]() as
as
![]() plus successive correction terms, it is well-structured for the case in which
plus successive correction terms, it is well-structured for the case in which ![]() is not too volatile. The same remark applies to the more general case of Proposition 1, but the logic is more transparent when a single parameter controls the scaled higher cumulants. Second, in the special case of Assumption 3, the coefficients
is not too volatile. The same remark applies to the more general case of Proposition 1, but the logic is more transparent when a single parameter controls the scaled higher cumulants. Second, in the special case of Assumption 3, the coefficients ![]() depend only on the chosen family of processes for
depend only on the chosen family of processes for ![]() and not on its parameters
and not on its parameters
![]() . In econometric applications, there can be millions of calls to the function
. In econometric applications, there can be millions of calls to the function
![]() , so the ability to pre-calculate the
, so the ability to pre-calculate the ![]() can result in
significant efficiencies.
can result in
significant efficiencies.
The three-parameter tempered stable subordinator is a flexible and widely-used family of subordinators. We can reparameterize the standard form of the Laplace exponent given by Cont and Tankov (2004, 4.2.2) in terms of our precision and scale parameters (
![]() and
and
![]() ) and a stability parameter
) and a stability parameter
![]() with
with
![]() . We obtain
. We obtain
It can easily be verified that
If
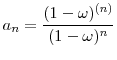
Two well-known examples of the tempered stable subordinator are the gamma subordinator (
![]() ) and the inverse Gaussian subordinator (
) and the inverse Gaussian subordinator (
![]() ). For the gamma subordinator, the constants
). For the gamma subordinator, the constants ![]() simplify
to
simplify
to ![]() , so
, so
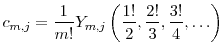
for
In the inverse Gaussian case (
![]() ), the
), the ![]() parameters are
parameters are
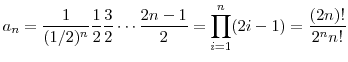
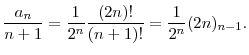
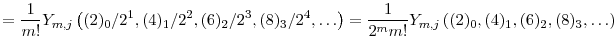
|
||
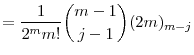 |
(2.17) |
where the last equality follows from identity (A.2).
3 Expansion in exponential functions
The method of this section relaxes the assumption that ![]() is a Lévy process, but is more restrictive on
is a Lévy process, but is more restrictive on ![]() . In the simplest case, we require that
. In the simplest case, we require that
where
Let ![]() denote the moment generating function for
denote the moment generating function for ![]() . We assume
. We assume
Assumption 5 can accommodate non-Lévy specifications as well. Since volatility spikes are often clustered in time, it may be desirable to allow for serial dependence in the rate of time change. Following Carr and Wu (2004) and Mendoza-Arriaga et al. (2010), we let a positive process ![]() be the instantaneous activity rate of business time, so that
be the instantaneous activity rate of business time, so that
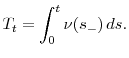
where
Under Assumptions 4 and 5, we have
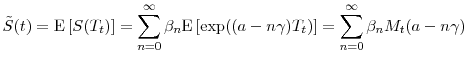
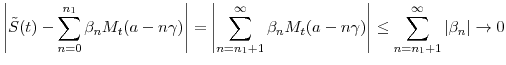
When ![]() is a Laplace transform of the time-integral of a nonnegative diffusion and when
is a Laplace transform of the time-integral of a nonnegative diffusion and when ![]() is a Lévy subordinator, Proposition 3 is equivalent to the eigenfunction expansion of Mendoza-Arriaga and Linetsky (2012).11 However, because our approach is agnostic with respect to the interpretation of
is a Lévy subordinator, Proposition 3 is equivalent to the eigenfunction expansion of Mendoza-Arriaga and Linetsky (2012).11 However, because our approach is agnostic with respect to the interpretation of ![]() , it can be applied in situations
when spectral decomposition is unavailable, e.g., when the background process is a time-integral of a process containing jumps. All that is needed is that
, it can be applied in situations
when spectral decomposition is unavailable, e.g., when the background process is a time-integral of a process containing jumps. All that is needed is that ![]() has a convergent Taylor series
expansion as specified in Assumption 4. Moreover, our approach makes clear that
has a convergent Taylor series
expansion as specified in Assumption 4. Moreover, our approach makes clear that ![]() need not be a Lévy subordinator.
need not be a Lévy subordinator.
As we will see in the next section, there are situations in which Assumption 4 does not hold, so neither Proposition 3 nor the corresponding eigenfunction expansion of Mendoza-Arriaga and
Linetsky (2012) pertains. However, our method can be adapted so long as ![]() has a suitable expansion in powers of an affine function of
has a suitable expansion in powers of an affine function of
![]() . We will make use of this alternative in particular:
. We will make use of this alternative in particular:
This leads to
Although Assumption 4' is not a sufficient condition for Assumption 2, it is sufficient for purposes of approximating
![]() by the expansion in derivatives of Section 2. Let
by the expansion in derivatives of Section 2. Let ![]() denote the approximation to
denote the approximation to ![]() given by the finite expansion
given by the finite expansion
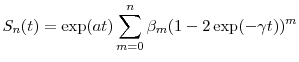
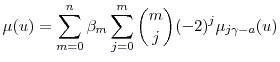
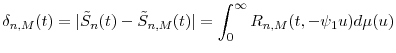
4 Application to credit risk modeling
We now apply the two expansion methods to the widely-used default intensity class of models for pricing credit-sensitive corporate bonds and credit default swaps. In these models, a firm's default occurs at the first event of a non-explosive counting process. Under the business-time clock, the
intensity of the counting process is
![]() . The intuition driving the model is that
. The intuition driving the model is that
![]() is the probability of default before business time
is the probability of default before business time ![]() ,
conditional on survival to business time
,
conditional on survival to business time ![]() . We define
. We define ![]() as the time-integral of
as the time-integral of
![]() , which is also known as the compensator.
, which is also known as the compensator.
Let
![]() denote the calendar default time, and let
denote the calendar default time, and let
![]() be the corresponding time under the business clock. Current time is normalized to zero under both clocks. The probability of survival to future business time
be the corresponding time under the business clock. Current time is normalized to zero under both clocks. The probability of survival to future business time ![]() is
is
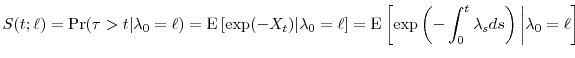
It is easily seen that time-changing the default time is equivalent to time-changing the compensator, i.e., that the survival probability in calendar time is equal to
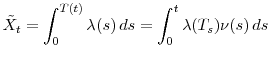
When ![]() is a Lévy subordinator, the
is a Lévy subordinator, the ![]() process is not differentiable, so
the change of variable cannot be applied. We have so far fixed the current time to zero to minimize notation. To accommodate analysis of time-series behavior, let us define
process is not differentiable, so
the change of variable cannot be applied. We have so far fixed the current time to zero to minimize notation. To accommodate analysis of time-series behavior, let us define
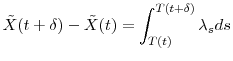
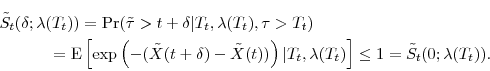
Since this holds for any nonnegative
We acknowledge that the assumption of independence between ![]() and
and ![]() may be
strong. In the empirical literature on stochastic volatility in stock returns, there is strong evidence for dependence between the volatility factor and stock returns (e.g., Jones, 2003;
Andersen et al., 2002; Jacquier et al., 2004). In the credit risk literature, however, the evidence is less compelling. Across the firms in their sample, Jacobs and Li (2008) find a median correlation of around 1% between the default intensity
diffusion and the volatility factor. Nonetheless, for a significant share of the firms, the correlation appears to be material. We hope to relax the independence assumption in future work.
may be
strong. In the empirical literature on stochastic volatility in stock returns, there is strong evidence for dependence between the volatility factor and stock returns (e.g., Jones, 2003;
Andersen et al., 2002; Jacquier et al., 2004). In the credit risk literature, however, the evidence is less compelling. Across the firms in their sample, Jacobs and Li (2008) find a median correlation of around 1% between the default intensity
diffusion and the volatility factor. Nonetheless, for a significant share of the firms, the correlation appears to be material. We hope to relax the independence assumption in future work.
We re-introduce the basic affine process, which we earlier defined in Section 3. Under the business clock,
![]() follows the stochastic differential equation
follows the stochastic differential equation
where
for functions
We digress briefly to consider whether the method of Carr and Wu (2004) can be applied in this setting. The compensator ![]() is not Lévy, but can be
expressed as a time-changed time-integral of a constant intensity, where the time change in this case is the time-integral of the basic affine process in (4.2). Thus, we can write
is not Lévy, but can be
expressed as a time-changed time-integral of a constant intensity, where the time change in this case is the time-integral of the basic affine process in (4.2). Thus, we can write
![]() as
as
![]() where
where ![]() is trivially a Lévy process and
is trivially a Lévy process and ![]() is a compound time change. However, this approach leads nowhere, because
is a compound time change. However, this approach leads nowhere, because ![]() is equivalent to
is equivalent to
![]() . Put another way, we are still left with the problem of solving the Laplace transform for
. Put another way, we are still left with the problem of solving the Laplace transform for
![]() .
.
To apply our expansion in exponential functions, we show that Assumption 4 is satisfied when
![]() and Assumption 4' is always satisfied. In Appendix C, we prove
and Assumption 4' is always satisfied. In Appendix C, we prove
Assume
For the case
In each case,
When
![]() and in the absence of jumps (
and in the absence of jumps (
![]() ), the expansion in (ii) is equivalent to the eigenfunction expansion in Davydov and Linetsky (2003, 4.3).13Therefore, the associated solution to
), the expansion in (ii) is equivalent to the eigenfunction expansion in Davydov and Linetsky (2003, 4.3).13Therefore, the associated solution to
![]() under a Lévy subordinator is identical to the solution in Mendoza-Arriaga and Linetsky (2012). Our result is more general in
that it permits non-stationarity (i.e.,
under a Lévy subordinator is identical to the solution in Mendoza-Arriaga and Linetsky (2012). Our result is more general in
that it permits non-stationarity (i.e.,
![]() ) in expansion (i) and accommodates the presence of jumps in the intensity process in expansions (i) and
(ii). Furthermore, it is clear in our analysis that our expansions can be applied to non-Lévy specifications of time-change as well, such as the mean-reverting activity rate model in (3.2).
) in expansion (i) and accommodates the presence of jumps in the intensity process in expansions (i) and
(ii). Furthermore, it is clear in our analysis that our expansions can be applied to non-Lévy specifications of time-change as well, such as the mean-reverting activity rate model in (3.2).
Subject to the technical caveat at the end of Section 3, Assumptions 1 and 4' are together sufficient for application of expansion in derivatives without restrictions on
![]() . To implement, we need an efficient algorithm to obtain derivatives of
. To implement, we need an efficient algorithm to obtain derivatives of ![]() . Let
. Let
![]() be the family of functions defined by
be the family of functions defined by
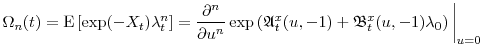
5 Numerical examples
We explore the effect of time-change on the behavior of the model, as well as the efficacy of our two series solutions. To fix a benchmark model, we assume that
![]() follows a CIR process in business time with parameters
follows a CIR process in business time with parameters
![]() ,
,
![]() and
and
![]() . This calibration is consistent in a stylized fashion with median parameter values under the physical measure as reported by Duffee (1999). Our
benchmark specification adopts inverse Gaussian time change. In all the examples discussed below, the behavior under gamma time-change is quite similar.
. This calibration is consistent in a stylized fashion with median parameter values under the physical measure as reported by Duffee (1999). Our
benchmark specification adopts inverse Gaussian time change. In all the examples discussed below, the behavior under gamma time-change is quite similar.
The survival probability function is falling monotonically and almost linearly, so is not scaled well for our exercises. Instead, following the presentation in Duffie and Singleton (2003, 3), we work with the forward default rate,
![]() .14 In our benchmark calibration, we set starting condition
.14 In our benchmark calibration, we set starting condition
![]() well below its long-run mean
well below its long-run mean ![]() in order to
give reasonable variation across the term structure in the forward default rate. Both
in order to
give reasonable variation across the term structure in the forward default rate. Both ![]() and
and ![]() are scale-invariant processes, so we fix the scale parameter
are scale-invariant processes, so we fix the scale parameter
![]() with no loss of generality.
with no loss of generality.
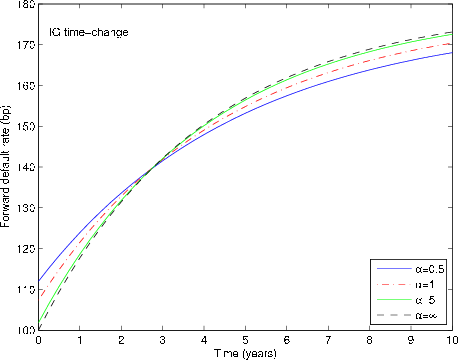
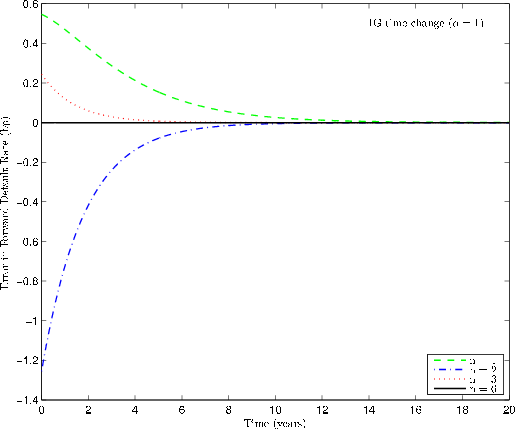
Figure 1 shows how the term structure of the forward default rate changes with the precision parameter
![]() . We see that lower values of
. We see that lower values of
![]() flatten the term-structure, which accords with the intuition that the time-changed term-structure is a mixture across time of the business-time term-structure. Above
flatten the term-structure, which accords with the intuition that the time-changed term-structure is a mixture across time of the business-time term-structure. Above
![]() , it becomes difficult to distinguish
, it becomes difficult to distinguish
![]() from the term structure
from the term structure ![]() for the CIR model without
time-change.
for the CIR model without
time-change.
Finding that time-change has negligible effect on the term structure
![]() for moderate values of
for moderate values of
![]() does not imply that time-change has a small effect on the time-series behavior of the default intensity. For a given time-increment
does not imply that time-change has a small effect on the time-series behavior of the default intensity. For a given time-increment ![]() , we obtain by simulation the kurtosis of calendar time increments of the default intensity (that is,
, we obtain by simulation the kurtosis of calendar time increments of the default intensity (that is,
![]() ) under the stationary law. For the limiting CIR model without time-change, moments for the increments
) under the stationary law. For the limiting CIR model without time-change, moments for the increments
![]() have simple closed-form solutions provided by Gordy (2012). The kurtosis is equal to
have simple closed-form solutions provided by Gordy (2012). The kurtosis is equal to
![]() , which is invariant to the time-increment
, which is invariant to the time-increment ![]() .
.
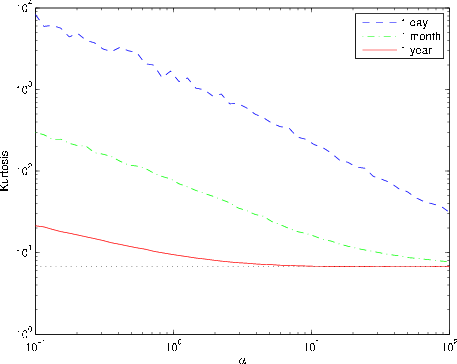
In Figure 2, we plot kurtosis as a function of
![]() on a log-log scale. Using the same baseline model specification as before, we plot separate curves for a one day horizon (
on a log-log scale. Using the same baseline model specification as before, we plot separate curves for a one day horizon (
![]() , assuming 250 trading days per year), a one month horizon (
, assuming 250 trading days per year), a one month horizon (
![]() ), and an annual horizon (
), and an annual horizon (![]() ). As we expect, kurtosis at all
horizons tends to its asymptotic CIR limit (dotted line) as
). As we expect, kurtosis at all
horizons tends to its asymptotic CIR limit (dotted line) as
![]() . For fixed
. For fixed
![]() , kurtosis also tends to its CIR limit as
, kurtosis also tends to its CIR limit as
![]() . This is because an unbiased trend stationary time-change has no effect on the distribution of a stationary process far into the future. For intermediate values of
. This is because an unbiased trend stationary time-change has no effect on the distribution of a stationary process far into the future. For intermediate values of
![]() (say, between 1 and 10), we see that time-change has a modest impact on kurtosis beyond one year, but a material impact at a one month horizon, and a very large impact at
a daily horizon.
(say, between 1 and 10), we see that time-change has a modest impact on kurtosis beyond one year, but a material impact at a one month horizon, and a very large impact at
a daily horizon.
Next, we explore the convergence of the series expansion in exponentials. Let
![]() denote the estimated forward default rate using the first
denote the estimated forward default rate using the first ![]() terms
of the series for
terms
of the series for
![]() and the corresponding expansion for
and the corresponding expansion for
![]() . Figure 3 shows that the convergence of
. Figure 3 shows that the convergence of
![]() to
to
![]() is quite rapid. We proxy the series solution with
is quite rapid. We proxy the series solution with ![]() terms as the
true forward default rate, and plot the error
terms as the
true forward default rate, and plot the error
![]() in basis points (bp). The error is decreasing in
in basis points (bp). The error is decreasing in ![]() , as
the series in Proposition 5 is an asymptotic expansion. With only
, as
the series in Proposition 5 is an asymptotic expansion. With only ![]() terms, the error is 0.25bp at
terms, the error is 0.25bp at ![]() , which corresponds to a relative error under 0.25%. With
, which corresponds to a relative error under 0.25%. With ![]() terms, relative error is negligible (under 0.0005%) at
terms, relative error is negligible (under 0.0005%) at ![]() .
.
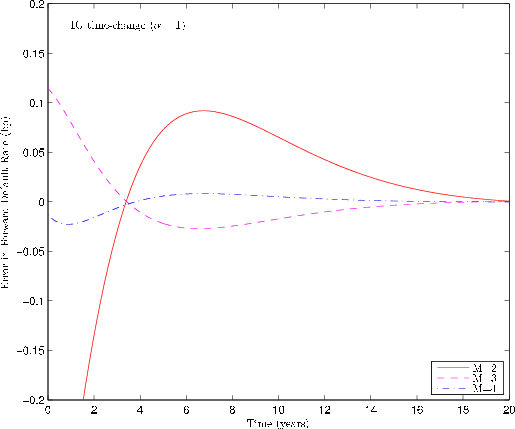
We turn now to the convergence of the expansion in derivatives. In Figure 4, we plot the error against the benchmark for ![]() terms in expansion (2.10). The benchmark curve is calculated, as before, using the series expansion in exponential functions with 12 terms. The magnitude of the relative error is generally largest at small values of
terms in expansion (2.10). The benchmark curve is calculated, as before, using the series expansion in exponential functions with 12 terms. The magnitude of the relative error is generally largest at small values of ![]() . For
. For ![]() , the forward default rate is off by nearly 0.5bp at
, the forward default rate is off by nearly 0.5bp at ![]() . Observed bid-ask spreads in the credit default swap market are an order of magnitude larger, so this degree of accuracy is already likely to be sufficient for empirical application. For
. Observed bid-ask spreads in the credit default swap market are an order of magnitude larger, so this degree of accuracy is already likely to be sufficient for empirical application. For ![]() , the gap is never over 0.025bp at any
, the gap is never over 0.025bp at any ![]() .
.
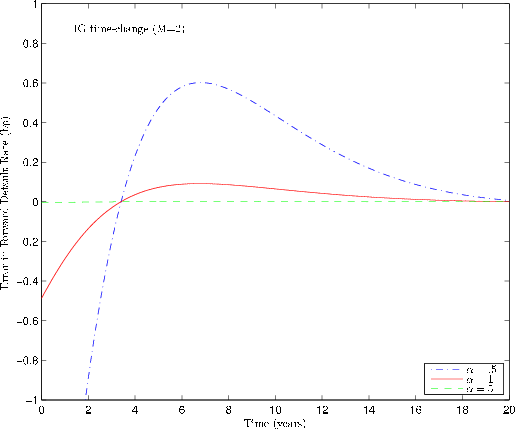
In Figure 5, we hold fixed ![]() and explore how error varies with
and explore how error varies with
![]() . As the expansion is in powers of
. As the expansion is in powers of
![]() , it is not surprising that error vanishes as
, it is not surprising that error vanishes as
![]() grows, and is negligible (under 0.005bp in absolute magnitude) at
grows, and is negligible (under 0.005bp in absolute magnitude) at
![]() . Experiments with other model parameters suggest that absolute relative error increases with
. Experiments with other model parameters suggest that absolute relative error increases with ![]() and
and ![]() and decreases with
and decreases with ![]() .
.
6 Options on credit default swaps
In the previous section, we observe that stochastic time-change has a negligible effect on the term structure of default probability for moderate values of
![]() , which implies that introducing time-change should have little impact on the term-structure of credit spreads on corporate bonds and credit default swaps (CDS).
Nonetheless, time-change has a large effect on the forecast density of the default intensity at short horizon. Consequently, introducing time-change should have material impact on the pricing of short-dated options on credit instruments.15 In this section, we develop a pricing methodology for European options on single-name CDS in the time-changed CIR model.
, which implies that introducing time-change should have little impact on the term-structure of credit spreads on corporate bonds and credit default swaps (CDS).
Nonetheless, time-change has a large effect on the forecast density of the default intensity at short horizon. Consequently, introducing time-change should have material impact on the pricing of short-dated options on credit instruments.15 In this section, we develop a pricing methodology for European options on single-name CDS in the time-changed CIR model.
At present, the CDS option market is dominated by index options. The market for single-name CDS options is less liquid, but trades do occur. A payer option gives the right to buy protection of maturity
![]() at a fixed spread
at a fixed spread ![]() (the "strike" or "pay premium") at a fixed
expiry date
(the "strike" or "pay premium") at a fixed
expiry date
![]() . A payer option is in-the-money if the par CDS spread at date
. A payer option is in-the-money if the par CDS spread at date
![]() is greater than
is greater than ![]() . A receiver option gives the right
to sell protection. We focus here on the pricing of payer options, but all results extend in an obvious fashion to the pricing of receiver options. An important difference between the index and single-name option markets is that single-name options are sold with knock-out, i.e., the option expires
worthless if the reference entity defaults before
. A receiver option gives the right
to sell protection. We focus here on the pricing of payer options, but all results extend in an obvious fashion to the pricing of receiver options. An important difference between the index and single-name option markets is that single-name options are sold with knock-out, i.e., the option expires
worthless if the reference entity defaults before
![]() . As we will see, this complicates the analysis. Willemann and Bicer (2010) provide an overview of CDS option trading and its
conventions.
. As we will see, this complicates the analysis. Willemann and Bicer (2010) provide an overview of CDS option trading and its
conventions.
To simplify the analysis and to keep the focus on default risk, we assume a constant risk free interest rate ![]() and a constant recovery rate
and a constant recovery rate ![]() . In the next section, we generalize our methods to accommodate a multi-factor model governing both the short rate and default intensity. The assumption of constant recovery can be relaxed by adopting the stochastic recovery model of
Chen and Joslin (2012) in business time. We assume that
. In the next section, we generalize our methods to accommodate a multi-factor model governing both the short rate and default intensity. The assumption of constant recovery can be relaxed by adopting the stochastic recovery model of
Chen and Joslin (2012) in business time. We assume that
![]() follows a mean-reverting (
follows a mean-reverting (
![]() ) CIR process in business time, and that the clock
) CIR process in business time, and that the clock ![]() is
a Lévy process satisfying Assumption 1 with Laplace exponent
is
a Lévy process satisfying Assumption 1 with Laplace exponent
![]() . All probabilities and expectations are under the risk-neutral measure.
. All probabilities and expectations are under the risk-neutral measure.
In the event of default at date
![]() , the receiver of CDS protection receives a single payment of
, the receiver of CDS protection receives a single payment of ![]() at
at
![]() . Therefore, the value at date
. Therefore, the value at date ![]() of the protection leg of a CDS of
maturity
of the protection leg of a CDS of
maturity
![]() is
is
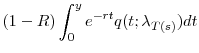
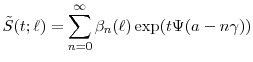
To price the premium leg, we make the simplifying assumption that the spread
![]() is paid continuously until default or maturity. The value at date
is paid continuously until default or maturity. The value at date ![]() of the premium leg of a CDS of maturity
of the premium leg of a CDS of maturity
![]() is then
is then
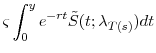
The par spread
To simplify exposition, we assume that CDS are traded on a running spread basis.16 Let
![]() be the net value of the CDS for the buyer of protection at time
be the net value of the CDS for the buyer of protection at time ![]() given
given
![]() and the spread
and the spread
![]() , i.e.,
, i.e., ![]() is the difference in value between the protection
leg and the premium leg. Note that
is the difference in value between the protection
leg and the premium leg. Note that ![]() does not depend directly on time
does not depend directly on time ![]() . This
simplifies to
. This
simplifies to
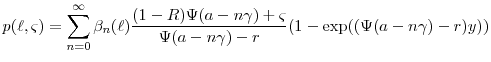
The value at time 0 of the payer option is the expectation of expression (6.3) over the joint distribution of
![]() under the risk-neutral measure:
under the risk-neutral measure:
Let
| (6.4) |
This expectation is most easily obtained by Monte Carlo simulation. In each trial
![]() , we draw a single value of the business clock expiry date
, we draw a single value of the business clock expiry date
![]() from the distribution of
from the distribution of
![]() . Next, we draw
. Next, we draw ![]() from the noncentral chi-squared
transition distribution for
from the noncentral chi-squared
transition distribution for
![]() given
given
![]() and
and
![]() . The transition law for the CIR process is given by Broadie and Kaya (2006, Eq. 8). The option value is estimated by
. The transition law for the CIR process is given by Broadie and Kaya (2006, Eq. 8). The option value is estimated by
Observe that we can efficiently calculate option values across a range of strike spreads with the same sample of
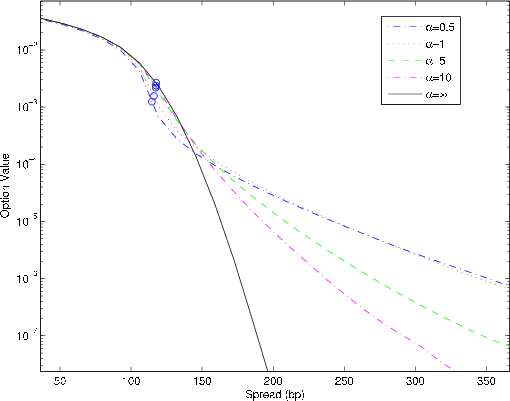
Figure 6 depicts the effect of
![]() on the value of a one month payer option on a five year CDS. Model parameters are taken from the baseline values of Section 5. The riskfree
rate is fixed at 3% and the recovery rate at 40%. Depending on the choice of
on the value of a one month payer option on a five year CDS. Model parameters are taken from the baseline values of Section 5. The riskfree
rate is fixed at 3% and the recovery rate at 40%. Depending on the choice of
![]() , the par spread is in the range of 115-120bp (marked with circles). For deep out-of-the-money options, i.e., for
, the par spread is in the range of 115-120bp (marked with circles). For deep out-of-the-money options, i.e., for
![]() , we see that option value is decreasing in
, we see that option value is decreasing in
![]() . Stochastic time-change opens the possibility that the short horizon to option expiry will be greatly expanded in business time, and so increases the likelihood of
extreme changes in the intensity. The effect is important even at large values of
. Stochastic time-change opens the possibility that the short horizon to option expiry will be greatly expanded in business time, and so increases the likelihood of
extreme changes in the intensity. The effect is important even at large values of
![]() for which the term-structure of forward default rate would be visually indistinguishable from the CIR case in Figure 1. For example, at a
strike spread of 200bp, the value of the option is nearly 700 times greater for the time-changed model with
for which the term-structure of forward default rate would be visually indistinguishable from the CIR case in Figure 1. For example, at a
strike spread of 200bp, the value of the option is nearly 700 times greater for the time-changed model with
![]() than for the CIR model without time-change.
than for the CIR model without time-change.
Perhaps counterintuitively, the value of the option is increasing in
![]() for near-the-money options. Because the transition variance of
for near-the-money options. Because the transition variance of
![]() is concave in
is concave in ![]() , introducing stochastic time-change
actually reduces the variance of the default intensity at option expiry even as it increases the higher moments. Relative to out-of-the-money options, near-the-money options are more sensitive to the variance and less sensitive to higher moments.
, introducing stochastic time-change
actually reduces the variance of the default intensity at option expiry even as it increases the higher moments. Relative to out-of-the-money options, near-the-money options are more sensitive to the variance and less sensitive to higher moments.
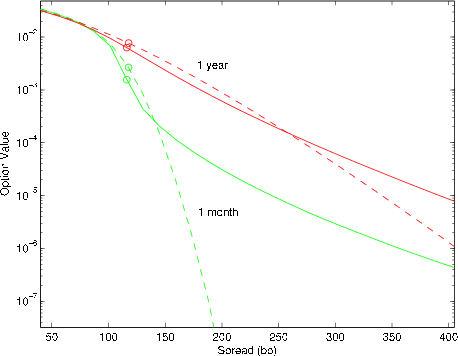
The effect of time to expiry on option value is depicted in Figure 7. The solid lines are for the model with stochastic time-change (![]() ), and the
dashed lines are for the CIR model without time-change. Relative to the case of the short-dated (one month) option, stochastic time-change has a small effect on the value of the long-dated (one year) option. This is consistent with our observation in Figure 2 that the
kurtosis of
), and the
dashed lines are for the CIR model without time-change. Relative to the case of the short-dated (one month) option, stochastic time-change has a small effect on the value of the long-dated (one year) option. This is consistent with our observation in Figure 2 that the
kurtosis of
![]() converges to that of
converges to that of
![]() as
as ![]() grows large.
Because the Lévy subordinator lacks persistence, stochastic time-change simply washes out at long horizon.
grows large.
Because the Lévy subordinator lacks persistence, stochastic time-change simply washes out at long horizon.
7 Multi-factor affine models
We have so far taken the business-time default intensity to be a single-factor basic affine process. In this section, we show that our methods of Sections 2 and 3 can be applied to a much wider class of multi-factor affine jump-diffusion models. For the sake of brevity, we limit our analysis here to stationary models.
Let
![]() be a
be a ![]() -dimensional affine jump-diffusion, and let the
default intensity at business time
-dimensional affine jump-diffusion, and let the
default intensity at business time ![]() be given by an affine function
be given by an affine function
![]() . We now obtain a convergent series expansion of
. We now obtain a convergent series expansion of
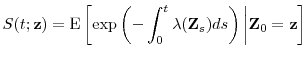
By Proposition 1 of Duffie et al. (2000, 2),
![]() has exponential-affine solution
has exponential-affine solution
![]() , where
, where ![]() denotes
the inner product. Functions
denotes
the inner product. Functions ![]() and
and
![]() satisfy complex-valued ODEs which we represent simply as
satisfy complex-valued ODEs which we represent simply as
where
which we study under assumptions guaranteeing stability of the equilibrium.
- (i)
-
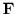 is analytic in a polydisk centered at zero.
is analytic in a polydisk centered at zero. - (ii)
-
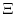 is a diagonalizable matrix of constants. Its eigenvalues
is a diagonalizable matrix of constants. Its eigenvalues
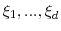 are nonresonant, i.e., for
are nonresonant, i.e., for
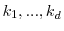 nonnegative integers with
nonnegative integers with
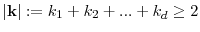 , we have
, we have
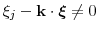 for
for 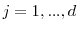 .
. - (iii)
-
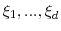 are in the left half plane,
are in the left half plane,
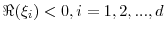 .
.
The following is a classical theorem due to Poincaré (see e.g., Ilyashenko and Yakovenko, 2008).
Under Assumption 7, there is a positive tuple
with a conjugation map tangent to the identity.
satisfies (7.3). Tangent to the identity simply means the fact that the linear part of the conjugation map is the identity, as seen in (7.4).
Let
![]() denote the common polydisk of analyticity of
denote the common polydisk of analyticity of
![]() and
and
![]() .
.
The general solution of (7.2) with initial condition
where
where
where
Let
![]() be a ball in which
be a ball in which
![]() is analytic and
is analytic and
The existence of
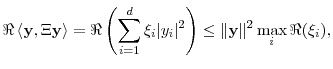
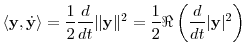
Under Assumption 7, the domain of analyticity of
We turn now to the second equation in the ODE system (7.1). Assume, without loss of generality, that
![]() is analytic in the same polydisk as
is analytic in the same polydisk as
![]() , i.e., in
, i.e., in
![]() , which implies that the expansion converges uniformly and absolutely inside
, which implies that the expansion converges uniformly and absolutely inside
![]() . Imposing Assumption 7, we substitute (7.6) to obtain a uniformly and absolutely convergent expansion in
. Imposing Assumption 7, we substitute (7.6) to obtain a uniformly and absolutely convergent expansion in
![]() , and integrate term-by-term to get
, and integrate term-by-term to get
where
The absolute and uniform convergence of the expansions of ![]() and
and ![]() extends to the expansion of
extends to the expansion of
![]() , which is the multi-factor extension of Proposition 5(ii). Thus, subject to Assumption 7 and
, which is the multi-factor extension of Proposition 5(ii). Thus, subject to Assumption 7 and
![]() , expansion in exponentials can be applied to the multi-factor model. Furthermore, the construction in (3.1) of a finite
signed measure satisfying Assumption 2 extends naturally, so expansion in derivatives also applies.
, expansion in exponentials can be applied to the multi-factor model. Furthermore, the construction in (3.1) of a finite
signed measure satisfying Assumption 2 extends naturally, so expansion in derivatives also applies.
The multi-factor extension can be applied to a joint affine model of the riskfree rate and default intensity. Let ![]() be the short rate in business time and let
be the short rate in business time and let ![]() be the recovery rate as a fraction of market value at
be the recovery rate as a fraction of market value at ![]() . We assume that
. We assume that
![]() is an affine function of the affine jump-diffusion
is an affine function of the affine jump-diffusion
![]() , and solve for the business-time default-adjusted discount function
, and solve for the business-time default-adjusted discount function
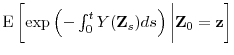 . Subject to the regularity
conditions in Assumption 7, we can thereby introduce stochastic time-change to the class of models studied by Duffie and Singleton (1999) and estimated by Duffee (1999). The possibility of handling
stochastic interest rates in our framework is also recognized by Mendoza-Arriaga and Linetsky (2012, Remark 4.1).
. Subject to the regularity
conditions in Assumption 7, we can thereby introduce stochastic time-change to the class of models studied by Duffie and Singleton (1999) and estimated by Duffee (1999). The possibility of handling
stochastic interest rates in our framework is also recognized by Mendoza-Arriaga and Linetsky (2012, Remark 4.1).
Conclusion
We have derived and demonstrated two new methods for obtaining the Laplace transform of a stochastic process subjected to a stochastic time change. Each method provides a simple way to extend a wide variety of constant volatility models to allow for stochastic volatility. More generally, we can abstract from the background process, and view our methods simply as ways to calculate the expectation of a function of stochastic time. The two methods are complements in their domains of application. Expansion in derivatives imposes strictly weaker conditions on the function, whereas expansion in exponentials imposes strictly weaker conditions on the stochastic clock. We have found both methods to be straightforward to implement and computationally efficient.
Relative to the earlier literature, the primary advantage of our approach is that the background process need not be Lévy or even Markov. Thus, our methods are especially well-suited to application to default intensity models of credit risk. Both of our methods apply to the survival probability function under the ubiquitous basic affine specification of the default intensity. The forward default rate is easily calculated as well. Therefore, we can easily price both corporate bonds and credit default swaps in the time-changed model. In a separate paper, a time-changed default intensity model is estimated on panels of CDS spreads (across maturity and observation time) using Bayesian MCMC methods.
In contrast to the direct approach of modeling time-varying volatility as a second factor, stochastic time-change naturally preserves important properties of the background model. In particular, so long as the default intensity is bounded nonnegative in the background model, it will be bounded nonnegative in the time-changed model. In numerical examples in which the business-time default intensity is a CIR process, we find that introducing a moderate volatility in the stochastic clock has hardly any impact on the term-structure of credit spreads, yet a very large impact on the intertemporal variation of spreads. Consequently, the model preserves the cross-sectional behavior of the standard CIR model in pricing bonds and CDS at a fixed point in time, but allows for much greater flexibility in capturing kurtosis in the distribution of changes in spreads across time. The model also has a first-order effect on the pricing of deep out-of-the-money CDS options.
A. Identities for the Bell polynomials
Bell polynomial identities arise frequently in our analysis, so we gather the important results together here for reference. In this appendix, ![]() and
and ![]() are scalar constants, and
are scalar constants, and ![]() and
and ![]() are infinite sequences
are infinite sequences
![]() and
and
![]() . Unless otherwise noted, results are drawn from Comtet (1974, 3.3), in some cases with slight rearrangement.
. Unless otherwise noted, results are drawn from Comtet (1974, 3.3), in some cases with slight rearrangement.
We begin with the incomplete Bell polynomials,
![]() . The homogeneity rule is
. The homogeneity rule is
From Mihoubi (2008, Example 2), we can obtain the identity
for any
For ![]() , the complete Bell polynomials,
, the complete Bell polynomials,
![]() , are obtained from the incomplete Bell polynomials as
, are obtained from the incomplete Bell polynomials as
Note that
B. Generalized transform for the basic affine process
In this appendix, we set forth the closed-form solution to functions
![]() in the generalized transform
in the generalized transform
The process
We follow the presentation in Duffie (2005, Appendix D.4), but with slightly modified notation. All functions and parameters associated with the generalized transform are written in Fraktur script. Let
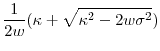 |
|||
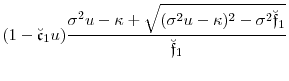 |
|||
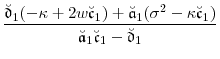
|
|||
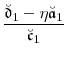 |
We next define for ![]()
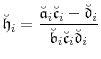
|
(B.2) |
and the functions
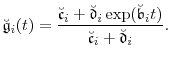
|
(B.3) |
Then the functions
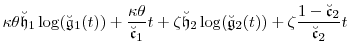
|
(B.4a) | ||
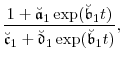 |
(B.4b) |
The discount function is
![]() where
where
![]() and
and
![]() . To obtain these, let
. To obtain these, let
![]() be the value of
be the value of
![]() when
when ![]() and
and ![]() for
for ![]() , and similarly define
, and similarly define
![]() ,
,
![]() , etc. These simplify to
, etc. These simplify to
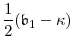 |
|||
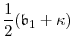 |
|||
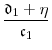 |
For the special case of
| (B.5a) | |||
| (B.5b) |
The
C. Expansion of the BAP survival probability function
We draw on the notation and results of Appendix B, and begin with the expansion in (i) of Proposition 5. Let
![]() , and introduce the change of variable
, and introduce the change of variable
![]() . Then for
. Then for ![]() , we can expand
, we can expand
where
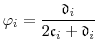
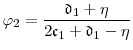
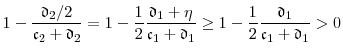
Using the same change of variable, the function ![]() has expansion
has expansion
Again, since
We combine these results to obtain
where
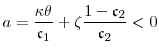
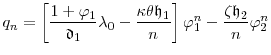
Since the composition of two analytic functions is analytic, a series expansion of ![]() in powers of
in powers of ![]() is absolutely convergent for
is absolutely convergent for ![]() (equivalently,
(equivalently, ![]() ). Thus, Proposition 5 holds with
). Thus, Proposition 5 holds with
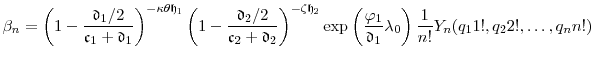
|
(C.4) |
These coefficients are most conveniently calculated via a recurrence rule easily derived from (A.6):
We now assume
![]() and derive the expansion in (ii) of Proposition 5. Here we introduce the change of variable
and derive the expansion in (ii) of Proposition 5. Here we introduce the change of variable
![]() . Following the same steps as above, we find that
. Following the same steps as above, we find that
![]() for
for ![]() can be expanded as
can be expanded as
Since
Using the same change of variable, the function ![]() has expansion
has expansion
Again, since
We combine these results to obtain
where
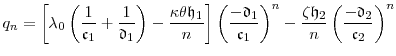
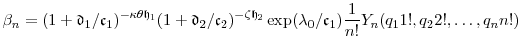
|
(C.9) |
Recurrence rule (C.5) applies in this case as well.
D. Derivatives of the generalized transform
Here we provide analytical expressions for
![]() . As in the previous appendix, the process
. As in the previous appendix, the process
![]() is assumed to follow a basic affine process with parameters
is assumed to follow a basic affine process with parameters
![]() . Recall that
. Recall that
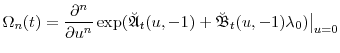
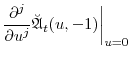 |
|||
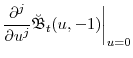 |
Then by Faà di Bruno's formula,
where
The functions ![]() and
and ![]() appear to be quite tedious (and the higher
order
appear to be quite tedious (and the higher
order ![]() and
and ![]() presumably even more so), as they depend on partial
derivatives of
presumably even more so), as they depend on partial
derivatives of
![]() ,
,
![]() , and so on. Fortunately, these derivatives simplify dramatically when evaluated at
, and so on. Fortunately, these derivatives simplify dramatically when evaluated at ![]() . Define
. Define
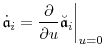
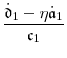 |
|||
An especially useful result is
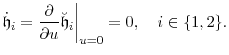
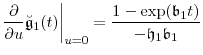 |
|||
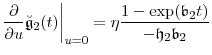 |
We arrive at
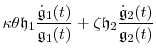 |
|||
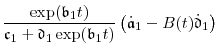 |
Perhaps surprisingly, there are no further complications for ![]() and
and ![]() for
for ![]() . Proceeding along the same lines, we find
. Proceeding along the same lines, we find
These expressions imply that the cost of computing
E. Differentiation of the
 functions
functions
As in the previous appendix, the process
![]() is assumed to follow a basic affine process with parameters
is assumed to follow a basic affine process with parameters
![]() . Let us define
. Let us define
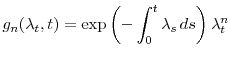
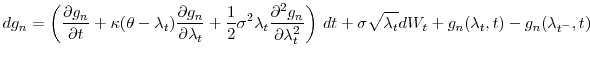
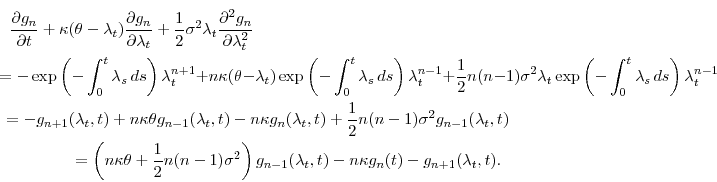
Taking expectations,
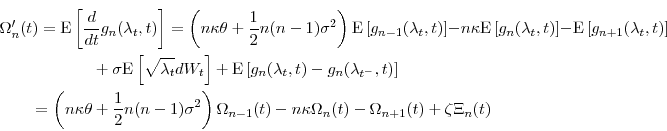
where we define
We interpret ![]() as the expected jump in
as the expected jump in ![]() conditional on a jump in
conditional on a jump in
![]() at time
at time ![]() . Let
. Let ![]() be the jump at time
be the jump at time ![]() . Noting that
. Noting that ![]() is distributed exponential with parameter
is distributed exponential with parameter
![]() , we have
, we have
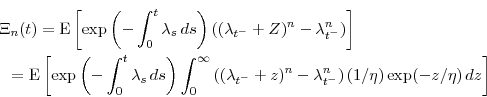
For
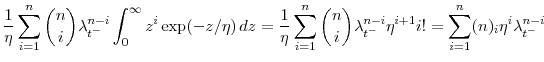
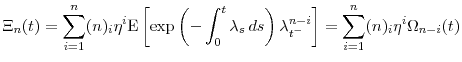
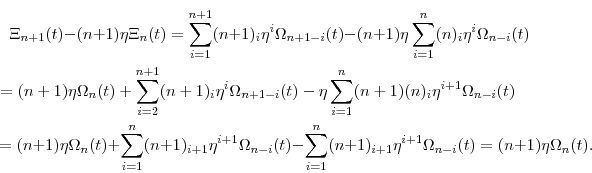
Journal of Banking and Finance, 32:, 1008
Journal of Finance, 57(3):, 1239
Functional Analysis and its Applications, 3(1):1-5, January-March, 1969.
Finance and Stochastics, 2(1):41-68, November, 1998.
Journal of Finance, 31(2):351-367, May , 1976.
Operations Research, 54(2):217-231, March-April, 2006.
Publicacions Matemàtiques, 49(1):197-212, 2005.
Journal of Financial Economics, 71:113-141, 2004.
Mathematical Finance, 13(3):345-382, July , 2003.
Comptes rendus de l'Académie des sciences, 17:370-376, August, 1843.
Review of Financial Studies, 25(7):, 2257
D. Reidel Publishing Company, Dordrecht, 1974.
Chapman & Hall, Boca Raton, 2004.
Proceedings: Mathematical, Physical and Engineering Sciences, 455, (1985)
Operations Research, 51(2):185-209, March-April, 2003.
Operations Research, 57(4):990-1005, July-August, 2009.
Review of Financial Studies, 12:197-226, 1999.
Journal of Banking and Finance, 29:, 2751
Review of Financial Studies, 12:687-720, 1999.
Princeton University Press, Princeton, 2003.
Econometrica, 68:, 1343
In Dana Schlomiuk, editor, Bifurcations and Periodic Orbits of Vector Fields, pages 75-184. Kluwer, Dordrecht, 1993.
Journal of Portfolio Management, 17(4):41-46, Summer, 1991.
Applied Mathematical Finance, 13(3):215-244, September, 2006.
FEDS, 2012
Management Science, 58(3):476-492, March , 2012.
Journal of Business and Economics Statistics, 28(3):438-451, July, 2010.
International Journal of Theoretical and Applied Finance, 12(8):, 1213
American Mathematical Society, Providence, RI, 2008.
Management Science, 54(6):, 1176
Journal of Econometrics, 122(1):185-212, September, 2004.
Journal of Finance, 50(1):53-86, March , 1995.
Mathematical Finance, 15(1):1-26, January , 2005.
Journal of Econometrics, 116:181-224, 2003.
Risk, 19(7):78-83, July, 2006.
Technical report, Barclays Capital, February, 2010.
Journal of Business, 63(4):511-524, October, 1990.
European Finance Review, 2:79-105, 1998.
September, 2012.
Mathematical Finance, 20(4):527-569, October, 2010.
Journal of Finance, 29(2):449-470, May , 1974.
Discrete Mathematics, 308:, 2450
Chicago Lectures in Mathematics. University of Chicago Press, Chicago, 1971.
Springer-Verlag, Berlin, 1992.
John Wiley & Sons, New York, 1968.
Journal of Computational and Applied Mathematics, 2012.
Transactions of the Cambridge Philosophical Society, 10(1):105-128, 1864.
Credit Research, Barclays Capital, 14 May, 2010.
Review of Financial Studies, 22(12):, 5099
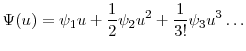
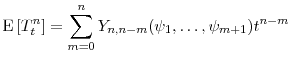
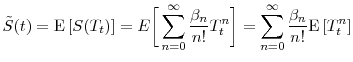
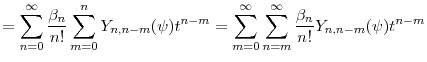
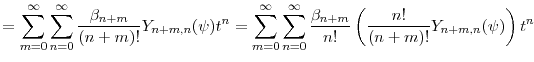
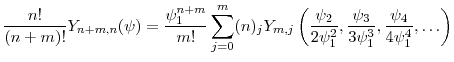
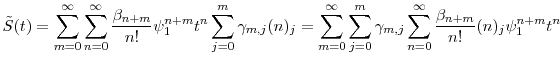
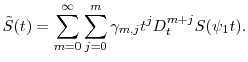
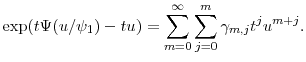
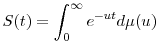
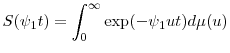
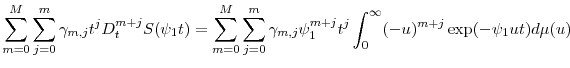
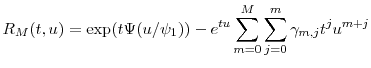
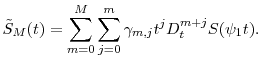
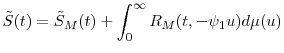
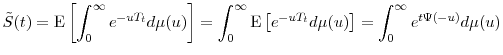
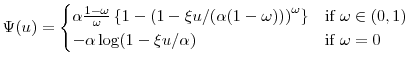
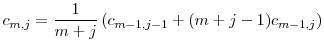
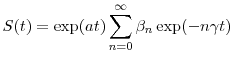
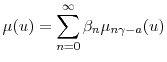
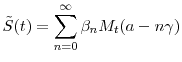
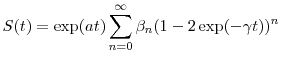
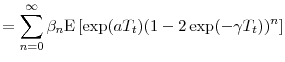
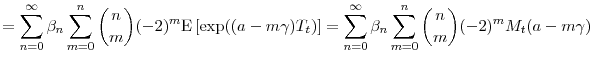
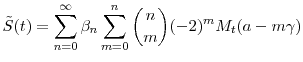
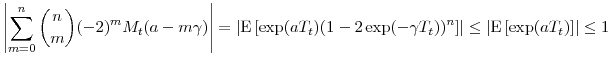
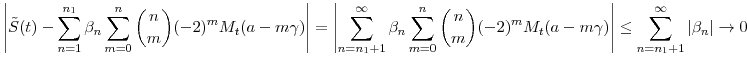
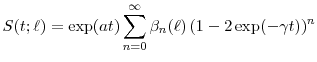
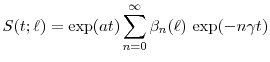
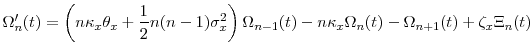
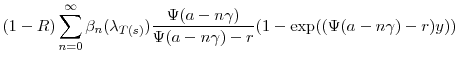
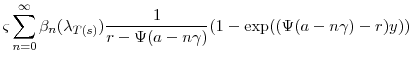
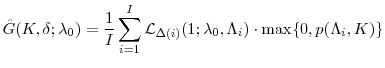
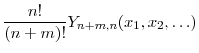
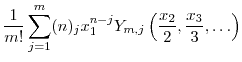
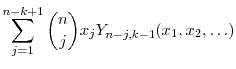
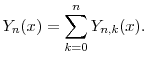
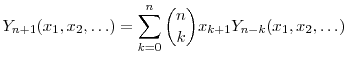
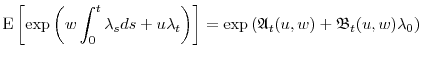
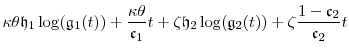
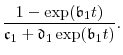
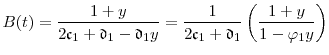
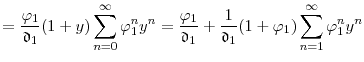
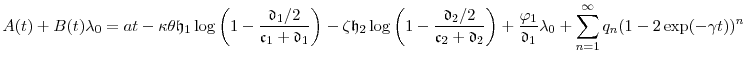
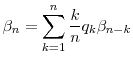
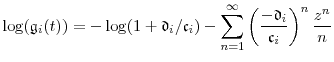
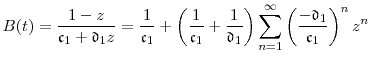
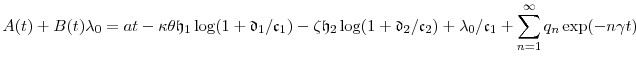
![\displaystyle (j-1)!\left( (-1)^{j+1}\ensuremath{\kappa}\theta \ensuremath{\mathfrak{h}}_1\left(\frac{\ensuremath{\dot{\ensuremath{\mathfrak{g}}}}_1(t)}{\ensuremath{\mathfrak{g}}_1(t)}\right)^j +\ensuremath{\zeta}\ensuremath{\mathfrak{h}}_2\left[\ensuremath{\eta}^j - \left(\ensuremath{\eta}-\frac{\ensuremath{\dot{\ensuremath{\mathfrak{g}}}}_2(t)}{\ensuremath{\mathfrak{g}}_2(t)}\right)^j\right] \right)](img576.gif)