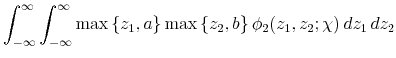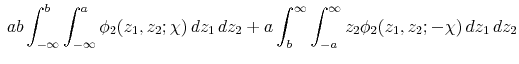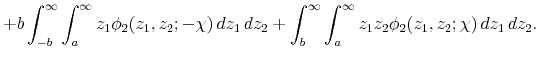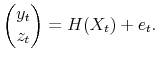Computing Arbitrage-Free Yields in Multi-Factor Gaussian Shadow-Rate Term Structure Models
PRELIMINARY DRAFT
Abstract:
1 Introduction
In late-2008, short-term nominal interest rates in the U.S. fell to their effective "zero lower bound" (see Bernanke et al., 2004 ). Since standard Gaussian term structure models do not rule out the possibility of negative model-implied yields, they provide a poor approximation to the behavior of nominal yields when the lower bound is binding (Kim and Singleton, 2012; Christensen and Rudebusch, 2013; Bauer and Rudebusch, 2013). Kim and Singleton (2012) find that shadow-rate models in the spirit of Black (1995) successfully capture yield-curve properties observed near the zero lower bound. However, arbitrage-free multi-factor versions of these models tend to be computationally intractable (Christensen and Rudebusch, 2013). Gorovoi and Linetsky (2004) show that bond prices in a one-factor shadow-rate model can be computed analytically by an eigenfunction expansion, but their approach does not generalize to multiple dimensions. Kim and Singleton (2012) and Ichiue and Ueno (2007) successfully estimate shadow-rate models with up to two factors, but they compute bond prices using discretization schemes that are subject to the curse of dimensionality. Christensen and Rudebusch (2013) use a yield formula proposed by Krippner (2012) to estimate shadow-rate Nelson-Siegel models with up to three factors, but 's derivation deviates from the usual no-arbitrage approach. Bauer and Rudebusch (2013) evaluate bond prices by Monte Carlo simulation for given model parameters from an unconstrained Gaussian term structure model, but they do not estimate a shadow-rate version of the model due to the computational burden.
This paper develops and applies a new technique for fast and accurate approximation of arbitrage-free zero-coupon bond yields in multi-factor Gaussian shadow-rate models of the term structure of interest rates. The computational complexity of the method does not increase with the number of yield curve factors, and, empirically, it produces yields that are accurate to within about half a basis point. The method is sufficiently fast to estimate a flexible, arbitrage-free, three-factor term structure model in which the shadow rate follows a Gaussian process. For illustration purposes, I estimate such a model by quasi-maximum likelihood on a sample of U.S. Treasury yields, using the unscented Kalman filter to account for the non-linear mapping between factors and yields.
2 Model
Consider first the standard, continuous-time N-factor Gaussian term structure model. In particular, let
![]() be
be ![]() -dimensional standard Brownian motion on a complete
probability space
-dimensional standard Brownian motion on a complete
probability space
![]() with canonical filtration
with canonical filtration
![]() . Assume there is a pricing measure
. Assume there is a pricing measure
![]() on
on
![]() that is equivalent to
that is equivalent to
![]() , and denote by
, and denote by
![]() Brownian motion under
Brownian motion under
![]() as derived from Girsanov's Theorem (Karatzas and Shreve, 1991). Suppose
as derived from Girsanov's Theorem (Karatzas and Shreve, 1991). Suppose ![]() latent factors (or states) representing uncertainty underlying term-structure securities follow the multivariate Ornstein-Uhlenbeck process
latent factors (or states) representing uncertainty underlying term-structure securities follow the multivariate Ornstein-Uhlenbeck process
were
Then by definition, the arbitrage-free time
with associated zero-coupon bond yield
Bond prices (and hence yields) can equivalently be defined in terms of forward rates:
where
Since ![]() is a Gaussian process (Karatzas and Shreve, 1991), it follows from (2) that the short rate
is a Gaussian process (Karatzas and Shreve, 1991), it follows from (2) that the short rate ![]() takes on strictly negative values with strictly positive probability. To modify the model in a way that accounts for the zero lower bound on nominal yields, Black (1995) proposes to think of
takes on strictly negative values with strictly positive probability. To modify the model in a way that accounts for the zero lower bound on nominal yields, Black (1995) proposes to think of ![]() as a shadow short rate (and, analogously, of
as a shadow short rate (and, analogously, of ![]() ,
,
![]() and
and ![]() as shadow bond price, shadow yield, and shadow
instantaneous forward rate, respectively) and define the observed short rate as the shadow rate censored at zero:
as shadow bond price, shadow yield, and shadow
instantaneous forward rate, respectively) and define the observed short rate as the shadow rate censored at zero:
With the observed short rate
3 Parameterizing the Lower Bound
The theoretical argument for a lower bound at zero on the nominal short rate (and hence on nominal yields) is based on arbitrage between bonds and currency Black (1995). In practice, the two assets may not be perfect substitutes for reasons such as
convenience, default risk, or legal requirements. This may push the empirical lower bound into slightly negative or slightly positive territory. The derivations in Section 2 are easily modified to accommodate a lower bound at
![]() . In particular, suppose
. In particular, suppose
![\displaystyle =-\frac{1}{T-t}\mathbf{E}_{t}^{\mathbb{Q}}\left[\exp\left(-\int_{t}^{T}\underline{r}_{s} ds\right) \right]](img36.gif) |
||
![\displaystyle =r_{\min}-\frac{1}{T-t}\mathbf{E}_{t}^{\mathbb{Q}}\left[\exp\left(-\int_{t}^{T}\max\{r_{s}-r_{\min},0\}\ ds\right)\right].](img37.gif) |
The last term is equal to the expression for the yield when the lower bound is zero, except that ![]() is subtracted from the shadow rate. Therefore, since
is subtracted from the shadow rate. Therefore, since
![]() , when the lower bound is nonzero we can compute zero-coupon yields as if the bound were zero, with
, when the lower bound is nonzero we can compute zero-coupon yields as if the bound were zero, with
![]() in place of
in place of ![]() , and then add
, and then add ![]() to the final result. The lower bound
to the final result. The lower bound ![]() can be set to a specific value based on
a priori reasoning, or treated as a free parameter in estimation.
can be set to a specific value based on
a priori reasoning, or treated as a free parameter in estimation.
4 Bond Price Computation
A central task in term-structure modeling is the (analytical and/or numerical) computation of arbitrage-free bond prices (and hence yields) based on equation (3). Section 4.1 reviews the standard approach using differential equations formalized by Duffie and Kan (1996), best suited to affine models. While it can be adapted to the shadow-rate framework, it loses much of its analytical tractability, and becomes computationally infeasible as the number of factors increases. Section 4.2 discusses an alternative method proposed by Krippner (2012). It defines a pseudo-forward rate that satisfies the lower bound (though differs from the arbitrage-free forward rate), and uses relationship (5) to approximate bond prices. Finally, Section 4.3 proposes a new approximation technique for yields in the shadow-rate model based on the expansion of a cumulant-generating function.
4.1 Partial Differential Equation
Like any conditional expectation of an
![]() -measurable random variable,
-measurable random variable,
![]() (the time
(the time ![]() price of a zero-coupon bond
maturing at time
price of a zero-coupon bond
maturing at time ![]() in the unconstrained Gaussian model, discounted to time 0 ) follows a martingale under
in the unconstrained Gaussian model, discounted to time 0 ) follows a martingale under
![]() . This is an immediate consequence of the definition of a martingale, after an application of the Law of Iterated Expectations. Using It
. This is an immediate consequence of the definition of a martingale, after an application of the Law of Iterated Expectations. Using It![]() 's Lemma and the Martingale Representation Theorem, we can therefore represent
's Lemma and the Martingale Representation Theorem, we can therefore represent ![]() by the function
by the function
![]() , where
, where ![]() solves the partial differential equation (PDE)
solves the partial differential equation (PDE)
with boundary condition
solves (7), where
with
assuming
A PDE analogous to (7) can be set up for the observed bond price in the shadow-rate model,
![]() . The only required modification is to replace the expression for the shadow short rate,
. The only required modification is to replace the expression for the shadow short rate,
![]() , by that for the observed short rate,
, by that for the observed short rate,
![]() . Unfortunately, when this non-linearity is introduced, the separation-of-variables procedure no longer applies, and no solution as
straightforward as (8) is available. It is possible to solve the modified version of (7) directly by numerical methods. This is the approach taken by Kim and Singleton (2012). It requires discretizing
. Unfortunately, when this non-linearity is introduced, the separation-of-variables procedure no longer applies, and no solution as
straightforward as (8) is available. It is possible to solve the modified version of (7) directly by numerical methods. This is the approach taken by Kim and Singleton (2012). It requires discretizing ![]() and
and ![]() on a multidimensional grid, which is computationally intensive and subject to the curse of dimensionality. Kim and Singleton (2012) therefore do not estimate models with more than two factors.
on a multidimensional grid, which is computationally intensive and subject to the curse of dimensionality. Kim and Singleton (2012) therefore do not estimate models with more than two factors.
4.2 Forward Rate Approximation
Krippner (2012) proposes an alternative approach to computing yields in shadow-rate models, which is implemented empirically by Christensen and Rudebusch (2013). It is based on an approximation to the forward rate
![]() . Substituting for
. Substituting for
![]() from the shadow-rate version of (3), and differentiating, we obtain
from the shadow-rate version of (3), and differentiating, we obtain
where
![\displaystyle \frac{d\underline{\mathbb{Q}}_{T}}{d\mathbb{Q}}=\frac{e^{-\int_{0}^{T}\underline{r}_{s}\, ds}}{\mathbf{E}^{\mathbb{Q}}\bigl[e^{-\int_{0}^{T}\underline{r}_{s}\, ds}\bigr]},](img68.gif)
Analogously,
expresses the shadow forward rate as the expectation under the shadow
The distribution of the shadow forward rate ![]() under
under
![]() can be derived more explicitly. First, from (5) and (8),
can be derived more explicitly. First, from (5) and (8),
Thus,
The final equality uses the It
Krippner (2012) takes advantage of this distributional property of
![]() . He defines a pseudo-forward rate as a hybrid between observed forward rate (12) and shadow forward rate (13):
. He defines a pseudo-forward rate as a hybrid between observed forward rate (12) and shadow forward rate (13):
This is the expectation under the shadow
This is formula (32) in Krippner (2012).3 Note from (17) that
Zero-coupon bond prices
![]() and yields
and yields
![]() can be approximated by substituting
can be approximated by substituting
![]() from (17) into (5) and (4).
from (17) into (5) and (4).
4.3 Cumulants
Since the PDE approach to pricing bonds in shadow-rate models becomes computationally intractable as the number of factors increases, and the approach proposed by Krippner (2012) relies on a forward rate that is not equal to the arbitrage-free forward rate, I propose a new cumulant-based technique to approximating yields in Gaussian shadow-rate models.
The quantity
![]() appearing in the shadow-rate version of (4) is the conditional cumulant-generating function4 under
appearing in the shadow-rate version of (4) is the conditional cumulant-generating function4 under
![]() , evaluated at -1 , of the random variable
, evaluated at -1 , of the random variable
![]() . It has the series representation
. It has the series representation
where
and the second-order approximation
where I make use of the fact that the first two cumulants of any random variable coincide with its first two centered moments.5
The first-order approximation (19) is equivalent to the method proposed independently and contemporaneously by Ichiue and Ueno (2013). I present it here both for comparison and to assess its relative performance in Section 5 below. I will, however, mostly focus on the
second-order approximation (20), which I argue is particularly promising a priori because it is exact in the Gaussian benchmark case.6
It can therefore be expected to perform well both for short maturities (where the higher-order terms in (18) are relatively small), and for long maturities as long as
![]() is small for large
is small for large ![]() (in which case
(in which case
![]() will behave approximately like a Gaussian process over sufficiently long horizons). Indeed, empirically, the second-order approximation turns out to be
highly accurate across maturities both during normal times and when rates are low (see Section 5).
will behave approximately like a Gaussian process over sufficiently long horizons). Indeed, empirically, the second-order approximation turns out to be
highly accurate across maturities both during normal times and when rates are low (see Section 5).
4.3.1 Computation of the First Moment
Evaluating the first- and second-order approximations (19) and (20) to zero-coupon yields requires computation of the first two cumulants (equivalently, centered moments) of
![]() . This subsection will be concerned with the first moment. As an initial step,
. This subsection will be concerned with the first moment. As an initial step,
by an application of Fubini's Theorem. Since
where
4.3.2 Computation of the Second Moment
Once we know the first moment of
![]() , it remains to evaluate
, it remains to evaluate
where the equality uses Fubini's Theorem and symmetry of the integrand. Since
where
![]() ,
,
![]() ,
,
![]() , and
, and
![]() denotes the decumulative bivariate normal cdf.
denotes the decumulative bivariate normal cdf.
That is, we can compute
![]() analytically up to the bivariate normal cdf, and we can then integrate this expression
numerically over
analytically up to the bivariate normal cdf, and we can then integrate this expression
numerically over ![]() and
and ![]() to obtain the second cumulant of
to obtain the second cumulant of
![]() .
.
4.3.3 Numerical Implementation
The following steps summarize the approximation procedure for zero-coupon yields for a given set of parameters
![]() and state vector
and state vector ![]() :
:
- Compute the conditional mean and covariance matrix of
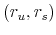 , for
, for 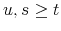 , using (A.4)
and (A.5).
, using (A.4)
and (A.5). - Using the results from step 1, compute
![\mathbf{E}_{t}^{\mathbb{Q}}\left[\underline{r}_{s}\right]](img113.gif) and
and
![\mathbf{E}_{t}^{\mathbb{Q}}\left[\underline{r}_{u}\underline{r}_{s}\right]](img129.gif) , for
, for 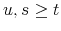 , as described in 4.3.1 and 4.3.2.
, as described in 4.3.1 and 4.3.2. - Integrate
![\mathbf{E}_{t}^{\mathbb{Q}}\left[\underline{r}_{s}\right]](img113.gif) numerically to obtain
numerically to obtain
![\mathbf{E}_{t}^{\mathbb{Q}}\left[\underline{R}_{t}^{T}\right]](img134.gif) , and integrate
, and integrate
![\mathbf{E}_{t}^{\mathbb{Q}}\left[\underline{r}_{u}\underline{r}_{s}\right]](img129.gif) numerically to obtain
numerically to obtain
![\mathbf{E}_{t}^{\mathbb{Q}}[\left(\underline{R}_{t}^{T}\right)^{2}]](img135.gif) .
. - Using the moments computed in step 3, approximate
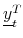 by
by
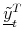 or
or
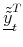 as defined in (19) and (20).
as defined in (19) and (20).
Note that the complexity of the algorithm does not depend on the number of yield curve factors ![]() , so it is not subject to the curse of dimensionality in the same way that some other
methods are.9
, so it is not subject to the curse of dimensionality in the same way that some other
methods are.9
For illustration purposes, in Appendix B I apply the second-order approximation method to estimate a three-factor shadow-rate model of the U.S. Treasury term structure.
5 Accuracy of Yield Approximation Methods
Section 4.3 argued intuitively that the second-order yield approximation (20) should be relatively precise. This section quantifies that claim. To get an initial sense of the relative numerical accuracy, I consider the stylized model used for illustration by Gorovoi and Linetsky (2004), and replicated for the same purpose in Krippner (2012). It is a one-factor model with
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . Gorovoi and Linetsky (2004) derive model-implied yield curves for states
. Gorovoi and Linetsky (2004) derive model-implied yield curves for states
![]() corresponding to shadow short rates
corresponding to shadow short rates
![]() . The four panels of Figure 1 plot the model-implied yield curves for each initial state. Within each panel, I compare four different yield approximation
schemes: Solving PDE (7) numerically (which, in a one-factor setting, is computationally feasible and can be considered the "exact" solution for comparison purposes), Krippner's (2012) approach described in Section 4.2, and the first- and second-order approximations proposed in Section
4.3. As the figure shows, the second-order approximation matches the exact PDE solution most closely, and consistently across states. The yield approximation error is uniformly less than one basis point. The first-order approximation generally overstates yields (an implication of the alternating
nature of series expansion (18)), with approximation errors increasing both in yield maturity and the level of the shadow short rate (in both cases, the first-order approximation is off by an increasingly large convexity adjustment arising from Jensen's inequality). Krippner's (2012) method generally undershoots yields, and is relatively more accurate when the shadow short rate is higher. Why this is the case can be seen intuitively by comparing the
. The four panels of Figure 1 plot the model-implied yield curves for each initial state. Within each panel, I compare four different yield approximation
schemes: Solving PDE (7) numerically (which, in a one-factor setting, is computationally feasible and can be considered the "exact" solution for comparison purposes), Krippner's (2012) approach described in Section 4.2, and the first- and second-order approximations proposed in Section
4.3. As the figure shows, the second-order approximation matches the exact PDE solution most closely, and consistently across states. The yield approximation error is uniformly less than one basis point. The first-order approximation generally overstates yields (an implication of the alternating
nature of series expansion (18)), with approximation errors increasing both in yield maturity and the level of the shadow short rate (in both cases, the first-order approximation is off by an increasingly large convexity adjustment arising from Jensen's inequality). Krippner's (2012) method generally undershoots yields, and is relatively more accurate when the shadow short rate is higher. Why this is the case can be seen intuitively by comparing the
![]() -measure expressions for the arbitrage-free forward rate (12) and Krippner's (2012) approximate forward rate (16): While both use the same time
-measure expressions for the arbitrage-free forward rate (12) and Krippner's (2012) approximate forward rate (16): While both use the same time ![]() short rate
short rate
![]() , Krippner's (2012) formula discounts by the shadow rate rather than the observed short rate. This means the discount factor tends to be larger than it
should be when
, Krippner's (2012) formula discounts by the shadow rate rather than the observed short rate. This means the discount factor tends to be larger than it
should be when
![]() is low, reducing the covariance between discount factor and
is low, reducing the covariance between discount factor and
![]() , and thus lowering the expectation of their product,
, and thus lowering the expectation of their product,
![]() .
.
To compare the relative performance of the different yield approximations in a more realistic empirical setting, I use the estimated model parameters and smoothed states from Appendix B.3 to compute model-implied yield curves for all dates in the sample.10 Since this is a three-factor model, solving PDE (7) numerically is no longer practicable. I therefore replace this benchmark by a simulated yield
![]() that consistently estimates the true yield
that consistently estimates the true yield
![]() based on
based on
![]() randomly drawn
randomly drawn
Figure 1: Yield curves (zero-coup on yield against maturity in years) implied by a one factor shadow-rate model with ρ0-0.01, ρ1-1, K
 0-0. K
0-0. K
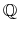 1- -0.1, and ∑ -0.02.The different panels corresp ond to di erent initial shadow short rates. Within each panel, the yield curve is computed using four metho ds: Numerical solution of PDE (7), Krippner's (2012) approach describ ed in Section 4.2,and the first- and second-order approximations proposed in Section 4.3.
1- -0.1, and ∑ -0.02.The different panels corresp ond to di erent initial shadow short rates. Within each panel, the yield curve is computed using four metho ds: Numerical solution of PDE (7), Krippner's (2012) approach describ ed in Section 4.2,and the first- and second-order approximations proposed in Section 4.3.
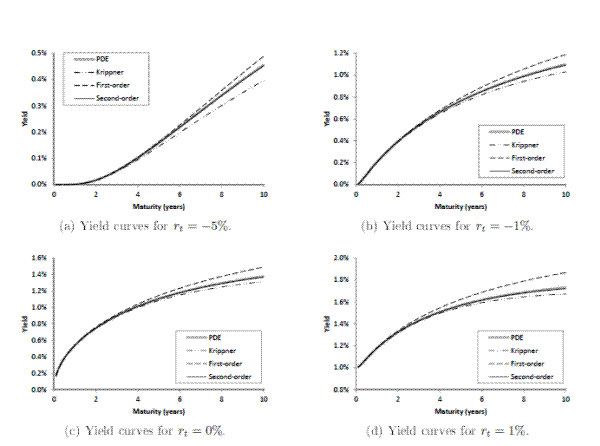 Figure 1 Data
Figure 1 Data
short-rate paths per sample date.11,12 Table 1 shows the mean simulation error of
![]() , and the root-mean-square errors (RMSE) against
, and the root-mean-square errors (RMSE) against
![]() of the yield
of the yield
![]() computed by Krippner's (2012) method, the first-order approximation
computed by Krippner's (2012) method, the first-order approximation
![]() defined in (19), and the second-order approximation
defined in (19), and the second-order approximation
![]() defined in (20). The table is divided into two panels. The top panel shows errors for the sub-sample Jan 1990-Nov 2008 (when
interest rates were at normal levels), and the bottom panel shows errors for the sub-sample Dec 2008-Dec 2012 (when the lower bound on nominal yields was binding at the short end of the yield curve). All methods are generally more precise at shorter maturities. As the first column in both panels
shows, the simulated yields are accurate to within approximately one fifth of a basis point at the ten-year maturity point. As shown in the second column of the tables, Krippner's (2012) method produces ten-year yields that are accurate to about one basis point during normal times, and to within four basis
points when the lower bound is binding. While the first-order method is more accurate when rates are low (the bottom panel), its errors remain substantial at the long end. The second-order method, the final column in the tables, produces ten-year yields that are accurate to approximately half a
basis point, both during normal times and when the lower bound is binding.
defined in (20). The table is divided into two panels. The top panel shows errors for the sub-sample Jan 1990-Nov 2008 (when
interest rates were at normal levels), and the bottom panel shows errors for the sub-sample Dec 2008-Dec 2012 (when the lower bound on nominal yields was binding at the short end of the yield curve). All methods are generally more precise at shorter maturities. As the first column in both panels
shows, the simulated yields are accurate to within approximately one fifth of a basis point at the ten-year maturity point. As shown in the second column of the tables, Krippner's (2012) method produces ten-year yields that are accurate to about one basis point during normal times, and to within four basis
points when the lower bound is binding. While the first-order method is more accurate when rates are low (the bottom panel), its errors remain substantial at the long end. The second-order method, the final column in the tables, produces ten-year yields that are accurate to approximately half a
basis point, both during normal times and when the lower bound is binding.
To further illustrate the time-varying relative performance of the three approximation schemes, Figure 2 plots the difference over time between the simulated ten-year yield and the three approximated yields. Krippner's (2012) method and the second-order approximation appear to be equally precise in the first few years of the sample,
| Maturity |
|
|
|
|
| 6m Sub-sample Kam 1990-Nov 2008 | 0.04 | 0.04 | 0.05 | 0.04 |
| 1y Sub-sample Kam 1990-Nov 2008 | 0.06 | 0.06 | 0.18 | 0.06 |
| 2y Sub-sample Kam 1990-Nov 2008 | 0.09 | 0.10 | 0.88 | 0.10 |
| 3y Sub-sample Kam 1990-Nov 2008 | 0.12 | 0.14 | 2.26 | 0.13 |
| 4y Sub-sample Kam 1990-Nov 2008 | 0.14 | 0.18 | 4.22 | 0.15 |
| 5y Sub-sample Kam 1990-Nov 2008 | 0.16 | 0.27 | 6.60 | 0.17 |
| 7y Sub-sample Kam 1990-Nov 2008 | 0.19 | 0.47 | 12.22 | 0.21 |
| 10y Sub-sample Kam 1990-Nov 2008 | 0.21 | 0.93 | 21.81 | 0.35 |
| 6m Sub-sample Dec 2008-Dec 2012 | 0.01 | 0.01 | 0.01 | 0.01 |
| 1y Sub-sample Dec 2008-Dec 2012 | 0.02 | 0.04 | 0.04 | 0.02 |
| 2y Sub-sample Dec 2008-Dec 2012 | 0.05 | 0.19 | 0.33 | 0.05 |
| 3y Sub-sample Dec 2008-Dec 2012 | 0.07 | 0.51 | 1.07 | 0.07 |
| 4y Sub-sample Dec 2008-Dec 2012 | 0.10 | 0.94 | 2.31 | 0.09 |
| 5y Sub-sample Dec 2008-Dec 2012 | 0.12 | 1.42 | 3.99 | 0.12 |
| 7y Sub-sample Dec 2008-Dec 2012 | 0.15 | 2.43 | 8.38 | 0.23 |
| 10y Sub-sample Dec 2008-Dec 2012 | 0.17 | 3.87 | 16.63 | 0.52 |
with fluctuations presumably largely due to simulation error.13 The discrepancy between simulated yield and Krippner's (2012) method increases over time as the level of yields declines, and exceeds five basis points by December 2012. The discrepancy between simulated yield and second-order approximation remains small and appears to show little systematic variation over time, perhaps trending up modestly towards the end of the sample. The first-order approximation has a large negative discrepancy initially, which shrinks over time but remains at a high absolute level even at the end of the sample.
Figure 2 also confirms that, just like in the simple one-factor model in Figure 1, the approximation errors under Krippner's (2012) method and the first-order scheme are largely systematic (rather than mere noise), in that the first-order approximation overstates arbitrage-free yields while Krippner's (2012) method tends to understate them.
In sum, the analysis above suggests that, empirically, the second-order yield approximation
![]() is accurate to within about one half of a basis point at maturities up to ten years, both during normal times and when the lower bound is binding. The
approximation error is one order of magnitude smaller than both the model-implied observation error in yields (see Table 3) and the next best approximation method proposed by Krippner's (2012). In contrast, the first-order approximation is acceptable at most at the very short end of
the yield curve.
is accurate to within about one half of a basis point at maturities up to ten years, both during normal times and when the lower bound is binding. The
approximation error is one order of magnitude smaller than both the model-implied observation error in yields (see Table 3) and the next best approximation method proposed by Krippner's (2012). In contrast, the first-order approximation is acceptable at most at the very short end of
the yield curve.
To add perspective, the approximation error in
![]() is no greater than commonly accepted fitting error in the derivation of constant-maturity zero-coupon bond yields from observed coupon-bearing
Treasuries (e.g., Gürkaynak et al., 2006). This puts the second-order approximation roughly on par with the numerical accuracy achieved
is no greater than commonly accepted fitting error in the derivation of constant-maturity zero-coupon bond yields from observed coupon-bearing
Treasuries (e.g., Gürkaynak et al., 2006). This puts the second-order approximation roughly on par with the numerical accuracy achieved
Figure 2: Deviation from simulated ten-year yield
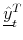 +10 of Krippner's (2012) yield approximation
+10 of Krippner's (2012) yield approximation
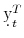 +10, the first-order yield appproximation
+10, the first-order yield appproximation
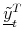 +10, and the second-order yield approximation
+10, and the second-order yield approximation
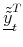 +10. Model parameters and filtered states are taken from Appendix B.
+10. Model parameters and filtered states are taken from Appendix B.
 Figure 2 Data
Figure 2 Data
by "exact" bond pricing methods in standard affine models, to the extent that they rely on numerical methods (say, to solve the system of ODEs (9)-(10)).14
6 Conclusion
This paper develops an approximation to arbitrage-free zero coupon bond yields in Gaussian shadow-rate term structure models. The complexity of the scheme does not depend on the number of factors. Further, I demonstrate that the method is computationally feasible by estimating a three-factor shadow-rate model of the U.S. Treasury yield curve. Based on Monte Carlo simulation, I also show that the yield approximation is approximately as precise as conventional approaches that are considered to be "exact."
A.1 Moments of 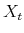
Consider the continuous time stochastic process ![]() defined in (1). The following derivations hold under both the
defined in (1). The following derivations hold under both the
![]() -measure and the
-measure and the
![]() -measure, hence for notational simplicity I will suppress dependence of moments and parameters on the measure. Since
-measure, hence for notational simplicity I will suppress dependence of moments and parameters on the measure. Since ![]() is a Gaussian process, all its finite-dimensional distributions are Gaussian Karatzas and Shreve, 1991). In particular, for
is a Gaussian process, all its finite-dimensional distributions are Gaussian Karatzas and Shreve, 1991). In particular, for ![]() , the
vectors
, the
vectors
![]() are jointly conditionally Gaussian, with
are jointly conditionally Gaussian, with
If
where "
and
A.2 Moments of Censored Gaussian Random Variables
This section derives two useful mathematical results involving the moments of censored Gaussian random variables.
Thus, it only remains to compute
![]() where
where ![]() is a standard normal
random variable, for arbitrary
is a standard normal
random variable, for arbitrary
![]() . By direct computation of the integral defining the expectation,
. By direct computation of the integral defining the expectation,
where ![]() is the standard normal cdf. Further,
is the standard normal cdf. Further,
Recursively substituting from (A.8) into (A.7), and finally into (A.6), establishes the result. ![]()
If
![\displaystyle \begin{pmatrix}X_{1}\ X_{2} \end{pmatrix}\sim N\left[\begin{pmatrix}\mu_{1}\ \mu_{2} \end{pmatrix},\begin{pmatrix}\sigma_{1}^{2} & \sigma_{12}\ \sigma_{12} & \sigma_{2}^{2} \end{pmatrix}\right]](img186.gif)
where
![]() ,
,
![]() ,
,
![]() ,
, ![]() denotes the univariate
standard normal pdf,
denotes the univariate
standard normal pdf, ![]() denotes the univariate standard normal cdf,
denotes the univariate standard normal cdf,
![]() denotes the bivariate normal pdf when both variables have zero means, unit variances, and correlation
denotes the bivariate normal pdf when both variables have zero means, unit variances, and correlation ![]() , and
, and ![]() and
and
![]() denote the corresponding cumulative and decumulative bivariate Gaussian distribution functions, where in particular
denote the corresponding cumulative and decumulative bivariate Gaussian distribution functions, where in particular
![]() .
.
The second and third terms can be evaluated using Lemma A.1. For the first term, it suffices to be able to compute
![]() for random variables
for random variables ![]() and
and ![]() that are bivariate normal with zero means, unit variances, and correlation
that are bivariate normal with zero means, unit variances, and correlation ![]() , and for arbitrary
, and for arbitrary
![]() . Using the properties of
. Using the properties of ![]() , this expectation can be
expanded as follows:
, this expectation can be
expanded as follows:
The first double integral is simply
![]() , the bivariate normal cdf. The second and third double integrals correspond to expected values of truncated bivariate normal random variables, and the last integral is
the expected cross product of a truncated bivariate normal random vector. These expected values are known up to the univariate standard normal cdf and the bivariate normal cdf, respectively (see Rosenbaum (1961)). Using the formulas in Rosenbaum (1961) to evaluate the integrals in (A.9), and substituting into (A.10), we obtain (A.9) after simplification.
, the bivariate normal cdf. The second and third double integrals correspond to expected values of truncated bivariate normal random variables, and the last integral is
the expected cross product of a truncated bivariate normal random vector. These expected values are known up to the univariate standard normal cdf and the bivariate normal cdf, respectively (see Rosenbaum (1961)). Using the formulas in Rosenbaum (1961) to evaluate the integrals in (A.9), and substituting into (A.10), we obtain (A.9) after simplification. ![]()
B. Empirical Implementation
This appendix empirically estimates a three-factor Gaussian shadow-rate term structure model using the yield approximation methodology proposed in Section 4.3. The main purpose is to demonstrate the computational tractability of the method in the context of a realistic application. For more in-depth discussion and empirical analysis, see Kim and Priebsch (2013).
B.1 Data
I use end-of-month zero-coupon U.S. Treasury yields from January 1990 through December 2012, for maturities of 6 months, 1-5, 7, and 10 years. I derive the 6-month yield from the corresponding T-bill quote, while longer-maturity zero yields are extracted from the CRSP U.S. Treasury Database using the unsmoothed Fama and Bliss (1987) methodology.15
I augment the yield data with survey forecasts from Blue Chip, interpolated to constant horizons of 1-4 quarters (available monthly), as well as annually out to 5 years and for 5-to-10 years (available every six months).16 Model-implied survey forecasts are subject to the same lower-bound constraint as yields,17 but their computation is substantially simpler: Forecasters report their expectation of the arithmetic mean of future observed short rates,
![]() . This is exactly (19) with the data-generating measure
. This is exactly (19) with the data-generating measure
![]() in place of pricing measure
in place of pricing measure
![]() . Therefore, the first-order method described in Section 4.3 produces exact model-implied survey forecasts. Intuitively, unlike yields, survey forecasts
are not subject to compounding, so there are no higher-order Jensen's inequality terms to consider.
. Therefore, the first-order method described in Section 4.3 produces exact model-implied survey forecasts. Intuitively, unlike yields, survey forecasts
are not subject to compounding, so there are no higher-order Jensen's inequality terms to consider.
B.2 Filtering and Estimation
Since the statistical properties of the term structure model laid out in Section 2 are formulated in terms of the latent state vector ![]() , but the data actually observed by the
econometrician consist of yields,
, but the data actually observed by the
econometrician consist of yields, ![]() , and survey expectations,
, and survey expectations, ![]() (see
Appendix B.1), I set up a joint estimation and filtering problem to obtain estimates of the model's parameters
(see
Appendix B.1), I set up a joint estimation and filtering problem to obtain estimates of the model's parameters
![]() .18 When discretely sampled at intervals
.18 When discretely sampled at intervals
![]() , the state vector
, the state vector ![]() follows a first-order Gaussian vector
autoregression,
follows a first-order Gaussian vector
autoregression,
where
Next, denote by
![]() the (non-linear) mapping from states
the (non-linear) mapping from states ![]() and parameters
and parameters ![]() to model-implied yields
to model-implied yields ![]() , and by
, and by
![]() the analogous mapping from states and parameters to model-implied survey forecasts
the analogous mapping from states and parameters to model-implied survey forecasts ![]() . For estimation purposes, I compute
. For estimation purposes, I compute ![]() through the second-order approximation (20), and
through the second-order approximation (20), and
![]() through the exact first-order method discussed in Appendix B.1. To simplify notation, denote the stacked mapping
through the exact first-order method discussed in Appendix B.1. To simplify notation, denote the stacked mapping
![]() by
by ![]() . If we assume that all yields
and survey expectations are observed with iid additive Gaussian errors, we obtain the observation equation
. If we assume that all yields
and survey expectations are observed with iid additive Gaussian errors, we obtain the observation equation
Together, equations (B.1) and (B.2) form a non-linear filtering problem.
The simple (linear) Kalman filter--optimal when measurement and observation equation are linear and all shocks are Gaussian--has been modified in a number of ways to accommodate nonlinearity as in (B.2). The unscented Kalman filter, proposed by Julier
et al. (1995), aims to deliver improved accuracy and numerical stability relative to the more traditional extended Kalman filter, without substantially increasing the computational burden.19,20 The algorithm is described in detail in Wan and van der Merwe (2001).
As a by-product of the filtering procedure, it conveniently produces estimates of the mean and covariance matrix of
![]() conditional on the econometrician's information set as of time
conditional on the econometrician's information set as of time ![]() . I use these to set up a quasi-maximum likelihood function based on (B.2),21 which I maximize numerically to obtain estimates of
the parameters
. I use these to set up a quasi-maximum likelihood function based on (B.2),21 which I maximize numerically to obtain estimates of
the parameters ![]() as well as their asymptotic standard errors (following Bollerslev and Wo oldridge, 1992).
as well as their asymptotic standard errors (following Bollerslev and Wo oldridge, 1992).
B.3 Estimation Results
To achieve econometric identification of the parameters ![]() in light of invariant transformations resulting in observationally equivalent models with different parameters (see Dai and Singleton, 2000 ), I follow Joslin et al. (2011) and impose the normalizations
in light of invariant transformations resulting in observationally equivalent models with different parameters (see Dai and Singleton, 2000 ), I follow Joslin et al. (2011) and impose the normalizations
![]() ,
,
![]() ,
,
![]() is diagonal and therefore completely determined by its ordered eigenvalues
is diagonal and therefore completely determined by its ordered eigenvalues
![]() , and
, and ![]() is lower triangular.
is lower triangular.
I estimate the model on the data set described in Appendix B.1, using the quasi-maximum likelihood (QML) procedure discussed in Appendix B.2. Table 2 displays the estimated model parameters
![]() , as well as their asymptotic standard errors.
, as well as their asymptotic standard errors.
| 0.0738 | |
| (0.0043) | |
| 0.0010 | |
| (0.0001) | |
| - 0.1038 | |
| (0.0226) | |
| - 0.3566 | |
| (0.1177) | |
| - 0.8574 | |
| (0.2876) | |
| - 0.0193 | |
| (0.0052) | |
| - 0.0099 | |
| (0.0224) | |
| 0.0278 | |
| (0.0233) | |
| 0.0268 | |
| (0.0084) | |
| - 0.0324 | |
| (0.0110) | |
| 0.0416 | |
| (0.0295) | |
| 0.0068 | |
| (0.0100) | |
| - 0.0397 | |
| (0.0302) | |
| - 0.0090 | |
| (0.0007) | |
| - 0.4679 | |
| (0.1574) | |
| - 0.3415 | |
| (0.1490) | |
| 0.3785 | |
| (0.6798) | |
| - 0.5752 | |
| (0.6303) | |
| - 1.1881 | |
| (1.1335) | |
| - 1.1875 | |
| (0.5740) | |
| 0.8908 | |
| (0.6982) | |
| 1.3060 | |
| (1.0641) | |
| 0.3990 | |
| (1.3561) |
Table 3 shows the QML-estimated standard deviations of the measurement errors in yields and survey variables (![]() in equation (B.2)). The average yield error is
8 basis points, and the average error in surveys is 21 basis points. For both yields and surveys, errors follow a U-shaped pattern, being largest at the short and long ends.
in equation (B.2)). The average yield error is
8 basis points, and the average error in surveys is 21 basis points. For both yields and surveys, errors follow a U-shaped pattern, being largest at the short and long ends.
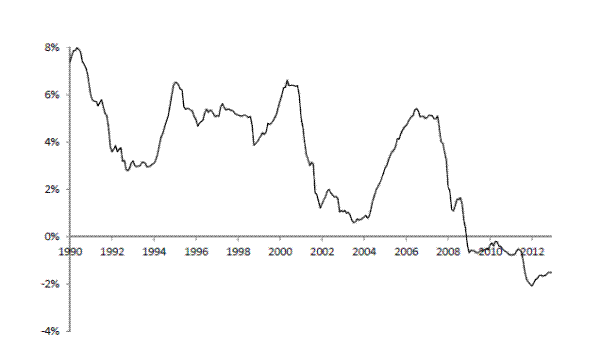
Figure 3 plots the model-implied shadow short rate ![]() over the sample period, based on the states implied by the Kalman smoother (that is, incorporating all information up to December
2012, the end of the sample). The shadow rate turned negative in December 2008, after the FOMC established a target federal funds rate range of 0 to 0.25 percent and the effective lower bound became binding, and has stayed negative through the end of the sample.
over the sample period, based on the states implied by the Kalman smoother (that is, incorporating all information up to December
2012, the end of the sample). The shadow rate turned negative in December 2008, after the FOMC established a target federal funds rate range of 0 to 0.25 percent and the effective lower bound became binding, and has stayed negative through the end of the sample.
| Maturity |
|
| 6m | 0.0017 |
| 1y | 0.0014 |
| 2y | 0.0006 |
| 3y | 0.0003 |
| 4y | 0.0004 |
| 5y | 0.0003 |
| 7y | 0.0006 |
| 10y | 0.0015 |
| Average | 0.0008 |
| Maturity |
|
| 1q | 0.0014 |
| 2q | 0.0002 |
| 3q | 0.0009 |
| 4q | 0.0014 |
| 2y | 0.0028 |
| 3y | 0.0026 |
| 4y | 0.0027 |
| 5y | 0.0031 |
| 5y-10y | 0.0034 |
| Average | 0.0021 |
References
Bauer, M., and Rudebusch, G. (2013), "Monetary Policy Exp ectations at the Zero Lower Bound," Working Paper, Federal Reserve Bank of San Francisco
Bernanke, B., Reinhart, V., and Sack, B. (2004), Monetary Policy Alterna- tives at the Zero Bound: An Empirical Assessment, "Brookings Papers on Economic Activity", 2:1-100
Black, F. (1995), Interest Rates as Options, Journal of Finance, 50(5):1371 1376
Bollerslev, T., and Wo oldridge, J. (1992), "Quasi-Maximum Likelihoodd Esti- mation and Inference in Dynamic Mo dels with Time-Varying Covariances, Econo- metric Reviews, 11(2):143-172
Chen, R. (1995), A Two-Factor, Preference-Free Mo del for Interest Rate Sensivite Claims, Journal of Futures Markets, 15(3):345-372
Christensen, J., and Rudebusch, G. (2013), Estimating Shadow-Rate Term Structure Mo dels with Near-Zero Yields, Working Paper, Federal Reserve Bank of San Francisco
Christoffersen, P., Dorion, C., Jacobs, K., and Karoui, L. (2012), Nonlinear Kalman Filtering in Affine Term Structure Mo dels, CREATES Research Paper 2012-49, Aarhus University
Dai, Q., and Singleton, K. (2000), Specification Analysis of Affine Term Structure Models, Journal of Finance, 60(5):1943-1978
Duan, J.-C., and Simonato, J.-G. (1999), "Estimating and Testing Exponential-Affine Term Structure Mo dels by Kalman Filter," Review of Quantitative Finance and Accounting, 13:111-135
Duffie, D., and Kan, R. (1996), "A Yield-Factor Mo del of Interest Rates," Mathematical Finance, 6:369-406
Fama, E., and Bliss, R. (1987) ,"The Information in Long-Maturity Forward Rates," American Economic Review, 77(4):680-692
Genz, A. (2004),"Numerical Computation of Rectangular Bivariate and Trivariate Normal and t Probabilities," Statistics and Computing, 14:251-260
Gorovoi, V., and Linetsky, V. (2004), "Black's Model of Interest Rates as Op- tions, Eigenfunction Expansions and Japanese Interest Rates," Mathematical Fi- nance, 14(1):49-78
Hamilton, J. (1994), The Time Series Analysis, Princeton University Press
Ichiue, H., and Ueno, Y. (2007), "Equilibrium Interest Rate and the Yield Curve in a Low Interest Environment," Bank of Japan Working Paper
(2013), "Estimating Term Premia at the Zero Bound: An Analysis of Japanese, U.S., and U.K. Yields," Bank of Japan Working Pap er No. 13-E-8
Joslin, S., Singleton, K., and Zhu, H. (2011), "A New Persp ective on Gaussian Dynamic Term Structure Mo dels," Review of Financial Studies, 24(3):926-970
Julier, S., Uhlmann, J., and Durrant-Whyte, H. (1995), "A New Approach for Filtering Nonlinear Systems," in Proceedings of the American Control Conference , pp. 1628-1632
Karatzas, I., and Shreve, S. (1991),Brownian Motion and Stochastic Calculus , Graduate Texts in Mathematics Series, Springer, London
Kim, D., and Orphanides, A. (2005), "Term Structure Estimation with Survey Data on Interest Rate Forecasts," Staff Working Pap er 2005-48, Federal Reserve Board
Kim, D., and Priebsch, M. (2013), "Estimation of Multi-Factor Shadow Rate Models," Working Pap er in Progress, Federal Reserve Board, Washington D.C.
Kim, D., and Singleton, K. (2012),"Term Structure Models and the Zero Bound: An Empirical Investigation of Japanese Yields," Journal of Econometrics, 170(1):32-49
Krippner, L. (2012), "Modifying Gaussian Term Structure Mo dels When Interest Rates are Near the Zero Lower Bound," Reserve Bank of New Zealand Discussion Paper 2012/02
Lund, J. (1997), Non-Linear Kalman Filtering Techniques for Term Structure Mo d-els, Working Paper, Aarhus Scho ol of Business
Piazzesi, M. (2010), "Affine Term Structure Models," in Handbook of Financial Econometrics , ed. by Y. Ait-Sahalia, and L. P. Hansen. North-Holland, Amsterdam
Rosenbaum, S. (1961),"Moments of a Truncated Bivariate Normal Distribution," Journal of the Royal Statistical Society, 23(2):405-408
Severini, T. (2005), Elements of Distribution Theory, Cambridge Series in Statistical and Probabilistic Mathematics, Cambridge University Press
Wan, E., and van der Merwe, R. (2001), "The Unscented Kalman Filter," in Kalman Filtering and Neural Networks, ed. by S. Haykin, pp. 221-280
Wu, S. (2010), Non-Linear Filtering in the Estimation of a Term Structure Mo del of Interest Rates WSEAS Transactions on Systems, 9(7):724-733
![\displaystyle {P}_{t}^{T}=\mathbf{E}_{t}^{\mathbb{Q}}\left[\exp\left(-\int_{t}^{T}{r}_{s}\, ds\right)\right]](img20.gif)
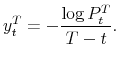
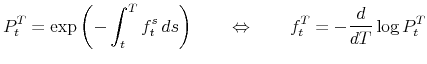

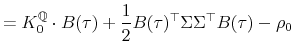
![\displaystyle \underline{f}_{t}^{T}=\mathbf{E}_{t}^{\mathbb{Q}}\Biggl[\frac{e^{-\int_{t}^{T}\underline{r}_{s}\, ds}}{\underline{P}_{t}^{T}}\underline{r}_{T}\Biggr]=\mathbf{E}_{t}^{\underline{\mathbb{Q}}_{T}}\left[\underline{r}_{T}\right]=\mathbf{E}_{t}^{\underline{\mathbb{Q}}_{T}}\left[\max\{{r_{T},0}\}\right]](img66.gif)
![\displaystyle f_{t}^{T}=\mathbf{E}_{t}^{\mathbb{Q}}\Biggl[\frac{e^{-\int_{t}^{T}r_{s}\, ds}}{P_{t}^{T}}r_{T}\Biggr]=\mathbf{E}_{t}^{\mathbb{Q}_{T}}\left[r_{T}\right]](img70.gif)
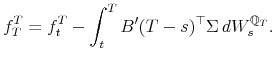
![\displaystyle \mathbf{E}_{t}^{\mathbb{Q}_{T}}\left[\left(\int_{t}^{T}B'(T-s)^{\top}\Sigma\, dW_{s}^{\mathbb{Q}_{T}}\right)^{2}\right]]](img79.gif)

![\displaystyle \d{f}_{t}^{T}=\mathbf{E}_{t}^{\mathbb{Q}}\Biggl[\frac{e^{-\int_{t}^{T}r_{s}\, ds}}{P_{t}^{T}}\underline{r}_{T}\Biggr]=\mathbf{E}_{t}^{\mathbb{Q}_{T}}\left[\underline{r}_{T}\right]=\mathbf{E}_{t}^{\mathbb{Q}_{T}}\left[\max\{{r_{T},0}\}\right].](img83.gif)
![\displaystyle \d{f}_{t}^{T}=\mathbf{E}_{t}^{\mathbb{Q}_{T}}\left[\max\{f_{T}^{T},0\}\right]=f_{t}^{T}\Phi\left(\frac{f_{t}^{T}}{\omega(T-t)}\right)+\omega(T-t)\phi\left(\frac{f_{t}^{T}}{\omega(T-t)}\right).](img85.gif)
![\displaystyle \log\mathbf{E}_{t}^{\mathbb{Q}}\left[\exp\left(-\underline{R}_{t}^{T}\right)\right]=\sum_{j=1}^{\infty}(-1)^{j}\frac{\kappa_{j}^{\mathbb{Q}}}{j!}](img96.gif)
![\displaystyle \underline{\tilde{y}}_{t}^{T}=\frac{1}{\tau}\kappa_{1}^{\mathbb{Q}}=\frac{1}{T-t}\mathbf{E}_{t}^{\mathbb{Q}}\left[\int_{t}^{T}\underline{r}_{s}\, ds\right]](img100.gif)
![\displaystyle \underline{\tilde{\tilde{y}}}_{t}^{T}=\frac{1}{T-t}\left(\kappa_{1}^{\mathbb{Q}}-\frac{1}{2}\kappa_{2}^{\mathbb{Q}}\right)=\frac{1}{T-t}\left(\mathbf{E}_{t}^{\mathbb{Q}}\left[\int_{t}^{T}\underline{r}_{s}\, ds\right]-\frac{1}{2}\mathrm{Var}_{t}^{\mathbb{Q}}\left[\int_{t}^{T}\underline{r}_{s}\, ds\right]\right)](img101.gif)
![\displaystyle \mathbf{E}_{t}^{\mathbb{Q}}\left[\int_{t}^{T}\underline{r}_{s}\, ds\right]=\int_{t}^{T}\mathbf{E}_{t}^{\mathbb{Q}}\left[\underline{r}_{s}\right]\, ds](img105.gif)
![\displaystyle \mathbf{E}_{t}^{\mathbb{Q}}\left[\int_{t}^{T}\underline{r}_{s}\, ds\right]=\int_{t}^{T}\left[\mu_{t\rightarrow s}\Phi\left(\frac{\mu_{t\rightarrow s}}{\sigma_{t\rightarrow s}}\right)+\sigma_{t\rightarrow s}\phi\left(\frac{\mu_{t\rightarrow s}}{\sigma_{t\rightarrow s}}\right)\right]\, ds](img110.gif)
![\displaystyle \mathbf{E}_{t}^{\mathbb{Q}}\left[\left(\int_{t}^{T}\underline{r}_{s}\, ds\right)^{2}\right]=2\int_{t}^{T}\int_{t}^{s}\mathbf{E}_{t}^{\mathbb{Q}}\left[\underline{r}_{u}\underline{r}_{s}\right]\, du\, ds](img114.gif)
![\displaystyle \mathbf{E}_{t}^{\mathbb{Q}}\left[\left(\int_{t}^{T}\underline{r}_{s}\, ds\right)^{2}\right]](img120.gif)
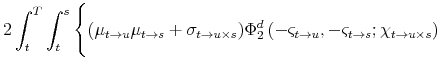
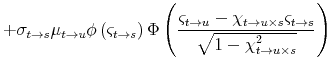
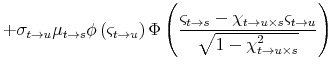
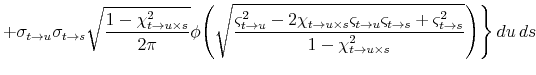
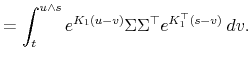
![\displaystyle \mathbf{E}[\max\{X,0\}]=\mu+\sigma\mathbf{E}\left[\max\left\{ \frac{X-\mu}{\sigma},-\frac{\mu}{\sigma}\right\} \right].](img180.gif)
![\displaystyle \mathbf{E}\left[\max\left\{ Z,a\right\} \right]=a\Phi(a)+\frac{1}{\sqrt{2\pi}}\int_{a}^{\infty}z\exp\left(-\frac{1}{2}z^{2}\right)\, dz,\\](img184.gif)
![\displaystyle \int_{a}^{\infty}z\exp\left(-\frac{1}{2}z^{2}\right)\, dz=\left[-\exp\left(-\frac{1}{2}z^{2}\right)\right]_{a}^{\infty}=\exp\left(-\frac{1}{2}a^{2}\right)=\sqrt{2\pi}\phi(a).](img185.gif)
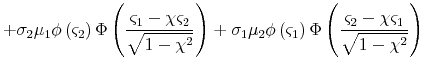
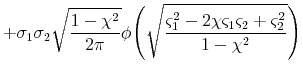
![\displaystyle \sigma_{1}\sigma_{2}\mathbf{E}^{\mathbb{}}\left[\max\left\{ \frac{X_{1}-\mu_{1}}{\sigma_{1}},-\frac{\mu_{1}}{\sigma_{1}}\right\} \max\left\{ \frac{X_{2}-\mu_{2}}{\sigma_{2}},-\frac{\mu_{2}}{\sigma_{2}}\right\} \right]\nonumber](img200.gif)