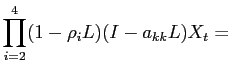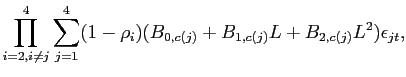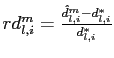Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 792, January 2004, Revised Version: March 2005--Screen Reader Version*
Can Long-Run Restrictions Identify Technology Shocks?
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Gal�'s innovative approach of imposing long-run restrictions on a vector autoregression (VAR) to identify the effects of a technology shock has become widely utilized. In this paper, we investigate its reliability through Monte Carlo simulations using calibrated business cycle models. We find it encouraging that the impulse responses derived from applying the Gal� methodology to the artificial data generally have the same sign and qualitative pattern as the true responses. However, we find considerable estimation uncertainty about the quantitative impact of a technology shock on macroeconomic variables, and little precision in estimating the contribution of technology shocks to business cycle fluctuations. More generally, our analysis emphasizes that the conditions under which the methodology performs well appear considerably more restrictive than implied by the key identifying assumption, and depend on model structure, the nature of the underlying shocks, and variable selection in the VAR. This cautions against interpreting responses derived from this approach as model-independent stylized facts.
Keywords: Technology shocks, vector autoregressions, business cycle models.
* Corresponding author: Board of Governors of the Federal Reserve System, Washington D.C. 20551-0001. Telephone (202) 452 2550. E-mail [email protected]. Return to text
** The authors are economists at the Board of Governors of the Federal Reserve System. We thank Olivier Blanchard, James Nason, Adrian Pagan, Robert Vigfusson, Chao Wei, and seminar participants at the Federal Reserve Bank of Atlanta, Federal Reserve Board, George Washington University, MIT, the Society for Computational Economics 2004 Meeting, and the Society for Economic Dynamics 2003 Meeting. We especially thank Jon Faust, Roberto Perotti (the editor), and three anonymous referees for their comments. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1 Introduction
The pioneering work of Blanchard and Quah (1989), King, Plosser, Stock, and Watson (1991), and Shapiro and Watson (1988) has stimulated widespread interest in using vector autoregressions (VARs) that impose long-run restrictions to identify the effects of shocks. This methodology has proved appealing because it does not require a fully-articulated structural model or numerous model-specific assumptions.
One important recent application of this approach, introduced by Gali (1999), involves using long-run restrictions to identify the effects of a technology shock. The key identifying assumption in this approach is that only technology innovations can affect labor productivity in the long-run. As discussed in Gali (1999), this assumption holds in a broad class of models under relatively weak assumptions about the form of the production function. Numerous researchers have used this approach to assess how technology shocks affect macroeconomic variables, and to quantify the importance of technology shocks in accounting for output and employment fluctuations.1
While the simplicity of Galí's methodology has contributed to its broad appeal, the recent literature has suggested reasons to question whether it is likely to yield reliable inferences about the effects of technology shocks. One reason is that it is difficult to estimate precisely the long-run effects of shocks using a short data sample. Accordingly, as emphasized by Faust and Leeper (1997), structural VARs (SVARs) that achieve identification through long-run restrictions may perform poorly when estimated over the sample periods typically utilized. A second reason, discussed by Cooley and Dwyer (1998) and Lippi and Reichlin (1993), is that a short-ordered VAR may provide a poor approximation of the dynamics of the variables in the VAR if the true data-generating process has a VARMA representation.
In this paper, we critique the reliability of the Galí methodology by using Monte Carlo simulations of reasonably-calibrated dynamic general equilibrium models. In particular, we compare the response of macroeconomic variables to a technology innovation derived from applying Galí's identifying scheme with the ``true'' response implied by our models. We utilize two alternative models of the business cycle as the data-generating process. The first is a standard real business cycle (RBC) model with endogenous capital accumulation that includes shocks to total factor productivity, labor income tax rates, government spending, and labor supply. The second model incorporates some of the dynamic complications that have been identified in the recent literature as playing an important role in accounting for the effects of real and monetary shocks.2 These features include habit persistence in consumption, costs of changing investment, variable capacity utilization, and nominal price and wage rigidity. The latter model, which we call the sticky price/wage model, provides an alternative perspective on how technology shocks affect the labor market in the short-run, since hours worked decline sharply after a positive innovation in technology rather than exhibit a modest rise as in the RBC model.
We generate Monte Carlo simulations from each model using an empirically-reasonable sample length of 180 quarters. The SVAR that we estimate using the simulated data includes labor productivity growth, the level of hours worked, the ratio of nominal consumption to output, and the ratio of nominal investment to output.3 One appealing feature of this specification is that a low-ordered VAR (i.e., four lags) provides a close approximation to the true data-generating process in the benchmark parameterizations of each of the models considered.4 This allows us to interpret the bias in the estimated impulse responses as arising almost exclusively due to the small sample problems emphasized by Faust and Leeper (1997).
Broadly speaking, the shocks derived from application of the Galí methodology to the simulated data ``look like'' true technology shocks in both of the models we consider. In particular, the mean impulse response functions (IRFs) of output, investment, consumption, and hours worked derived from the Monte Carlo simulations uniformly have the same sign and qualitative pattern as the true responses. Moreover, we find that the probability of inferring a response of output, consumption, or investment that has the qualitatively incorrect sign (even for only a few quarters) is generally low.
However, we find that small-sample bias poses quantitative problems for this identifying scheme. There is substantial downward bias in the estimated responses of output, labor productivity, consumption, and investment derived from the Monte Carlo simulations in each of the models. Moreover, given the bias and substantial spread in the distribution of the impulse responses, we find that the probability that a researcher would estimate a response for output that lies uniformly more than 33 percent away from the true response (for the first four quarters following the shock) is about 25 percent in each of the models.
We show that the bias in the estimated impulse responses is dependent on model structure. Within the context of the benchmark models, the bias can be attributed to two related sources. First, the slow adjustment of capital makes it hard to gauge the long-run impact of a technology shock on labor productivity, contributing to downward bias in the estimated impulse responses.5 Second, the identification procedure has difficulty disentangling technology shocks from other shocks that have highly persistent, even if not permanent, effects on labor productivity (such as labor supply or tax rate shocks).6 As a result, even in the absence of shocks that would violate Galí's long-run identifying assumption, the estimated technology shock may incorporate a sizeable non-technology component. Accordingly, the bias in the estimated response of a given variable to a technology shock depends on the relative magnitude of technology and non-technology shocks, and on its response to non-technology shocks.
Our results also have implications for a principal application of the Galí methodology, which has involved using estimates derived from SVARs to evaluate the plausibility of alternative models of the business cycle.7 Interestingly, though there is considerable uncertainty about the estimated response of hours worked, our results suggest that the SVAR approach may provide some basis for discriminating between models that have sufficiently divergent implications about how technology shocks affect the labor market. For instance, we find that the probability of finding an initial decline in hours that persists for two quarters is 93 percent in the model with nominal rigidities, but only 26 percent in the RBC model. Accordingly, a researcher who found that hours worked declined after a positive innovation in technology in the data could reasonably interpret this finding as providing some evidence in favor of the sticky price/wage model. While our results are encouraging on this dimension, our analysis cautions that appropriate specification of the SVAR (i.e., variables included and their transformations) appears to play a key role in allowing tests to have sufficient power to discriminate between alternative models.
By contrast, we find that there is very little precision in estimating the contribution of technology shocks to output fluctuations at business cycle frequencies. For example, the 90 percent confidence intervals for the contribution range between 7 and 90 percent for the benchmark RBC model, and between 7 and 80 percent for the sticky price/wage model.
Our analysis also illustrates how the performance of the Galí procedure may be influenced by the selection of variables in the VAR, the transformations applied, and the nature of the underlying shocks. We find that the performance of the Galí procedure may exhibit noticeable sensitivity to the specification of variables in the VAR. This sensitivity in part reflects that for some variable choices a low-ordered VAR may perform poorly in capturing the VARMA representations implied by our models.8 We also find that the performance of the Galí methodology deteriorates on some dimensions with the inclusion in the RBC model of technology shocks that are stationary but highly persistent.
Overall, Galí's methodology appears to offer a fruitful approach to uncovering the effects of technology shocks, and it is encouraging that our baseline, four-variable SVAR specification performs reasonably well across the alternative models considered. However, our analysis emphasizes that the conditions under which the Galí methodology performs well appear considerably more restrictive than implied by the key identifying restriction, and depend on model structure, the nature of the underlying shocks, and on variable selection in the SVAR. Accordingly, we caution that empirical estimates of the effects of technology shocks should not be regarded as model-independent stylized facts. Instead, the interpretation of results derived from the Galí approach should be informed by the model or class of models that the researcher regards as most plausible, with the model serving as a guidepost about biases likely to arise and the limitations of the approach.
The rest of this paper is organized as follows. Section 2 outlines our baseline RBC model and describes the calibration. Section 3 reviews the Galí identification scheme. Section 4 reports our results for the RBC model, and Section 5 discusses the results for the sticky price/wage model. Section 6 concludes.
2 The RBC Model
We begin by outlining a relatively standard real business cycle model. The model structure is very similar to that analyzed by King, Plosser, and Rebelo (1988), though we include a broader set of shocks.
2.1 Household Behavior
The utility function of the representative household is
where the discount factor
where
The representative household's budget constraint in period
![]() states that its
expenditure on consumption and investment goods (
states that its
expenditure on consumption and investment goods (![]() and net purchases of bonds
and net purchases of bonds
![]() must equal its
after-tax disposable income:
must equal its
after-tax disposable income:
The household earns after-tax labor income of
In every period ![]() , the
household maximizes utility (1)
with respect to its consumption, labor supply, investment,
(end-of-period) capital stock, and real bond holdings, subject to
its budget constraint (3), and the
transition equation for capital (4).
, the
household maximizes utility (1)
with respect to its consumption, labor supply, investment,
(end-of-period) capital stock, and real bond holdings, subject to
its budget constraint (3), and the
transition equation for capital (4).
2.2 Firms
The representative firm uses capital and labor to produce a final output good that can either be consumed or invested. This firm has a constant returns-to-scale Cobb-Douglas production function of the form:
In the above,
and
| (7) |
with
The firm purchases capital services and labor in perfectly
competitive factor markets, so that it takes as given the rental
price of capital ![]() and the aggregate wage
and the aggregate wage ![]() Since the firm behaves as a price taker in the
output market as well as in factor markets, the following
efficiency conditions hold for the choice of capital and labor:
Since the firm behaves as a price taker in the
output market as well as in factor markets, the following
efficiency conditions hold for the choice of capital and labor:
2.3 Government
Some of the final output good is purchased by the government, so that the market-clearing condition is:
Government purchases are assumed to have no direct effect on the utility function of the representative household. We also assume that government purchases as a fraction of output,
where
The government's budget is balanced every period, so that total
taxes - which include both distortionary taxes on labor and capital
income - equal the sum of government purchases of the final output
good and net lump-sum transfers to households.9Hence, the government's budget
constraint at date ![]() is:
is:
The tax rates on capital and labor are assumed to be exogenous and evolve according to:
where
2.4 Solution and Calibration
To analyze the behavior of the model, we first apply a
stationary-inducing transformation to those real variables that
share a common trend with the level of technology. This entails
detrending real GDP, the GDP expenditure components, and the real
wage by ![]() and the
capital stock,
and the
capital stock, ![]() ,
by
,
by ![]() . We then
compute the solution of the model using the numerical algorithm of
Anderson and Moore (1985), which provides an efficient implementation of the
solution method proposed by Blanchard and Kahn (1980).
. We then
compute the solution of the model using the numerical algorithm of
Anderson and Moore (1985), which provides an efficient implementation of the
solution method proposed by Blanchard and Kahn (1980).
Table 1 summarizes the calibrated
values of most of the model's parameters. The model is calibrated
at a quarterly frequency so that
![]() and
and
![]() . The
utility function parameter
. The
utility function parameter ![]() is set to 1.5 so as to imply a Frisch elasticity
of labor supply of 2/3, an elasticity well within the range of most
empirical estimates.10 The
capital share parameter
is set to 1.5 so as to imply a Frisch elasticity
of labor supply of 2/3, an elasticity well within the range of most
empirical estimates.10 The
capital share parameter ![]() is set to 0.35, and we normalized
is set to 0.35, and we normalized
![]() , as
, as
![]() does not
affect the model's log-linear dynamics.
does not
affect the model's log-linear dynamics.
Using data on the share of government consumption to U.S. GDP,
we fit a first order autoregression for ![]() (allowing for a linear time
trend) and estimated
(allowing for a linear time
trend) and estimated ![]() and
and
![]() in equation
(10) to be 0.98 and 0.003, respectively. We
set
in equation
(10) to be 0.98 and 0.003, respectively. We
set ![]() so that the ratio of
government spending to output is 20% in the model's non-stochastic
steady state.
so that the ratio of
government spending to output is 20% in the model's non-stochastic
steady state.
For the parameters governing the two tax rate series, we
estimated equation (12) using OLS after
constructing these tax rates series based on U.S. data from
1958-2002 following the methodology described in
Jones (2002).11 Our
estimates implied
![]() ,
,
![]() ,
and
,
and
![]() for the labor tax rate and
for the labor tax rate and
![]() ,
,
![]() ,
and
,
and
![]() for the capital tax rate.
for the capital tax rate.
For reasons that we discuss below, it is convenient to exclude
capital tax rate and temporary technology shocks from our benchmark
calibration of the RBC model; thus, we set
![]() . In this case, we can
obtain a time series for
. In this case, we can
obtain a time series for ![]() by defining the Solow residual as:
by defining the Solow residual as:
and noting that
 . We then estimate
. We then estimate
In the absence of labor-supply shocks, our calibrated RBC model
would significantly underestimate the volatility in hours worked -
a familiar problem in the real business cycle literature. To see
this, Table 2 compares the second
moments of several key variables that are implied by our model with
their sample counterparts based on U.S. data. As shown in the
column labelled ``
![]() '',
the model significantly understates the ratio of the standard
deviation of HP-filtered hours to the standard deviation of
HP-filtered output. For our benchmark calibration, we address this
issue by incorporating labor supply shocks.12 In particular, we set
'',
the model significantly understates the ratio of the standard
deviation of HP-filtered hours to the standard deviation of
HP-filtered output. For our benchmark calibration, we address this
issue by incorporating labor supply shocks.12 In particular, we set
![]() and
choose an innovation variance
and
choose an innovation variance
![]() that
allows the model to match the observed standard deviation of
HP-filtered hours relative to the standard deviation of HP-filtered
output.
that
allows the model to match the observed standard deviation of
HP-filtered hours relative to the standard deviation of HP-filtered
output.
Table 2 shows the selected moments for the benchmark RBC model. A comparison of the model's implications for the volatility of output, investment, and consumption to the corresponding sample moments suggests that this calibrated model performs fairly well on these dimensions, even though it was not calibrated specifically to match these moments.
3 The SVAR Specification
In this section, we outline the estimation procedure that a researcher would follow given a single realization of data. The structural VAR takes the form:
where
In our benchmark specification of the VAR, ![]() contains the log difference of
average labor productivity, the log of hours worked, the log of the
consumption-to-output ratio, and the log of the
investment-to-output ratio. All variables are expressed as a
deviation from the model's nonstochastic steady state, and average
labor productivity is defined as
contains the log difference of
average labor productivity, the log of hours worked, the log of the
consumption-to-output ratio, and the log of the
investment-to-output ratio. All variables are expressed as a
deviation from the model's nonstochastic steady state, and average
labor productivity is defined as
![]() . The
inclusion of average labor productivity growth in
. The
inclusion of average labor productivity growth in ![]() is standard in the empirical
literature using VARs to identify technology shocks. While the
empirical literature is divided on whether hours worked are best
included in levels or differences, the former specification is
selected, because the DGE model implies that hours are stationary
in levels. The ratios of investment and consumption to output are
included in the VAR, in part because Christiano, Eichenbaum, and Vigfusson (2003) have
found these variables to be important in controlling for
omitted-variable bias when using U.S. data.
is standard in the empirical
literature using VARs to identify technology shocks. While the
empirical literature is divided on whether hours worked are best
included in levels or differences, the former specification is
selected, because the DGE model implies that hours are stationary
in levels. The ratios of investment and consumption to output are
included in the VAR, in part because Christiano, Eichenbaum, and Vigfusson (2003) have
found these variables to be important in controlling for
omitted-variable bias when using U.S. data.
The identification of the technology shock is achieved in the following way. First, it is assumed that the innovations are orthogonal and have been normalized to unity so that
| (15) |
where
Here, R(L) is the reduced-form moving average representation of the VAR given by
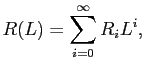 |
(17) |
where
In our Monte Carlo study, we generate 10,000 data samples from the relevant DGE model, and apply the estimation strategy discussed above to each sample. Every data sample consists of 180 quarterly observations.13
4 Estimation results for the RBC Model
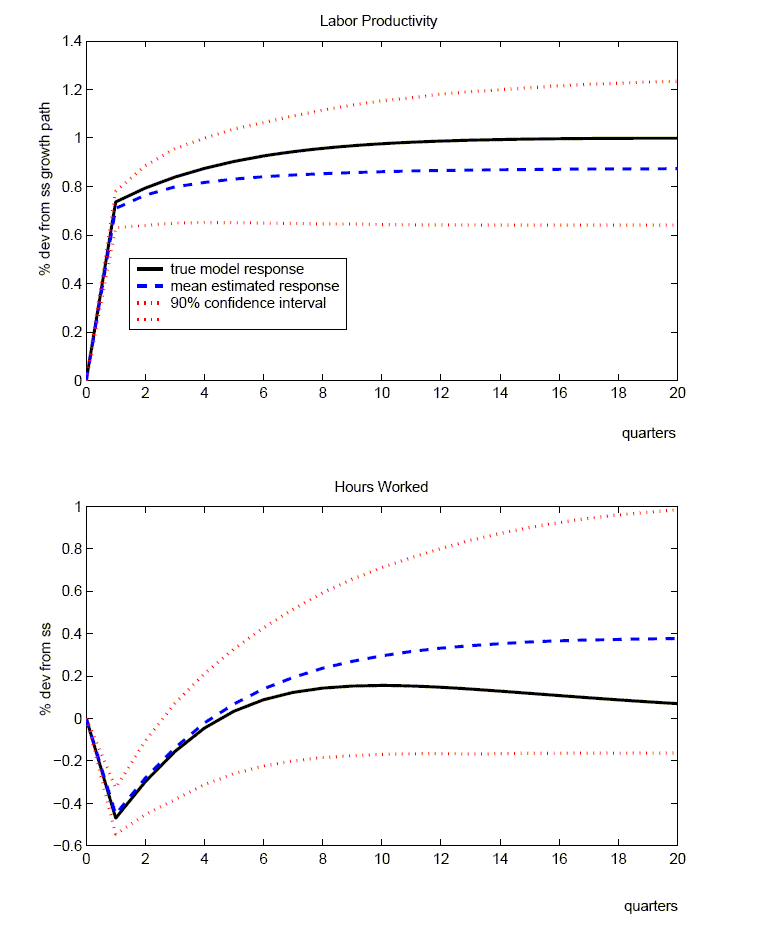
Figure 1 reports the response of labor productivity, hours worked, consumption, investment, and output to a technology shock for the benchmark calibration of the RBC model.14 In each panel, the solid lines show the true responses from the DGE model. The innovation occurs at date 1 and has been scaled so that the level of labor productivity rises by one percent in the long run.
The dashed lines show the mean of the impulse responses derived from applying our benchmark, four-variable SVAR to the 10,000 artificial data samples (the median response is nearly identical).15 The dotted lines show the 90 percent pointwise confidence interval of the SVAR's impulse responses.16
As shown in Figure 1, the mean responses of labor productivity, consumption, investment, and output have the same sign and qualitative pattern as the true responses. As indicated by the pointwise confidence intervals, the SVAR is likely to give the appropriate sign of the response for these variables. For hours worked, the mean estimate is also qualitatively in line with the true response; however, the confidence interval is wide, indicating that there is a non-negligible probability of a negative estimate.
Quantitatively, the SVAR does not perform as well. As seen in Figure 1, the mean responses of the SVAR systematically underestimate labor productivity, consumption, investment, and output, while overestimating hours worked. To gauge the size of the bias, the top row of Table 3 reports the average absolute percent difference between the mean response and the true response over the first twelve quarters for each of the variables except hours worked.17 For hours, Table 3 reports the absolute value of the difference between the mean estimated response and the true response (we simply report the difference because the true response is very small). As reported in the first row of Table 3, labor productivity is underestimated by the SVAR by 40% on average over the first 12 quarters after the innovation to technology, while output is underestimated by 25%. We defer our explanation of these results to Section 4.1.
While useful for illustrating the bias associated with the
SVAR's estimates, the relative distance measure does not capture
the uncertainty that a researcher confined to a single draw of the
data would confront. After all, the impulse response derived using
a single realization of the data may diverge substantially from the
mean. Accordingly, we consider an alternative measure of how well
the SVAR's point estimates of the impulse responses match the
truth. For variable ![]() , this
measure is defined as
, this
measure is defined as
where
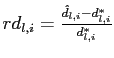 and
and
While the probability of underestimating labor productivity, consumption, output, and investment is substantial, the probability of inferring an incorrect sign for several quarters is very low (not reported). It is also interesting to assess the probability of inferring a response of hours worked that has the incorrect sign in the first few periods, given the significant attention recent research has devoted to this question. Accordingly, for hours worked, Tables 4, 5, and 6 report the probability that the estimated response of hours worked is incorrect (negative in this model) in each of the first 2, 4, and 12 quarters, respectively. As shown in Figure 1, the true response of hours is positive, and there is upward bias in the mean estimated response. Nevertheless, Table 5 shows that there is a 23% chance a researcher would find that hours worked fell for four straight quarters in the year following a technology shock.18
Gali (1999), Gali (2004), and Christiano, Eichenbaum, and Vigfusson (2003) have
employed SVARs with long-run restrictions to estimate the
contribution of technology shocks to business cycle fluctuations,
and have used these estimates to conclude that technology shocks
only play a small role in driving output fluctuations over the
business cycle.19 We use
our framework to assess the reliability of these estimates. The top
left panel of Figure 2 shows the cumulative
distribution function derived from Monte Carlo simulations of our
estimator of the contribution of technology shocks to output
fluctuations. This contribution is defined as
![]() where
where
![]() denotes
the unconditional variance of HP-filtered output in the model and
denotes
the unconditional variance of HP-filtered output in the model and
![]() is the variance of HP-filtered output conditional on only unit-root
technology shocks.20 The
distribution function appears close to uniform over the unit
interval, so that the 90% confidence bands for the estimator
include contributions ranging from 7 to 91 percent (confidence
bands are indicated by stars on the x-axis). Therefore, for the
benchmark RBC model, this application of the SVAR methodology
yields uninformative estimates of the contribution of technology
shocks to output fluctuations at business cycle frequencies.
is the variance of HP-filtered output conditional on only unit-root
technology shocks.20 The
distribution function appears close to uniform over the unit
interval, so that the 90% confidence bands for the estimator
include contributions ranging from 7 to 91 percent (confidence
bands are indicated by stars on the x-axis). Therefore, for the
benchmark RBC model, this application of the SVAR methodology
yields uninformative estimates of the contribution of technology
shocks to output fluctuations at business cycle frequencies.
4.1 Interpreting the Bias
In this section, we estimate the contribution of two sources of bias in the impulse responses shown in Figure 1. We then provide an interpretation of the economic mechanisms accounting for the bias in the RBC model.
The first source of bias, which we call ``truncation bias,'' arises because the finite-ordered VAR chosen by our estimation procedure only provides an approximation to the true dynamics implied by the model. In particular, our model produces an exact VARMA(4,5) representation and even though this VARMA process is invertible, a finite-ordered VAR may be misspecified to some degree.21Cooley and Dwyer (1998) emphasized that most popular DGE models imply VARMA representations; thus, truncation bias is a fairly general phenomenon. The second source of bias is the small sample bias that arises in all time series work. Faust and Leeper (1997) highlighted small sample imprecision as a problem in this context, although they did not focus on bias in particular.
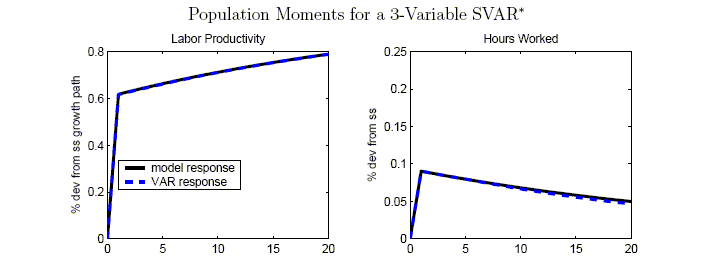
To measure the truncation bias, we calculate the population limit of a VAR(4) based on our model. In principle, we could estimate this using one very long sample drawn from the model, but we simply use the relevant population moments from the model to derive the VAR(4).22
Figure 3 compares the effects of a technology shock derived from the population SVAR with the true model responses. Though the four variables in the VAR have a VARMA(4,5) representation in our benchmark RBC model, it is clear that the truncation bias appears negligible for each of the variables depicted. Thus, for the benchmark calibration of the RBC model, the assumption that a short-ordered VAR provides a good approximation to the true data-generating process seems warranted. This proves attractive heuristically, because we can interpret almost all of the bias as arising from a small sample.
Accordingly, we further decompose the small-sample bias into two parts, and show that most of the small sample bias is attributable to the difficulty in precisely estimating the long-run response of variables to the innovations in the VAR. Noticing that equation (14) can be expressed as:
it is evident that the response of
Returning to the lower right panel of panel of Figure 1, we provide a decomposition of the overall bias in the mean response of labor productivity. The overall bias is represented by the solid line labelled ``total bias'', and is simply the difference between the mean estimated response of labor productivity to a technology innovation and the true response. The dotted line labelled ``T bias'' for truncation bias shows the bias introduced by assuming that the variables in the VAR can be represented by a VAR with only four lags. As suggested by Figure 3, this source of bias comprises only a tiny fraction of the bias in the mean response of labor productivity. From the dashed-dotted line labelled ``A bias'', it is clear that most of the small-sample bias initially is attributable to the error in transforming the reduced form into its structural form using the long-run restriction.24 Eventually, however, imprecision in estimating the long-run responses has a roughly commensurate effect on each component, so that the R bias contributes about as much to the bias as the A bias.
We now use the benchmark RBC model to provide an economic interpretation of the small sample bias that illustrates how it depends on model structure. This bias can be attributed largely to two related factors in our RBC model. First, the slow adjustment of capital makes it hard to estimate the long-run impact of a technology shock on labor productivity, which serves as a source of downward bias in the estimated impulse responses. Second, the SVAR has difficulty disentangling technology shocks from highly persistent non-technology shocks, so that the estimated technology shock may incorporate a sizeable non-technology component. The second source of bias has more pronounced effects on the estimated responses to a technology shock as the relative magnitude of non-technology shocks rises, and as the non-technology shocks become more persistent.
We conduct two experiments to show that the small sample bias is
greatly reduced when the exogenous and endogenous sources of
persistence in the model are decreased. First, as seen in the rows
of Tables 3 to 6 labelled ``with lower persistence'', we
analyze the effects of halving all of the AR(1) parameters of the
non-technology shocks from their benchmark values. Table 3 shows that the (percentage) distance between
the mean and the true response narrows for all variables and
especially for labor productivity, and Tables 4 to 6
indicate that there are sizeable declines in the frequencies of
large misses for all the variables we consider. Our second
experiment combines the lower persistence of non-technology shocks
with an increase in the depreciation rate of capital from
![]() to
to
![]() . In this
case, labor productivity adjusts more quickly in response to both
technology and non-technology shocks. Table 3 shows that the mean bias falls below 10% for
all the variables.25
. In this
case, labor productivity adjusts more quickly in response to both
technology and non-technology shocks. Table 3 shows that the mean bias falls below 10% for
all the variables.25![]() 26
26
Our final experiment in this section illustrates the important
influence that the non-technology shocks may have on the SVAR's
estimated responses. We reduce the innovation variance of the
technology shock to 0.0049, or one-third of its benchmark value,
thus effectively increasing the relative size of the non-technology
shocks. The mean estimated responses and true responses to a
technology shock under this alternative parameterization are
depicted in Figure 4 (and reported in
Table 3 in the row labelled ``with
![]() '').
With this increase in the relative size of the non-technology
shocks, the estimated responses look more like the effects that
arise from labor supply shocks (the dominant non-technology shock
in the benchmark calibration). To see this, we also plot the true
responses to a labor supply shock in the same figure. Observe that
relative to their effects on labor productivity, labor supply
shocks have much larger effects on hours worked and investment than
a true technology shock. Given that estimates derived from the SVAR
approach confound labor supply with true technology innovations,
the former shocks are a source of upward bias in the estimated
responses of hours worked and investment to a technology shock.
Thus, with the increased importance of labor supply shocks in this
alternative calibration, the upward bias in the mean response of
hours worked is much more pronounced than under our benchmark
calibration, and the bias in investment shifts from negative to
noticeably positive.
'').
With this increase in the relative size of the non-technology
shocks, the estimated responses look more like the effects that
arise from labor supply shocks (the dominant non-technology shock
in the benchmark calibration). To see this, we also plot the true
responses to a labor supply shock in the same figure. Observe that
relative to their effects on labor productivity, labor supply
shocks have much larger effects on hours worked and investment than
a true technology shock. Given that estimates derived from the SVAR
approach confound labor supply with true technology innovations,
the former shocks are a source of upward bias in the estimated
responses of hours worked and investment to a technology shock.
Thus, with the increased importance of labor supply shocks in this
alternative calibration, the upward bias in the mean response of
hours worked is much more pronounced than under our benchmark
calibration, and the bias in investment shifts from negative to
noticeably positive.
4.2 Sensitivity Analysis
We next use sensitivity analysis to illustrate how the performance of the Galí procedure may be influenced by the selection of variables in the VAR, the transformations applied, and the inclusion of a wider array of shocks.
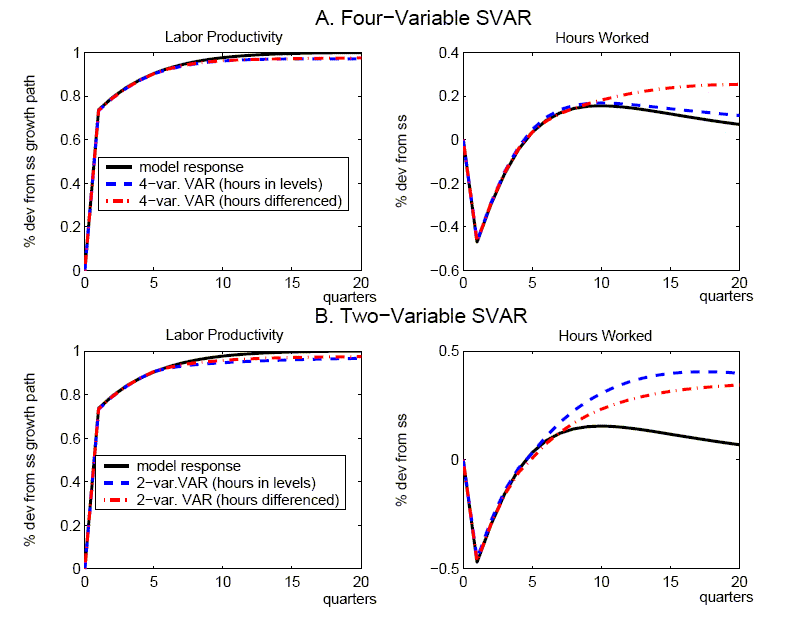
Figure 3 shows the responses derived from a four-variable VAR that is modified to include hours in differences rather than levels. As above, it is convenient to begin by abstracting from small-sample issues, and hence replace sample moments with the model's population moments in estimating the VAR (again we use four lags in the VAR). Our model implies that hours worked are stationary so that it might be expected that differencing hours would impair the ability of a short-ordered VAR to recover the true responses.27 However, it still does very well in capturing the quantitative effects of a technology shock for the other variables, even though the SVAR implies some upward bias in the response of hours. Turning to the small sample results in Tables 3 -6, there is only modest evidence of a deterioration in performance.
Figure 5 shows responses derived from alternative specifications of bivariate SVARs that include labor productivity growth and either the level of hours worked (the dashed lines) or the first difference of hours worked (the dash-dotted line). These specifications have often been utilized in the empirical literature applying the Galí methodology. The upper panel uses the population moments to derive each of the VARs (using four lags), while the lower panel reports the mean impulses derived from the Monte Carlo simulations (as in section 3, the Schwartz criterion is used to select lag length). It is clear from the upper panel that the two-variable specifications perform less adeptly than our four-variable specification in recovering the true responses: there is upward bias in the hours in levels specification, while there is pronounced downward bias for the hours in differences specification. The lower panel shows that the truncation bias is reflected in the mean bias observed in small samples.
Our results for these bivariate SVARs are quite similar to those reported by Chari, Kehoe, and McGratten (2005). These authors also highlight (what we term) truncation bias as a significant problem for the two-variable specification, and provide an insightful discussion about the origin of this bias in the RBC model: namely, it occurs primarily because capital is omitted from the SVAR, and this variable has a significant and long-lasting influence on the dynamic responses of labor productivity growth and hours worked. They proceed to argue that the poor performance of the bivariate SVARs (especially with hours in differences) makes this approach wholly unsuited to evaluating the plausibility of the RBC model relative to various alternatives, and thus provide a rebuttal to a substantial literature that has utilized SVARs to question the empirical relevance of that model. Finally, insofar as they regard the RBC model as representing a best case for the SVAR methodology, they surmise that application of the SVAR approach to other models would also be likely to yield highly imprecise estimates, and lead to mistaken inferences.
While we defer a more detailed response to the critique of Chari, Kehoe, and McGratten (2005) to Section 5.4, we believe that our analysis that considers both a wider set of SVAR specifications and models provides a broader perspective for evaluating the SVAR approach. Clearly, our analysis of the four-variable SVAR specifications above (with hours in levels and differences) suggests that certain specifications can perform reasonably well in eliciting the true responses in the RBC model: the problem of truncation bias highlighted by Chari, Kehoe, and McGratten (2005) is minimized in our benchmark RBC model insofar as the consumption and investment shares help proxy for the omitted capital stock.28 Although Chari, Kehoe, and McGratten (2005) may be justified in criticizing some of the specific empirical research critiquing RBC models, we believe the SVAR approach has much greater potential to yield informative estimates than these authors suggest.
Finally, while we show below that our four-variable VAR also performs reasonably well in the model with nominal rigidities, we caution that variable selection should be tailored to the model(s) that the researcher wishes to evaluate. In particular, our analysis suggests that if shocks other than the unit root shock to technology have a large impact on labor productivity, the ability of a low-ordered VAR to approximate the underlying VARMA process may deteriorate markedly, even using our four-variable VAR specification: while the VARMA process in this case is invertible, the additional shocks contribute to a very slowly-decaying moving average component. This potential sensitivity is illustrated in Figure 6, which reports responses from a four-variable SVAR that has four lags and is derived using population moments from an alternative calibration of the RBC model that includes capital tax rate and temporary technology shocks.29 There is a sizeable deterioration in the performance of the population SVAR in this case, with most of the divergence attributable to the temporary technology shocks.30
5 Sticky Price/Wage Model
In this section, we examine the robustness of our results by modifying the real business model to include nominal and real frictions that have been found useful in accounting for the observed behavior of aggregate data. These frictions include sticky wages and prices, variable capacity utilization, costs of adjustment for investment, and habit persistence in consumption. As noted above, one of the principal differences between this model and the RBC model is that hours worked decline initially in response to a technology shock rather than rise as in the RBC model. Since our sticky price/wage model is similar to Christiano, Eichenbaum, and Evans (2001) and Smets and Wouters (2003), we provide only a brief account of how it can be derived by modifying the RBC model discussed above.
5.1 Model Description
We assume that nominal wages and prices are set in Calvo-style staggered contracts in a framework similar to that discussed in Erceg, Henderson, and Levin (2000). The wage and price contracts have a mean duration of four quarters, and we set the wage and price markups both equal to 1/3. The inclusion of nominal rigidities into the model requires us to specify a monetary policy rule. We assume that the central bank adjusts the quarterly nominal interest rate (expressed at an annual rate) in response to the four-quarter inflation rate and to the four-quarter rate of growth of output:
where
We introduce habit persistence in consumption by modifying the utility function of the representative household in the following way:32
Our approach follows Smets and Wouters (2003), among others, by assuming that an individual cares about his consumption relative to the lagged value of aggregate consumption,
We incorporate variable capacity utilization into the sticky
price/wage model so that variation in the Solow residual reflects
both changes in technology and movements in the unobserved level of
capacity utilization in response to all of the underlying shocks.
The production function modified to include variable capacity
utilization, ![]() , is
given by:
, is
given by:
| (22) |
where
In our decentralized economy, households rent capital services (
![]() to firms,
and choose how intensively the capital is utilized. We follow
Christiano, Eichenbaum, and Evans (2001) and assume that households pay a cost to
varying
to firms,
and choose how intensively the capital is utilized. We follow
Christiano, Eichenbaum, and Evans (2001) and assume that households pay a cost to
varying ![]() in units
of the consumption good. These adjustment costs alter the budget
constraint of the representative household as follows:
in units
of the consumption good. These adjustment costs alter the budget
constraint of the representative household as follows:
In the above, the term,
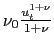 , reflects the cost
of adjusting the utilization rate, where
, reflects the cost
of adjusting the utilization rate, where As in our benchmark calibration of the RBC model, our benchmark
calibration of the sticky price/wage model abstracts from capital
tax rate and temporary technology shocks by setting
![]() . We used the method of
moments to estimate the innovation variances of the permanent
technology shock (0.0152) and the labor supply shock (0.069) by
exactly matching the model's implications for the volatility of the
Solow residual growth rate and the standard deviation of
(HP-filtered) hours worked relative to output to their sample
counterparts. For the other model parameters, shown in Table
1, we used the same values as for
the RBC model.
. We used the method of
moments to estimate the innovation variances of the permanent
technology shock (0.0152) and the labor supply shock (0.069) by
exactly matching the model's implications for the volatility of the
Solow residual growth rate and the standard deviation of
(HP-filtered) hours worked relative to output to their sample
counterparts. For the other model parameters, shown in Table
1, we used the same values as for
the RBC model.
5.2 Estimation Results
Figure 7 exhibits the response of labor productivity, hours worked, consumption, investment, and output to a technology shock for the benchmark sticky price/wage model. In each panel the solid lines show the true responses from the DGE model. In the same panels, the dashed lines show the mean responses from the SVAR derived from Monte Carlo simulations (as described in Section 3). As in the case of the benchmark RBC model, the mean response of each of these variables has the same sign and qualitative pattern as the true response. Moreover, as suggested by the pointwise confidence intervals, the SVAR is likely to correctly imply a rise in labor productivity, consumption, and output in response to the technology shock. The SVAR is also likely to capture the initial decrease in hours worked that occurs following a technology shock.34 Both the mean response and the 90% confidence intervals fall below zero in the two periods following the shock, in line with the model's response.
As in the case of the RBC model, the SVAR does not perform as well quantitatively. The mean responses underestimate the true responses of labor productivity, output, consumption, and investment by roughly 30-35 percent (see Table 3). This downward bias helps account for the substantial probability of making large errors in estimating these variables, as shown in Tables 4-6. Overall, the probability of making a large error in estimating most of the variables seems commensurate with that of the RBC model, with the exception of investment. Interestingly, we found that while the probability of estimating a response of labor productivity, output, or consumption that was uniformly positive for four quarters following the shock exceeded 90%, there was only a 63% chance of estimating a uniformly positive response of investment. Thus, in this model, there appears to be considerably more qualitative uncertainty about the effects of a technology shock on investment.
The bottom left panel of Figure 2 shows the cumulative distribution function derived from Monte Carlo simulations of the estimator of the contribution of technology shocks to explaining variations in HP-filtered output. The 90% confidence bands for the estimator include contributions ranging from 7 to 80 percent. Therefore, as in the benchmark RBC model, the Galí identification scheme provides little information about the importance of technology shocks in explaining output fluctuations at business cycle frequencies.
We next examine the sources of bias in the mean responses using the same analytical framework that was applied to the RBC model. The dashed lines in the top panel of Figure 8 show the responses to a technology shock derived from a SVAR with four lags that uses the model's population moments. While these responses diverge slightly from the true responses, it is clear that a short-ordered population VAR performs well in approximating the true VARMA process. Accordingly, as in the benchmark RBC model, most of the bias in the estimated impulse responses is attributable to the small-sample problems emphasized by Faust and Leeper (1997).
The small-sample bias in this model depends on many of the same
model characteristics as identified using the RBC model. In
particular, the bias arises because the identification scheme has
difficulty disentangling unit root technology shocks from other
shocks that may have highly persistent effects on labor
productivity, and because of slow capital adjustment (the latter
plays less of a role in accounting for bias, since variable
capacity utilization induces labor productivity to rise more
quickly to its long-run level). As shown in Table 3, the bias is reduced when we decrease the
persistence of the non-technology shocks and accelerate capital
adjustment by setting
![]() ; however,
the change in the bias is somewhat less dramatic than in the RBC
model.
; however,
the change in the bias is somewhat less dramatic than in the RBC
model.
5.3 Sensitivity Analysis in the Sticky Price/Wage Model
We next investigate the sensitivity of our results to including a different set of variables in the SVAR, to differencing hours worked, and to adding capital tax rate and temporary technology shocks.35
The bottom panels of Figure 8 show results for the two bivariate population SVARs considered in Section 4.2 (i.e., each SVAR has four lags and is derived by replacing sample moments with corresponding population moments). The dashed lines show the responses for the SVAR with labor productivity growth and hours in levels, while the dash-dotted lines show the responses of the alternative specification with hours in differences. Notably, in stark contrast with their performance in the RBC model, each specification does very well in accounting for the short-run response of hours worked. The bivariate SVARs also perform quite well in small samples. For example, Figure 9 illustrates the responses derived from estimating the bivariate specification with hours in differences. The mean response of hours lies very close to the true response in the short-run and the confidence intervals are somewhat narrower than in the four-variable specification with hours in levels (see Figure 7).
Thus, the model with nominal rigidities provides an interesting
example of a model that could rationalize the use of the bivariate
SVAR in estimation (as often employed in the empirical literature).
These results should help dispel the presumption of Chari, Kehoe, and McGratten (2005)
that the RBC model presents a best case for the SVAR approach. The
considerably improved performance of the bivariate VAR in this
model may indeed seem surprising, insofar as it includes a much
larger set of endogenous state variables than the RBC model (e.g.,
lagged consumption, investment, and the real wage). However, it
turns out that the dynamics of labor productivity growth and hours
worked in this model are simple enough that they can be more easily
approximated by a short-ordered VAR. This reflects the inclusion of
variable capacity utilization in the sticky price/wage model, which
allows firms to vary their effective capital stock,
![]() , in
response to shocks. As a result, the capital stock,
, in
response to shocks. As a result, the capital stock, ![]() , has a diminished influence on
the dynamics of labor productivity and hours relative to the RBC
model (this is particularly evident in the response of labor
productivity, which reaches its long-run level much more quickly
than in the RBC model). It also reflects that the additional state
variables such as consumption and investment exert only a small
influence on the dynamics of labor productivity, and their effect
on hours is fairly transient.36
, has a diminished influence on
the dynamics of labor productivity and hours relative to the RBC
model (this is particularly evident in the response of labor
productivity, which reaches its long-run level much more quickly
than in the RBC model). It also reflects that the additional state
variables such as consumption and investment exert only a small
influence on the dynamics of labor productivity, and their effect
on hours is fairly transient.36
Overall, we find relatively little sensitivity of our results derived from this model to the transformation applied to hours worked in the SVAR (levels vs. differences). This applies both to our four-variable specification (shown in Figure 8 using population moments, with small sample results in Tables 3-6) and to the bivariate SVARs. Thus, the pronounced sensitivity to the transformation of hours evident in the bivariate SVARs derived from the RBC model appears exceptional among the cases we consider; and to the extent we do see some sensitivity, there is no clear pattern of bias in the hours worked variable (e.g., in the sticky price/wage model, differencing hours implies upward bias in the hours response for both the two and four-variable SVAR specifications, in sharp contrast with the RBC model, where hours is downward biased in the bivariate specification). To the extent that empirical results appear noticeably more sensitive to the transformation of hours, this may reflect other factors not captured in either of our models, e.g. demographic shifts or other shocks to labor force participation.37
We also find that the sticky price/wage model is somewhat less sensitive to the inclusion of the additional shocks than the RBC model.38 Using the population moments of the sticky price/wage model with these additional shocks, the four-variable SVAR with four lags displays a deterioration (not shown) in its ability to approximate the true dynamics; however, this deterioration is less pronounced than in the RBC model. Similarly to the RBC model, there is no evident deterioration in small sample performance in this case (see Tables 3 -6).
Taking stock of our sensitivity analysis across the two models, our results suggest that specification choice should be suited to the particular use or interpretation to be attached to the results, and to the researcher's beliefs about the plausibility of alternative models. Thus, a researcher exclusively interested in estimating the effects of technology shocks who had high confidence in the model with nominal rigidities might find it desirable to use a bivariate VAR specification with hours in differences, even if this specification performed relatively poorly in the RBC model. By contrast, a researcher interested in evaluating the plausibility of alternative models would presumably want to adopt a SVAR specification that performed well enough across models to help differentiate between them. As one might conjecture and as we verify below, the four-variable SVAR would appear to offer a useful basis for discriminating between the implications of the two benchmark models we have examined.
5.4 Discriminating Between Models Based on the Response of Hours
A key objective of Galí's (1999) seminal paper applying the SVAR approach to technology shocks was to differentiate between alternative business cycle models. In this vein, Galí interpreted his result that hours worked fell in response to a technology shock as contravening the RBC paradigm, and suggested that his findings might be more consistent with a model that incorporated nominal rigidities. Galí's provocative conclusion generated considerable subsequent empirical research examining the robustness of inferences drawn from SVARs to changes in data and specification. This research has included papers by Francis and Ramey (2003) and Gali and Rabanal (2005), that broadly lent support to Galí's original conclusion, while Christiano, Eichenbaum, and Vigfusson (2003) favored a VAR specification that implies a rise in hours worked following a technology shock. But notwithstanding the lively debate that has emerged about specification issues, these papers share the common thread that they regard the SVAR approach as a useful methodological approach in helping to discriminate between alternative business cycle models.
The recent paper by Chari, Kehoe, and McGratten (2005) diverges from this literature in its complete rejection of the use of the SVAR approach to evaluate the plausibility of alternative models. As noted above, these authors (hence CKM) concluded based on the performance of bivariate SVARs estimated using artificial data from an RBC model that inferences from the SVAR approach are likely to be uninformative or misleading.
We are certainly sympathetic with CKM's specific point that the SVAR methodology may perform poorly even if the data-generating process satisfies Galí's headline identifying assumptions. Complementary to our own analysis, the CKM results should provide strong caution against interpreting the results of SVARs in a model-independent fashion: inferences about technology shocks, and tests of alternative models using the SVAR approach, are invariably more model-specific than has been recognized in the literature. As applied to the literature, we concur with CKM that at least some of the evidence brought to bear against the RBC model, such as that derived from a two-variable SVAR with hours in differences, probably can be dismissed.
But do we agree with CKM that the SVAR methodology is completely ill-suited to discriminating between alternative models of the business cycle? Our answer is an emphatic ``no.'' To the contrary, we interpret our results as suggesting that the SVAR approach may indeed be a useful tool in this regard, provided that the models have sufficiently divergent implications about the effects of technology shocks on the labor market, and that the SVAR performs reasonably well in each model.
We illustrate this by assessing the ability of the SVAR to discriminate between our two benchmark models based on the response of hours worked. We use a four-variable SVAR with hours in levels, since we have shown that it performs reasonably well in both the RBC model, and in the model with nominal rigidities. The upper panel of Figure 10 shows the probabilities that the estimated response of hours is uniformly negative in the first two and four quarters, respectively. The probability of finding an initial decline in hours that persists for two quarters is 93 percent in the model with nominal rigidities, but only 26 percent in the RBC model. Accordingly, a researcher who found that hours worked declined after a positive innovation in technology in the data could reasonably interpret this finding as providing some evidence in favor of the sticky price/wage model. By contrast, a researcher who found that hours worked rose after a technology shock could regard this finding as offering evidence in support of the RBC model: as shown in the lower panel, the probability of finding an initial rise in hours that persists for two quarters is 71 percent in the RBC model, but less than 1 percent in the sticky price/wage model.
Interestingly, fairly similar results obtain for a two-variable VAR specification in which hours is specified in levels. For example, for this specification we find that the probability of finding an initial decline in hours that persists for two quarters is 87 percent in the model with nominal rigidities, but only 23 percent in the RBC model. Ironically, while there is admittedly some upward bias in the two-variable SVAR when applied to the RBC model - a feature which CKM highlight in pejorative terms - such bias may actually facilitate differentiating between models. This is because the bias induces a larger wedge between the implications of these models for hours worked, making it less probable that an observed decline in hours would be consistent with the RBC model.
Several recent papers have in fact examined the implications of bivariate SVARs with hours in levels, including Gali (2004), Francis and Ramey (2004), and Christiano, Eichenbaum, and Vigfusson (2003). The empirical results appear quite sensitive to measurement of the hours worked variable, with no consensus on the most appropriate measure (e.g., Galí and Rabanal and Francis and Ramey find that hours decline for most of their measures, while Christiano, Eichenbaum, and Vigfusson report a rise in hours for their preferred measure). While identifying the proper empirical counterpart to the hours concept in our theoretical model is an issue beyond the scope of the present paper, our analysis does provide a rationale for using such a SVAR specification; and it would appear to offer a much better test of the RBC model than SVAR specifications involving hours in differences.
From a more general perspective, our analysis suggests that the SVAR methodology may offer a plausible means of differentiating between alternative business-cycle models, as envisioned in Galí's original article and in most of the subsequent empirical literature. However, it is important that a researcher is aware of the limitations of alternative SVAR specifications in evaluating the models considered, and that he adopt a specification that is well-suited to differentiate between the particular models of interest.
6 Conclusion
While identifying technology shocks and their effects is a difficult task, our analysis suggests that Galí's methodology is a useful tool. We find it encouraging that our four-variable VAR specification performs reasonably well across the RBC and sticky price/wage models in characterizing the qualitative effects of a technology shock on a range of macro variables. But our analysis highlights that the conditions under which the Galí methodology performs well appear considerably more restrictive than implied by the key identifying restriction. Accordingly, it will be useful in future research to delineate further the class of models for which this methodology works well, and also to examine empirically realistic conditions that might exacerbate some of the problems we have identified in our analysis (e.g., stationary technology shocks). Moreover, it will be beneficial to identify VAR specifications that appear to be robust across a class of plausible models, insofar as this would enhance the latitude to use this methodology in discriminating across models.
References
Altig, D., L. J. Christiano, M. Eichenbaum, and J. Lind� (2003). Technology Shocks and Aggregate Fluctuations. Mimeo, Northwestern University.
Anderson, G. and G. Moore (1985). A Linear Algebraic Procedure for Solving Linear Perfect Foresight Models. Economic Letters 17, 247--52.
Blanchard, O. J. and C. M. Kahn (1980). The Solution of Linear Difference Models under Rational Expectations. Econometrica 48(5), 1305--1312.
Blanchard, O. J. and D. Quah (1989). The Dynamic Effects of Aggregated Demand and Supply Disturbances. American Economic Review 79(4), 655--673.
Chari, V. V., P. J. Kehoe, and E. R. McGrattan (2005). A Critique of Structural VARs Using Real Business Cycle Theory. Federal Reserve Bank of Minneapolis, Working Paper No 631.
Christiano, L. J., M. Eichenbaum, and C. L. Evans (2005). Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy. Journal of Political Economy 113(1), 1--45.
Christiano, L. J., M. Eichenbaum, and R. Vigfusson (2003). What Happens after a Technology Shock. NBER Working Paper No.w9819.
Christiano, L. J. and J. D. Fisher (1995). Tobin's q and Asset Returns: Implications for Business Cycle Analysis. NBER Working Paper No.5292.
Cogley, T. and J. M. Nason (1995). Output Dynamics in Real-Business-Cycle Models. American Economic Review 85(3), 492--462.
Cooley, T. and M. Dwyer (1998). Business Cycle Analysis without much Theory: A Look at Structural VARs. Journal of Econometrics 83, 57--88.
Erceg, C. J., D. W. Henderson, and A. T. Levin (2000). Optimal Monetary Policy with Staggered Wage and Price Contracts. Journal of Monetary Economics 46, 281--313.
Evans, C. L. (1992). Productivity Shocks and Real Business Cycles. Journal of Monetary Economics 29, 191--208.
Faust, J. and E. M. Leeper (1997). When Do Long-Run Identifying Restrictions Give Reliable Results? Journal of Business and Economic Statistics 15(3), 345--353.
Fisher, J. D. M. (2002). Technology Shocks Matter. Mimeo, Federal Reserve Bank of Chicago.
Francis, N. and V. A. Ramey (2003). Is the Technology-Driven Real Business Cycle Hypothesis Dead? Shocks and Aggregate Fluctuations Revisited. Mimeo, University of California at San Diego.
Francis, N. and V. A. Ramey (2004). A New Measure of Hours Per Capita with Implications for the Technology-Hours Debate. Mimeo, University of California at San Diego.
Gal�, J. (1999). Technology, Employment, and the Business Cycle: Do Technology Shocks Explain Aggregate Fluctuations? American Economic Review 89(1), 249--271.
Gal�, J. (2004). On the Role of Technology Shocks as a Source of Business Cycles: Some New Evidence. Journal of the European Economic Association 2, 372--380.
Gal�, J. and P. Rabanal (2005). Technology Shocks and Aggregate Fluctuations: How Well Does the Real Business Cycle Model Fit Postwar U.S. Data? In M. Gertler and K. Rogoff (Eds.), NBER Macroeconomics Annual 2004, pp. 225--288. MIT Press.
Hall, R. E. (1997). Macroeconomic Fluctuations and the Allocation of Time. Journal of Labor Economics 15(1), S223--S250.
Hansen, L. and T. Sargent (2004). Recursive Models of Dynamic Linear Economies. Mimeo, New York University.
Jones, J. B. (2002). Has Fiscal Policy Helped Stabilize the Postwar U.S. Economy? Journal of Monetary Economics 49, 709--746.
Killingsworth, M. and J. Heckman (1986). Female Labor Supply: A Survey. In O. Ashenfelter and R. Layard (Eds.), Handbook of Labor Economics, Volume 1 of Handbooks in Economics Series, pp. 103--204. Elsevier Science B.V.
King, R. G., C. I. Plosser, and S. Rebelo (1988). Production, Growth and Business Cycles. Journal of Monetary Economics 21, 195--232.
King, R. G., C. I. Plosser, J. H. Stock, and M. W. Watson (1991). Stochastic Trends and Economic Fluctuations. American Economic Review 81, 819--840.
Lippi, M. and L. Reichlin (1993). The Dynamic Effects of Aggregate Supply and Demand Disturbances: Comment. American Economic Review 83, 644--652.
Lutkepohl, H. (1991). Introduction to Multiple Time Series Analysis. Berlin: Springer-Verlag.
Pagan, A. R. and J. C. Robertson (1998). Structural Models of the Liquidity Effect. Review of Economics and Statistics 80, 202--217.
Parkin, M. (1988). A Method for Determining Whether Parameters in Aggregative Models are Structural. Carnegie-Rochester Conference Series on Public Policy 29, 215--252.
Pencavel, J. (1986). Labor Supply of Men: A Survey. In O. Ashenfelter and R. Layard (Eds.), Handbook of Labor Economics, Volume 1 of Handbooks in Economics Series, pp. 3--102. Elsevier Science B.V.
Pencavel, J. (2002). A Cohort Analysis of the Association Between Work and Wages Among Men. The Journal of Human Resources 37(2), 251--274.
Schwarz, G. (1978). Estimating the Dimension of a Model. The Annals of Statistics 6(2), 461--464.
Shapiro, M. and M. Watson (1988). Sources of Business Cycle Fluctuations. NBER Macroeconomics Annual, 111--148.
Smets, F. and R. Wouters (2003). An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area. Journal of the European Economic Association 1(5), 1124--1175.
Vigfusson, R. J. (2004). The Delayed Response To A Technology Shock. A Flexible Price Explanation. International Finance Discussion Papers, Number 810, Board of Governors of the Federal Reserve System.
|
|
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Moment | U.S. Data |
Real Business Cycle
|
Real Business Cycle Benchmark |
Real Business Cycle with Additional Shocks |
Sticky Prices and Wages Benchmark |
Sticky Prices and Wages with Additional Shocks |
|---|---|---|---|---|---|---|
|
|
2.17 | 1.38 | 1.72 | 1.67 | 2.00 | 1.82 |
|
|
0.80 | 0.28 | 0.80 | 0.80 | 0.80 | 0.80 |
|
|
0.47 | 0.73 | 0.61 | 0.56 | 0.78 | 0.72 |
|
|
2.91 | 1.98 | 2.26 | 2.55 | 2.35 | 2.53 |
|
|
0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 |
| Parameter Values | Real Business Cycle
|
Real Business Cycle Benchmark |
Real Business Cycle with Additional Shocks |
Sticky Prices and Wages Benchmark |
Sticky Prices and Wages with Additional Shocks |
|
|
|
0.0148 | 0.0148 | 0.0104 | 0.0152 | 0.0103 | |
|
|
0 | 0.024 | 0.0198 | 0.0619 | 0.0335 | |
|
|
0 | 0 | 0.008 | 0 | 0.008 | |
|
|
0 | 0 | 0.0103 | 0 | 0.0102 | |
![]()
![]() and
and
![]() were
computed using BLS data on nonfarm business sector output and hours
from 1958-2002.
were
computed using BLS data on nonfarm business sector output and hours
from 1958-2002.
![]() and
and
![]() were taken from Christiano and Fisher (1995) who used DRI data from
1947-1995.
were taken from Christiano and Fisher (1995) who used DRI data from
1947-1995.
| Experiment | Labor Productivity | Output | Hours | Consumption | Investment |
|---|---|---|---|---|---|
| RBC Model | 0.40 | 0.25 | 0.09 | 0.28 | 0.19 |
| with
|
0.49 | 0.02 | 0.34 | 0.11 | 0.21 |
| with lower
persistence |
0.17 | 0.16 | 0.01 | 0.16 | 0.15 |
| with lower
persistence |
0.10 | 0.10 | 0.00 | 0.09 | 0.10 |
| with hours differenced | 0.24 | 0.33 | 0.08 | 0.30 | 0.34 |
| with additional
shocks |
0.22 | 0.02 | 0.14 | 0.13 | 0.15 |
| Sticky Price/Wage Model | 0.34 | 0.33 | 0.05 | 0.34 | 0.32 |
| with lower
persistence |
0.19 | 0.20 | 0.03 | 0.20 | 0.30 |
| with hours differenced | 0.38 | 0.37 | 0.06 | 0.37 | 0.37 |
| with additional
shocks |
0.29 | 0.29 | 0.05 | 0.29 | 0.29 |
![]() Absolute value of
percent difference between mean estimated response and true model
response averaged over first twelve periods. For hours worked, we
report the absolute value of the difference from the true model
response.
Absolute value of
percent difference between mean estimated response and true model
response averaged over first twelve periods. For hours worked, we
report the absolute value of the difference from the true model
response.
![]() Lower persistence refers to the case where AR(1)
parameters of non-technology shocks are set to half the benchmark
values.
Lower persistence refers to the case where AR(1)
parameters of non-technology shocks are set to half the benchmark
values.
![]() The additional shocks are capital tax rate and
temporary technology shocks.
The additional shocks are capital tax rate and
temporary technology shocks.
| Experiment | Labor Productivity | Output | Hours | Consumption | Investment |
|---|---|---|---|---|---|
| RBC Model | 0.48 | 0.27 | 0.26 | 0.31 | 0.35 |
| with
|
0.61 | 0.67 | 0.28 | 0.52 | 0.78 |
| with lower
persistence |
0.10 | 0.08 | 0.16 | 0.04 | 0.15 |
| with lower
persistence |
0.03 | 0.08 | 0.37 | 0.07 | 0.10 |
| with hours differenced | 0.27 | 0.39 | 0.42 | 0.34 | 0.44 |
| with additional
shocks |
0.34 | 0.40 | 0.23 | 0.26 | 0.61 |
| Sticky Price/Wage Model | 0.35 | 0.31 | 0.02 | 0.36 | 0.79 |
| with lower
persistence |
0.12 | 0.16 | 0.00 | 0.15 | 0.70 |
| with hours differenced | 0.41 | 0.35 | 0.03 | 0.41 | 0.80 |
| with additional
shocks |
0.38 | 0.35 | 0.10 | 0.30 | 0.86 |
![]() Lower persistence refers to the case where AR(1)
parameters of non-technology shocks are set to half the benchmark
values.
Lower persistence refers to the case where AR(1)
parameters of non-technology shocks are set to half the benchmark
values.
![]() The additional shocks are capital tax rate and
temporary technology shocks.
The additional shocks are capital tax rate and
temporary technology shocks.
| Experiment | Labor Productivity | Output | Hours | Consumption | Investment |
|---|---|---|---|---|---|
| RBC Model | 0.43 | 0.24 | 0.23 | 0.28 | 0.28 |
| with
|
0.54 | 0.58 | 0.25 | 0.44 | 0.70 |
| with lower
persistence |
0.05 | 0.03 | 0.04 | 0.03 | 0.05 |
| with lower
persistence |
0.02 | 0.04 | 0.20 | 0.04 | 0.05 |
| with hours differenced | 0.22 | 0.35 | 0.38 | 0.30 | 0.39 |
| with additional
shocks |
0.30 | 0.31 | 0.21 | 0.22 | 0.51 |
| Sticky Price/Wage Model | 0.31 | 0.26 | 0.02 | 0.32 | 0.71 |
| with lower
persistence |
0.10 | 0.12 | 0.00 | 0.13 | 0.30 |
| with hours differenced | 0.37 | 0.30 | 0.03 | 0.38 | 0.71 |
| with additional
shocks |
0.34 | 0.30 | 0.07 | 0.28 | 0.78 |
![]() Lower persistence refers to the case where AR(1)
parameters of non-technology shocks are set to half the benchmark
values.
Lower persistence refers to the case where AR(1)
parameters of non-technology shocks are set to half the benchmark
values.
![]() The additional shocks are capital tax rate and
temporary technology shocks.
The additional shocks are capital tax rate and
temporary technology shocks.
| Experiment | Labor Productivity | Output | Hours | Consumption | Investment |
|---|---|---|---|---|---|
| RBC Model | 0.36 | 0.17 | 0.16 | 0.22 | 0.16 |
| with
|
0.40 | 0.36 | 0.19 | 0.32 | 0.46 |
| with lower
persistence |
0.02 | 0.01 | 0.00 | 0.01 | 0.01 |
| with lower
persistence |
0.01 | 0.01 | 0.06 | 0.01 | 0.01 |
| with hours differenced | 0.13 | 0.29 | 0.32 | 0.25 | 0.31 |
| with additional
shocks |
0.22 | 0.19 | 0.17 | 0.15 | 0.30 |
| Sticky Price/Wage Model | 0.25 | 0.23 | NA | 0.25 | 0.61 |
| with lower
persistence |
0.05 | 0.07 | NA | 0.07 | 0.15 |
| with hours differenced | 0.30 | 0.26 | NA | 0.30 | 0.61 |
| with additional
shocks |
0.24 | 0.25 | NA | 0.22 | 0.63 |
![]() Lower persistence refers to the case where AR(1)
parameters of non-technology shocks are set to half the benchmark
values.
Lower persistence refers to the case where AR(1)
parameters of non-technology shocks are set to half the benchmark
values.
![]() The additional shocks are capital tax rate and
temporary technology shocks.
The additional shocks are capital tax rate and
temporary technology shocks.
Figure 1: Responses to technology Shocks in the benchmark RBC Model*
![Figure 1 has six panels. The first five report the response of labor productivity, hours worked, consumption, investment, and output to a technology shock for the benchmark calibration of the RBC model. More precisely, the responses shown are the deviations of the log level of each variable from the steady-state growth path. In each panel, the solid lines show the true responses from the DGE model. The innovation has been scaled so that the level of labor productivity rises by one percent in the long run. An additional panel shows the bias decomposition for the estimated response for labor productivity to technology shocks.
In each of the first five panels additional dashed lines show the mean of the impulse responses derived from applying our benchmark, four-variable SVAR to the 10,000 artificial data samples (the median response is nearly identical). [Note: We scale up the technology innovation derived from the SVAR by the same constant factor as applied to the true innovation.] Moreover, dotted lines show the 90 percent pointwise confidence interval of the SVAR's impulse responses. [Note: These confidence intervals are also constructed from the estimated impulse responses derived from applying the SVAR to the 10,000 artificial data samples from our model.]
The mean responses of labor productivity, consumption, investment, and output have the same sign and qualitative pattern as the true responses. As indicated by the pointwise confidence intervals, the SVAR is likely to give the appropriate sign of the response for these variables. For hours worked, the mean estimate is also qualitatively in line with the true response; however, the confidence interval is wide, indicating that there is a non-negligible probability of a negative estimate.
Quantitatively, the SVAR does not perform as well. Figure 1 shows that the mean responses of the SVAR systematically underestimate labor productivity, consumption, investment, and output, while overestimating hours worked.
Finally, the bias decomposition presented in the sixth panel displays three sources of bias: T bias that arises from approximating the true VARMA process with a VAR of order 4; R bias that reflects small-sample bias from estimating the reduced-form VAR; A bias that reflects small-sample bias associated with the transformation of the reduced-form to the structural form. Over the first few quarters the A bias dominates.](Figure1.gif)
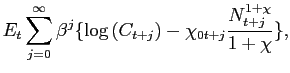
![\begin{displaymath}\begin{array}[c]{c} C_{t}+I_{t} + \frac{1}{1+r_{t}}B_{t+1}-B_... ...}+ (1-\tau_{Kt})R_{Kt}K_{t}+\tau _{Kt}\delta K_{t}. \end{array}\end{displaymath}](img18.gif)

![$\displaystyle \begin{tabular}[c]{l} $T_{t}+G_{t}=\tau_{Nt}W_{t}N_{t}+\tau_{Kt}(R_{Kt}-\delta)K_{t}$. \end{tabular}$](img43.gif)
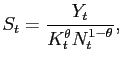
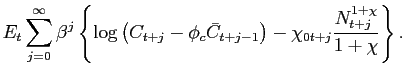
![\begin{displaymath}\begin{array}[c]{c} C_{t}+I_{t}+\frac{1}{1+r_{t}}B_{t+1}-B_{t... ...} {I_{t-1}^{2}}-\nu_{0}\frac{u_{t}^{1+\nu}}{1+\nu}. \end{array}\end{displaymath}](img130.gif)
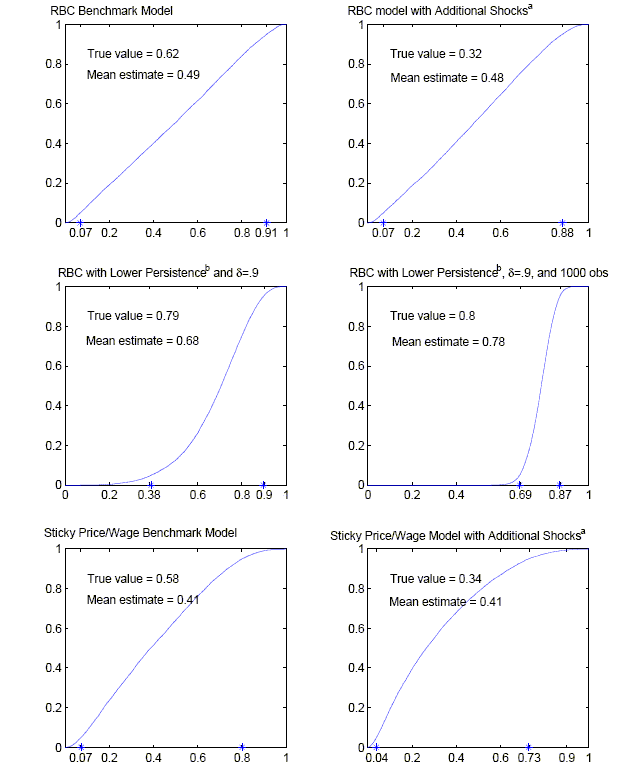
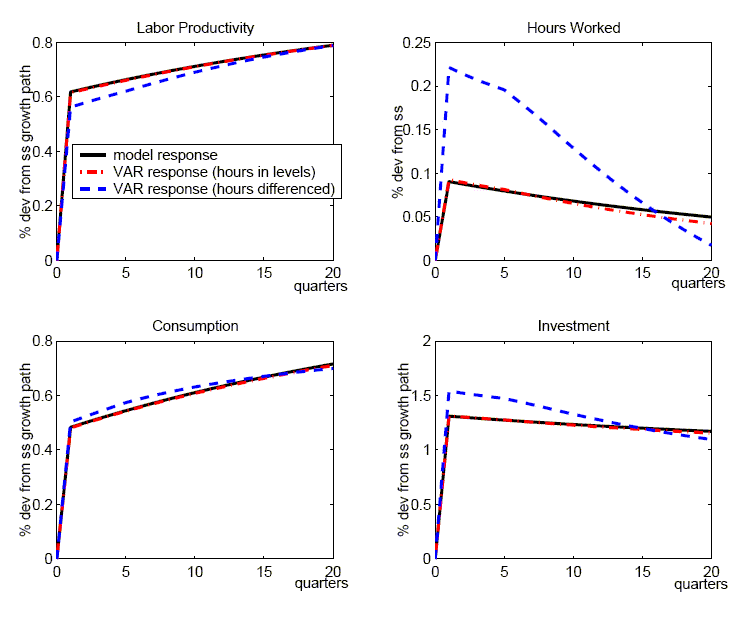
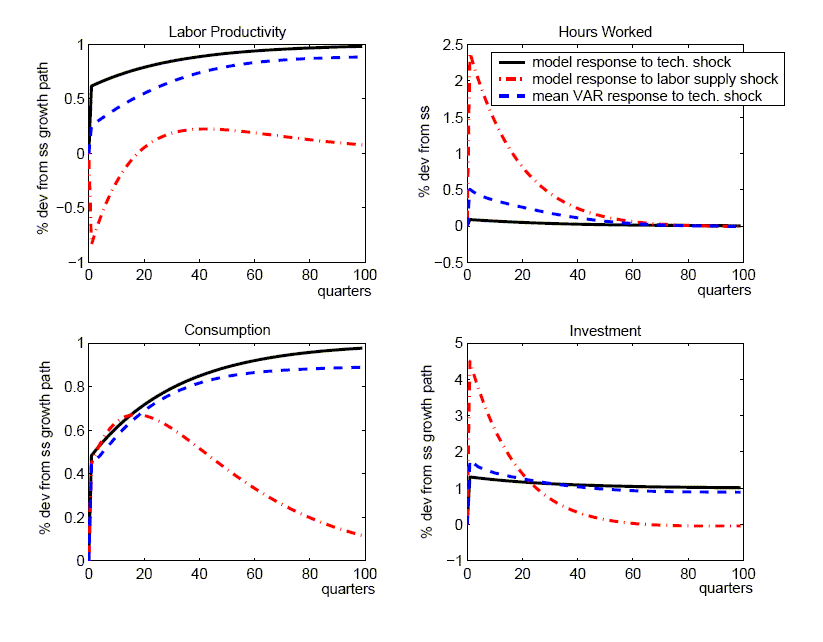
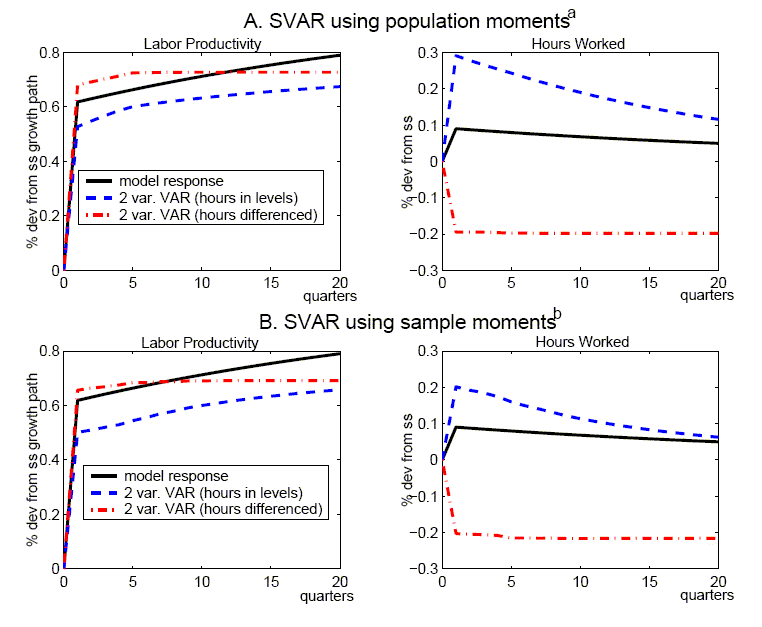
![Figure 6 illustrates that if shocks other than the unit root shock to technology have a large impact on labor productivity, the ability of a low-ordered VAR to approximate the underlying VARMA process may deteriorate markedly, even using our four-variable VAR specification. Figure 6 reports responses from a four-variable SVAR that has four lags and is derived using population moments from an alternative calibration of the RBC model that includes capital tax rate and temporary technology shocks.[Note: In this alternative calibration, the temporary technology shock contributes 50 percent of the variation to the growth rate of the Solow residual, while the parameters of the capital tax rate process are estimated using historical data (see Tables 1 and 2 for parameter estimates and selected second moments).] In the figure, there are four panels for the responses to a technology shock of labor productivity, hours worked, consumption, and investment. There is a sizeable deterioration in the performance of the population SVAR in this case, with most of the divergence attributable to the temporary technology shocks. The VAR responses for hours worked and investment on impact are, respectively, 4 times and 2 times the model responses.](Figure6.gif)
![Figure 7 matches the content of figure 1, but focuses on the sticky price model, rather than on the benchmark RBC model.
Figure 7 has six panels. The first five report the response of labor productivity, hours worked, consumption, investment, and output to a technology shock for the benchmark calibration of the RBC model. More precisely, the responses shown are the deviations of the log level of each variable from the steady-state growth path. In each panel, the solid lines show the true responses from the DGE model. The innovation has been scaled so that the level of labor productivity rises by one percent in the long run. An additional panel shows the bias decomposition for the estimated response for labor productivity to technology shocks.
In each of the first five panels additional dashed lines show the mean of the impulse responses derived from applying our benchmark, four-variable SVAR to the 10,000 artificial data samples (the median response is nearly identical). [Note: We scale up the technology innovation derived from the SVAR by the same constant factor as applied to the true innovation.] Moreover, dotted lines show the 90 percent pointwise confidence interval of the SVAR's impulse responses. [Note: These confidence intervals are also constructed from the estimated impulse responses derived from applying the SVAR to the 10,000 artificial data samples from our model.]
The mean responses of labor productivity, consumption, investment, and output have the same sign and qualitative pattern as the true responses. As indicated by the pointwise confidence intervals, the SVAR is likely to give the appropriate sign of the response for these variables. For hours worked, the mean estimate is also qualitatively in line with the true response; however, the confidence interval is wide, indicating that there is a non-negligible probability of a negative estimate.
Quantitatively, the SVAR does not perform as well. Figure 1 shows that the mean responses of the SVAR systematically underestimate labor productivity, consumption, investment, and output, while overestimating hours worked.
Finally, the bias decomposition presented in the sixth panel displays three sources of bias: T bias that arises from approximating the true VARMA process with a VAR of order 4; R bias that reflects small-sample bias from estimating the reduced-form VAR; A bias that reflects small-sample bias associated with the transformation of the reduced-form to the structural form. Over the first few quarters the A bias dominates.](Figure7.gif)