
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 797, April 2004 --- Screen Reader Version*
Indeterminacy with Inflation-Forecast-Based Rules in a Two-Bloc Model*
International Finance Discussion Papers numbers 797-807 were presented on November 14-15, 2003 at the second conference sponsored by the International Research Forum on Monetary Policy sponsored by the European Central Bank, the Federal Reserve Board, the Center for German and European Studies at Georgetown University, and the Center for Financial Studies at the Goethe University in Frankfurt.
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We examine the performance of forward-looking inflation-forecast-based rules in open economies. In a New Keynesian two-bloc model, a methodology first employed by Batini and Pearlman (2002) is used to obtain analytically the feedback parameters/horizon pairs associated with unique and stable equilibria. Three key findings emerge: first, indeterminacy occurs for any value of the feedback parameter on inflation if the forecast horizon lies too far into the future. Second, the problem of indeterminacy is intrinsically more serious in the open economy. Third, the problem is compounded further in the open economy when central banks respond to expected consumer, rather than producer price inflation.
Keywords: Taylor rules, inflation-forecast-based rules, indeterminacy, open economy
JEL Classification: E52, E37, E58
Contents
- 1. Introduction
- 2. Recent Related Literature
- 3. The
Model
- 3.1. Households
- 3.2. Firms
- 3.3. The Equilibrium and the Trade Balance
- 3.4. Linearization
- 3.5. Sum and Difference Systems
- 4. Designing and Implementing Optimal Policy
- 5. The
Stability and Determinacy of IFB Rules
- 6. Conclusions
- A. The Optimal Rule
- B. A Topological Guide to The Root Locus Technique
- C. Calibration
- Bibliography
NON-TECHNICAL SUMMARY
Under inflation targeting, the task of the central bank is to alter monetary conditions to keep inflation close to a pre-announced target. Since current inflation is usually predetermined by existing price contracts and so cannot be readily affected via monetary impulses, one class of rules widely proposed under inflation targeting are 'inflation-forecast-based' (IFB) rules (Batini and Haldane (1999)). IFB rules are 'simple' rules as in Taylor (1993), but where the policy instrument responds to deviations of expected, rather than current inflation from target and so allow to bypass the policy lags that exist when inflation is sticky.
These rules are of special interest because similar reaction functions are used in the Quarterly Projection Model of the Bank of Canada (see Coletti et al. (1996)), and in the Forecasting and Policy System of the Reserve Bank of New Zealand (see Black et al. (1997)) - two prominent inflation targeting central banks. Besides, estimates of IFB-type rules appear to offer a good description of the actual monetary policy in the US and Europe of recent years.
However, IFB rules have been criticized on various grounds. One recurrent crit- icism by much of the literature has to do with the fact that forward-looking Taylor-type rules tend to lead to real indeterminacy. This implies that when a shock displaces the economy from its equilibrium, there are many possible paths for the real variables leading back to equilibrium. The fact that these rules may introduce indeterminacy and generate so called 'sunspot equilibria' is of interest because sunspot fluctuations-i.e. persistent movements in inflation and output that materialize even in the absence of shocks to preferences or technology-are typically welfare reducing and can potentially be quite large. In practice, the problem of real indeterminacy with these rules seems to take two forms: if the response of interest rates to a rise in expected inflation is insufficient, then real interest rates fall thus raising demand and confirming any exogenous expected inflation. But indeterminacy is also possible if the rule is overly aggressive. Most of the literature in this area assumes that the economy is closed.
In this paper we extend this literature by studying the uniqueness and stability conditions for an equilibrium under IFB rules for various feedback horizons in open economies. In particular, we study determinacy under these rules in a New Keynesian sticky-price two-bloc model similar to Benigno and Benigno (2001) - BB henceforth - and Clarida et al. (2002) - CGG (2002) henceforth. We modify the BB/CGG (2002) model to include habit formation in consumption and price indexing, changes that help to improve the ability of the model to capture the inflation and output dynamics observed in the Euro area and the US. We also generalize the model to allow for the possibility that agents in the two blocs exhibit home bias in consumption patterns. This produces short-run and long-run deviations from consumption-based purchasing power parity, and improves the model's ability to replicate the large and protracted swings in the real euro/dollar rate observed since the launch of the euro. Analyzing a two-bloc model is particularly interesting because it allows us to explore the implications for rational-expectations equilibria of concurrent monetary policy strategies of the European Central Bank (ECB) and the Federal Reserve.
Three key findings emerge from this paper. First, we find that indeterminacy occurs for any value of the feedback parameter on inflation in the forward-looking rule if the forecast horizon lies too far into the future. This reaffirms, for the open-economy case, results found in the literature for the closed-economy case. Second, we find that the problem of indeterminacy is intrinsically more serious in an open than in a closed economy. Third, we find that the probability of indeterminacy is compounded further in the open economy when central banks in the two blocs respond to expected consumer, rather than expected producer price, inflation. Since both the ECB and the Federal Reserve focus primarily on consumer price inflation, and not on producer price inflation, our results on the poor performance of consumer price based rules have important normative implications.
1 Introduction
Under inflation targeting, the task of the central bank is to alter monetary conditions to keep inflation close to a pre-announced target. Since current inflation is usually predetermined by existing price contracts and so cannot be readily affected via monetary impulses, one class of rules widely proposed under inflation targeting are `inflation-forecast-based' (IFB) rules (Batini and Haldane (1999)). IFB rules are `simple' rules as in Taylor (1993), but where the policy instrument responds to deviations of expected, rather than current inflation from target. In most applications, the inflation forecasts underlying IFB rules are taken to be the endogenous rational-expectations forecasts conditional on an intertemporal equilibrium of the model. These rules are of specific interest because similar reaction functions are used in the Quarterly Projection Model of the Bank of Canada (see Coletti et al. (1996)), and in the Forecasting and Policy System of the Reserve Bank of New Zealand (see Black et al. (1997)) - two prominent inflation targeting central banks. As shown in Clarida et al. (2000) - CGG (2000) henceforth- and Castelnuovo (2003), estimates of IFB-type rules appear to be a good fit to the actual monetary policy in the US and Europe of recent years.1
However, IFB rules have been criticized on various grounds. Svensson (2001, 2003) criticizes Taylor-type rules in general and argues for policy based on explicit maximization procedures: we discuss his critique in section 5. Much of the literature, however, focusses on a more specific possible with Taylor-type rules -that of equilibrium indeterminacy when they are forward-looking. Nominal indeterminacy arising from an interest rate rule was first shown by Sargent and Wallace (1975) in a flexible price model. In sticky-price New Keynesian models this nominal indeterminacy disappears because the previous period's price level serves as a nominal anchor. But now a problem of real indeterminacy emerges taking two forms: if the response of interest rates to a rise in expected inflation is insufficient, then real interest rates fall thus raising demand and confirming any exogenous expected inflation (see CGG (2000) and Batini and Pearlman (2002)). But indeterminacy is also possible if the rule is overly aggressive (Bernanke and Woodford (1997); Batini and Pearlman (2002); Giannoni and Woodford (2002)).2 Here we extend this literature by studying the uniqueness and stability conditions for an equilibrium under IFB rules for various feedback horizons in open economies. 3
In a New Keynesian closed-economy model, Batini and Pearlman (2002) illustrate analytically that long-horizon IFB rules (with or without additional feedbacks on the output gap) and with interest rate smoothing can lead to indeterminacy.4 This paper employs the same root locus methodology to show analytically the feedback parameters/horizon pairs that are associated with unique and stable equilibria in a New Keynesian sticky-price two-bloc model similar to Benigno and Benigno (2001) - BB henceforth- and Clarida et al. (2002) - CGG (2002) henceforth. We modify the BB/CGG (2002) model to include habit formation in consumption and price indexing, changes that help to improve the ability of the model to capture the inflation and output dynamics observed in the Euro area and the US. We also generalize the model to allow for the possibility that agents in the two blocs exhibit home bias in consumption patterns. This produces short-run and long-run deviations from consumption-based purchasing power parity, and improves the model's ability to replicate the large and protracted swings in the real euro/dollar rate observed since the launch of the euro. Analyzing a two-bloc model is particularly interesting because it allows us to explore the implications for rational-expectations equilibria of concurrent monetary policy strategies of the European Central Bank (ECB) and the Federal Reserve. In addition, by assuming that the two blocs are identical in both fundamental parameters and in policy, we can use the Aoki (1981) decomposition of the model into sum and differences forms; we can then examine whether findings in the literature on the stability and uniqueness of equilibria based on a closed-economy assumption translate to the open-economy case.
Three key findings emerge from this paper. First, we find that indeterminacy occurs for any value of the feedback parameter on inflation in the forward-looking rule if the forecast horizon lies too far into the future. 5 This reaffirms, for the open-economy case, results found in the literature for the closed-economy case. Second, we find that the problem of indeterminacy is intrinsically more serious in an open than in a closed economy. Third, we find that the probability of indeterminacy is compounded further in the open economy when central banks in the two blocs respond to expected consumer, rather than expected producer price, inflation.
The plan of the paper is as follows. Section 2 offers an overview of the main related papers. Section 3 sets out our two-bloc model. Section 4 compares IFB rules with monetary policy based on explicit optimization and addresses the `Svensson Critique'. Section 5 uses the root locus analysis technique to investigate the stability and uniqueness conditions for IFB rules based on producer price or consumer price inflation, allowing for the possibility of home consumption bias. Section 6 offers some concluding remarks and some possible directions for future research.
2 Recent Related Literature
So far, research on monetary policy strategy has identified a series of circumstances under which forward-looking optimal and simple IFB-type rules might result in multiple equilibria or instability. One of the earliest contributions on indeterminacy under inflation-targeting forward-looking rules is Bernanke and Woodford (1997). Assuming that agents form their expectations rationally, they showed that the equilibrium associated with forward-looking optimal inflation-targeting rules under commitment may not be unique when the central bank targets current (exogenously-determined) private-sector forecasts of inflation, either those made explicitly by professional forecasters or those implicit in asset prices. In this sense, their finding squares with the more general one in Sargent and Wallace (1975), who showed that any policy rule responding uniquely to exogenous factors may induce multiple rational-expectations equilibria.
Subsequent work by Svensson and Woodford (2003), again assuming rational expectations and commitment on the side of the central bank, revealed however that forward-looking optimal inflation targeting based instead on endogenously-determined forecasts as opposed to exogenous, private-sector forecasts might not necessarily lead to superior results. As their work emphasizes, the purely forward-looking procedure, often assumed in discussions of inflation forecast targeting, prevents the target variables from depending on past conditions. In other words, the target variables are not `history-dependent'.6 This feature makes the rules sub-optimal, perhaps seriously so (Currie and Levine (1993)), and can lead to indeterminacy of the equilibrium (Woodford (1999)). Work on simple IFB rules also revealed that with these rules (i) responding to exogenous, private-sector forecasts, (ii) lacking `history dependence', and/or (iii) disregarding the way in which the private sector forms expectations when agents are not fully rational can result in multiple or unstable equilibria (see Svensson and Woodford (2003); and Evans and Honkapoja (2001, 2002)).
Perhaps the best-known theoretical result in the literature on IFB rules is that to avoid indeterminacy the monetary authority must respond aggressively, that is with a coefficient above unity, but not excessively large, to expected inflation in the closed-economy context (see, among others, CGG (2000) and, in the small-open-economy context, see De Fiore and Liu (2002)). Bullard and Mitra (2001) reaffirmed this result in a closed-economy model where private agents form forecasts using recursive learning algorithms.
Empirically, CGG (2000) found that the Federal Reserve appears to have indeed responded to expected inflation either one-quarter or one-year-ahead. Furthermore, the coefficient for the interest rate response to expected inflation has been considerably greater than 1 during the Volcker-Greenspan era. They also found that the same coefficient was significantly less than 1 in the pre-Volcker era, a possible cause, they argue, of the poor macroeconomic outcomes at the time. Estimates of an IFB rule augmented with an output gap feedback for the euro area by Castelnuovo (2003), using area-wide synthetic data going back to 1980 Q1, suggest that at an aggregate level, European monetary authorities have also responded to expected inflation one-year-ahead with a coefficient well above unity. This result would explain the successful disinflation observed in Europe in the 1980s, and accords with findings in Faust et al. (2001) on estimates of a similar reaction function for the Bundesbank over a slightly shorter period.7
The case for an aggressive rule however has been questioned by a number of recent theoretical studies. First, the result depends entirely on: (a) the way in which money is assumed to enter preferences and technology; and (b) how flexible prices are. In the closed-economy context, both Carlstrom and Fuerst (2000) and Benhabib et al. (2001) showed, for example, that with sticky prices the result is overturned when money enters the utility function either as in Sidrauski-Brock or via more realistic cash-in-advance timing assumptions.8 With these assumptions, if the monetary authority responds aggressively to future expected inflation it makes indeterminacy more likely, whereas if it does so to past inflation it makes determinacy less likely.
Second, the result rests on the assumption that, in its attempt to look forward, the central bank responds only to next quarter's inflation forecast, not to forecasts at later quarters. However, real-world procedures typically involve stabilizing inflation in the medium-run, one to two years out. It follows that the above result may not translate into sound policy prescriptions for inflation targeters. Complementing numerical results by Levin et al. (2001)-LWW henceforth- Batini and Pearlman (2002) showed analytically that IFB rules may lead to indeterminacy in the standard IS-AS optimizing forward-looking model used, for example, by Woodford (1999). They also showed that this problem is alleviated if: (i) the central bank responds to averages of expected inflation, instead of expected one-period inflation at a specific horizon; (ii) the response is very gradual (i.e., when interest rate smoothing is high); or (iii) if the rule is augmented with a response to the output gap. Below we build on this work to study indeterminacy with IFB rules responding beyond one quarter in the context of a dynamic two-bloc New-Keynesian model. In doing so we consider the impact of various degrees of openness and price flexibility on our indeterminacy results, but stick to the conventional timing used in most open-economy optimizing-agents models whereby real money entering the utility function refers to end-of-period balances.9
3 The Model
Our model is essentially a generalization of CGG (2002) and BB to incorporate a bias for consumption of home-produced goods, habit formation in consumption, and Calvo price setting with indexing of prices for those firms who, in a particular period, do not re-optimize their prices. The latter two aspects of the model follow Christiano et al. (2001) and, as with these authors, our motivation is an empirical one: to generate sufficient inertia in the model so as to enable it, in calibrated form, to reproduce commonly observed output, inflation and nominal interest rate responses to exogenous shocks.
There are two equally-sized10 symmetric blocs with the same household preferences and technologies. In each bloc there is one traded risk-free nominal bond denominated in the home bloc's currency. The exchange rate is perfectly flexible. A final homogeneous good is produced competitively in each bloc using a CES technology consisting of a continuum of differentiated non-traded goods. Intermediate goods producers and household suppliers of labor have monopolistic power. Nominal prices of intermediate goods, expressed in the currency of producers, are sticky.
The monetary policy of the central banks in the two blocs takes the same form; namely, that of an IFB nominal interest rate rule with identical parameters. The money supply accommodates the demand for money given the setting of the nominal interest rate according to such a rule. Since the paper is exclusively concerned with the possible indeterminacy or instability of IFB rules, we confine ourselves to a perfect foresight equilibrium in a deterministic environment with monetary policy responding to unanticipated transient exogenous TFP shocks.11 The decisions of households and firms are as follows:
3.1 Households
A representative household ![]() in the `home' bloc maximizes
in the `home' bloc maximizes
The representative household ![]() must obey a budget constraint:
must obey a budget constraint:
where
![$W_{t}=\left[\int_0^1 W_t(r)^{1-\eta} dr \right]^{ \frac{1}{1-\eta}}$](img46.gif) is an average wage index and
is an average wage index and
We assume that the consumption index depends on the consumption
of a single type of final good in each of two identically sized
blocs, and is given by
with the consumer price index
where
Thus (since
In a perfect foresight equilibrium, maximizing (1) subject to (2) and (3) and imposing symmetry on households (so that
![]() , etc)
yields standard results:
, etc)
yields standard results:
(9) is the familiar Keynes-Ramsey rule adapted to take into account of the consumption habit. In (10), the demand for money balances depends positively on consumption relative to habit and negatively on the nominal interest rate. Given the central bank's setting of the latter, (10) is completely recursive to the rest of the system describing our macro-model and will be ignored in the rest of the paper. (11) reflects the market power of households arising from their monopolistic supply of a differentiated factor input with elasticity
Households can accumulate assets in the form of either home or
foreign bonds. Uncovered interest rate parity then gives
3.2 Firms
Competitive final goods firms use a continuum of non-traded
intermediate goods according to a constant returns CES technology
to produce aggregate output
where
![$P_{Ht}=\left[ \int_0^1 P_{Ht}(m)^{1-\zeta} dm \right]^{ \frac{1}{1-\zeta}}$](img87.gif) .
. In the intermediate goods sector each good ![]() is produced by a single firm
is produced by a single firm
![]() using only
differentiated labour with another constant returns CES
technology:
using only
differentiated labour with another constant returns CES
technology:
For later analysis it is useful to define the real marginal cost as the wage relative to domestic producer price. Using (11) and (16) this can be written as
Now we assume that there is a probability of ![]() at each period that the price of
each intermediate good
at each period that the price of
each intermediate good ![]() is
set optimally to
is
set optimally to ![]() . If the price is not re-optimized, then
it is indexed to last period's aggregate producer price
inflation.14 With
indexation parameter
. If the price is not re-optimized, then
it is indexed to last period's aggregate producer price
inflation.14 With
indexation parameter ![]() , this implies that successive prices
with no reoptimization are given by
, this implies that successive prices
with no reoptimization are given by
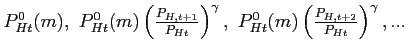 . For each intermediate producer
. For each intermediate producer ![]() the objective is at time
the objective is at time ![]() to choose
to choose ![]() to maximize discounted
profits
to maximize discounted
profits
and by the law of large numbers the evolution of the price index is given by
3.3 The Equilibrium and the Trade Balance
In equilibrium, goods markets, money markets and the bond market
all clear. Equating the supply and demand of the home consumer good
and using (5) and the foreign counterpart of
(6) we obtain
Given interest rates
Combining the Keynes-Ramsey equations with the UIP condition we
have that
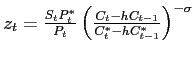 . Then (22) implies that
. Then (22) implies that
The model as it stands with habit persistence (![]() ),
), ![]() and
and
![]() exhibits net foreign
asset dynamics. This can be shown by writing the trade balance
exhibits net foreign
asset dynamics. This can be shown by writing the trade balance
![]() in the
home bloc as exports minus imports denominated its own
currency:
in the
home bloc as exports minus imports denominated its own
currency:
3.4 Linearization
We linearize around a baseline symmetric steady state in which
consumption and prices in the two blocs are equal and constant.
Then inflation is zero,
![]() and
hence from (24) trade is balanced. Output is then
at its sticky-price, imperfectly competitive natural rate and from
the Keynes-Ramsey condition (9) the nominal
rate of interest is given by
and
hence from (24) trade is balanced. Output is then
at its sticky-price, imperfectly competitive natural rate and from
the Keynes-Ramsey condition (9) the nominal
rate of interest is given by
![]() . Now define all lower
case variables (including
. Now define all lower
case variables (including ![]() ) as proportional deviations from this baseline
steady state17. Home
producer and consumer inflation are defined as
) as proportional deviations from this baseline
steady state17. Home
producer and consumer inflation are defined as
![]() and
and
![]() respectively. Similarly, define foreign producer inflation
and consumer price inflation. Combining (19)
and (20), we can eliminate
respectively. Similarly, define foreign producer inflation
and consumer price inflation. Combining (19)
and (20), we can eliminate ![]() to obtain in linearized
form
to obtain in linearized
form
The first term on the right-hand-side of (26) is a TFP shock. The second term is a risk-sharing effect: a rise in habit-adjusted consumption leads to an increase in the real wage (see (11)) and hence the marginal cost. The last term is a terms of trade effect, which implies that marginal costs falls if the terms of trade,
Linearizing the remaining equations (8), (9), (12), (21) and (23) yields18
Note that (30) and its foreign counterpart imply that
Turning to spillover effects in our
linearized form of the model, consider the case of no home bias.
Then from (30) and (26) we
obtain
(33) indicates that the risk-sharing effect exceeds the terms of trade effect and there is positive spillover from output onto the marginal cost of the second bloc--implying a negative spillover on output--iff
3.5 Sum and Difference Systems
Since the economies are symmetric, the easiest way of analyzing
them is to use the sum and difference systems, as introduced by
Aoki (1981). We denote all
sums of home and foreign variables with the superscript
![]() , while we denote
differences by
, while we denote
differences by ![]() . The
first thing to note when inspecting the equations above is that the
sum system is independent of home bias, and can be written
as
. The
first thing to note when inspecting the equations above is that the
sum system is independent of home bias, and can be written
as
where
However the difference system does depend on the home bias
parameter, ![]() ,
Writing
,
Writing
![]() ,
,
![]() , etc., it can
be written as
, etc., it can
be written as
For the case of no home consumption bias (
In addition, when there is no home bias, the remainder of the difference system reduces to
Note, as with other models of the same New Keynesian genre, there is a long-run inflation-unemployment trade-off.20
The sum and difference systems can now be set up in state-space form given the nominal interest rate rule. This Aoki decomposition enables us to decompose the open economy into two decoupled dynamic systems; the sum system, that captures the properties of a closed world economy, and a difference system that instead portrays the open-economy case. In principle, we could close the model with a number of different Taylor-type rules and also, given a policymaker's objective function, with optimal rules for coordinated or independent policies. Here we choose to focus uniquely on IFB rules that feedback exclusively on expected inflation. Before doing so, in the next section we first offer answers to the more general question of why is it interesting to look at simple rules. We also discuss why, within the broader class of simple rules, we consider non-optimal simple rules rather than simple rules which are optimal within the constraints defining their Taylor form of simplicity.
4 Designing and Implementing Optimal Policy
4.1 Formulating the Optimal Rule
The analysis of IFB rules set out in the next section
contributes to a large literature on monetary policy rules that
focusses primarily on the properties of these non-optimizing simple
rules, thereby neglecting the possibility that central banks set
monetary conditions by means of some explicit optimizing procedure.
This approach has been criticized by Svensson (2001, 2003), and in
this section we attempt to address his critique. We start with a
commonly used objective function at time ![]() for the home bloc of the
form
for the home bloc of the
form
Our linearized model can be expressed in state-space form
as
say, where
4.2 Implementing the Optimal Policy and Simple Rules
The optimal cooperative policy then consists of trajectories for
nominal interest rates that would be followed in the absence of
initial shocks to TFP (or, in a stochastic setting, in the absence
of random shocks) and a reaction function consisting of a feedback
on the lagged predetermined variables with geometrically declining
weights with lags extending back to time ![]() , the time of the formulation and
announcement of the policy. Together these components constitute an
explicit instrument rule. 24As is well-known, there are two
fundamental problems with implementing such a rule. First it is
time-inconsistent: having announced the policy at time
, the time of the formulation and
announcement of the policy. Together these components constitute an
explicit instrument rule. 24As is well-known, there are two
fundamental problems with implementing such a rule. First it is
time-inconsistent: having announced the policy at time ![]() , at any time
, at any time ![]() there emerges an incentive for
the social planner to redesign both open-loop and feedback
components of policy. Second, the cooperative policy is not a Nash
equilibrium so there exists at any time, including
there emerges an incentive for
the social planner to redesign both open-loop and feedback
components of policy. Second, the cooperative policy is not a Nash
equilibrium so there exists at any time, including ![]() , an incentive to renege and adopt
a policy that is the best response to that of the other bloc.
, an incentive to renege and adopt
a policy that is the best response to that of the other bloc.
One way of implementing the optimal policy that addresses both the time-inconsistency and cooperation problems is to design objective functions for the two blocs that do not coincide with the true welfare. The aim of the exercise is to choose this design, or `regime', so that if the two blocs independently optimize in a discretionary fashion, then in a non-cooperative time-consistent equilibrium the optimal policy will be implemented. Thus BB, in addressing the cooperation problem, force the central banks to be `inward-looking' in the sense that their loss function only includes domestic target (e.g., producer inflation rather than consumer inflation which implies an exchange rate target). Svensson and Woodford (2003) adopt this modified loss function approach to the time-inconsistency problem for a closed economy. The idea of modifying loss functions so that players in a game have the `wrong' welfare criteria is, of course, not new and is the basis of Rogoff-delegation and Walsh contracts. To a greater or lesser extent all these solutions are susceptible to the critique by McCallum (1995) of Walsh contracts, that they do not solve either the credibility or the coordination problem, but ``merely relocate'' them to demonstrating the commitment of the policymakers to their modified loss functions.
A second way of implementing optimal policy is to build up a reputation for commitment to both the second bloc and to the private sector. In a more realistic incomplete information setting where policymakers' objectives are not known to the public, but policy rules can be observed, the public can learn about the rule by observing the relevant data and applying standard econometric techniques. In principle this should be possible for rules of the form (45), but the New Keynesian features of the model (namely output and inflation persistence) make it particularly complex. This highlights the importance of rules being simple in the sense that the instrument is constrained to feed back on a limited number of variables and their lags such as in a Taylor rule, or their forecasts as in IFB rules.
As well as being more easily verifiable, simple rules may have other advantages. As shown in Currie and Levine (1993) and Tetlow and von zur Muehlen (2001), it is easier to learn about simple rules that (by definition) feed back on a limited selection of easily verifiable macro-variables, than to learn about complex optimal rules such as (45) . Taking this ability to learn into account, simple rules may then outperform their optimal counterparts. Finally it has been suggested that simple rules may be robust with respect to modelling errors (LWW, Taylor (1999)).
Simple rules can be designed to approximate the optimal rule by
choosing the feedback parameters so as to maximize an objective
function of the form (43). However the
simplicity constraint means that the optimal simple rule is not
certainty equivalent, unlike the
optimal rule unconstrained to be simple. This means that if at time
![]() we designed a
optimal simple rule of a particular form for our model above,
optimal feedback parameters would depend on the transient shocks to
TFPs,
we designed a
optimal simple rule of a particular form for our model above,
optimal feedback parameters would depend on the transient shocks to
TFPs, ![]() and
and ![]() and, in a stochastic
setting, on the variance-covariance matrix of white noise
disturbances in the stochastic process defining these
shocks.25 Then
rules that perform well, in the sense of achieving a welfare
outcome close to that of the optimal rule, under one assumed set of
initial displacements and covariance matrix may well lack
robustness in that they may perform badly under a different set of
assumptions. However some structures of simple rule may be more
robust than others.26
and, in a stochastic
setting, on the variance-covariance matrix of white noise
disturbances in the stochastic process defining these
shocks.25 Then
rules that perform well, in the sense of achieving a welfare
outcome close to that of the optimal rule, under one assumed set of
initial displacements and covariance matrix may well lack
robustness in that they may perform badly under a different set of
assumptions. However some structures of simple rule may be more
robust than others.26
Defining what we mean by the optimal simple rule is then problematic. The literature on determinacy, to which our paper contributes, has a more modest objective of providing guidelines to policymakers in the form of simple criteria for avoiding very bad outcomes that lead to multiple equilibria or explosive behaviour. In our set-up, these guidelines focus on the choice of feedback, interest rate smoothing and feedback horizon parameters. In the following section we pursue this research objective by looking at how such guidelines are affected when we proceed from the closed to the open economy and by the degree of openness in the latter.
5 The Stability and Determinacy of IFB Rules
This section studies two particular forms of simple rule, IFB
rules either of the form
which is a feedback on producer price inflation. Both rules are in deviation form about some long-run zero-inflation steady state and could represent the feedback component of monetary policy that complements a (possibly optimal) open-loop trajectory designed as in the previous section. We assume that the foreign bloc has a similar rule with the same parameters and forecast horizon.
With rules (46) and (47), policymakers set the nominal interest rate so as
to respond to deviations of the inflation term from target. In
addition, policymakers smooth rates, in line with the idea that
central banks adjust the short-term nominal interest rate only
partially towards the long-run inflation target, which is set to
zero for simplicity in our set-up.27 The parameter
![]() measures the degree of interest rate smoothing.
measures the degree of interest rate smoothing. ![]() is the feedback horizon of the
central bank. When
is the feedback horizon of the
central bank. When ![]() , the
central bank feeds back from current dated variables only. When
, the
central bank feeds back from current dated variables only. When
![]() , the central
bank feeds back instead from deviations of forecasts of variables
from target. This is a proxy for actual policy in inflation
targeting countries that apparently respond to deviations of
current inflation from its short or medium forecast (see Batini and Nelson (2001)).
Finally,
, the central
bank feeds back instead from deviations of forecasts of variables
from target. This is a proxy for actual policy in inflation
targeting countries that apparently respond to deviations of
current inflation from its short or medium forecast (see Batini and Nelson (2001)).
Finally, ![]() is the feedback parameter: the larger is
is the feedback parameter: the larger is ![]() , the faster is the pace at which
the central bank acts to eliminate the gap between expected
inflation and its target value. We now show that, for given degrees
of interest rate smoothing
, the faster is the pace at which
the central bank acts to eliminate the gap between expected
inflation and its target value. We now show that, for given degrees
of interest rate smoothing ![]() , the stabilizing characteristics of these rules
depend both on the magnitude of
, the stabilizing characteristics of these rules
depend both on the magnitude of ![]() and the length of the feedback horizon
and the length of the feedback horizon
![]() .
.
5.1 Conditions for the Uniqueness and Stability
To understand better how the precise combination of the pair
![]() , IFB rules
can lead the economy into instability or indeterminacy consider the
model economy (44) with interest rate rules of
the form (46) or (47) with
, IFB rules
can lead the economy into instability or indeterminacy consider the
model economy (44) with interest rate rules of
the form (46) or (47) with
![]() . Shocks to TFP
are exogenous stable processes and play no part in the stability
analysis. Furthermore we are only concerned with the feedback
component of policy. We therefore set
. Shocks to TFP
are exogenous stable processes and play no part in the stability
analysis. Furthermore we are only concerned with the feedback
component of policy. We therefore set
![]() in (44). Write the IFB rules in the
form28
in (44). Write the IFB rules in the
form28
![\begin{displaymath} \left[ \begin{array}{l} i_{t} \ i_{t}^{\ast } \end{array}\... ...array}{l} \mathsf{z}_{t} \ \mathsf{x}_{t} \end{array}\right] \end{displaymath}](img239.gif)
|
(48) |
![\begin{displaymath} \left[ \begin{array}{l} \mathsf{z}_{t+1} \ \mathcal{E}_{t}... ...array}{l} \mathsf{z}_{t} \ \mathsf{x}_{t} \end{array}\right] \end{displaymath}](img242.gif)
|
(49) |
The condition for a stable and unique equilibrium depends on the
magnitude of the eigenvalues of the matrix ![]() . If the number of eigenvalues
outside the unit circle is equal to the number of non-predetermined
variables, the system has a unique equilibrium which is also stable
with saddle-path
. If the number of eigenvalues
outside the unit circle is equal to the number of non-predetermined
variables, the system has a unique equilibrium which is also stable
with saddle-path ![]() where
where ![]() . (See Blanchard and Kahn (1980);
Currie and Levine
(1993)). In our model under control, with
. (See Blanchard and Kahn (1980);
Currie and Levine
(1993)). In our model under control, with ![]() , there are 4 non-predetermined
variables in total, 2 each for the sum and difference systems and 6
predetermined variables in total, 3 each for the sum and difference
systems. Instability occurs when the number of eigenvalues of
, there are 4 non-predetermined
variables in total, 2 each for the sum and difference systems and 6
predetermined variables in total, 3 each for the sum and difference
systems. Instability occurs when the number of eigenvalues of
![]() outside the unit
circle is larger than the number of non-predetermined variables.
This implies that when the economy is pushed off its steady state
following a shock, it cannot ever converge back to it, but rather
finishes up with explosive inflation dynamics (hyperinflation or
hyperdeflation).
outside the unit
circle is larger than the number of non-predetermined variables.
This implies that when the economy is pushed off its steady state
following a shock, it cannot ever converge back to it, but rather
finishes up with explosive inflation dynamics (hyperinflation or
hyperdeflation).
By contrast, indeterminacy occurs when the number of eigenvalues
of ![]() outside the unit
circle is smaller than the number of non-predetermined variables.
Put simply, this implies that when a shock displaces the economy
from its steady state, there are many possible paths leading back
to equilibrium, i.e. there are multiple well-behaved rational
expectations solutions to the model economy. With forward-looking
rules this can happen when policymakers respond to private sector's
inflation expectations and these in turn are driven by
non-fundamental exogenous random shocks (i.e. not based on
preferences or technology), usually referred to as `sunspots'. If
policymakers set the coefficients of the rule so that this
accommodates such expectations, the latter become self-fulfilling.
Then the rule is unable to uniquely pin down the behavior of one or
more real and/or nominal variables, making many different paths
compatible with equilibrium (see Kerr and King (1996); Chari et al.
(1998); CGG (2000); Carlstrom and Fuerst (1999)
and Carlstrom and
Fuerst (2000); Svensson and Woodford
(1999); and Woodford
(2000)). The fact that the rule itself may introduce
indeterminacy and generate so called `sunspot equilibria' is of
interest because sunspot fluctuations - i.e., persistent movements
in inflation and output that materialize even in the absence of
shocks to preferences or technology - are typically
welfare-reducing and can potentially be quite large.
outside the unit
circle is smaller than the number of non-predetermined variables.
Put simply, this implies that when a shock displaces the economy
from its steady state, there are many possible paths leading back
to equilibrium, i.e. there are multiple well-behaved rational
expectations solutions to the model economy. With forward-looking
rules this can happen when policymakers respond to private sector's
inflation expectations and these in turn are driven by
non-fundamental exogenous random shocks (i.e. not based on
preferences or technology), usually referred to as `sunspots'. If
policymakers set the coefficients of the rule so that this
accommodates such expectations, the latter become self-fulfilling.
Then the rule is unable to uniquely pin down the behavior of one or
more real and/or nominal variables, making many different paths
compatible with equilibrium (see Kerr and King (1996); Chari et al.
(1998); CGG (2000); Carlstrom and Fuerst (1999)
and Carlstrom and
Fuerst (2000); Svensson and Woodford
(1999); and Woodford
(2000)). The fact that the rule itself may introduce
indeterminacy and generate so called `sunspot equilibria' is of
interest because sunspot fluctuations - i.e., persistent movements
in inflation and output that materialize even in the absence of
shocks to preferences or technology - are typically
welfare-reducing and can potentially be quite large.
In order to gain insight into the stabilizing properties of IFB
rules, following Batini
and Pearlman (2002) we analyze their performance by using
root locus analysis, a method that we
borrow from the control engineering literature. Appendix B outlines
how this method works. Use of this method allows us to identify
analytically the range of stabilizing parameters
![]() in our
sticky-price/sticky-inflation models before indeterminacy sets in.
The method produces geometrical representations that show how
system eigenvalues change as a function of the change in any
parameter in the system. In our particular case we are interested
in detecting how the characteristic roots of the model economy
evolve as we vary the inflation feedback parameter
in our
sticky-price/sticky-inflation models before indeterminacy sets in.
The method produces geometrical representations that show how
system eigenvalues change as a function of the change in any
parameter in the system. In our particular case we are interested
in detecting how the characteristic roots of the model economy
evolve as we vary the inflation feedback parameter ![]() , for given forecast horizons
, for given forecast horizons
![]() in the policy rule.
As the conditions for stability and determinacy of the model hinge
on the value of these roots, from these diagrams we can infer which
regions of the
in the policy rule.
As the conditions for stability and determinacy of the model hinge
on the value of these roots, from these diagrams we can infer which
regions of the
![]() parameter space are associated
with unique and well-behaved REE. Since we condition on
increasingly distant forecast horizons in the policy rule, the
method entails deriving a separate diagram for each value of
parameter space are associated
with unique and well-behaved REE. Since we condition on
increasingly distant forecast horizons in the policy rule, the
method entails deriving a separate diagram for each value of
![]() . However, in the
majority of cases a clear pattern emerges quickly, so in what
follows we only draw these diagrams at most for
. However, in the
majority of cases a clear pattern emerges quickly, so in what
follows we only draw these diagrams at most for ![]() = 0, 1,...,4.
= 0, 1,...,4.
In the following subsections, we use the Aoki method to analyze separately the sum and difference systems of two symmetric blocs pursuing symmetric IFB rules of the form (46) or (47). The results for the sum system can be thought of as applying to a closed economy. For open economies both sum and difference systems must be saddle-path stable for a stable and unique equilibrium. As previously mentioned, the central banks'choice of responding to consumer or price inflation as well as the existence of a home bias in consumption patterns are all irrelevant in the case of the sum system. In the case of the difference system this is no longer true, and so we investigate changes to these assumptions separately for that case.
5.2 The Sum System
The sum form of the IFB rule is given by
where we have defined
Equation (51) shows that the minimal
state-space form of the sum system has dimension
![]() .
Recalling that there are 3 predetermined variables in each of the
sum and difference systems, it follows that the saddle-path
condition for a unique stable rational expectations solution in the
general version of our model is that the number of stable roots
(i.e., roots inside the unit circle of the complex plane) is 3 and
the number of unstable roots is
.
Recalling that there are 3 predetermined variables in each of the
sum and difference systems, it follows that the saddle-path
condition for a unique stable rational expectations solution in the
general version of our model is that the number of stable roots
(i.e., roots inside the unit circle of the complex plane) is 3 and
the number of unstable roots is ![]() .
.
To identify values of ![]() that involve exactly three roots of
equation (51) we use the root locus
technique. In particular, this technique can help us uncover how
the range of values of
that involve exactly three roots of
equation (51) we use the root locus
technique. In particular, this technique can help us uncover how
the range of values of ![]() that are consistent with determinacy changes as
the feedback horizon
that are consistent with determinacy changes as
the feedback horizon ![]() changes. The root locus technique provides topological proofs of
our main results (Appendix B describes this technique in detail).
The technique involves starting from a polynomial equation and
using a set of topological theorems to track the equation's roots
as parameters in the system vary. The locus describing the
evolution of the roots when parameters change is called the `root
locus'. In our analysis here, the polynomial equation is the
characteristic equation (51), and we use the
technique to graph the locus of
changes. The root locus technique provides topological proofs of
our main results (Appendix B describes this technique in detail).
The technique involves starting from a polynomial equation and
using a set of topological theorems to track the equation's roots
as parameters in the system vary. The locus describing the
evolution of the roots when parameters change is called the `root
locus'. In our analysis here, the polynomial equation is the
characteristic equation (51), and we use the
technique to graph the locus of
![]() pairs that traces how the
roots change as
pairs that traces how the
roots change as ![]() varies between 0 and
varies between 0 and ![]() .
Other parameters in the system, including the feedback horizon
parameter
.
Other parameters in the system, including the feedback horizon
parameter ![]() in the IFB
rule, are kept constant. So to plot root loci for different
feedback horizon we have to generate separate charts, each
conditioning on a different horizon assumption. Each chart shows
the complex plane (indicated by the solid thin line),29 the unit circle (indicated by the
dashed line), and the root locus tracking zeroes of equation
(51) as
in the IFB
rule, are kept constant. So to plot root loci for different
feedback horizon we have to generate separate charts, each
conditioning on a different horizon assumption. Each chart shows
the complex plane (indicated by the solid thin line),29 the unit circle (indicated by the
dashed line), and the root locus tracking zeroes of equation
(51) as ![]() varies between 0 and
varies between 0 and ![]() (indicated by the solid bold
line). The arrows indicate the direction of the arms of the root
locus as
(indicated by the solid bold
line). The arrows indicate the direction of the arms of the root
locus as ![]() increases. Throughout we experiment with both a `higher' and a
`lower'
increases. Throughout we experiment with both a `higher' and a
`lower'
![]() ,
as defined in (52). The economic
interpretation of these cases is as follows: from the definitions
in (52), the high
,
as defined in (52). The economic
interpretation of these cases is as follows: from the definitions
in (52), the high
![]() case corresponds to low
case corresponds to low ![]() (i.e., more flexible prices) and low
(i.e., more flexible prices) and low
![]() .
From section 3.4 we have seen that the latter implies small
spillover effects and hence low interdependence between the two
blocs. Hence in the high
.
From section 3.4 we have seen that the latter implies small
spillover effects and hence low interdependence between the two
blocs. Hence in the high
![]() case, prices are relatively flexible and interdependence not as
strong when compared with the low
case, prices are relatively flexible and interdependence not as
strong when compared with the low
![]() case.
case.
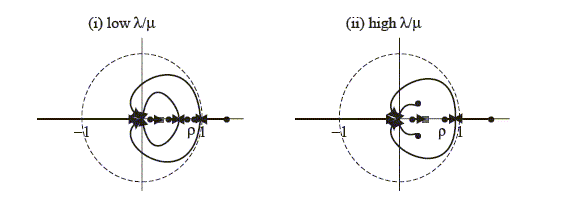
The term inside the square brackets in equation (51) corresponds to no nominal interest rate policy at
all. With no policy rule in place, rule (46) or
(47) is switched off and so the lagged term
![]() disappears from
our model; the system now requires exactly two stable roots for determinacy. Figure 1 plots
the root locus in this case. Since with no policy
disappears from
our model; the system now requires exactly two stable roots for determinacy. Figure 1 plots
the root locus in this case. Since with no policy ![]() is set to 0, the root locus is
just a set of dots: namely, the roots of equation (51) when
is set to 0, the root locus is
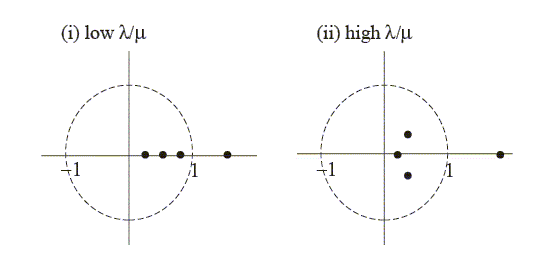
just a set of dots: namely, the roots of equation (51) when ![]() . Note that depending on the value of
. Note that depending on the value of
![]() , the
position of these roots varies, and in the flexible price, low
independence case where
, the
position of these roots varies, and in the flexible price, low
independence case where
![]() is
high, there are complex roots indicating oscillatory
dynamics.30 The
diagram shows that there are too many stable roots in both cases
(i.e. 3 instead of 2), which implies that with no monetary policy
there will always be indeterminacy in the sum system.
is
high, there are complex roots indicating oscillatory
dynamics.30 The
diagram shows that there are too many stable roots in both cases
(i.e. 3 instead of 2), which implies that with no monetary policy
there will always be indeterminacy in the sum system.
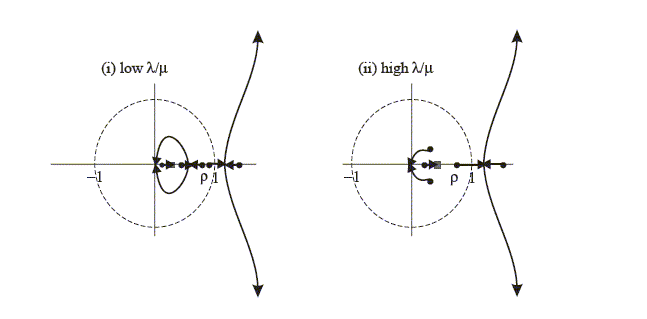
Figure 1: Possible position of zeroes when
If the nominal interest rate rule is switched on and now feeds
back on current rather than expected inflation, i.e. ![]() = 0, then the root locus technique
yields a pattern of zeros as depicted in Figure 2. Interest rate
smoothing brings about a lag in the short-term nominal interest
rate and so means that the system is stable if it has exactly
three stable roots (as we now have
three predetermined variables in the system). The figure
illustrates that if
= 0, then the root locus technique
yields a pattern of zeros as depicted in Figure 2. Interest rate
smoothing brings about a lag in the short-term nominal interest
rate and so means that the system is stable if it has exactly
three stable roots (as we now have
three predetermined variables in the system). The figure
illustrates that if ![]() is
sufficiently large, one arm of the root locus starting originally
at
is
sufficiently large, one arm of the root locus starting originally
at ![]() exits the unit
circle, turning one root from stable to unstable so that there are
now three - as required - instead of four stable roots and the
system has a determinate equilibrium. As
exits the unit
circle, turning one root from stable to unstable so that there are
now three - as required - instead of four stable roots and the
system has a determinate equilibrium. As
![]() , there are roots at
, there are roots at
![]() , two
roots at
, two
roots at ![]() , and one at
, and one at
![]() , the
latter shown as a square.
, the
latter shown as a square.
Figure 2: Position of zeroes as
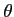 changes using
current inflation
changes using
current inflation
Note that when ![]() , the characteristic equation has the value
0, confirming that the branch of the root locus moving away from
, the characteristic equation has the value
0, confirming that the branch of the root locus moving away from
![]() crosses the
unit circle at a value
crosses the
unit circle at a value ![]() . Thus we conclude that for a rule feeding
back on current inflation the sum system exhibits determinacy if
and only if
. Thus we conclude that for a rule feeding
back on current inflation the sum system exhibits determinacy if
and only if ![]() .
For higher values of
.
For higher values of ![]() we can draw the sequence of root locus diagrams shown in Figures
3-6, and so confirm the well-known `Taylor Principle' that interest
rates need to react to inflation with a feedback greater than
unity. However for
we can draw the sequence of root locus diagrams shown in Figures
3-6, and so confirm the well-known `Taylor Principle' that interest
rates need to react to inflation with a feedback greater than
unity. However for ![]() our diagrams show that an arm of the root locus re-enters the unit
circle for some high
our diagrams show that an arm of the root locus re-enters the unit
circle for some high ![]() and indeterminacy re-emerges. Therefore
and indeterminacy re-emerges. Therefore
![]() is
necessary but not sufficient for stability and determinacy. Our
results up to this point are summarized in proposition 1 below.
is
necessary but not sufficient for stability and determinacy. Our
results up to this point are summarized in proposition 1 below.
Figure 3: Position of zeroes as
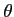 changes: 1-period
ahead expected inflation
changes: 1-period
ahead expected inflation
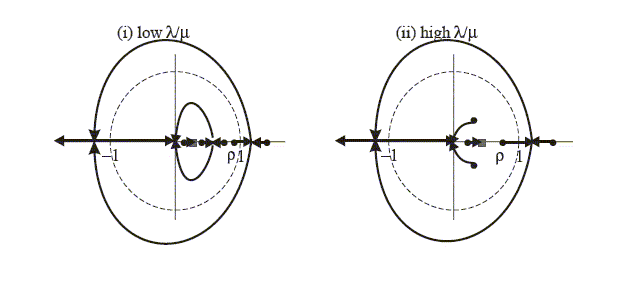
Figure 4: Position of zeroes as
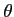 changes: 2-period
ahead expected inflation
changes: 2-period
ahead expected inflation
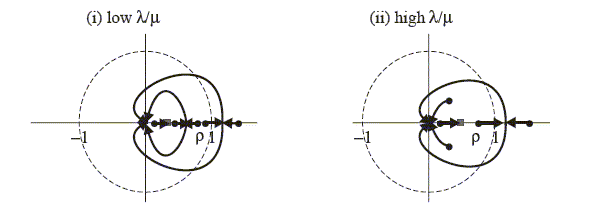
Figure 5: Position of zeroes as
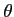 changes: 3-period
ahead expected inflation
changes: 3-period
ahead expected inflation
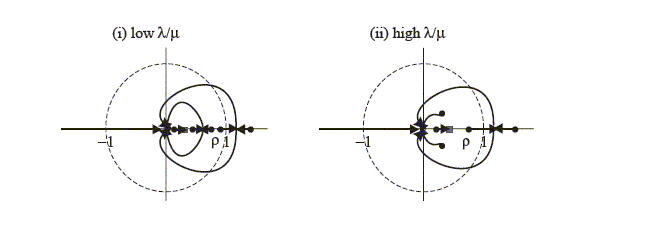
Figure 6: Position of zeroes as
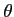 changes: 4-period
ahead expected inflation
changes: 4-period
ahead expected inflation
Proposition 1: In the sum system, for a rule feeding back on current inflation (
When the rule starts responding to inflation expectations at
longer horizons (![]()
![]() 1),
self-fulfilling inflationary expectations and sunspot equilibria
are once again possible as
1),
self-fulfilling inflationary expectations and sunspot equilibria
are once again possible as ![]() becomes too large. These manifest themselves as
soon as the arms of the root locus that were outside the unit
circle when
becomes too large. These manifest themselves as
soon as the arms of the root locus that were outside the unit
circle when ![]() = 0 and
for small values of
= 0 and
for small values of ![]() start entering the unit circle as
start entering the unit circle as ![]() increases. Let
increases. Let
![]() be the
upper critical value of
be the
upper critical value of ![]() for the sum system for a feedback horizon
for the sum system for a feedback horizon
![]() . Figure 3 shows that
for the case
. Figure 3 shows that
for the case ![]() , i.e.
one-quarter ahead forecasts which corresponds to a case studied by
CGG (2000), indeterminacy occurs when this portion of the root
locus enters the unit circle at
, i.e.
one-quarter ahead forecasts which corresponds to a case studied by
CGG (2000), indeterminacy occurs when this portion of the root
locus enters the unit circle at ![]() .31 The
critical upper value for
.31 The
critical upper value for
![]() when this occurs is obtained by substituting
when this occurs is obtained by substituting ![]() and
and ![]() into the characteristic equation
(51) to obtain:
into the characteristic equation
(51) to obtain:
One important thing to note looking at this expression is that
the greater is the degree of smoothing captured by the parameter
![]() in the interest
rate rule, the larger the maximum permissible value of
in the interest
rate rule, the larger the maximum permissible value of ![]() before indeterminacy sets in.
For
before indeterminacy sets in.
For ![]() , Figures 4-6
show that indeterminacy occurs when the root locus enters the unit
circle at
, Figures 4-6
show that indeterminacy occurs when the root locus enters the unit
circle at
![]() for some
for some
![]() . In this case, the
threshold
. In this case, the
threshold
![]() for
for
![]() must be found
numerically. Given
must be found
numerically. Given ![]() , write
the characteristic equation as
, write
the characteristic equation as
which can be solved numerically for
As well as locating an upper threshold
![]() , an even more significant result concerning indeterminacy emerges
from Figures 4, 5 and 6 for
, an even more significant result concerning indeterminacy emerges
from Figures 4, 5 and 6 for ![]() . These have been drawn in such a way that the
two rightmost poles of the root locus are joined by straight lines
that meet outside the unit circle. The
implication is that for some values of
. These have been drawn in such a way that the
two rightmost poles of the root locus are joined by straight lines
that meet outside the unit circle. The
implication is that for some values of ![]() , these yield unstable
roots of the system, and therefore the system will have exactly
three stable roots which is what is required for determinacy. (Note
that if the arms of the root locus from
, these yield unstable
roots of the system, and therefore the system will have exactly
three stable roots which is what is required for determinacy. (Note
that if the arms of the root locus from ![]() cross the unit circle before
these latter meet, then there may anyway be too many stable roots).
However, for a lower value of
cross the unit circle before
these latter meet, then there may anyway be too many stable roots).
However, for a lower value of ![]() it could happen that rather than meeting to the
right of
it could happen that rather than meeting to the
right of ![]() , the two
arms instead meet to the left of
, the two
arms instead meet to the left of ![]() , that is inside the
unit circle and then remain within it, as in figure 7. This would
imply that for all
, that is inside the
unit circle and then remain within it, as in figure 7. This would
imply that for all ![]() there are always more than three stable roots, which would entail,
in turn, indeterminacy for all values of
there are always more than three stable roots, which would entail,
in turn, indeterminacy for all values of ![]() . We therefore conclude that
there is determinacy for
. We therefore conclude that
there is determinacy for ![]() slightly greater than 1 if the root locus
passes through
slightly greater than 1 if the root locus
passes through ![]() from the left, as in figures 3-6. Conversely, there is
indeterminacy for all
from the left, as in figures 3-6. Conversely, there is
indeterminacy for all ![]() if the root locus passes through
if the root locus passes through ![]() from the right, as in Figure 7;
this equivalent to the condition
from the right, as in Figure 7;
this equivalent to the condition
![]() at
at ![]() . We now use this topological
argument to prove the following proposition:
. We now use this topological
argument to prove the following proposition:
Proposition 2:
Whatever the combination of parameter values, there is always some
lead ![]() given by
(56) below such that for
given by
(56) below such that for ![]() there is indeterminacy for
all values of
there is indeterminacy for
all values of ![]() .
.
Proof:
Write (51) as ![]() . Taking derivatives with respect to
. Taking derivatives with respect to
![]() , and evaluating
at
, and evaluating
at ![]() yields
yields
![]() . By inspection
. By inspection ![]() , so that the root locus crosses
, so that the root locus crosses ![]() from the right if
from the right if
![]() . Substituting from
(51), this is a requirement that
. Substituting from
(51), this is a requirement that
![]() and
and
![]() .
Since
.
Since ![]() guarantees the
latter condition, there is always indeterminacy if
guarantees the
latter condition, there is always indeterminacy if
Figure 7: Position of zeros as
 changes: 3-period
ahead expected inflation, and low
changes: 3-period
ahead expected inflation, and low 
The value of ![]() is
crucial in determining the critical value of the lead
is
crucial in determining the critical value of the lead ![]() beyond which indeterminacy sets in.
The lower
beyond which indeterminacy sets in.
The lower ![]() , the lower
the maximum-permitted inflation horizon the central bank can
respond to, and hence, the larger the region of indeterminacy under
IFB rules.
, the lower
the maximum-permitted inflation horizon the central bank can
respond to, and hence, the larger the region of indeterminacy under
IFB rules.
5.3 The Difference System
In this section we analyze the effect of the IFB rule in the
difference system. We shall see that, in this case, there are
important differences in the conditions for determinacy depending
on (i) whether the central banks react to producer or consumer
price inflation and on (ii) the degree of openness of the two
economies (as captured by the parameter ![]() ). We start by considering the
case of complete integration (i.e.
). We start by considering the
case of complete integration (i.e.
![]() and
no home bias), looking first at IFB rules based on producer price
inflation and then at IFB rules based on consumer price inflation.
Then we consider the case when there is home bias, however
restricting ourselves to the case of no habit formation
(
and
no home bias), looking first at IFB rules based on producer price
inflation and then at IFB rules based on consumer price inflation.
Then we consider the case when there is home bias, however
restricting ourselves to the case of no habit formation
(![]() ) and a unit
elasticity of substitution in the utility function (
) and a unit
elasticity of substitution in the utility function (![]() ). These more restrictive
assumptions imply no foreign asset dynamics about a balanced trade
steady state (since trade is always balanced), as when we assumed
no home bias. Without these restrictions we need to address the
well-known problems associated with Ramsey consumers in open
economies (see, for example, Schmitt-Grohe and Uribe,
2001).33
). These more restrictive
assumptions imply no foreign asset dynamics about a balanced trade
steady state (since trade is always balanced), as when we assumed
no home bias. Without these restrictions we need to address the
well-known problems associated with Ramsey consumers in open
economies (see, for example, Schmitt-Grohe and Uribe,
2001).33
5.3.1 No Home Bias and IFB Rules Based on Producer Price Inflation
With interest rates feeding back on producer price inflation,
the IFB rule in difference form is given by
The root locus diagrams for this characteristic equation will have qualitatively the same features as those for the sum system. So propositions 1 and 2 apply to the difference system as well. By analogy with our earlier results, the critical upper value
and a sufficient condition for indeterminacy is now:
It follows from a little algebra that
Proposition 3. With IFB rules responding to producer price inflation and with no home bias, if
Figure 8: Areas of Determinacy for the Sum Difference Systems: Feedback on Producer Price Inflation and No Home Bias.
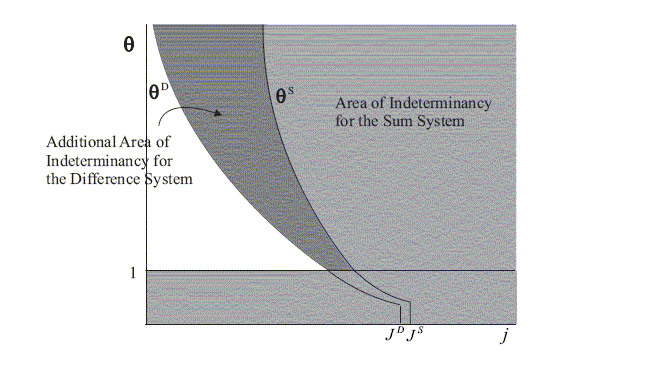
Figure 8 illustrates proposition 3 by showing
![]() and
and
![]() . As the
proposition suggests, the area of indeterminacy is larger in the
open-economy case (this area now being equivalent to the sum of the
dark and light grey areas in the diagram) than in the
closed-economy case. As
. As the
proposition suggests, the area of indeterminacy is larger in the
open-economy case (this area now being equivalent to the sum of the
dark and light grey areas in the diagram) than in the
closed-economy case. As ![]() and
and ![]() grow in magnitude, the dark area in the diagram expands, thus
increasing the negative output spillovers between the two blocs.
Also from (56) and (60) as
interest rate smoothing
grow in magnitude, the dark area in the diagram expands, thus
increasing the negative output spillovers between the two blocs.
Also from (56) and (60) as
interest rate smoothing ![]() increases, both
increases, both
![]() and
and
![]() shift to
the right alleviating the indeterminacy problem for both closed and
open economies alike. Table 1 quantifies numerically upper critical
values for
shift to
the right alleviating the indeterminacy problem for both closed and
open economies alike. Table 1 quantifies numerically upper critical
values for ![]() in the
sum and difference system cases, respectively when we calibrate the
model's parameters as described in Appendix C using US data
(central values), and we set the interest rate smoothing parameter
for the central banks at
in the
sum and difference system cases, respectively when we calibrate the
model's parameters as described in Appendix C using US data
(central values), and we set the interest rate smoothing parameter
for the central banks at ![]() .
.
| j | j=1 | j=2 | j=3 | j=4 | j=5 | j=6 | j=7 | j=8 | j=9 | j=10 | j=11 |
|
|
369 | 60.2 | 12 | 5.5 | 3.5 | 2.62 | 2.05 | 1.67 | 1.40 | 1.18 | 1.02 |
|
|
247 | 38.2 | 9.6 | 5.1 | 3.4 | 2.57 | 2.04 | 1.66 | 1.39 | 1.18 | 1.02 |
5.3.2 No Home Bias and IFB Rules Based on Consumer Price Inflation
With no home bias purchasing power parity applies to the
consumer index and therefore
![]() . Hence using (40) the interest rate rule of the difference system
is given by
. Hence using (40) the interest rate rule of the difference system
is given by
Proposition 4: When IFB rules in the two blocs respond to consumer price inflation and there is no home bias in consumption, a rule for both blocs feeding off inflation expected at any time horizon
Proof: From (61),
Root locus analysis of this equation for values of
5.3.3 The Effect of Home Bias
As discussed earlier, allowing for home bias in consumption
patterns has no implications for the sum system, and we therefore
only need to consider its impact on the difference system. In this
system, we can ignore problems arising from foreign asset dynamics
by focussing on the case ![]() and
and ![]() . Writing
. Writing
![]() in linearized form, this
yields a representation for the difference system:
in linearized form, this
yields a representation for the difference system:
Consider first feedback from forward-looking producer price
inflation, given for the difference system by (57). Together with (63) and
the UIP condition, which we write in terms of the terms of trade
as
For the case of feedback from forward-looking consumer price
inflation, we can use (66) to write the
difference system for interest rates as
Inspection of the system of dynamic equations shows that determinacy requires exactly two stable roots. For the case
Figure 9: Position of zeroes as
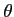 changes, for
changes, for
 in the home bias
difference system with CPI inflation based IFB
rules.
in the home bias
difference system with CPI inflation based IFB
rules.

Note that there is a branch point into the complex plane, which
returns to the real axis for a larger value of ![]() ; as
; as ![]() approaches a further critical
value, one of the zeroes tends to
approaches a further critical
value, one of the zeroes tends to ![]() , and beyond this critical value it heads along
the real axis from
, and beyond this critical value it heads along
the real axis from ![]() . Finally, there is a critical value of
. Finally, there is a critical value of
![]() at which
at which
![]() , and any higher
values of
, and any higher
values of ![]() yield
indeterminacy. For
yield
indeterminacy. For ![]() we can
evaluate the upper bound on
we can
evaluate the upper bound on ![]() as before by putting
as before by putting ![]() and
and ![]() in (68). For
the case under consideration with feedback from consumer price
inflation and home bias
in (68). For
the case under consideration with feedback from consumer price
inflation and home bias
![]() , denote this threshold at
, denote this threshold at
![]() by
by
![]() . Then we obtain for j = 1.
. Then we obtain for j = 1.
For ![]() , from Figure
10 the critical value at which indeterminacy occurs is not
associated with
, from Figure
10 the critical value at which indeterminacy occurs is not
associated with ![]() .
.
Figure 10: Position of zeroes as
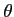 changes, for
changes, for
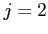 in the home bias
difference system with CPI inflation based IFB
rules.
in the home bias
difference system with CPI inflation based IFB
rules.
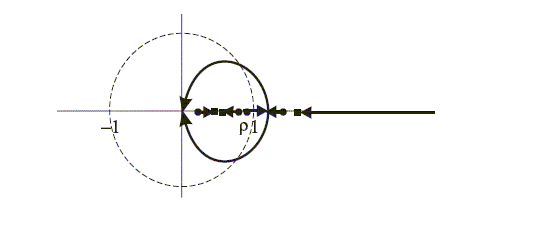
Similar root locus diagrams to the ones we have seen earlier can
then be drawn for values of ![]() . Using the same technique as before, it is easy
to show that indeterminacy occurs for all
. Using the same technique as before, it is easy
to show that indeterminacy occurs for all ![]() provided that the
derivative of the LHS of (68) at
provided that the
derivative of the LHS of (68) at
![]() is greater
than 0. The threshold values of
is greater
than 0. The threshold values of ![]() must then satisfy
must then satisfy
We can now compare the difference systems with home bias under
rules based on producer price, and on consumer price inflation.
Denote the ![]() -threshold at
-threshold at ![]() and the
and the ![]() -threshold for producer price based rules by
-threshold for producer price based rules by
![]() and
and
![]() respectively. We have shown that for
respectively. We have shown that for ![]() and
and ![]() we obtain
we obtain
![]() and
and
![]() obtained previously without home bias. Gathering together these
results, after some algebra we arrive at:
obtained previously without home bias. Gathering together these
results, after some algebra we arrive at:
Clearly
Proposition 5. With home consumption bias, the potential indeterminacy of IFB rules is worse when based on consumer rather than producer price inflation, and becomes increasingly worse as the degree of openness of the two blocs increases.
6 Conclusions
This paper has examined conditions for a unique stable rational expectations equilibrium for a symmetric two-bloc world economy where monetary authorities in both blocs pursue IFB rules. Most of the literature in this area assumes that the economy is closed. In the open economy changes to nominal interest rate affect aggregate demand through both intertemporal substitution effects (as in a closed economy) and terms of trade effects, working in opposite directions. Given the additional terms of trade effect, it is reasonable to expect that IFB rules would perform differently in the open economy, and indeed we find this to be the case.
Our results are best synthesized by focussing on the critical
upper bound for the expected inflation feedback parameter beyond
which there is indeterminacy,
![]() and
and
![]() for the
sum and difference systems respectively, where
for the
sum and difference systems respectively, where ![]() is the feedback horizon. The diverse
performance of rules in the closed and open economy can be
summarized by the difference
is the feedback horizon. The diverse
performance of rules in the closed and open economy can be
summarized by the difference
![]() . Consider first the case
when there is no home bias and the degree of openness is at its
maximum. For IFB rules based on producer price inflation this
difference is positive, indicating that indeterminacy is a more
serious problem for the open economy. If rules are based on
consumer price inflation the problem worsens; indeed, in the case
of no home bias, an IFB rule responding to consumer price inflation
at any horizon
. Consider first the case
when there is no home bias and the degree of openness is at its
maximum. For IFB rules based on producer price inflation this
difference is positive, indicating that indeterminacy is a more
serious problem for the open economy. If rules are based on
consumer price inflation the problem worsens; indeed, in the case
of no home bias, an IFB rule responding to consumer price inflation
at any horizon ![]()
![]() (i.e.,
including feedback on current consumer price inflation) leads to
indeterminacy.35 With
consumer price inflation feedback and some home bias, the
indeterminacy problem is less severe, but it rapidly deteriorates
towards the extreme case as the bias diminishes and the economies
become more open, since in that case the
(i.e.,
including feedback on current consumer price inflation) leads to
indeterminacy.35 With
consumer price inflation feedback and some home bias, the
indeterminacy problem is less severe, but it rapidly deteriorates
towards the extreme case as the bias diminishes and the economies
become more open, since in that case the
![]() increases. The rationale
behind the poorer performance of IFB rules based on consumer price
inflation lies with the familiar beggar-thy-neighbour behavior.
This develops between two blocs when central banks in each bloc
attempt simultaneously to lower domestic consumer price inflation,
now including an imported component, by improving their own bloc's
terms of trade.
increases. The rationale
behind the poorer performance of IFB rules based on consumer price
inflation lies with the familiar beggar-thy-neighbour behavior.
This develops between two blocs when central banks in each bloc
attempt simultaneously to lower domestic consumer price inflation,
now including an imported component, by improving their own bloc's
terms of trade.
Although the euro area and the US are not very open, and so they probably do not fall foul of our worst case scenario, our results are nevertheless an important warning for the ECB and the Federal Reserve, since they imply that concurrent excessive preemptiveness in response to shocks may expose both to self-fulfilling sunspot sequences for any feedback on inflation forecasts. Since both the ECB and the Federal Reserve focus primarily on consumer price inflation 36 and not on producer price inflation, our results on the poor performance of consumer price based rules also have normative implications.
Of course these results may well depend on our modelling assumptions; future work could usefully examine the extent to which this is, in fact, the case. Among many possible sensitivity studies, two in particular seem to deserve prioritization. First, our treatment of money demand is conventional, whereas we have seen from the related literature section that the indeterminacy of IFB rules may be sensitive to how money enters the utility function or to whether a cash-in-advance approach is adopted. Second, in our model the length of Calvo contracts is exogenous, whereas it is sensible to expect firms to increase the frequency with which they update their prices as inflation increases.37
This paper has examined IFB rules for given ad hoc settings for
the choice of horizon and feedback parameters. An often-stated
benefit of simple rules is that they have good robustness
properties in the face of modelling errors. One aspect of
robustness is that the economy under control should remain stable
and determinate even when the assumed model turns out to be wrong
in some respect. An advantage of using the root locus technique is
that it enables one to clearly track all the eigenvalues associated with the rule as the
feedback parameter changes. This suggests that, for a given model,
a robust rule should be designed so that in ![]() space it is far from the
indeterminacy boundary. Assessing the truth of this conjecture for
a broader range of rules38 is
another possible area for research.
space it is far from the
indeterminacy boundary. Assessing the truth of this conjecture for
a broader range of rules38 is
another possible area for research.
A. The Optimal Rule
The deterministic two-bloc model of the paper can be written in the following general formwhere
![\begin{equation*} s_t=\Gamma \left[ \begin{array}{l} z_t\ x_t \end{array} \rig... ... \Theta \left[ \begin{array}{l} w_t\ w_t^* \end{array} \right] \end{equation*}](img387.gif)
Let
![\begin{equation*} \Omega_0=-\sum_{t=0}^{\infty} \beta^t \left[ s_t^TQ_1s_t+w_t^TQ_2w_t \right] \end{equation*}](img389.gif)
which we rewrite as
![\begin{equation*} \Omega_0=-\sum_{t=0}^{\infty} \beta^t \left[ y^T_t Qy_t+2y_t^T... ...\left[ \begin{array}{l} w_t\ w^*_t \end{array} \right] \right] \end{equation*}](img390.gif) where
where
For the optimal rule, we take as the joint cooperative objective
function a linear combination
![]() given
by
given
by
![\begin{eqnarray*} \left[ \begin{array}{l} w_t\ w^*_t \end{array} \right] &=& -(R^c+B^TSB)^{-1}(B^TSA+U^T_c)y_t= -Fy_t \end{eqnarray*}](img403.gif)
say, where
If we define ![]() by
by
![\begin{equation*} N = - \left[ \begin{array}{cc} S_{11}-S_{12}S^{-1}_{22}S_{21}&... ..._{22}^{-1}\ -S_{22}^{-1}S_{21}&S_{22}^{-1} \end{array} \right] \end{equation*}](img406.gif)
where ![]() has been
partitioned so that
has been
partitioned so that ![]() is
is
![]() and
and
![]() is
is ![]() , then we have that
, then we have that
is the saddle-path of the system under control,
![\begin{equation*} T=\left[ \begin{array}{ll} I&0\ S_{21}&S_{22} \end{array} \right] \end{equation*}](img413.gif)
and the free variables
![\begin{equation*} x_t=-\left[ \begin{array}{ll} N_{21}&N_{22} \end{array} \right] \left[ \begin{array}{l} z_t\ p_{21} \end{array} \right] \end{equation*}](img414.gif)
The initial conditions in (A.4) are
Equation (A.3) expresses the
cooperative, optimal policy in feedback form. Putting
![]() in
(A.4) and partitioning, we have
in
(A.4) and partitioning, we have
![]()
from which (A.3) may be written in the
form (45) of the text
![\begin{displaymath} \left[ \begin{array}{l} w_t\ w^*_t \end{array} \right]=D_1z_t+D_2C_{21} \sum_{\tau=1}^{t}(C_{22})^{\tau-1}z_{t-\tau} \end{displaymath}](img418.gif)
|
(A.5) |
B. A Topological Guide to The Root Locus Technique
Here we present a brief guide to how to use the root locus technique. We start by some standard `rules' as provided in control theory textbooks, and then summarize their practical implications in more plain language.
The idea behind the root locus technique is to track the zeroes
of the polynomial equation
![]() as
as
![]() moves from 0 to
moves from 0 to
![]() . Clearly for
. Clearly for
![]() , the roots are
those of
, the roots are
those of ![]() ,
whereas when
,
whereas when
![]() , the roots are those of
, the roots are those of
![]() . The root locus
then connects the first set of roots to the second set by a series
of lines and curves. We shall assume without loss of generality
that the coefficient of the highest power of each of
. The root locus
then connects the first set of roots to the second set by a series
of lines and curves. We shall assume without loss of generality
that the coefficient of the highest power of each of ![]() and
and ![]() is unity.
is unity.
There are a number of different ways of stating the standard control `rules' that underly the technique. One popular way (see Evans (1954)) involves just 7 steps:
1(a). Define ![]() no. of zeros of
no. of zeros of ![]() ,
, ![]() no. of zeros of
no. of zeros of ![]() .
.
1(b). Loci start at the zeros of ![]() , and end at the zeros of
, and end at the zeros of
![]() and at
and at
![]() if
if ![]() .
.
1(c). Loci start at the zeros of ![]() and at
and at ![]() , and end at the zeros of
, and end at the zeros of
![]() if
if ![]() .
.
2. Number of loci must be equal to
![]()
3. A point on the real axis is on the root
locus if the number of zeros of ![]() and
and ![]() on the
real axis to its right is odd.
on the
real axis to its right is odd.
4. Loci ending or beginning at ![]() do so at angles to the
do so at angles to the
![]() real axis given by
real axis given by
![]() ,
where
,
where ![]() goes from 0 to
goes from 0 to
![]() .
.
5. Asymptotes at ![]() intersect the real axis at the center of
gravity of the zeros of
intersect the real axis at the center of
gravity of the zeros of ![]() and
and ![]() , i.e. [Sum of zeros
of
, i.e. [Sum of zeros
of ![]() - Sum of zeros of
- Sum of zeros of
![]() ]/
]/![]() .
.
6. If all coefficients of ![]() and
and ![]() are real, then the root locus is symmetric about the
real axis.
are real, then the root locus is symmetric about the
real axis.
7. Loci leave the real axis where
![]() .
.
Let us now look at how this set of rules can be used in practice
to construct root locus diagrams. In what follows, we always assume
for convenience that the coefficient of the highest power of
![]() in both
in both ![]() and
and ![]() is equal to 1. At heart, the idea is that when all
zeros of
is equal to 1. At heart, the idea is that when all
zeros of ![]() and
and
![]() are real, it is easy
to map out a unique path for the various branches of the root
loci.
are real, it is easy
to map out a unique path for the various branches of the root
loci.
For example, suppose that ![]() is of order 2, and
is of order 2, and ![]() is of order 3, then for any value of
is of order 3, then for any value of ![]() the polynomial
the polynomial
![]() is also of
order 3. We then need 3 branches of the root locus to connect with
the 3 roots of
is also of
order 3. We then need 3 branches of the root locus to connect with
the 3 roots of ![]() .
To unveil how the branches connect to the roots, we need to examine
what happens when
.
To unveil how the branches connect to the roots, we need to examine
what happens when ![]() is
very small. In this case it is easy to see that one of the roots
corresponds to
is
very small. In this case it is easy to see that one of the roots
corresponds to
![]() ,
i.e. at
,
i.e. at ![]() ,
while the other two roots are located very close to the roots of
,
while the other two roots are located very close to the roots of
![]() . Likewise if
. Likewise if
![]() is of order 2, and
is of order 2, and
![]() is of order 4, then
there will be another two roots located at
is of order 4, then
there will be another two roots located at
![]() approximately, i.e. at
approximately, i.e. at
![]() .
.
Continuing in this vein, if ![]() is of order 2, and
is of order 2, and ![]() is of order 5, then there will be two roots for very
small
is of order 5, then there will be two roots for very
small ![]() located where
located where
![]() i.e. one at
i.e. one at ![]() and the others at 120
degrees to this. When
and the others at 120
degrees to this. When ![]() is a polynomial of higher order than
is a polynomial of higher order than ![]() , then there will be similar zeroes at infinity, but
this time not at
, then there will be similar zeroes at infinity, but
this time not at ![]() ,
but instead as
,
but instead as
![]() .
.
Now that we know the full behavior at ![]() and
and
![]() , the next thing we need to learn is how to draw the diagram. To
simplify matters, from now on we refer to the roots of
, the next thing we need to learn is how to draw the diagram. To
simplify matters, from now on we refer to the roots of ![]() as `poles', while we refer to the
roots of
as `poles', while we refer to the
roots of ![]() as `zeroes'.
The root locus diagram is then a set of lines or curves joining
poles to zeroes. One rule is that these never cross, although they
can meet, and then branch off. If they branch off, it is into the
complex part of the complex plane, and this occurs in complex
conjugate pairs.
as `zeroes'.
The root locus diagram is then a set of lines or curves joining
poles to zeroes. One rule is that these never cross, although they
can meet, and then branch off. If they branch off, it is into the
complex part of the complex plane, and this occurs in complex
conjugate pairs.
The simplest root locus diagram is when there is just one pole
and one zero. The root locus is then a straight line connecting the
pole to the zero. This is usually a straightforward case, apart
from when it implies two completely different root locus diagrams
for ![]() and
and
![]() . Take for
instance a polynomial like
. Take for
instance a polynomial like
![]() . This
case is easy: the root locus is a straight line from
. This
case is easy: the root locus is a straight line from ![]() to
to ![]() . On the other hand, consider
. On the other hand, consider
![]() .
Clearly, for
.
Clearly, for ![]() there is a root at infinity, where the root can be any real number
other than those between
there is a root at infinity, where the root can be any real number
other than those between ![]() and
and ![]() . If
. If ![]() , then the root locus heads
toward
, then the root locus heads
toward ![]() from
the pole at
from
the pole at ![]() , and hits
the zero at
, and hits
the zero at ![]() from
from
![]() .
.
The next simplest case is when the poles and zeroes alternate
with one another on the real line; thus the ordering can be
expressed as ![]() . In
this case, the root locus is just a set of straight lines
connecting each
. In
this case, the root locus is just a set of straight lines
connecting each ![]() to
each
to
each ![]() in their ordering on
the real line.
in their ordering on
the real line.
Suppose however that the ordering is ![]() . In the case
. In the case ![]() , the root locus starts
with straight lines from the poles heading towards one another.
Where they meet, they then branch into the complex plane
(symmetrically about the real axis), and eventually curve back down
on to the real line, meeting somewhere between the two zeroes. They
then head in a straight line towards the two zeroes. In the case
, the root locus starts
with straight lines from the poles heading towards one another.
Where they meet, they then branch into the complex plane
(symmetrically about the real axis), and eventually curve back down
on to the real line, meeting somewhere between the two zeroes. They
then head in a straight line towards the two zeroes. In the case
![]() , the
leftmost
, the
leftmost ![]() heads to
heads to
![]() , and
re-emerges from
, and
re-emerges from ![]() to meet the rightmost zero, while there is straight line
representing the part of the root locus connecting the inner
to meet the rightmost zero, while there is straight line
representing the part of the root locus connecting the inner
![]() to the inner
to the inner
![]() .
.
Similarly, consider the ordering ![]() . For
. For ![]() , the inner
, the inner ![]() and
and ![]() are
connected by a straight line, whereas the two outer poles have loci
along the real axis that head for one another, then branch out into
the complex plane, and meet the real line between the two outer
zeroes; from here they head along the real axis for the latter. In
the case
are
connected by a straight line, whereas the two outer poles have loci
along the real axis that head for one another, then branch out into
the complex plane, and meet the real line between the two outer
zeroes; from here they head along the real axis for the latter. In
the case ![]() ,
the outermost
,
the outermost ![]() has a locus
that heads for
has a locus
that heads for ![]() , which re-emerges at
, which re-emerges at ![]() to meet the outermost
to meet the outermost
![]() , while the remaining
loci branch into the complex plane in the manner already
described.
, while the remaining
loci branch into the complex plane in the manner already
described.
More general cases are just variants of the simpler ones
described above. A specific example is provided by (51) without an interest rate rule:
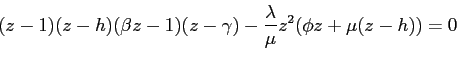
|
We first note that as
![]() , there is a root
at
, there is a root
at ![]() , which must be
connected to the root at
, which must be
connected to the root at
![]() .
Secondly we note that there cannot be an arm of the root locus
connecting
.
Secondly we note that there cannot be an arm of the root locus
connecting ![]() to 0,
because it would then be impossible for either arm starting at 1 or
at
to 0,
because it would then be impossible for either arm starting at 1 or
at ![]() to also get to 0. It
therefore follows that there must be an arm connecting
to also get to 0. It
therefore follows that there must be an arm connecting ![]() to
to
![]() .
In order for the arms starting at 1 and
.
In order for the arms starting at 1 and ![]() to then get to 0, they must head
towards one another and then branch off into the complex plane.
Logically therefore, there is only one way of drawing the diagram,
as shown.
to then get to 0, they must head
towards one another and then branch off into the complex plane.
Logically therefore, there is only one way of drawing the diagram,
as shown.
Figure 11: Position of zeros for varying
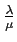
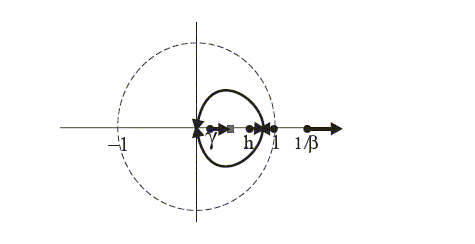
This diagram explains the position of the zeros as depicted in
Figure 11 for low and high
![]() .
Finally if
.
Finally if
![]() , it is easy to show
that the root locus diagram changes very little.
, it is easy to show
that the root locus diagram changes very little. ![]() will still have an arm
connecting it to
will still have an arm
connecting it to
![]() ,
but the arrow will point in the opposite direction.
,
but the arrow will point in the opposite direction.
C. Calibration
So far we have we have derived conditions for unique and stable equilibria with IFB rules in our two-bloc model in parametric form. To carry out the numerical procedure to calculate thresholdsTable 2 below describes these parameters and explains where they
come from. Most of the calibration is based on Smets and Wouters
(2002, 2003. SW02 and SW03 henceforth) Bayesian estimates on US and
area-wide data, respectively, of a one-country dynamic stochastic
general equilibrium model. SW's model is similar to Christiano
et al. (2001), CEE). SW's model differs from our
two-bloc model inasmuch as: (i) in addition to nominal rigidities
in both the price level and its growth rate, it assumes rigidities
also in the wage level and its growth rate. In practice, SW02 and
SW03 find that, for both the US and the euro area, rigidities in
wages tend to be neither important nor significant. So SW03 provide
alternative estimates of the structural parameters in their model
obtained when they relax the wage stickiness assumption. It is
these estimates to which we calibrate our model, given that we
assume throughout that wages are flexible;(ii) it assumes capital
accumulation with capital adjustment costs, whereas we assume that
capital is constant in our model; (iii) finally, SW's model assumes
a Cobb-Douglas technology for firms, whereas we, as Clarida et al
(2002), assume that technology is of the CES form. Given these
model differences, we cannot infer all parameters we need from
SW02, SW03 estimates, so we calibrate the remaining parameters as
in CEE and Erceg et al (2000, EHL) for the US bloc.
Table 2: Calibrated Values
| Parameter | Notation | US Value | US Source | EA Value | EA Source |
| Discount factor | 0.99 | SW03,EHL | 0.99 | SW02 | |
| Risk Aversion | 2.01 | SW03 | 1.61 | SW02 | |
| Disutility of Effort | 0.83 | SW03 | 0.76 | SW03 | |
| Indexation | 0.48 | SW03 | 0.41 | SW02 | |
| Calvo Probability | 0.5-0.9 | EHL, SW03 | 0.91 | SW02 | |
| Habit | h | 0.49-0.63-0.7 | SW03,CEE | 0.54 | SW02 |
References
Aoki, M. (1981). Dynamic Analysis of Open Economies. Academic Press.
Batini, N. and Haldane, A. G. (1999).Forward-looking rules for monetary policy. In J. B. Taylor, editor, Monetary Policy Rules, pages 157-202. Chicago: University of Chicago Press.
Batini, N. and Nelson, E. (2001). Optimal horizons for Inflation Targeting. Journal of Economic Dynamics and Control, 25, 891-910.
Batini, N. and Pearlman, J. (2002). Too Much Too Soon: Instability and Indeterminacy With Forward-Looking Rules. Bank of England External MPC Discussion Paper No. 8.
Batini, N., Harrison, R., and Millard, S. (2003). Monetary Policy Rules for Open Economies. Journal of Economic Dynamics and Control, forthcoming.
Benhabib, J., Schmitt-Grohe, S., and Uribe, M. (2001). Monetary Policy and Multiple Equilibria. American Economic Review, 91(1), 167-86.
Benigno, G. and Benigno, P. (2001). Implementing Monetary Cooperation through Inflation Targeting. New York University, Mimeo.
Bernanke, B. and Woodford, M. (1997). Inflation Forecasts and Monetary Policy. Journal of Money Credit and Banking, 24, 653-684.
Black, R., Cassino, V., Aaron, D., Hansen, E., Hunt, B., Rose, D., and Scott, A. (1997). The Forecasting and policy System: The Core Model. Research Paper No. 43, Reserve Bank of New Zealand, Wellington.
Blanchard, O. J. and Kahn, C. M. (1980). The Solution of Linear Difference Models under Rational Expectations. Econometrica, 48(5), 1305-11.
Bullard, J. and Mitra, K. (2001). Learning about monetary policy rules. Journal of Monetary Economics.
Carlstrom, C. T. and Fuerst, T. S. (1999). Real indeterminacy in monetary models with nominal interest rate distortions. Federal Reserve Bank of Cleveland working paper.
Carlstrom, C. T. and Fuerst, T. S. (2000). Forward-looking versus backward-looking Taylor rules. Federal Reserve Bank of Cleveland working paper.
Castelnuovo, E. (2003). Taylor Rules and Interest Rate Smoothing in the US and EMU. mimeo, Bocconi University.
Chari, V. V., Christiano, L. J., and Eichenbaum, M. (1998). Expectation traps and discretion. Journal of Economic Theory, 81(2), 462-92.
Christiano, L. J., Eichenbaum, M., and Evans, C. (2001). Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy. NBER Working Paper, no. 8403.
Clarida, R., Galí, J., and Gertler, M. (1999). The Science of Monetary Policy: A New Keynesian Perspective. Journal of Economic Literature, 37(4), 1661-1707.
Clarida, R., Galí, J., and Gertler, M. (2000). Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory. Quarterly Journal of Economics, 115(1), 147-80.
Clarida, R., Galí, J., and Gertler, M. (2002). A Simple Framework for International Monetary Policy Analysis. NBER Working Paper w8870 .
Coletti, D., Hunt, B., Rose, D., and Tetlow, R. (1996). Bank of Canada's New Quarterly Projection Model. Part 3, The Dynamic Model: QPM. Technical Report No. 75, Bank of Canada, Ottawa.
Corsetti, G., Dedola, L., and Leduc, S. (2002). Consumption and Real Exchange Rates with Goods and Asset Markets Frictions. University of Rome III, Mimeo.
Currie, D. and Levine, P. (1993). Rules, Reputation and Macroeconomic Policy Coordination. CUP.
De Fiore, F. and Liu, Z. (2002). Openness and Equilibrium Determinancy under Interest Rate Rules. European Central Bank, WP. no. 173.
Devereux, M. B. and Yetman, J. (2002). Menu costs and the long-run output-inflation trade-off. Economic Letters, 76(1), 95-100.
Erceg, C. J., Henderson, D., and Levin, A. T. (2000). Optimal monetary policy with staggered wage and price contracts. Journal of Monetary Economics, 46(2), 281-313.
Evans, G. W. and Honkapoja, S. (2001). Expectations and the stability problem for optimal monetary policies. working paper, www.valt.helsinki.fi/RAKA/seppo.html.
Evans, G. W. and Honkapoja, S. (2002). Monetary policy, expectations and commitment. mimeo.
Evans, W. R. (1954). Control Systems Dynamics. McGraw Hill.
Faust, J., Rogers, J., and Wright, J. (2001). An Empirical Comparison of Bundesbank and ECB Monetary Policy Rules. International Finance Discussion Papers No. 705, Board of Governors of the Federal Reserve System.
Giannoni, M. and Woodford, M. (2002). Optimal Interest-Rate Rules: I. General Theory. NBER Working Paper no. 9419.
Karanassou, M., Sala, H., and Snower, D. (2003). A Reappraisal of the Inflation-Unemployment Trade-off. IZA Discussion paper No. 636, Bonn.
Kerr, W. and King, R. G. (1996). Limits on interest rates rules in the IS model. Economic Quarterly, 82(2), 47-76.
Levin, A., Wieland, V., and C, W. J. (2001). The performance of inflation forecast-based rules under model uncertainty. Federal Reserve Board International Finance Discussion Paper No.
McCallum, B. T. (1995). Two fallacies concerning central bank independence. American Economic Review, AEA papers and proceedings.
Sargent, T. and Wallace, N. (1975). Rational expectations, the optimal monetary instrument and the optimal money supply rule. Journal of Political Economy, 83, 241-54.
Smets, F. and Wouters, R. (2002). An estimated stochastic dynamic general equilibrium model of the Euro Area. European Central Bank, WP. no. 171.
Smets, F. and Wouters, R. (2003). Shocks and frictions in US business cycles: a Bayesian DSGE approach. paper presented at the conference `Dynamic Models Useful for Policy' held at the Bank of Canada, July 2003.
Sutherland (2002). International monetary policy coordination and financial market integration. mimeo, Board of Governors of the Federal Reserve System.
Svensson, L. E. O. (2001). Requiem for Forecast-Based Instrument Rules. mimeo, Stockholm University.
Svensson, L. E. O. (2003). What is wrong with Taylor Rules? Using judgement in monetary policy through targeting rules. Journal of Economic Literature, forthcoming.
Svensson, L. E. O. and Woodford, M. (1999). Implementing Optimal Policy through Inflation-Forecast Targeting. mimeo, Princeton University.
Svensson, L. E. O. and Woodford, M. (2003). Implementing Optimal Policy through Inflation-Forecast Targeting. mimeo, Princeton University.
Taylor, J. B. (1993). Discretion versus policy rules in practice. Carnegie-Rochester Conference Series on Public Policy, 39, 195-214.
Taylor, J. B. (1999). A Historical Analysis of Monetary Policy Rules. In J. B. Taylor, editor, Monetary Policy Rules, pages 319-41. Chicago: University of Chicago Press.
Tetlow, R. J. (2000). The Fed is Not as Ignorant as You Think. mimeo, Board of Governors of the Federal Reserve System.
Tetlow, R. J. and von zur Muehlen, P. (2001). Simplicity vesus optimality: The choice of monetary policy rules when agents must learn. Journal of Economic Dynamics and Control, 25, 245-79.
Woodford, M. (1999). Commentary: How Should Monetary Policy Be Conducted in an Era of Price Stability? In F. R. B. of Kansas City, editor, New Challenges for Monetary Policy. Kansas City: Federal Reserve Bank of Kansas City.
Woodford, M. (2000). Pitfalls of forward-looking monetary policy. American Economic Review, 90(2), 100-104.
Woodford, M. (2003). Foundations of a Theory of Monetary Policy. Princeton University Press.
Footnotes
* The paper is partly based on research conducted while Levine and Pearlman were visiting the European Central Bank (ECB) July-August 2003 as part of their Research Visitors Programme. Thanks are owing to the ECB for this hospitality and to numerous resident and visiting researchers for stimulating discussions. Views expressed in this paper do not re�ect those of the BoE or the ECB. This paper was presented at the International Research Forum on Monetary Policy in Washington, DC, November 14-15, 2003. Insightful comments from discussants Giancarlo Cosetti and Marc Giannoni, and from other participants are acknowledged. Useful comments from an anonymous referee and from participants at seminars in Pompeu Fabra, the University of Frankfurt, the ECB, the Bank of England, the Bank of Canada and the Swiss National Bank are also gratefully acknowledged. Return to text
† Research Adviser, MPC Unit, Bank of England, Threadneedle Street, London EC2R 8AH, United Kingdom. E-mail: [email protected]. Return to text
‡ Professor of Economics, University of Surrey, Guildford, Surrey GU2 7XH, United Kingdom. Email: [email protected]. Return to text
§ Professor of Economics, London Metropolitan University, 31 Jewry St, London EC3N 2EY, United Kingdom. Email: [email protected]. Return to text
1. However, as we discuss in the next section, it has been argued that results such as these may be susceptible to the Lucas Critique. Return to text
2. Both types of real indeterminacy
can be illustrated in a very simple closed economy model: consider
a special case of `Phillips Curve' set out in this paper,
![]() , where
, where
![]() denotes
inflation and
denotes
inflation and ![]() is the
deviation of output from its equilibrium level. Close the model
with an ad hoc `IS' curve
is the
deviation of output from its equilibrium level. Close the model
with an ad hoc `IS' curve
![]() where
where
![]() is the nominal
interest rate which is set according to an IFB-Taylor rule
is the nominal
interest rate which is set according to an IFB-Taylor rule
![]() .
Substituting out for
.
Substituting out for ![]() and
and
![]() we arrive at
we arrive at
![]() which has a unique rational expectations solution
which has a unique rational expectations solution
![]() iff
iff
![]() and a
stable trajectory, tending to zero inflation in the long run,
consistent with any initial inflation rate otherwise- that is there
is indeterminacy if
and a
stable trajectory, tending to zero inflation in the long run,
consistent with any initial inflation rate otherwise- that is there
is indeterminacy if ![]() or
or
![]() . In the latter case,
overly aggressive feedback produces cycles of positive and negative
inflation. Thus the inclusion of a feedback on output reduces the
region of indeterminacy. Empirical estimates of
. In the latter case,
overly aggressive feedback produces cycles of positive and negative
inflation. Thus the inclusion of a feedback on output reduces the
region of indeterminacy. Empirical estimates of ![]() appear to be small, as discussed
in section 2. So, in our subsequent analysis, we focus exclusively
on `pure' IFB rules, i.e. rules without an output gap
term. Return to text
appear to be small, as discussed
in section 2. So, in our subsequent analysis, we focus exclusively
on `pure' IFB rules, i.e. rules without an output gap
term. Return to text
3. Perhaps the closest paper to ours is De Fiore and Liu (2002) which explores indeterminacy in a small open-economy model with one-quarter-ahead IFB rules. Return to text
4. Giannoni and Woodford (2002) obtain similar results for IFB rules, but without interest rate smoothing. Return to text
5. The fact that forward-looking
behavior is a source of indeterminacy can again be illustrated
using the simple model of the previous footnote. Consider a rule
involving a feedback on current
inflation and the current output gap:
![]() . Then re-working the
analysis we arrive at
. Then re-working the
analysis we arrive at
![]() which has a unique RE solution
which has a unique RE solution ![]() iff
iff ![]() . For this current-looking
rule there is no upper-bound on
. For this current-looking
rule there is no upper-bound on ![]() : all values above 1 ensure
determinacy. Return to text
: all values above 1 ensure
determinacy. Return to text
6. As we shall see in section 5, this a property of the optimal commitment rule. Return to text
7. Although empirical evidence seems to lend support to the idea that the US and European central banks follow IFB-type rules, the Lucas Critique suggests that there is a logical distinction between observing that a simple reduced-form relationship holds between variables and assuming that such a relation holds as a structural equation. For example, Tetlow (2000) demonstrates that a Taylor rule may seem to explain US monetary policy even if monetary policy is set optimally, conditioning on literally hundreds of state variables. Return to text
8. De Fiore and Liu (2002) assume this latter type of cash-in-advance assumption. Return to text
9. Batini et al. (2003), however, present a small open-economy model with a timing assumption on transactions as in Carlstrom and Fuerst (1999). De Fiore and Liu (2002) show that indeterminacy results are sensitive to the various assumptions on the timing of transactions in the context of a small open-economy model. Return to text
10. The population in each bloc is normalized at unity. It is straightforward to allow for different sized blocs, as in CGG (2002) and BB. Then in the Aoki decomposition, aggregates must be population-weighted and differences expressed in per capita terms. Return to text
11. Any welfare analysis and the formulation of optimal rules of the IFB form would require a stochastic treatment that now characterizes much of the New Keynesian literature. Return to text
12. When ![]() ,
, ![]() is merely an index of the curvature of the
utility function. Return to text
is merely an index of the curvature of the
utility function. Return to text
13. The effect of home bias in open economies is studied in Corsetti et al. (2002) and De Fiore and Liu (2002). Return to text
14. Thus we can interpret
![]() as the
average duration for which prices are left unchanged. Return to text
as the
average duration for which prices are left unchanged. Return to text
15. In a stochastic setting with complete asset markets, (23) is simply the risk-sharing condition for consumption, because it equates marginal rate of substitution to relative price, as would be obtained if utility were being jointly maximized by a social planner (see Sutherland (2002)). Return to text
16. In effect, this is the case studied by De Fiore and Liu (2002) in a small open-economy context. Return to text
17. That is, for a typical variable
![]() ,
,
![]() where
where ![]() is the
baseline steady state. Return to
text
is the
baseline steady state. Return to
text
18. Our linearized system is in agreement with that of Christiano et al. (2001), BB and CGG(2002). Return to text
19. If ![]() , this replicates the result in CGG
(2002). Return to text
, this replicates the result in CGG
(2002). Return to text
20. Empirical work by Karanassou et al. (2003) gives a inflation rate -unemployment rate slope of around 3. Using calibrated values given in Appendix C, our model also suggests a significant long-run trade-off, but a rather smaller one than that estimated by these authors. Return to text
21. The correspondence is not exact as the quadratic approximation is about a carefully chosen cooperative flexible price steady state in which a subsidy rate is used to correct the distortion caused by imperfect competition. Moreover the inflation rates are for producer price and not consumer inflation as in (43). In an earlier paper Clarida et al. (1999) provide a strong defence of the pragmatic approach which is also adopted by Svensson (2001, 2003). Return to text
22. In a stochastic version of the
model, if we assume simple AR(1) stochastic processes for the TFP
shocks, i.e.,
![]() ,
,
![]() , then a term
, then a term
![]() where
where ![]() and
and
![]() are white
noise disturbances would be added to the right-hand-side of
(44). Return to
text
are white
noise disturbances would be added to the right-hand-side of
(44). Return to
text
23. Alternatively the policymaker
might penalize changes in the interest rate. If neither penalty
applies (i.e., ![]() ), then the optimization problem must be set
up as a two-stage procedure in which inflation rates are chosen
optimally and then interest rates are set to achieve the resulting
optimal paths for inflation. Return to
text
), then the optimization problem must be set
up as a two-stage procedure in which inflation rates are chosen
optimally and then interest rates are set to achieve the resulting
optimal paths for inflation. Return to
text
24. See Svensson and Woodford (2003). An alternative form of the rule is as a specific targeting rule which takes the form of the first-order conditions that lead up to (45). Return to text
25. Non-certainty equivalence also
has the consequence that optimal simple rules designed at time
![]() for displacements
for displacements
![]() will be
sub-optimal at any later date t where
will be
sub-optimal at any later date t where
![]() ; i.e.,
optimal simple rules are time inconsistent,
even in the absence of forward-looking behaviour in the
model. This, in essence, is the main point made in Svensson (2001). Return to text
; i.e.,
optimal simple rules are time inconsistent,
even in the absence of forward-looking behaviour in the
model. This, in essence, is the main point made in Svensson (2001). Return to text
26. These issues concerning the design of simple rules are addressed extensively in Currie and Levine (1993). Return to text
27. For instance (46) can be written as
![]() which is a partial adjustment to a static IFB rule
which is a partial adjustment to a static IFB rule
![]() . Return to text
. Return to text
28. For the case of ![]() , we can substitute out for
, we can substitute out for
![]() and
and
![]() from (44). Return to text
from (44). Return to text
29. In this plane, the horizontal
axis depicts real numbers, and the vertical axis depicts imaginary
numbers. If a root is complex, i.e. ![]() , then its complex conjugate
, then its complex conjugate ![]() is also a root. Thus the root
locus is symmetric about the real axis. Return to text
is also a root. Thus the root
locus is symmetric about the real axis. Return to text
30. How we find the position of these zeros is main example of Appendix B. Return to text
31. Thus Figure 3 portrays
diagrammatically the result shown analytically by Woodford (2003), chapter 4, that
there is a value of
![]() say, beyond which there is indeterminacy. Return to text
say, beyond which there is indeterminacy. Return to text
32. Results using MATLAB are reported in the next section. Return to text
33. An alternative way of handling
the foreign assets problem is to follow BB and CGG, among others,
and recast the model as stochastic with complete asset markets.
Then, as mentioned in footnote 10, the relationship between foreign
and domestic consumption and the real exchange rate derived in our
perfect foresight model from the Euler equations and the UIP
condition is still valid, but now becomes a risk-sharing condition.
The linearized stochastic model has an identical deterministic
component and therefore the stability analysis, which is all that
concerns us in this paper, all goes through as before. Furthermore,
in that case the analysis is valid without restrictions
![]() and
and ![]() for the home bias case.
Although now trade balance is not zero, the current account is
balanced with any trade imbalance automatically offset by payoffs
from income-contingent assets (see Sutherland (2002)).
Return to text
for the home bias case.
Although now trade balance is not zero, the current account is
balanced with any trade imbalance automatically offset by payoffs
from income-contingent assets (see Sutherland (2002)).
Return to text
34. Note that the decoupled interest
rate process has a characteristic equation
![]() . By the root locus
method it can be shown that this system also has an indeterminate
equilibrium for
. By the root locus
method it can be shown that this system also has an indeterminate
equilibrium for ![]() and for
and for ![]() when
when
![]() . However, for the
system as a whole the indeterminacy is determined by that of the
. However, for the
system as a whole the indeterminacy is determined by that of the
![]() system
as given in the proof. Return to
text
system
as given in the proof. Return to
text
35. In fact it is straightforward to
show that proposition 4 also holds for any backward lag,
![]() . Return to text
. Return to text
36. As measured respectively by changes in the Harmonized Index of Consumer Prices, HICP; and changes in the Personal Consumption Expenditure, PCE, in the form of either the chain-weighted index or the deflator. Return to text
37. See Devereux and Yetman (2002) for a recent paper with endogenous Calvo price adjustments. Return to text
38. This range could include rules which also feedback on output and on future average inflation over a given time horizon j, rather than one-period inflation j periods ahead as in this paper. Return to text
This version is optimized for use by screen readers. A printable pdf version is available.
![\begin{displaymath} \mathcal{E}_{0}\sum_{t=0}^{\infty }\beta ^{t}\left[ \frac{ (... ...1-\varphi }-\kappa \frac{N_{t}(r)^{1+\phi }}{ 1+\phi }\right] \end{displaymath}](img23.gif)
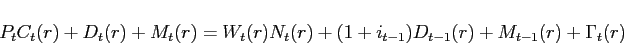
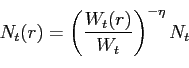
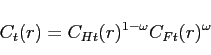
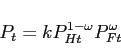
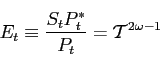
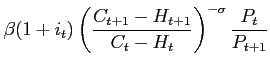
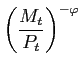
![$\displaystyle \frac{(C_t-H_t)^{-\sigma}}{\chi P_t}\left[ \frac{i_t}{1+i_t} \right]$](img77.gif)
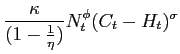
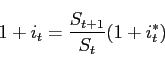
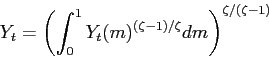
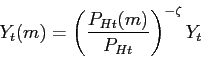
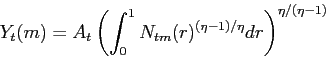
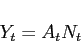
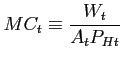
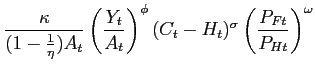
![\begin{displaymath} \mathcal{E}_{t}\sum_{k=0}^{\infty }\left(\frac{\xi}{1+i_t} \... ...t+k}}{P_{Ht}}\right) ^{\gamma }-\frac{W_{t+k}}{A_{t}} \right] \end{displaymath}](img102.gif)
![\begin{displaymath} \mathcal{E}_{t}\sum_{k=0}^{\infty }\left(\frac{ \xi}{1+i_t} ... ...amma }-\frac{1}{ (1-1/\zeta) }\frac{W_{t+k}}{A_{t}}\right] =0 \end{displaymath}](img104.gif)
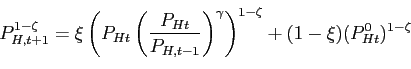
![$\displaystyle C_{Ht}+C_{Ht}^*=\frac{P}{P_H} \left[(1-\omega) C+ \omega E C^* \right]$](img107.gif)
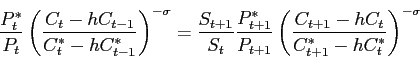
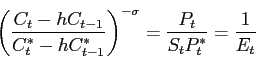
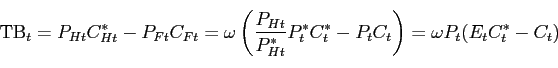
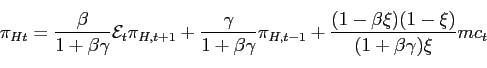
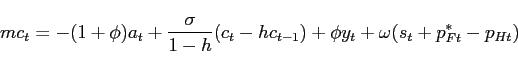
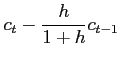
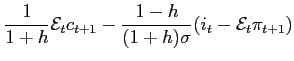
![\begin{displaymath} mc_{t}=\frac{\sigma }{2(1-h)}\left[ y_{t}-hy_{t-1}+y_{t}^{\a... ...ht] +\phi y_{t}+\frac{1}{2}\left[ y_{t}-y_{t}^{\ast } \right] \end{displaymath}](img162.gif)
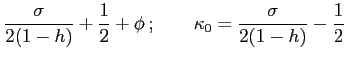
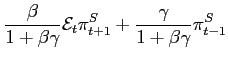
![$\displaystyle \frac{(1-\beta\xi)(1-\xi)}{(1+\beta\gamma)\xi}[(\phi+\frac{\sigma}{1-h}) y_t^S-\frac{\sigma h}{1-h}y_{t-1}^S-(1+\phi)a_t^S]$](img176.gif)
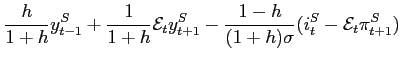
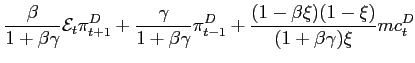
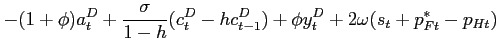
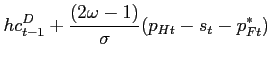
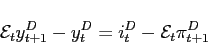
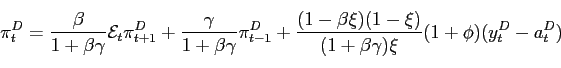
![\begin{displaymath} \Omega _{0}=-\mathcal{E}_{0}\sum_{t=0}^{\infty }\beta ^{t}[\pi _{t}^{2}+\alpha _{y}(y_{t}-k)^{2}+\alpha _{i}i_{t}^{2}] \end{displaymath}](img196.gif)
![\begin{displaymath} \left[ \begin{array}{l} z_{t+1} \ \mathcal{E}_t x_{ t+1} \... ...hsf{B}\left[ \begin{array}{l} i_t \ i_t^* \end{array}\right] \end{displaymath}](img198.gif)
![\begin{displaymath} \left[ \begin{array}{l} i_t \ i^*_t \end{array}\right]=D_1z_t+D_2C_{21} \sum_{\tau=1}^{t}(C_{22})^{\tau-1}z_{t-\tau} \end{displaymath}](img214.gif)
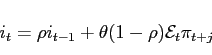
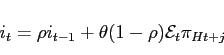
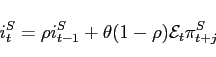
![$\displaystyle (z-\rho )[(z-1)(z-h)(\beta z-1)(z-\gamma )-\frac{\lambda }{\mu }z^{2}(\phi z+\mu (z-h))]$](img249.gif)
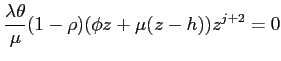
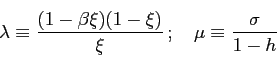
![\begin{displaymath} \theta ^{S}(1)=\frac{1+\rho }{1-\rho }\left[ 1+\frac{2(1+h)(1+\beta )(1+\gamma )\mu }{\lambda (\phi +\mu (1+h))}\right] \end{displaymath}](img281.gif)
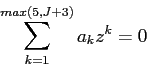
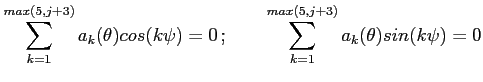
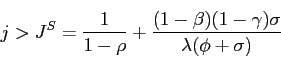
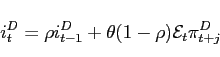
![\begin{displaymath} (z-\rho )[(z-1)(\beta z-1)(z-\gamma )-\lambda (1+\phi )z^{2}]+\lambda \theta (1-\rho )(1+\phi )z^{j+2}=0 \end{displaymath}](img309.gif)
![\begin{displaymath} \theta ^{D}(1)=\frac{1+\rho }{1-\rho }\left[ 1+\frac{2(1+\beta )(1+\gamma )\mu }{\lambda (\phi +1))}\right] \end{displaymath}](img311.gif)
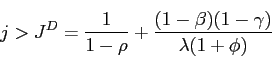
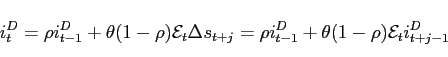
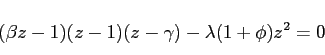
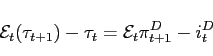
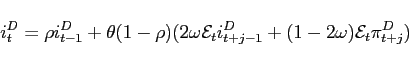
![\begin{displaymath} (z-\rho )[(\beta z-1)(z-1)(z-\gamma )-\lambda (1+\phi )z^{2}... ...[2\omega (\beta z-1)(z-1)(z-\gamma )-\lambda (1+\phi )z^{2}]=0 \end{displaymath}](img348.gif)
![\begin{displaymath} \theta ^{D}(CP,\omega )=\frac{1+\rho }{1-\rho }\left[ 1+\fra... ...) }{4\omega (\beta +1)(1+\gamma )+\lambda (\phi +1))} \right] \end{displaymath}](img353.gif)
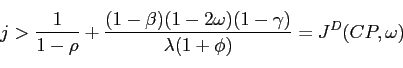
![\begin{displaymath} \theta^D(PP, \omega)-\theta^D(CP, \omega) = \frac{4(1+\rho)(... ...\lambda(1+\phi)[4 \omega(1+\beta)(1+\gamma)+\lambda(1+\phi) ]} \end{displaymath}](img363.gif)
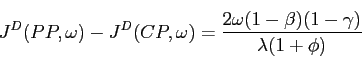
![\begin{displaymath} \left[ \begin{array}{l} z_{t+1}\ x^e_{t+1,t} \end{array} \... ...] + B \left[ \begin{array}{l} w_t\ w^*_t \end{array} \right] \end{displaymath}](img372.gif)
![\begin{displaymath} \Omega_0^c=\frac{1}{2}\sum_{i=0}^{\infty} \beta^t \left[ y^T... ...eft[ \begin{array}{l} w_t\ w^*_t \end{array} \right] \right] \end{displaymath}](img399.gif)
![\begin{displaymath} \left[ \begin{array}{l} w_t\ w^*_t \end{array} \right]=F \... ... = G \left[ \begin{array}{l} z_t\ p_{2t} \end{array} \right] \end{displaymath}](img411.gif)
![\begin{displaymath} \left[ \begin{array}{l} z_{t+1}\ p_{2t+1} \end{array} \rig... ...} \left[ \begin{array}{l} z_t\ p_{2t} \end{array} \right]\ \end{displaymath}](img412.gif)