
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 801, April 2004, Revised Version: late 2004--Screen Reader Version*
This HTML version of this discussion paper is a revised and updated version of the same paper available as a PDF file at http://www.federalreserve.gov/pubs/ifdp/2004/801/ifdp801.pdf.
The Optimal Degree of Discretion in Monetary Policy
International Finance Discussion Papers numbers 797-807 were presented on November 14-15, 2003 at the second conference sponsored by the International Research Forum on Monetary Policy sponsored by the European Central Bank, the Federal Reserve Board, the Center for German and European Studies at Georgetown University, and the Center for Financial Studies at the Goethe University in Frankfurt.
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
How much discretion should the monetary authority have in setting its policy? This question is analyzed in an economy with an agreed-upon social welfare function that depends on the economy's randomly fluctuating state. The monetary authority has private information about that state. Well-designed rules trade off society's desire to give the monetary authority discretion to react to its private information against society's need to prevent that authority from giving in to the temptation to stimulate the economy with unexpected inflation, the time inconsistency problem. Although this dynamic mechanism design problem seems complex, its solution is simple: legislate an inflation cap. The optimal degree of monetary policy discretion turns out to shrink as the severity of the time inconsistency problem increases relative to the importance of private information. In an economy with a severe time inconsistency problem and unimportant private information, the optimal degree of discretion is none.
Keywords: Rules vs. discretion, time inconsistency, optimal monetary policy, inflation targets, inflation caps
JEL Classification: E5, E6, E52, E58, E61
Suppose that society can credibly impose on the monetary authority rules governing the conduct of monetary policy. How much discretion should be left to the monetary authority in setting its policy? The conventional wisdom from policymakers is that optimal outcomes can be achieved only if some discretion is left in the hands of the monetary authority. But starting with Kydland and Prescott (1977), most of the academic literature has contradicted that view. In summarizing this literature, Taylor (1983) and Canzoneri (1985) argue that when the monetary authority does not have private information about the state of the economy, the debate is settled: there should be no discretion; the best outcomes can be achieved by rules that specify the action of the monetary authority as a function of observables. The unsettled question in this debate is Canzoneri's: What about when the monetary authority does have private information? What, then, is the optimal degree of monetary policy discretion?
To answer this question, we use a model of monetary policy similar to that of Kydland and Prescott (1977) and Barro and Gordon (1983). In our legislative approach to monetary policy, we suppose that society designs the optimal rules governing the conduct of monetary policy by the monetary authority. The model includes an agreed-upon social welfare function that depends on the random state of the economy. We begin with the assumption that the monetary authority observes the state and individual agents do not. In the context of our model, we say that the monetary authority has discretion if its policy is allowed to vary with its private information.2
The assumption of private information creates a tension between discretion and time inconsistency.3 Tight constraints on discretion mitigate the time inconsistency problem in which the monetary authority is tempted to claim repeatedly that the current state of the economy justifies a monetary stimulus to output. However, tight constraints leave little room for the monetary authority to fine tune its policy to its private information. Loose constraints allow the monetary authority to do that fine tuning, but they also allow more room for the monetary authority to stimulate the economy with surprise inflation.
We find the constraints on monetary policy that, in the presence of private information, optimally resolve this tension between discretion and time inconsistency. Formally, we cast this problem as a dynamic mechanism design problem. Canzoneri (1985) conjectures that because of the dynamic nature of the problem, the resulting optimal mechanism with regard to monetary policy is likely to be quite complex. We find that, in fact, it is quite simple. For a broad class of economies, the optimal mechanism is static and can be implemented by setting an inflation cap, an upper limit on the permitted inflation rate.
More formally, our model can be described as follows. Each period, the monetary authority observes one of a continuum of possible privately observed states of the economy. These states are i.i.d. over time. In terms of current payoffs, the monetary authority prefers to choose higher inflation when higher values of this state are realized and lower inflation when lower values are realized. Here a mechanism specifies what monetary policy is chosen each period as a function of the history of the monetary authority's reports of its private information. We say that a mechanism is static if policies depend only on the current report by the monetary authority and dynamic if policies depend also on the history of past reports.
Our main technical result is that, as long as a monotone hazard condition is satisfied, the optimal mechanism is static. We also give examples in which this monotone hazard condition fails, and the optimal mechanism is dynamic.
We then show that our result on the optimality of a static
mechanism implies that the optimal policy has one of two forms:
either it has bounded discretion or it has no discretion. Under
bounded discretion, there is a cutoff
state: for any state less than this, the monetary authority chooses
its static best response, which is an
inflation rate that increases with the state, and for any
state![]() greater than this
cutoff state
greater than this
cutoff state![]() the monetary
authority chooses a constant inflation rate. Under no discretion, the monetary authority chooses some
constant inflation rate regardless of its information
the monetary
authority chooses a constant inflation rate. Under no discretion, the monetary authority chooses some
constant inflation rate regardless of its information![]()
We then show that we can implement the optimal policy as a repeated static equilibrium of a game in which the monetary authority chooses its policy subject to an inflation cap and in which individual agents' expectations of future inflation do not vary with the monetary authority's policy choice. In general, the inflation cap would vary with observable states, but to keep the model simple, we abstract from observable states, and the inflation cap is a single number. Depending on the realization of the private information, sometimes the cap will bind, and sometimes it will not.
These results imply that the optimal constraints on discretion take the form of an inflation cap: the monetary authority is allowed to choose any inflation rate below this cap, but cannot choose one above it. We say that a given inflation cap implies less discretion than another cap if it is more likely to bind. We show that the optimal degree of discretion for the monetary authority is smaller in an economy the more severe the time inconsistency problem is and the less important private information is. It is immediate that we can equivalently implement the optimal policy by choosing a range of acceptable inflation rates. The optimal range will decrease as the time inconsistency problem becomes more severe relative to the importance of private information.
Here the rationale for discretion clearly depends in a critical way on the monetary authority having some private information that the other agents in the economy do not have. Of course, if the amount of such private information is thought to be very small in actual economies, relative to time inconsistency problems, then our work argues that in such economies the logical case for a sizable amount of discretion is weak, and the monetary authority should follow a rather tightly specified rule.
One interpretation of our work is that we solve for the optimal inflation targets. As such, our work is related to the burgeoning literature on inflation targeting. (See the work of Cukierman and Meltzer (1986), Bernanke and Woodford (1997), and Faust and Svensson (2001), among many others.) In terms of the practical application of inflation targets, Bernanke and Mishkin (1997) discuss how inflation targets often take the form of ranges or limits on acceptable inflation rates similar to the ranges we derive. Indeed, our work here provides one theoretical rationale for the type of constrained discretion advocated by Bernanke and Mishkin.
Here we have assumed that the monetary authority maximizes the welfare of society. As such, the monetary authority is viewed as the conduit through which society exercises its will. An alternative approach is to view the monetary authority as an individual or an organization motivated by concerns other than that of society's well-being. If, for example, the monetary authority is motivated in part by its own wages, then, as Walsh (1995) has shown, the full-information, full-commitment solution can be implemented. Hence, with such a setup, monetary policy has no binding incentive problems to begin with. As Persson and Tabellini (1993) note, there many reasons such contracts are either difficult or impossible to implement, and the main issue for research following this approach is why such contracts are, at best, rarely used.
Our work is related to several other literatures. One is some work on private information in monetary policy games. See, for example, that of Backus and Driffill (1985); Ireland (2000); Sleet (2001); Da Costa and Werning (2002); Angeletos, Hellwig, and Pavan (2003); Sleet and Yeltekin (2003); and Stokey (2003). The most closely related of these is the work of Sleet (2001), who considers a dynamic general equilibrium model in which the monetary authority sees a noisy signal about future productivity before it sets the money growth rate. Sleet finds that, depending on parameters, the optimal mechanism may be static, as we find here, or it may be dynamic.
Our work is also related to a large literature on dynamic contracting. Our result on the optimality of a static mechanism is quite different from the typical result in this literature, that static mechanisms are not optimal. (See, for example, Green (1987), Atkeson and Lucas (1992), and Kocherlakota (1996).) We discuss the relation between our work and these literatures in more detail after we present our results.
At a technical level, we draw heavily on the literature on recursive approaches to dynamic games. We use the technique of Abreu, Pearce, and Stacchetti (1990), which has been applied to monetary policy games by Chang (1998) and is related to the policy games studied by Phelan and Stacchetti (2001), Albanesi and Sleet (2002), and Albanesi, Chari, and Christiano (2003).
The mechanism design problem that we study is related, at an abstract level, to some work on supporting collusive outcomes in cartels by Athey, Bagwell, and Sanchirico (2004), work on risk-sharing with nonpecuniary penalties for default by Rampini (forthcoming), and work on the tradeoff between flexibility and commitment in savings plans for consumers with hyperbolic discounting by Amador, Werning, and Angeletos (2004). However, our paper is both substantively and technically quite different from those. We discuss the details of the relation after we present our results.
1 The Economy
A The Model
Here we describe our simple model of monetary policy. The
economy has a monetary authority and a continuum of individual
agents. The time horizon is infinite, with periods indexed by
![]()
At the beginning of each period, agents choose individual action
![]() from some compact
set. We interpret
from some compact
set. We interpret ![]() as (the
growth rate of) an individual's nominal wage and let
as (the
growth rate of) an individual's nominal wage and let ![]() denote the (growth of the)
average nominal wage. Next, the monetary authority observes the
current realization of its private information about the state of
the economy. This private information
denote the (growth of the)
average nominal wage. Next, the monetary authority observes the
current realization of its private information about the state of
the economy. This private information
![]() is an i.i.d.,
mean 0 random variable with support
is an i.i.d.,
mean 0 random variable with support
![]() ,
with a strictly positive density
,
with a strictly positive density ![]() and a distribution function
and a distribution function ![]() . Given this private
information
. Given this private
information
![]() , referred to
as the state, the monetary authority
chooses money growth
, referred to
as the state, the monetary authority
chooses money growth ![]() in some large compact set
in some large compact set
![]()
The monetary authority maximizes a social welfare function
![]() that depends on the
average nominal wage growth
that depends on the
average nominal wage growth ![]() the monetary growth rate
the monetary growth rate ![]() , and a privately observed
state
, and a privately observed
state
![]() . We interpret
. We interpret
![]() to be private
information of the monetary authority regarding the impact of a
monetary stimulus on social welfare in the current period.
Throughout, we assume that
to be private
information of the monetary authority regarding the impact of a
monetary stimulus on social welfare in the current period.
Throughout, we assume that ![]() is strictly concave in
is strictly concave in ![]() and twice continuously
differentiable.
and twice continuously
differentiable.
A leading interpretation of the private information in our economy follows that of Sleet and Yeltekin (2003) and Sleet (2004). Individual agents in the economy have either heterogeneous preferences or heterogeneous information regarding the optimal inflation rate, and the monetary authority sees an aggregate of that information which the private agents do not see. (Informally, we imagine this private information takes resources to acquire, so that while agents in the economy feasibly can acquire the information, the costs involved in doing so outweigh the benefits.) When we pose our optimal policy problem as a mechanism design problem, we are presuming that the mechanism designer is a separate agent with no independent information of its own. We interpret the society's objective as a weighted average of the preferences of the heterogeneous agents.
As a benchmark example, we use this function:
| (1) | ![$\displaystyle R(x_{t},\mu_{t},\theta_{t})=-\frac{1}{2}\left[ (U+x_{t}-\mu_{t})^{2}+(\mu _{t}-\alpha\theta_{t})^{2}\right] .$](img18.gif)
|
We interpret (1) as the reduced form that results from a monetary authority which maximizes a social welfare function that depends on unemployment, inflation, and the monetary authority's private information
| (2) |
where
| (3) | 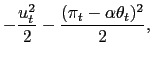
|
which is similar to that used by Kydland and Prescott (1977) and Barro and Gordon (1983). Using (2) and
Throughout, a policy for the
monetary authority in any given period, denoted
![]() specifies
the money growth rate
specifies
the money growth rate
![]() for each
level of the state
for each
level of the state ![]() For any
For any ![]() we define
the static best response to be the
policy
we define
the static best response to be the
policy
![]() that solves
that solves ![]() (
(
![]() )
)
![]() We assume that if
We assume that if
![]() then
then
| (4) |
B Two Ramsey Benchmarks
Before we analyze the economy in which the monetary authority has private information, we consider two alternative economies. The optimal policies in these economies are useful as benchmarks for the optimal policy in the private information economy.
One benchmark, the Ramsey policy,
denoted
![]() yields
the highest payoff that can be achieved in an economy with full
information. The gap between that Ramsey payoff and the payoff in
the economy with private information measures the welfare loss due
to private information.
yields
the highest payoff that can be achieved in an economy with full
information. The gap between that Ramsey payoff and the payoff in
the economy with private information measures the welfare loss due
to private information.
The other benchmark, the expected Ramsey
policy, denoted ![]() yields the highest payoff that can be
achieved when the policy is restricted to not depend on private
information. In our environment, there is no publicly observed
shock to the economy; hence, this policy is a constant. The
expected Ramsey policy is a useful benchmark because it is the best
policy that can be achieved by a rule which specifies policies as a
function only of observables. This policy is analogous to the
strict targeting rule discussed by Canzoneri (1985).
yields the highest payoff that can be
achieved when the policy is restricted to not depend on private
information. In our environment, there is no publicly observed
shock to the economy; hence, this policy is a constant. The
expected Ramsey policy is a useful benchmark because it is the best
policy that can be achieved by a rule which specifies policies as a
function only of observables. This policy is analogous to the
strict targeting rule discussed by Canzoneri (1985).
For the Ramsey policy benchmark, consider an economy with full
information with the following timing scheme. Before the state
![]() is realized, the
monetary authority commits to a schedule for money growth rates
is realized, the
monetary authority commits to a schedule for money growth rates
![]() . Next,
individual agents choose their nominal wages
. Next,
individual agents choose their nominal wages ![]() with associated average nominal wages
with associated average nominal wages
![]() Then the state
Then the state
![]() is realized, and
the money growth rate
is realized, and
the money growth rate
![]() is
implemented. The optimal allocations and policies in this economy
solve the Ramsey problem:
is
implemented. The optimal allocations and policies in this economy
solve the Ramsey problem:
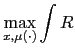 (
(For the other benchmark, consider an economy in which the
monetary authority is restricted to choosing money growth
![]() that does not vary
with its private information. The equilibrium allocations and
policies in the economy with these constraints solve the
expected Ramsey problem:
that does not vary
with its private information. The equilibrium allocations and
policies in the economy with these constraints solve the
expected Ramsey problem:
| (5) | 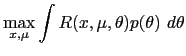
|
subject to
For our example (1), the Ramsey policy
obviously yields strictly higher welfare than does the expected
Ramsey policy. More generally, when
![]() the Ramsey policy
the Ramsey policy
![]() is
strictly increasing in
is
strictly increasing in ![]() and yields strictly higher welfare than does
the expected Ramsey policy.
and yields strictly higher welfare than does
the expected Ramsey policy.
C The Dynamic Mechanism Design Problem
To analyze the problem of finding the optimal degree of discretion, we use the tools of dynamic mechanism design. Without loss of generality, we formulate the problem as a direct revelation game. In this problem, society specifies a monetary policy, the money growth rate as a function of the history of the monetary authority's reports of its private information about the state of the economy. Given the specified monetary policy, the monetary authority chooses a strategy for reporting its private information. Individual agents choose their wages as functions of the history of reports of the monetary authority.
A monetary policy in this environment is a sequence of
functions
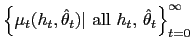 , where
, where
![]() specifies the money
growth rate that will be chosen in period
specifies the money
growth rate that will be chosen in period ![]() following the history
following the history
![]() of past reports together with the current report
of past reports together with the current report
![]() The
monetary authority chooses a reporting strategy
The
monetary authority chooses a reporting strategy
![]() all
all ![]() ,
,
![]() in period
in period ![]() where
where
![]() is the
current realization of private information and
is the
current realization of private information and
![]()
![]() is the
reported private information in
is the
reported private information in ![]() As is standard, we restrict attention to public
strategies, those that depend only on public histories and the
current private information, not on the history of private
information.5 Also, from
the Revelation Principle, we need only restrict attention to
truth-telling equilibria, in which
As is standard, we restrict attention to public
strategies, those that depend only on public histories and the
current private information, not on the history of private
information.5 Also, from
the Revelation Principle, we need only restrict attention to
truth-telling equilibria, in which
![]() for all
for all
![]() and
and
![]()
In each period, each agent chooses the action ![]() as a function of the history of
reports
as a function of the history of
reports ![]() Since
agents are competitive, the history need not include either agents'
individual past actions or the aggregate of their past
actions.6
Since
agents are competitive, the history need not include either agents'
individual past actions or the aggregate of their past
actions.6
Each agent chooses nominal wage growth equal to expected
inflation. For each history ![]() with monetary policy
with monetary policy
![]() given, agents set
given, agents set
![]() equal to
expected inflation:
equal to
expected inflation:
| (6) | 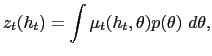
|
where we have used the fact that agents expect the monetary authority to report truthfully, so that
The optimal monetary policy maximizes the discounted sum of social welfare:
| (7) | 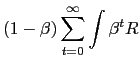 (
( |
where the future histories
A perfect Bayesian equilibrium of
this revelation game is a monetary policy, a reporting strategy, a
strategy for wage-setting by agents
![]() and
average wages
and
average wages
![]() such that (6) is satisfied in every period
following every history
such that (6) is satisfied in every period
following every history ![]() average wages equal individual wages in that
average wages equal individual wages in that
![]() , and the monetary policy is
incentive-compatible in the standard sense that, in every period,
following every history
, and the monetary policy is
incentive-compatible in the standard sense that, in every period,
following every history ![]() and realization of the private information
and realization of the private information
![]() the
monetary authority prefers to report
the
monetary authority prefers to report
![]() rather than any
other value
rather than any
other value
![]() Note that since average wages
Note that since average wages
![]() always
equal wages of individual agents
always
equal wages of individual agents
![]() we need
only record average wages from now on.
we need
only record average wages from now on.
Note that this definition of a perfect Bayesian equilibrium includes no notion of optimality for society. Instead, it simply requires that in response to a given monetary policy, private agents respond optimally and truth-telling for the monetary authority is incentive-compatible. The set of perfect Bayesian equilibria outcomes is the set of incentive-compatible outcomes that are implementable by some monetary policy.
The mechanism design problem is to choose a monetary policy, a reporting strategy, and a strategy for average wages, the outcomes of which maximize social welfare (7) subject to the constraint that these strategies are incentive-compatible.
D A Recursive Formulation
Here we formulate the problem of characterizing the solution to
this mechanism design problem recursively. The repeated nature of
the model implies that the set of incentive-compatible payoffs that
can be obtained from any period ![]() on is the same that can be obtained from period
on is the same that can be obtained from period
![]() Thus, the payoff
from any incentive-compatible outcome for the repeated game can be
broken down into payoffs from current actions for the players and
continuation payoffs that are themselves drawn from the set of
incentive-compatible payoffs. Following this logic, Abreu, Pearce,
and Stacchetti (1990) show that the set of incentive-compatible
payoffs can be found using a recursive method that we exploit
here.
Thus, the payoff
from any incentive-compatible outcome for the repeated game can be
broken down into payoffs from current actions for the players and
continuation payoffs that are themselves drawn from the set of
incentive-compatible payoffs. Following this logic, Abreu, Pearce,
and Stacchetti (1990) show that the set of incentive-compatible
payoffs can be found using a recursive method that we exploit
here.
In our environment, this recursive method is as follows.
Consider an operator on sets of the following form. Let
![]() be some compact
subset of the real line, and let
be some compact
subset of the real line, and let ![]() be the largest element of
be the largest element of ![]() . The set
. The set ![]() may be interpreted as a candidate
set of incentive-compatible levels of social welfare. In our
recursive formulation, the current actions are average wages
may be interpreted as a candidate
set of incentive-compatible levels of social welfare. In our
recursive formulation, the current actions are average wages
![]() and a report
and a report
![]() for every realized value of the state
for every realized value of the state ![]() For each possible report
For each possible report
![]() there is
a corresponding continuation payoff
there is
a corresponding continuation payoff
![]() that
represents the discounted utility for the monetary authority from
the next period on. Clearly, these continuation payoffs cannot vary
directly with the privately observed state
that
represents the discounted utility for the monetary authority from
the next period on. Clearly, these continuation payoffs cannot vary
directly with the privately observed state ![]()
We say that the actions ![]() and
and
![]() and the
continuation payoff
and the
continuation payoff ![]() are enforceable by
are enforceable by ![]() if
if
| (8) |
| (9) | 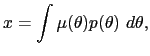 |
and the incentive constraints
| (10) |
are satisfied for all
The payoff corresponding to
![]() and
and
![]() is
is
| (11) |
Define the operator
| (12) | ||
| s.t. |
As demonstrated by Abreu, Pearce, and Stacchetti (1990), the set of incentive-compatible payoffs is the largest set
| (13) |
For any given candidate set of incentive-compatible payoffs
![]() we are interested
in finding the largest payoff that is enforceable by
we are interested
in finding the largest payoff that is enforceable by ![]() or the largest element
or the largest element
![]()
![]() We find this
payoff by solving the following problem, termed the best payoff problem:
We find this
payoff by solving the following problem, termed the best payoff problem:
| (14) | 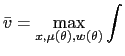 [
[ |
subject to the constraint that
The best payoff problem is a mechanism design problem of
choosing an incentive-compatible allocation
![]() which maximizes utility. Following the language of mechanism
design, we now refer to
which maximizes utility. Following the language of mechanism
design, we now refer to ![]() as the type of the
monetary authority, which changes every period. When we solve this
problem with
as the type of the
monetary authority, which changes every period. When we solve this
problem with
![]() (13) implies that the resulting payoff is the highest
incentive-compatible payoff. We will prove our main result in
Proposition 1 for any
(13) implies that the resulting payoff is the highest
incentive-compatible payoff. We will prove our main result in
Proposition 1 for any ![]() Hence, we will not have to explicitly solve the fixed-point problem
of finding
Hence, we will not have to explicitly solve the fixed-point problem
of finding ![]()
Moreover, to prove our main result, we also need focus only on
the best payoff problem, which gives the highest payoff that can be
obtained from period 0 onward. For
completeness, however, notice that given some
![]() from the
best payoff problem, a period
from the
best payoff problem, a period ![]() policy and continuation value,
policy and continuation value,
![]() and
and
![]() that satisfy
that satisfy
| (15) | ![$\displaystyle w_{0}(\theta)=\int\left[ (1-\beta)R\mbox{{\large (}}x_{w_{0}(\the... ...{w_{0}(\theta)}(z),z\mbox{{\large )}}+\beta w_{w_{0}(\theta)}(z)\right] p(z)~dz$](img135.gif)
|
exist by the definition of
2 Characterizing the Optimal Mechanism
Now we solve the best payoff problem and use the solution to characterize the optimal mechanism. Our main result here is that under two simple conditions, a single-crossing condition and a monotone hazard condition, the optimal mechanism is static. To highlight the importance of the monotone hazard condition for this result, we discuss in an appendix three examples which show that if the monotone hazard condition is violated, the optimal mechanism is dynamic.
A Preliminaries
We begin with some definitions. In our recursive formulation, we
say that a mechanism is static if the
continuation value
![]() for
(almost) all
for
(almost) all ![]() We say
that a mechanism is dynamic if
We say
that a mechanism is dynamic if
![]() for some set of
for some set of ![]() which is realized with strictly positive probability.
which is realized with strictly positive probability.
Our characterization of the solution to the best payoff problem
does not depend on the exact value of ![]() Hence, to simplify the
notation, we suppress explicit dependence on
Hence, to simplify the
notation, we suppress explicit dependence on ![]() and think of the term
and think of the term
![]() as being
subsumed in the
as being
subsumed in the ![]() function and
function and ![]() as
being subsumed in the
as
being subsumed in the ![]() function.
function.
We assume that the preferences are differentiable and satisfy a standard single-crossing assumption, that
| (A1) |
This implies that higher types of monetary authority have a stronger preference for current inflation. Standard arguments can be used to show that the static best response
Under the single-crossing assumption (A1), a standard lemma lets
us replace the global incentive constraints (10)
with some local versions of them. We say that an allocation is
locally incentive-compatible if it
satisfies three conditions:
![]() is
nondecreasing in
is
nondecreasing in ![]() ;
;
| (16) | 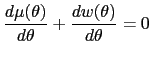
|
wherever
| (17) |
Standard arguments give the following result: under the single-crossing assumption (A1), the allocation (
Given any incentive-compatible allocation, we define the
utility of the allocation at
![]() to be
to be
| (18) | 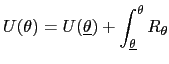 (
( |
while integrating
| (19) | 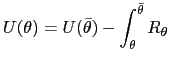 (
( |
With integration by parts, it is easy to show that for interval endpoints
| (20) | 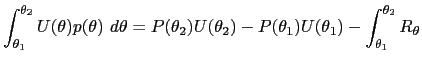 (
( |
Using (18) and (20), we can write the value of the objective function
| (21) | 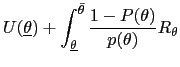 (
( |
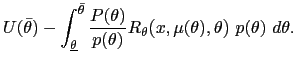
Next we make some joint assumptions on the probability
distribution and the social welfare function. Assume that, for any
action profile
![]() with
with
![]() nondecreasing,
nondecreasing,
| (A2a) | 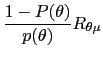 (
( |
| (A2b) | 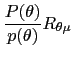 (
( |
We refer to assumptions (A2a) and (A2b) together as (A2) and, in a
slight abuse of terminology, call them the monotone hazard condition. In our benchmark example
(1),
![]() (
(
![]() )
)
![]() , so that (A2)
reduces to the standard monotone hazard condition familiar from the
mechanism design literature, that
, so that (A2)
reduces to the standard monotone hazard condition familiar from the
mechanism design literature, that
![]() be strictly decreasing and
be strictly decreasing and
![]() be
strictly increasing.
be
strictly increasing.
B Showing That the Optimal Mechanism Is Static
Here we show that the optimal mechanism is static by proving this proposition:
Proposition 1: Under assumptions (A1) and A2), the optimal mechanism is static.
The approach we take in proving Proposition 1 is different from the standard approach used by Fudenberg and Tirole (1991, Chapter 7.3) for solving a mathematically related principal-agent problem. To motivate our approach, we first show why the standard approach does not work for our problem. We discuss the forces that lead to the failure of the standard approach here because these forces suggest a variational argument we use to prove Proposition 1.
The best payoff problem can be written as follows: Choose
![]() to maximize
social welfare
to maximize
social welfare
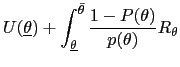 (
(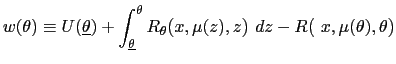
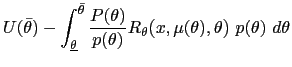
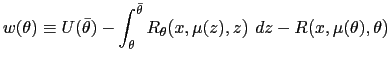
The standard approach to solving either version of this problem
is to guess that the analog of constraints ![]() and
and ![]() do not bind, take the
corresponding first-order conditions of either version to find the
implied
do not bind, take the
corresponding first-order conditions of either version to find the
implied
![]() and then
verify that constraints
and then
verify that constraints ![]() and
and ![]() are in fact satisfied at that choice of
are in fact satisfied at that choice of
![]() If we take
that approach here, it fails. The first-order conditions with
respect to
If we take
that approach here, it fails. The first-order conditions with
respect to
![]() are
are
| (22) | 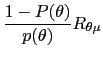 (
( |
for the first version of the best payoff problem and
| (23) | 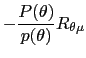 (
( |
for the second version, where
We also cannot use the ironing approach designed to deal with
cases in which the monotonicity constraint ![]() binds, because in our problem,
the constraint that binds is constraint
binds, because in our problem,
the constraint that binds is constraint ![]() , which is not dealt with in
that approach. Instead, in the proof of Proposition 1 that follows,
we use a variational argument to show that constraint
, which is not dealt with in
that approach. Instead, in the proof of Proposition 1 that follows,
we use a variational argument to show that constraint ![]() binds for all
binds for all ![]() at the solution to the best
payoff problem. (We discuss below the reason our model differs from
others in the literature.)
at the solution to the best
payoff problem. (We discuss below the reason our model differs from
others in the literature.)
Before proving Proposition 1, we sketch our basic argument. Our
discussion of the first-order conditions of the relaxed problem
(22) and (23)
suggests that given any strictly increasing
![]() schedule, a
variation that flattens this schedule will improve welfare if it is
feasible in the sense that the associated continuation value
satisfies constraint
schedule, a
variation that flattens this schedule will improve welfare if it is
feasible in the sense that the associated continuation value
satisfies constraint ![]() Our proof of Lemma 1 formalizes this logic.
Our proof of Lemma 1 formalizes this logic.
Our objective is to show that the optimal continuation value
![]() is constant at
is constant at
![]() We prove this
by contradiction. We start with the observation that
We prove this
by contradiction. We start with the observation that ![]() is piecewise-differentiable
since
is piecewise-differentiable
since
![]() is
piecewise-differentiable and (16) holds. We
first show that
is
piecewise-differentiable and (16) holds. We
first show that ![]() must be a step function. If not, there is some interval over which
must be a step function. If not, there is some interval over which
![]() is
nonzero, and hence, from local incentive-compatibility,
is
nonzero, and hence, from local incentive-compatibility,
![]() is strictly
increasing. In Lemma 2, we show that a variation that flattens
is strictly
increasing. In Lemma 2, we show that a variation that flattens
![]() over that
interval is feasible. From Lemma 1, we know it is
welfare-improving.
over that
interval is feasible. From Lemma 1, we know it is
welfare-improving.
We next show that ![]() must be continuous, and since it is a step function, it must be
constant. We prove this by showing that if either
must be continuous, and since it is a step function, it must be
constant. We prove this by showing that if either
![]() or
or
![]() are
discontinuous at some point
are
discontinuous at some point ![]() then (17) implies that
then (17) implies that
![]() must be
increasing in the sense that it jumps up at that point. In Lemma 3,
we show that a variation that flattens
must be
increasing in the sense that it jumps up at that point. In Lemma 3,
we show that a variation that flattens
![]() in a
neighborhood of that point is feasible, and again from Lemma 1, we
know that it is welfare-improving.
in a
neighborhood of that point is feasible, and again from Lemma 1, we
know that it is welfare-improving.
It is convenient in the proof of Proposition 1 to use a
definition of increasing on an interval
which covers the cases we will deal with in Lemmas 2 and 3. This
definition subsumes the case of Lemma 2 in which
![]() for some interval and the
case of Lemma 3 in which
for some interval and the
case of Lemma 3 in which
![]() jumps up at
jumps up at
![]() We say
that
We say
that
![]() is
increasing on
is
increasing on
![]() if
if
![]() is weakly
increasing on this interval and there is some
is weakly
increasing on this interval and there is some
![]() in this
interval such that
in this
interval such that
![]() for
for
![]() and
and
![]() for
for
![]() , where
, where
![]() is the
conditional mean of
is the
conditional mean of
![]() on this
interval, namely,
on this
interval, namely,
| (24) | 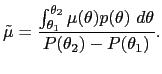
|
In words, on this interval, the function
Consider now some dynamic mechanism (
![]() ) in
which the policy
) in
which the policy
![]() is
increasing on some interval, say,
is
increasing on some interval, say,
![]() In our variation, we
marginally move the function
In our variation, we
marginally move the function
![]() toward its
conditional mean on this interval and adjust the continuation
values to preserve incentive-compatibility. In particular, our
variation moves our original policy
toward its
conditional mean on this interval and adjust the continuation
values to preserve incentive-compatibility. In particular, our
variation moves our original policy
![]() marginally
toward a policy
marginally
toward a policy
![]() defined by
defined by
| (25) | ![$\displaystyle \tilde{\mu}(\theta)=\left\{ \begin{array}[c]{c} \tilde{\mu}\mbox{... ...\in(\theta_{1},\theta_{2})\\ \mu(\theta)\mbox{ otherwise} \end{array} \right. .$](img211.gif)
|
This policy
We let (
![]() )
and
)
and
![]() denote our
variation and the associated utility. The policy
denote our
variation and the associated utility. The policy
![]() in our
variation is a convex combination of the policy
in our
variation is a convex combination of the policy
![]() and
the original policy
and
the original policy
![]() and is
defined by
and is
defined by
| (26) |
for
The delicate part of the variation is to construct the
continuation value
![]() so as to
satisfy the feasibility constraint
so as to
satisfy the feasibility constraint
![]() for all
for all ![]() in addition to
incentive-compatibility. It turns out that we can ensure
feasibility if we use one of two ways to adjust continuation
values. In the up variation, we leave
the continuation values unchanged below
in addition to
incentive-compatibility. It turns out that we can ensure
feasibility if we use one of two ways to adjust continuation
values. In the up variation, we leave
the continuation values unchanged below
![]() and pass up
any changes induced by our variation in the policy to higher types
by suitably adjusting the continuation values to maintain
incentive-compatibility. In the down
variation, we leave the continuation values unchanged above
and pass up
any changes induced by our variation in the policy to higher types
by suitably adjusting the continuation values to maintain
incentive-compatibility. In the down
variation, we leave the continuation values unchanged above
![]() and pass
down any changes induced by our variation in the policy to lower
types by suitably adjusting the continuation values to maintain
incentive-compatibility.
and pass
down any changes induced by our variation in the policy to lower
types by suitably adjusting the continuation values to maintain
incentive-compatibility.
In the up variation, we determine the continuation values by
substituting
![]()
![]() (
(
![]() )
)
![]()
![]() into
(18) to get that
into
(18) to get that
![]() is defined
by
is defined
by
| (27) | 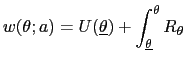 (
( |
In the down variation, we use (19) in a similar way to get that
| (28) | 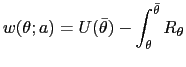 (
( |
By construction, these variations are incentive-compatible. In the following lemma, we show that, if either variation is feasible, it improves welfare.
LEMMA 1: Assume (A1)
and (A2), and
let (
![]() )
)![]() be an allocation in
which
be an allocation in
which
![]() is increasing on some interval
is increasing on some interval
![]() Then the
up variation and the down variation both improve welfare by
increasing the objective function (
Then the
up variation and the down variation both improve welfare by
increasing the objective function (
![]()
PROOF: To see that the up variation improves welfare, use (21) to write the value of the objective function under this variation as
| (29) | 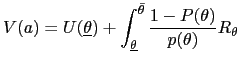 (
( |
To evaluate the effect on welfare of a marginal change of this type, take the derivative of
| (30) | 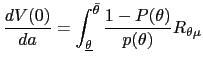 (
( |
which, with the form of
| (31) | 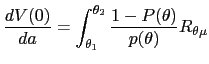 (
( |
If we divide (31) by the positive constant
The down variation also improves welfare. The value of the objective function under this variation is
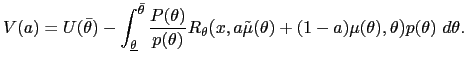
| (32) | 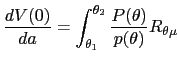 (
( |
by arguments similar to those given before. Q.E.D.
To gain some intuition for how these variations improve welfare,
we begin by emphasizing a critical insight: changing the inflation
for any given type not only has direct effects on the welfare of
that type, but also has indirect effects on the welfare of other
types through the incentive constraints. For example, making a
given type better off not only helps that type, but also makes that
type less tempted to mimic higher types. Thus, the continuation
values of those higher types can then be increased, if that is
feasible, as in the up variation. In that variation, the term
![]() measures the importance
of higher types
measures the importance
of higher types
![]() relative
to the rate at which changing
relative
to the rate at which changing
![]() affects
expected inflation as measured by
affects
expected inflation as measured by
![]() When
continuation values are adjusted for types below a given type
When
continuation values are adjusted for types below a given type
![]() (as in the down
variation)
(as in the down
variation)![]() the term
the term
![]() measures the importance
of lower types
measures the importance
of lower types ![]() relative to
relative to ![]() . In each variation, the term
. In each variation, the term
![]() relates to the
rate at which changing inflation for type
relates to the
rate at which changing inflation for type ![]() relaxes incentive
constraints.
relaxes incentive
constraints.
Using these ideas, let us now focus on the up variation, and
consider the effects of increasing ![]() as formalized in (31). The
variation affects inflation within the interval
as formalized in (31). The
variation affects inflation within the interval
![]() and the expression inside
the integral represents, for each
and the expression inside
the integral represents, for each
![]() the direct and
indirect effects of changing inflation for type
the direct and
indirect effects of changing inflation for type ![]() We now argue that the
flattening of the inflation schedule has a positive effect for a type in the bottom part of
the interval, namely, for some
We now argue that the
flattening of the inflation schedule has a positive effect for a type in the bottom part of
the interval, namely, for some
![]() , due to
an increase in the inflation, which in turn relaxes the incentive
constraint for
, due to
an increase in the inflation, which in turn relaxes the incentive
constraint for
![]() and
enables the continuation value
and
enables the continuation value
![]() to
increase. This also creates a positive indirect effect for all
types
to
increase. This also creates a positive indirect effect for all
types
![]() since the increase in
continuation values can be passed upward without violating
incentive constraints. In contrast, for a type in the top part of
the interval, namely, for some
since the increase in
continuation values can be passed upward without violating
incentive constraints. In contrast, for a type in the top part of
the interval, namely, for some
![]() the flattening of the inflation schedule has a negative effect, an effect that is passed on
through the incentive constraints in the form of lower continuation
values for all types
the flattening of the inflation schedule has a negative effect, an effect that is passed on
through the incentive constraints in the form of lower continuation
values for all types
![]() Our monotone hazard
rate assumption (A2a) ensures that the positive effect outweighs
the negative effect: when appropriately normalized, help to lower
types is more important than harm to higher types, because relative
to
Our monotone hazard
rate assumption (A2a) ensures that the positive effect outweighs
the negative effect: when appropriately normalized, help to lower
types is more important than harm to higher types, because relative
to
![]() type
type
![]() exerts
greater indirect effects on types above
exerts
greater indirect effects on types above
![]() .
.
More formally, let us derive expressions for the impact of the
flattening of the policy on the current payoffs ![]() of the directly affected types on
of the directly affected types on
![]() as well as the continuation
values
as well as the continuation
values ![]() of directly
and indirectly affected types. The impact of increasing
of directly
and indirectly affected types. The impact of increasing
![]() on the current
payoff for type
on the current
payoff for type
![]() is
is
| (33) | 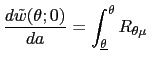 (
( |
Hence, the impact on the utility of type
| (34) | 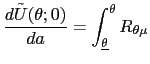 (
( |
Notice from (34) that any change in the policy for some particular type
| (35) |
in the integral (30) can be thought of as the sum of the change in welfare for all types
In the down variation, the intuition for the derivative
(32) is the same as that for (31), except that, in this variation, a change in the
inflation rate chosen by type ![]() affects the continuation value of all types
below
affects the continuation value of all types
below ![]() . Making a type
. Making a type
![]() at the top of the interval worse off (by flattening the inflation
schedule) leaves nearby types less tempted to mimic
at the top of the interval worse off (by flattening the inflation
schedule) leaves nearby types less tempted to mimic
![]() thus, the
continuation value for
thus, the
continuation value for
![]() can be
increased without inducing mimicry, and this increase can be passed
on to all types
can be
increased without inducing mimicry, and this increase can be passed
on to all types
![]() .
Making a type
.
Making a type
![]() at the
bottom of the interval better off necessitates a lower continuation
value for
at the
bottom of the interval better off necessitates a lower continuation
value for
![]() in order to
deter mimicry by nearby types, and again this decrease is passed on
to types
in order to
deter mimicry by nearby types, and again this decrease is passed on
to types
![]() .
Condition (A2b) ensures that, when weighted by the effects on
average inflation, the indirect effect generated by
.
Condition (A2b) ensures that, when weighted by the effects on
average inflation, the indirect effect generated by
![]() dominates that generated by
dominates that generated by
![]() , so that
flattening the schedule increases expected welfare.
, so that
flattening the schedule increases expected welfare.
The following lemma proves that if ![]() is not a step function, then
is not a step function, then
![]() is
increasing on some interval, and there is a feasible variation that
flattens
is
increasing on some interval, and there is a feasible variation that
flattens
![]() and improves
welfare.
and improves
welfare.
LEMMA 2: Under (A1)
and (A2), in the
optimal mechanism, the continuation value function
![]() is a step function.
is a step function.
PROOF: Since by assumption
![]() is
piecewise-differentiable, we know from (16) that
is
piecewise-differentiable, we know from (16) that
![]() is too. By way
of contradiction, assume that
is too. By way
of contradiction, assume that ![]() is not a step function. Then there is an
interval over which
is not a step function. Then there is an
interval over which
![]() exists and does not equal zero. Clearly, then, there is a
subinterval
exists and does not equal zero. Clearly, then, there is a
subinterval
![]() over which
over which
![]() is
either strictly positive or strictly negative, and
is
either strictly positive or strictly negative, and
![]() for some
for some
![]() From
local incentive-compatibility, we know that
From
local incentive-compatibility, we know that
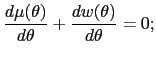
To complete the proof, we show that either the up variation or
the down variation is always feasible. Under the up variation, (
![]() and
(27) imply that
and
(27) imply that
![]() equals
equals
![]() for
for
![]() and
and
![]() for
for
![]() where
where
| (36) | 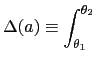 [
[ |
Figure 2 is a graph of
![]() in the up
variation
in the up
variation![]() This graph
illustrates several features of
This graph
illustrates several features of
![]() : it
coincides with
: it
coincides with ![]() for
for
![]() it differs from
it differs from ![]() by the constant
by the constant ![]() for
for
![]() and it jumps at both
and it jumps at both
![]() and
and
![]() This last
feature follows from (17) and the fact that
This last
feature follows from (17) and the fact that
![]() jumps at
these points. Notice in the graph that
jumps at
these points. Notice in the graph that
![]() for
for
![]()
Under the down variation, (
![]() and
(28) imply that
and
(28) imply that
![]() equals
equals
| (37) |
for
To ensure that the continuation value satisfies feasibility, we
use the up variation when the term
![]() and the
down variation when that term is positive. By doing so, we ensure
that outside the interval
and the
down variation when that term is positive. By doing so, we ensure
that outside the interval
![]() the continuation value under
this variation is no larger than the original continuation value
the continuation value under
this variation is no larger than the original continuation value
![]() , which, by
assumption, is feasible. We know that inside the interval
, which, by
assumption, is feasible. We know that inside the interval
![]() ,
,
![]() Since
Since ![]() is continuous in
is continuous in ![]() , we can choose
, we can choose ![]() small enough to ensure that
small enough to ensure that
![]()
Q.E.D.
In the next lemma, we show that
![]() and
and
![]() are
continuous. Since we know from Lemma 2 that
are
continuous. Since we know from Lemma 2 that ![]() is a step function, we
conclude that
is a step function, we
conclude that ![]() is a
constant. Optimality implies that this constant is
is a
constant. Optimality implies that this constant is ![]()
LEMMA 3: Under (A1)
and (A2),
![]() and
and ![]() are continuous.
are continuous.
In Appendix A, we prove that ![]() is continuous by contradiction. We show that
if
is continuous by contradiction. We show that
if ![]() jumps at some
point
jumps at some
point
![]() , then
the same up variation and down variation we used in Lemma 1 will
improve welfare. The only difficult part of the proof is showing
that when the appropriate interval
, then
the same up variation and down variation we used in Lemma 1 will
improve welfare. The only difficult part of the proof is showing
that when the appropriate interval
![]() is selected that contains the
jump point
is selected that contains the
jump point
![]() the
associated continuation values are feasible. Here it may turn out
that the feasibility constraint binds inside the interval
the
associated continuation values are feasible. Here it may turn out
that the feasibility constraint binds inside the interval
![]() in that the original
allocation has
in that the original
allocation has
![]() for
some
for
some ![]() in
in
![]() Thus, we cannot simply shrink
the size of the weight
Thus, we cannot simply shrink
the size of the weight ![]() in the variation to ensure feasibility on
in the variation to ensure feasibility on
![]() , as we did in the proof of
Lemma 2. Instead we show that the variation is feasible inside the
interval
, as we did in the proof of
Lemma 2. Instead we show that the variation is feasible inside the
interval
![]() with arguments that we
relegate to Appendix A.
with arguments that we
relegate to Appendix A.
Together Lemmas 2 and ![]() establish Proposition 1, that under our assumptions, the optimal
mechanism is static. Our characterization of optimal policy relied
on the monotone hazard condition (A2). Under this condition, we
showed that the dynamic mechanism design problem has a static
solution. In Appendix B, we give three simple examples in which the
monotone hazard condition (A2) is violated, and the dynamic
mechanism design problem does not have a static solution. In the
first two examples, (A2) fails because [
establish Proposition 1, that under our assumptions, the optimal
mechanism is static. Our characterization of optimal policy relied
on the monotone hazard condition (A2). Under this condition, we
showed that the dynamic mechanism design problem has a static
solution. In Appendix B, we give three simple examples in which the
monotone hazard condition (A2) is violated, and the dynamic
mechanism design problem does not have a static solution. In the
first two examples, (A2) fails because [
![]() ]
]
![]() is not
monotone; in the third, (A2) fails because
is not
monotone; in the third, (A2) fails because
![]() is
increasing at a sufficiently rapid rate.
is
increasing at a sufficiently rapid rate.
3 The Optimal Degree of Discretion
So far we have demonstrated that the optimal mechanism is static. Now we describe three key implications of an optimal static mechanism for monetary policy: The optimal policy has either bounded discretion or no discretion; the optimal policy can be implemented by society setting an upper limit, or cap, on the inflation rate that the monetary authority is allowed to choose; and the optimal degree of discretion is decreasing the more severe is the time inconsistency problem and the less important is private information.
A Characterizing the Optimal Policy
In the optimal static mechanism, the monetary policy
![]() maximizes
maximizes
| (38) |
subject to the constraints that
We say that a monetary policy
![]() has
bounded discretion if it takes the
form
has
bounded discretion if it takes the
form
| (39) | ![$\displaystyle \mu(\theta)=\left\{ \begin{array}[c]{c} \mu^{\ast}(\theta;x)\mbox... ...x)\mbox{ if }\theta\in\lbrack\theta^{\ast },\bar{\theta}] \end{array} \right. ,$](img333.gif)
|
where
We now show that the optimal policy has either bounded
discretion or no discretion. Here, as before, we can replace the
global incentive constraint in (38) with the
local incentive constraints, with the restriction that
![]() In
particular, Lemma 3 implies that
In
particular, Lemma 3 implies that
![]() is
continuous, while (16), the condition that
is
continuous, while (16), the condition that
![]() implies that for all
implies that for all ![]()
![]() is either
flat or equal to the static best response. Clearly, if
is either
flat or equal to the static best response. Clearly, if
![]() is flat
everywhere, it is a constant; hence, it equals the expected Ramsey
policy, which by definition is the best constant policy. If
is flat
everywhere, it is a constant; hence, it equals the expected Ramsey
policy, which by definition is the best constant policy. If
![]() is not flat
everywhere, then it must be of the following form for some
is not flat
everywhere, then it must be of the following form for some
![]() and
and
![]() :
:
| (40) | ![$\displaystyle \mu(\theta)=\left\{ \begin{array}[c]{c} \mu_{1}=\mu^{\ast}(\theta... ...theta_{2};x)\mbox{ if }\theta\in(\theta_{2},\bar{\theta}] \end{array} \right. ,$](img346.gif)
|
where
In the following proposition, we show that if the optimal policy
is not the expected Ramsey policy, then it must be of the form (
![]() with
with
![]() equal to
equal to
![]() , so
that the policy's form reduces to the bounded discretion form
(39).
, so
that the policy's form reduces to the bounded discretion form
(39).
Proposition 2: Under assumptions(A1) and (A2), the optimal policy
![]() has either bounded discretion or no discretion.
has either bounded discretion or no discretion.
Proof: We have argued that if the optimal policy is constant, then it must be an expected Ramsey policy, which has
no discretion. If the optimal policy is not constant, then it must
be of the form (
![]() But
But
![]() having the
form (40) with
having the
form (40) with
![]() cannot be optimal.
To see this, observe that an alternative policy
cannot be optimal.
To see this, observe that an alternative policy
![]() of
the same form would exist with
of
the same form would exist with
![]() and
and
![]() We illustrate this
alternative policy in Figure 4. This alternative policy
We illustrate this
alternative policy in Figure 4. This alternative policy
![]() would be closer to
would be closer to
![]() wherever it differs from
wherever it differs from
![]() and would
satisfy
and would
satisfy
![]() Hence, this alternative policy
Hence, this alternative policy
![]() would be strictly preferred to
would be strictly preferred to
![]() ; the change
from
; the change
from
![]() to
to
![]() directly improves welfare for all types
directly improves welfare for all types
![]() with
with ![]() held fixed. The
change also reduces
held fixed. The
change also reduces ![]() which
by (4) contributes to improving total
welfare. More formally, observe that the marginal impact on welfare
of a marginal reduction in
which
by (4) contributes to improving total
welfare. More formally, observe that the marginal impact on welfare
of a marginal reduction in
![]() is given by
is given by
![]() equal to
equal to
![$\displaystyle \int_{\underline{\theta}}^{\theta_{1}}\left[ R_{\mu}\mbox{{\large... ...\mu(\theta),\theta\mbox{{\large )}}\Delta x\mbox{{\large ]}}p(\theta)~d\theta, $](img360.gif)
B Implementing Optimal Policy with an Inflation Cap or a Range of Inflation Rates
We have characterized the solution to a dynamic mechanism design
problem. We now imagine implementing the resulting outcome with an
inflation cap, a highest allowable
level of inflation
![]() We imagine
that society legislates this highest allowable level and that doing
so restricts the monetary authority's choices to be
We imagine
that society legislates this highest allowable level and that doing
so restricts the monetary authority's choices to be
![]() If this cap is appropriately set and agents simply play the
repeated one-shot equilibrium of the resulting game with this
inflation cap, then the monetary authority will optimally choose
the outcome of the mechanism design problem. In this sense, the
repeated one-shot game with an inflation cap implements the policy
that solves the best payoff problem.
If this cap is appropriately set and agents simply play the
repeated one-shot equilibrium of the resulting game with this
inflation cap, then the monetary authority will optimally choose
the outcome of the mechanism design problem. In this sense, the
repeated one-shot game with an inflation cap implements the policy
that solves the best payoff problem.
The intuition for this result--that a policy with either bounded
discretion or no discretion can be implemented by setting an upper
limit on permissible inflation rates--is simple. In our
environment, the only potentially beneficial deviations from either
type of policy are ones that raise inflation. Under bounded
discretion, the types in
![]() are choosing their
static best response to wages and, hence, have no incentive to
deviate, whereas the types in
are choosing their
static best response to wages and, hence, have no incentive to
deviate, whereas the types in
![]() have an incentive to
deviate to a higher rate than
have an incentive to
deviate to a higher rate than
![]() Similarly,
from Proposition 3 (stated and proved below), we know that if the
expected Ramsey policy is optimal, then at this policy all types
have an incentive to deviate to higher rates of inflation. Hence,
an inflation cap of
Similarly,
from Proposition 3 (stated and proved below), we know that if the
expected Ramsey policy is optimal, then at this policy all types
have an incentive to deviate to higher rates of inflation. Hence,
an inflation cap of
![]() implements such a policy. (For completeness, we formalize this
argument in Appendix C.)
implements such a policy. (For completeness, we formalize this
argument in Appendix C.)
Clearly, we can also implement the optimal policy with a range
of inflation rates denoted
![]()
![]() The top
end of such a range is the inflation cap,
The top
end of such a range is the inflation cap,
![]() just
discussed. The bottom end of the range,
just
discussed. The bottom end of the range,
![]() , is
simply the optimal policy chosen by the lowest type
, is
simply the optimal policy chosen by the lowest type
![]() in
the optimal static mechanism. Under a policy of bounded discretion,
in
the optimal static mechanism. Under a policy of bounded discretion,
![]() while under a policy of
no discretion,
while under a policy of
no discretion,
![]() .
.
C Linking Discretion With Time Inconsistency and Private Information
So far we have shown that the optimal policy has either bounded discretion or no discretion and discussed how to implement such a policy. Here we link the optimal degree of discretion to the severity of the time inconsistency problem and the importance of private information. We show that the optimal degree of discretion shrinks as the time inconsistency problem becomes more severe and private information becomes less important.
The literature using general equilibrium models to study optimal
monetary policies suggests a qualitative way to measure the
severity of the time inconsistency problem. In most of this
literature, the time inconsistency problem is extremely severe, in
that the static Nash equilibrium is always at the highest feasible
inflation rate
![]() This result
follows because the static best response of the monetary authority
to any given level of expected inflation is always above that
level; thus, the monetary authority is always tempted to generate a
monetary surprise. Examples of the models with the more severe
problems are those of Ireland (1997); Chari, Christiano, and
Eichenbaum (1998); and Sleet (2001). In the rest of the literature,
the problem is less severe, in that the static Nash equilibrium is
interior. Examples of the models with the less severe problems are
those of Chang (1998), Nicolini (1998), and Albanesi, Chari, and
Christiano (2003).
This result
follows because the static best response of the monetary authority
to any given level of expected inflation is always above that
level; thus, the monetary authority is always tempted to generate a
monetary surprise. Examples of the models with the more severe
problems are those of Ireland (1997); Chari, Christiano, and
Eichenbaum (1998); and Sleet (2001). In the rest of the literature,
the problem is less severe, in that the static Nash equilibrium is
interior. Examples of the models with the less severe problems are
those of Chang (1998), Nicolini (1998), and Albanesi, Chari, and
Christiano (2003).
In our reduced-form model, we can mimic the general equilibrium
models with the more severe problems by choosing a payoff function
![]() for which
for which
![]() for all
for all ![]() That is, in response to any
choice of wages
That is, in response to any
choice of wages ![]() the
monetary authority wants to choose inflation higher than
the
monetary authority wants to choose inflation higher than
![]() , regardless of its
type. Under (A1), this condition is equivalent to requiring that
the static best response function satisfies
, regardless of its
type. Under (A1), this condition is equivalent to requiring that
the static best response function satisfies
![]() for all
for all
![]() ,
,
![]() . We show in
the next proposition that this condition implies that the optimal
policy has no discretion.
. We show in
the next proposition that this condition implies that the optimal
policy has no discretion.
We can mimic the general equilibrium models with less severe
problems by choosing a payoff function ![]() for which the static Nash
equilibrium best response is interior. For such a payoff function,
the optimal policy will typically depend on parameters. When the
time inconsistency problem is sufficiently mild, however, we can
show a general result: that optimal policy must have bounded
discretion. Here, by mild, we mean that when wages are set at the
expected Ramsey level, the lowest type wants to set inflation at
some level lower than the expected Ramsey level. Technically, we
can state this condition as that the static best response satisfies
for which the static Nash
equilibrium best response is interior. For such a payoff function,
the optimal policy will typically depend on parameters. When the
time inconsistency problem is sufficiently mild, however, we can
show a general result: that optimal policy must have bounded
discretion. Here, by mild, we mean that when wages are set at the
expected Ramsey level, the lowest type wants to set inflation at
some level lower than the expected Ramsey level. Technically, we
can state this condition as that the static best response satisfies
![]() or, equivalently, that the payoff function satisfies
or, equivalently, that the payoff function satisfies
![]()
We summarize this discussion in a proposition:
PROPOSITION 3: Assume
(A1) and (A2). Two
cases follow: (i) if the static best response satisfies
![]() for all
for all
![]() ,
,
![]() then the optimal policy has no discretion,
and (ii) if
the static best response satisfies
then the optimal policy has no discretion,
and (ii) if
the static best response satisfies
![]() , then the optimal policy has bounded
discretion.
, then the optimal policy has bounded
discretion.
PROOF: Under (A1) and (A2), the optimal mechanism is static. To prove (i), note that in any equilibrium with bounded discretion,
| (41) | ![$\displaystyle x=\int_{\underline{\theta}}^{\theta^{\ast}}\mu^{\ast}(\theta,x)p(\theta )d\theta+[1-P(\theta^{\ast})]\mu^{\ast}(\theta^{\ast},x).$](img385.gif)
|
Under
We prove (ii) by contradiction.
Assume that
![]() but that the optimal policy has no discretion. The variation used
in Proposition 2 immediately implies that such a policy cannot be
optimal. Thus, the optimal policy must have bounded discretion.
but that the optimal policy has no discretion. The variation used
in Proposition 2 immediately implies that such a policy cannot be
optimal. Thus, the optimal policy must have bounded discretion.
![]()
In Proposition ![]() we
have characterized the form of the optimal policy for two cases for
which this can be done independently of parameters. To characterize
the optimal policy in the remaining case (iii) in which
we
have characterized the form of the optimal policy for two cases for
which this can be done independently of parameters. To characterize
the optimal policy in the remaining case (iii) in which
![]() but there exists an
but there exists an ![]() such
that
such
that
![]() we return to
our benchmark example (1).
we return to
our benchmark example (1).
In general, the choice of the optimal inflation cap depends on
the importance of private information relative to the severity of
the time inconsistency problem. In our benchmark example, the
parameter ![]() indexes
the importance of private information, and the parameter
indexes
the importance of private information, and the parameter
![]() indexes the severity
of the time inconsistency problem. To see why
indexes the severity
of the time inconsistency problem. To see why ![]() indexes the importance of
private information, note that the Ramsey policy is
indexes the importance of
private information, note that the Ramsey policy is
![]() so that the slope of
the policy increases with
so that the slope of
the policy increases with ![]() . Hence, as
. Hence, as ![]() increases, the Ramsey policy responds more to
the private information
increases, the Ramsey policy responds more to
the private information ![]() , and the gap in welfare between the Ramsey
policy and the expected Ramsey policy grows. To see why
, and the gap in welfare between the Ramsey
policy and the expected Ramsey policy grows. To see why
![]() indexes the severity
of the time inconsistency problem, note that the Nash inflation
rate is
indexes the severity
of the time inconsistency problem, note that the Nash inflation
rate is ![]() , and
the Nash policies are
, and
the Nash policies are
![]() The Ramsey
inflation rate is
The Ramsey
inflation rate is ![]() and the Ramsey policies are
and the Ramsey policies are
![]() Thus, for each type
Thus, for each type
![]() the Nash
policies are simply the Ramsey policies shifted up by
the Nash
policies are simply the Ramsey policies shifted up by ![]() As
As ![]() gets smaller, the Nash policies converge to the
Ramsey policies. When
gets smaller, the Nash policies converge to the
Ramsey policies. When ![]() is zero, the Nash and Ramsey policies coincide.
is zero, the Nash and Ramsey policies coincide.
When the objective function satisfies (1), the
condition
![]() in Proposition 3 reduces to
in Proposition 3 reduces to
![]() , where
, where
![]() is
a negative number. Proposition 3 thus implies that bounded
discretion is optimal when private information is important
relative to the severity of the time inconsistency problem. We
characterize the optimal mechanism in the benchmark case more fully
in the next proposition, to get a more precise link between the
severity of the time inconsistency problem and the optimal degree
of discretion.
is
a negative number. Proposition 3 thus implies that bounded
discretion is optimal when private information is important
relative to the severity of the time inconsistency problem. We
characterize the optimal mechanism in the benchmark case more fully
in the next proposition, to get a more precise link between the
severity of the time inconsistency problem and the optimal degree
of discretion.
For policies of the bounded discretion form (39), we think of
![]() as
indexing the degree of discretion. If
as
indexing the degree of discretion. If
![]() then all types
then all types
![]() are on their
static best responses; hence, we say there is complete discretion.
As
are on their
static best responses; hence, we say there is complete discretion.
As
![]() decreases, fewer types are on their static best responses; hence,
we say there is less discretion. We then have this proposition:
decreases, fewer types are on their static best responses; hence,
we say there is less discretion. We then have this proposition:
PROPOSITION 4: Assume
(1), (A1), and (A2a).
If
![]() then the optimal policy has complete
discretion. If
then the optimal policy has complete
discretion. If
![]() then that policy has bounded discretion
with
then that policy has bounded discretion
with
![]() The optimal degree of discretion
The optimal degree of discretion
![]() is decreasing in
is decreasing in ![]() As
As ![]() approaches
approaches
![]() ,
the cutoff
,
the cutoff
![]() approaches
approaches
![]() .
If
.
If
![]() then the optimal policy is the expected Ramsey policy with
no discretion.
then the optimal policy is the expected Ramsey policy with
no discretion.
We prove this proposition in Appendix D. Figure 5 illustrates
the proposition for two economies with different degrees of
relative importance of private information and severity of time
inconsistency problems,
![]() . In these two
economies, we denote the optimal policies by
. In these two
economies, we denote the optimal policies by
![]() indexed
by
indexed
by
![]() and
and
![]() indexed
by
indexed
by
![]() ,
along with the inflation caps
,
along with the inflation caps
![]() and
and
![]()
4 Comparison to the Literature
Our result on the optimality of a static mechanism is quite different from what is typically found in dynamic contracting problems, that static mechanisms are not optimal. Using a recursive approach, we have shown how our dynamic mechanism design problem reduces to a simple quasi-linear mechanism design problem. Our result is thus also directly comparable to the large literature on mechanism design with broad applications, including those in industrial organization, public finance, and auctions. (See Fudenberg and Tirole's 1991 book for an introduction to mechanism design and its applications.) In this comparison, the continuation values in our framework correspond to the contractual compensation to the agent in the mechanism design literature. Our result that the optimal mechanism is static, so that the continuation values do not vary with type, stands in contrast to the standard result in the mechanism design literature that under the optimal contract, the compensation to the agent varies with the agent's type. In this sense, our result is also quite different from what is found in the mechanism design literature.
The key feature of our model that distinguishes it from much of the dynamic incentive literature is the feasibility constraint
| (42) |
The implication of this constraint is that in our model the continuation values of one type cannot be traded off against other types as they can be in many other models. To highlight the importance of this constraint, we consider a highly stylized example in Appendix E that replaces the constraint
| (43) | 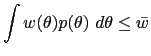 |
and show that the resulting optimal value of
A large class of dynamic incentive models include a feature like (43); they might usefully be thought of as debt models. Early versions of these include the private debt models of Green (1987), Thomas and Worrall (1990), Atkeson (1991), and Atkeson and Lucas (1992, 1995) while later versions include the government debt models of Sleet and Yeltekin (2003) and Sleet (2004). All of these models share the feature that optimal contracts are dynamic because in each of these settings a low continuation for one type can be traded off against a high continuation value for another type. In this sense, the debt models share many of the features of models with constraints of the form (43) rather than those with constraints of the form (42).
Having a constraint like (42) rather than (43) is important for our result that the optimal mechanism is static, but it is not sufficient, for at least two reasons. First, even in our model, we have given examples in which the optimal mechanism is dynamic when our monotone hazard condition is violated. Second, the information structure also matters. In our model, private agents receive no direct information about the state of the economy. If private agents receive a noisy signal about the state before the monetary authority takes its action, then our result goes through pretty much unchanged; the noisy signal is just a publicly observed variable upon which the inflation cap is conditioned. If, however, private agents receive a noisy signal about the information the monetary authority received after the monetary authority takes its action, then dynamic mechanisms in which continuation values vary with this signal may be optimal.
Sleet (2001) considers such an information structure and shows that the optimality of the dynamic mechanism depends on the parameters governing the noise. He finds that when the public signal about the monetary authority's information is sufficiently noisy, having the monetary authority's action depend on its private information is not optimal; hence, the optimal mechanism is static. In contrast, when this public signal is sufficiently precise, the optimal mechanism is dynamic. The logic of why a dynamic mechanism is optimal is roughly similar to that in the literature of industrial organization which follows Green and Porter (1984) on optimal collusive agreements that are supported by periodic reversion to price wars, even though these price wars lower all firms' profits.
Our work here is also related to some of the repeated game literature in industrial organization about supporting collusion in oligopolies. Athey and Bagwell (2001) and Athey, Bagwell, and Sanchirico (2004) solve for the best trigger strategy-type equilibria in games with hidden information about cost types. Athey and Bagwell (2001) show that, in general, the best equilibrium is dynamic (nonstationary). In this equilibrium, a firm which sets low prices gets a lower discounted value of profits from then on. Athey, Bagwell, and Sanchirico (2004) show that when strategies are restricted to be strongly symmetric, so that all firms receive the same continuation values even though they take observably different actions, a different result emerges. In particular, under some conditions, the best equilibrium is stationary and entails pooling of all cost types. When those conditions fail, and when firms are sufficiently patient, there may be a set of stationary and nonstationary equilibria that yield the same payoffs. (The latter result relies heavily on the Revenue Equivalence Theorem from auction theory.)
5 Conclusion
What is the optimal degree of discretion in monetary policy? For economies in which private information is not important and time inconsistency problems are severe, the optimal degree of discretion is zero. For economies in which private information is important and time inconsistency problems are less severe, it is not zero, but bounded. More generally, the optimal degree of discretion is decreasing the more severe is the time inconsistency problem and the less important is private information. For all of these economies, the optimal policy can be implemented by legislating and enforcing a simple inflation cap.
In our simple model, the optimal inflation cap is a single number because there is no publicly observed state. If the model were extended to have a publicly observed state, then the optimal policy would respond to this state, but not to the private information. To implement optimal policy, therefore, society would need to specify a rule for setting the inflation cap, where the cap would vary with public information. Equivalently, society could specify a rule for setting ranges for acceptable inflation, where these ranges would vary with public information. We interpret these rules as a type of inflation targeting that is broadly similar to the types actually practiced by a fair number of countries. (For a discussion of inflation targeting in practice, see Bernanke and Mishkin (1997).)
To keep our theoretical model simple, we have abstracted from exotic events which are both unforeseeable and unquantifiable. Anyone interpreting the implications of our results for an actual society, therefore, should keep in mind that to handle such exotic events, the optimal policy rule would need to be adapted to deal with them, perhaps by the addition of some type of escape clauses.
Appendix A: Proof of Lemma 3
Here we prove Lemma 3, that under (A1) and (A2), the optimal
allocation
![]() is continuous. The proof is by
contradiction.
is continuous. The proof is by
contradiction.
PROOF. In Lemma 2, we showed that in an optimal
allocation ![]() must be a step function. Thus, two types of potential
discontinuities in the allocation
must be a step function. Thus, two types of potential
discontinuities in the allocation
![]() must be ruled out. In the
first type,
must be ruled out. In the
first type,
![]() and,
potentially,
and,
potentially, ![]() jump
at some point
jump
at some point
![]() and are
both constant in some intervals
and are
both constant in some intervals
![]() and
and
![]() on either side of the jump
point
on either side of the jump
point
![]() In the
second type of discontinuity,
In the
second type of discontinuity,
![]() and
and
![]() both jump at
the point
both jump at
the point
![]() , and
, and
![]() is equal to
the static best response in some interval
is equal to
the static best response in some interval
![]() or
or
![]() on either side of the jump
point
on either side of the jump
point
![]()
Consider now the first type of discontinuity, when
![]() and
and
![]() are constant
on some intervals
are constant
on some intervals
![]() and
and
![]() on either side of the
point of discontinuity
on either side of the
point of discontinuity
![]() Let
Let
![]() denote
the allocation on
denote
the allocation on
![]() and
and
![]() denote
the allocation on
denote
the allocation on
![]() . By the continuity of
. By the continuity of
![]() , we can choose
the interval
, we can choose
the interval
![]() small enough so that if
small enough so that if
![]() is strictly
positive, then so is
is strictly
positive, then so is
![]() , and if
, and if
![]() is strictly
negative, then so is
is strictly
negative, then so is
![]()
Under these assumptions,
![]() is
increasing on the interval
is
increasing on the interval
![]() We next show
that if, for the chosen interval
We next show
that if, for the chosen interval
![]() the term
the term ![]() , defined in (36), is negative for small
, defined in (36), is negative for small ![]() then the up variation is feasible.
That this variation is feasible outside the interval
then the up variation is feasible.
That this variation is feasible outside the interval
![]() is clear from the proof of
Lemma 2. What needs to be proved is that this variation is also
feasible inside the interval
is clear from the proof of
Lemma 2. What needs to be proved is that this variation is also
feasible inside the interval
![]() Using essentially the same
argument, we show that if
Using essentially the same
argument, we show that if ![]() is positive for small
is positive for small ![]() then the down variation is
feasible. Hence, by the same logic as in the proof of Lemma 2, the
optimal allocation cannot have this first type of
discontinuity.
then the down variation is
feasible. Hence, by the same logic as in the proof of Lemma 2, the
optimal allocation cannot have this first type of
discontinuity.
Suppose that for the chosen interval
![]() the term
the term ![]() is negative for small
is negative for small
![]() Since
Since
![]() this
implies that
this
implies that
![]() Using the form of
Using the form of
![]() on the
interval
on the
interval
![]() , we have that
, we have that
| (44) | 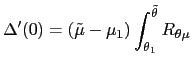 (
(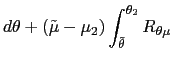 (
( |
To show that the up variation is feasible inside the interval
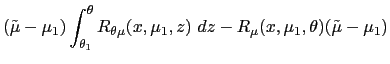 for
for | (45) | 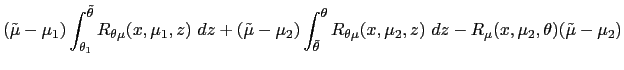 for
for |
Using
| (46) |  for
for |
| (47) | -R_{\mu }(x,\mu_{2},\tilde{\theta})(\tilde{\mu}-\mu_{2})$](img452.gif) for
for |
Consider first (46). By construction
Consider next (47). Note that we can rewrite (44) as
Now consider the second type of discontinuity, when
![]() is constant
on one side of
is constant
on one side of
![]() and
equal to the static best response on the other side of
and
equal to the static best response on the other side of
![]() .
Suppose, for example, that
.
Suppose, for example, that
![]() equals the
static best response for
equals the
static best response for ![]() on some interval
on some interval
![]() . Clearly,
. Clearly,
![]() is
increasing on the interval
is
increasing on the interval
![]() Since
Since
![]() jumps up at
jumps up at
![]() it
must be true that
it
must be true that
![]() (
(
![]() )
)
![]() (
(
![]() )
)![]() Hence, from
condition (17) in local
incentive-compatibility, we know that
Hence, from
condition (17) in local
incentive-compatibility, we know that
![]() Thus, for
Thus, for
![]()
![]() . Hence, either the up
variation or the down variation can be applied to this allocation
in the interval
. Hence, either the up
variation or the down variation can be applied to this allocation
in the interval
![]() as in the proof of Lemma
2, and thus, such an allocation cannot be optimal. With an
analogous argument, we can rule out the case in which
as in the proof of Lemma
2, and thus, such an allocation cannot be optimal. With an
analogous argument, we can rule out the case in which
![]() equals the
static best response for
equals the
static best response for ![]() on the other side of the jump point, on some
interval
on the other side of the jump point, on some
interval
![]() .
. ![]()
Appendix B: Optimal Policy without Monotone Hazards
Here we give three examples in which our monotone hazard
condition (A2) is violated and in which the optimal mechanism is
dynamic. In the first two examples, we assume that the hazard
![]() is decreasing in
is decreasing in ![]() at all points except the point
at all points except the point
![]() , where the
hazard jumps up. We also assume that
, where the
hazard jumps up. We also assume that
![]() is
increasing throughout. In the third example, we shed light on the
role of
is
increasing throughout. In the third example, we shed light on the
role of
![]() in (A2)
by assuming that the hazard
in (A2)
by assuming that the hazard
![]() is decreasing throughout but
that
is decreasing throughout but
that
![]() is not.
is not.
For the first two examples, assume that at the point
![]()
| (48) | 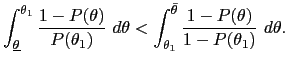
|
To interpret this inequality, note that the left side is the conditional mean of the function
It is easy to show that a two-piece uniform distribution with
![]() if
if
![]() and
and
![]() if
if
![]() will satisfy (48) if
will satisfy (48) if ![]() is chosen to be sufficiently
small relative to
is chosen to be sufficiently
small relative to ![]() In this case, illustrated in Figure 6, the
function
In this case, illustrated in Figure 6, the
function
![]() will jump up sufficiently at
will jump up sufficiently at
![]() so that the
conditional mean of this function over the higher interval
so that the
conditional mean of this function over the higher interval
![]() is larger than the
conditional mean over the lower interval
is larger than the
conditional mean over the lower interval
![]()
In the first example, the linear
example, we make the calculations trivial by assuming that
![]() with
with
![]() . In the
second example, which is the benchmark
example of (1), we assume that
. In the
second example, which is the benchmark
example of (1), we assume that
| (49) | ![$\displaystyle R(x,\mu,\theta)=-\frac{1}{2}\left[ (U+x-\mu)^{2}+(\mu-\alpha\theta )^{2}\right] .$](img489.gif)
|
In the third example, the discrete example,
All three of these examples satisfy the single-crossing property
(A1). In the first two examples,
![]() , so
that the condition (A2) reduces to the standard monotone hazard
condition. Note that for the first two examples, any distribution
that satisfies (
, so
that the condition (A2) reduces to the standard monotone hazard
condition. Note that for the first two examples, any distribution
that satisfies (
![]() is
inconsistent with the monotone hazard condition (A2a).
is
inconsistent with the monotone hazard condition (A2a).
The Linear Example
Any solution to the mechanism design problem must have the two-piece form
| (50) | ![$\displaystyle (\mu(\theta),w(\theta))=\left\{ \begin{array}[c]{cc} (\mu_{1},w_{... ...)\mbox{ \ for} & \theta\in\lbrack\theta_{1},\bar{\theta}] \end{array} \right. .$](img493.gif)
|
This follows because the arguments used in Lemmas 1 and 2 can be applied separately to the intervals
The mechanism design problem then reduces to the linear problem
of choosing ![]() ,
,
![]() , and
, and
![]() to maximize
to maximize
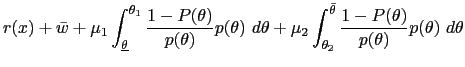
| (51) | ![$\displaystyle \left[ -\int_{\underline{\theta}}^{\theta_{1}}\frac{1-P(\theta)}{... ...}\frac{1-P(\theta)} {1-P(\theta_{1})}~d\theta\right] P(\theta_{1})\Delta_{1}>0,$](img514.gif)
|
where the inequality follows from (
The Benchmark Example
Now assume that the policy
![]() which
solves the static mechanism design problem, has bounded discretion
and that
which
solves the static mechanism design problem, has bounded discretion
and that
![]() so that the jump point
in the hazard occurs on the flat portion of that policy. (We can
construct a numerical example in which this assumption holds.) We
will show that there is a dynamic mechanism that improves on the
optimal static mechanism. The basic idea is to use a variation that
spreads out the inflation schedule as a function of type instead of
flattens it as did the variation in Lemmas 1 and 2.
so that the jump point
in the hazard occurs on the flat portion of that policy. (We can
construct a numerical example in which this assumption holds.) We
will show that there is a dynamic mechanism that improves on the
optimal static mechanism. The basic idea is to use a variation that
spreads out the inflation schedule as a function of type instead of
flattens it as did the variation in Lemmas 1 and 2.
This variation is similar to the one in the linear example.
Consider an alternative policy that lowers inflation for types at
or below
![]() raises it
for types above
raises it
for types above
![]() , and keeps
expected inflation constant:
, and keeps
expected inflation constant:
![\begin{displaymath} \tilde{\mu}(\theta)=\left\{ \begin{array}[c]{cc} \mu(\theta)... ...a)+\Delta_{1} & \mbox{if }\theta>\theta_{1} \end{array}\right. \end{displaymath}](img519.gif)
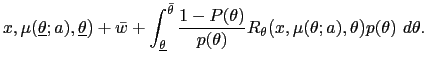
| (52) | 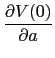 |
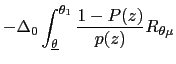 (
( |
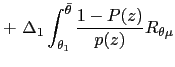 (
( |
Since
It is straightforward, but somewhat tedious, to show that the
associated continuation values
![]() defined by
defined by
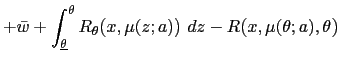
Note that if
![]() has no
discretion, then we need a different condition on the distribution
to show that the static mechanism is not optimal. This is because
when
has no
discretion, then we need a different condition on the distribution
to show that the static mechanism is not optimal. This is because
when
![]() has no
discretion, we can have
has no
discretion, we can have ![]() (
(
![]() )
) ![]() , and
the above argument that
, and
the above argument that
![]() for
all
for
all ![]() does not go
through. When
does not go
through. When
![]() has no
discretion, the analog of the condition (48) is that at
has no
discretion, the analog of the condition (48) is that at
![]() there
exists a
there
exists a
![]() such that
such that
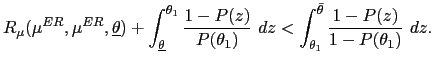
The Discrete Example
Now let the types be
![]() for
for
![]() with
associated probabilities
with
associated probabilities ![]() , and let
, and let
![]() Then it is easy to show
that under the discrete analog of (A1), the only relevant incentive
constraints are
Then it is easy to show
that under the discrete analog of (A1), the only relevant incentive
constraints are
| (53) |
for
![$\displaystyle \frac{1-P_{1}}{p_{2}}\left[ R_{\mu}(x,\mu_{2},\theta_{2})-R_{\mu}... ...}}\left[ R_{\mu}(x,\mu _{3},\theta_{3})-R_{\mu}(x,\mu_{3},\theta_{2})\right] , $](img553.gif)
| (54) | ![$\displaystyle \frac{1-P_{1}}{p_{2}}\left[ g(\theta_{2})-g(\theta_{1})\right] >\frac{1-P_{2}}{p_{3}}\left[ g(\theta_{3})-g(\theta_{2})\right] .$](img554.gif)
|
We now give an example in which the hazard (
![]() is
monotone but
is
monotone but ![]() is so
convex that (54) is violated, and the optimal
policy is dynamic. Suppose that
is so
convex that (54) is violated, and the optimal
policy is dynamic. Suppose that
![]() is
part of a candidate optimal policy. Consider the variation of
decreasing
is
part of a candidate optimal policy. Consider the variation of
decreasing ![]() and
and
![]() by
by
![]() and increasing
and increasing
![]() by (
by (
![]() , so that expected inflation
, so that expected inflation
![]() is constant. We can
maintain incentives by keeping
is constant. We can
maintain incentives by keeping ![]() and
and ![]() unchanged and lowering
unchanged and lowering ![]() by
by
![]() This variation leads to a
change in welfare of
This variation leads to a
change in welfare of
In Sum
In each of the three examples, we have shown that welfare could be improved relative to a static policy by raising inflation for high types and lowering inflation for low types so as to keep expected inflation constant. In the first two examples, this improved welfare because there were sufficiently few high types relative to low types; we could raise inflation a lot for the types who valued it more and lower it only a little for the types who valued it less. In the third example, even though the distribution of types is uniform, the high types valued inflation so much more than the low types that raising inflation for the high types and lowering it for the low types still improved welfare.
Appendix C: Implementation with an Inflation Cap
Here we prove that the equilibrium outcome in an economy with an inflation cap is the optimal outcome of the mechanism design problem. We show this result formally using a one-shot game in which we drop time subscripts.
With an inflation cap of ![]() in the current period, the problem of the
monetary authority at a given
in the current period, the problem of the
monetary authority at a given ![]() is, given aggregate wages
is, given aggregate wages ![]() , to choose money growth
, to choose money growth
![]() for the
state
for the
state ![]() to maximize
to maximize
![]() subject to
subject to
![]() The private agents'
decisions on wages are summarized by
The private agents'
decisions on wages are summarized by
![]()
An equilibrium of this one-shot game consists of aggregate wages
![]() and a money growth
policy
and a money growth
policy
![]() such that
(i) with
such that
(i) with ![]() given,
given,
![]() satisfies
satisfies
![]() , and (ii)
, and (ii)
![]() We denote the optimal
choice of the monetary authority as
We denote the optimal
choice of the monetary authority as
![]() This notation reflects
the fact that the monetary authority is choosing a static best
response to
This notation reflects
the fact that the monetary authority is choosing a static best
response to ![]() given that
its choice set is restricted by
given that
its choice set is restricted by ![]() , which we call the inflation cap.
, which we call the inflation cap.
To implement the best equilibrium in the dynamic game, we choose
![]() as follows.
Whenever the expected Ramsey policy is optimal, we choose the
inflation cap to be
as follows.
Whenever the expected Ramsey policy is optimal, we choose the
inflation cap to be
| (55) |
Whenever bounded discretion is optimal, we choose the cap to be the money growth rate chosen by the cutoff type
| (56) |
where
PROPOSITION 5: Assume
(A1), (A2), and that the inflation cap
![]() is set according to (55)
and (56).
Then the equilibrium outcome of the one-shot
game with the inflation cap for each period coincides with the
optimal equilibrium outcome of the dynamic game.
is set according to (55)
and (56).
Then the equilibrium outcome of the one-shot
game with the inflation cap for each period coincides with the
optimal equilibrium outcome of the dynamic game.
PROOF: We establish this result in two steps. We
first show that the monetary authority will choose the upper bound
![]() when the expected Ramsey policy is optimal in the dynamic game.
Note that Proposition 3 implies that whenever the expected Ramsey
policy is optimal,
when the expected Ramsey policy is optimal in the dynamic game.
Note that Proposition 3 implies that whenever the expected Ramsey
policy is optimal,
![]() Also, recall that the single-crossing assumption (A1) implies that
the best response is strictly increasing in
Also, recall that the single-crossing assumption (A1) implies that
the best response is strictly increasing in ![]() . Thus,
. Thus,
![]() for all
for all ![]() Hence, at the expected Ramsey policy and the associated inflation
rate, all types want to deviate by increasing their inflation above
Hence, at the expected Ramsey policy and the associated inflation
rate, all types want to deviate by increasing their inflation above
![]() ; hence, the
constraint
; hence, the
constraint
![]() binds, and all types choose the expected Ramsey level.
binds, and all types choose the expected Ramsey level.
We next show that if bounded discretion is optimal in the
dynamic game, then in the associated static game with the inflation
cap, all types choose the bounded discretion policies. For all
types
![]() the policies under bounded
discretion are simply the static best responses, and these clearly
coincide with those in the static game. For all types
the policies under bounded
discretion are simply the static best responses, and these clearly
coincide with those in the static game. For all types ![]() above
above
![]() the
policies under bounded discretion are the static best responses of
the
the
policies under bounded discretion are the static best responses of
the
![]() type,
namely,
type,
namely,
![]() , where
, where ![]() is the equilibrium expected
inflation rate under bounded discretion. Under assumption (A1), the
static best responses are increasing in the type, so that the best
response of any type
is the equilibrium expected
inflation rate under bounded discretion. Under assumption (A1), the
static best responses are increasing in the type, so that the best
response of any type
![]() is above
is above
![]() Thus, in the one-shot
game with the inflation cap, the constraint (56)
binds for such types. Thus, the equilibrium outcomes of the two
games coincide.
Thus, in the one-shot
game with the inflation cap, the constraint (56)
binds for such types. Thus, the equilibrium outcomes of the two
games coincide.
![]()
Appendix D: Proof of Proposition 4
Here we prove Proposition 4, which links monetary policy discretion to both time inconsistency and private information.
PROOF: The optimal policy with bounded discretion
is found as the solution to the problem of choosing
![]() and
and
![]() to maximize
to maximize
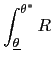 (
(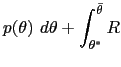 (
(| (57) | 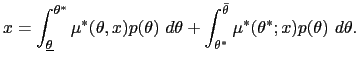
|
Let
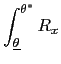 (
(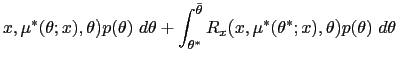
![$\displaystyle +\left[ \int_{\theta^{\ast}}^{\bar{\theta}}R_{\mu}\mbox{{\large (... ...rac{\partial\mu^{\ast}(\theta^{\ast},x)}{\partial x}p(\theta)~d\theta\right] . $](img593.gif)
| (58) | ![$\displaystyle \left[ \int_{\theta^{\ast}}^{\bar{\theta}}\mbox{{\large (}}\theta... ... ~d\theta\right] \left[ 1-\frac{P(\theta^{\ast})}{2}\right] -\frac{U} {\alpha}.$](img594.gif)
|
We can show that, under (A2a), this derivative is strictly decreasing in
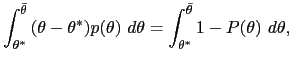
![$\displaystyle \left[ \int_{\theta^{\ast}}^{\bar{\theta}}\frac{1-P(\theta)}{p(\t... ...~d\theta\right] \left[ 1-\frac {P(\theta^{\ast})}{2}\right] -\frac{U}{\alpha}, $](img596.gif)
The fact that (58) is strictly decreasing in
![]() implies
that three possible cases characterize the optimal policy with
bounded discretion, all of which depend on the value of
implies
that three possible cases characterize the optimal policy with
bounded discretion, all of which depend on the value of
![]() In one case,
the derivative (58) is positive for all
In one case,
the derivative (58) is positive for all
![]() , and the
solution is
, and the
solution is
![]() Since the first term of
(58) equals zero when
Since the first term of
(58) equals zero when
![]() this case occurs only
when
this case occurs only
when
![]() As is
clear, in this case, there is no time inconsistency problem, and
the Ramsey policy is incentive-compatible. In a second case, the
derivative (58) is negative for all
As is
clear, in this case, there is no time inconsistency problem, and
the Ramsey policy is incentive-compatible. In a second case, the
derivative (58) is negative for all
![]() , and the
solution is
, and the
solution is
![]() Since the derivative
(58) evaluated at
Since the derivative
(58) evaluated at
![]() reduces to
reduces to
![]() this case occurs when
this case occurs when
![]() Note that in
this case, the optimal policy with bounded discretion specifies a
constant inflation rate and, hence, is dominated, at least weakly,
by the expected Ramsey policy with no discretion. Hence, we say
that in this case, the optimal policy has no discretion. In the
third case, there is an interior
Note that in
this case, the optimal policy with bounded discretion specifies a
constant inflation rate and, hence, is dominated, at least weakly,
by the expected Ramsey policy with no discretion. Hence, we say
that in this case, the optimal policy has no discretion. In the
third case, there is an interior
![]() that
sets the derivative (58) to zero. This case
occurs when
that
sets the derivative (58) to zero. This case
occurs when
![]() Clearly, in this
case, the value of
Clearly, in this
case, the value of
![]() characterizing the optimal degree of discretion is decreasing in
characterizing the optimal degree of discretion is decreasing in
![]()
Finally, to complete the proof of Proposition 4, we must show
that when
![]() the optimal
policy with bounded discretion dominates the expected Ramsey
policy. To do so, we use part (ii) of
Proposition 3. Note that when
the optimal
policy with bounded discretion dominates the expected Ramsey
policy. To do so, we use part (ii) of
Proposition 3. Note that when
![]() , we have that
, we have that
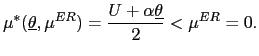
Appendix E: The Role of Our feasibility Constraint
Here we develop a highly stylized example (about traffic congestion) that illustrates the importance of the feasibility constraint
| (59) |
in generating our result that the optimal policy is static. In the example, we replace this constraint with the constraint
| (60) | 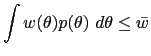 |
and show that the resulting optimal mechanism differs radically from ours.
To be concrete, consider a mechanism design problem of choosing
![]() and
and
![]() to solve
to solve
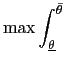 [
[| (61) |
| (62) | 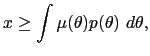 |
and
It is easy to see that here the optimal ![]() varies with
varies with ![]() Specifically,
Specifically, ![]() can be chosen in such a way
as to support the first best. (Here we are assuming (A1), so that
the first best schedule for
can be chosen in such a way
as to support the first best. (Here we are assuming (A1), so that
the first best schedule for
![]() is
upward-sloping. To see this result, drop the incentive constraint
(61) and solve for the first best
is
upward-sloping. To see this result, drop the incentive constraint
(61) and solve for the first best
![]() ;
then use the local incentive-compatibility condition to construct
the
;
then use the local incentive-compatibility condition to construct
the
![]() function, up to the constant
function, up to the constant
![]() , that makes
, that makes
![]() incentive-compatible. Finally,
choose the constant
incentive-compatible. Finally,
choose the constant
![]() to satisfy (60).) Clearly, the answer to this problem is very
different from the answer to our problem; here the optimal
to satisfy (60).) Clearly, the answer to this problem is very
different from the answer to our problem; here the optimal
![]() varies with
varies with
![]() while in ours
it does not and
while in ours
it does not and
![]()
Note that the result that the first best is incentive-compatible
is special to this functional form in which payoffs are linear in
![]() If instead we had
If instead we had
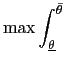 [
[How could we interpret our model and results in this road
congestion context? Suppose that using tolls is not feasible, and
the only way to ration road use is to make people wait to get on
the road. Let
![]() be the
amount of time someone has to wait to drive
be the
amount of time someone has to wait to drive
![]() and let
and let
![]() be the associated utility
from waiting
be the associated utility
from waiting
![]() Then
Then
![]() is, of
course, equivalent to
is, of
course, equivalent to
![]() In this context, we get a very different answer than when using
tolls is feasible. Under (A1) and (A2), the optimal scheme is to
have no one wait (
In this context, we get a very different answer than when using
tolls is feasible. Under (A1) and (A2), the optimal scheme is to
have no one wait (
![]() and let
everyone drive as much as they like, subject to a cap,
and let
everyone drive as much as they like, subject to a cap,
![]()
References
ABREU, D., D. PEARCE, and E. STACCHETTI (1990): `` Toward a Theory of Discounted Repeated Games with Imperfect Monitoring,'' Econometrica, 58, 1041-1063.
ALBANESI, S., V. CHARI, and L. CHRISTIANO (2003): `` Expectation Traps and Monetary Policy,'' Review of Economic Studies, 70, 715-741.
ALBANESI, S., and C. SLEET (2002): `` Optimal Policy with Endogenous Fiscal Constitutions,'' Manuscript, Fuqua School of Business, Duke University.
AMADOR, M., I. WERNING, and G. ANGELETOS (2004): `` Commitment vs. Flexibility,'' Manuscript, Massachusetts Institute of Technology.
ANGELETOS, G., C. HELLWIG, and A. PAVAN (2003): `` Coordination and Policy Traps,'' NBER Working Paper 9767.
ATHEY, S., and K. BAGWELL (2001): `` Optimal Collusion with Private Information,'' RAND Journal of Economics, 32, 428-465.
ATHEY, S., K. BAGWELL, and C. SANCHIRICO (2004): `` Collusion and Price Rigidity,'' Review of Economic Studies, 71, 317-349.
ATKESON, A. (1991): `` International Lending with Moral Hazard and Risk of Repudiation,'' Econometrica, 59, 1069-1089.
ATKESON, A., and R. LUCAS (1992): `` On Efficient Distribution with Private Information,'' Review of Economic Studies, 59, 427-453.
----- (1995): `` Efficiency and Equality in a Simple Model of Efficient Unemployment Insurance,'' Journal of Economic Theory, 66, 64-88.
BACKUS, D., and J. DRIFFILL (1985): `` Inflation and Reputation,'' American Economic Review, 75, 530-538.
BARRO, R., and D. GORDON (1983): `` Rules, Discretion and Reputation in a Model of Monetary Policy,'' Journal of Monetary Economics, 12, 101-121.
BERNANKE, B., and F. MISHKIN (1997): `` Inflation Targeting: A New Framework for Monetary Policy?'' Journal of Economic Perspectives, 11, 97-116.
BERNANKE, B., and M. WOODFORD (1997): `` Inflation Forecasts and Monetary Policy,'' Journal of Money, Credit, and Banking, 39, 653-684.
CANZONERI, M. (1985) `` Monetary Policy Games and the Role of Private Information,'' American Economic Review, 75, 1056-1070.
CHANG, R. (1998): `` Credible Monetary Policy in an Infinite Horizon Model: Recursive Approaches,'' Journal of Economic Theory, 81, 431-461.
CHARI, V., L. CHRISTIANO, and M. EICHENBAUM (1998): `` Expectation Traps and Discretion,'' Journal of Economic Theory, 81, 462-492.
CHARI, V., and P. KEHOE (1990): `` Sustainable Plans,'' Journal of Political Economy, 98, 783-802.
CUKIERMAN, A., and A. MELTZER (1986): `` A Theory of Ambiguity, Credibility, and Inflation under Discretion and Asymmetric Information,'' Econometrica, 54, 1099-1128.
DA COSTA, C., and I. WERNING (2002): `` On the Optimality of the Friedman Rule with Heterogeneous Agents and Non-Linear Income Taxation,'' Manuscript, Massachusetts Institute of Technology.
FAUST, J., and L. SVENSSON (2001): `` Transparency and Credibility: Monetary Policy with Unobservable Goals,'' International Economic Review, 42, 369-397.
FUDENBERG, D., and J. TIROLE (1991): Game Theory. Cambridge, Mass.: MIT Press.
GREEN, E. (1987): `` Lending and the Smoothing of Uninsurable Income,'' in Contractual Arrangements for Intertemporal Trade. Minneapolis: University of Minnesota Press.
GREEN, E., and R. PORTER (1984): `` Noncooperative Collusion under Imperfect Price Information,'' Econometrica, 52, 87-100.
IRELAND, P. (1997): `` Sustainable Monetary Policies,'' Journal of Economic Dynamics and Control, 22, 87-108.
----- (2000): `` Expectations, Credibility, and Time-Consistent Monetary Policy,'' Macroeconomic Dynamics, 4, 448-466.
KOCHERLAKOTA, N. (1996): `` Implications of Efficient Risk Sharing without Commitment,'' Review of Economic Studies, 63, 595-609.
KYDLAND, F., and E. PRESCOTT (1977): `` Rules Rather Than Discretion: The Inconsistency of Optimal Plans,'' Journal of Political Economy, 85, 473-491.
NICOLINI, J. (1998): `` More on the Time Consistency of Monetary Policy,'' Journal of Monetary Economics, 41, 333-350.
PERSSON, T., and G. TABELLINI (1993): `` Designing Institutions for Monetary Stability,'' Carnegie-Rochester Conference Series on Public Policy,'' 39, 53-84.
PHELAN, C., and E. STACCHETTI (2001): `` Sequential Equilibria in a Ramsey Tax Model,'' Econometrica, 69, 1491-1518.
RAMPINI, A. (Forthcoming): `` Default and Aggregate Income,'' Journal of Economic Theory.
ROMER, C., and D. ROMER (2000): `` Federal Reserve Information and the Behavior of Interest Rates,'' American Economic Review, 90, 429-457.
SLEET, C. (2001): `` On Credible Monetary Policy and Private Government Information,'' Journal of Economic Theory, 99, 338-376.
----- (2004): `` Optimal Taxation with Private Government Information,'' Review of Economic Studies, 71, 1217-1239.
SLEET, C., and S. YELTEKIN (2003): `` Credible Monetary Policy with Private Government Preferences,'' Manuscript, Kellogg School of Management, Northwestern University.
STOKEY, N. (2003): ```Rules versus Discretion' After Twenty-Five Years,'' in NBER Macroeconomics Annual 2002, vol. 17, ed. by M. Gertler and K. Rogoff. Cambridge, Mass.: MIT Press.
TAYLOR, J. (1983): `` Rules, Discretion and Reputation in a Model of Monetary Policy: Comments,'' Journal of Monetary Economics, 12, 123-125.
THOMAS, J., and T. WORRALL (1990): `` Income Fluctuation and Asymmetric Information: An Example of a Repeated Principal-Agent Problem,'' Journal of Economic Theory, 51, 367-390.
WALSH, C. (1995): `` Optimal Contracts for Central Bankers,'' American Economic Review, 85, 150-167.
Figure 1
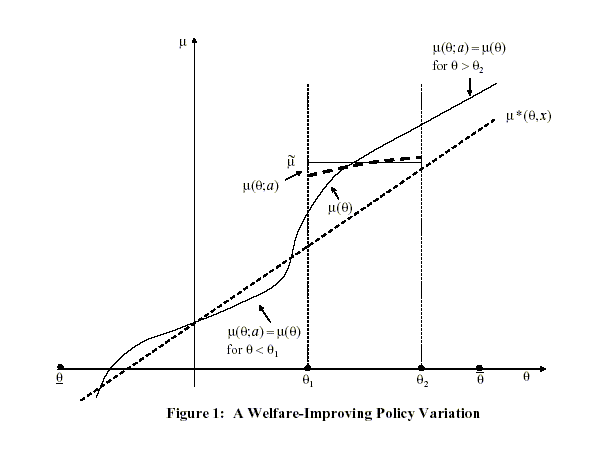
Figure 2
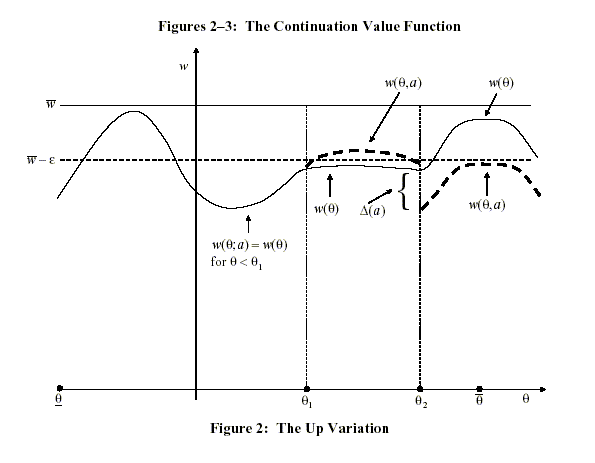
Figure 3
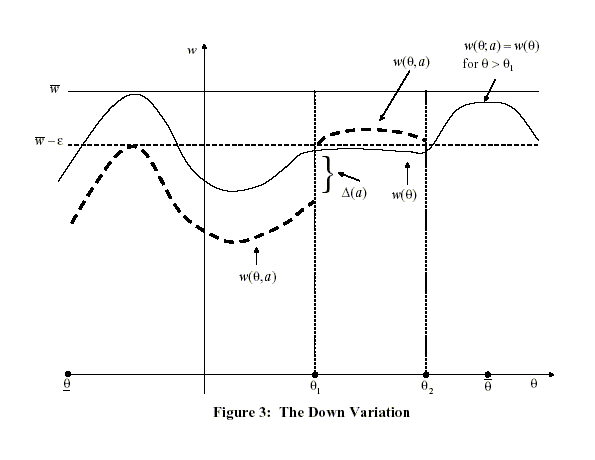
Figure 4
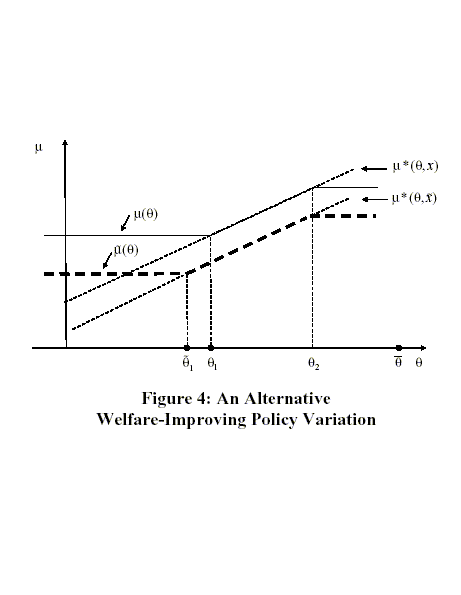
Figure 5
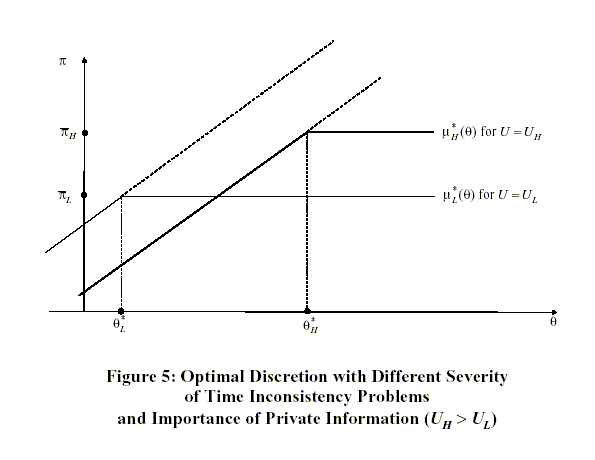
Figure 6
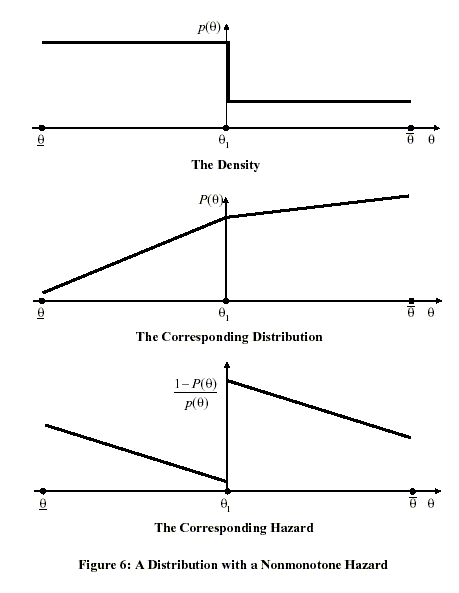
Footnotes
1. The authors thank the editor and the referees for very useful comments, Kathy Rolfe for excellent editorial assistance, and the NSF for generous financial assistance. The views expressed are those of the authors and not necessarily those of the Federal Reserve Bank of Minneapolis or the Federal Reserve System. Return to text
2. Our approach here is different from that in the early literature on rules vs. discretion, as is our notion of discretion. The early literature assumes that society has no mechanism for committing to rules governing monetary policy. As does Taylor (1983), we find the legislative approach more appealing for advanced economies. Return to text
3. For some potential empirical support for the idea that the Federal Reserve possesses some nontrivial private information, see the work of Romer and Romer (2000). As we discuss below, we interpret this private information in our economy along the lines of Sleet and Yeltekin (2003) and Sleet (2004). Return to text
4. Note that the inflation rate that
enters the period ![]() social
welfare function is the current inflation rate, that from period
social
welfare function is the current inflation rate, that from period
![]() to period
to period
![]() As has often been
noted, this formulation captures the distortions in a sticky price
model with multiple sectors. As the current inflation rate rises or
falls, the prices of goods in sectors that can currently change
prices rise or fall relative to the prices in sectors that cannot.
Movements in the current inflation rate thus create resource
allocation distortions.
As has often been
noted, this formulation captures the distortions in a sticky price
model with multiple sectors. As the current inflation rate rises or
falls, the prices of goods in sectors that can currently change
prices rise or fall relative to the prices in sectors that cannot.
Movements in the current inflation rate thus create resource
allocation distortions.
Also, for simplicity, our formulation abstracts from direct costs due to future inflation. One interpretation of this feature is that it captures what happens in the cashless limit of a sticky price model. Return to text
5. For a discussion of the large class of environments for which this restriction does not alter the set of equilibrium payoffs, see Fudenberg and Tirole's 1991 text. Return to text
6. For details of why this is true, see the work of Chari and Kehoe (1990). Return to text
7. Note that this definition of
increasing is stronger than the
definition of a function weakly
increasing on an interval because our definition rules out a
function that is constant over the interval. But our definition is
weaker than the definition of a function strictly increasing over an interval because ours
allows for subintervals over which
![]() is
constant. Return to text
is
constant. Return to text
8. Note that the best policy with no
discretion, the expected Ramsey policy,
will not typically be a special case of a policy with bounded
discretion. Specifically, when
![]() , the form (39) yields one particular policy with no discretion:
, the form (39) yields one particular policy with no discretion:
![]() for all
for all
![]() . But this policy
does not typically coincide with the expected Ramsey policy
. But this policy
does not typically coincide with the expected Ramsey policy
![]() since the
best response of the lowest type is not typically the expected
Ramsey policy. Return to text
since the
best response of the lowest type is not typically the expected
Ramsey policy. Return to text
This version is optimized for use by screen readers. A printable pdf version is available.