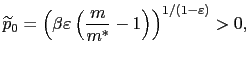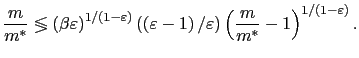Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 802, April 2004--Screen Reader Version*
Monetary Discretion, Pricing Complementarity and Dynamic Multiple Equilibria
International Finance Discussion Papers numbers 797-807 were presented on November 14-15, 2003 at the second conference sponsored by the International Research Forum on Monetary Policy sponsored by the European Central Bank, the Federal Reserve Board, the Center for German and European Studies at Georgetown University, and the Center for Financial Studies at the Goethe University in Frankfurt.
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
In a plain-vanilla New Keynesian model with two-period staggered price-setting, discretionary monetary policy leads to multiple equilibria. Complementarity between the pricing decisions of forward-looking firms underlies the multiplicity, which is intrinsically dynamic in nature. At each point in time, the discretionary monetary authority optimally accommodates the level of predetermined prices when setting the money supply because it is concerned solely about real activity. Hence, if other firms set a high price in the current period, an individual firm will optimally choose a high price because it knows that the monetary authority next period will accommodate with a high money supply. Under commitment, the mechanism generating complementarity is absent: the monetary authority commits not to respond to future predetermined prices. Multiple equilibria also arise in other similar contexts where (i) a policymaker cannot commit, and (ii) forward-looking agents determine a state variable to which future policy responds.
Keywords: monetary policy, discretion, time-consistency, multiple equilibria, complementarity
JEL Classification: E5, E61, D78
Non-technical summary
In the debate over rules versus discretion for monetary policy, the primary argument against discretion has been that it leads to higher average inflation than is optimal with commitment. In the consensus basic model which has developed following Kydland and Prescott [1977] and Barro and Gordon [1983], the discretionary monetary authority seeks to produce unexpected inflation to stimulate real output, which is inefficiently low because of distortions in the economy. But since it cannot fool agents in rational expectations equilibrium, the discretionary monetary authority produces expected inflation that has a negligible real effect on output, while imposing other costs on the economy.
By contrast, this paper provides an example of a different, potentially adverse, consequence of discretionary monetary policy: it can lead to multiple equilibria and, thus, to the possibility of endogenous fluctuations in inflation and real activity that are not related to the economy's fundamentals. We illustrate this possibility within a simple dynamic macroeconomic model that has important New Keynesian features: (i) monopolistic competition, making output inefficiently low; and (ii) a staggered pricing structure in which firms set nominal prices that must be held fixed for two periods. These two features give the monetary authority some leverage over real activity.
In this simple setting, the multiplicity of equilibria derives from interaction between two features of the economy. First, firms adopt forward-looking pricing rules because their nominal prices are held fixed for two periods. In choosing a price, firms in the current period need to form expectations about the behavior of the monetary authority - and firms - in the next period. A higher future money supply leads to a higher future nominal marginal cost, which raises the optimal price for a firm in the current period. Second, under discretion, the monetary authority takes as given prices set in previous periods in determining its choice of the money stock in each period. Since its concern is to maximize the welfare of the representative agent, which depends on real variables, it chooses a money stock that is proportional to the price set by firms in the previous period, which we call a homogenous money stock rule.
The combination of forward-looking pricing with discretionary policy leads to complementarity between the price-setting actions of firms: if all other firms set a higher price in the current period, the monetary authority will set a higher money supply in the subsequent period, raising the desired price for a single firm in the current period.
We show that this policy-induced complementarity implies that there are typically two private-sector equilibria which can prevail at any point in time and two steady-state equilibria. In general, there is one equilibrium in which firms expect small adjustments and the newly set price is relatively close to the price that firms set last period. But there is another in which the adjusting firms make a much larger adjustment.
Because this multiplicity of equilibria arises for arbitrary homogenous monetary policies, it also arises with an optimizing monetary authority who cannot commit to future actions. We begin by considering settings of perfect foresight, in which the monetary authority and private agents each assume that only one of the two types of private sector equilibria will occur. We show that there are two steady-state discretionary equilibria, one with low inflation bias and one with high inflation bias. It is notable that the complementarity which generates multiple equilibria is entirely due, in our model, to the nature of monetary policy under discretion. That is: our specification of preferences and the labor market is such that there is no complementarity in the price-setting behavior of firms if the central bank maintains a fixed nominal money stock. Our setup thus highlights the role of discretionary monetary policy in generating complementarity.
While our results concern the interaction between a monetary policymaker and a forward-looking private sector that sets prices for only two periods, they are indicative of a more general phenomenon, both in the context of monetary policy and in other areas of economics. The necessary features for the kind of phenomenon we describe are as follows: (i) a policymaker that cannot commit to future actions, and (ii) forward-looking private agents whose current actions determine a state-variable to which the policymaker responds in the future. These features seem quite widespread, suggesting that lack of commitment may be an important cause of economic instability.
1 Introduction
In the debate over rules versus discretion for monetary policy, the primary argument against discretion has been that it leads to higher average inflation than is optimal with commitment. In the consensus basic model which has developed following Kydland and Prescott [1977] and Barro and Gordon [1983], the discretionary monetary authority seeks to produce unexpected inflation to stimulate real output, which is inefficiently low because of distortions in the economy. But since it cannot fool agents in rational expectations equilibrium, the discretionary monetary authority produces expected inflation that has a negligible real effect on output, while imposing other costs on the economy.
By contrast, this paper provides an example of a different, potentially adverse, consequence of discretionary monetary policy: it can lead to multiple equilibria and, thus, to the possibility of endogenous fluctuations in inflation and real activity that are not related to the economy's fundamentals. We illustrate this possibility within a simple dynamic macroeconomic model that has important New Keynesian features: (i) monopolistic competition, making output inefficiently low; and (ii) a staggered pricing structure in which firms set nominal prices that must be held fixed for two periods. These two features give the monetary authority some leverage over real activity.
In this simple setting, the multiplicity of equilibria derives from interaction between two features of the economy. First, firms adopt forward-looking pricing rules because their nominal prices are held fixed for two periods. In choosing a price, firms in the current period need to form expectations about the behavior of the monetary authority - and firms - in the next period. A higher future money supply leads to a higher future nominal marginal cost, which raises the optimal price for a firm in the current period. Second, under discretion, the monetary authority takes as given prices set in previous periods in determining its choice of the money stock in each period. Since its concern is to maximize the welfare of the representative agent, which depends on real variables, it chooses a money stock that is proportional to the price set by firms in the previous period, which we call a homogenous money stock rule.
The combination of forward-looking pricing with discretionary policy leads to complementarity between the price-setting actions of firms: if all other firms set a higher price in the current period, the monetary authority will set a higher money supply in the subsequent period, raising the desired price for a single firm in the current period.
We show that this policy-induced complementarity implies that there are typically two private-sector equilibria which can prevail at any point in time and two steady-state equilibria. In general, there is one equilibrium in which firms expect small adjustments and the newly set price is relatively close to the price that firms set last period. But there is another in which the adjusting firms make a much larger adjustment.
Because this multiplicity of equilibria arises for arbitrary homogenous monetary policies, it also arises with an optimizing monetary authority who cannot commit to future actions. We begin by considering settings of perfect foresight, in which the monetary authority and private agents each assume that only one of the two types of private sector equilibria will occur. We show that there are two steady-state discretionary equilibria, one with low inflation bias and one with high inflation bias. It is notable that the complementarity which generates multiple equilibria is entirely due, in our model, to the nature of monetary policy under discretion. That is: our specification of preferences and the labor market is such that there is no complementarity in the price-setting behavior of firms if the central bank maintains a fixed nominal money stock. Our setup thus highlights the role of discretionary monetary policy in generating complementarity.
There is a rich literature on the importance of commitment for monetary policy. In section 6 we relate our analyses to three branches of the existing literature. The first comprises the seminal works of Kydland and Prescott [1977] and Barro and Gordon [1983]; they studied reduced-form linear models in which the policymaker had quadratic preferences, and emphasized that discretion led to inflation bias. The second branch is associated with the recent optimizing sticky-price models, which have typically been analyzed using LQ approximations. The emphasis in this work has been on inflation bias and stabilization bias. Finally, Albanesi, Chari and Christiano [2003] have show that discretion leads to multiple equilibria in a different kind of sticky price model - one without the endogenous state variables which play such a crucial role here.
While our results concern an interaction between a monetary policymaker and a forward-looking private sector that sets prices for only two periods, they are indicative of a more general phenomenon, both in the context of monetary policy and in other areas of economics. In section 7, we discuss some empirical implications of our model, consider the consequences of extending it to multiple periods of price-setting, and describe other potential settings in which similar phenomena might arise. Section 8 concludes.
2 Model
The model economy that we study is a particular fully articulated ``New Keynesian'' framework, featuring monopolistic competition and nominal prices which are fixed for two periods. There is staggered pricing, with one-half of a continuum of firms adjusting price in each period. Since all of the firms have the same technology and face the same demand conditions, it is natural to think of all adjusting firms as choosing the same price. We impose this symmetry condition in our analysis.
There are many different types of New Keynesian models, which differ in terms of their implications for the extent of complementarity in price-setting. Our model assumes that (i) there is a constant elasticity demand structure originating from a Dixit-Stiglitz aggregator of differentiated products; (ii) there is a centralized labor market so that the common marginal cost for all firms is powerfully affected by aggregate demand; and (iii) preferences for goods and leisure display exactly offsetting income and substitution effects of wage changes, as is common in the literature on real business cycles. Kimball [1995] and Woodford [2002] have stressed that these assumptions make it difficult to generate complementarity between price-setters when there is an exogenous money stock. As we will, see our model has exactly zero complementarity in this situation. From our perspective, this is a virtue because it highlights the importance of the policy-based complementarity that arises from monetary policy under discretion.
2.1 Households
There is a representative household, which values consumption
(![]() ) and leisure
(
) and leisure
(![]() ) according to a
standard time separable expected utility objective,
) according to a
standard time separable expected utility objective,
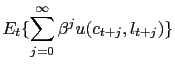
|
(1) |
with
| (2) |
which implies that there are exactly off-setting income and substitution effects of wage changes. It also has some other convenient implications that we describe later.
As is standard in the analyses of imperfect competition macro
models that follow Blanchard and Kiyotaki [1987] and Rotemberg
[1987], we assume that consumption is an aggregate of a continuum
of individual goods,
![]() . Households distribute their expenditure efficiently across
these goods, resulting in constant-elasticity demands for
individual products from each of the two types of firms which they
will encounter in the equilibrium below:
. Households distribute their expenditure efficiently across
these goods, resulting in constant-elasticity demands for
individual products from each of the two types of firms which they
will encounter in the equilibrium below:
The subscript
We assume that households also hold money to finance expenditure, according to
so that our model imposes a constant, unit velocity, in common with many macroeconomic analyses.2 We adopt this specification because it allows us to abstract from all the wealth and substitution effects that normally arise in optimizing models of money demand, so as to focus on the consequences of price-stickiness. With constant-elasticity demands for each good, the money-demand specification in (5) implies
Since this is a representative agent model and since no real accumulation is possible given the technologies described below, we are not too explicit about the consumption-saving aspect of the household's problem; it will be largely irrelevant in general equilibrium except for asset-pricing. We simply assume that there is a Lagrange multiplier that takes the form
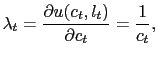
|
(7) |
and that households equate the marginal rate of substitution between leisure and consumption to the real wage rate prevailing in the competitive labor market, i.e.,
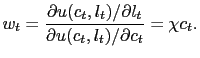
|
(8) |
In each case, the second equality indicates the implications of the specific utility function introduced above.
2.2 Firms
Firms produce output according to a linear technology, where for convenience we set the marginal product of labor to one. So, for each type of firm, the production function is
| (9) |
This implies that real marginal cost is unrelated to the scale of the firm or its type and is simply
Much of our analysis will focus on the implications of efficient
price-setting by the monopolistically competitive firm. The
adjusting firms in period t are assumed to set prices so as to
maximize the expected present discounted value of their revenues,
using the household's marginal utility as a (possibly stochastic)
discount factor. That is, they choose ![]() to maximize their market
value,
to maximize their market
value,
![$\displaystyle \lbrack\lambda_{t}(P_{0,t}-\Psi_{t})c_{0,t}+\beta E_{t}\lambda_{t+1} \frac{P_{t}}{P_{t+1}}(P_{0,t}-\Psi_{t+1})c_{1,t+1}]. $](img25.gif)
where we again give the result under the specific momentary utility function. In fact, this reveals one motivation for the form of the particular utility function chosen. In general, both aggregate demand (
the optimal price is a constant markup
The weights on current and future nominal marginal cost represent the shares of marginal revenue associated with the current and future periods.
2.3 Defining Complementarity in Price Setting
The standard definition of complementarity - contained, for
example, in Cooper and John [1988]- is that the optimal action of
one decision-maker is increasing in the actions of other similar
decision-makers. In our context, we are interested in
complementarity in price-setting in equation (11). The left-hand side of this expression is the
action of the particular decision-maker under study: the optimal
price of an individual monopolistically competitive firm that is
currently making a price adjustment. Other monopolistically
competitive firms are also simultaneously adjusting prices: these
firms take an action ![]() that influences the right-hand of (11). The
price chosen by the representative adjusting firm influences the
price level directly because
that influences the right-hand of (11). The
price chosen by the representative adjusting firm influences the
price level directly because
![]() and may also affect current nominal marginal cost. Given
that prices are sticky, there can be real effects of variations in
the price level, so that these could influence nominal marginal
cost. Finally, the weights on the present and the future in
(11) also depend on the price level. To
determine whether there is complementarity, we must work through
these mechanisms and determine the sign of the relevant partial
derivative. The extent of complementarity will depend on the
behavior of the monetary authority.
and may also affect current nominal marginal cost. Given
that prices are sticky, there can be real effects of variations in
the price level, so that these could influence nominal marginal
cost. Finally, the weights on the present and the future in
(11) also depend on the price level. To
determine whether there is complementarity, we must work through
these mechanisms and determine the sign of the relevant partial
derivative. The extent of complementarity will depend on the
behavior of the monetary authority.
2.4 Timing
The sequence of actions within a period is as follows. In the
first stage, the monetary authority chooses the money stock,
![]() taking as given
taking as given
![]() the price set
by firms in the previous period. In the second stage, adjusting
firms set prices (
the price set
by firms in the previous period. In the second stage, adjusting
firms set prices (![]() ). Simultaneously, wages are determined and
exchange occurs in labor and goods markets.
). Simultaneously, wages are determined and
exchange occurs in labor and goods markets.
There are two important consequences of these timing assumptions. First, since price-setters move after the monetary authority, they cannot be surprised by the monetary authority during the initial period that their price is in effect. Accordingly, the monetary authority faces an economy in which it can surprise some agents (those with pre-set prices) but not others (those adjusting prices) within a period. This gives rise to a relative price distortion across firms in the discretionary equilibrium that we construct, which in turn means that there is an interior solution for the monetary authority's choice problem. If we reversed the timing order so that the monetary authority moved last, we conjecture that there would not be a discretionary equilibrium unless some other aspect of the economy were modified, such as allowing firms to reset their prices after paying an adjustment cost.3 Second, the fact that the price-setters move after the monetary authority means that there is the potential for more than one equilibrium price to correspond to a given monetary policy action.
2.5 Complementarity with an exogenous money stock
We now consider a situation in which
![]() . Under
the assumptions of our model, it turns out to be easy to
investigate the influence of other adjusting firm's actions, i.e.,
to compute the effect of
. Under
the assumptions of our model, it turns out to be easy to
investigate the influence of other adjusting firm's actions, i.e.,
to compute the effect of ![]() on the right-hand side of (11). The constant velocity assumption (
on the right-hand side of (11). The constant velocity assumption (
![]() ) and
the particular utility function together imply
) and
the particular utility function together imply
![]() . Hence,
equilibrium nominal marginal cost is exactly proportional to the
money stock,
. Hence,
equilibrium nominal marginal cost is exactly proportional to the
money stock,
![]() .
Since the nominal money stock is assumed constant over time,
nominal marginal cost is also constant over time and (11) becomes
.
Since the nominal money stock is assumed constant over time,
nominal marginal cost is also constant over time and (11) becomes
2.6 Summarizing the economy by
 and
and 
Under discretionary policy, the monetary authority will not
choose to keep the nominal money supply constant. Therefore, the
optimal pricing condition (11) will not
simplify to a static equation. In general, however, equilibrium
will be a function of just two variables: a measure of the price
set by adjusting firms and a measure of monetary policy. We
construct these variables by normalizing nominal prices and money
by the single nominal state variable in this economy, the price set
by firms in the previous period (
![]() ).
Define the normalized money supply as
).
Define the normalized money supply as
| (13) |
and the normalized price set by adjusting firms in the current period as
| (14) |
We can then express all variables of interest as functions of these two normalized variables. From (4), the normalized price level is a function of only
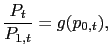
![$\displaystyle g(p_{0,t})\equiv\lbrack\frac{1}{2}p_{0,t}^{1-\varepsilon}+\frac{1}{2} ]^{\frac{1}{1-\varepsilon}}. $](img47.gif)
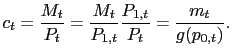
![$\displaystyle n_{t}=n(p_{0,t},m_{t})\equiv\frac{1}{2}\cdot c(p_{0,t},m_{t})\cdo... ...t}\right) \right] ^{\varepsilon}\cdot\left( p_{0,t} ^{-\varepsilon}+1\right) . $](img53.gif)
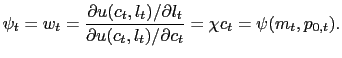
This follows directly from writing the inflation rate as a a ratio of normalized variables:
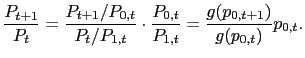
2.7 Two distortions and monetary policy
The monetary authority in this model faces two distortions that are present in the private economy and can be influenced by its actions. First, there is a markup distortion that represents the wedge between price and marginal cost: it has consequences similar to those of a tax on labor income. The markup is just the reciprocal of real marginal cost,
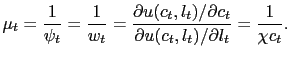
![$\displaystyle n_{t}/c_{t}=\delta(p_{0,t})\equiv\frac{1}{2}\cdot\left[ g\left( p... ...t}\right) \right] ^{\varepsilon}\cdot\left( p_{0,t}^{-\varepsilon }+1\right) . $](img62.gif)
Just as we showed above that all real variables could be
described in terms of ![]() and
and ![]() the distortions can be described similarly. The summary role of
the distortions can be described similarly. The summary role of
![]() and
and ![]() together with the fact that at any
point in time the monetary authority can choose
together with the fact that at any
point in time the monetary authority can choose ![]() (i.e. choosing
(i.e. choosing ![]() in the current period is no different
than choosing
in the current period is no different
than choosing ![]() ) has a
strong implication for the analysis of discretionary monetary
policy.4 It implies
that the level of the predetermined nominal price
) has a
strong implication for the analysis of discretionary monetary
policy.4 It implies
that the level of the predetermined nominal price ![]() does not restrict the outcomes
a discretionary policymaker can achieve, as long as the monetary
authority in future periods behaves in the same manner.5
does not restrict the outcomes
a discretionary policymaker can achieve, as long as the monetary
authority in future periods behaves in the same manner.5
We now analyze outcomes under monetary discretion, proceeding in three steps (with each a separate section of the paper). We begin by studying perfect foresight settings. In section 3, we detail the nature of perfect foresight private sector equilibria under a particular class of monetary policy rules. In section 4, we describe a full discretionary equilibrium - with optimization by the monetary authority--in which policy is shown to be in this class of rules. Finally, in section 5, we discuss stochastic discretionary equilibria.
3 Equilibrium with homogeneous policy
We begin by studying the nature of equilibrium price-setting
(![]() ) given an
arbitrary action by the monetary authority and given perfect
foresight. We assume that the monetary authority adopts a policy
rule of the form
) given an
arbitrary action by the monetary authority and given perfect
foresight. We assume that the monetary authority adopts a policy
rule of the form
where
A homogenous money supply rule means that the future money supply depends on the price set by adjusting firms today,
in equilibrium. The derivation of (17) from (11) involves (i) using the fact that nominal marginal cost is
The weight on future nominal marginal cost, which was defined in (12), can be written in terms of current and future normalized prices as
where we are now explicit about how
We view ![]() on the
left-hand side of (18) as describing
what an individual firm finds optimal given the actions of other
price-setters and the monetary authority. On the right hand side,
on the
left-hand side of (18) as describing
what an individual firm finds optimal given the actions of other
price-setters and the monetary authority. On the right hand side,
![]() then represents
all other adjusting firms' pricing behavior, and the function on
the right hand side represents the implications of those firms'
behavior for the marginal revenues and costs of an individual firm.
In other words,
then represents
all other adjusting firms' pricing behavior, and the function on
the right hand side represents the implications of those firms'
behavior for the marginal revenues and costs of an individual firm.
In other words, ![]() is
a best-response function for the
individual firm. We restrict attention to symmetric equilibria, so
that prices chosen by all adjusting firms are identical. We define
complementarity in terms of a positive partial derivative of the
response function with respect to its first argument. That is: with
perfect foresight, there is complementarity if
is
a best-response function for the
individual firm. We restrict attention to symmetric equilibria, so
that prices chosen by all adjusting firms are identical. We define
complementarity in terms of a positive partial derivative of the
response function with respect to its first argument. That is: with
perfect foresight, there is complementarity if
![]() .
.
In sections 3.2 and 3.3 below, we will make intensive
use of the perfect-foresight best-response function (18). First, we will use it to describe
point-in-time equilibria; this involves characterizing the fixed
points for ![]() ,
taking as given
,
taking as given
![]() , and
, and
![]() . Second, we
will use it to determine the model's steady-state equilibria under
constant arbitrary policy. That is, we will impose
. Second, we
will use it to determine the model's steady-state equilibria under
constant arbitrary policy. That is, we will impose
![]() and
and
![]() and
determine the equilibrium value(s) (fixed points) for
and
determine the equilibrium value(s) (fixed points) for ![]() . Both of these exercises will
then serve as inputs to our analysis of discretionary equilibria.
There, (18) will summarize private
sector equilibrium for any action that the monetary authority
contemplates, under perfect foresight.8 With uncertainty, (18) will not hold exactly, but the mechanisms
discussed here will still be relevant.
. Both of these exercises will
then serve as inputs to our analysis of discretionary equilibria.
There, (18) will summarize private
sector equilibrium for any action that the monetary authority
contemplates, under perfect foresight.8 With uncertainty, (18) will not hold exactly, but the mechanisms
discussed here will still be relevant.
3.1 Complementarity under homogeneous monetary policy
There are two mechanisms for complementarity in (17) and (18) that
will be operative in our analysis of both point-in-time and
steady-state equilibria. First, holding fixed the weights,
![]() has a positive
effect on the right-hand side in (17): it enters linearly with a coefficient of
has a positive
effect on the right-hand side in (17): it enters linearly with a coefficient of
![]() , which is positive because firms are forward-looking and
the monetary authority raises nominal
, which is positive because firms are forward-looking and
the monetary authority raises nominal ![]() proportionately with
proportionately with
![]() Hence the
specification of monetary policy has introduced some
complementarity into an economy in which it was previously
absent.
Hence the
specification of monetary policy has introduced some
complementarity into an economy in which it was previously
absent.
Second, the weights in these expressions vary with the current
price ![]() (or its
normalized counter part
(or its
normalized counter part ![]() ). This additional channel plays an important
role in our analysis. A reference value for the weight
). This additional channel plays an important
role in our analysis. A reference value for the weight
![]() is
one-half, since (12) implies that the weight
is
is
one-half, since (12) implies that the weight
is
![]() with
with
![]() close to one if if
close to one if if
![]() . An
upper bound on this weight is one: this is a situation where firms
place full weight on the future. Increases in the weight raise the
extent of the effect discussed above, i.e., they raise the
coefficient
. An
upper bound on this weight is one: this is a situation where firms
place full weight on the future. Increases in the weight raise the
extent of the effect discussed above, i.e., they raise the
coefficient
![]() that measures the extent of complementarity. The second
mechanism is then that an increase in
that measures the extent of complementarity. The second
mechanism is then that an increase in ![]() (or its normalized counterpart
(or its normalized counterpart
![]() ) raises the
weight on the future. This occurs because a firm's profits are not
symmetric around its optimal price. As the firm's relative price
rises, its profits decline gradually, asymptotically reaching zero
as the price goes to infinity. By contrast, as the price falls, the
firms profits decline sharply toward zero and may even become
highly negative if the firm is not allowed to shut down its
operations.9 Thus, when
) raises the
weight on the future. This occurs because a firm's profits are not
symmetric around its optimal price. As the firm's relative price
rises, its profits decline gradually, asymptotically reaching zero
as the price goes to infinity. By contrast, as the price falls, the
firms profits decline sharply toward zero and may even become
highly negative if the firm is not allowed to shut down its
operations.9 Thus, when
![]() increases for
all other firms, future monetary accommodation - and the associated
higher nominal price set by firms in
the future - automatically lower's the firm's future relative
price. The costliness of a low relative price leads the firm to put
increased weight on future marginal cost.
increases for
all other firms, future monetary accommodation - and the associated
higher nominal price set by firms in
the future - automatically lower's the firm's future relative
price. The costliness of a low relative price leads the firm to put
increased weight on future marginal cost.
3.2 Equilibrium analysis of steady states
To characterize steady-state equilibria for arbitrary constant,
homogeneous monetary policies, we impose constant ![]() and
and ![]() on the right hand side of (18). Steady-state equilibria are fixed points of
the resulting steady-state best-response function for
on the right hand side of (18). Steady-state equilibria are fixed points of
the resulting steady-state best-response function for ![]() :
:
with a weight on the future of
Fixed points of the steady-state best-response function are constructed by simultaneously varying current and future
3.2.1 Uniqueness occurs at zero inflation
A zero inflation steady state involves ![]() Such a steady state exists
when the normalized quantity of money is
Such a steady state exists
when the normalized quantity of money is
![]() In this case, the weight on the future is
In this case, the weight on the future is
![]() which is roughly one-half. The zero-inflation steady state is
asymptotically optimal under full commitment in this model (see
King and Wolman [1999]) and provides an important benchmark.
Furthermore, if
which is roughly one-half. The zero-inflation steady state is
asymptotically optimal under full commitment in this model (see
King and Wolman [1999]) and provides an important benchmark.
Furthermore, if
![]() zero
inflation is the unique steady state;
that is,
zero
inflation is the unique steady state;
that is, ![]() is
the unique solution to (20) when
is
the unique solution to (20) when
![]() .
.
3.2.2 Multiplicity or nonexistence must occur with positive inflation
We refer to any
![]() as an
inflationary monetary policy, because if inflation is positive in a
steady state, then
as an
inflationary monetary policy, because if inflation is positive in a
steady state, then
![]() as we
now show. From (20), given that
as we
now show. From (20), given that
![]() in steady
state, we have
in steady
state, we have
![$\displaystyle m=\frac{1}{(\frac{\varepsilon}{\varepsilon-1}\chi)}\frac{\pi}{[1-... ...theta\pi]}=\frac{1}{[\theta+\left( 1-\theta\right) (\frac{1}{\pi} )]}m^{\ast}. $](img105.gif)
Proposition 1 states that under an arbitrary inflationary
monetary policy, for low values of ![]() there are two steady-state equilibrium values of
there are two steady-state equilibrium values of
![]() . For high values
of
. For high values
of ![]() , no steady-state
equilibrium exists. In a knife edge case there is a unique
steady-state equilibrium.
, no steady-state
equilibrium exists. In a knife edge case there is a unique
steady-state equilibrium.
From (20), steady-state equilibria for a
given ![]() are fixed points of
are fixed points of
![]() where we write the
best-response function as
where we write the
best-response function as
for the discussion of proposition 1.
Figure 1 provides the basis for a heuristic discussion of
Proposition 1, based on the best-response function
![]() .
The dashed line in Figure 1 is the
.
The dashed line in Figure 1 is the ![]() line; when
line; when
![]() crosses this line the action of a representative adjusting firm
(the horizontal axis) coincides with the optimal action of an
individual firm as described by
crosses this line the action of a representative adjusting firm
(the horizontal axis) coincides with the optimal action of an
individual firm as described by
![]() .
The solid line is
.
The solid line is
![]() for
for
![]() When
When
![]() it is easy
to see from (22) that there is one steady
state, and it occurs at
it is easy
to see from (22) that there is one steady
state, and it occurs at ![]() . An increase in
. An increase in ![]() shifts
shifts
![]() upwards. It is thus clear that
upwards. It is thus clear that ![]() is not an equilibrium point with
is not an equilibrium point with
![]() , but
that there is a prospect for an intersection point somewhere to the
right as in the case illustrated in Figure 1. At any such ``low''
stationary equilibrium, it must be the case that the slope is less
than one (if
, but
that there is a prospect for an intersection point somewhere to the
right as in the case illustrated in Figure 1. At any such ``low''
stationary equilibrium, it must be the case that the slope is less
than one (if
![]() crosses the
crosses the
![]() line) or the
slope is exactly equal to one (if it is a tangency). Let us call
this first equilibrium
line) or the
slope is exactly equal to one (if it is a tangency). Let us call
this first equilibrium
![]()
Suppose the slope at a ``low'' stationary equilibrium is less
than one, so that it is not a tangency and corresponds to the case
illustrated in Figure 1. As ![]() becomes arbitrarily large,
becomes arbitrarily large,
![]() .
For large
.
For large ![]() , then, it
follows that
, then, it
follows that
![]() approaches
the line
approaches
the line
![]() from
below. For high enough
from
below. For high enough ![]() then,
then,
![]() since we are considering an inflationary monetary policy (
since we are considering an inflationary monetary policy (
![]() ). We
have assumed there was a fixed point at which
). We
have assumed there was a fixed point at which
![]() and we have shown that
and we have shown that
![]() lies above the 45
lies above the 45![]() line for high enough
line for high enough ![]() , so
there must be some other ``high''
, so
there must be some other ``high'' ![]() for which there is an equilibrium
for which there is an equilibrium
![]() . If
. If ![]() is high enough, the first fixed point
does not exist, and
is high enough, the first fixed point
does not exist, and
![]() lies everywhere above the
lies everywhere above the ![]() line. We label the two equilibria with an
asterisk (*) and carry them over to our discussion below.
line. We label the two equilibria with an
asterisk (*) and carry them over to our discussion below.
There are two mechanisms at work to produce multiple steady-state rates of inflation for arbitrary constant, homogeneous monetary policy. The first is that monetary policy is accommodative: if higher prices are set by other firms today, the future nominal money stock will be higher in proportion. The second is that if all other firms raise prices today and in the future, then the future inflation rate will rise and a single firm today places higher weight on future nominal marginal costs, so that future monetary endogeneity becomes more influential on current price-setting. Looking ahead, the discretionary equilibria we will construct below will involve constant, homogeneous monetary policy. Necessarily, then, there will be multiple steady-state equilibria under discretion. However, in order to construct those equilibria we cannot rely on the steady-state best-response function.
3.3 Point-in-time equilibria
Solving the monetary authority's problem under discretion means
computing the point-in-time equilibria that correspond to all
possible current policy actions, and then picking the best action.
Before studying this topic in detail in section 4, we here begin by
characterizing point-in-time equilibria for an arbitrary policy
action in the current period. Point-in-time equilibrium refers to
the values of ![]() that
solve (18) for given current and future
monetary actions, and a given future price
that
solve (18) for given current and future
monetary actions, and a given future price
![]() The
mechanisms described earlier lead to the potential for multiple
point-in-time equilibria. We assume that the future money supply is
given by
The
mechanisms described earlier lead to the potential for multiple
point-in-time equilibria. We assume that the future money supply is
given by
![]() (i.e.
steady-state equilibria do exist for the assumed value of
(i.e.
steady-state equilibria do exist for the assumed value of
![]() and are
inflationary) and that the future relative price is consistent with
one of the two steady-state equilibria that may prevail if that
level of
and are
inflationary) and that the future relative price is consistent with
one of the two steady-state equilibria that may prevail if that
level of ![]() is
maintained forever. Under these assumptions, there are either two
equilibria in the current period or equilibrium does not exist.
Again, in a knife edge case equilibrium is unique.
is
maintained forever. Under these assumptions, there are either two
equilibria in the current period or equilibrium does not exist.
Again, in a knife edge case equilibrium is unique.
Point-in-time equilibria are fixed points of the best-response function for current period price-setters, which we write without time subscripts, using superscript prime to denote next period:
No expectation operator appears because we are assuming, for the purposes of this section, that there is no uncertainty about future
Figure 2 illustrates the multiplicity of point-in-time
equilibria for
![]() for two different beliefs
about future
for two different beliefs
about future ![]() . As
above, the dashed line is the 45
. As
above, the dashed line is the 45![]() line that identifies fixed points: the two points
marked with asterisks (`*') on the
line that identifies fixed points: the two points
marked with asterisks (`*') on the ![]() line are the steady states from Figure 1. The
solid line is the best-response function when agents expect
line are the steady states from Figure 1. The
solid line is the best-response function when agents expect
![]()
![]() in
the future, with certainty. The low steady state is a point-in-time
equilibrium when agents expect
in
the future, with certainty. The low steady state is a point-in-time
equilibrium when agents expect ![]()
![]() in the future, but the high
steady state is not, because in that steady state agents expect
in the future, but the high
steady state is not, because in that steady state agents expect
![]() rather than
rather than ![]()
![]() in
the future. In fact, the second point-in-time equilibrium must be
at a higher
in
the future. In fact, the second point-in-time equilibrium must be
at a higher ![]() because expectations make the future less important than in the
steady-state analysis of Figure 1: a larger increase in the weight
on the future is required for the second fixed point to occur. The
dotted line shows the best-response function when agents expect
because expectations make the future less important than in the
steady-state analysis of Figure 1: a larger increase in the weight
on the future is required for the second fixed point to occur. The
dotted line shows the best-response function when agents expect
![]() in
the future, with certainty. In this case the higher of the two
steady-state equilibria survives as a point-in-time equilibrium,
but the the low-inflation point-in-time equilibrium is now higher
than the low-inflation steady state.
in
the future, with certainty. In this case the higher of the two
steady-state equilibria survives as a point-in-time equilibrium,
but the the low-inflation point-in-time equilibrium is now higher
than the low-inflation steady state.
From (23), note that for given
![]() lower
lower
![]() drives down the lower
price equilibrium and drives up the higher price equilibrium. Lower
current
drives down the lower
price equilibrium and drives up the higher price equilibrium. Lower
current ![]() shifts the
best-response function down, with lower current marginal cost
reducing the firm's optimal price for any price set by other firms.
The lower fixed point falls, but because the basic properties of
the response function are unchanged, there is still a second fixed
point, now at a higher level of
shifts the
best-response function down, with lower current marginal cost
reducing the firm's optimal price for any price set by other firms.
The lower fixed point falls, but because the basic properties of
the response function are unchanged, there is still a second fixed
point, now at a higher level of ![]() at this high level of
at this high level of ![]() high future marginal cost
offsets the lower current marginal cost. Current monetary policy
actions thus affect the two equilibria in very different ways.
high future marginal cost
offsets the lower current marginal cost. Current monetary policy
actions thus affect the two equilibria in very different ways.
Figure 2 illustrates that beliefs about both current and future
equilibrium selection can affect the opportunities available to a
discretionary monetary authority. Raising the current money supply
shifts out the best-response function for firms, resulting in a
lower high-![]() equilibrium and higher low-
equilibrium and higher low-![]() equilibrium. The likelihood of each equilibrium
in the present will thus alter the trade-off facing the monetary
authority. Beliefs about future
equilibrium selection shift the current period best-response
function for a given current money supply, and thus also alter the
trade-off facing the current monetary authority.
equilibrium. The likelihood of each equilibrium
in the present will thus alter the trade-off facing the monetary
authority. Beliefs about future
equilibrium selection shift the current period best-response
function for a given current money supply, and thus also alter the
trade-off facing the current monetary authority.
4 Discretion under perfect foresight
In a perfect foresight discretionary equilibrium, the current monetary authority sets the money stock to maximize the representative private agent's welfare, subject to
- The behavior of the future monetary authority (
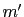 ).
). - The behavior of firms in the future (
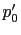 ).
). - Optimal pricing by firms in the current period (
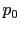 ). The monetary authority must
have beliefs about the selection rule used to determine
). The monetary authority must
have beliefs about the selection rule used to determine
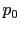 when a
contemplated value of
when a
contemplated value of 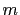 leads to multiple equilibrium values of
leads to multiple equilibrium values of 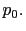
Two conditions define a stationary perfect foresight equilibrium with discretion: (i) the current and future monetary authority each choose the same action; and (ii) the selection rule specifies that only one equilibrium will prevail in every period. It is common knowledge which equilibrium will prevail.
As we noted above, it is the essence of discretion in monetary
policy that certain predetermined nominal variables are taken as
given by the monetary authority. Here, the current money supply is
set proportionally to the previously set price,
![]() This leads us to view
This leads us to view ![]() as
the monetary authority's choice variable. Our analysis of
equilibrium under arbitrary choice of
as
the monetary authority's choice variable. Our analysis of
equilibrium under arbitrary choice of ![]() revealed that in general there were
either two point-in-time equilibria or no point-in-time equilibria,
as long as future policy was expected to be inflationary. This
leads us to expect multiple discretionary equilibria. In this
section we analyze discretionary equilibria where there is a
constant probability of
revealed that in general there were
either two point-in-time equilibria or no point-in-time equilibria,
as long as future policy was expected to be inflationary. This
leads us to expect multiple discretionary equilibria. In this
section we analyze discretionary equilibria where there is a
constant probability of ![]() on one of the two private sector equilibria.
on one of the two private sector equilibria.
4.1 Constructing Discretionary Equilibria
We look for a stationary, discretionary equilibrium, which is a
value of ![]() that
maximizes
that
maximizes ![]() subject to the constraints above when
subject to the constraints above when
![]() . We have
used two computational approaches to find this fixed point. A
comparison of the two approaches is revealing about the nature of
the multiple equilibria we encounter.
. We have
used two computational approaches to find this fixed point. A
comparison of the two approaches is revealing about the nature of
the multiple equilibria we encounter.
The first computational method involves iterating on steady
states. We assume that all future monetary authorities follow some
fixed rule
![]() . Next, we
determine the steady state that prevails including the value of
. Next, we
determine the steady state that prevails including the value of
![]() . Then,
we confront the current monetary policy authority with these
beliefs and ask her to optimize, given the constraints including
the selection rule. If she chooses an
. Then,
we confront the current monetary policy authority with these
beliefs and ask her to optimize, given the constraints including
the selection rule. If she chooses an ![]() such that
such that
![]() is sufficiently small, then we
have an approximate fixed point. If not, then we adjust the future
monetary policy rule in the direction of her choice and go through
the process again until we have achieved an approximate fixed
point. This approach conceptually matches our discussion throughout
the text, but leaves open an important economic question: are the
equilibria that we construct critically dependent on the infinite
horizon nature of the problem?
is sufficiently small, then we
have an approximate fixed point. If not, then we adjust the future
monetary policy rule in the direction of her choice and go through
the process again until we have achieved an approximate fixed
point. This approach conceptually matches our discussion throughout
the text, but leaves open an important economic question: are the
equilibria that we construct critically dependent on the infinite
horizon nature of the problem?
The second computational method involves backward induction on
finite horizon economies. We begin with a last period, in which
firms are not forward-looking in their price setting and deduce
that there is a single equilibrium, including an optimal action for
the monetary authority
![]() and
a unique equilibrium relative price
and
a unique equilibrium relative price ![]() . Then, we step back one period, taking as
given the future monetary action and the future relative price. We
find that there are two private sector equilibria. In fact, this is
inevitable, because the first step backwards creates a version of
our point-in-time analysis above. Consequently, this approach
establishes that the phenomena are associated with forward-looking
pricing and homogenous monetary policy, rather than with an
infinite horizon. To construct stationary nonstochastic equilibria
using this approach, we can iterate backwards from the last period,
computing the optimal policy,
. Then, we step back one period, taking as
given the future monetary action and the future relative price. We
find that there are two private sector equilibria. In fact, this is
inevitable, because the first step backwards creates a version of
our point-in-time analysis above. Consequently, this approach
establishes that the phenomena are associated with forward-looking
pricing and homogenous monetary policy, rather than with an
infinite horizon. To construct stationary nonstochastic equilibria
using this approach, we can iterate backwards from the last period,
computing the optimal policy,
![]() and stop the process when
and stop the process when
![]() is small, taking
is small, taking ![]() as an approximate fixed
point.
as an approximate fixed
point.
In either computational approach, our work begins from the perspective that the relevant dynamic equilibrium is one that is Markovian, in the sense of Krusell and Rios-Rull [1999]. In general, this equilibrium concept restricts the actions of the policymaker to depend on a set of fundamental state variables that have intrinsic relevance to the equilibrium. In our setting, there are no such state variables, so that search for a nonstochastic Markov equilibrium corresponds to determining constant levels of public and private actions. When we do so, we find that there is more than one nonstochastic Markov equilibrium. We then consider a stochastic discretionary equilibrium in which each period's equilibrium outcome is determined by a sunspot that shifts private sector beliefs. When we consider this extension, we continue to assume that the monetary authority makes its actions a function of the state variables that are relevant to the private sector. We focus on Markov equilibria because these impose the most structure on the problem (making clear that our multiplicity arises from a single source) and provide the most tractable solution. Furthermore, the Markov equilibria of the model have natural analogues in a finite-horizon version of the model, making it clear that our results do not depend on whether the model is literally an infinite horizon one or simply the convenient stationary limit of a sequence of finite horizon models.
The numerical examples that we study next have the following
common elements. The demand elasticity (
![]() ) is
) is
![]() implying a gross
markup of
implying a gross
markup of ![]() in a
zero inflation steady state. The preference parameter (
in a
zero inflation steady state. The preference parameter (![]() ) is
) is ![]() and for convenience we set the
time endowment to
and for convenience we set the
time endowment to ![]() Taken together with the markup, this implies that agents will work
one fifth of their time
Taken together with the markup, this implies that agents will work
one fifth of their time
![]() in
a zero inflation steady state. With zero inflation,
in
a zero inflation steady state. With zero inflation, ![]() since there are no relative
price distortions, and thus
since there are no relative
price distortions, and thus
![]() . Further,
leisure (
. Further,
leisure (![]() ) is then
) is then
![]() . Accordingly, in a
zero inflation stationary state, utility is just
. Accordingly, in a
zero inflation stationary state, utility is just
![]() .
A first-best outcome would dictate that
.
A first-best outcome would dictate that ![]() be maximized subject to
be maximized subject to
![]() . For the
specified preferences, this leads to a first order condition
. For the
specified preferences, this leads to a first order condition
![]() or
an efficient level of work (
or
an efficient level of work (![]() ) of
) of ![]() .
So, the increase in work from cutting the gross markup to one is
11.1%.
.
So, the increase in work from cutting the gross markup to one is
11.1%.
4.2 Optimistic Equilibrium
If the discretionary monetary authority knows that the low equilibrium will prevail, then its problem is to maximize
where
4.2.1 Exploiting initial conditions
Figure 3 provides some insight into the nature of the monetary
authority's choice when it knows that the ![]() equilibrium will prevail for all time. For this figure, we assume
that future monetary policy is noninflationary
equilibrium will prevail for all time. For this figure, we assume
that future monetary policy is noninflationary
![]() ,
,
![]() The
current monetary authority optimally adopts an inflationary
monetary policy (choosing
The
current monetary authority optimally adopts an inflationary
monetary policy (choosing
![]() )
because it can reduce the markup and stimulate consumption toward
the first-best level. It does not completely drive the gross markup
to one because an increase in
)
because it can reduce the markup and stimulate consumption toward
the first-best level. It does not completely drive the gross markup
to one because an increase in ![]() produces relative price distortions. While the
relative price distortions are negligible near the noninflationary
steady state, they increase convexly as monetary policy stimulates
the economy. Figure 3 illustrates the sense in which New Keynesian
models capture the incentive for stimulating the economy at zero
inflation, as described in Kydland and Prescott [1977] and Barro
and Gordon [1983].
produces relative price distortions. While the
relative price distortions are negligible near the noninflationary
steady state, they increase convexly as monetary policy stimulates
the economy. Figure 3 illustrates the sense in which New Keynesian
models capture the incentive for stimulating the economy at zero
inflation, as described in Kydland and Prescott [1977] and Barro
and Gordon [1983].
4.2.2 An inflation bias equilibrium
Figure 4 displays the consistent steady-state equilibrium, in
which agents correctly forecast the incentives of the monetary
authority. Panel A shows the policymaker's objective function,
which can be thought of as an indirect utility function: the
relevant portion for the current discussion is the solid line,
which reaches a maximum at the value of
![]() 1.01. This
implies a stationary relative price (
1.01. This
implies a stationary relative price (![]() ) of
) of ![]() , which is determined along the lines of Figure 2
with agents expecting
, which is determined along the lines of Figure 2
with agents expecting
![]() and
and
![]() . Given
that there is a steady state,
. Given
that there is a steady state, ![]() and this relative price thus implies an
inflation rate of 2.2 % per quarter. At this inflation rate, the
monetary authority faces sufficiently increasing marginal relative
price distortions that it chooses not to further increase
and this relative price thus implies an
inflation rate of 2.2 % per quarter. At this inflation rate, the
monetary authority faces sufficiently increasing marginal relative
price distortions that it chooses not to further increase
![]() in an effort to
further reduce the markup. Notably, the stationary markup departs
little from its value at zero inflation. Stationary consumption is
99.96% of its zero inflation value, so that the markup has changed
negligibly (recall that the markup and consumption are directly
related by
in an effort to
further reduce the markup. Notably, the stationary markup departs
little from its value at zero inflation. Stationary consumption is
99.96% of its zero inflation value, so that the markup has changed
negligibly (recall that the markup and consumption are directly
related by
![]() with the
preference specification used here).
with the
preference specification used here).
4.3 Pessimistic Equilibrium
We next suppose that the monetary authority instead knows that
the high ![]() equilibrium will always prevail. Its incentives are sharply
different. Looking at Figure 4, we can see these incentives in the
dashed lines, which describe a
non-equilibrium situation in which the
private sector and the monetary authority assume that the future is
described by
equilibrium will always prevail. Its incentives are sharply
different. Looking at Figure 4, we can see these incentives in the
dashed lines, which describe a
non-equilibrium situation in which the
private sector and the monetary authority assume that the future is
described by ![]()
![]() while the present is described by
while the present is described by
![]() . The
monetary authority has a clear incentive to raise
. The
monetary authority has a clear incentive to raise
![]() since this lowers the markup and
relative price distortions, with utility being maximized when
since this lowers the markup and
relative price distortions, with utility being maximized when
![]() is sufficiently high
that there is exactly a tangency equilibrium in the temporary
equilibrium analysis of Figure 2. Here the monetary authority
``takes policy to the limit'' of the set of equilibria that are
imposed as its constraints. Because Figure 4 assumes optimism (that
is, the low-
is sufficiently high
that there is exactly a tangency equilibrium in the temporary
equilibrium analysis of Figure 2. Here the monetary authority
``takes policy to the limit'' of the set of equilibria that are
imposed as its constraints. Because Figure 4 assumes optimism (that
is, the low-![]() outcome
occurs with probability one) , there are some inconsistencies in
using Figure 4 to discuss an equilibrium with pessimistic
expectations. Notably, the monetary authority can lower the markup
to less than one, in which case some of the firms in the economy
are making losses. But the picture tells the right story: nearer
the consistent discretionary equilibrium that is described by a
level
outcome
occurs with probability one) , there are some inconsistencies in
using Figure 4 to discuss an equilibrium with pessimistic
expectations. Notably, the monetary authority can lower the markup
to less than one, in which case some of the firms in the economy
are making losses. But the picture tells the right story: nearer
the consistent discretionary equilibrium that is described by a
level
![]() , the
monetary authority still has the same incentives to raise
, the
monetary authority still has the same incentives to raise
![]() , but it does so
without producing the curious behavior of the markup shown
here.
, but it does so
without producing the curious behavior of the markup shown
here.
In fact, it is not necessary to make a complicated set of fixed
point computations in this case. A tangency equilibrium is one in
which
![]() . Therefore, we can simply solve the stationary version of
the equation,
. Therefore, we can simply solve the stationary version of
the equation,
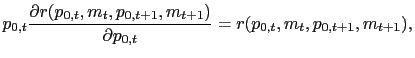
In our numerical example, there is a consistent equilibrium with
![]() , so that
there is a 17% quarterly inflation rate in the pessimistic
equilibrium with optimal discretionary policy. The associated value
of
, so that
there is a 17% quarterly inflation rate in the pessimistic
equilibrium with optimal discretionary policy. The associated value
of
![]() is
is
![]() . This value is
larger than the one used to construct Figure 3, as it should be: a
higher level of
. This value is
larger than the one used to construct Figure 3, as it should be: a
higher level of ![]() is
necessary to produce a tangency equilibrium in the pessimistic
case.
is
necessary to produce a tangency equilibrium in the pessimistic
case.
There are thus two steady-state equilibria with discretionary optimal monetary policy in our quantitative example, one with low inflation and one with high inflation. The levels of the inflation rates are quite different: about 2 percent (per quarter) in one case and about 17 percent in the other.
5 Stochastic equilibria
The generic existence of two point-in-time equilibria and two
steady-state equilibria for arbitrary homogeneous policy suggests
that it may be possible to construct discretionary equilibria that
involve stochastic fluctuations. We now provide an example of such
an equilibrium. We assume that there is an i.i.d. sunspot realized
each period which selects between the two private sector
equilibria: in each period, the low-![]() outcome occurs with probability 0.6, the
high-
outcome occurs with probability 0.6, the
high-![]() outcome occurs
with probability of 0.4, and this is common knowledge.10
outcome occurs
with probability of 0.4, and this is common knowledge.10
In order for its maximization problem to be well-defined, the
monetary authority must have beliefs about the current and future
distribution over private-sector equilibria. Above, these beliefs
were degenerate. Now that they are nondegenerate, the problem is
slightly more complicated. Letting ![]() be the probability of the low-
be the probability of the low-![]() outcome, the monetary authority
maximizes
outcome, the monetary authority
maximizes
where expectations are taken over the distribution of the sunspot variable. For example,
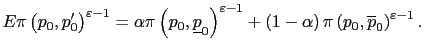
5.1 Constructing Discretionary Equilibria
We can again apply the two computational approaches described in the previous section to construct Nash equilibria. In implementing these, we assume that the monetary authority and the private sector share the same probability beliefs.
5.2 Optimal discretionary policy
The relevant trade-offs for the discretionary monetary authority
are illustrated in Figure 5. In panel A, there is a light solid
line between the objective function for the low-![]() private-sector equilibrium (the
dark solid line) and the objective function for the
high-
private-sector equilibrium (the
dark solid line) and the objective function for the
high-![]() private sector
equilibrium (the dashed line): this is the monetary authority's
expected utility objective, which is a weighted average of the two
other objectives. The monetary authority chooses an optimal action
that is about 1.0202, which is more stimulative than the earlier
equilibrium action (1.01, shown in Figure 4) that was appropriate
under extreme optimism (
private sector
equilibrium (the dashed line): this is the monetary authority's
expected utility objective, which is a weighted average of the two
other objectives. The monetary authority chooses an optimal action
that is about 1.0202, which is more stimulative than the earlier
equilibrium action (1.01, shown in Figure 4) that was appropriate
under extreme optimism (![]() ). But it is smaller than the equilibrium
action appropriate under extreme pessimism (
). But it is smaller than the equilibrium
action appropriate under extreme pessimism (![]() ).
).
Figure 5 also highlights that the specific values taken on by
![]() in the optimistic
and pessimistic equilibrium are endogenously determined in our
setup, by current monetary policy and the sunspot probabilities. By
contrast, in the essentially static models of Albanesi, Chari and
Christiano [2002], the values of endogenous variables are not
affected by the probability structure of extrinsic uncertainty.
in the optimistic
and pessimistic equilibrium are endogenously determined in our
setup, by current monetary policy and the sunspot probabilities. By
contrast, in the essentially static models of Albanesi, Chari and
Christiano [2002], the values of endogenous variables are not
affected by the probability structure of extrinsic uncertainty.
5.3 Effects of sunspots
Consider now the effects of a sunspot on equilibrium quantities.
We take as the reference point the levels in the low-![]() private-sector equilibrium, which
involve a markup of about 1.11 (close to the zero inflation markup)
and a normalized price that is close to one. If the economy
suddenly shifts to the high-
private-sector equilibrium, which
involve a markup of about 1.11 (close to the zero inflation markup)
and a normalized price that is close to one. If the economy
suddenly shifts to the high-![]() private sector equilibrium as a result of the
sunspot, then firms become much more aggressive in their
adjustments. With the nominal money stock fixed (
private sector equilibrium as a result of the
sunspot, then firms become much more aggressive in their
adjustments. With the nominal money stock fixed (
![]() ),
there is a decline in real aggregate demand since the price level
rises. Consumption and work effort accordingly fall. Alternatively,
the average markup rises dramatically, increasing distortions in
the economy, to bring about this set of results. Quantitatively, in
Figure 5, the rise in the markup is from about 1.12 to about 1.17,
so that there is roughly a 4.5% increase in the markup. Given that
markups and consumption are (inversely) related proportionately,
there is a 4.5% decline in consumption and work effort.
),
there is a decline in real aggregate demand since the price level
rises. Consumption and work effort accordingly fall. Alternatively,
the average markup rises dramatically, increasing distortions in
the economy, to bring about this set of results. Quantitatively, in
Figure 5, the rise in the markup is from about 1.12 to about 1.17,
so that there is roughly a 4.5% increase in the markup. Given that
markups and consumption are (inversely) related proportionately,
there is a 4.5% decline in consumption and work effort.
6 Relationship to existing monetary policy literature
The study of monetary policy under discretion began with the seminal papers by Kydland and Prescott [1977] and Barro and Gordon [1983], which we will refer to as KPBG. In this early literature, output is inefficiently low, but can be raised by policies that also produce unexpected inflation. There are costs of actual inflation, so that a consistent equilibrium exhibits an inflation bias. The model that captures these ideas involves a quadratic monetary authority objective and an economic model consisting of linear behavioral equations. There is a unique discretionary equilibrium in the standard model (absent reputational effects or trigger strategies).
In recent years attention has shifted to optimization based models, such as the one here. Models very close to ours have been studied extensively, without uncovering multiplicity under discretion. We explain why below, and we contrast the multiplicity here with that found by Albanesi, Chari and Christiano [2002] in a different type of sticky price model.
6.1 New Keynesian Models
There is an important recent literature that works out how the standard Kydland-Prescott-Barro-Gordon (KPBG) model can be derived from a fully articulated New Keynesian framework. The key ingredients of the models in this literature are that output is inefficiently low due to monopoly distortions; the monetary authority has temporary leverage over the real economy because of staggered price setting; and the costs of actual inflation are welfare losses associated with relative price distortions. Analyses of discretionary equilibrium in New Keynesian models has been conducted within linearized versions of those models, and using a primal approach to policy (more on this below). Just as in KPBG, there is a unique discretionary equilibrium, and it is characterized by inflation bias.11
Our analysis takes the most basic fully articulated New Keynesian model, without linearizing, and shows that there are multiple equilibria.12 Our model features costs of stimulative policies - which bring about actual inflation - that stem from relative price distortions across goods. It also features benefits from unexpected stimulative policies, which lower monopoly markups and raise output toward the first best level. The model is explicitly dynamic, with firms forecasting future inflation when setting nominal prices for two periods. Multiple equilibria occur because of complementarity among price-setting firms that is induced by the response of future policy to current prices.
It should be clear from figure 2 that nonlinearity is central to the multiplicity of point-in-time equilibria we describe: the best response function of a price-setting firm is nonlinear, and without nonlinearity there could not be multiple fixed points to that best response function. Multiplicity of steady state equilibria could survive linearization, in that one could approximate linearly around either of the two steady state discretionary equilibria. Previous analyses of discretionary equilibrium in New Keynesian models have not uncovered multiple steady states because they have used a ``primal approach;'' instead of specifying a policymaker who chooses an instrument and must accept whatever equilibria correspond to the instrument setting, they have specified a planner who can choose allocations (thus, prices), subject to those allocations being consistent with private-sector equilibrium.
If the policymaker can commit to future actions, the distinction
between planning problem and policy problem is immaterial in New
Keynesian models. However, absent commitment the distinction
becomes important; the planner's formulation rules out the steady
state with lower welfare. To see this, consider a planner in the
current period who knows that the future will be characterized by
the steady state with lower welfare (higher ![]() ). It is optimal for the planner
to pick allocations that correspond to a low value of
). It is optimal for the planner
to pick allocations that correspond to a low value of ![]() in the current period, and thus
the low-welfare steady state is not an equilibrium to the planning
problem.13 In
contrast, a policymaker- who can only
choose
in the current period, and thus
the low-welfare steady state is not an equilibrium to the planning
problem.13 In
contrast, a policymaker- who can only
choose ![]() - must
respect private agents' beliefs. If agents are pessimistic today
and in the future, then the current policymaker chooses an
- must
respect private agents' beliefs. If agents are pessimistic today
and in the future, then the current policymaker chooses an
![]() such that the
low-welfare steady state outcome is realized today.
such that the
low-welfare steady state outcome is realized today.
Without commitment, it is also important what the policy
instrument is. If the policy instrument is the nominal interest
rate instead of the money supply, Dotsey and Hornstein [2004] show
that there is a unique Markov equilibrium, corresponding to the
low-![]() steady state of
our model. This ``Sargent and Wallace on their head'' result is
somewhat misleading however: the focus on Markov equilibria rules
out a continuum of equilibria that would exist for exogenous fixed
nominal interest rate policies.
steady state of
our model. This ``Sargent and Wallace on their head'' result is
somewhat misleading however: the focus on Markov equilibria rules
out a continuum of equilibria that would exist for exogenous fixed
nominal interest rate policies.
6.2 Albanesi, Chari and Christiano
Third, our paper is closely related to recent work by Albanesi, Chari and Christiano [2002]. They find multiple equilibria in an essentially static model where a portion of monopolistically competitive firms must set prices before the monetary authority's action in each period. At the same time, the structure of the model they study is quite different from ours. The stimulative policies that produce inflation in their model also raise nominal interest rates and lead to money demand distortions, either by driving a relative price wedge between the cost of buying goods on cash and credit or by increasing transactions time. A monetary authority thus faces a trade-off between the benefits of driving down the markup and these costs. In our model, instead of the costs of realized inflation being related to money demand, they involve price distortions across goods whose prices were set in different periods.14
If there are sunspots which switch the economy between equilibria, there are also important differences in the consequences that are suggested by our model from those suggested by the ACC models. In our setting, if a high inflation equilibrium occurs when agents attach low probability to such an event, then there will be a decline in output because aggregate demand will fall and the average markup will increase. By contrast, in the ACC models, a switch from low inflation to high inflation will have little effect on the average markup or output, with the main difference being the extent of money demand distortions. Since the ACC models are essentially static ones, there is also another difference: there is no feedback between the likelihood that economic agents attach to future equilibria and the levels of inflation and output at a point in time. Accordingly beliefs about the future are of no bearing for current events. In our model, beliefs about future outcomes affect the nature of the current policy problem because firms setting their price in the current period care about both current and future monetary policy.
7 Discretion and Multiplicity more Generally
Multiple equilibria arise under discretion in our model because of policy-induced complementarity among private agents. The complementarity involves interaction between forward-looking firms and a future policymaker who will respond to the state variable determined by those firms. We will argue here that similar types of complementarity are present more generally when policy is formulated without commitment. For generalizations of our staggered pricing model we know this to be true, and thus we speculate on some empirical implications of monetary discretion. We then describe some other contexts in which discretion can lead to multiple equilibria because of policy-induced complementarity among private agents.
7.1 Greater Price Stickiness
Multiplicity of equilibrium under discretion is not an artifact of two-period staggered pricing. The key model element generating multiplicity is the existence of a nominal state variable (here, the nominal price set by firms that adjusted their price in the previous period). With prices set for more than two periods, such a nominal state variable would still exist, but it would be an index of those nominal prices charged in the current period but chosen in previous periods. Furthermore, there would be real state variables, namely ratios of the current period nominal prices chosen by firms in previous periods. Solving for an equilibrium under discretion is more complicated when there is a real state that constrains the monetary authority. In Khan, King and Wolman [2001], we show that multiple equilibria still arise with three-period staggered pricing. However, that analysis is conducted using backward induction on a finite horizon model, and already with a two period horizon we encounter some headaches. There are discontinuities in the monetary authority's policy functions, which makes it computationally difficult - though not impossible - to extend the horizon beyond two periods. For this reason we chose to focus here on the model without a state variable, where we are able to characterize equilibrium with an infinite horizon.
7.2 Empirical implications
There are tantalizing empirical implications of the kind of model we have discussed here. First, a model with multiple steady state rates of inflation can potentially explain why monetary policymakers can be caught at a high rate of inflation, in what Chari, Christiano and Eichenbaum [1998] call an ``expectations trap.'' This could explain wide variation in inflation rates across countries or time periods displaying similar structural features.
Second, the effect of sunspots on economic activity that we just discussed in section 5.3 is a situation of ``unexpected stagflation'' arising because of shifting beliefs. Goodfriend [1993] describes post-war U.S. recessions as arising from ``inflation scares'', situations in which markets suddenly come to expect higher inflation and a contraction in aggregate demand occurs. The effect that we describe above seems to capture some aspects of this perspective, but it does not involve the increases in long-term expectations of inflation reflected in market interest rates. To consider such effects, which may be important for understanding the interaction of the U.S. central bank with the real economy during the post-war period, one could introduce persistence into the sunspot process determining equilibrium selection.
7.3 Discretionary policy in other contexts
Our emphasis in this paper has been on the link between lack of commitment for monetary policy and multiple equilibria. However, the nature of the mechanism by which lack of commitment leads to multiple equilibria suggests that the phenomenon is more general. Whenever private agents' forecasts of future policy affect an endogenous state variable to which future policy responds, there is the potential for policy-induced complementarity among private agents actions. Just as in our model, even without ``structural'' complementarity among private agents, discretionary policy can create complementarity and lead to multiple equilibria.
A slight modification of Kydland and Prescott's flood control example fits into this framework. Suppose private agents choose among two locations, one of which experiences flooding with positive probability. Agents have idiosyncratic preferences over the two locations. After agents choose locations, a government chooses whether to impose taxes and undertake costly flood control. Suppose that the government is willing to let a small number of inhabitants be flooded, but will undertake flood control if enough agents move to the flood plain. There can be multiple equilibria here of the sort that arise in our model. When a single agent believes that no others will move to the flood plain, she knows that the government will not protect her, and chooses not to locate in the flood plain. When the agent believes that many others will move to the flood plain, she knows that the government will protect her, and she chooses to live in the flood plain. Thus, there is complementarity in agents' location decisions. That complementarity is not intrinsic, but is induced by the fact that location decisions determine a state (population in the floodplain) to which the future policymaker responds. If the policymaker could commit in advance to its action, it would determine a unique equilibrium.
Another example of lack of commitment leading to multiple equilibria comes from Glomm and Ravikumar's [1995] model of public expenditure on education. In their OLG model, young agents choose how much time to devote to learning, given their expectation of the income tax rate in the next period. Individual young agents' decisions in the current period determine next period's individual and aggregate stock of human capital. In turn, next period's government chooses the optimal tax rate as a function of the aggregate stock of human capital, in order to fund valued public education. Thus, the future tax rate effectively responds to expectations of the future tax rate. Or, equivalently, an individual agent's current decision about human capital accumulation depends on aggregate decisions because the aggregate determines the future state (capital) to which policy will respond. For certain parameterizations the policy response induces sufficiently complementarity among private agents' decisions that there are multiple equilibria. Again, with commitment the multiplicity disappears.
8 Summary and conclusions
We have described equilibria under discretionary monetary policy in a basic New-Keynesian model with two-period staggered price setting. The trade-off that our monetary authority faces is a familiar one. Output is inefficiently low because firms have monopoly power. This creates an incentive for the monetary authority to provide unexpected stimulus, exploiting the pre-set prices and raising output. However, when it exploits pre-set prices, the monetary authority also raises the dispersion of prices, leading to an inefficient allocation of resources. In equilibrium, the monetary authority is balancing the marginal contribution of these two effects.
While the monetary policy trade-off is familiar, the nature of equilibrium is not. Discretionary monetary policy leads to multiple equilibria. The multiplicity occurs because of complementarity in pricing behavior that is induced by the monetary authority's natural tendency to treat the level of pre-set nominal prices as a bygone. Under discretion, in each period the monetary authority moves the nominal money supply proportionately with the nominal level of pre-set prices. This feature of monetary policy means that higher prices set by firms in the current period will lead to a higher money supply (and even higher prices) in the subsequent period. Understanding this mechanism, an individual firm adjusting its price in the current period finds it optimal to raise its price in response to higher prices set by other firms. There is complementarity in pricing, and it leads to multiple equilibria.
When we consider discretionary equilibria that are driven by a sunspot variable, the equilibria involve random fluctuations between different real outcomes.15 If all firms choose to raise prices by a large amount because they (rationally) believe that others are raising prices, the result is a reduction in real aggregate demand and a decline in output relative to the level that would prevail if smaller price adjustments took place. Economic volatility then, as well as high inflation, may be a cost of discretion in monetary policy.
The mechanism leading to complementarity and multiple equilibria here transcends our example of monetary policy in a staggered pricing model. Other environments which share two features have the potential to generate similar results. First, private agents must be forward-looking and their actions must be influenced by their expectations about future policy. Second, private agents' actions must determine a state variable to which future policy responds. These features seem quite widespread, suggesting that lack of commitment may be an important cause of economic instability.
References
[1] Albanesi, Stefania, V.V. Chari and Lawrence Christiano (2002), ``Expectations Traps and Monetary Policy,'' NBER Working Paper 8912.
[2] Barro, Robert and David B. Gordon (1983), ``A Positive Theory of Monetary Policy in a Natural Rate Model,'' Journal of Political Economy 91, 589-610.
[3] Blanchard, Olivier J. and Nobuhiro Kiyotaki (1987), ``Monopolistic Competition and the Effects of Aggregate Demand,'' American Economic Review 77, 647-666.
[4] Chari, V.V., Lawrence J. Christiano and Martin Eichenbaum (1998), ``Expectations Traps and Discretion,'' Journal of Economic Theory.81, 462-492.
[5] Clarida, Richard, Jordi Gali and Mark Gertler (1999), ``The Science of Monetary Policy: A New Keynesian Perspective,'' Journal of Economic Literature 37, 1661-1707.
[6] Cooper, Russell W. and A. Andrew John (1988), ``Coordinating Coordination Failures in Keynesian Models,'' Quarterly Journal of Economics 103, 441-463.
[7] Dedola, Luca (2000), ``Credibility and the Gains from Commitment in a General Equilibrium Model,'' University of Rochester Ph.D. thesis.
[8] Dotsey, Michael and Andreas Hornstein (2004), unpublished notes on Discretionary Monetary Policy and Instrument Choice.
[9] Dotsey, Michael and Andreas Hornstein (2003), ``Should a monetary policymaker look at money?'' Journal of Monetary Economics 50, 547-79.
[10] Ennis, Huberto M. and Todd Keister (forthcoming), ``Government Policy and the Probability of Coordination Failures,'' European Economic Review.
[11] Glomm, Gerhard and B. Ravikumar (1995), ``Endogenous Public Policy and Multiple Equilibria.'' European Journal of Political Economy 11, 653-662.
[12] Goodfriend, Marvin (1993), ``Interest Rate Policy and the Inflation Scare Problem: 1979-92,'' Federal Reserve Bank of Richmond Economic Quarterly (Winter), pp. 1-24.
[13] Ireland, Peter (1997), ``Sustainable Monetary Policies.'' Journal of Economic Dynamics and Control 22 (November): 87-108.
[14] Khan, Aubhik, Robert G. King and Alexander L. Wolman (2001), ``The Pitfalls of Monetary Discretion,'' Federal Reserve Bank of Richmond Working Paper 01-8.
[15] Kimball, Miles S. (1995). ``The Quantitative Analytics of the Basic Neomonetarist Model'', Journal of Money, Credit, and Banking, 27, 1241-1277.
[16] King, Robert G. and Alexander L. Wolman (1999), ``What Should the Monetary Authority Do When Prices Are Sticky?'' in Monetary Policy Rules, John Taylor, ed. University of Chicago Press, 349-398
[17] Krusell, Per and Jose-Victor Rios-Rull (1999), ``On the Size of U.S. Government: Political Economy in the Neoclassical Growth Model,'' American Economic Review 89, 1156-1181.
[18] Kydland, Finn E. and Edward C. Prescott (1977), ``Rules Rather than Discretion: The Inconsistency of Optimal Plans,'' Journal of Political Economy 85, 473-492.
[19] Rotemberg, Julio J. (1987), ``The New Keynesian Microfoundations,'' NBER Macroeconomics Annual, MIT Press: Cambridge, MA.
[20] Wolman, Alexander L. (2001), ``A Primer on Optimal Monetary Policy in Sticky Price Models,'' Federal Reserve Bank of Richmond Economic Quarterly 87, 27-52.
[21] Woodford, Michael, (2003) Interest and Prices, Princeton University Press: Princeton, NJ, Chapter 3.
A Appendix
A.1 Proofs
where
Steady-state equilibria are thus fixed points of
(ii) For ![]() the function
the function
![]() is
strictly positive, strictly increasing, and strictly
convex
is
strictly positive, strictly increasing, and strictly
convex![]()
(iii) Define
![]() implicitly as follows:
implicitly as follows:
and
Convexity of
![]() implies that if
implies that if
![]() then
then
![]() does not have a fixed point, and if
does not have a fixed point, and if
![]() then
then
![]() has
two fixed points. We now need to show that for low
has
two fixed points. We now need to show that for low ![]()
![]() and for high
and for high ![]()
![]() From (27) and (26),
From (27) and (26),
![]() is equivalent to
is equivalent to
It is straightforward to show from (28) that there is a unique value of
for fixed
(i) The left side is strictly concave and increasing; the right
hand side is strictly increasing (since
![]() , and
either strictly concave (if
, and
either strictly concave (if
![]() ) or
strictly convex (if
) or
strictly convex (if
![]() ).
).
(ii)
![]() as
as
![]() ,
and
,
and
![]()
(iii)
![]()
![]() as
as
![]()
(iv) Thus, this equation has either two solutions or no solutions.
(v) Can show there is a unique ![]() call it
call it ![]() such that
such that ![]() and
and ![]() are
tangent.
are
tangent.
(iv) As ![]() increases
above
increases
above ![]() , solution
disappears; as
, solution
disappears; as ![]() decreases below
decreases below ![]() two solutions emerge
two solutions emerge
![]()
Figure 1. Steady-state best-response function for m > m*
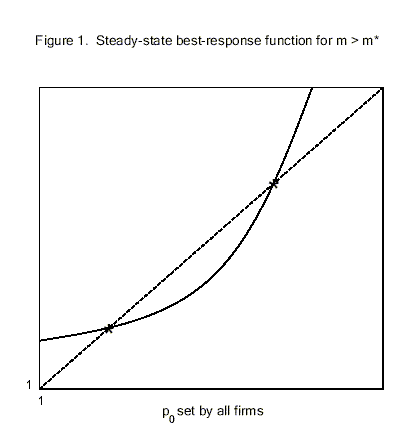
Figure 2. Point-in-time best response function for m=m' > m*
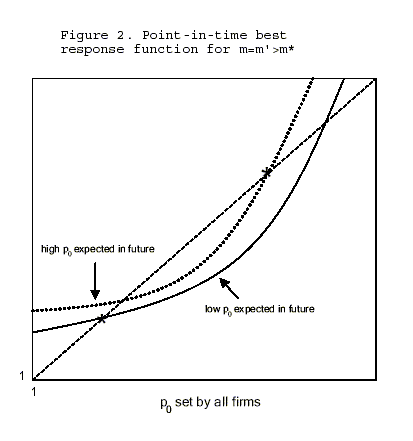
Figure 3. The temptation to stimulate a zero-inflation economy (m'=1.0)
Figure 4. Discretionary equilibrium with optimism (low 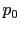 expectations) Equilibrium m=1.010
expectations) Equilibrium m=1.010
Figure 5. Discretionary equilibrium with Prob(low  )=0.6 . Equilibrium m=1.020156
)=0.6 . Equilibrium m=1.020156
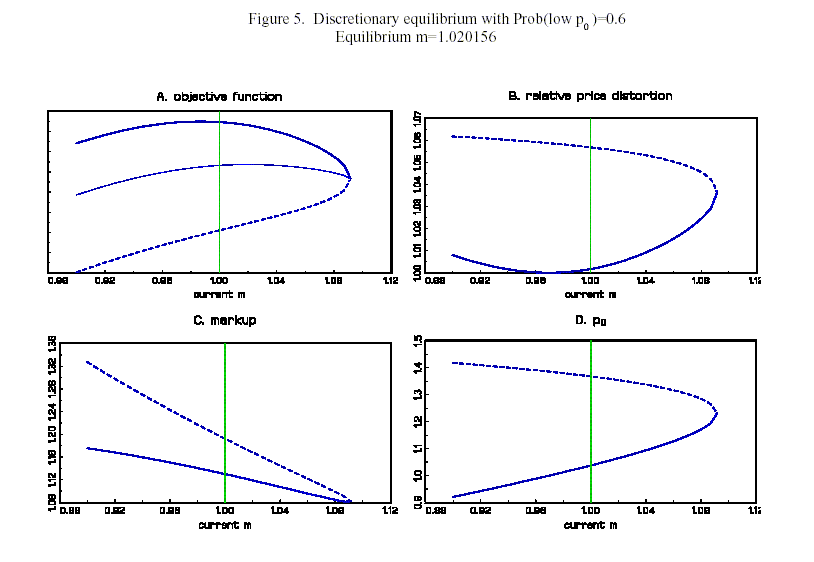
Footnotes
1. [email protected], Boston University and [email protected], Federal Reserve Bank of Richmond. This paper is an outgrowth of the authors' work in progress with Aubhik Khan, available at http://www.rich.frb.org/pubs/wpapers/pdfs/wp01-8.pdf; it does not necessarily represent the views of the Federal Reserve System, the Federal Reserve Board, or the Federal Reserve Bank of Richmond. We have benefited from converstations with Russell Cooper, Huberto Ennis, Mark Gertler, Andreas Hornstein, Olivier Jeanne, John Leahy and Henry Siu, and from presentations at Harvard, Iowa, MIT, the New York Fed, UQAM, Western Ontario, Wharton, York, the conference on Dynamic Models at the Bank of Canada, July 2003, and the International Research Forum on Monetary Policy, November 2003. Return to text
2. We think of this quantity equation as the limiting version of a standard money demand function which occurs as the own return on money is raised toward the nominal interest rate (see King and Wolman [1999] for some additional discussion). Return to text
3. The nonexistence of a discretionary equilibrium is a feature of Ireland's [1997] analysis of a model in which all prices are set simultaneously, before the monetary authority determines the current money supply. Return to text
4. It is important not to
misinterpret the parenthetical statement: any choice of
![]() can be replicated
by choosing
can be replicated
by choosing
![]() However, a policy of keeping
However, a policy of keeping
![]() constant is not
the same as a policy of keeping
constant is not
the same as a policy of keeping ![]() constant. Return to
text
constant. Return to
text
5. If the future monetary authority paid attention to nominal levels, it might be optimal for the current monetary authority to do the same. We do not consider equilibria with this property. Return to text
6. The word `` necessarily'' appears
because one could construct non-Markov equilibria in which all
agents agreed that ![]() did constrain the monetary authority. See previous footnote. We do
not study such equilibria. Return to
text
did constrain the monetary authority. See previous footnote. We do
not study such equilibria. Return to
text
7. By contrast, under commitment,
the monetary authority commits not to
respond to ![]() and
the choice is over sequences of
and
the choice is over sequences of ![]() King and Wolman (1999) study optimal policy
with commitment in the model used here. Return to text
King and Wolman (1999) study optimal policy
with commitment in the model used here. Return to text
8. If we impose
![]() but allow
but allow
![]() to differ from
to differ from
![]() then
(18) describes the dynamics of
then
(18) describes the dynamics of
![]() for constant
homogeneous policy. Such analysis might reveal interesting
dynamics. However, it is not an input into our analysis of
discretionary equilibrium. Return to
text
for constant
homogeneous policy. Such analysis might reveal interesting
dynamics. However, it is not an input into our analysis of
discretionary equilibrium. Return to
text
9. At this point in the analysis, we do not explicitly take into account the shut-down possibility. But, when we calculate discretionary equilibria, we do verify that the equilibria are robust to allowing firms to shut down. Return to text
10. Our model does not pin down the
distribution of the sunspot variable. However, some restrictions on
that distribution are imposed by the requirement that every firm's
profits be nonnegative in each period. For example, if ![]() is 0.75 rather than 0.6, this
condition is violated in the
is 0.75 rather than 0.6, this
condition is violated in the
![]() state, and no discretionary equilibrium exists. As in Ennis and
Keister (forthcoming), it would be interesting to study whether
adaptive learning schemes would further restrict the distribution
of the sunspot variable. Return to
text
state, and no discretionary equilibrium exists. As in Ennis and
Keister (forthcoming), it would be interesting to study whether
adaptive learning schemes would further restrict the distribution
of the sunspot variable. Return to
text
11. For a textbook treatment, see the derivation in Woodford [2002, chapter 3]. The inflation bias result under discretion within such optimizing New Keynesian models has been popularized by Clarida, Gali and Gertler [1999]. Return to text
12. Much of the New Keynesian literature uses the Calvo assumption of a constant probability of price adjustment. The Calvo assumption implies that a positive fraction of firms charge a price set arbitrarily far in the past. However, for many purposes this formulation has the advantage of tractability. For our purposes however the Calvo assumption is more complicated than two period staggered pricing, because it would add a real state variable to the monetary authority's problem. As we discuss below, adding a real state variable leaves intact the fundamental mechanism generating multiplicity. Return to text
13. Wolman [2001] illustrates the exact discretionary solution to the planner's problem in this model, and Dotsey and Hornstein [2003] solve the discretionary planner's problem of this model using an LQ approximation. In neither case does multiplicity arise. Return to text
14. Dedola (2000) studies discretionary policy in a Rotemberg-style model of pricing, and finds multiple equilibria. Dedola models money demand using a cash-in-advance constraint, and like Albanesi, Chari and Christiano, the multiple equilibria are related to the money demand specification. Return to text
15. The distribution of the sunspot variable shifts the equilibrium, and while we do not pin down that distribution, it is an integral part of the definition of equilibrium. Thus far, we have only considered i.i.d. sunspot variations, so as to produce the simplest possible explanation of the source and nature of multiple equilibria. In future work, we plan to extend the analysis to the implications of persistent sunspots. This extension would allow us to take the model more seriously as a potential explanation for some of the volatility observed in actual macroeconomic time series. Return to text
This version is optimized for use by screen readers. A printable pdf version is available.
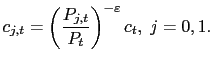
![$\displaystyle P_{t}=[\frac{1}{2}P_{0,t}^{1-\varepsilon}+\frac{1}{2}P_{1,t}^{1-\varepsilon }]^{\frac{1}{1-\varepsilon}}.$](img17.gif)
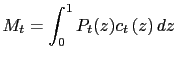
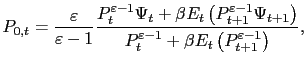
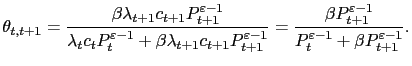
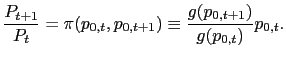
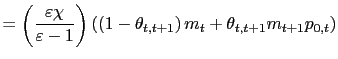
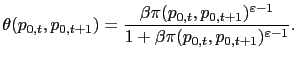
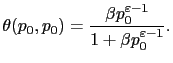
![$\displaystyle p_{0}=r\left( p_{0},m,p_{0}^{\prime},m^{\prime}\right) =\frac{1}{... ...ight) \right) m+\theta\left( p_{0},p_{0}^{\prime}\right) m^{\prime}p_{0}\right]$](img132.gif)
![$\displaystyle p_{0}=\frac{1}{m^{\ast}}\left[ \left( \frac{1}{1+\beta E\pi\left(... ...left( p_{0},p_{0}^{\prime}\right) ^{\varepsilon -1}m^{\prime}\right\} \right] ,$](img198.gif)