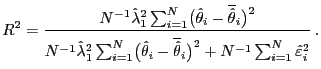Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 895, May 2007--- Screen Reader
Version*
A Note on the Coefficient of Determination in Models with Infinite Variance Variables1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Since the seminal work of Mandelbrot (1963), ![]() -stable distributions with infinite variance have been
regarded as a more realistic distributional assumption than the
normal distribution for some economic variables, especially
financial data. After providing a brief survey of theoretical
results on estimation and hypothesis testing in regression models
with infinite-variance variables, we examine the statistical
properties of the coefficient of determination in models with
-stable distributions with infinite variance have been
regarded as a more realistic distributional assumption than the
normal distribution for some economic variables, especially
financial data. After providing a brief survey of theoretical
results on estimation and hypothesis testing in regression models
with infinite-variance variables, we examine the statistical
properties of the coefficient of determination in models with ![]() -stable variables. If the regressor and
error term share the same index of stability
-stable variables. If the regressor and
error term share the same index of stability ![]() , the coefficient of determination has a
nondegenerate asymptotic distribution on the entire [0, 1] interval, and the density of this distribution is
unbounded at 0 and 1. We provide closed-form expressions
for the cumulative distribution function and probability density
function of this limit random variable. In contrast, if the indices
of stability of the regressor and error term are unequal, the
coefficient of determination converges in probability to
either 0 or 1, depending on which variable has the
smaller index of stability. In an empirical application, we revisit
the Fama-MacBeth two-stage regression and show that in the
infinite-variance case the coefficient of determination of the
second-stage regression converges to zero in probability even if
the slope coefficient is nonzero.
, the coefficient of determination has a
nondegenerate asymptotic distribution on the entire [0, 1] interval, and the density of this distribution is
unbounded at 0 and 1. We provide closed-form expressions
for the cumulative distribution function and probability density
function of this limit random variable. In contrast, if the indices
of stability of the regressor and error term are unequal, the
coefficient of determination converges in probability to
either 0 or 1, depending on which variable has the
smaller index of stability. In an empirical application, we revisit
the Fama-MacBeth two-stage regression and show that in the
infinite-variance case the coefficient of determination of the
second-stage regression converges to zero in probability even if
the slope coefficient is nonzero.
Keywords: Regression models, ![]() -stable distributions, infinite variance, coefficient
of determination, Fama-MacBeth regression, Monte Carlo simulation,
signal-to-noise ratio, density transformation theorem.
-stable distributions, infinite variance, coefficient
of determination, Fama-MacBeth regression, Monte Carlo simulation,
signal-to-noise ratio, density transformation theorem.
JEL classification: C12, C13, C21, G12
1 Introduction
Granger and Orr (1972) begin their article, " 'Infinite variance' and research strategy in time series analysis," by questioning the uncritical use of the normal distribution assumption in economic modelling and estimation:
Due in part to the influential seminal work of Mandelbrot
(1963), ![]() -stable distributions are often
considered to provide the basis for more realistic distributional
assumptions for some economic data, especially for high-frequency
financial time series such as those of exchange rate fluctuations
and stock returns. Financial time series are typically fat-tailed
and excessively peaked around their mean--phenomena that can be
better captured by
-stable distributions are often
considered to provide the basis for more realistic distributional
assumptions for some economic data, especially for high-frequency
financial time series such as those of exchange rate fluctuations
and stock returns. Financial time series are typically fat-tailed
and excessively peaked around their mean--phenomena that can be
better captured by ![]() -stable distributions
with
-stable distributions
with
![]() rather than by the normal
distribution, for which
rather than by the normal
distribution, for which ![]() .4 The
.4 The ![]() -stable distributional assumption with
-stable distributional assumption with
![]() is thus a generalization of rather
than an alternative to the Gaussian distributional assumption. If
an economic series fluctuates according to an
is thus a generalization of rather
than an alternative to the Gaussian distributional assumption. If
an economic series fluctuates according to an ![]() -stable distribution with
-stable distribution with ![]() , it
is known that many of the standard methods of statistical analysis,
which often rest on the asymptotic properties of sample second
moments, do not apply in the conventional way. In particular, as we
demonstrate in this paper, the coefficient of determination--a
standard criterion for judging goodness of fit in a regression
model--has several nonstandard statistical properties if
, it
is known that many of the standard methods of statistical analysis,
which often rest on the asymptotic properties of sample second
moments, do not apply in the conventional way. In particular, as we
demonstrate in this paper, the coefficient of determination--a
standard criterion for judging goodness of fit in a regression
model--has several nonstandard statistical properties if
![]() .
.
The linear regression model is one of the most commonly used and basic econometric tools, not only for the analysis of macroeconomic relationships but also for the study of financial market data. Typical examples for the latter case are estimation of the ex-post version of the capital asset pricing model (CAPM) and the two-stage modelling approach of Fama and MacBeth (1973). Because of the prevalence of heavy-tailed distributions in financial time series, it is of interest to study how regression models perform when the data are heavy-tailed rather normally distributed.
The first purpose of the present paper is to survey theoretical results of estimation and hypothesis testing in regression models with infinite-variance distributions, and the second is to establish that infinite variance of the regression variables has important consequences for the statistical properties of the coefficient of determination and tests of the hypothesis that this coefficient is equal to zero. Third, we revisit the Fama-MacBeth two-stage regression approach and demonstrate that infinite variance of the regression variables can affect decisively the interpretation of the empirical results.
The rest of our paper is structured as follows. In
Section 2 we provide a
brief summary of the properties of ![]() -stable
distributions and of aspects of estimation, hypothesis testing, and
model diagnostic checking in regression models with
infinite-variance regressors and disturbance terms.
Section 3
provides a detailed analysis of the asymptotic properties of the
coefficient of determination in regression models with
infinite-variance variables. In our empirical application,
presented in Section 4, we revisit the
data used in Fama and French (1992), and we show that the
statistical and/or economic interpretation of their findings can be
quite different under the maintained assumption of
-stable
distributions and of aspects of estimation, hypothesis testing, and
model diagnostic checking in regression models with
infinite-variance regressors and disturbance terms.
Section 3
provides a detailed analysis of the asymptotic properties of the
coefficient of determination in regression models with
infinite-variance variables. In our empirical application,
presented in Section 4, we revisit the
data used in Fama and French (1992), and we show that the
statistical and/or economic interpretation of their findings can be
quite different under the maintained assumption of ![]() -stable distributions from an interpretation based on
the assumption of normal distributions. Section 5 summarizes the
paper and offers some concluding remarks.
-stable distributions from an interpretation based on
the assumption of normal distributions. Section 5 summarizes the
paper and offers some concluding remarks.
2 Framework
2.1  -stable
distributions
-stable
distributions
A random variable ![]() is said to have a stable
distribution if, for any positive integer
is said to have a stable
distribution if, for any positive integer ![]() ,
there exist constants
,
there exist constants ![]() and
and
![]() such that
such that
![]() , where
, where
![]() are independent copies
of
are independent copies
of ![]() and
and
![]() signifies equality in
distribution. The coefficient
signifies equality in
distribution. The coefficient ![]() above is
necessarily of the form
above is
necessarily of the form
![]() for some
for some
![]() (see Feller, 1971,
Section VI). The parameter
(see Feller, 1971,
Section VI). The parameter ![]() is called the
index of stability of the distribution, and a random
variable
is called the
index of stability of the distribution, and a random
variable ![]() with index
with index ![]() is
called
is
called ![]() -stable. An
-stable. An ![]() -stable
distribution is described by four parameters and will be denoted by
-stable
distribution is described by four parameters and will be denoted by
![]() . Closed-form
expressions for the probability density functions of
. Closed-form
expressions for the probability density functions of ![]() -stable distributions are known to exist only for
three special cases.5 However, closed-form expressions for
the characteristic functions of
-stable distributions are known to exist only for
three special cases.5 However, closed-form expressions for
the characteristic functions of ![]() -stable
distributions are readily available. One parameterization of the
logarithm of the characteristic function of
-stable
distributions are readily available. One parameterization of the
logarithm of the characteristic function of
![]() is
is
where
The tail shape of an ![]() -stable distribution is
determined by its index of stability
-stable distribution is
determined by its index of stability
![]() . Skewness is governed by
. Skewness is governed by
![]() ; the distribution is symmetric
about
; the distribution is symmetric
about ![]() if and only if
if and only if ![]() . The scale and location parameters of
. The scale and location parameters of ![]() -stable distributions are denoted by
-stable distributions are denoted by ![]() and
and
![]() , respectively. When
, respectively. When
![]() , the log characteristic function
given by equation (1) reduces to
, the log characteristic function
given by equation (1) reduces to
![]() , which is that
of a Gaussian random variable with mean
, which is that
of a Gaussian random variable with mean ![]() and variance
and variance
![]() . For
. For ![]() and
and
![]() , the tail properties of
an
, the tail properties of
an ![]() -stable random
variable
-stable random
variable ![]() satisfy
satisfy
i.e., both tails of the probability density function (pdf)
of ![]() are asymptotically Paretian. For
are asymptotically Paretian. For
![]() and
and ![]() (
(![]() ), the distribution is maximally
right-skewed (left-skewed) and only the right (left) tail is
asymptotically Paretian.6 The term
), the distribution is maximally
right-skewed (left-skewed) and only the right (left) tail is
asymptotically Paretian.6 The term ![]() in
equations (2)
and (3) is
given by
in
equations (2)
and (3) is
given by
and
Because
![]() , it follows that
, it follows that
![]() for
for
![]() and
and
![]() for
for
![]() if
if ![]() is
is
![]() -stable with
-stable with
![]() .8 Only moments of order
up to but not including
.8 Only moments of order
up to but not including ![]() are finite if
are finite if
![]() , and a non-Gaussian stable
distribution's index of stability is also equal to its maximal
moment exponent.9 In particular, if
, and a non-Gaussian stable
distribution's index of stability is also equal to its maximal
moment exponent.9 In particular, if
![]() , the variance is infinite but
the mean exists. For
, the variance is infinite but
the mean exists. For ![]() , it follows that
, it follows that
![]() ; in addition, for
; in addition, for ![]() ,
, ![]() is equal to the
distribution's mode and median irrespective of the value
of
is equal to the
distribution's mode and median irrespective of the value
of ![]() , justifying the use of the term
``central location parameter'' for
, justifying the use of the term
``central location parameter'' for ![]() in the
finite-mean or symmetric cases. In addition, for
in the
finite-mean or symmetric cases. In addition, for
![]() , one can show that
, one can show that
![]() .10 We make use of this property below
in the derivations of Theorem 1 and
Remark 3.
.10 We make use of this property below
in the derivations of Theorem 1 and
Remark 3.
The class of ![]() -stable distributions is an
interesting distributional candidate for disturbances in regression
models because (i) it is able to capture the relative frequencies
of extreme vs.observations in the economic variables, (ii) it has
the convenient statistical property of closure under convolution,
and (iii) only
-stable distributions is an
interesting distributional candidate for disturbances in regression
models because (i) it is able to capture the relative frequencies
of extreme vs.observations in the economic variables, (ii) it has
the convenient statistical property of closure under convolution,
and (iii) only ![]() -stable distributions can
serve as limiting distributions of sums of independent and
identically distributed (iid) random variables, as proven in
Zolotarev (1986). The latter two properties are appealing for
regression analysis, given that disturbances can be viewed as
random variables which represent the sum of all external effects
not captured by the regressors. For more details on the properties
of
-stable distributions can
serve as limiting distributions of sums of independent and
identically distributed (iid) random variables, as proven in
Zolotarev (1986). The latter two properties are appealing for
regression analysis, given that disturbances can be viewed as
random variables which represent the sum of all external effects
not captured by the regressors. For more details on the properties
of ![]() -stable distributions, we refer to
Gnedenko and Kolmogorov (1954), Feller (1971), Zolotarev (1986),
and Samorodnitsky and Taqqu (1994). The role of the
-stable distributions, we refer to
Gnedenko and Kolmogorov (1954), Feller (1971), Zolotarev (1986),
and Samorodnitsky and Taqqu (1994). The role of the ![]() -stable distribution in financial market and
econometric modelling is surveyed in McCulloch (1996) and Rachev
et al.1999).
-stable distribution in financial market and
econometric modelling is surveyed in McCulloch (1996) and Rachev
et al.1999).
2.2 Regression models with infinite-variance variables
Let ![]() and
and ![]() be two jointly
symmetric
be two jointly
symmetric ![]() -stable (henceforth,
-stable (henceforth, ![]() ) random variables with
) random variables with ![]() ,
i.e., we require
,
i.e., we require ![]() and
and ![]() to have
finite means. Our main reason for concentrating on the case
to have
finite means. Our main reason for concentrating on the case
![]() lies in its empirical relevance.
Estimated maximal moment exponents for most empirical financial
data, such as exchange rates and stock prices, are generally
greater than 1.5; see, for example, de Vries (1991) and
Loretan and Phillips (1994). An econometric (purposeful) reason for
studying the case
lies in its empirical relevance.
Estimated maximal moment exponents for most empirical financial
data, such as exchange rates and stock prices, are generally
greater than 1.5; see, for example, de Vries (1991) and
Loretan and Phillips (1994). An econometric (purposeful) reason for
studying the case ![]() is that, for
is that, for
![]() -stable distributions with
-stable distributions with ![]() , regression analysis that is based on sample
second moments, such as least squares, is still asymptotically
consistent for the regression coefficients, even though the limit
distributions of these regression coefficients are
nonstandard.11 Suppose that the regression of a
random variable
, regression analysis that is based on sample
second moments, such as least squares, is still asymptotically
consistent for the regression coefficients, even though the limit
distributions of these regression coefficients are
nonstandard.11 Suppose that the regression of a
random variable ![]() on a random
variable
on a random
variable ![]() is linear, i.e., there exists a
constant
is linear, i.e., there exists a
constant ![]() such that
such that
with
![$\displaystyle \theta=\frac{[Y,X]_{\alpha}}{{\gamma_{x}}^{\alpha}}X, $](img145.gif)
where
![]() is the scale parameter of the
is the scale parameter of the
![]() variable
variable ![]() and
and
![]() in the numerator is
covariation (covariance in the Gaussian case), which can be
calculated as
in the numerator is
covariation (covariance in the Gaussian case), which can be
calculated as
![]() , for all
, for all
![]() with
with
![]() .
.
For estimation and diagnostics, the relation (5) can be written as a regression model with a constant term,
where the maintained hypothesis is that ![]() is iid
is iid
![]() , with
, with
![]() . The econometric issues of
interest are to estimate
. The econometric issues of
interest are to estimate ![]() properly, to test the
hypothesis of significance for the estimated parameter, usually
based on the
properly, to test the
hypothesis of significance for the estimated parameter, usually
based on the ![]() -statistic, as well as to compute model
diagnostics, such as the coefficient of determination, the
Durbin-Watson statistic, and the
-statistic, as well as to compute model
diagnostics, such as the coefficient of determination, the
Durbin-Watson statistic, and the ![]() -test of parameter
constancy across subsamples.
-test of parameter
constancy across subsamples.
The effects of infinite variance in the regressor and
disturbance term can be substantial. If the variables share the
same index of stability ![]() , the ordinary
least squares (OLS) estimate of
, the ordinary
least squares (OLS) estimate of ![]() is
still consistent, but its asymptotic distribution is
is
still consistent, but its asymptotic distribution is ![]() -stable with the same
-stable with the same ![]() as the
underlying variables. Furthermore, the convergence rate to the true
parameter is
as the
underlying variables. Furthermore, the convergence rate to the true
parameter is
![]() , smaller than the rate
, smaller than the rate
![]() which applies in the finite-variance
case. If
which applies in the finite-variance
case. If ![]() , OLS loses its best linear
unbiased estimator (BLUE) property, i.e., it is no longer the
minimum-dispersion estimator in the class of linear estimators
of
, OLS loses its best linear
unbiased estimator (BLUE) property, i.e., it is no longer the
minimum-dispersion estimator in the class of linear estimators
of ![]() . In addition, the asymptotic
efficiency of the OLS estimator converges to zero as the index of
stability
. In addition, the asymptotic
efficiency of the OLS estimator converges to zero as the index of
stability ![]() declines to
declines to ![]() .
Blattberg and Sargent (1971) (henceforth, BS) derived the BLUE
for
.
Blattberg and Sargent (1971) (henceforth, BS) derived the BLUE
for ![]() in (6) if the value
of
in (6) if the value
of ![]() is known. The BS estimator is given
by
is known. The BS estimator is given
by
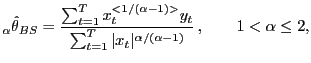
|
(7) |
which coincides with the OLS estimator if ![]() .
Kim and Rachev (1999) prove that the asymptotic distribution of the
BS estimator is also
.
Kim and Rachev (1999) prove that the asymptotic distribution of the
BS estimator is also ![]() -stable. Samorodnitsky
et al.2007) consider an optimal power estimate based on the BS
estimator for unknown
-stable. Samorodnitsky
et al.2007) consider an optimal power estimate based on the BS
estimator for unknown ![]() , and they
also provide an optimal linear estimator of the regression
coefficients for various configurations of the indices of stability
of
, and they
also provide an optimal linear estimator of the regression
coefficients for various configurations of the indices of stability
of ![]() and
and ![]() . Other
efficient estimators of the regression coefficients have been
studied as well; Kanter and Steiger (1974) propose an unbiased
. Other
efficient estimators of the regression coefficients have been
studied as well; Kanter and Steiger (1974) propose an unbiased
![]() -estimator, which excludes very large
shocks in its estimation to avoid excess sensitivity due to
outliers. Using a weighting function, McCulloch (1998) considers a
maximum-likelihood estimator which is based on an approximation to
a symmetric stable density.
-estimator, which excludes very large
shocks in its estimation to avoid excess sensitivity due to
outliers. Using a weighting function, McCulloch (1998) considers a
maximum-likelihood estimator which is based on an approximation to
a symmetric stable density.
Hypothesis testing is also affected considerably when the
regressors and disturbance terms have infinite-variance stable
distributions. For example, the ![]() -statistic,
commonly used to test the null hypothesis of parameter
significance, no longer has a conventional Student-
-statistic,
commonly used to test the null hypothesis of parameter
significance, no longer has a conventional Student-![]() distribution if
distribution if ![]() . Rather, as established
by Logan et al.1973), its pdf has modes at
. Rather, as established
by Logan et al.1973), its pdf has modes at ![]() and
and ![]() ; for
; for ![]() these modes are infinite. Kim (2003) provides
empirical distributions of the
these modes are infinite. Kim (2003) provides
empirical distributions of the ![]() -statistic for
finite degrees of freedom and various values of
-statistic for
finite degrees of freedom and various values of ![]() by simulation. The usual applied goodness-of-fit test
statistics, such as the likelihood ratio, Lagrange multiplier, and
Wald statistics, also no longer have the conventional asymptotic
by simulation. The usual applied goodness-of-fit test
statistics, such as the likelihood ratio, Lagrange multiplier, and
Wald statistics, also no longer have the conventional asymptotic
![]() distribution, but have a stable
distribution, but have a stable
![]() distribution, a term that was
introduced by Mittnik et al.1998).
distribution, a term that was
introduced by Mittnik et al.1998).
In time series regressions with infinite-variance innovations,
Phillips (1990) shows that the limit distribution of the augmented
Dickey-Fuller tests for a unit root are functionals of Lévy
processes, whereas they are functionals of Brownian motion
processes in the finite-variance case. The ![]() -test
statistic for parameter constancy that is based on the residuals
from a sample split test has an
-test
statistic for parameter constancy that is based on the residuals
from a sample split test has an ![]() -distribution in
the conventional, finite-variance case. Kurz-Kim et al.2005)
obtain the limiting distribution of the
-distribution in
the conventional, finite-variance case. Kurz-Kim et al.2005)
obtain the limiting distribution of the ![]() -test if the
random variables have infinite variance. As shown by the authors,
as well as by Runde (1993), the limiting distribution of the
-test if the
random variables have infinite variance. As shown by the authors,
as well as by Runde (1993), the limiting distribution of the
![]() -statistic for
-statistic for ![]() behaves completely differently from the Gaussian
case: whereas in the latter case the statistic converges to 1
under the null as the degrees of freedom for both numerator and
denominator of the statistic approach infinity, in the former case
the statistic converges to a ratio of two independent, positive,
and maximally right-skewed
behaves completely differently from the Gaussian
case: whereas in the latter case the statistic converges to 1
under the null as the degrees of freedom for both numerator and
denominator of the statistic approach infinity, in the former case
the statistic converges to a ratio of two independent, positive,
and maximally right-skewed
![]() -stable distributions. This result
is used below to derive closed-form expressions for the pdf and
cumulative distribution function (cdf) of the limiting distribution
of the
-stable distributions. This result
is used below to derive closed-form expressions for the pdf and
cumulative distribution function (cdf) of the limiting distribution
of the ![]() statistic if the regressor and
disturbance term share the same index of stability
statistic if the regressor and
disturbance term share the same index of stability ![]() .
.
Moreover, commonly used criteria for judging the validity of
some of the maintained hypotheses of a regression model, such as
the Durbin-Watson statistic and the Box-Pierce ![]() -statistic, would be inappropriate if one were to rely on
conventional critical values. Phillips and Loretan (1991) study the
properties of the Durbin-Watson statistic for regression residuals
with infinite variance, and Runde (1997) examines the properties of
the Box-Pierce
-statistic, would be inappropriate if one were to rely on
conventional critical values. Phillips and Loretan (1991) study the
properties of the Durbin-Watson statistic for regression residuals
with infinite variance, and Runde (1997) examines the properties of
the Box-Pierce ![]() -statistic for random variables
with infinite variance. Loretan and Phillips (1994) and Phillips
and Loretan (1994) establish that both the size of tests of
covariance stationarity under the null and their rate of divergence
of these tests under the alternative are strongly affected by
failure of standard moment conditions; indeed, standard tests of
covariance stationarity are inconsistent if population
second moments do not exist.
-statistic for random variables
with infinite variance. Loretan and Phillips (1994) and Phillips
and Loretan (1994) establish that both the size of tests of
covariance stationarity under the null and their rate of divergence
of these tests under the alternative are strongly affected by
failure of standard moment conditions; indeed, standard tests of
covariance stationarity are inconsistent if population
second moments do not exist.
3 Asymptotic properties of the
coefficient of determination in models with  -stable regressors and error terms
-stable regressors and error terms
3.1 Basic results
For the general asymptotic theory of stochastic processes with stable random variables, we refer to Resnick (1986) and Davis and Resnick (1985a, 1985b, 1986). Our results in this section are, in large part, an application of their work to the regression diagnostic context.
The maintained assumptions are:
- The relationship between the dependent and independent variable
conforms to the classical bivariate linear regression model,
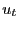 is iid
is iid 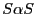
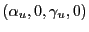 , with
, with
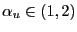 .
.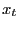 is exogenous and is also iid
is exogenous and is also iid
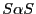
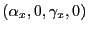 , with
, with
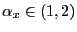 .
.- The regressor and the error term have the same index of
stability, i.e.,
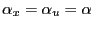 .
. - The coefficients
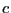 and
and 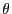 are consistently estimated
by
are consistently estimated
by 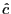 and
and
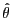 .12
.12
The fourth assumption, that the regressor and the error term
have the same index of stability, is rather strong, and its
validity may be difficult to ascertain in empirical applications.
In Corollary 2
below, we examine the consequences of having unequal values for the
indices of stability for ![]() and
and ![]() for the asymptotic properties of the coefficient of
determination.
for the asymptotic properties of the coefficient of
determination.
The coefficient of determination measures the proportion of the total squared variation in the dependent variable that is explained by the regression:
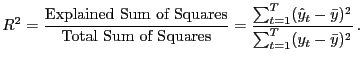
Because
![]() and
and
![]() , where
, where
![]() and
and ![]() are the
respective sample averages of
are the
respective sample averages of ![]() and
and ![]() , and because
, and because
![]() =0 by
construction, the coefficient of determination may be written as
=0 by
construction, the coefficient of determination may be written as
Since ![]() and
and ![]() are
in the normal domain of attraction of a stable distribution with
index of stability
are
in the normal domain of attraction of a stable distribution with
index of stability
![]() , norming by
, norming by
![]() rather than
by
rather than
by ![]() is required to obtain non-degenerate
limits for the sums of the squared variables. Because
is required to obtain non-degenerate
limits for the sums of the squared variables. Because
![]() by the assumption
of consistent estimation, an application of the law of large
numbers to
by the assumption
of consistent estimation, an application of the law of large
numbers to ![]() , the continuous mapping
theorem, and the results of Davis and Resnick (1985b) yield the
following expression for the joint limiting distribution of the
elements in equation (9):
, the continuous mapping
theorem, and the results of Davis and Resnick (1985b) yield the
following expression for the joint limiting distribution of the
elements in equation (9):
For ![]() , the random variables
, the random variables
![]() and
and ![]() are
independent, maximally right-skewed, and positive stable random
variables with index of stability
are
independent, maximally right-skewed, and positive stable random
variables with index of stability
![]() ,
, ![]() ,
,
![]() ,13
,13 ![]() , and log characteristic function
, and log characteristic function
We therefore conclude that, under the five maintained
assumptions of this section, the ![]() statistic of
the regression model (8) has the
following asymptotic distribution.
statistic of
the regression model (8) has the
following asymptotic distribution.
where
Thus, for ![]() and
and ![]() , the coefficient of determination does not
converge to a constant but has a nondegenerate asymptotic
distribution on the interval
, the coefficient of determination does not
converge to a constant but has a nondegenerate asymptotic
distribution on the interval ![]() . This
contrasts starkly with the standard, finite-variance result, which
is stated here for completeness.
. This
contrasts starkly with the standard, finite-variance result, which
is stated here for completeness.
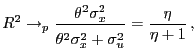
In the finite-variance case, the model's asymptotic
signal-to-noise ratio,
![]() , is
constant, as is therefore the limit of the coefficient of
determination. In contrast, in the infinite-variance case the
model's limiting signal-to-noise ratio is given by
, is
constant, as is therefore the limit of the coefficient of
determination. In contrast, in the infinite-variance case the
model's limiting signal-to-noise ratio is given by ![]() , where
, where
![]() and
and
![]() , and is therefore a random
variable even asymptotically; it is this feature that causes the
randomness of
, and is therefore a random
variable even asymptotically; it is this feature that causes the
randomness of
![]() . We postpone a
fuller discussion of the intuition that underlies this result to
the end of this section, after we provide a detailed analysis of
the statistical properties of
. We postpone a
fuller discussion of the intuition that underlies this result to
the end of this section, after we provide a detailed analysis of
the statistical properties of
![]() .
.
Before doing so, however, we note that the fourth maintained
assumption, i.e., that the indices of stability of the regressor
and error term in (8) be the same, is
crucial for obtaining the result that the asymptotic distribution
of
![]() is nondegenerate. Indeed, if
the two indices of stability differ, the asymptotic properties of
the
is nondegenerate. Indeed, if
the two indices of stability differ, the asymptotic properties of
the ![]() statistic are as follows.
statistic are as follows.
Corollary 2
Suppose that the maintained assumptions of
Theorem 1 apply
except that
![]() , i.e., suppose that
the indices of stability of the regressor and error term are
unequal. Let
, i.e., suppose that
the indices of stability of the regressor and error term are
unequal. Let
![]() to rule out the trivial case from
further consideration. Then,
to rule out the trivial case from
further consideration. Then,
- if
 ,
,
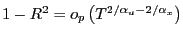 ;
and
;
and - if
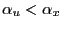 ,
,
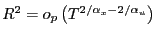 .
.
Thus, ![]() converges to
converges to ![]() in probability if
in probability if
![]() , and it converges
to 0 in probability if
, and it converges
to 0 in probability if
![]() .
.
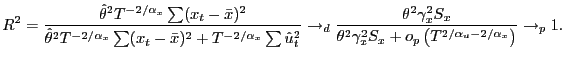
|
Similarly, if
Heuristically, if
![]() and
and
![]() , the limiting distribution of the
, the limiting distribution of the
![]() statistic is degenerate at 0
or 1 because the model's asymptotic signal-to-noise ratio is
either zero (if
statistic is degenerate at 0
or 1 because the model's asymptotic signal-to-noise ratio is
either zero (if
![]() ) or infinite (if
) or infinite (if
![]() ). From an
examination of the proof of this corollary, we can also deduce that
if
). From an
examination of the proof of this corollary, we can also deduce that
if
![]() , the fifth
maintained assumption--that the regression coefficients are
estimated consistently--could be relaxed, to require merely that an
estimation method be employed that guarantees
, the fifth
maintained assumption--that the regression coefficients are
estimated consistently--could be relaxed, to require merely that an
estimation method be employed that guarantees
![]() ; the result that
; the result that
![]() converges either to 0 or 1
would continue to hold in this case.
converges either to 0 or 1
would continue to hold in this case.
3.2 Qualitative properties of
Returning to the main case of
![]() , we note that
the random variable
, we note that
the random variable
![]() is defined for all values of
is defined for all values of
![]() , even though in a regression
context one would typically assume that
, even though in a regression
context one would typically assume that
![]() . We now establish some
important qualitative properties of
. We now establish some
important qualitative properties of
![]() .
.
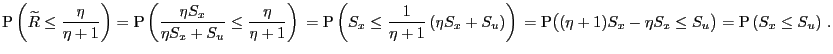
|
Because
Thus, ![]() is equal to the non-random limit
of
is equal to the non-random limit
of ![]() in the finite-variance case. Since
in the finite-variance case. Since
![]() and
and ![]() are positive
a.s., we also have
are positive
a.s., we also have
![]() ,
i.e., the median of
,
i.e., the median of ![]() is equal to 1,
regardless of the value of
is equal to 1,
regardless of the value of ![]() . As we will
demonstrate rigorously later in this paper, the probability mass
of
. As we will
demonstrate rigorously later in this paper, the probability mass
of ![]() is highly concentrated around 1 for
values of
is highly concentrated around 1 for
values of ![]() close to 2. Conversely, for
small values of
close to 2. Conversely, for
small values of ![]() ,
, ![]() is unlikely to be close to 1; instead, it is very
likely that one will obtain a draw of
is unlikely to be close to 1; instead, it is very
likely that one will obtain a draw of ![]() that is
either very small, i.e., close to 0, or very large. A small or
large draw of
that is
either very small, i.e., close to 0, or very large. A small or
large draw of ![]() has a crucial effect on the
model's signal-to-noise ratio,
has a crucial effect on the
model's signal-to-noise ratio, ![]() , and
therefore also on
, and
therefore also on ![]() . This suggests that an
informal measure of the effect of infinite variance in the
regression variables on the value of
. This suggests that an
informal measure of the effect of infinite variance in the
regression variables on the value of ![]() in
a given sample may be based on the difference between the
model's coefficient of determination and a consistent estimate of
its median
in
a given sample may be based on the difference between the
model's coefficient of determination and a consistent estimate of
its median ![]() , say
, say
![]() , where
, where
![]() . The larger the difference between
. The larger the difference between ![]() and
and ![]() , the more important the effect is of
having obtained a small (or large) value of
, the more important the effect is of
having obtained a small (or large) value of ![]() .
.
The following remark shows that a finite-variance property
of
![]() for
for ![]() ,
viz.,
,
viz.,
![]() , carries over in
a natural way to
, carries over in
a natural way to
![]() .
.
or equivalently,
The distribution of
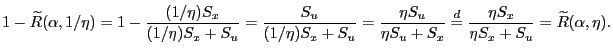
|
The symmetry of ![]() about
about ![]() for
for
![]() follows immediately from this result
and the fact that the distribution's support is the
interval [0, 1].
follows immediately from this result
and the fact that the distribution's support is the
interval [0, 1].
Next, as the following remark shows, the pdf of
![]() has infinite modes
at 0 and
has infinite modes
at 0 and ![]() , i.e., at the
endpoints of its support.
, i.e., at the
endpoints of its support.

|
where the joint pdf
![]() is nonzero on
is nonzero on
![]() . The case
. The case
![]() can occur only if
can occur only if ![]() ; if
; if ![]() , however, the random
variables
, however, the random
variables ![]() and
and ![]() are
perfectly dependent, their joint pdf is nonzero only on the
positive
are
perfectly dependent, their joint pdf is nonzero only on the
positive ![]() -halfline, and the joint pdf
-halfline, and the joint pdf
![]() reduces to
reduces to
![]() ,
, ![]() .
Hence, for
.
Hence, for ![]() we find
we find
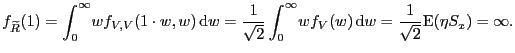
|
By Remark 2, we have
![]() as well. The continuity
of the cdf of
as well. The continuity
of the cdf of ![]() on
on ![]() for
for
![]() follows from the continuity of the
cdfs of
follows from the continuity of the
cdfs of ![]() and
and ![]() on
on
![]() and the fact that their pdfs
are equal to zero at the origin. For example, one finds that
and the fact that their pdfs
are equal to zero at the origin. For example, one finds that
![]() ; the result
; the result
![]() then follows from
Remark 2.
then follows from
Remark 2.
The fact that the probability density function of
![]() has infinite singularities
may seem unusual. However, the presence of singularities is a
regular feature of pdfs that are based on ratios of stable
random variables. For example, Logan et al.1973) and Phillips
and Hajivassiliou (1987) showed that if
has infinite singularities
may seem unusual. However, the presence of singularities is a
regular feature of pdfs that are based on ratios of stable
random variables. For example, Logan et al.1973) and Phillips
and Hajivassiliou (1987) showed that if ![]() ,
the density of the
,
the density of the ![]() -statistic has infinite
modes at
-statistic has infinite
modes at ![]() and
and ![]() ; similarly,
Phillips and Loretan (1991) demonstrated that if
; similarly,
Phillips and Loretan (1991) demonstrated that if ![]() , this feature is also present in the asymptotic
distributions of the von Neuman ratio and the normalized
Durbin-Watson test statistic.
, this feature is also present in the asymptotic
distributions of the von Neuman ratio and the normalized
Durbin-Watson test statistic.
3.3 The cdf and pdf of
The remarks in the preceding subsection provide important
qualitative information about some of the distributional properties
of
![]() . However, they do not
address issues such as whether the distribution has modes beyond
those at 0 and 1, whether the discontinuity of the pdf at
the endpoints is simple or if
. However, they do not
address issues such as whether the distribution has modes beyond
those at 0 and 1, whether the discontinuity of the pdf at
the endpoints is simple or if
![]() diverges--and, if so,
at which rate--as
diverges--and, if so,
at which rate--as
![]() or
or
![]() , or how much of the
distribution's mass is concentrated near the endpoints of the
support. To examine these issues, we provide expressions for the
cdf and pdf of
, or how much of the
distribution's mass is concentrated near the endpoints of the
support. To examine these issues, we provide expressions for the
cdf and pdf of
![]() in this subsection.
It is possible to do so because
in this subsection.
It is possible to do so because
![]() is a continuously
differentiable and invertible function of the ratio of two
independent, maximally right-skewed, and positive
is a continuously
differentiable and invertible function of the ratio of two
independent, maximally right-skewed, and positive ![]() -stable random variables, and because closed-form
expressions for the cdf and pdf of this ratio are known. The latter
expressions are provided in the following proposition.
-stable random variables, and because closed-form
expressions for the cdf and pdf of this ratio are known. The latter
expressions are provided in the following proposition.
Differentiating this expression with respect to
As
The cdf of the random variable ![]() is shown in
Figure 2 for various values of
is shown in
Figure 2 for various values of ![]() between 1.98 and 0.25.18The random variable
between 1.98 and 0.25.18The random variable
![]() has several interesting properties. First,
note that
has several interesting properties. First,
note that
![]() and that
the rate of divergence to infinity of
and that
the rate of divergence to infinity of ![]() as
as
![]() is given by
is given by
![]() ; thus, the pdf
of
; thus, the pdf
of ![]() has a one-sided infinite singularity
at 0. Second, as
has a one-sided infinite singularity
at 0. Second, as
![]() ,
,
![]() for a suitable
constant
for a suitable
constant ![]() . This result, along with
. This result, along with
![]() , implies that
, implies that ![]() lies in the normal domain of attraction of a positive
stable distribution, say
lies in the normal domain of attraction of a positive
stable distribution, say
![]() , with index of stability
, with index of stability
![]() and
and ![]() , the
same parameters as that of the variables
, the
same parameters as that of the variables ![]() and
and ![]() .19 Hence, the mean
of
.19 Hence, the mean
of ![]() is infinite for all values of
is infinite for all values of ![]() . Third, in the special case of
. Third, in the special case of ![]() ,
, ![]() and
and ![]() are
each distributed as a Lévy
are
each distributed as a Lévy ![]() -stable
random variable, which is well known to be equivalent to the
inverse of a
-stable
random variable, which is well known to be equivalent to the
inverse of a
![]() random variable. For
random variable. For ![]() , then, the pdf of
, then, the pdf of ![]() reduces to
reduces to
![]() , which is
also the pdf of an
, which is
also the pdf of an ![]() distribution; see
Runde (1993).
distribution; see
Runde (1993).
As was noted earlier, the median of ![]() is
equal to 1 for all values of
is
equal to 1 for all values of
![]() . The regression model's
signal-to-noise ratio is given by the random
variable
. The regression model's
signal-to-noise ratio is given by the random
variable ![]() if
if ![]() ,
whereas it is given by the constant
,
whereas it is given by the constant ![]() in
the standard, i.e., finite-variance case. The fact that the random
variable which multiplies
in
the standard, i.e., finite-variance case. The fact that the random
variable which multiplies ![]() has a median
of 1 helps to develop further the intuition that underlies the
result of Remark 1, viz.,the
median of
has a median
of 1 helps to develop further the intuition that underlies the
result of Remark 1, viz.,the
median of
![]() ,
,
![]() , is the same in both the
finite-variance and the infinite-variance cases. Finally, an
inspection of equation (13) reveals that
, is the same in both the
finite-variance and the infinite-variance cases. Finally, an
inspection of equation (13) reveals that
![]() and
and
![]() ; put
differently,
; put
differently,
![]() . The
probability mass of
. The
probability mass of ![]() therefore becomes perfectly
concentrated at 1 as
therefore becomes perfectly
concentrated at 1 as
![]() , even though, of course, its
mean remains infinite as long as
, even though, of course, its
mean remains infinite as long as ![]() .
.
From Theorem 1, we have
![]() , say.
Note that
, say.
Note that
![]() satisfies the conditions
of Proposition 1 and that the
function
satisfies the conditions
of Proposition 1 and that the
function
![]() is continuously differentiable and strictly increasing in the
interior of its domain. We are therefore able to provide the
following expressions for the cdf and pdf of
is continuously differentiable and strictly increasing in the
interior of its domain. We are therefore able to provide the
following expressions for the cdf and pdf of
![]() by an application of the
density transformation theorem.20
by an application of the
density transformation theorem.20
Furthermore,
The pdf of
![]() for
for ![]() is given by
is given by
As
The probability density functions and cumulative distribution
functions of
![]() for values of
for values of
![]() between 0.25 and 1.98 are
graphed in Figures 3 and 4. (In all cases, we have set
between 0.25 and 1.98 are
graphed in Figures 3 and 4. (In all cases, we have set
![]() .) The pdfs in Figure 3 are shown
with a logarithmic scale on the ordinate. Since we know that
.) The pdfs in Figure 3 are shown
with a logarithmic scale on the ordinate. Since we know that
![]() , we
graph the functions only for
, we
graph the functions only for
![]() . The
graphs show that
. The
graphs show that
- If
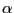 is close to but less than 2,
e.g., if
is close to but less than 2,
e.g., if
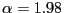 or
or
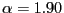 , the pdf has an interior mode,
and most of the probability mass of
, the pdf has an interior mode,
and most of the probability mass of
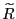 is concentrated near its
median. Conversely, only very little mass is located near 0
and 1, and the pdfs register only mild increases
as
is concentrated near its
median. Conversely, only very little mass is located near 0
and 1, and the pdfs register only mild increases
as 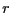 approaches either edge of the
distribution's support.
approaches either edge of the
distribution's support. - For
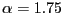 and
and
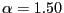 , the distribution of
, the distribution of
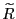 continues to have an
interior mode (as well as, of course, the two unbounded modes
at 0 and 1). However, the distribution is noticeably less
concentrated around the interior mode than if
continues to have an
interior mode (as well as, of course, the two unbounded modes
at 0 and 1). However, the distribution is noticeably less
concentrated around the interior mode than if 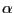 is closer to 2.
is closer to 2. - By
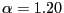 , the interior mode has
disappeared and the distribution is nearly uniform over the entire
interval
, the interior mode has
disappeared and the distribution is nearly uniform over the entire
interval ![$ [0,1]$](img545.gif) .
. - If
 takes on even smaller values, less
and less of the probability mass of
takes on even smaller values, less
and less of the probability mass of
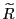 is located near the median,
and more and more of it is concentrated close to 0
and 1.
is located near the median,
and more and more of it is concentrated close to 0
and 1. - If
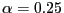 , about 75 percent of the
probability mass lies within 0.001 of the two endpoints of the
distribution, while the probability of observing a realization
of
, about 75 percent of the
probability mass lies within 0.001 of the two endpoints of the
distribution, while the probability of observing a realization
of
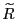 for
for
![$ r\in[0.25,0.75]$](img550.gif) is less than 5 percent.
is less than 5 percent.
A heuristic summary of these properties of
![]() is straightforward. We begin
by recalling that the multiplicative term
is straightforward. We begin
by recalling that the multiplicative term
![]() , shown in equation (4) and
Figure 1, affects the probability of tail-region values of the
random variables in question, and that the rate of decline in the
tail areas of density of
, shown in equation (4) and
Figure 1, affects the probability of tail-region values of the
random variables in question, and that the rate of decline in the
tail areas of density of ![]() -stable random
variables increases as
-stable random
variables increases as
![]() . Suppose first
that
. Suppose first
that ![]() is very close to 2; then,
is very close to 2; then,
![]() is close to 0, and the
fraction of observations of
is close to 0, and the
fraction of observations of ![]() and
and ![]() that fall into the respective
Paretian-tail regions is therefore very low; moreover, given the
fairly rapid decay of the density's tails for
that fall into the respective
Paretian-tail regions is therefore very low; moreover, given the
fairly rapid decay of the density's tails for ![]() close to 2, the likelihood of obtaining a very
large draw, conditional on obtaining a draw from the Paretian tail
area, is also low. As a result, the probability of observing large
observations of
close to 2, the likelihood of obtaining a very
large draw, conditional on obtaining a draw from the Paretian tail
area, is also low. As a result, the probability of observing large
observations of ![]() and
and ![]() is
quite low. This, in turn, makes it unlikely to observe a very large
draw of either
is
quite low. This, in turn, makes it unlikely to observe a very large
draw of either ![]() or
or ![]() and thus
of observing a value of
and thus
of observing a value of ![]() that is either
close to 0 or very large. Therefore, if
that is either
close to 0 or very large. Therefore, if ![]() is very close to 2,
is very close to 2, ![]() is likely
close to its median of 1, and most of the mass of
is likely
close to its median of 1, and most of the mass of
![]() is concentrated near its
median,
is concentrated near its
median,
![]() . Next, as
. Next, as ![]() moves down and away from 2, say to
around 1.5,
moves down and away from 2, say to
around 1.5, ![]() increases rapidly, leading
to a higher frequency of observing tail-region draws
for
increases rapidly, leading
to a higher frequency of observing tail-region draws
for ![]() and
and ![]() . In
addition, as the density in the tail region declines more slowly
for smaller values of
. In
addition, as the density in the tail region declines more slowly
for smaller values of ![]() , it is much
more likely of obtaining very large draws of the regressor and
error term than if
, it is much
more likely of obtaining very large draws of the regressor and
error term than if ![]() is close to 2. In
consequence, if
is close to 2. In
consequence, if ![]() is around 1.5, it is
quite likely to obtain draws of
is around 1.5, it is
quite likely to obtain draws of ![]() that are
either very close to zero or very large, and thus more of the
probability mass of
that are
either very close to zero or very large, and thus more of the
probability mass of
![]() is located near the edges of
its support. Conversely the interior mode of
is located near the edges of
its support. Conversely the interior mode of
![]() is considerably less
pronounced than if
is considerably less
pronounced than if ![]() is close to 2.
Finally, as
is close to 2.
Finally, as ![]() decreases further,
decreases further, ![]() rises further, and both the frequency of tail
observations and the likelihood that any draws from the tail areas
will be very large increase. Therefore, it is very likely that the
largest few observations of
rises further, and both the frequency of tail
observations and the likelihood that any draws from the tail areas
will be very large increase. Therefore, it is very likely that the
largest few observations of ![]() or
or ![]() will dominate the realization
of
will dominate the realization
of ![]() and therefore the realization of
and therefore the realization of
![]() . As a result, if
. As a result, if
![]() is small the central mode of
is small the central mode of
![]() vanishes entirely and
almost all of its probability mass is located very close to the
endpoints of the distribution's support. In the limit, as
vanishes entirely and
almost all of its probability mass is located very close to the
endpoints of the distribution's support. In the limit, as
![]() ,
,
![]() converges to a Bernoulli
random variable, for which all of the probability mass is located
at 0 and 1.
converges to a Bernoulli
random variable, for which all of the probability mass is located
at 0 and 1.
4 An empirical application
Fama and MacBeth (1973) proposed the so-called Fama-MacBeth
regression to test the hypothesis of a linear relationship between
risk and risk premium in stock returns in a cross-sectional
setting. Let ![]() be the return on market
portfolio
be the return on market
portfolio ![]() at time
at time ![]() ,
where
,
where
![]() and
and
![]() ; denote the average return of
portfolio
; denote the average return of
portfolio ![]() as
as
![]() ;
denote the average portfolio return at time
;
denote the average portfolio return at time ![]() as
as
![]() ; and
denote the average portfolio return across all time periods by
; and
denote the average portfolio return across all time periods by
![]() . The
first-stage Fama-MacBeth regression is an ex post CAPM,
. The
first-stage Fama-MacBeth regression is an ex post CAPM,
where
![]() ,
,
![]() , and
, and ![]() is iid
is iid ![]() the same index
the same index
![]() as
as ![]() .
We may assume that the distribution of
.
We may assume that the distribution of
![]() has a finite mean and variance,
say,
has a finite mean and variance,
say,
![]() and
and
![]() . Denote the OLS
estimates of the regression coefficients in equation (17) by
. Denote the OLS
estimates of the regression coefficients in equation (17) by
![]() and
and
![]() . The second-stage
Fama-MacBeth regression is given by
. The second-stage
Fama-MacBeth regression is given by
where
![]() is iid
is iid ![]() the same index
the same index ![]() as
as
![]() ,
,
![]() , and
, and
![]() .
.
The ![]() statistic of the second-stage
Fama-MacBeth regression is given by
statistic of the second-stage
Fama-MacBeth regression is given by
This statistic has the following asymptotic properties.
- If
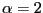 ,
,
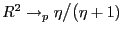 , where
, where
 ; and
; and - If
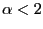 ,
,
 .
.
Thus, if ![]() ,
,
![]() , at a rate that is
proportional to
, at a rate that is
proportional to
![]() .
.
This result does not conflict with the one provided in
Theorem 1, as the present case is one of an unbalanced
regression design: the regressor has an asymptotically finite
variance, whereas the error term has infinite variance, implying
that the asymptotic signal-to-noise ratio is zero. Instead, this
result is closely related to the one provided in Corollary 2,
which examined the asymptotic limit of ![]() if
if
![]() . We note that even
if
. We note that even
if ![]() is fixed (as is generally taken to be the
case in Fama-MacBeth regressions), the dispersion of
is fixed (as is generally taken to be the
case in Fama-MacBeth regressions), the dispersion of
![]() will likely be quite a bit
smaller than that of
will likely be quite a bit
smaller than that of
![]() , indicating that the
model's signal-to-noise ratio,
, indicating that the
model's signal-to-noise ratio, ![]() , and
hence the median of
, and
hence the median of ![]() , in the second-stage
regression will be quite small unless
, in the second-stage
regression will be quite small unless
![]() is sufficiently large in
absolute value.
is sufficiently large in
absolute value.
These qualitative observations are confirmed by a small-scale
Monte Carlo simulation, shown in Table 1, in which we
report the median value of ![]() as a function
of two values of
as a function
of two values of ![]() and selected values
of
and selected values
of ![]() ,
, ![]() ,
and
,
and ![]() .21 It is evident for
both
.21 It is evident for
both
![]() and
and
![]() that the median value
of
that the median value
of ![]() declines as
declines as ![]() increases if
increases if ![]() is fixed, that this effect
is particularly strong if
is fixed, that this effect
is particularly strong if ![]() is large, and that
this effect is more pronounced for
is large, and that
this effect is more pronounced for
![]() than it is for
than it is for
![]() . The final result is as one
would expect, given that Theorem 3 states that the
rate of convergence of
. The final result is as one
would expect, given that Theorem 3 states that the
rate of convergence of ![]() to zero
increases as
to zero
increases as ![]() moves down further
from 2.
moves down further
from 2.
On the basis of the small value of coefficient of determination
from the Fama-MacBeth regression, Jagannathan and Wang (1996)
confirm the finding of Fama and Macbeth (1973) of a ``flat''
relation between average return and market beta. They report a very
low coefficient of determination of 1.35%=0.0135 for the
Sharpe-Lintner-Black (SLB) static CAPM. Regarding ``thick-tailed''
phenomena in empirical data, Fama and French (1992) conjectured
that neglecting the heavy-tails phenomenon of the data does not
lead to serious errors in the interpretation of empirical results.
In the following, we use the same CRSP dataset as was used by
Jagannathan and Wang (1996); the data are very similar to those
that were used in the study of Fama and French (1992). The data
consist of stock returns of nonfinancial firms listed on the NYSE
and AMEX from July 1963 until December 1990 covered by CRSP alone;
the frequency of observation is monthly. In the preceding notation,
we have ![]() and
and ![]() . Figure 5
displays the time series of these monthly returns.
. Figure 5
displays the time series of these monthly returns.
For our analysis we need to obtain point estimates the index of
stability of the stock returns and determine whether the estimates
are less than 2. Under the assumption of symmetry, which
implies that the left and right tails of the returns distribution
possess the same maximal moment exponent and dispersion
coefficient, the point estimate of ![]() for
monthly stock returns in the CRSP dataset using the Hill method
(Hill, 1975) is 1.77, with a standard deviation
of 0.15.22 On the basis of these estimates,
normality (
for
monthly stock returns in the CRSP dataset using the Hill method
(Hill, 1975) is 1.77, with a standard deviation
of 0.15.22 On the basis of these estimates,
normality (![]() ) can be excluded only at a
confidence level of approximately 87.5 percent. However,
inference about the width of the confidence interval for the Hill
estimator is valid only asymptotically; in finite samples, the
Hill-method estimates are known to be quite sensitive to even minor
departures from exactly Paretian tail behavior.23 In contrast, the
method of Dufour and Kurz-Kim (2007) provides exact confidence
intervals for finite samples. By their method, the point estimate
of
) can be excluded only at a
confidence level of approximately 87.5 percent. However,
inference about the width of the confidence interval for the Hill
estimator is valid only asymptotically; in finite samples, the
Hill-method estimates are known to be quite sensitive to even minor
departures from exactly Paretian tail behavior.23 In contrast, the
method of Dufour and Kurz-Kim (2007) provides exact confidence
intervals for finite samples. By their method, the point estimate
of ![]() for the monthly stock returns data
is 1.78, and the exact finite-sample 90interval for this point
estimate is [1.64, 1.99]. This result also does not offer very
strong evidence against the hypothesis
for the monthly stock returns data
is 1.78, and the exact finite-sample 90interval for this point
estimate is [1.64, 1.99]. This result also does not offer very
strong evidence against the hypothesis ![]() .
Nevertheless, because of estimation uncertainty in small samples,
and because this uncertainty is especially severe if
.
Nevertheless, because of estimation uncertainty in small samples,
and because this uncertainty is especially severe if ![]() is close to 2, the data can be regarded as being
in the domain of attraction of a stable distribution with
is close to 2, the data can be regarded as being
in the domain of attraction of a stable distribution with ![]() .24 We therefore proceed
to investigate the consequences of this finding for the proper
interpretation of the low
.24 We therefore proceed
to investigate the consequences of this finding for the proper
interpretation of the low ![]() statistic
reported by Jegannathan and Wang (1996).
statistic
reported by Jegannathan and Wang (1996).
We designed Monte Carlo simulations to obtain the cdf of
![]() for our empirical data, first under
the assumption that the returns data are in the domain of
attraction of an
for our empirical data, first under
the assumption that the returns data are in the domain of
attraction of an ![]() -stable distribution with
-stable distribution with
![]() , and second under the assumption
of normality (
, and second under the assumption
of normality (![]() ). The simulation was calibrated
to the main characteristics the empirical data; we set
). The simulation was calibrated
to the main characteristics the empirical data; we set
![]() ,
, ![]() ,
,
![]() , and we set the expected return equal
to the average annual return in the full sample, i.e.,
, and we set the expected return equal
to the average annual return in the full sample, i.e.,
![]() . The number of replications
of the first-stage and second-stage Fama-MacBeth regressions is
100,000, for the both values of
. The number of replications
of the first-stage and second-stage Fama-MacBeth regressions is
100,000, for the both values of ![]() . The
simulated cdfs of the
. The
simulated cdfs of the ![]() -statistic are shown in
Figure 6, where a vertical line is drawn at
-statistic are shown in
Figure 6, where a vertical line is drawn at
![]() to indicate the in-sample value
of the coefficient of determination. The shapes of the two curves
are rather different, with the one for
to indicate the in-sample value
of the coefficient of determination. The shapes of the two curves
are rather different, with the one for
![]() rising much more quickly for
small values of
rising much more quickly for
small values of ![]() .
.
The simulated median ![]() of the
second-stage Fama-MacBeth regression is 0.384 for
of the
second-stage Fama-MacBeth regression is 0.384 for ![]() , but it is only 0.072 for
, but it is only 0.072 for
![]() . The simulated probability of
obtaining
. The simulated probability of
obtaining
![]() is a minuscule
1.55 percent for
is a minuscule
1.55 percent for ![]() , but it is a much
more sizable 21.88 percent for
, but it is a much
more sizable 21.88 percent for
![]() ; thus, if
; thus, if
![]() the event
the event
![]() is about 14 times more
probable than if
is about 14 times more
probable than if ![]() . On the basis of these
findings, we conclude that the inference drawn from the low value
of
. On the basis of these
findings, we conclude that the inference drawn from the low value
of ![]() by Fama and French (1992)--that the
empirical usefulness of the SLB CAPM is refuted--does not seem to
be robust once proper allowance is made for the distributional
properties of the data that give rise to this statistic.
by Fama and French (1992)--that the
empirical usefulness of the SLB CAPM is refuted--does not seem to
be robust once proper allowance is made for the distributional
properties of the data that give rise to this statistic.
5 Concluding remarks
After providing a brief overview of some of the properties of
![]() -stable distributions, this paper
surveys the literature on the estimation of linear regression
models with infinite-variance variables and associated methods of
conducting hypothesis and specification tests. Our paper adds to
the already-wide body of knowledge that there are substantial
differences between regression models with infinite-variance and
finite-variance regressors and error terms by examining the
properties of the coefficient of determination. In the
infinite-variance case with iid regressors and error terms that
share the same index of stability
-stable distributions, this paper
surveys the literature on the estimation of linear regression
models with infinite-variance variables and associated methods of
conducting hypothesis and specification tests. Our paper adds to
the already-wide body of knowledge that there are substantial
differences between regression models with infinite-variance and
finite-variance regressors and error terms by examining the
properties of the coefficient of determination. In the
infinite-variance case with iid regressors and error terms that
share the same index of stability ![]() , we
find that the
, we
find that the ![]() statistic does not converge to a
constant but instead that it has a nondegenerate asymptotic
distribution on the
statistic does not converge to a
constant but instead that it has a nondegenerate asymptotic
distribution on the ![]() interval, with a pdf
that has infinite singularities at 0 and 1. We provide
closed-form expressions for the cdf and pdf of this limit random
variable. If the regressors and error term do not have the same
index of stability, we show that the coefficient of determination
collapses either to 0 or to 1, depending on whether the model's
signal-to-noise ratio converges asymptotically to zero or infinity.
Finally, we provide an empirical application of our methods to the
Fama-MacBeth two-stage regression setup, and we show that the
coefficient of determination asymptotically converges to 0 in
probability if the regression variables have infinite variance.
This, in turn, strongly suggests that low values of the
interval, with a pdf
that has infinite singularities at 0 and 1. We provide
closed-form expressions for the cdf and pdf of this limit random
variable. If the regressors and error term do not have the same
index of stability, we show that the coefficient of determination
collapses either to 0 or to 1, depending on whether the model's
signal-to-noise ratio converges asymptotically to zero or infinity.
Finally, we provide an empirical application of our methods to the
Fama-MacBeth two-stage regression setup, and we show that the
coefficient of determination asymptotically converges to 0 in
probability if the regression variables have infinite variance.
This, in turn, strongly suggests that low values of the ![]() statistic should not, by themselves, be taken as proof
of a ``flat'' relationship between the dependent variable and the
regressor.
statistic should not, by themselves, be taken as proof
of a ``flat'' relationship between the dependent variable and the
regressor.
In view of the random nature of the limit law
![]() if the regressors and error
terms share the same index of stability, and given our related
finding that the coefficient of determination converges to zero in
probability if the tail index of the disturbance term is smaller
than that of the regressor, a case that may be difficult to rule
out in empirical practice unless the sample size is very large, we
view our results as establishing that one should not rely
on
if the regressors and error
terms share the same index of stability, and given our related
finding that the coefficient of determination converges to zero in
probability if the tail index of the disturbance term is smaller
than that of the regressor, a case that may be difficult to rule
out in empirical practice unless the sample size is very large, we
view our results as establishing that one should not rely
on ![]() as a measure of the goodness of fit of
a regression model whenever the regressors and disturbance terms
are sufficiently heavy-tailed to call into question the existence
of second (population) moments. At the very least, if one chooses
to report the coefficient of determination in regressions with
infinite-variance variables at all, one should also report a point
estimate of the median of
as a measure of the goodness of fit of
a regression model whenever the regressors and disturbance terms
are sufficiently heavy-tailed to call into question the existence
of second (population) moments. At the very least, if one chooses
to report the coefficient of determination in regressions with
infinite-variance variables at all, one should also report a point
estimate of the median of
![]() ,
,
![]() ,
where
,
where ![]() is as in Theorem 1. In
addition, one should indicate whether the error terms and
regressors may reasonably be assumed to share the same index of
stability. If the validity of that assumption is in doubt, the
authors should also indicate which of the two parameters is likely
to be smaller and how far apart the two parameters may plausibly
be.
is as in Theorem 1. In
addition, one should indicate whether the error terms and
regressors may reasonably be assumed to share the same index of
stability. If the validity of that assumption is in doubt, the
authors should also indicate which of the two parameters is likely
to be smaller and how far apart the two parameters may plausibly
be.
It is widely known, and it is certainly stressed in all
introductory econometrics textbooks, that a high value
of ![]() does not provide a sufficient basis
for concluding that an empirical regression model is a ``good''
explanation of the dependent variable, or even that the regression
is correctly specified. Nevertheless, one suspects, researchers may
view low values of
does not provide a sufficient basis
for concluding that an empirical regression model is a ``good''
explanation of the dependent variable, or even that the regression
is correctly specified. Nevertheless, one suspects, researchers may
view low values of ![]() in an
empirical regression as an indication that the (linear)
relationship is either weak or unreliable. A direct implication of
the work presented in this paper is that whenever the data are
characterized by significant outlier activity, a low value
of
in an
empirical regression as an indication that the (linear)
relationship is either weak or unreliable. A direct implication of
the work presented in this paper is that whenever the data are
characterized by significant outlier activity, a low value
of ![]() should not, by itself, be used to
disqualify the model from further consideration.
should not, by itself, be used to
disqualify the model from further consideration.
Several extensions to the work presented here are possible.
First, the regression ![]() -statistic is a simple
function of the coefficient of determination; e.g.,
-statistic is a simple
function of the coefficient of determination; e.g.,
![]() in the
bivariate regression case. Given the close connection between the
two statistics, it seems useful to study if and how the
distributional properties of the regression
in the
bivariate regression case. Given the close connection between the
two statistics, it seems useful to study if and how the
distributional properties of the regression ![]() -statistic are affected by the presence of
-statistic are affected by the presence of ![]() -stableand error terms under both the null hypothesis,
-stableand error terms under both the null hypothesis,
![]() , and the alternative hypothesis,
, and the alternative hypothesis,
![]() . It would also be useful to
elaborate on our idea, offered after Remark 1 in
subsection 3.2,
that the difference between the estimate of
. It would also be useful to
elaborate on our idea, offered after Remark 1 in
subsection 3.2,
that the difference between the estimate of ![]() and a consistent estimate of its median may serve as a
diagnostic check of the size of the effect of infinite variance
on
and a consistent estimate of its median may serve as a
diagnostic check of the size of the effect of infinite variance
on ![]() . For example, it may be feasible to
develop an asymptotic theory of the distributional properties of
this difference.
. For example, it may be feasible to
develop an asymptotic theory of the distributional properties of
this difference.
It also seems desirable to study how well the distribution
of
![]() approximates the empirical
distribution of
approximates the empirical
distribution of ![]() in finite samples, for
various types of heavy-tailed distributions that are in the domain
of attraction of
in finite samples, for
various types of heavy-tailed distributions that are in the domain
of attraction of ![]() distributions, and for
various types of estimators (such as OLS, Blattberg-Sargent's BLUE,
and the least-absolute deviation estimator). In addition, an
extension to a multiple-regression framework may produce additional
insights into the properties of the coefficient of determination in
the infinite-variance case. Finally, the theoretical results
presented in our paper depend crucially on the assumption that the
random variables are iid. Relaxing this assumption would seem
to be useful, as many economic and financial time
series--especially if they are sampled at very high
frequencies--are characterized by interesting dependence and
heterogeneity features. Introducing serial dependence and
heterogeneity, especially conditional heterogeneity, would serve
the purpose of studying how the properties of
distributions, and for
various types of estimators (such as OLS, Blattberg-Sargent's BLUE,
and the least-absolute deviation estimator). In addition, an
extension to a multiple-regression framework may produce additional
insights into the properties of the coefficient of determination in
the infinite-variance case. Finally, the theoretical results
presented in our paper depend crucially on the assumption that the
random variables are iid. Relaxing this assumption would seem
to be useful, as many economic and financial time
series--especially if they are sampled at very high
frequencies--are characterized by interesting dependence and
heterogeneity features. Introducing serial dependence and
heterogeneity, especially conditional heterogeneity, would serve
the purpose of studying how the properties of
![]() may be affected by such
departures from the basic case of iid variables. The authors are
considering conducting research to extend the work presented in
this paper along these lines.
may be affected by such
departures from the basic case of iid variables. The authors are
considering conducting research to extend the work presented in
this paper along these lines.
References
Blattberg, R. and T. Sargent (1971): Regression with non-Gaussian stable disturbances: Some sampling results, Econometrica 39, 501-510.
Brockwell, P.J. and R.A. Davis (1991): Time Series: Theory and Models (2nd ed). Springer: New York.
Davis, R.A. and S.I. Resnick (1985a): Limit theory for moving averages of random variables with regularly varying tail probabilities, Annals of Probability 13, 179-195.
Davis, R.A. and S.I. Resnick (1985b): More limit theory for sample correlation functions of moving averages, Stochastic Processes and Their Applications 20, 257-279.
Davis, R.A. and S.I. Resnick (1986): Limit theory for sample covariance and correlation functions of moving averages, Annals of Statistics 14, 533-558.
De Vries, C. (1991): On the relation between GARCH and stable processes, Journal of Econometrics 48, 313-324.
Dufour, J.-M. and J.-R. Kurz-Kim (2007): Exact inference and optimal invariant estimation for the stability parameter of symmetric alpha-stable, Journal of Empirical Finance, forthcoming.
Fama, E.F. and K.R. French (1992): The cross-section of expected stock returns, Journal of Finance 47, 427-465.
Fama, E.F. and J.D. MacBeth (1973): Risk, return, and equilibrium: Empirical tests, Journal of Political Economy 71, 607-636.
Feller, W. (1971): An Introduction to Probability Theory and its Applications, Vol. (2nd ed). Wiley: New York.
Gnedenko, B.V. and A.N. Kolmogorov (1954): Limit Distributions for Sums of Independent Random Variables. Addison-Wesley: Reading, Mass.
Granger, C.W.J. and D. Orr (1972): ``Infinite variance'' and research strategy in time series analysis, Journal of the American Statistical Association 67, 275-285.
Ibragimov, I.A. and Yu.V. Linnik (1971): Independent and Stationary Sequences of Random Variables. Wolters-Noordhoff: Groningen.
Hill, B.M. (1975): A simple general approach to inference about the tail of a distribution, Annals of Statistics 3, 1163-1174.
Jagannathan, R. und Z. Wang (1996): The conditional CAPM and cross-section of expected returns, Journal of Finance 51, 3-53.
Kanter, M. and W.L. Steiger (1974): Regression and autoregression with infinite variance, Advances in Applied Probability 6, 768-783.
Kim, J.-R. (2003): Finite-sample distributions of self-normalized sums, Computational Statistics 18, 493-504.
Kim, J.-R. and S.T. Rachev (1999): Asymptotic distributions of BLUE in the presence of infinite variance residuals, Unpublished manuscript.
Kurz-Kim, J.-R., S.T. Rachev and G. Samorodnitsky (2005):
![]() -type Distributions for Heavy-tailed
Variates, Unpublished manuscript.
-type Distributions for Heavy-tailed
Variates, Unpublished manuscript.
Logan, B.F., C.L. Mallows, S.O. Rice and L.A. Shepp (1973): Limit distributions of self-normalized sums, Annals of Probability 1, 788-809.
Loretan, M. and P.C.B. Phillips (1994): Testing the covariance stationarity of heavy-tailed time series, Journal of Empirical Finance 1, 211-248.
Mood, A.M., F.A. Graybill and D.C. Boes (1974): Introduction to the Theory of Statistics (3rd ed). McGraw-Hill: New York.
Mandelbrot, B. (1963): The variation of certain speculative prices, Journal of Business 36, 394-419.
McCulloch, J.H. (1986): Simple consistent estimators of stable distribution parameters, Communications in Statistics, Computation and Simulation 15, 1109-1136.
McCulloch, J.H. (1996): Financial applications of stable distributions, in: Handbook of Statistics--Statistical Methods in Finance, Vol. 14, 393-425, eds..S. Maddala and C.R. Rao. Elsevier Science: Amsterdam.
McCulloch, J.H. (1997): Measuring tail thickness to estimate
the stable index ![]() : A critique,
Journal of Business and Economic Statistics 15, 74-81.
: A critique,
Journal of Business and Economic Statistics 15, 74-81.
McCulloch, J.H. (1998): Linear regression with stable disturbances, in: A Practical Guide to Heavy Tails, 359-376, eds.. Adler, R. Feldman, and M.S. Taqqu. Birkhäuser: Berlin and Boston.
Mittnik, S., S.T. Rachev and J.-R. Kim (1998): Chi-square-type distributions for heavy-tailed variates, Econometric Theory 14, 339-354.
Phillips, P.C.B. (1990): Time series regression with a unit root and infinite-variance errors, Econometric Theory 6, 44-62.
Phillips, P.C.B. and V.A. Hajivassiliou (1987): Bimodal
![]() -ratios, Cowles Foundation Discussion
Paper No. 842.
-ratios, Cowles Foundation Discussion
Paper No. 842.
Phillips, P.C.B. and M. Loretan (1991): The Durbin-Watson ratio under infinite-variance errors, Journal of Econometrics 47, 85-114.
Phillips, P.C.B. and M. Loretan (1994): On the theory of testing covariance stationarity under moment condition failure, in: Advances in Econometrics and Quantiative Economics. Essays in Honor of Professor C.R. Rao, 198-233, eds..S. Maddala, P.C.B. Phillips, and T.N. Srinivasan. Blackwell: Oxford.
Rachev, S.T., J.-R. Kim and S. Mittnik (1999): Stable Paretian econometrics, Part I and II, The Mathematical Scientists 24, 24-55 and 113-127.
Rachev, S.T., C. Menn and F.J. Fabozzi (2005): Fat-Tailed and Skewed Asset Return Distributions. Wiley: New York.
Resnick, S.I. (1986): Point processes regular variation and weak convergence, Advances in Applied Probability 18, 66-138.
Resnick, S.I. (1999): A Probability Path. Birkhäuser: Berlin and Boston.
Resnick, S.I. (2006), Heavy-Tail Phenomena: Probabilistic and Statistical Modeling. Springer: New York.
Runde, R. (1993): A note on the asymptotic distribution of the
![]() -statistic for random variables with
infinite variance, Statistics & Probability Letters
18, 9-12.
-statistic for random variables with
infinite variance, Statistics & Probability Letters
18, 9-12.
Runde, R. (1997): The asymptotic null distribution of the
Box-Pierce ![]() -statistic for random variables with
infinite variance, with an application to German stock returns,
Journal of Econometrics 78, 205-216.
-statistic for random variables with
infinite variance, with an application to German stock returns,
Journal of Econometrics 78, 205-216.
Samorodnitsky, G., S.T. Rachev, J.-R. Kurz-Kim and S. Stoyanov (2007): Asymptotic distribution of linear unbiased estimators in the presence of heavy-tailed stochastic regressors and residuals, Probability and Mathematical Statistics, forthcoming.
Samorodnitsky, G. and M.S. Taqqu (1994): Stable Non-Gaussian Random Processes. Chapman & Hall: New York.
Zolotarev, V.M. (1986): One-Dimensional Stable
Distributions, Translations of Mathematical Monographs,
Vol. 65. American Mathematical Society: Providence. Empty
`thebibliography' environment
Table 1. Median Value of ![]() as a Function of
as a Function of ![]() ,
, ![]() ,
, ![]() , and
, and ![]()
| 1.50 | 100 | 30 | 0.0404 | 0.0425 | 0.0576 | 0.1009 | 0.2963 |
|---|---|---|---|---|---|---|---|
| 1.50 | 100 | 100 | 0.0162 | 0.0172 | 0.0292 | 0.0596 | 0.2019 |
| 1.50 | 100 | 500 | 0.0068 | 0.0075 | 0.0147 | 0.0325 | 0.1206 |
| 1.50 | 100 | 1000 | 0.0046 | 0.0055 | 0.0114 | 0.0264 | 0.0973 |
| 1.50 | 250 | 30 | 0.0402 | 0.0426 | 0.0779 | 0.1598 | 0.4417 |
| 1.50 | 250 | 100 | 0.0161 | 0.019 | 0.0448 | 0.1058 | 0.3304 |
| 1.50 | 250 | 500 | 0.0064 | 0.0075 | 0.022 | 0.0565 | 0.202 |
| 1.50 | 250 | 1000 | 0.0047 | 0.0058 | 0.0172 | 0.0452 | 0.1667 |
| 1.50 | 1000 | 30 | 0.0387 | 0.0484 | 0.1499 | 0.332 | 0.6748 |
| 1.50 | 1000 | 100 | 0.0162 | 0.0223 | 0.094 | 0.2272 | 0.5558 |
| 1.50 | 1000 | 500 | 0.0065 | 0.0104 | 0.0521 | 0.1341 | 0.3994 |
| 1.50 | 1000 | 1000 | 0.0046 | 0.0072 | 0.0399 | 0.1079 | 0.3443 |
| 1.50 | 2500 | 30 | 0.0403 | 0.058 | 0.2478 | 0.4806 | 0.7962 |
| 1.50 | 2500 | 100 | 0.0155 | 0.0294 | 0.1621 | 0.3581 | 0.6973 |
| 1.50 | 2500 | 500 | 0.0066 | 0.013 | 0.0883 | 0.2243 | 0.5507 |
| 1.50 | 2500 | 1000 | 0.0047 | 0.0103 | 0.0737 | 0.1896 | 0.497 |
| 1.75 | 100 | 30 | 0.0488 | 0.0543 | 0.1332 | 0.2944 | 0.641 |
| 1.75 | 100 | 100 | 0.026 | 0.0328 | 0.1032 | 0.2413 | 0.5756 |
| 1.75 | 100 | 500 | 0.0177 | 0.0222 | 0.0779 | 0.1941 | 0.5055 |
| 1.75 | 100 | 1000 | 0.0149 | 0.0199 | 0.072 | 0.1778 | 0.4792 |
| 1.75 | 250 | 30 | 0.0474 | 0.0642 | 0.2509 | 0.4899 | 0.7993 |
| 1.75 | 250 | 100 | 0.0265 | 0.043 | 0.2066 | 0.4264 | 0.756 |
| 1.75 | 250 | 500 | 0.0169 | 0.029 | 0.1571 | 0.35 | 0.695 |
| 1.75 | 250 | 1000 | 0.0143 | 0.0251 | 0.144 | 0.3273 | 0.673 |
| 1.75 | 1000 | 30 | 0.047 | 0.1193 | 0.5351 | 0.7665 | 0.9309 |
| 1.75 | 1000 | 100 | 0.0265 | 0.0871 | 0.4612 | 0.7124 | 0.9115 |
| 1.75 | 1000 | 500 | 0.0169 | 0.0635 | 0.391 | 0.6507 | 0.8865 |
| 1.75 | 1000 | 1000 | 0.0144 | 0.0579 | 0.3663 | 0.6257 | 0.8744 |
| 1.75 | 2500 | 30 | 0.048 | 0.2185 | 0.7214 | 0.8804 | 0.9677 |
| 1.75 | 2500 | 100 | 0.0255 | 0.1704 | 0.6599 | 0.8474 | 0.9578 |
| 1.75 | 2500 | 500 | 0.0169 | 0.1251 | 0.59 | 0.8066 | 0.9452 |
| 1.75 | 2500 | 1000 | 0.0149 | 0.1202 | 0.5674 | 0.7902 | 0.9394 |
The numbers in the body of the table are the medians from simulated distributions with 100,000 replications.
Figure 1. The Function ![]() , 0 <
, 0 < 
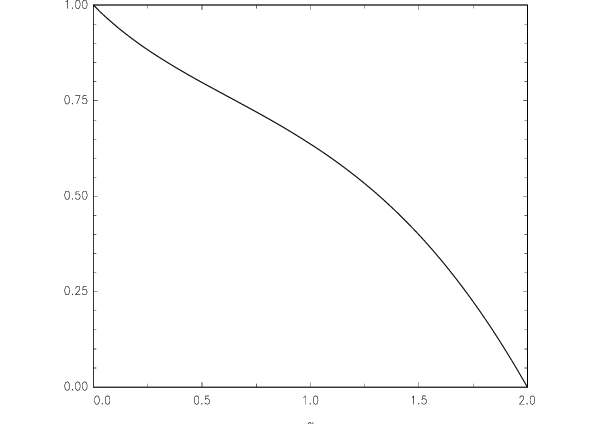
Figure 2. Cumulative Distribution Functions of ![]()

Figure 3. Probability Density Functions of ![]() ,
,![]()
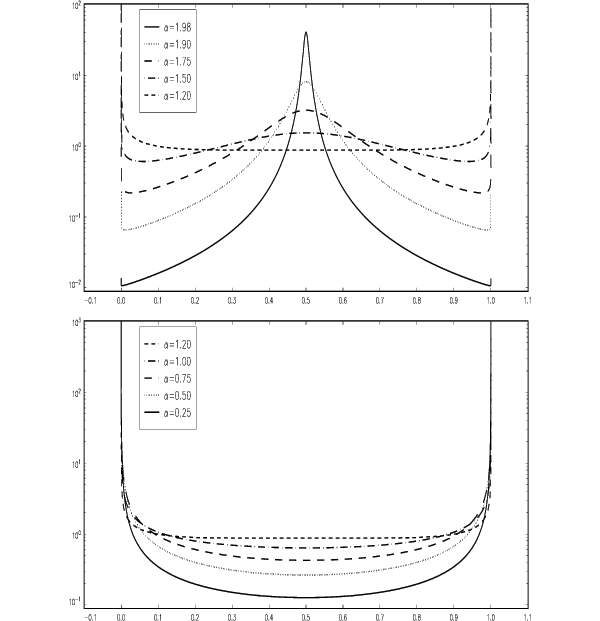
Figure 4. Cumulative Distribution Functions of ![]() ,
,![]()

Figure 5. CRSP Returns, July 1963 to December 1992

Figure 6. Simulated cdf of ![]() , Second-Stage Fama-MacBeth Regressions
, Second-Stage Fama-MacBeth Regressions
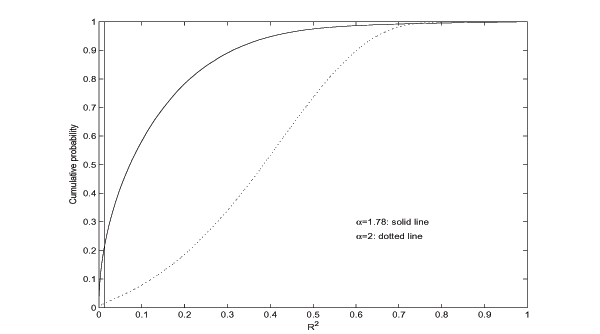
Footnotes
1. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the staff of the Deutsche Bundesbank, the Board of Governors of the Federal Reserve System, or of any other person associated with the Federal Reserve System. We are grateful to Jean-Marie Dufour, Neil R. Ericsson, Peter C.B. Phillips, Werner Ploberger, Jonathan H. Wright, and participants of a workshop at the Federal Reserve Board for valuable comments, and to Zhenyu Wang for the data used in the empirical section of this paper. Return to text
2. Corresponding author. Research support from the Alexander von Humboldt Foundation is gratefully acknowledged. Deutsche Bundesbank, Wilhelm-Epstein-Strasse 14, 60431 Frankfurt am Main, Germany; Email: [email protected]; Tel: +49-69-9566-4576, Fax: +49-69-9566-2982. Return to text
3. Mailstop 18, Board of Governors of the Federal Reserve System, Washington DC 20551, USA; Email: [email protected]; Tel: +1-202-452-2219; Fax: +1-202-263-4850. Return to text
4. The normal distribution is the only
member of the family of ![]() -stable distributions
that has finite second (and higher-order) moments; all other
members of this family have infinite variance. Return to text
-stable distributions
that has finite second (and higher-order) moments; all other
members of this family have infinite variance. Return to text
5. The three special cases are: (i) the
Gaussian distribution
![]() , (ii) the
symmetric Cauchy distribution
, (ii) the
symmetric Cauchy distribution
![]() , and (iii) the
Lévy distribution
, and (iii) the
Lévy distribution
![]() ; see Zolotarev
(1986), Section 2, and Rachev et al. (2005),
Section 7. Return to text
; see Zolotarev
(1986), Section 2, and Rachev et al. (2005),
Section 7. Return to text
6. For ![]() and
and
![]() ,
,
![]() , i.e., the distribution's
support is bounded below by
, i.e., the distribution's
support is bounded below by ![]() . Zolotarev
(1986, Theorem 2.5.3) and Samorodnitsky and Taqqu (1994, pp. 17-18)
provide expressions for the rate of decline of the non-Paretian
tail if
. Zolotarev
(1986, Theorem 2.5.3) and Samorodnitsky and Taqqu (1994, pp. 17-18)
provide expressions for the rate of decline of the non-Paretian
tail if
![]() and
and
![]() . Return
to text
. Return
to text
7. The function ![]() is smooth on the entire interval
is smooth on the entire interval ![]() . The numerator
and the second term in the denominator of equation (4) both converge
to 0 as
. The numerator
and the second term in the denominator of equation (4) both converge
to 0 as
![]() ;
;
![]() therefore follows from an
application of L'Hôpital's Rule. Return to text
therefore follows from an
application of L'Hôpital's Rule. Return to text
8. Ibragimov and Linnik (1971,
Theorem 2.6.4) show that this result holds not only for
![]() -stable distributions, but that it
pertains to all distributions that are in the domain of
attraction of an
-stable distributions, but that it
pertains to all distributions that are in the domain of
attraction of an ![]() -stable distribution.
Ibragimov and Linnik (1971, Theorem 2.6.1) provide necessary and
sufficient conditions for a probability distribution to lie in the
domain of attraction of an
-stable distribution.
Ibragimov and Linnik (1971, Theorem 2.6.1) provide necessary and
sufficient conditions for a probability distribution to lie in the
domain of attraction of an ![]() -stable
law. Return to text
-stable
law. Return to text
9. The maximal moment exponent of a
distribution is either a finite positive number, or it is infinite
if a distribution has finite moments of all orders. For a
Student-![]() distribution, the degrees of freedom
parameter is equal to its maximal moment exponent. Return to text
distribution, the degrees of freedom
parameter is equal to its maximal moment exponent. Return to text
10. This result also holds for the case
![]() and
and ![]() . Return to text
. Return to text
11. Another reason for this restriction
comes from the viewpoint of statistical modelling. The conditional
expectation of the bivariate symmetric stable distribution
in (5) is, as in
the Gaussian case, linear in ![]() only if
only if
![]() . The regression function is
in general nonlinear, or rather only asymptotically linear, under
other conditions. For more on bivariate linearity, see
Samorodnitsky and Taqqu (1994, Sections 4
and 5). Return to text
. The regression function is
in general nonlinear, or rather only asymptotically linear, under
other conditions. For more on bivariate linearity, see
Samorodnitsky and Taqqu (1994, Sections 4
and 5). Return to text
12. If
![]() , OLS is known to
generate consistent estimates of
, OLS is known to
generate consistent estimates of ![]() and
and ![]() . See Samorodnitsky et al. (2007) for an overview
and discussion of estimation methods that are consistent for
various combinations of
. See Samorodnitsky et al. (2007) for an overview
and discussion of estimation methods that are consistent for
various combinations of
![]() and
and
![]() . Return to text
. Return to text
13. To prove that ![]() ,
see equation (13.3.14) on p. 529 of Brockwell and Davis
(1991). In that equation, put
,
see equation (13.3.14) on p. 529 of Brockwell and Davis
(1991). In that equation, put
![]() , where
, where ![]() is given by equation (4), and employ the
recursive relationship
is given by equation (4), and employ the
recursive relationship
![]() .
Return to text
.
Return to text
14. Observe that ![]() if
and only if
if
and only if ![]() , as the dispersion
parameters
, as the dispersion
parameters
![]() and
and
![]() are necessarily
positive. Return to text
are necessarily
positive. Return to text
15. Recall that in the finite-variance
case,
![]() ; therefore, norming
by
; therefore, norming
by
![]() and
and
![]() in
equation (10)
produces a constant of
in
equation (10)
produces a constant of ![]() . Return to text
. Return to text
16. See, e.g., Resnick (1999, p. 155). Return to text
17. See, e.g., Mood, Graybill, and Boes (1974), p. 187. Return to text
18. Runde (1993) graphs pdfs of
![]() for values of
for values of ![]() between
between
![]() and
and ![]() . Return to text
. Return to text
19. See Mittnik et al. (1998) for a
discussion of some of the properties of the stable law
![]() . Return to text
. Return to text
20. See, e.g., Mood, Graybill, and Boes (1974, p. 200). Return to text
21. The design of the simulation and the
choices of values for ![]() ,
, ![]() ,
,
![]() and
and ![]() were
influenced by a desire to maximize the empirical relevance of the
simulation exercise. We chose
were
influenced by a desire to maximize the empirical relevance of the
simulation exercise. We chose
![]() and
and
![]() because
because
![]() for most empirical
economic data. We study the cases of
for most empirical
economic data. We study the cases of ![]() ,
,
![]() ,
, ![]() , and
, and
![]() because
because ![]() corresponds approximately to the number of business days in a
calendar year. The values of
corresponds approximately to the number of business days in a
calendar year. The values of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() correspond to the numbers of stocks contained in certain well-known
stock price indices, such as the U.S. Dow-Jones Industial and
German DAX indices, the U.K. FTSE-100 index, the U.S. S&P-500
index, etc. The choice of
correspond to the numbers of stocks contained in certain well-known
stock price indices, such as the U.S. Dow-Jones Industial and
German DAX indices, the U.K. FTSE-100 index, the U.S. S&P-500
index, etc. The choice of ![]() provides a
reference to contrast the cases of
provides a
reference to contrast the cases of
![]() and
and
![]() ;
;
![]() is particularly relevant for the
empirical study provided below. Return
to text
is particularly relevant for the
empirical study provided below. Return
to text
22. In this estimation, we used 0.0031 as the centering offset for the empirical data; this adjustment is necessary because the Hill estimator is not location-invariant. The offset is equal to the estimated location parameter obtained by the quantile estimation method of McCulloch (1986). The choice of the number of order statistics to include in the Hill method used was determined by the Monte Carlo method of Dufour and Kurz-Kim (2007). For the present dataset, this method indicated the use of 43% of all observations.
The Hill estimator uses extreme observations from both tails of
the empirical distribution under the assumption of symmetry, but it
uses only observations from the right (left) tail under the
assumption of right-skewed (left-skewed) asymmetry. In the case of
the monthly stock returns, the distribution is clearly left-skewed,
i.e., the largest negative returns are larger in the sample than
the largest positive returns; see Figure 5. Under the
assumption of left-skewed asymmetry, the point estimate
of ![]() for the left tail using the Hill
method is 1.47, with one standard deviation
of 0.18. Return to text
for the left tail using the Hill
method is 1.47, with one standard deviation
of 0.18. Return to text
23. Stable distributions have tails that
are asymptotically Paretian. In finite samples, and
especially if the index of stability is not far below 2, it is
known that the tails of stable distributions are not approximated
particularly well by Pareto distributions with the same value
of ![]() . See Resnick (2006, pp. 86-9) for
a discussion of the consequences of these finite-sample features
for the reliability of the Hill estimator. Return to text
. See Resnick (2006, pp. 86-9) for
a discussion of the consequences of these finite-sample features
for the reliability of the Hill estimator. Return to text
24. For a broader discussion of how to
decide if ![]() , see McCulloch
(1997). Return to text
, see McCulloch
(1997). Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text
 for
for
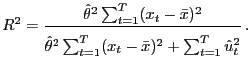
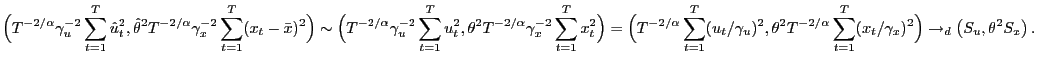
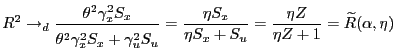 , say,
, say,
![$\displaystyle f_{Z}(z) = \frac{\d }{\d z}F_{Z}(z) = \frac{\sin(\pi{\alpha /2})}{\pi z\bigl[ z^{-{\alpha/2}}+z^{{\alpha/2}}+ 2\cos(\pi{\alpha/2}) \bigr] }\,.$](img445.gif)
![$\displaystyle f_{{\widetilde{R}}}(r) = \left\vert \frac{\d }{\d r} g^{-1}(r) \right\vert f_{Z}\bigl[g^{-1}(r)\bigr] = \frac{1}{\eta(1-r)^{2}} \cdot\frac{\sin(\pi{\alpha/2})}{\pi g^{-1} (r)\Bigl( [g^{-1}(r)]^{-{\alpha/2}}+[g^{-1}(r)] ^{{\alpha/2}}+ 2\cos (\pi{\alpha/2}) \Bigr) } = \frac{\sin(\pi{\alpha/2})}{\pi\,r(1-r)} \cdot\bigl[ z^{-{\alpha/2}} +z^{{\alpha/2}}+ 2\cos(\pi{\alpha/2})\bigr]^{-1}$](img513.gif) where
where