
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 944, September 2008 --- Screen Reader
Version*
The Macroeconomic Effects of External Pressures on Monetary Policy*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Central banks, whether independent or not, may occasionally be subject to external pressures to change policy objectives. We analyze the optimal response of central banks to such pressures and the resulting macroeconomic consequences. We consider several alternative scenarios regarding policy objectives, the degree of commitment and the timing of external pressures. The possibility to adopt "more liberal" objectives in the future increases current inflation through an accommodation effect. Simultaneously, the central bank tries to anchor inflation by promising to be even "more conservative" in the future. The immediate effect is an output contraction, the opposite of what the pressures to adopt " more liberal" objectives may be aiming. We also discuss the opposite case, where objectives may become " more conservative" in the future, which may be the relevant case for countries considering the adoption of inflation targeting.
Keywords: Monetary policy, time-consistency, political disagreement
JEL classification: E52, E58, E61
1 Introduction
In the last decades, there has been a big effort to build monetary institutions that are independent from political forces and other types of external pressures. In most cases, this process has implied the definition of specific goals to be assigned to central banks, typically in terms of inflation and output stabilization. However, it has often been the case that central banks are subject to some pressures to change their policy goals. For instance, the European Central Bank has been recently criticized for adopting policies that do not properly take into account output growth. In other cases, as it is currently happening in the United States, the adoption of inflation targeting or other institutional reforms are being discussed. Even if there is not an immediate reaction to such pressures, the central bank and the public may attach some probability that monetary policy may change its objectives in the future. Changes in policy objectives may also simply be due to the the appointment of a new central bank chairman or staff, who may have different views from the predecessors.
The aim of this paper is to study how the possibility of changes in future policy goals affects current economic outcomes. It is widely accepted in the modern macroeconomic literature that firms and households, when setting current prices and wages, take into account their expectations about future inflation. In this context, when a policy that generates a higher inflation bias (henceforth, a "liberal policy") is expected in the future, inflation expectations increase and will be reflected in current prices and wages. As a consequence, given the policy chosen by the central bank, the possibility of a future change in policy objectives affects the economic variables already in the current period. In this paper, we analyze the optimal response of a central bank in such situation and its macroeconomic effects.
Optimal monetary policy is typically characterized under the assumptions that a central bank is in charge for an infinite horizon, it can credibly commit to future policy plans, and its policy goals do not change. In this paper, we relax these assumptions. First, we need to consider that current and future policy objectives may not necessarily coincide. Second, when considering the possibility of changes in policy objectives, the assumption about the credibility of the central bank needs to be rethought. For instance, if the central bank has received some external pressures to change its policy goals, it will adopt the best possible policy to fulfill its new objectives, and the plans made when priorities were different will become irrelevant.
We consider several alternative scenarios regarding policy objectives, the degree of commitment and the timing of external pressures. The main part of our analysis refers to the case where an independent central bank has been appointed, possibly one with more conservative objectives than society.1 The central bank is not completely insulated from the opinions prevailing in the economic environment, and may occasionally be subject to some external pressures to adopt more liberal objectives in the future. This typically happens when countries face adverse economic conditions, like recessions or financial crisis. In all the settings taken into consideration, the possibility that liberal policies may be implemented implies an increase in current inflation through an accommodation effect. At the same time, the central bank tries to anchor inflation expectations by promising to be even more conservative in the future. The immediate effect is an output contraction, which is the opposite of what the pressures to implement liberal policies may be aiming for. These effects are stronger the higher is the probability that objectives change. In this respect, adopting inflation targeting may be better than appointing a conservative central banker. In the former case, changing objectives usually requires costly institutional reform. In the latter, it just requires that the central bank chairman and advisors, at the end of their term of office, are substituted by ones with different policy objectives.
We also analyze the opposite case, where objectives may become more conservative in the future. This is the relevant scenario for countries discussing the adoption of more stringent and explicit inflation objectives, which is, arguably, the case of the United States. In this context, the possibility of more conservative policy in the future creates a positive externality.
Our paper is related to the literature about political economy in monetary policy, following the seminal contribution of Alesina (1987). We want to emphasize that our goal is not to provide a partisan analysis of monetary policy, where one attributes economic cycles to political parties. According to the empirical literature, it seems difficult to match timely and systematically certain parties with effective changes in monetary policy.2 It seems implausible that all governments have always successfully influenced central bank's objectives, and that they did so as soon as they were elected. However, there have been frequent cases where central banks have been subject to external pressures. Our goal is to understand what are the effects of certain types of pressures, and what is the optimal response of a central bank in such situation. Also, our analysis can provide a rationale for the changes in interest rate rules, as analyzed by Davig and Leeper (2007).
We carry out our analysis in the framework commonly used in the literature on monetary policy design. As it has become standard, we do not assume a New Classical Phillips curve and consider instead its New Keynesian counterpart. The features of modern science of monetary policy considered here have important consequences, and induce different mechanisms than the ones modeled in Alesina (1987) and other "partisan models" of monetary policy. In the New Keynesian framework and unlike its New Classical counterpart, the possibility of a future change in policy objectives implies a different level of inflation and output in earlier periods. This is because firms and households, when setting current prices and wages, take into account future economic conditions. With respect to the partisan theory of economic fluctuations, our analysis suggests that it is difficult to find a link between economic outcomes and the objectives of certain policymakers.
We also study the importance of central bank credibility when policy objectives can change. To do so, we relax the discretion assumption, typical of the political economy literature. Instead, and following the recent contributions of Schaumburg and Tambalotti (2007) and Debortoli and Nunes (2006a), we model the central bank as possessing a loose commitment technology. In this context, in order to lower inflation expectations created by the possibility to adopt liberal policies, a conservative central bank optimally promises to be even more conservative in the future. If the conservative central bank does not possess a commitment technology, as in Alesina (1987) or Rogoff (1985), such policy is not possible and the effects of future liberal objectives are stronger. Even for a Rogoff central banker, our analysis suggests that, besides other considerations, credibility or commitment is important to counteract the negative externalities generated by the pressures for liberal policies.
We first consider a simplified model where changes in policy objectives can occur in any period. This simplification allows us to obtain several analytical results. However, in reality, policy objectives can not always be changed immediately because of institutional features and policy implementation lags. We then consider a richer model where the central bank has complete insulation from external pressures in the short-run, but understands that objectives may change in the future. For example, this can be due to the fact that the current chairman, at the end of his tenure can then be replaced by one with different views about the conduct of monetary policy. This second model also identifies more clearly the key effects arising from possible changes in future objectives.
The paper is organized as follows. Section 2, examines a simple model with an analytical solution. In that framework, we discuss the importance of commitment and inflation targeting. In section 3, we solve a model where external pressures do not materialize immediately. Section 4 examines several alternative scenarios where the basic mechanisms identified are still present. It considers different types of changes in the policy objectives, the strategic use of lagged inflation in a hybrid Phillips curve, and a case with full-commitment and no disagreement. Section 5 concludes.
2 The model
We base our analysis on a simple monetary model. Inflation dynamics are described by a New Keynesian Phillips curve (NKPC). As it is well known, the NKPC is a reduced form approximation of the relationship between inflation and output in an economy with monopolistic competition and staggered price setting.3 The NKPC takes the form:
| (1) |
where ![]() denotes price inflation and
denotes price inflation and
![]() measures the output-gap, i.e. the
difference between current output and the output level that would
prevail under flexible prices.
measures the output-gap, i.e. the
difference between current output and the output level that would
prevail under flexible prices.
As it is standard in the optimal monetary policy literature, we assume that the central bank controls inflation directly.4 The objectives of the monetary authority are characterized by a period quadratic loss function taking the following form:
![$\displaystyle U =\frac{1}{2}\left[ \pi_{t}^{2}+w(y_{t}-\widetilde{y}_{t})^{2}\right]$](img5.gif)
|
(2) |
The monetary policy authority aims at minimizing a weighted
average of deviations of inflation and output-gap from their
respective targets. The parameter ![]() measures the
relative importance of output vs. inflation stabilization. The
inflation target is normalized to zero, while
measures the
relative importance of output vs. inflation stabilization. The
inflation target is normalized to zero, while
![]() represents the
(exogenously given) output target. The latter variable indicates
that monetary policy aims at correcting some inefficiencies in the
economy, like the presence of monopolistic power, distortionary
taxes, frictions in the labor market, etc. The parameter
represents the
(exogenously given) output target. The latter variable indicates
that monetary policy aims at correcting some inefficiencies in the
economy, like the presence of monopolistic power, distortionary
taxes, frictions in the labor market, etc. The parameter
![]() can therefore be
interpreted as the difference between the efficient level of output
and the output that would prevail under flexible prices. This
difference generates a trade-off between output and inflation
stabilization around their respective targets.
can therefore be
interpreted as the difference between the efficient level of output
and the output that would prevail under flexible prices. This
difference generates a trade-off between output and inflation
stabilization around their respective targets.
In what follows, we consider that the objectives of the central
bank, depending on the values assigned to
![]() and
and ![]() , can be
either "liberal" (
, can be
either "liberal" (![]() ) or "conservative"
(
) or "conservative"
(![]() ). For convenience, we use the term "liberal central bank" to refer to a case where the output target
and the relative weight to output stabilization are higher than a
" conservative central bank", that is
). For convenience, we use the term "liberal central bank" to refer to a case where the output target
and the relative weight to output stabilization are higher than a
" conservative central bank", that is
![]() ,
,
![]() , or both.
, or both.
2.1 Modeling policy changes
To keep the problem as simple as possible, we start by considering a case where a conservative central bank is in charge. At any point in time, the monetary authority is subject to external pressures and may adopt more liberal objectives. In this simplified model, we can derive analytical results that illustrate the main points of our analysis. In section 3, we consider the case where the central bank faces some insulation from external pressures, and hence policy objectives can change in the future but not immediately.
Consider that the objectives of a conservative central bank are
characterized by a relative weight for output ![]() , and a target for the output gap
, and a target for the output gap
![]() .5 At any point in
time, with probability
.5 At any point in
time, with probability ![]() the objectives of
the central bank will remain unchanged, while with probability
the objectives of
the central bank will remain unchanged, while with probability
![]() the central bank will be subject to
external pressures and more liberal objectives will be adopted,
i.e. setting
the central bank will be subject to
external pressures and more liberal objectives will be adopted,
i.e. setting
![]() ,
,
![]() or both.6
or both.6
Moreover, we assume that the central bank can only make credible commitments about future policy while objectives remain unchanged. If objectives do change, the more liberal central bank will set a new policy, and previous commitments will be disregarded. This assumption can be justified on the grounds that if the central bank has received some external pressures to change its policy goals, it will adopt the best possible policy to fulfill its new objectives, and thus disregards the plans made when priorities were different.7
In this context, it can be shown that the central bank makes its policy plans to solve the following problem:
![$\displaystyle =\underset{\{\pi_{t},y_{t}\}_{t=0}^{\infty}}{\max} \sum _{t=0}^{\infty} \left( \beta q\right) ^{t}\{-\frac{1}{2}\left[ \pi_{t} ^{2}+w^{c}(y_{t}-\widetilde{y}^{c})^{2}\right] +\beta(1-q)V^{c,\ell }\}$](img23.gif)
|
(3) | |
| (4) |
The objective function is given by an infinite sum, discounted
at the rate ![]() . This reflects the positive
probability that objectives will remain unchanged over the infinite
future. Each term in the summation is composed by two parts. The
first part, in the square brackets, is the period loss function.
The second part is the value function
. This reflects the positive
probability that objectives will remain unchanged over the infinite
future. Each term in the summation is composed by two parts. The
first part, in the square brackets, is the period loss function.
The second part is the value function
![]() , summarizing the utility the
central bank obtains if next period policy objectives
change.8
, summarizing the utility the
central bank obtains if next period policy objectives
change.8
Table 1: Possible settings
Value of q | Same Objectives: ( | Different objectives: ( |
|---|---|---|
q = 1 | Full Commitment (Objectives never change) | Full Commitment (Objectives never change) |
0 < q < 1 | Loose Commitment | Probabilistic changes Commitment only if no changes |
q = 0 | Discretion | Objectives change every period Commitment is not possible |
The central bank faces a sequence of constraints represented by
the NKPC, where for any period ![]() inflation
expectations are an average between two terms. The first term, with
weight
inflation
expectations are an average between two terms. The first term, with
weight ![]() , is the inflation that would prevail under
the current (conservative) central bank
, is the inflation that would prevail under
the current (conservative) central bank
![]() and upon which there is credible
commitment. The second term, with weight
and upon which there is credible
commitment. The second term, with weight ![]() , is
the inflation that would be implemented under liberal objectives
, is
the inflation that would be implemented under liberal objectives
![]() , which is taken as given by
the current central bank. In equilibrium, such level of inflation
is determined by solving a symmetric problem to the one described
above, using as preferences those of a more liberal central
bank.
, which is taken as given by
the current central bank. In equilibrium, such level of inflation
is determined by solving a symmetric problem to the one described
above, using as preferences those of a more liberal central
bank.
This framework nests many possible alternative settings, as
summarized in table 1. For example, if
we set
![]() and
and
![]() we have a typical problem of a
central bank, without changes in policy goals. In addition, setting
we have a typical problem of a
central bank, without changes in policy goals. In addition, setting
![]() we have the standard full-commitment
case, while by setting
we have the standard full-commitment
case, while by setting ![]() , we have the problem of a
central bank operating under discretion.
, we have the problem of a
central bank operating under discretion.
2.2 Effects of changes in the output target
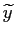
We start analyzing the case where a change in policy objectives
only implies a change in the output target, while keeping unchanged
the relative weight of output stabilization (
![]() ). It can be shown that while
the current conservative objective function prevails, the output
gap and inflation evolve according to
). It can be shown that while
the current conservative objective function prevails, the output
gap and inflation evolve according to
| (5) | ||
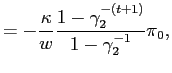
|
(6) |
where
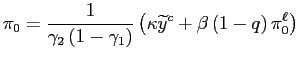
|
(7) |
and
![]() are
coefficients satisfying
are
coefficients satisfying
![]() and
and
![]() ,
which are thus independent of the policy objectives.9
Such coefficients can also be shown to be strictly increasing in
,
which are thus independent of the policy objectives.9
Such coefficients can also be shown to be strictly increasing in
![]() .10
.10
Equation (6) implies that the output gap is always below its target and that such difference increases over time. Inflation is always positive, declines over time and converges asymptotically to zero. In the initial period, the central bank can use inflation to expand output towards its efficient level. To do so, it also needs to keep inflation expectations at a low level by promising to reduce inflation in the subsequent periods. As time passes by, inflation is then reduced and output converges to a permanently and inefficiently low level. The policy plan prescribed by (5) and (6) is in general time-inconsistent. Whenever the central bank is allowed to review its policies, it has an incentive to surprise the economy and to implement a higher inflation than expected.
From these equations we can observe that, at any point in time,
the distance between output gap and inflation from their respective
targets can be expressed as increasing functions of the initial
level of inflation ![]() . The latter variable,
as we can see in (7), depends on two
factors. First, on the output target of the current policymaker
. The latter variable,
as we can see in (7), depends on two
factors. First, on the output target of the current policymaker
![]() , which is a measure of the
amplitude of the distortions in the economy. Second, it depends on
the inflation that is implemented if liberal objectives are
adopted,
, which is a measure of the
amplitude of the distortions in the economy. Second, it depends on
the inflation that is implemented if liberal objectives are
adopted,
![]() . This reflects the externality
that the possibility of changing the policy objectives generates on
the current central bank. In this respect, it is worth noticing the
presence of an inflation bias even when
. This reflects the externality
that the possibility of changing the policy objectives generates on
the current central bank. In this respect, it is worth noticing the
presence of an inflation bias even when
![]() , that is in the absence,
according to the current objectives, of any trade-off between
output and inflation stabilization. Section 2.3 discusses this
particular case in detail. Moreover, we must emphasize that
equation (5)
holds independently of the specific institutional setting (in terms
of the central bank credibility, duration of the tenure, etc.)
prevailing once the liberal objectives are adopted. The only factor
that matters is the initial level of inflation
, that is in the absence,
according to the current objectives, of any trade-off between
output and inflation stabilization. Section 2.3 discusses this
particular case in detail. Moreover, we must emphasize that
equation (5)
holds independently of the specific institutional setting (in terms
of the central bank credibility, duration of the tenure, etc.)
prevailing once the liberal objectives are adopted. The only factor
that matters is the initial level of inflation
![]() implemented in such
circumstance. For convenience, we assume that once the change in
objectives occurs, the central bank faces a symmetric problem to
the one described above.11
implemented in such
circumstance. For convenience, we assume that once the change in
objectives occurs, the central bank faces a symmetric problem to
the one described above.11
We first study the effects of limited commitment alone, assuming
that policy goals cannot be changed, but that the monetary
authority is not fully credible. In particular, we consider that at
any given point in time a reoptimization may occur with probability
![]() , but the objectives of the
central bank will be the same, i.e.
, but the objectives of the
central bank will be the same, i.e.
![]() . As
shown by Schaumburg and Tambalotti (2007) the optimal
path of inflation under limited commitment is given by:12
. As
shown by Schaumburg and Tambalotti (2007) the optimal
path of inflation under limited commitment is given by:12
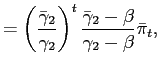 |
(8) |
where
![]() is the level of inflation
prevailing under the assumption of full commitment and no
uncertainty about policy objectives, as derived in appendix
A.1. Since
is the level of inflation
prevailing under the assumption of full commitment and no
uncertainty about policy objectives, as derived in appendix
A.1. Since
![]() we have that
in any period,
we have that
in any period,
![]() . This means
that limited commitment introduces an inflation bias. Since
. This means
that limited commitment introduces an inflation bias. Since
![]() , such bias is
decreasing in the probability of commitment q.
, such bias is
decreasing in the probability of commitment q.
We can now turn to the main part of our analysis, namely the
effects of the possibility that policy goals may change. In this
context, at any point in time and with probability ![]() , the central bank may adopt more liberal objectives, thus
setting
, the central bank may adopt more liberal objectives, thus
setting
![]() . It
can be shown that in that case
. It
can be shown that in that case
![$\displaystyle = \underset{ \begin{array}[c]{c} \text{{\scriptsize {Limited Commitment}}}\\ >1 \end{array} } {\underbrace{\left( \frac{\bar{\gamma}_{2}}{\gamma_{2}}\right) ^{t} \frac{\bar{\gamma}_{2}-\beta}{\gamma_{2}- \beta}}} \underset{ \begin{array}[c]{c} \text{{\scriptsize {Liberal Objectives}}}\\ >1 \end{array} }{\underbrace{\frac{\widetilde{y}^{c}+\Phi\widetilde{y}^{\ell}}{\widetilde {y}^{c}\left( 1+\Phi\right) }}}\bar{\pi}_{t}$](img75.gif)
|
(9) |
where
![]() and
and
![]() .
.
When more liberal objectives may be adopted in the future, two
different forces affect current inflation, independently of whether
such changes ultimately occur or not. The first is related to the
reduction in credibility associated with the possibility of a
change in policy objectives. This is represented by the first
fraction on the left-hand side of equation (9), which is
the same as in (8). The second
force is related to the adoption of more liberal objectives, as
represented by the second fraction on the left-hand side. We can
thus conclude that the possibility that policy objectives become
more liberal introduces an additional inflation bias with respect
to the limited commitment case. Such additional bias can be shown
to be increasing in the difference between
![]() and
and
![]() and in the probability
of policy changes
and in the probability
of policy changes ![]() .13 In other words,
the more liberal the alternative objectives are and the more likely
the change, the higher is current inflation. Moreover, higher
inflation is associated with a reduction in output. This can be
clearly seen in equation (6), a higher
initial inflation (
.13 In other words,
the more liberal the alternative objectives are and the more likely
the change, the higher is current inflation. Moreover, higher
inflation is associated with a reduction in output. This can be
clearly seen in equation (6), a higher
initial inflation (![]() ) lowers output in all
periods.
) lowers output in all
periods.
The main message of our analysis is twofold. First, consider an economy experiencing a low productivity level or a recession. In that case, discussing the adoption of more liberal monetary policy objectives may seem appropriate but is in fact detrimental for the economy. It generates inflationary pressures and it exacerbates the recession. Second, when there is the possibility that more liberal objectives are adopted, even the most conservative central bank should accommodate the inflationary pressures to avoid a stronger recession. In other words, the fact that inflation is higher in a given period should not be necessarily interpreted as a signal that a more liberal monetary policy is being implemented. It can be just the optimal reaction of a conservative central bank to the externalities generated by the possibility that liberal policies prevail in the future.
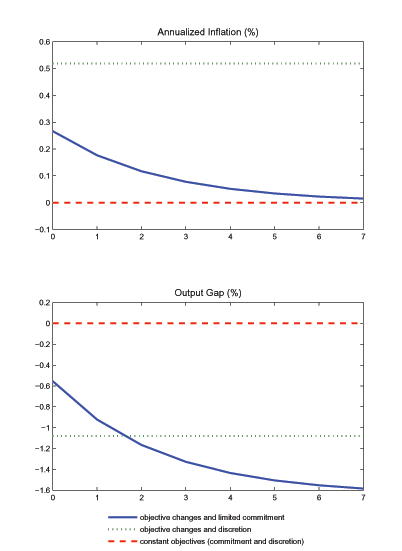
In order to give a quantification of the effects related to the
uncertainty about policy objectives, in figure 1 we plot the
optimal path of inflation and output gap while conservative
objectives prevail. We assume that the central bank has an output
target
![]() and that with
probability
and that with
probability ![]() it will adopt more liberal
objectives, i.e. setting
it will adopt more liberal
objectives, i.e. setting
![]() . For the remaining
parameters, we used a standard calibration of the model, with
. For the remaining
parameters, we used a standard calibration of the model, with
![]() ,
, ![]() , and
, and
![]() .14 For comparison, we also plot the
allocations prevailing under full-commitment and under limited
commitment. When there is the possibility that more liberal
objectives are adopted (solid line), in the first period there is a
0.25% increase in (annualized) inflation and a .5% reduction in
output with respect to the standard case with full-commitment and
no possibility of policy changes (dashed line). More importantly,
the reduction in output is even bigger at a longer horizon,
reaching a level of about 1.5%. From the picture, it is also clear
that most of the effects are due to the changes in objectives,
rather than to the associated loss of credibility, measured by the
difference between the full-commitment (dashed line) and the
limited commitment case (dashed-dotted line).
.14 For comparison, we also plot the
allocations prevailing under full-commitment and under limited
commitment. When there is the possibility that more liberal
objectives are adopted (solid line), in the first period there is a
0.25% increase in (annualized) inflation and a .5% reduction in
output with respect to the standard case with full-commitment and
no possibility of policy changes (dashed line). More importantly,
the reduction in output is even bigger at a longer horizon,
reaching a level of about 1.5%. From the picture, it is also clear
that most of the effects are due to the changes in objectives,
rather than to the associated loss of credibility, measured by the
difference between the full-commitment (dashed line) and the
limited commitment case (dashed-dotted line).
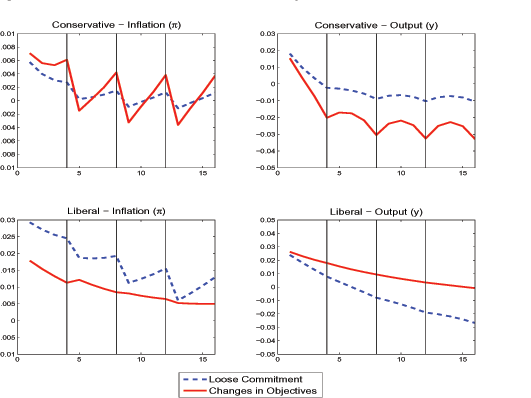
Figure 1: Adoption of liberal objectives: Optimal Inflation and Output under a conservative central bank
The figure plots inflation and the output gap that the conservative central bank implements under several scenarios. The figure plots the case of objective changes and limited commitment (continuous line), objective changes and discretion (dotted line), no objective changes and limited commitment (dashed-dotted line), and no objective changes and full commitment (dashed line).
Data for Figure 1: Panel A - Inflation
| Time | Constant objectives and full commitment |
Constant objectives and limited commitment |
Objective changes and discretion |
Objective changes and limited commitment |
|---|---|---|---|---|
| 0 | 0.1735 |
0.1928 |
0.8417 |
0.4324 |
| 1 | 0.1108 |
0.1278 |
0.8417 |
0.2866 |
| 2 | 0.0707 |
0.0847 |
0.8417 |
0.1899 |
| 3 | 0.0452 |
0.0561 |
0.8417 |
0.1259 |
| 4 | 0.0288 |
0.0372 |
0.8417 |
0.0834 |
| 5 | 0.0184 |
0.0247 |
0.8417 |
0.0553 |
| 6 | 0.0118 |
0.0163 |
0.8417 |
0.0366 |
| 7 | 0.0075 |
0.0108 |
0.8417 |
0.0243 |
Data for Figure 1: Panel B - Output
| Time | Constant objectives and full commitment | Constant objectives and limited commitment | Objective changes and discretion | Objective changes and limited commitment |
|---|---|---|---|---|
| 0 | 0.6385 | 0.5984 | -0.7536 | 0.0993 |
| 1 | 0.4076 | 0.3323 | -0.7536 | -0.4977 |
| 2 | 0.2603 | 0.1559 | -0.7536 | -0.8934 |
| 3 | 0.1662 | 0.0390 | -0.7536 | -1.1556 |
| 4 | 0.1061 | -0.0385 | -0.7536 | -1.3295 |
| 5 | 0.0677 | -0.0899 | -0.7536 | -1.4446 |
| 6 | 0.0432 | -0.1239 | -0.7536 | -1.5210 |
| 7 | 0.0276 | -0.1465 | -0.7536 | -1.5716 |
We can conclude that the mere possibility that more liberal policies can be adopted in the future, even if this ultimately never occurs, induces an increase in inflation in the short-run and a significant and permanent reduction in output. The intuition for this result goes as follows. Other things equal, the possibility of having more liberal policies in the future increases inflation expectations. As a consequence, on the one hand the central bank increases current inflation, thus accommodating the higher inflation expectations in the effort to limit the reduction in output. On the other hand, the central bank promises to reduce inflation in the future, for the case the conservative objectives still prevail.15 In this way, it reduces the inflation expectations, limiting the negative externality generated by the possibility that policy objectives become more liberal. This means that as time passes by, inflation will not be used to foster production, and thus output will be lower.
Finally, we want to understand how the credibility of the
central bank matters when policy objectives can change. To do so,
we compare two alternative settings. The first is the one described
above, where the central bank can make credible promises regarding
the policies that will be implemented if the objectives remain
unchanged. The second is a setting where, by assumption, the
central bank is not credible at all, no matter whether the policy
objectives may change or not. In that case, we have that inflation
(![]() ) and output (
) and output (![]() )
are constant over time and given by
)
are constant over time and given by
![$\displaystyle =\frac{1}{1+\frac{\kappa^{2}}{w}-\beta q}[\kappa\widetilde{y} ^{c}+\beta\left( 1-q\right) \pi_{0}^{\ell}]$](img92.gif)
|
(10) | |
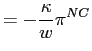 |
(11) |
In order to compare the two alternative settings, we combine
(5) and
(7) and
divide the resulting expression by (10),
considering that the inflation implemented with liberal objectives
(
![]() ) is the same in the two cases. We
then obtain that
) is the same in the two cases. We
then obtain that
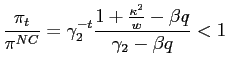
|
(12) |
where the last inequality follows from the fact that
![]() .
Moreover, dividing (6) by (11) we have
.
Moreover, dividing (6) by (11) we have

|
(13) |
which, at least for ![]() , is smaller than 1,
implying
, is smaller than 1,
implying
![]() .16
.16
The difference between the two alternative settings is also
shown in figure 1. In a context
where policy goals can be changed, when the central bank can commit
(solid line) inflation in the first period (![]() ) is
approximately half of the value prevailing when commitment is ruled
out (dotted line).
) is
approximately half of the value prevailing when commitment is ruled
out (dotted line).
Our analysis suggests that when policy objectives can change, having credibility is important. It allows to implement a lower inflation and, at least in the short-run, a higher output. This is because a credible central bank can keep inflation expectations relatively low by promising to lower inflation in case liberal objectives are not adopted. In other words, a credible institution can counteract more efficiently, the inflationary pressures arising from the possibility of adopting more liberal objectives.
To summarize, the possibility of adopting more liberal objectives generates the following effects on the conservative central bank:
- In any period, it generates an inflation bias, with respect to the case with full-commitment and constant objectives.
- In any period, it generates a lower output, with respect to the case with full-commitment and constant objectives. This is the opposite effect of what liberal pressures are aiming at.
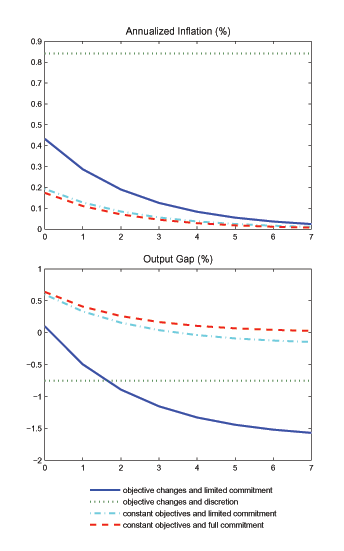
- The previous effects are due in part to the loss of credibility, and in part to the change in objectives, as described in (9). The latter seems quantitatively more important.
- The more liberal are the policies (i.e. the higher is
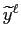 ) and the more likely
is the change in objectives (lower q), the higher
is the inflation bias.
) and the more likely
is the change in objectives (lower q), the higher
is the inflation bias. - The higher is the inflation bias, the bigger is the associated reduction in output, as described by (6).
- When there is the possibility policy goals can be changed, credibility of the central bank allows to keep inflation and output gap closer to their targets, as described in equation (12) and (13).
2.3 Discussion: commitment, the conservative central banker and inflation targeting
The optimal monetary policy literature has proposed many ways to limit the time-inconsistency problem. In a remarkable contribution, Rogoff (1985) suggested to appoint a conservative central bank that is more averse than society towards inflation.17 Rogoff shows that appointing a conservative central banker, even operating under discretion, can significantly reduce the time-inconsistency problem, and in some cases can implement the same policy of a benevolent planner with full-commitment, i.e. the best possible policy. As a result, it may be concluded that the credibility of a central bank may be of little importance, as long as its degree of inflation aversion is high enough.
We have shown previously, that when there is the possibility
that objectives may change, if the conservative central bank does
have some commitment then it can achieve more favorable
allocations. We can further illustrate this point in the following
example. Consider an (extreme) case where the conservative central
bank has a target for the output gap
![]() .18 In this case, the
central bank perceives that there are no distortions in the economy
to be corrected through the use of inflation. As a consequence, if
policy objectives cannot be changed, the central bank implements
the allocation
.18 In this case, the
central bank perceives that there are no distortions in the economy
to be corrected through the use of inflation. As a consequence, if
policy objectives cannot be changed, the central bank implements
the allocation ![]() and
and ![]() in all periods, no matter what is the degree of
commitment. In this context, appointing such a conservative central
bank is equivalent to the adoption of a strict inflation targeting
policy. The interesting question is to understand what happens if
such a conservative central bank faces the possibility that future
objectives can change to
in all periods, no matter what is the degree of
commitment. In this context, appointing such a conservative central
bank is equivalent to the adoption of a strict inflation targeting
policy. The interesting question is to understand what happens if
such a conservative central bank faces the possibility that future
objectives can change to
![]() .
.
As suggested from our discussion in the previous section, and as can be seen in figure 2, the conservative central bank, when facing possible changes in objectives, implements a positive inflation and a negative output gap.19 The figure also plots the policy where the conservative can make credible commitments (solid line), and the policy where credible commitments are ruled out (dotted line). The difference between the two lines indicates that introducing credible commitments helps significantly in keeping inflation and output close to their targets. Note that we have identified this effect even when the Rogoff conservative central banker implements the benevolent planner policy.
Figure 2: Changes in objectives and Inflation targeting: Optimal Inflation and Output
Note: The figure plots inflation and the output gap that the conservative central bank (with ![]() ) implements under several scenarios. The figure plots the case of objective changes and limited commitment (continuous line), objective changes and discretion (dotted line), and no objective changes (dashed line). In this calibration the case of no objective changes with discretion is equivalent to no objective changes with commitment.
) implements under several scenarios. The figure plots the case of objective changes and limited commitment (continuous line), objective changes and discretion (dotted line), and no objective changes (dashed line). In this calibration the case of no objective changes with discretion is equivalent to no objective changes with commitment.
Data for Figure 2: Panel A - Inflation
| Time | Constant objectives (commitment and discretion) | Objective changes and discretion | Objective changes and limited commitment |
|---|---|---|---|
| 0 | -1.962E-13 | 5.183E-01 | 2.662E-01 |
| 1 | -1.300E-13 | 5.183E-01 | 1.764E-01 |
| 2 | -8.618E-14 | 5.183E-01 | 1.169E-01 |
| 3 | -5.712E-14 | 5.183E-01 | 7.751E-02 |
| 4 | -3.786E-14 | 5.183E-01 | 5.137E-02 |
| 5 | -2.509E-14 | 5.183E-01 | 3.405E-02 |
| 6 | -1.663E-14 | 5.183E-01 | 2.257E-02 |
| 7 | -1.102E-14 | 5.183E-01 | 1.496E-02 |
Data for Figure 2: Panel B - Output
| Time | Constant objectives (commitment and discretion) |
Objective changes and discretion |
Objective changes and limited commitment |
|---|---|---|---|
| 0 | 4.087E-13 |
-1.080E+00 |
-5.546E-01 |
| 1 | 6.797E-13 |
-1.080E+00 |
-9.222E-01 |
| 2 | 8.592E-13 |
-1.080E+00 |
-1.166E+00 |
| 3 | 9.782E-13 |
-1.080E+00 |
-1.327E+00 |
| 4 | 1.057E-12 |
-1.080E+00 |
-1.434E+00 |
| 5 | 1.109E-12 |
-1.080E+00 |
-1.505E+00 |
| 6 | 1.144E-12 |
-1.080E+00 |
-1.552E+00 |
| 7 | 1.167E-12 |
-1.080E+00 |
-1.583E+00 |
Even independent and conservative central banks, may be subject to some external pressures. Our work emphasizes that even a Rogoff conservative central banker, or a central bank adopting an inflation targeting policy, can benefit from commitment. Besides other considerations, commitment is important to counteract the effects of the possibility of changes in policy objectives.
Another interesting point in our framework, is that the probability that objectives change in the future matters. In this respect, we can emphasize the difference between appointing a conservative central bank and implementing an inflation targeting regime. A conservative central bank puts more weight on inflation, and therefore can be equivalent to an inflation targeting regime, as in the example just shown. However, if an inflation targeting regime has been implemented, changing policy objectives is likely to be harder. It requires institutional reforms that are usually costly and lengthy. When a conservative central bank is in office, without a clearly specified target, changing policy objectives is easier. It is enough that the next chairman is not as conservative as the current one. Therefore, implementing an inflation targeting regime or appointing a conservative central bank is not equivalent. The two cases imply different probabilities that objectives change in the future, which immediately affects current outcomes.
3 A model with periodic objective changes
There are several examples of interference in central bank
policy in OECD countries. Nevertheless, it may not be entirely
plausible to assume that external pressures occur continuously, or
that the objectives of the central bank can be changed immediately.
In practice, objectives can only be changed with some delay due to
institutional features and policy implementation lags. In this
section, we add several features that make the model more
realistic. We consider the case where the conservative central bank
knows that it will decide the monetary policy course for at least
![]() periods. A possible interpretation of this
setting is that the central bank is independent and the chairman or
the members of the board of advisors are in charge for
periods. A possible interpretation of this
setting is that the central bank is independent and the chairman or
the members of the board of advisors are in charge for ![]() periods. At the end of their tenure, policy objectives can
change as long as officers with different views are appointed.
periods. At the end of their tenure, policy objectives can
change as long as officers with different views are appointed.
Both the conservative central bank and private agents know that
in ![]() periods the current conservative
objectives can persist (with probability
periods the current conservative
objectives can persist (with probability ![]() ) or
give place to liberal objectives (with probability
) or
give place to liberal objectives (with probability ![]() ). In the latter case, for simplicity, we assume the
central bank will face a symmetric problem, where liberal
objectives are unaltered for
). In the latter case, for simplicity, we assume the
central bank will face a symmetric problem, where liberal
objectives are unaltered for ![]() periods, and then
can change with probability
periods, and then
can change with probability ![]() . The model in
this section, besides being more realistic, allows us to better
understand how the possibility of changes in policy objectives
affects the conduct of monetary policy.
. The model in
this section, besides being more realistic, allows us to better
understand how the possibility of changes in policy objectives
affects the conduct of monetary policy.
As before, the central bank can commit to a plan as long as the
objectives remain unchanged. In this setting, analytical solutions
are not available, and one needs to use the tools of shown in
Debortoli and Nunes (2006a) and Debortoli and Nunes (2006b) to solve the model
numerically.20 In the present framework, the
problem of the conservative (![]() ) or liberal
(
) or liberal
(![]() ) central bank is the following. Taking
as given the sequence of policy
) central bank is the following. Taking
as given the sequence of policy
![]() and
the value function
and
the value function ![]() , with
, with ![]() , the problem of the central bank can be written
as:
, the problem of the central bank can be written
as:
![$\displaystyle E_{0}\sum_{m=0}^{\infty }\left( \beta^{T}q\right) ^{m}\left[ -\frac{1}{2}\sum_{t=0}^{T-1}\beta ^{t}\left[ \pi_{m+t}^{2}+w^{i}(y_{m+t}-{\widetilde{y}}^{i})^{2}\right] + \beta^{T}(1-q)V^{ij} \right]$](img125.gif)
|
(14) |
| (15) | ||
| (16) | ||
where ![]() indexes the number of tenures, each
lasting for
indexes the number of tenures, each
lasting for ![]() periods. The objective function
reflects the institutional setting the central bank faces. At the
end of any tenure (
periods. The objective function
reflects the institutional setting the central bank faces. At the
end of any tenure (![]() periods where objectives
can not change), current objectives (
periods where objectives
can not change), current objectives (![]() ) can remain
unaltered with probability
) can remain
unaltered with probability ![]() . This history is
summarized in the outer summation. Within each tenure, plans are
made for
. This history is
summarized in the outer summation. Within each tenure, plans are
made for ![]() periods, as indicated in the inner
summation. Finally, the central bank (
periods, as indicated in the inner
summation. Finally, the central bank (![]() )
internalizes that with some probability
)
internalizes that with some probability ![]() , at the
end of tenure the objectives will be of type (
, at the
end of tenure the objectives will be of type (![]() ). In this case, central bank (
). In this case, central bank (![]() ) will get
the loss function
) will get
the loss function ![]() . More formally, define
the sequence
. More formally, define
the sequence
![]()
![]() . The value function
. The value function
![]() ,
,
![]() and
and ![]() is given by
is given by
![$\displaystyle E_{0}\sum_{m=0}^{\infty}\left( \beta^{T}q\right) ^{m}\left[ -\frac{1}{2} \sum_{t=0}^{T-1}\beta^{t}\left[ {(\pi_{m+t}^{j})}^{2} +w^{i}(y_{m+t}^{j}-{\widetilde{y}}^{i})^{2}\right] + \beta^{T}(1-q)V^{ji} \right]$](img150.gif)
|
(17) |
The sequence of constraints (15) and (16) also reflects
the institutional setting. Within any tenure ![]() ,
we can divide the constraints into two groups, depending on how
inflation expectations are formed. In the periods
,
we can divide the constraints into two groups, depending on how
inflation expectations are formed. In the periods
![]() , inflation expectations
internalize that in the next period objectives do not change. In
the last period of the tenure
, inflation expectations
internalize that in the next period objectives do not change. In
the last period of the tenure ![]() , agents
recognize that with some probability
, agents
recognize that with some probability ![]() objectives
do not change, while with probability
objectives
do not change, while with probability ![]() objectives do change. We employ the following definition of
equilibrium:
objectives do change. We employ the following definition of
equilibrium:
- The value function
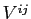 satisfies equation
(17).
satisfies equation
(17). - The sequence
 ,
solves (14)
subject to (15) and (16).
,
solves (14)
subject to (15) and (16).
In order to solve problem (14), we first write its recursive formulation. To do so we apply the technique of Marcet and Marimon (1998), and we write the problem as a saddle point functional equation that generalizes the usual Bellman equation. The proof of that result requires considering each tenure as one big period, and then applying the results of Debortoli and Nunes (2006a) to address the probabilistic switch at the end of each tenure. Proposition 1 in the appendix proves this result in detail. As stated in Proposition 1 in the appendix, we can then characterize the policy functions solving our problem as tenure invariant functions of the Lagrange multipliers associated with the constraints (15) and (16). We are not claiming that the policy functions are time-invariant. Indeed, the policy functions change in the different periods within a tenure.
In order to solve our problem we have to find, for both central
banks (![]() ), the policy functions satisfying
the equilibrium conditions stated above. In particular, for each
central bank, we need to find as many policy functions as the
number of periods within each tenure (
), the policy functions satisfying
the equilibrium conditions stated above. In particular, for each
central bank, we need to find as many policy functions as the
number of periods within each tenure (![]() ). Moreover,
as can be seen in (16), the policies
of central bank
). Moreover,
as can be seen in (16), the policies
of central bank ![]() enter the problem of central bank
enter the problem of central bank
![]() (and viceversa). This implies that we have
to solve a fixed point problem in such policy functions. In
addition, the implied value functions
(and viceversa). This implies that we have
to solve a fixed point problem in such policy functions. In
addition, the implied value functions ![]() and
and
![]() also enter the problem and need to be
solved for endogenously.21 We also have to take into account
the possibility of default on past promises, an event that occurs
whenever there is a change in objectives. The presence of default
significantly complicates the numerical procedure, since both the
levels and the derivatives of the policy functions enter the
first-order conditions of the problem.
also enter the problem and need to be
solved for endogenously.21 We also have to take into account
the possibility of default on past promises, an event that occurs
whenever there is a change in objectives. The presence of default
significantly complicates the numerical procedure, since both the
levels and the derivatives of the policy functions enter the
first-order conditions of the problem.
We solved the model numerically using the same calibration of
the previous section. Regarding the number of periods where
objectives remain unchanged (![]() ), and the
probability that objectives change, we could have considered
several calibrations. We considered that central bank objectives
remain unchanged with certainty for four periods (
), and the
probability that objectives change, we could have considered
several calibrations. We considered that central bank objectives
remain unchanged with certainty for four periods (![]() ), at that point there is a probability of that objectives
change equal to
), at that point there is a probability of that objectives
change equal to ![]() . This calibration is
convenient for illustrative purposes.22
. This calibration is
convenient for illustrative purposes.22
3.1 Results
We first consider the case of disagreement in the output gap target level. Figure 3 plots the optimal policy functions in the case where the conservative central bank may be temporarily replaced by a liberal one (continuous line). One can easily translate the policy functions to certain realizations of events. The conservative central bank implements the policy functions shown in the figure until policy objectives are changed. When such change occurs, the liberal policy is implemented until objectives become conservative again. In this model, the possibility that objectives change is only present every four periods - those periods are signaled in the pictures with continuous vertical lines. Therefore, once it is know that the liberal policies are not implemented, the conservative central bank is insulated from any external pressure for four periods. This feature of the model tries to capture the fact that in reality political pressures may not be able to change objectives immediately. The upper panel plots the policy functions of the conservative central bank for inflation and output, the lower panel refers to the liberal policy functions.
Figure 3: Model with Occasional Changes in Objectives
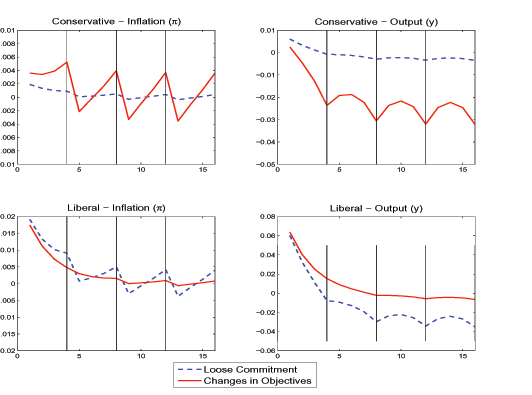
Note: This figure refers to the model where objectives can not change immediately. The upper two panels plot the policy functions (inflation and output gap) of a conservative central bank, and the lower two panels refer to a liberal central bank. Objectives changes (in the output gap target) can only occur every four periods - marked with continuous vertical lines. The case with objective changes and limited commitment is plotted with a continuous line. The case of no objective changes and limited commitment is plotted with a dashed line. In all panels the horizontal axis refers to the number of periods elapsed after the last change in objectives/reoptimization.
Data for Figure 3
| Time | Conservative: Inflation (π): Changes in Objectives | Conservative: Inflation (π): Loose Commitment | Conservative: Output (y): Changes in Objectives | Conservative: Output (y): Loose Commitment | Liberal: Inflation (π): Changes in Objectives | Liberal: Inflation (π): Loose Commitment | Liberal: Output (y): Changes in Objectives | Liberal: Output (y): Loose Commitment |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.00361381 | 0.00191580 | 0.00247123 | 0.00600875 | 0.01745961 | 0.01915766 | 0.06362582 | 0.06008821 |
| 2 | 0.00340069 | 0.00132815 | -0.00461354 | 0.00324176 | 0.01120911 | 0.01328165 | 0.04027350 | 0.03241810 |
| 3 | 0.00390106 | 0.00101412 | -0.01274074 | 0.00112902 | 0.00725431 | 0.01014126 | 0.02516036 | 0.01129048 |
| 4 | 0.00522740 | 0.00091032 | -0.02363117 | -0.00076748 | 0.00478613 | 0.00910324 | 0.01518925 | -0.00767461 |
| 5 | -0.00212530 | 0.00007835 | -0.01920346 | -0.00093070 | 0.00298678 | 0.00078315 | 0.00896679 | -0.00930618 |
| 6 | -0.00020702 | 0.00017309 | -0.01877217 | -0.00129131 | 0.00211121 | 0.00173108 | 0.00456843 | -0.01291260 |
| 7 | 0.00168707 | 0.00030528 | -0.02228689 | -0.00192731 | 0.00167108 | 0.00305287 | 0.00108701 | -0.01927274 |
| 8 | 0.00395531 | 0.00050304 | -0.03052712 | -0.00297531 | 0.00157816 | 0.00503045 | -0.00220083 | -0.02975284 |
| 9 | -0.00330208 | -0.00029842 | -0.02364779 | -0.00235361 | 0.00001919 | -0.00298446 | -0.00224081 | -0.02353521 |
| 10 | -0.00094677 | -0.00006375 | -0.02167535 | -0.00222080 | 0.00024573 | -0.00063732 | -0.00275274 | -0.02220747 |
| 11 | 0.00123310 | 0.00015993 | -0.02424430 | -0.00255400 | 0.00052627 | 0.00159943 | -0.00384913 | -0.02553960 |
| 12 | 0.00369447 | 0.00041953 | -0.03194111 | -0.00342801 | 0.00092038 | 0.00419534 | -0.00576659 | -0.03427989 |
| 13 | -0.00354338 | -0.00037567 | -0.02455908 | -0.00264537 | -0.00058930 | -0.00375700 | -0.00453888 | -0.02645281 |
| 14 | -0.00109845 | -0.00011231 | -0.02227064 | -0.00241139 | -0.00013678 | -0.00112295 | -0.00425392 | -0.02411334 |
| 15 | 0.00114001 | 0.00013013 | -0.02464566 | -0.00268250 | 0.00029153 | 0.00130140 | -0.00486126 | -0.02682460 |
| 16 | 0.00364099 | 0.00040240 | -0.03223105 | -0.00352084 | 0.00078551 | 0.00402410 | -0.00649774 | -0.03520814 |
For comparison, in figure 3, we also plot the policy functions that occur in a loose commitment setting (dashed line). Loose commitment refers to the fact that the central bank occasionally disregards previous commitments and makes a new plan, but where objectives do not change. In such case, the policy functions with the same objectives are implemented from the beginning until the next reoptimization occurs. The differences between the policy functions with loose commitment and with changes in objectives are only due to the possibility that objectives change. In both cases, there is a common commitment problem.
The possibility that a liberal central banker might be appointed in the future affects the optimal policy functions of the conservative central bank in several ways. First, when the conservative central bank starts (periods 1 to 4), inflation is now higher and output is lower. This is due to an accommodation effect. The possibility that the liberal policies with high inflation are implemented in the future affects current outcomes through inflation expectations. High inflation expectations either imply higher current inflation or lower output. The optimal policy of the conservative implies a combination of higher inflation and lower output.
Second, we also observe that the conservative central bank implements a low inflation level immediately after knowing that the pressures to adopt liberal policies have dissipated (periods 5, 9, 13,...), and that objectives will not change in the following four periods. The rationale of this policy is to anchor inflation expectations. When it is known that in the next period a liberal policy may be implemented, inflation expectations increase. In order to keep inflation expectations low, the conservative central bank finds it optimal to promise to reduce inflation if objectives remain unchanged. This promise regarding future policy affects beneficially the current period through inflation expectations. Note that this promise is extremely time-inconsistent, if there is not a change in objectives, the conservative central bank needs to fulfil its promise of implementing a very low inflation level. This case exemplifies how commitment is used to balance distortions across time and states of nature.
Finally, note that the first period of the conservative central bank (period 1) is fundamentally different from any first period after being confirmed in office (periods 5, 9, 13,...). As we had explained before, periods 5, 9, 13 are characterized by low inflation that was promised in the previous period. In the current setting, we are assuming that past promises are not binding in period 1 because the conservative central bank was not in office before. This is the reason why inflation is relatively high in period 1, when compared, for instance, with period 5.
Summarizing our results, we have found that the possibility that
liberal policies are implemented creates three effects in the
policies of the conservative. First, the conservative central bank
needs to raise inflation to accommodate inflation expectations -
the accommodation effect. The accommodation effect is higher the
closer is the period where liberal policies may take over. Second,
to counteract high inflation expectations, the conservative
promises to implement a low inflation if the objectives do not
change - the anchoring effect. The anchoring effect only
materializes when liberal objectives are not adopted. The
combination of the accommodation and anchoring effect explains why
the conservative starts with low inflation and then increases it.
In the model with one period tenure ![]() , the
strength of the anchoring and accommodation effect did not change
over time. And in that case, we proved analytically that the
possibility that liberal objectives could be adopted induced the
conservative to implement higher inflation in every period. Third,
the conservative experiences lower output due to the possibility
that liberal policies are implemented. This result may come as
surprising. If a liberal sector of the economy thinks that current
output is too low, and makes pressures for changing the central
bank policy, then the outcome is that the economy experiences an
even lower output. If the liberal policies are implemented in a
later period, then the economy will experience an expansion.
However, as long as the objectives do not change, the economy
experiences a recession, the opposite outcome of what the pressures
for liberal policies may be aiming.
, the
strength of the anchoring and accommodation effect did not change
over time. And in that case, we proved analytically that the
possibility that liberal objectives could be adopted induced the
conservative to implement higher inflation in every period. Third,
the conservative experiences lower output due to the possibility
that liberal policies are implemented. This result may come as
surprising. If a liberal sector of the economy thinks that current
output is too low, and makes pressures for changing the central
bank policy, then the outcome is that the economy experiences an
even lower output. If the liberal policies are implemented in a
later period, then the economy will experience an expansion.
However, as long as the objectives do not change, the economy
experiences a recession, the opposite outcome of what the pressures
for liberal policies may be aiming.
Table 2 reports welfare and the average allocations. The average inflation that the conservative implements is higher relative to the loose commitment case where the conservative is never substituted by a liberal policy. As expected, the overall output average when conservative and liberal objectives coexist is higher than the case where the conservative objectives are unchallenged. But, as we cautioned before, the conservative central bank experiences a lower output due to the pressures of liberal policies. Hence, as long as the central bank's objectives do not change, there is a negative effect on output. In terms of welfare, pressures to adopt liberal objectives create a negative externality on the conservative. Even though, overall output is slightly higher, inflation is further away from target.
Table 2: Inflation and Output in a Model with Occasional Changes in Objectives
| Variable | Changes in Objectives: Average with c | Changes in Objectives: Average with l | Changes in Objectives: Overall | Loose Commitment: c | Loose Commitment: l |
|---|---|---|---|---|---|
| π | 0.2254 | 0.57 | 0.3968 | 0.0723 | 0.7226 |
| y | -1.6888 | 1.7822 | 0.0382 | 0.0083 | 0.083 |
| welfare | -0.0036 | -0.0272 | . | -0.0003 | -0.0302 |
Note: The table reports the average allocations across different simulations of the model.
In a partisan theory of output and inflation, Alesina (1987) considered a classical Phillips curve where current inflation surprises affect current outcomes. In that context, the possibility of a future change in policy does not affect current outcomes. For instance, the possibility that a liberal policy is implemented in period 4, 8, 12 has no consequences on the economy and the optimal policy functions in any other periods. Here, we consider instead a (standard) New Keynesian Phillips curve, where future conditions also influence current outcomes. Therefore, our work has very different mechanisms from the analysis considered in Alesina (1987), where for instance the accommodation effect is simply absent. In addition, in those models it is assumed that the central bank acts with discretion in every period. Given the developments in central bank commitment, we are instead assuming that there is commitment to policies aimed at maximizing the same objectives. Since the anchoring effect found in our model is based on a commitment, that effect is also not present in Alesina's model.
4 Alternative scenarios
In this section, we consider some alternative scenarios where liberal and conservative objectives coexist. We consider a case where the relative weight of inflation stabilization can change, a case with a hybrid Phillips curve, and then a full commitment cooperative setting. In all these cases, the main intuition presented in the baseline case still holds. We finally discuss the reverse scenarios that we examined, the case where future policy objectives may become more conservative.
4.1 Changes on the relative weight of inflation stabilization
Consider the case where both conservative and liberal objectives
agree on the output target level, but disagree on the importance of
inflation stabilization. In particular, we assume
![]() and
and
![]() . In this context, if
policy objectives can change in every period (
. In this context, if
policy objectives can change in every period (![]() ) with probability
) with probability ![]() , we can show
that inflation evolves according to
, we can show
that inflation evolves according to
![$\displaystyle = \underset{ \begin{array}[c]{c} \text{{\scriptsize {Liberal Objectives}}}\\ >1 \end{array} }{\underbrace{\frac{(1+\Phi^{\ell})(1-\Phi^{c})}{1-\Phi^{c}\Phi^{\ell}}} }\underset{ \begin{array}[c]{c} \text{{\scriptsize {Limited Commitment}}}\\ >1 \end{array} } {\underbrace{\left( \frac{\bar{\gamma}_{2}}{\gamma_{2}}\right) ^{t} \frac{\bar{\gamma}_{2}-\beta}{\gamma_{2}- \beta}}} \bar{\pi}_{t},$](img178.gif)
|
where
Consistent with our analysis in section 2.2, we can conclude that pressures to increase the relative weight of output stabilization generates an inflation bias. This bias increases with the probability of a policy change (1 - q).
We provide a quantitative example, for the case where the tenure
of the central bank lasts for ![]() periods. More
specifically, we consider that
periods. More
specifically, we consider that
![]() ,
,
![]() and
and
![]() . This case is also plausible
since it has been argued that the full-commitment microfounded
calibration of
. This case is also plausible
since it has been argued that the full-commitment microfounded
calibration of ![]() is much lower than what policy
makers often implement in practice. Figure 4 presents the
policy functions and Table 3 presents the
average allocations in the economy. All the results and intuition
that we mentioned previously remain unaltered.
is much lower than what policy
makers often implement in practice. Figure 4 presents the
policy functions and Table 3 presents the
average allocations in the economy. All the results and intuition
that we mentioned previously remain unaltered.
Table 3: Inflation and Output - Changes in w
| Variable | Changes in Objectives: Average with c |
Changes in Objectives: Average with l |
Changes in Objectives: Overall |
Loose Commitment: c |
Loose Commitment: l |
|---|---|---|---|---|---|
| π | 0.336 |
1.1208 |
0.7265 |
0.2168 |
2.0627 |
| y | -1.3006 |
1.4567 |
0.0713 |
0.0249 |
0.2137 |
| welfare | -0.007 |
-0.0329 |
. |
-0.0027 |
-0.0483 |
Note: The table reports the average allocations across different simulations of the model.
Figure 4: Alternative Scenario: different weights of inflation stabilization
Note: This figure refers to the model where objectives can not change immediately. The upper two panels plot the policy functions (inflation and output gap) of a conservative central bank, and the lower two panels refer to a liberal central bank. Objectives changes (in weight on output stabilization) can only occur every four periods - marked with continuous vertical lines. The case with objective changes and limited commitment is plotted with a continuous line. The case of no objective changes and limited commitment is plotted with a dashed line. In all panels the horizontal axis refers to the number of periods elapsed after the last change in objectives/reoptimization.
Data for Figure 4
| Time | Conservative: Inflation (π): Changes in Objectives | Conservative: Inflation (π): Loose Commitment | Conservative: Output (y): Changes in Objectives | Conservative: Output (y): Loose Commitment | Liberal: Inflation (π): Changes in Objectives | Liberal: Inflation (π): Loose Commitment | Liberal: Output (y): Changes in Objectives | Liberal: Output (y): Loose Commitment |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.00707260 | 0.00574730 | 0.01526541 | 0.01802647 | 0.01787927 | 0.02927630 | 0.02627515 | 0.02390077 |
| 2 | 0.00560208 | 0.00398449 | 0.00359440 | 0.00972544 | 0.01540582 | 0.02715780 | 0.02306561 | 0.01824290 |
| 3 | 0.00529560 | 0.00304237 | -0.00743811 | 0.00338716 | 0.01323157 | 0.02558941 | 0.02030903 | 0.01291177 |
| 4 | 0.00610045 | 0.00273097 | -0.02014738 | -0.00230236 | 0.01131381 | 0.02454367 | 0.01795199 | 0.00779850 |
| 5 | -0.00148497 | 0.00023495 | -0.01705369 | -0.00279184 | 0.01215689 | 0.01873137 | 0.01541930 | 0.00389614 |
| 6 | 0.00022263 | 0.00051932 | -0.01751750 | -0.00387376 | 0.01072218 | 0.01852703 | 0.01318551 | 0.00003634 |
| 7 | 0.00199432 | 0.00091586 | -0.02167234 | -0.00578180 | 0.00949862 | 0.01871050 | 0.01120663 | -0.00386168 |
| 8 | 0.00420362 | 0.00150913 | -0.03042989 | -0.00892583 | 0.00846258 | 0.01928957 | 0.00944360 | -0.00788034 |
| 9 | -0.00323966 | -0.00089534 | -0.02368059 | -0.00706054 | 0.00811571 | 0.01128447 | 0.00775282 | -0.01023128 |
| 10 | -0.00088041 | -0.00019119 | -0.02184641 | -0.00666222 | 0.00741457 | 0.01243192 | 0.00620812 | -0.01282126 |
| 11 | 0.00131741 | 0.00047983 | -0.02459101 | -0.00766186 | 0.00686238 | 0.01385257 | 0.00477846 | -0.01570721 |
| 12 | 0.00381469 | 0.00125860 | -0.03253827 | -0.01028394 | 0.00644902 | 0.01557908 | 0.00343491 | -0.01895285 |
| 13 | -0.00359946 | -0.00112710 | -0.02503941 | -0.00793582 | 0.00526179 | 0.00602542 | 0.00233871 | -0.02020815 |
| 14 | -0.00110658 | -0.00033688 | -0.02273403 | -0.00723398 | 0.00507871 | 0.00812751 | 0.00128064 | -0.02190138 |
| 15 | 0.00117861 | 0.00039042 | -0.02518947 | -0.00804736 | 0.00500065 | 0.01042187 | 0.00023884 | -0.02407261 |
| 16 | 0.00373494 | 0.00120723 | -0.03297059 | -0.01056242 | 0.00502704 | 0.01295872 | -0.00080846 | -0.02677234 |
4.2 Hybrid Phillips curve
In this section, following Galí and Gertler (1999), we consider the possibility that the Phillips curve may also include a backward looking term. The hybrid Phillips curve takes the form
| (18) |
The presence of lagged inflation introduces a state variable in the model.23 The presence of such state variable is relevant for our analysis, since it allows the central bank to influence strategically future decisions. Whether there is a change in objectives or not, current policy will be affected by the past inflation level. Therefore, the central bank can strategically choose an inflation to influence next period decisions, even if objectives change.
For direct comparability purposes, we leave the central banks' objective functions as in the baseline scenario of section 3.24 This allows us to understand whether the presence of inflation as a state variable changes the interaction patterns between the conservative and liberal policies. Another important point is that the model with the hybrid Phillips curve actually alleviates the time-inconsistency problem. This is because the weight on expected future inflation is smaller. Since a reoptimization will now imply an inflation level that is not as high as before, the conservative central bank necessity to accommodate inflation expectations is not so strong.
In accordance with the empirical evidence in Galí and Gertler (1999) we set α to be 0.3. Figure 5 plots the policy functions.25 The qualitative features of the effects of the possibility of adopting liberal objectives are the same as in the baseline case. Table 4 reports the relevant statistics. The table mainly confirms the results explained previously.
Figure 5: Alternative Scenario: Hybrid Phillips Curve
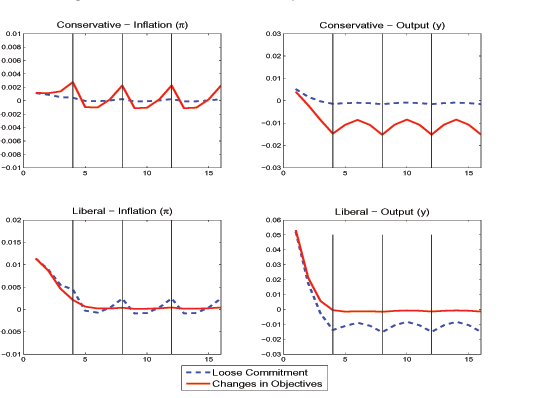
Note: This figure refers to the model where objectives can not change immediately, and the Phillips curve also has a backward-looking component. The upper two panels plot the policy functions (inflation and output gap) of a conservative central bank, and the lower two panels refer to a liberal central bank. Objectives changes (in the output gap target) can only occur every four periods - marked with continuous vertical lines. The case with objective changes and limited commitment is plotted with a continuous line. The case of no objective changes and limited commitment is plotted with a dashed line. In all panels the horizontal axis refers to the number of periods elapsed after the last change in objectives/reoptimization.
Data for Figure 5
| Time | Conservative: Inflation (π): Changes in Objectives |
Conservative: Inflation (π): Loose Commitment |
Conservative: Output (y): Changes in Objectives |
Conservative: Output (y): Loose Commitment |
Liberal: Inflation (π): Changes in Objectives |
Liberal: Inflation (π): Loose Commitment |
Liberal: Output (y): Changes in Objectives |
Liberal: Output (y): Loose Commitment |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.00117922 |
0.00114053 |
0.00402156 |
0.00520089 |
0.01136665 |
0.01140533 |
0.05318813 |
0.05200888 |
| 2 | 0.00112130 |
0.00089530 |
-0.00197746 |
0.00175934 |
0.00872704 |
0.00895302 |
0.02133001 |
0.01759339 |
| 3 | 0.00139801 |
0.00054925 |
-0.00855765 |
-0.00025771 |
0.00464379 |
0.00549250 |
0.00572274 |
-0.00257694 |
| 4 | 0.00277161 |
0.00044605 |
-0.01469438 |
-0.00137630 |
0.00213496 |
0.00446052 |
-0.00044475 |
-0.01376258 |
| 5 | -0.00094956 |
-0.00002729 |
-0.01076383 |
-0.00110832 |
0.00064934 |
-0.00027290 |
-0.00142771 |
-0.01108303 |
| 6 | -0.00100483 |
-0.00007062 |
-0.00855598 |
-0.00088930 |
0.00022804 |
-0.00070617 |
-0.00122637 |
-0.00889284 |
| 7 | 0.00019162 |
0.00003812 |
-0.01079614 |
-0.00108933 |
0.00022774 |
0.00038120 |
-0.00118657 |
-0.01089311 |
| 8 | 0.00226500 |
0.00024246 |
-0.01519380 |
-0.00152062 |
0.00040204 |
0.00242459 |
-0.00153287 |
-0.01520579 |
| 9 | -0.00111935 |
-0.00008924 |
-0.01072274 |
-0.00106188 |
0.00013769 |
-0.00089239 |
-0.00095790 |
-0.01061857 |
| 10 | -0.00103865 |
-0.00007946 |
-0.00843032 |
-0.00082668 |
0.00016461 |
-0.00079457 |
-0.00066332 |
-0.00826673 |
| 11 | 0.00019745 |
0.00004288 |
-0.01070622 |
-0.00104960 |
0.00027424 |
0.00042878 |
-0.00083949 |
-0.01049583 |
| 12 | 0.00227493 |
0.00024738 |
-0.01514582 |
-0.00150085 |
0.00044624 |
0.00247380 |
-0.00136341 |
-0.01500812 |
| 13 | -0.00111177 |
-0.00008593 |
-0.01070327 |
-0.00105436 |
0.00016654 |
-0.00085927 |
-0.00089466 |
-0.01054338 |
| 14 | -0.00103477 |
-0.00007788 |
-0.00842458 |
-0.00082470 |
0.00017817 |
-0.00077872 |
-0.00064724 |
-0.00824690 |
| 15 | 0.00019897 |
0.00004346 |
-0.01070555 |
-0.00104952 |
0.00027913 |
0.00043460 |
-0.00083932 |
-0.01049507 |
| 16 | 0.00227537 |
0.00024753 |
-0.01514643 |
-0.00150119 |
0.00044745 |
0.00247530 |
-0.00136651 |
-0.01501149 |
Table 4: Inflation and Output - Hybrid Phillips Curve
| Variable | Changes in Objectives: Average with c |
Changes in Objectives: Average with l |
Changes in Objectives: Overall |
Loose Commitment: c |
Loose Commitment: l |
|---|---|---|---|---|---|
| π | 0.0878 |
0.3567 |
0.2216 |
0.0404 |
0.4038 |
| y | -0.8503 |
0.9003 |
0.0207 |
0.0045 |
0.0449 |
| welfare | -0.0017 |
-0.0253 |
. |
-0.0002 |
-0.0264 |
Note: The table reports the average allocations across different simulations of the model.
4.3 A full commitment solution
For the sake of realism, we assumed an intermediate level of commitment where the central bank could make binding promises as long as external pressures do not alter policy objectives. This feature reflects the inherent disagreement on different policy objectives. In this section, we want to analyze a setting where the central bank has full commitment, even though the policy objectives may change over time. One interpretation of this framework is that the structural parameters of the economy, like the degree of nominal rigidities and the degree of firms' monopolistic power, evolve stochastically, thus changing the magnitude of the distortion the central bank aims to correct and the effectiveness of its policy.26 Another interpretation of this setting is that the central bank itself is subject to preferences shocks. The setting in this section models the central bank has being extremely forward-looking, since it already makes a plan and commits to certain policy actions even if future objectives differ from the current ones. Another essential assumption for the present setting is that there is no disagreement about policy objectives, in which case considering loose commitment would be necessary.
In the baseline setting described in section 3, when external pressures succeed in altering the objectives, policy is reset to achieve the new objectives disregarding previous objectives. In contrast, in the model of this section, policies are chosen to maximize the overall welfare. In fact, since there is no disagreement, we can think that there is a unique policymaker taking decisions.
More specifically, we assume the central bank's policy goals can
be
![]() or
or
![]() . For convenience, we
still refer to the terminology central bank
. For convenience, we
still refer to the terminology central bank ![]() or
or
![]() when the current output gap is
respectively
when the current output gap is
respectively
![]() or
or
![]() . Every four periods
(
. Every four periods
(![]() ) the objectives remain unchanged with
probability
) the objectives remain unchanged with
probability ![]() , while with probability
, while with probability
![]() the objectives do change. The problem of
the central bank can be written as:
the objectives do change. The problem of
the central bank can be written as:
![$\displaystyle =-\frac{1}{2}E_{0}\sum_{t=0}^{\infty }\beta^{t}\left[ \pi_{t}^{2}+w(y_{t}-\widetilde{y_{t}})^{2}\right]$](img199.gif)
|
||
where expectations are taken with respect to the variable
![]() . This problem can be written
recursively by considering a tenure as a unique period and then
applying standard dynamic programming techniques.
. This problem can be written
recursively by considering a tenure as a unique period and then
applying standard dynamic programming techniques.
Figure 6 plots the policy functions for both types of objectives.27 The policy functions of the conservative are extremely similar to the other cases considered previously. There is an accommodation effect, which becomes more visible the closer is the period where the liberal policies may emerge (periods 4, 8, 12 in the graph). In addition, whenever the objectives do not change, and thus the conservative objectives are kept (periods 5, 9, 13), inflation is reduced due to the anchoring effect. Also, as before, the conservative central bank experiences lower output due to the externalities generated by the possibility that more liberal objectives are adopted.28
Figure 6: Alternative Scenario: Full Commitment and objective changes
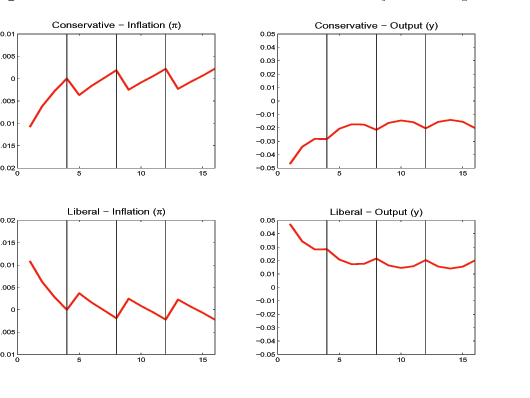
Note: This figure refers to the model where objectives can not change immediately, and the central bank commits to future policy, even if objectives do change. The upper two panels plot the policy functions (inflation and output gap) of a conservative central bank, and the lower two panels refer to a liberal central bank. Objectives changes (in the output gap target) can only occur every four periods - marked with continuous vertical lines. The case with objective changes and full commitment is plotted with a continuous line. The case of no objective changes and full commitment would correspond to zero inflation and zero output gap. In all panels the horizontal axis refers to the number of periods elapsed after the last change in objectives.
Data for Figure 6
| Time | Conservative: Inflation (π) | Conservative: Output (y) | Liberal: Inflation (π) | Liberal: Output (y) |
|---|---|---|---|---|
| 1 | -0.010815 | -0.046973 | 0.010903 | 0.047296 |
| 2 | -0.006180 | -0.034099 | 0.006235 | 0.034305 |
| 3 | -0.002797 | -0.028271 | 0.002833 | 0.028403 |
| 4 | 0.000030 | -0.028334 | -0.000007 | 0.028417 |
| 5 | -0.003670 | -0.020687 | 0.003685 | 0.020741 |
| 6 | -0.001618 | -0.017316 | 0.001627 | 0.017351 |
| 7 | 0.000115 | -0.017556 | -0.000109 | 0.017578 |
| 8 | 0.001889 | -0.021492 | -0.001886 | 0.021506 |
| 9 | -0.002483 | -0.016319 | 0.002486 | 0.016328 |
| 10 | -0.000860 | -0.014527 | 0.000861 | 0.014533 |
| 11 | 0.000599 | -0.015775 | -0.000598 | 0.015779 |
| 12 | 0.002198 | -0.020355 | -0.002198 | 0.020358 |
| 13 | -0.002286 | -0.015593 | 0.002286 | 0.015595 |
| 14 | -0.000734 | -0.014064 | 0.000734 | 0.014065 |
| 15 | 0.000679 | -0.015479 | -0.000679 | 0.015480 |
| 16 | 0.002250 | -0.020166 | -0.002250 | 0.020167 |
The main difference in the conservative policy between this model and the baseline one in section 3 resides in the initial period. In the present model, inflation in the first four periods is lower. The main reason is that in this model past plans are always fulfilled. Therefore, the anchoring effect is also present in the initial period. The other interesting feature is that this anchoring effect is much stronger when the conservative is newly appointed (period 1 in the graph) rather than when it is reappointed (periods 5, 9, 13). The reason is that in this setup there is no disagreement about policy objectives, and therefore there is cooperation between the liberal and the conservative central bank. The anchoring effect reduces inflation expectations, which allows to increase output for a given inflation rate. When current objectives are liberal, it is specially important to achieve a high output level. Therefore, a liberal central bank promises that inflation will be at a particularly low level when objectives become conservative.
The next table plots the average allocations in the economy. As before, under a conservative central bank, the possibility that liberal policies may be adopted lowers output. The anchoring effect is stronger and is present more frequently in this economy.29 In fact, when policy objectives may become more liberal, a conservative central bank implement a lower average inflation, which comes at the expense of a deeper recession.30 This model confirms our findings in previous sections. The possibility that future policy objectives may become less conservative affects considerably the current optimal policy of a conservative central bank. We still observe an anchoring and accommodation effect, while output is lowered.
Table 5: Inflation and Output - Full commitment case
| Variable | Changes in Objectives: Average with c |
Changes in Objectives: Average with l |
Changes in Objectives: Overall |
Loose Commitment: c |
Loose Commitment: l |
|---|---|---|---|---|---|
| π | -0.2429 |
0.2507 |
0.0027 |
0.0005 |
0.0048 |
| y | -2.5179 |
2.5466 |
0.002 |
0.0018 |
0.0176 |
Note: The table reports the average allocations across different simulations of the model.
4.4 The effects of adopting conservative objectives
We have solved our model where both the liberal and conservative policies are set optimally. We have mainly described the effects that external pressures to adopt a liberal policy have on a conservative central bank. This may seem the most reasonable case in the OECD economies, where politicians occasionally exert some influence for more expansionary policies. Nevertheless, our model yields implications for the opposite case, when a central bank expects that more conservative objectives may be adopted in the future. This may be the relevant case for economies where the adoption of more stringent inflation objectives, like a specific low inflation target, is being discussed. Arguably, and subject to interpretation, this may be what it is currently happening in the United States.
In the baseline case, the possible adoption of more conservative objectives makes the liberal to implement a lower inflation rate. In addition, inflation expectations become lower, which allows the liberal central bank to achieve higher output. Both these effects make the liberal to achieve a better welfare outcome. In this sense, the possibility that more conservative objectives are adopted constitutes a positive externality for a liberal central bank. All these conclusions are mainly robust to the other scenarios that we have considered.31
5 Conclusions
Both central bankers and politicians frequently discuss whether central bank's objectives should be changed. These discussions may result in institutional reforms, or may influence in a particular direction the appointment of a new chairman or board members of the central bank. This paper analyzes the macroeconomic effects induced by the fact that central bank objectives may change in the future. We analyze optimal policy in such situation and its economic implications.
The paper is not aimed at providing a theoretical basis for partisan economic fluctuations, as for instance in Alesina (1987) and Drazen (2000). In practice, it may be hard to match directly political parties with systematic and successful changes in central bank policy. In this respect, the novelty of our analysis is to show how the possibility of future policy changes already produces effects in earlier periods. Following the recent literature on monetary policy, we model inflation dynamics with a New Keynesian Phillips curve, where expectations about future economic conditions affect current outcomes. Our analysis thus clarifies the theoretical difficulties to find a clear relationship between economic outcomes and policymakers' objectives. We indeed show that if liberal objectives can be adopted in the future, high inflation may be the optimal response of a conservative central bank. We can thus observe a high level of inflation no matter whether liberal objectives are eventually adopted or not.
The most common case in reality is the one where a conservative central bank faces pressures to pursue more expansionary policies. In this circumstances, the optimal response of a conservative central bank is to increase current inflation through an accommodation effect. Simultaneously, the central bank tries to anchor inflation expectations by promising to be even more conservative in the future. Overall, we find that the possibility that policy objectives may become more liberal generates a negative externality for the conservative central bank. More interestingly, we also find that they lead to a contraction in current output, which is precisely the opposite of what pressures to adopt liberal policies may be aiming for. The more likely is the adoption of liberal objectives, the stronger are these effects. Along this dimension, the adoption of an inflation targeting regime seems to be preferable to a conservative central bank a la Rogoff, namely one with higher aversion towards inflation than society. An inflation targeting regime insulates more the central bank from external pressures. Changing policy objectives indeed requires an institutional reform, rather than simply appointing a chairman or advisors with different views.
We have also discussed to which extent credibility matters, in a context where policy objectives can be changed. This is done by taking into account several commitment settings, following the recent contributions of Schaumburg and Tambalotti (2007) and our methods developed in Debortoli and Nunes (2006a). In particular, we show how credible institutions are able to partially counteract the bad externalities generated by the possibility that policy objectives may become more liberal. This result is interesting since it clarifies that having a central bank with sufficient aversion towards inflation, as suggested by Rogoff (1985), or equivalently adopting an inflation targeting policy, does not eliminate the scope for having credible institutions.
Finally, our paper draws conclusions about the reverse case, where the current central bank may perceive that policy objectives may become more conservative in the future. This case may be relevant for countries that are discussing the adoption of inflation targeting regimes, which is, arguably, the case of the United States. In this case, the possibility of more conservative policy in the future creates a positive externality for the liberal central bank. Also, inflation expectations become lower, which is translated into lower current inflation and higher current output.
References
Alesina, A., 1987. Macroeconomic policy in a two-party system as a repeated game. Quarterly Journal of Economics 102 (3), 651-678.
Alesina, A., Roubini, N., Cohen, G., 1997. Political Cycles and the Macroeconomy. The MIT Press.
Aoki, K., 2003. On the optimal monetary policy response to noisy indicators. Journal of Monetary Economics 50, 501-523.
Chappell, H., Havrilesky, T., McGregor, R., 1993. Partisan monetary policies: Presidential influence through the power of appointment. The Quarterly Journal of Economics 108 (1), 185-218.
Davig, T., Leeper, E., 2007. Generalizing the Taylor principle. American Economic Review 97 (3), 607-635.
Debortoli, D., Nunes, R., 2006a. Loose commitment. Universitat Pompeu Fabra. Manuscript.
Debortoli, D., Nunes, R., 2006b. Political disagreement, lack of commitment and the level of debt. Universitat Pompeu Fabra. Manuscript.
Drazen, A., 2000. The political business cycle after 25 years. NBER macroeconomics annual.
Faust, J., Irons, J., 1999. Money, politics and the post-war business cycle. Journal of Monetary Economics 43 (1), 61-89.
Galí, J., 2008. Monetary Policy, Inflation, and the Business Cycle: An Introduction to the New Keynesian Framework. Princeton University Press.
Galí, J., Gertler, M., 1999. Inflation dynamics: A structural econometric analysis. Journal of Monetary Economics 44 (2), 195-222.
Hansen, L., Sargent, T., 2007. Robustness. Princeton University Press.
Marcet, A., Marimon, R., 1998. Recursvie contracts. Universitat Pompeu Fabra. Working Paper.
Roberds, W., 1987. Models of policy under stochastic replanning. International Economic Review 28 (3), 731-755.
Rogoff, K., 1985. The optimal degree if commitment to an intermediate monetary target. Quarterly Journal of Economics 100 (4), 1169-89.
Schaumburg, E., Tambalotti, A., 2007. An investigation of the gains from commitment in monetary policy. Journal of Monetary Economics 54 (2), 302-324.
Sheffrin, S., 1989. Evaluating rational partisan business cycle theory. Economics and Politics 1, 239-259.
Svensson, L., 1997. Optimal inflation contracts, conservative central banks, and linear inflation contracts. American Economic Review 87 (1), 98-114.
Walsh, C., 1995. Optimal contracts for central bankers. American Economic Review 85 (1), 150-167.
Woodford, M., 2003. Interest and Prices: Foundations of a Theory of Monetary Policy. Princeton University Press.
Appendix
A Optimal monetary policy with changes in policy objectives
We derive the solution to the optimal policy problem described in section 2. To do so, we write the first-order necessary conditions of the planner's problem described in (3), given by
| (A-1) | ||
| (A-2) | ||
| (A-3) |
where
![]() is the Lagrange multiplier
associated with the NKPC. Rearranging equations (A-1)-(A-3) we obtain the
second-order difference equation
is the Lagrange multiplier
associated with the NKPC. Rearranging equations (A-1)-(A-3) we obtain the
second-order difference equation
![$\displaystyle \left[ \beta qL^{-2}-\left( 1+\beta q+\frac{\kappa^{2}}{w^{c}}+1\right) L^{-1}+1\right] \lambda_{t-1}=\kappa\widetilde{y}^{c}+\beta\left( 1-q\right) \pi_{0}^{\ell} $](img207.gif)
whose solution is given by
| (A-4) |
where,
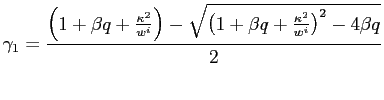
|
(A-5) |
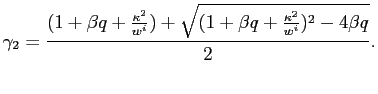
|
(A-6) |
It is convenient to emphasize that
![]() and
and
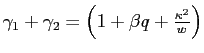 and
and
![]() .
Moreover,
.
Moreover,
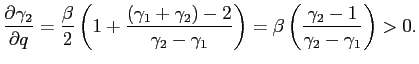
The unique stable solution to (A-4) is given by the expression
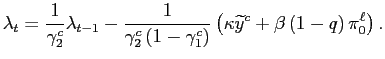
Solving backward and imposing the initial condition
![]() , we obtain
, we obtain
![$\displaystyle =\frac{1-(\gamma_{2}^{c})^{-(t+1)}}{\left( 1-\gamma_{1} ^{c}\right) \left( 1-\gamma_{2}^{c}\right) }\left[ \kappa\widetilde{y} ^{c}+\beta\left( 1-q\right) \pi_{0}^{\ell}\right] .$](img218.gif)
|
Using (A-1) we obtain the following expression for the evolution of inflation and output
![$\displaystyle \pi_{0}=-\lambda_{0}=\frac{1}{\gamma_{2}^{c}\left( 1-\gamma_{1}^{c}\right) }\left[ \kappa\widetilde{y}^{c}+\beta\left( 1-q\right) \pi_{0}^{\ell }\right] $](img219.gif)
and
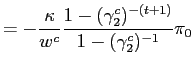
|
which corresponds to equations (5)-(7).
For later convenience, we notice that since the liberal central bank is facing a problem that is symmetric with the one described above, using a symmetric expression to (7) we have
![$\displaystyle \pi_{0}^{\ell}=\frac{1}{\gamma_{2}^{\ell}\left( 1-\gamma_{1}^{\ell}\right) }\left[ \kappa\widetilde{y}^{\ell}+\beta\left( 1-q\right) \pi_{0} ^{c}\right]$](img224.gif)
|
(A-7) |
A.1The case of full-commitment and constant policy objectives
The standard case of full-commitment and no uncertainty about
policy objectives is a special case of the problem described above
where
![]() ,
,
![]() and
and ![]() . In this case, we have that
. In this case, we have that
![]() . Defining
. Defining
![]() as the value taken by
(A-6) when
as the value taken by
(A-6) when
![]() we have
we have
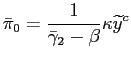
|
(A-8) |
where
![]() is the value taken by
is the value taken by
![]() when
when ![]() . Moreover,
from (5)
and (6)
. Moreover,
from (5)
and (6)
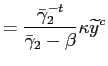
|
(A-9) | |
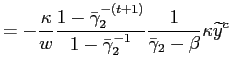
|
(A-10) |
A.2 The case of limited commitment
The case of limited commitment is one where policy objectives do
not change. However, the monetary authority is not fully credible
because at any point in time there is a probability ![]() that its previous promises are disregarded and that a
reoptimization occurs. This case corresponds to one where
that its previous promises are disregarded and that a
reoptimization occurs. This case corresponds to one where
![]() ,
,
![]() and
and ![]() . As in the full-commitment case, we have that
. As in the full-commitment case, we have that
![]() . The resulting
allocations are given by similar expressions to (A-8)-(A-10), substituting
the value of
. The resulting
allocations are given by similar expressions to (A-8)-(A-10), substituting
the value of
![]() as given by (A-6), instead of
as given by (A-6), instead of
![]() . As a consequence, we have
that inflation and output are given by
. As a consequence, we have
that inflation and output are given by
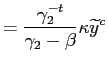
|
|
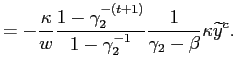
|
Since
![]() we have that the higher is the probability of commitment, the lower
are inflation and output. Finally, equation (8) is obtained
dividing the above expression by (A-9).
we have that the higher is the probability of commitment, the lower
are inflation and output. Finally, equation (8) is obtained
dividing the above expression by (A-9).
A.3 The case of changes in the output target
We now analyze the case where there is uncertainty about the
output target, i.e. where the current conservative target can be
replaced by
![]() ,
but keeping unchanged the weight on output stabilization,
,
but keeping unchanged the weight on output stabilization,
![]() . Substituting this into
(7), and
using the fact that in this case, being the output target the only
difference among the two types of policymakers,
. Substituting this into
(7), and
using the fact that in this case, being the output target the only
difference among the two types of policymakers,
![]() and
and
![]() we obtain
we obtain
![$\displaystyle \pi_{0}^{c}\left( 1-\frac{\beta^{2}\left( 1-q\right) ^{2}}{\left[ \gamma_{2}\left( 1-\gamma_{1}\right) \right] ^{2}}\right) =\frac{1} {\gamma_{2}\left( 1-\gamma_{1}\right) }\left[ \kappa\widetilde{y}^{c} +\frac{\beta\left( 1-q\right) }{\gamma_{2}\left( 1-\gamma_{1}\right) }\kappa\widetilde{y}^{\ell}\right] \text{.} $](img255.gif)
For convenience, we define
![]() and notice that
and notice that
![]() .
.
We thus have
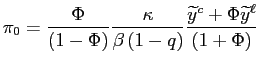
Using this expression to substitute for ![]() in
(5) and
then dividing everything by (A-9) one obtains
in
(5) and
then dividing everything by (A-9) one obtains
![$\displaystyle = \underset{ \begin{array}[c]{c} \text{{\scriptsize {Liberal Objectives}}}\\ >1 \end{array} }{\underbrace{\frac{\widetilde{y}^{c}+\Phi\widetilde{y}^{\ell}}{\widetilde {y}^{c}\left( 1+\Phi\right) }}}\underset{ \begin{array}[c]{c} \text{{\scriptsize {Limited Commitment}}}\\ >1 \end{array} } {\underbrace{\left( \frac{\bar{\gamma}_{2}}{\gamma_{2}}\right) ^{t} \frac{\bar{\gamma}_{2}-\beta}{\gamma_{2}- \beta}}} \bar{\pi}_{t},$](img261.gif)
|
which is the same as (9).
Finally, it easy to see that ![]() is
increasing in the difference between
is
increasing in the difference between
![]() and
and
![]() . We can also show that it
is strictly decreasing in
. We can also show that it
is strictly decreasing in ![]() , indeed
, indeed
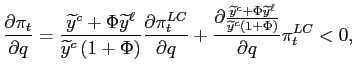
|
since both terms of the sum are negative. The first term is negative because of our result in the previous section, while the second term can be written as
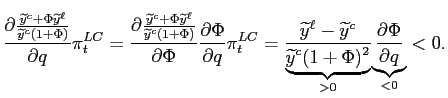
|
A.4 The case of changes in the relative weight of output w
When there is uncertainty about the output weight, we have that
the current conservative weight can be replaced by
![]() , while keeping unchanged
the output target
, while keeping unchanged
the output target
![]() .
Substituting (A-7) into (5) one obtains
.
Substituting (A-7) into (5) one obtains
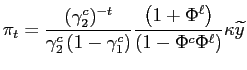
|
which divided by (A-9) delivers the expression in section 4.1.
B Recursive formulation of the problem of section 3
For notational convenience only, we abstract from the presence of uncertainty other than the one regarding the policy objective changes.
Proposition 1
Being ![]() the vector of lagrange
multipliers associated with the constraints (15) and (16), problem
(14) can
be written as a saddle point functional equation (SPFE) as
follows:
the vector of lagrange
multipliers associated with the constraints (15) and (16), problem
(14) can
be written as a saddle point functional equation (SPFE) as
follows:
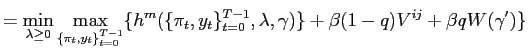
|
|
where
![$\displaystyle \equiv\sum_{t=0}^{T-1}\beta^{t}\left[ {\pi_{t}}^{2}+w^{i}(y_{t}-{\widetilde{y}})^{2}\right]$](img280.gif)
|
|
![$\displaystyle \equiv\left[ \begin{array}[c]{c} \pi_{0}-\kappa y_{0}-\beta\pi_{1}\\ \vdots\\ \pi_{T-2}-\kappa y_{T-2}-\beta\pi_{T-1}\\ \pi_{T-1}-\kappa y_{T-1}-\beta(1-q)\pi_{T}^{j} \end{array} \right]$](img282.gif)
|
|
![$\displaystyle \equiv\left[ \begin{array}[c]{c} 0\\ \vdots\\ 0\\ \pi_{0}^{i} \end{array} \right]$](img284.gif)
|
Proof. of Proposition 1 Define the
real valued function ![]() as follows:
as follows:
![$\displaystyle \equiv-\frac{1}{2}\sum_{t=0}^{T-1} \beta^{t}\left[ \pi_{t}^{2}+w^{i}(y_{t}-{\widetilde{y}}^{i})^{2}\right] +\beta^{T}(1-q)V^{ij}$](img288.gif)
|
Moreover,
![]() and
and
![]() are defined as in the second
part of the proposition.
are defined as in the second
part of the proposition.
Problem (14) is therefore equivalent to:
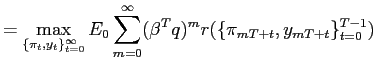
|
|
This formulation fits the definition of Program 1 in Marcet Marimon (1998). We can therefore write the problem as a saddle point functional equation in the sense that there exists a unique function satisfying:
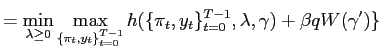
|
|
where:
or in a more intuitive formulation define:
![$\displaystyle \equiv\sum_{t=0}^{T-1}\beta^{t}\left[ {\pi_{t}}^{2}+w^{i}(y_{t}-{\widetilde{y}})^{2}\right]$](img304.gif)
|
and the saddle point functional equation is:
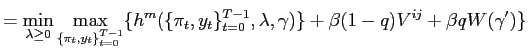
|
|
|
||
Proof. of Proposition 2: Using Proposition 1, this proof follows directly from the results of Marcet and Marimon (1998).
Footnotes
* We are grateful to Gabriel Fagan, Jordi Galí, Albert Marcet and seminar participants at the 2008 Royal Economic Society, the Federal Reserve of Dallas, 2008 Conference Computing on Computing in Economics and Finance for helpful comments. We gratefully acknowledge financial support from IAE-CSIC (Debortoli) and Fundação para a Ciência e Tecnologia (Nunes). Any remaining errors are our own. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. E-mail address: [email protected] Return to text
1. As shown by Rogoff (1985), appointing a central banker with higher aversion towards inflation than the overall society reduces the inefficiencies associated with time-inconsistency. Return to text
2. Alesina et al. (1997) point out several empirical successes of the Alesina (1987) model, while Sheffrin (1989) and Drazen (2000) point out some empirical failures. Chappell et al. (1993) conclude that political influences on the Federal Reserve are not clearly connected with a party tenure, since they occur indirectly through the appointments of FOMC members and thus different ideologies overlap in the committee. Faust and Irons (1999) conclude that partisan effects in US macroeconomic data are fragile, and that there is little evidence that the partisan effects on the economy operate through changes in monetary policy. Return to text
3. The theoretical framework underlying such relationship is described in Woodford (2003) and Galí (2008). This specification of the NKPC holds in a neighborhood of a zero inflation steady state. Throughout our analysis, we abstract from the changes that may derive from having a different steady state level of inflation. Return to text
4. The interest rate it required to implement the desired inflation level can be obtained from the demand side of the economy, not modeled here. Return to text
5. The simple case where ![]() is discussed in section 2.3. Return to text
is discussed in section 2.3. Return to text
6. Our analysis can be easily extended to analyze the symmetric case where a liberal central bank faces the possibility of adopting more conservative objectives. We discuss this case in section 4.4. Return to text
7. In section 4.3, we analyze the case where the central bank can make credible commitments contingent on its policy objectives. Return to text
8. In the present framework, the function
![]() is just a constant, and is
irrelevant for the maximization problem. The current policymaker
does not have a state variable to influence the choices when policy
objectives change. This analysis changes in a model with endogenous
state variables, like the one considered in section 4.2. Return to text
is just a constant, and is
irrelevant for the maximization problem. The current policymaker
does not have a state variable to influence the choices when policy
objectives change. This analysis changes in a model with endogenous
state variables, like the one considered in section 4.2. Return to text
9. In the definition of
![]() and
and
![]() (see equations (A-5) and (A-6) in the appendix
A), the
only parameter related to the policy objectives is the relative
weight of output stability
(see equations (A-5) and (A-6) in the appendix
A), the
only parameter related to the policy objectives is the relative
weight of output stability ![]() , which is assumed
to be constant. This assumption is relaxed in section 4.1. Return to text
, which is assumed
to be constant. This assumption is relaxed in section 4.1. Return to text
10. See appendix A for the derivation of these results. Return to text
11. The previous assumption can be easily relaxed without affecting qualitatively our results. Return to text
12. See appendix A.2 for the derivation of these results. Return to text
13. For the derivation of these results see appendix A.3. Return to text
14. This calibration is used for instance in Woodford (2003) and Schaumburg and Tambalotti (2007). Return to text
15. These two effects, namely the accommodation effect and the anchoring expectations effect, can be better disentangled in a framework where policy objectives can change only occasionally, say every T periods, as the one considered in section 3.1. Return to text
16. To see this result notice that, from
(11),
![]() . Return to text
. Return to text
17. Walsh (1995) and Svensson (1997) also suggested alternative ways to solve the time-inconsistency problem. Return to text
18. Our result is still valid if the
conservative central banker is one assigning zero weight on output
stabilization (![]() ) as long as cost-push shocks are
added to the NKPC. Return to
text
) as long as cost-push shocks are
added to the NKPC. Return to
text
19. Figure 2 plots inflation
and output gap for the case of
![]() and
and
![]() , while keeping all
the other parameters as in the previous section. Return to text
, while keeping all
the other parameters as in the previous section. Return to text
20. The present work combines the tools developed in Debortoli and Nunes (2006a) for the probabilistic model and the T-periods model. The probabilistic model was also addressed in Roberds (1987) and Schaumburg and Tambalotti (2007). We also use features of Debortoli and Nunes (2006b), where we considered disagreement among successive policymakers. Return to text
21. Note that ![]() and
and
![]() are value functions in the presence
of disagreement between successive policymakers, therefore unlike
in Debortoli and Nunes (2006a) one can not use an
envelope result. Return to text
are value functions in the presence
of disagreement between successive policymakers, therefore unlike
in Debortoli and Nunes (2006a) one can not use an
envelope result. Return to text
22. This calibration implies that objective changes on average every 8 periods, roughly the same as in the case considered in the previous section. Return to text
23. Under this specification, propositions 1 and 2 in the appendix also apply. Return to text
24. We do not have the goal to characterize policy with indexation, where the functional forms of policy objectives may differ from the ones considered here. Return to text
25. We have set initial inflation to be 0. Considering other values does not affect qualitatively the results. Return to text
26. This interpretation of the model is partly related to the literature on robust control of Hansen and Sargent (2007), and to the literature about optimal monetary policy in the presence of noisy indicators as in Aoki (2003). In our analysis, however, we focus on the effects of evolving objectives, and assume the structural relationships describing the economy and the exogenous shocks are known and common knowledge. Return to text
27. In the model of section 3.1, when policy objectives are changed the lagrange multiplier is reset to zero. Afterwards, the policy functions depend on the evolution of the lagrange multiplier. There, we plotted the policy functions depending on the time spent in office, because there is a unique mapping between the evolution of the lagrange multiplier and the time spent in office. In the setup of this section, the lagrange multiplier is never set to zero. Therefore, even when objectives change, policy functions depend on the entire history that occurred previously. Nevertheless, we found that the qualitative features of the policy functions are not affected by the previous history of events. Return to text
28. The analog of this model with no changes in objectives, is the usual full commitment solution where output converges to zero. Return to text
29. In the baseline model of section 3, the anchoring effect is not present in the initial 4 periods. Note that the policies of the conservative from period 1 to 4 are more likely to be implemented than the policies from period 5 to 8, which in turn are more likely to be implemented than subsequent policies. Return to text
30. We do not compare welfare between this case and the full-commitment benchmark, because the utility functions are different, and such comparisons are meaningless. Return to text
31. The only exception is the model with full commitment and no disagreement, as the one considered in section 4.3. There, liberal policies implement an even higher inflation level, and then reduce it over time achieving a specially high output. This policy is only possible because the conservative policies are cooperative, and anchor inflation expectations very firmly by promising a very low inflation level. The main feature that an expansion is obtained still holds in that case. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text