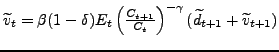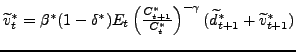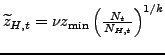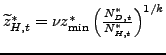Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 995, March 2010 --- Screen Reader
Version*
Offshore Production and Business Cycle Dynamics with Heterogeneous Firms1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Cross-country variation in production costs encourages the relocation of production facilities to other countries, a process known as offshoring through vertical foreign direct investment. I examine the effect of offshoring on the international transmission of business cycles. Unlike the existing macroeconomic literature, I distinguish between fluctuations in the number of offshoring firms (the extensive margin) and in the value added per offshoring firm (the intensive margin) as separate transmission mechanisms. The firms' decision to produce offshore depends on the firm-specific level of labor productivity, on fluctuations in the relative cost of effective labor, and on the fixed and trade costs of offshoring. The model replicates the procyclical pattern of offshoring and the dynamics along its two margins, which I document using data from U.S. manufacturing and Mexico's maquiladora sectors. O�shoring enhances the synchronization of business cycles, and dampens the real exchange rate appreciation generated by aggregate productivity di�erentials across countries.
Keywords: Offshore production, extensive margin, heterogeneous firms, firm entry, business cycle dynamics, terms of labor, real exchange rate
JEL classification: F23, F41
1 Introduction
Firms often follow strategies that involve the establishment of production affiliates at foreign locations with relatively lower production costs, a process known in the international trade literature as offshoring through vertical foreign direct investment (FDI).3 Unlike production under horizontal FDI - which means that foreign affiliates aim to gain market access by replicating the operations of their parent firms at the location where final consumption takes place - the type of offshoring that I model is primarily motivated by cross-country differences in the cost of effective labor, as in Helpman (1984), as foreign affiliates add value to goods consumed in the multinationals' country of origin.4 The number of offshoring firms (the extensive margin) and the real value added per offshoring firm (the intensive margin) fluctuate over the business cycle, and thus affect output, prices and wages in both the parent and the host countries.5
I document the business cycle features of offshoring motivated by lower production costs using data from U.S. manufacturing and Mexico's maquiladora sector.6 Using the number of maquiladora plants to reflect the extensive margin, I show that the total value added and the number of plants in Mexico are strongly procyclical with the U.S. manufacturing output (Figure 3). In addition, the business cycle dynamics of the maquiladora sector differ across the total value added and its extensive margin: The total value added co-moves almost contemporaneously with U.S. manufacturing, whereas the number of plants lags the expansions and contractions in U.S. manufacturing by about four quarters, a result which highlights the inter-temporal dynamics of the extensive margin of offshoring.
Despite this empirical evidence, the international macroeconomics literature does not fully capture the business cycle dynamics of offshoring along its extensive margin. Burstein, Kurz, and Tesar (2009) examine the role of production sharing in the transmission of business cycles in a two-country model in which the location of plants is fixed over time.7 Bergin, Feenstra, and Hanson (2007) focus on the importance of offshore production in amplifying the transmission of shocks across countries, in a model in which the number of offshoring firms adjusts instantly - rather than gradually over time as in the data - in response to simultaneous aggregate shocks in the parent and the host countries.
To address this issue, I introduce the endogenous creation of offshore production plants as a firm-specific decision, in a two-country (North and South), dynamic stochastic general equilibrium framework. The key features of the model include endogenous firm entry in the parent country and firm heterogeneity in labor productivity. Firm entry is subject to a sunk cost reflecting headquarter activities at home. Following entry in the North, each firm can use either domestic or foreign labor in the production of a different variety of goods. The use of foreign labor involves the establishment of an offshore plant, and is subject to fixed and trade costs every period.8 Since firms are heterogeneous in productivity, the decision to produce offshore is firm-specific: Despite the lower cost of effective labor abroad (i.e. the lower wage relative to aggregate productivity), only the more productive firms can afford the fixed and trade costs of offshoring. The cross-country asymmetry in the cost of effective labor also implies that offshoring takes place one-way; only some of the Northern firms have an incentive to produce offshore, whereas all Southern firms produce at home.
The key results of the paper are as follows. First, the model generates a procyclical pattern of offshoring that is consistent with the data from U.S. manufacturing and Mexico's maquiladora sector. In the model, the number of offshoring firms depends on the fluctuations in the relative cost of effective labor across countries. A positive shock to aggregate productivity in the North encourages domestic firm entry, and causes the domestic wage to rise above aggregate productivity as labor demand increases to accommodate firm entry requirements. Notably, the increase in the cost of effective labor in the North is gradual (because the number of firms is a stock variable), and causes a gradual increase in the number of offshoring firms (the extensive margin), as in the data. Second, offshoring enhances the co-movement of output across countries. The increase of output in the North (generated by a country-specific shock to aggregate productivity) and also in the South (caused by the immediate jump in Northern demand for offshored varieties, and also by the subsequent relocation of production by the Northern firms to the South) enhance the co-movement of output across the two economies.9 The result is consistent with the empirical regularity documented in Burstein, Kurz, and Tesar (2009) that country pairs with larger shares of offshoring-related bilateral trade exhibit larger correlations of manufacturing output. Third, offshoring narrows price dispersion across countries, as it reduces the appreciation of the real exchange rate that follows a domestic increase in aggregate productivity in the framework with firm entry and endogenously traded varieties. Thus, offshoring dampens the Harrod-Balassa-Samuelson effect through a number of channels, including the transfer of upward pressure from the domestic to the foreign wage, the reduced size of the domestic non-traded sector, and the decline in import prices that occurs as offshoring crowds out the less productive foreign exporters.
This paper is related to a growing body of macroeconomic literature that focuses on endogenous firm entry and adjustments along the extensive margin of exports (but not of offshoring).10 For example, Ghironi and Melitz (2005) study the export decision of firms in the presence of fixed exporting costs, in a framework with firm entry and firm heterogeneity. Alessandria and Choi (2007) analyze the extensive margin of exports in a model with sunk costs and continuation fixed costs that explains the "exporter hysteresis" behavior.11 Corsetti, Martin, and Pesenti (2007) examine the terms-of-trade implications of productivity improvements in the sectors of firm entry and production, in a model in which the extensive margin of exports is endogenous. Finally, Mejean (2006) studies the effect of endogenous firm entry in the tradable sector on the real exchange rate dynamics and the Harrod-Balassa-Samuelson effect.
The assumptions of the model considered in this paper are consistent with the empirical evidence on the determinants of offshore production provided by recent studies. Hanson, Mataloni, and Slaughter (2005) show that U.S. multinational firms attract larger shares of the sales of their foreign affiliates when the latter benefit from lower trade costs and lower wages abroad. Kurz (2006) shows that the U.S. plants and firms using imported components in production are larger and more productive than their domestically-oriented counterparts, as the larger productivity allows them to cover the fixed costs of offshoring.
The study of offshoring motivated by lower production costs is important to understand the macroeconomic interdependence between country pairs and economic areas separated by persistent differences in the cost of effective labor, such as the U.S. and Latin America, or Western Europe and the new member countries of the European Union (Marin, 2006; Meyer, 2006). In 2005, offshore production through vertical integration was responsible for as much as 50 percent of the manufacturing sales of the U.S. affiliates in Mexico, and for 26 percent of the sales of the U.S. affiliates in Latin America as a whole, shares which were directed towards the U.S. parent firms (BEA, 2007).
The rest of this paper is organized as follows: Section 2 introduces the model of offshoring with heterogeneous firms that allows for fluctuations in offshoring along its extensive and intensive margins. Section 3 translates the model with firm heterogeneity into an equivalent framework with two representative firms that produce domestically and offshore. Section 4 describes the model calibration. Section 5 presents the results; it shows the business cycle dynamics of offshoring in the presence of aggregate productivity shocks, and also compares the empirical moments of offshoring from the U.S. to Mexico with their model counterparts. Section 6 concludes with a summary and possible extensions of the model.
2 Model of Offshoring with Heterogeneous Firms
2.1 Markets and Production Strategies
The model consists of two economies, North and South. Each economy includes one representative household, and also a continuum of firms that are monopolistically competitive and heterogeneous in labor productivity, with each firm producing a different variety of goods. Every period, the existing firms choose the destination market(s) that they serve and the location of production, as follows:
- All firms serve their domestic market. For this purpose, the Northern firms produce their varieties using either domestic or foreign labor. The use of foreign labor involves the establishment of an offshore production plant, and offers the advantage of a lower production cost. However, offshoring is subject to per-period fixed and trade costs, as described below.12
- Some firms from each economy also serve the foreign market. They use exclusively domestic labor in production, and export their varieties subject to a per-period fixed cost, as in Ghironi and Melitz (2005).
Because the number of firms in each economy varies over time, and also because the existing firms re-optimize their offshoring and exporting strategies every period, the composition of consumption baskets in each economy changes over time.
2.2 Firms Serving the Domestic Market: Domestic vs. Offshore Production
This section illustrates the mechanisms of domestic and offshore
production as alternative choices for the Northern firms that
produce for their domestic market. Every period, the firm with
idiosyncratic labor productivity ![]() must choose one of
the two possible production strategies:
must choose one of
the two possible production strategies:
(a) Domestic production, with output being a function of the
aggregate productivity in the North ![]() , the
firm-specific labor productivity
, the
firm-specific labor productivity ![]() , and domestic labor
, and domestic labor
![]() :
:
| (1) |
(b) Alternatively, the firm with idiosyncratic labor
productivity ![]() may choose to produce offshore using
Southern labor
may choose to produce offshore using
Southern labor
![]() :
:
| (2) |
The Northern firm producing offshore becomes subject to the
Southern aggregate labor productivity ![]() but is
able to carry its own idiosyncratic labor productivity
but is
able to carry its own idiosyncratic labor productivity ![]() to the South.13
to the South.13
The monopolistically-competitive firm with idiosyncratic
productivity ![]() solves the profit-maximization problem
for the alternative scenarios of domestic and offshore
production:
solves the profit-maximization problem
for the alternative scenarios of domestic and offshore
production:
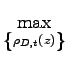 |
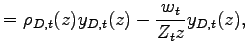
|
(3) |
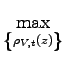 |
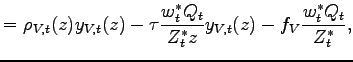
|
(4) |
where
![]() and
and
![]() are the prices associated with
each of the two production strategies,
are the prices associated with
each of the two production strategies, ![]() and
and
![]() are the real wages in the North
and the South, and
are the real wages in the North
and the South, and ![]() is the real exchange
rate. The cost of producing one unit of output either domestically
or offshore varies not only with the cost of effective labor
is the real exchange
rate. The cost of producing one unit of output either domestically
or offshore varies not only with the cost of effective labor
![]() and
and
![]() across
countries, but also with the level of idiosyncratic labor
productivity
across
countries, but also with the level of idiosyncratic labor
productivity ![]() across firms.14 In addition, the
Northern firms producing offshore incur a fixed offshoring cost
equal to
across firms.14 In addition, the
Northern firms producing offshore incur a fixed offshoring cost
equal to ![]() units of Southern effective
labor15 - that reflects the building and
maintenance of the offshore production facility - and also an
iceberg trade cost
units of Southern effective
labor15 - that reflects the building and
maintenance of the offshore production facility - and also an
iceberg trade cost ![]() associated with the
shipping of goods produced offshore back to the parent country. For
every
associated with the
shipping of goods produced offshore back to the parent country. For
every ![]() units produced offshore, only one unit
arrives in the North for consumption, as the difference is lost due
to trade barriers, transportation and insurance costs (Anderson and
Wincoop, 2004). The demand functions for the variety produced by
firm
units produced offshore, only one unit
arrives in the North for consumption, as the difference is lost due
to trade barriers, transportation and insurance costs (Anderson and
Wincoop, 2004). The demand functions for the variety produced by
firm ![]() domestically or offshore are
domestically or offshore are
![]() and
and
![]() ,
where
,
where ![]() is the aggregate consumption in the
North.
is the aggregate consumption in the
North.
The profit-maximization problem implies the equilibrium prices
![]() and
and
![]() for the alternative scenarios of domestic and offshore production.
The corresponding profits, expressed in units of the aggregate
consumption basket
for the alternative scenarios of domestic and offshore production.
The corresponding profits, expressed in units of the aggregate
consumption basket ![]() are:
are:
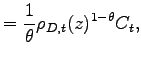 |
(5) | |
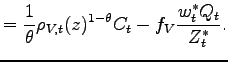
|
(6) |
When deciding upon the location of production every period, the
firm with productivity ![]() compares the profit
compares the profit
![]() that it would obtain from domestic
production with the profit
that it would obtain from domestic
production with the profit
![]() from producing the same variety
offshore. As a particular case, I define the productivity cutoff
level
from producing the same variety
offshore. As a particular case, I define the productivity cutoff
level ![]() on the support interval
on the support interval
![]() , so that the firm at the
cutoff obtains equal profits from producing domestically or
offshore:
, so that the firm at the
cutoff obtains equal profits from producing domestically or
offshore:
| (7) |
The productivity cutoff ![]() is a variable that
reacts to fluctuations in the relative cost of effective labor
across countries, and thus reflects the behavior of the extensive
margin of offshoring over the business cycle.
is a variable that
reacts to fluctuations in the relative cost of effective labor
across countries, and thus reflects the behavior of the extensive
margin of offshoring over the business cycle.
The model implies that only the relatively more productive
Northern firms find it profitable to produce their varieties
offshore. Despite the lower cost of effective labor in the South,
only firms with idiosyncratic productivity above a certain cutoff
(![]() ) obtain benefits from offshoring
that are large enough to cover the fixed and iceberg trade costs.
This feature of the model is consistent with the empirical evidence
in Kurz (2006), that the U.S. plants and firms using imported
components in production are larger and more productive than their
domestically-oriented counterparts, as the larger idiosyncratic
productivity levels allow them to cover the fixed costs of
offshoring.16
) obtain benefits from offshoring
that are large enough to cover the fixed and iceberg trade costs.
This feature of the model is consistent with the empirical evidence
in Kurz (2006), that the U.S. plants and firms using imported
components in production are larger and more productive than their
domestically-oriented counterparts, as the larger idiosyncratic
productivity levels allow them to cover the fixed costs of
offshoring.16
Existence of the equilibrium
productivity cutoff Next I show that the existence of the equilibrium productivity
cutoff ![]() requires a cross-country asymmetry in
the cost of effective labor, so that some of the Northern firms
will always have an incentive to produce offshore. I begin by
re-writing the per-period profits that would be obtained from
domestic and offshore production as
requires a cross-country asymmetry in
the cost of effective labor, so that some of the Northern firms
will always have an incentive to produce offshore. I begin by
re-writing the per-period profits that would be obtained from
domestic and offshore production as
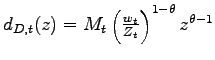 and
and
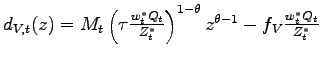 , where
, where
![]() measures the size of the Northern market. In Figure 1, I plot the
two profits as functions of the idiosyncratic productivity
parameter
measures the size of the Northern market. In Figure 1, I plot the
two profits as functions of the idiosyncratic productivity
parameter
![]() over the support interval
over the support interval
![]() . The vertical intercept is
zero for the case of domestic production; it is equal to the
negative of the fixed cost in the case of offshoring (
. The vertical intercept is
zero for the case of domestic production; it is equal to the
negative of the fixed cost in the case of offshoring (
![]() ).
).
Figure 1: The Firm specific productivity cutoff
![]()
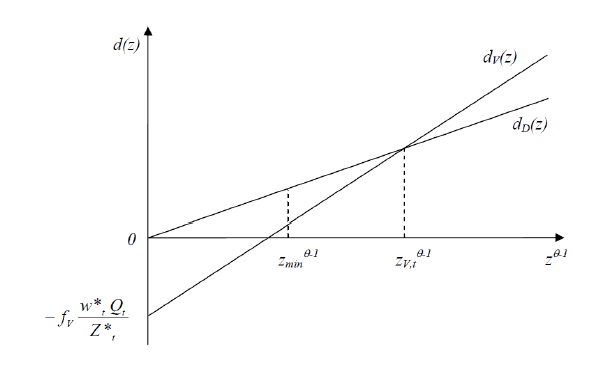
The existence of the equilibrium productivity cutoff ![]() in Figure 1 requires that the profit function from
offshoring must be steeper than the profit from domestic
production,
in Figure 1 requires that the profit function from
offshoring must be steeper than the profit from domestic
production,
![]() When this condition is met, offshoring generates greater profits
than domestic production for the subset of firms with idiosyncratic
productivity
When this condition is met, offshoring generates greater profits
than domestic production for the subset of firms with idiosyncratic
productivity ![]() along the upper range of the support
interval (
along the upper range of the support
interval (![]() ). The slope inequality is
equivalent to
). The slope inequality is
equivalent to
![]() which implies that the effective wage in the South must be
sufficiently lower than that in the North, so that the difference
covers both the fixed cost and the iceberg trade cost (
which implies that the effective wage in the South must be
sufficiently lower than that in the North, so that the difference
covers both the fixed cost and the iceberg trade cost (![]() ), and thus provides an incentive for some of the
Northern firms to produce offshore. The model calibration and the
magnitude of macroeconomic shocks ensure that this condition is
satisfied every period.17
), and thus provides an incentive for some of the
Northern firms to produce offshore. The model calibration and the
magnitude of macroeconomic shocks ensure that this condition is
satisfied every period.17
2.3 Exporting Firms
Firms from each economy can choose to serve the foreign market
through exports as in Ghironi and Melitz (2005), in addition to
producing for their domestic market. In the North, the firm with
idiosyncratic productivity ![]() would use an amount
of domestic labor
would use an amount
of domestic labor ![]() to produce for the
Southern market,
to produce for the
Southern market,
![]() .18 The Southern
firms that choose to export to the North face a similar
problem.
.18 The Southern
firms that choose to export to the North face a similar
problem.
Profit maximization implies the following equilibrium price and
profit functions for the Northern exporter with productivity factor
![]() :
:
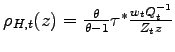 and
and
![]() , where
, where
![]() is the aggregate consumption in
the South. Producing for the foreign market generates additional
profits, but involves a fixed exporting cost equal to
is the aggregate consumption in
the South. Producing for the foreign market generates additional
profits, but involves a fixed exporting cost equal to ![]() units of Northern effective labor, and also an iceberg
trade cost
units of Northern effective labor, and also an iceberg
trade cost
![]() . Thus, the model implies that
only the subset of Northern firms with idiosyncratic labor
productivity above a productivity cutoff
. Thus, the model implies that
only the subset of Northern firms with idiosyncratic labor
productivity above a productivity cutoff ![]() find it profitable to export to the Southern market, as they can
afford the fixed and iceberg trade costs of exporting. The
time-varying productivity cutoff is:
find it profitable to export to the Southern market, as they can
afford the fixed and iceberg trade costs of exporting. The
time-varying productivity cutoff is:
| (8) |
2.4 Households and Consumption Baskets
The representative household in the North maximizes the expected
lifetime utility, which is
![$ \underset{\left\{ B_{t+1},\text{ }x_{t+1}\right\} } {\max}\left[ E_{t}\overset{\infty}{\underset{s=t}{\sum}}\beta^{s-t} \frac{C_{s}^{1-\gamma}}{1-\gamma}\right] ,$](img97.gif) subject to the budget constraint:
subject to the budget constraint:
| (9) |
where ![]() is the amount of aggregate consumption,
is the amount of aggregate consumption,
![]() is the subjective discount
factor, and
is the subjective discount
factor, and ![]() is the inverse of the
inter-temporal elasticity of substitution. (The representative
household in the South faces a similar problem.) The Northern
household starts every period with share holdings
is the inverse of the
inter-temporal elasticity of substitution. (The representative
household in the South faces a similar problem.) The Northern
household starts every period with share holdings ![]() in a mutual fund of
in a mutual fund of ![]() firms whose
average market value is
firms whose
average market value is
![]() , and also with real bond
holdings
, and also with real bond
holdings ![]() . It receives dividends equal to the
average firm profit
. It receives dividends equal to the
average firm profit
![]() in proportion with the
number of firms and with its share holdings, interest
in proportion with the
number of firms and with its share holdings, interest
![]() on bond holdings, and the real
wage
on bond holdings, and the real
wage ![]() for the amount of labor
for the amount of labor ![]() supplied inelastically.
supplied inelastically.
The Northern household purchases two types of assets every
period. First, it purchases ![]() shares in a
mutual fund of Northern firms that includes: (i)
shares in a
mutual fund of Northern firms that includes: (i) ![]() firms already producing at time
firms already producing at time ![]() , either
domestically or offshore, and (ii)
, either
domestically or offshore, and (ii) ![]() new
firms that enter the market in period
new
firms that enter the market in period ![]() . Each share
is worth its market value
. Each share
is worth its market value
![]() , equal to the net present
value of the expected stream of future profits of the average firm.
Second, the household also purchases the risk-free bond
, equal to the net present
value of the expected stream of future profits of the average firm.
Second, the household also purchases the risk-free bond ![]() denominated in units of the Northern consumption
basket.19 In addition, the household purchases
the consumption basket
denominated in units of the Northern consumption
basket.19 In addition, the household purchases
the consumption basket ![]() , which includes
varieties produced by the Northern firms either domestically
, which includes
varieties produced by the Northern firms either domestically
![]() or offshore
or offshore
![]() ; it also includes
varieties produced by Southern firms and imported by the North
; it also includes
varieties produced by Southern firms and imported by the North
![]() :
:
![$\displaystyle C_{t}=\left[ \underset{\omega\in\Omega_{t}^{NN}}{\underbrace{\underset {z_{\min}}{\overset{z_{V,t}}{\int}}y_{D,t}(\omega)^{\frac{\theta-1}{\theta} }d\omega}}+\underset{\omega\in\Omega_{t}^{NS}}{\underbrace{\underset{z_{V,t} }{\overset{\infty}{\int}}y_{V,t}(\omega)^{\frac{\theta-1}{\theta}}d\omega} }+\underset{\omega\in\Omega_{t}^{SS}}{\underbrace{\underset{z_{H,t}^{\ast} }{\overset{\infty}{\int}}y_{H,t}^{\ast}(\omega)^{\frac{\theta-1}{\theta} }d\omega}}\right] ^{\frac{\theta}{\theta-1}},$](img123.gif)
|
(10) |
where ![]() is the symmetric elasticity of
substitution across varieties. I use the home consumption basket
is the symmetric elasticity of
substitution across varieties. I use the home consumption basket
![]() as the numeraire good, so that the
price index in the North is
as the numeraire good, so that the
price index in the North is
![$ 1=\left[ \int\rho_{t}(\omega)^{1-\theta} d\omega\right] ^{\frac{1}{1-\theta}}$](img126.gif) , where
, where
![]() , and
, and
![]() is the real price of each
variety expressed in units of the Northern consumption basket. The
first-order conditions generate the following Euler equations for
bonds and stocks:
is the real price of each
variety expressed in units of the Northern consumption basket. The
first-order conditions generate the following Euler equations for
bonds and stocks:
| (11) | ||
![$\displaystyle =\beta(1-\delta)E_{t}\left[ \left( \frac{C_{t+1} }{C_{t}}\right) ^{-\gamma}(\widetilde{d}_{t+1}+\widetilde{v}_{t+1})\right] ,$](img132.gif)
|
(12) |
where ![]() is the exogenous rate of firm exit
every period.
is the exogenous rate of firm exit
every period.
2.5 Firm Entry and Exit
Firm entry takes place in both countries every period, as in
Ghironi and Melitz (2005). An unbounded pool of potential entrant
firms face a trade-off between the sunk entry cost (reflecting
headquarter activities in the parent country, such as research and
development, management, marketing) and the expected stream of
future monopolistic profits (discounted by the probability of exit
very period). In the North, firm entry requires a sunk entry cost
equal to ![]() units of Northern effective
labor.20 After paying the sunk entry cost,
each firm is randomly assigned an idiosyncratic labor productivity
factor
units of Northern effective
labor.20 After paying the sunk entry cost,
each firm is randomly assigned an idiosyncratic labor productivity
factor ![]() that is drawn independently from a common
distribution
that is drawn independently from a common
distribution ![]() with support over the interval
with support over the interval
![]() , and which the firm keeps
for the entire duration of its life.
, and which the firm keeps
for the entire duration of its life.
The ![]() firms entering at time
firms entering at time ![]() do not produce until period
do not produce until period ![]() .
Irrespective of their idiosyncratic productivity, all firms -
including the new entrants - are subject to a random exit shock
that occurs with probability
.
Irrespective of their idiosyncratic productivity, all firms -
including the new entrants - are subject to a random exit shock
that occurs with probability ![]() at the end of
every period. Thus, the law of motion for the number of producing
firms is
at the end of
every period. Thus, the law of motion for the number of producing
firms is
![]() where
where
![]() is the total number
of Northern firms that produce either domestically or offshore at
period
is the total number
of Northern firms that produce either domestically or offshore at
period ![]() .
.
The potential entrant firms anticipate their expected post-entry
value
![]() , which depends on the
expected stream of future profits
, which depends on the
expected stream of future profits
![]() , the stochastic discount
factor, and the exogenous probability
, the stochastic discount
factor, and the exogenous probability ![]() of exit
every period. The forward iteration of the Euler equation for
stocks (12) generates the
following expression for the expected post-entry value of the
average firm:
of exit
every period. The forward iteration of the Euler equation for
stocks (12) generates the
following expression for the expected post-entry value of the
average firm:
![$\displaystyle \widetilde{v_{t}}=E_{t}\left\{ \underset{s=t+1}{\overset{\infty}{\sum} }\left[ \beta(1-\delta)\right] ^{s-t}\left( \frac{C_{s}}{C_{t}}\right) ^{-\gamma}\widetilde{d_{s}}\right\} .$](img149.gif)
|
(13) |
In equilibrium, firm entry takes place until the expected value of the average firm is equal to the sunk entry cost expressed in units of the Northern consumption basket:
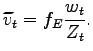 |
(14) |
3 Aggregation over Heterogeneous Firms
This section translates the model with firm heterogeneity into an equivalent framework with two representative Northern firms that produce domestically and offshore for their domestic market. Since offshoring takes place one-way, there is only one representative Southern firm that produces for the domestic market. In addition to the firm producing for the domestic market, one representative firm in each economy produces domestically for the export market.
3.1 Average Firm Productivity Levels
Domestic vs. offshore
production First I describe the average productivity levels of the two
representative Northern firms that produce domestically and
offshore for the Northern market. In Figure 2, I plot the density
of the firm-specific labor productivity levels ![]() over the support interval
over the support interval
![]() . Every period
. Every period ![]() , there are
, there are ![]() firms from the North
with idiosyncratic productivity levels below the offshoring cutoff
(
firms from the North
with idiosyncratic productivity levels below the offshoring cutoff
(![]() ) that produce domestically;
their average productivity is
) that produce domestically;
their average productivity is
![]() . There are also
. There are also
![]() firms with productivity factors
above the cutoff (
firms with productivity factors
above the cutoff (![]() ) that choose to
produce offshore; their average productivity is
) that choose to
produce offshore; their average productivity is
![]() .21 Since the
firm-specific labor productivity levels
.21 Since the
firm-specific labor productivity levels ![]() are random
draws from a common distribution
are random
draws from a common distribution ![]() with density
with density
![]() , I compute the two average productivity
levels as:
, I compute the two average productivity
levels as:
![$\displaystyle \widetilde{z}_{D,t}=\left[ \frac{1}{G(z_{V,t})}\underset{z_{\min}} {\overset{z_{V,t}}{\int}}z^{\theta-1}g(z)dz\right] ^{\frac{1}{\theta-1} }$](img165.gif) and
and ![$\displaystyle \widetilde{z}_{V,t}=\left[ \frac{1}{1-G(z_{V,t} )}\overset{\infty}{\underset{z_{V,t}}{\int}}z^{\theta-1}g(z)dz\right] ^{\frac{1}{\theta-1}}.$](img166.gif)
|
(15) |
Figure 2: Average labor productivity levels of
Northern firms that produce domestically (![]() ) and offshore (
) and offshore (![]() ) for the Northern market.
) for the Northern market.
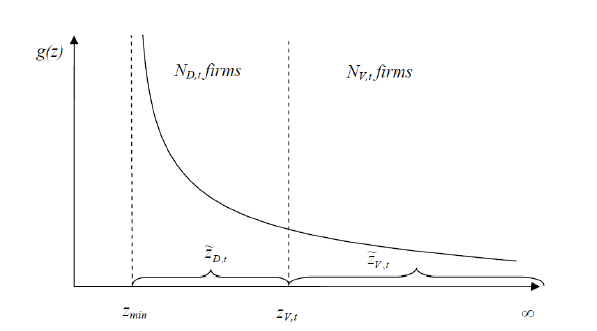
I assume that the firm-specific labor productivity draws
![]() are Pareto-distributed, with p.d.f.
are Pareto-distributed, with p.d.f.
![]() and c.d.f.
and c.d.f.
![]() over the support
interval
over the support
interval
![]() . Using this assumption, I
derive analytical solutions for the average productivity levels of
the two representative Northern firms that produce domestically and
offshore as functions of the time-variant productivity cutoff
. Using this assumption, I
derive analytical solutions for the average productivity levels of
the two representative Northern firms that produce domestically and
offshore as functions of the time-variant productivity cutoff
![]() :22
:22
![$\displaystyle \widetilde{z}_{D,t}=\nu z_{\min}z_{V,t}\left[ \frac{z_{V,t}^{k-(\theta -1)}-z_{\min}^{k-(\theta-1)}}{z_{V,t}^{k}-z_{\min}^{k}}\right] ^{\frac {1}{\theta-1}}$](img173.gif) and
and |
(16) |
where the productivity cutoff is
![]() , and
the parameters are
, and
the parameters are
![$ \nu\equiv\left[ \frac{k}{k-(\theta-1)}\right] ^{\frac {1}{\theta-1}}$](img176.gif) and
and
![]() .23 Since offshoring
takes place one-way, from the North to the South, the Southern
firms serve their domestic market exclusively through domestic
production. Their average productivity is constant,
.23 Since offshoring
takes place one-way, from the North to the South, the Southern
firms serve their domestic market exclusively through domestic
production. Their average productivity is constant,
![]() , as it covers
the entire support interval
, as it covers
the entire support interval
![]() .
.
Exporting firms Under the assumption of Pareto-distributed productivity draws, the average productivity levels of the exporting firms in each economy are as in Ghironi and Melitz (2005):
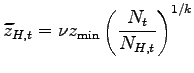 and
and 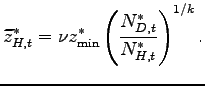
|
(17) |
3.2 Average Prices and Profits
Using the average productivity levels for the domestic, offshoring and exporting firms described above, I translate the model of offshoring in terms of three representative Northern firms: one produces domestically, another produces offshore (each serving the Northern market), while a third firm produces domestically and exports to the Southern market. There are only two representative Southern firms: one produces for the local market, and the other exports to the North.
I describe the average prices and profits for each representative firm in Table 1.Using the property that the Northern firm at the productivity
cutoff ![]() is indifferent between the two
production strategies, I derive the following relationship between
the average profits of the two representative firms that produce
domestically and offshore:24
is indifferent between the two
production strategies, I derive the following relationship between
the average profits of the two representative firms that produce
domestically and offshore:24
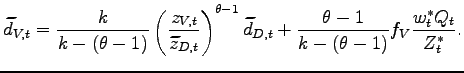
|
(18) |
In addition, using the property that the firm at the
productivity cutoff ![]() obtains zero profits
from exporting, the average profits from exports are:
obtains zero profits
from exporting, the average profits from exports are:
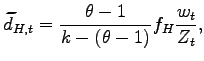 and
and 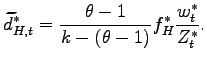
|
(19) |
Table 1: Average Prices and Profits
| Firm | Origin | Production | Market | Average Price | Average Profit |
|---|---|---|---|---|---|
| 1. | North | North | North | ||
| 2. | South | South | South | ||
| 3. | North | South | North | ||
| 4. | North | North | South | ||
| 5. | South | South | North |
Table 1 summarizes the average prices and profits of the firms that produce domestically for their local markets (rows 1 and 2); of the Northern firms that produce offshore (row 3); and of the firms that produce domestically for the export markets (rows 4 and 5).
Price indexes The consumption price index in the Northern economy is a function of the average prices of varieties produced domestically and offshore by the Northern firms, as well as the average price of the varieties imported from the South:
| (20) |
In the South, there is no representative firm producing offshore. The consumption price index depends on the average price of varieties produced domestically by the Southern firms, and also on that of varieties imported from the North:
| (21) |
Total profits The total profits of the Northern firms include the average profits from domestic and offshore production, as well as those from exports:
| (22) |
The total profits of the Southern firms combine the average profits from domestic sales and exports:
| (23) |
3.3 Aggregate Accounting and the Current Account Balance
I measure the aggregate income as the sum of the wage bill and
the amount of stock dividends that households in each economy
obtain every period,
![]() and
and
![]() The value added offshore, defined as the wage bill of the Southern
workers employed for production in the offshoring sector, is part
of the Southern output. The profits of the Northern firms producing
offshore are part of the Northern output.
The value added offshore, defined as the wage bill of the Southern
workers employed for production in the offshoring sector, is part
of the Southern output. The profits of the Northern firms producing
offshore are part of the Northern output.
Under financial autarky in the markets for bonds and stocks,
aggregate accounting implies that households spend their income
from labor and stock holdings on consumption and investment in new
firms,
![]() and
and
![]()
The current account in the North is:
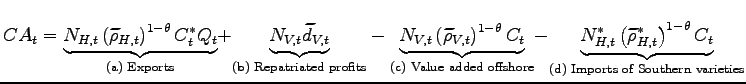
|
Under financial autarky, the balanced current account condition
(![]() ) states that the sum of (a) exports
by Northern firms to the South and (b) repatriated profits of
offshore affiliates must be equal to the sum of (c) the value added
by offshore affiliates imported in the North and (d) the imports of
varieties produced by the Southern firms.25
) states that the sum of (a) exports
by Northern firms to the South and (b) repatriated profits of
offshore affiliates must be equal to the sum of (c) the value added
by offshore affiliates imported in the North and (d) the imports of
varieties produced by the Southern firms.25
3.4 Model Summary
The baseline model with financial autarky for the Northern
economy is characterized by 16 equations in 16 endogenous
variables: ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() and
and ![]() . Since the
Southern firms do not produce in the high-cost North, the Southern
economy is described by only 11 equations in 11 endogenous
variables; there are no Southern counterparts for
. Since the
Southern firms do not produce in the high-cost North, the Southern
economy is described by only 11 equations in 11 endogenous
variables; there are no Southern counterparts for ![]() ,
, ![]() ,
,
![]() ,
,
![]() and
and
![]() . In particular, the
average labor productivity of the representative Southern firm
producing for the domestic market (
. In particular, the
average labor productivity of the representative Southern firm
producing for the domestic market (
![]() is constant over
time. Variables
is constant over
time. Variables ![]() ,
, ![]() ,
,
![]() and
and
![]() are predetermined.26
are predetermined.26
4 Calibration
I use a standard quarterly calibration by setting the subjective
rate of time discount
![]() to match an average annualized
interest rate of 4 percent. The coefficient of relative risk
aversion is
to match an average annualized
interest rate of 4 percent. The coefficient of relative risk
aversion is ![]() . Following Ghironi and Melitz
(2005), I set the intra-temporal elasticity of substitution
. Following Ghironi and Melitz
(2005), I set the intra-temporal elasticity of substitution
![]() , and the probability of firm exit
, and the probability of firm exit
![]() to match the annual 10 percent
job destruction in the U.S.
to match the annual 10 percent
job destruction in the U.S.
As summarized in Table 2, I calibrate the fixed costs of
offshoring (![]() ) and exporting (
) and exporting (![]() and
and
![]() ) as well as the Pareto
distribution parameter
) as well as the Pareto
distribution parameter ![]() , so that the model matches
the importance of offshoring and trade for the Mexican economy in
steady state, as illustrated by four empirical moments: (1) The
maquiladora value added represents about 20 percent of Mexico's
manufacturing GDP (INEGI, 2008), compared to 25 percent in the
model; (2) The maquiladora exports represent about half of Mexico's
total exports (Bergin, Feenstra, and Hanson, 2008), vs. 60 percent
in the model; (3) Employment in the maquiladora sector accounts for
approximately 25 percent of Mexico's total manufacturing employment
(Bergin, Feenstra, and Hanson, 2008), compared to 22 percent in the
model; (4) Total imports represent the equivalent of 33 percent of
Mexico's GDP (INEGI, 2008), and 32 percent in the model. To this
end, I set
, so that the model matches
the importance of offshoring and trade for the Mexican economy in
steady state, as illustrated by four empirical moments: (1) The
maquiladora value added represents about 20 percent of Mexico's
manufacturing GDP (INEGI, 2008), compared to 25 percent in the
model; (2) The maquiladora exports represent about half of Mexico's
total exports (Bergin, Feenstra, and Hanson, 2008), vs. 60 percent
in the model; (3) Employment in the maquiladora sector accounts for
approximately 25 percent of Mexico's total manufacturing employment
(Bergin, Feenstra, and Hanson, 2008), compared to 22 percent in the
model; (4) Total imports represent the equivalent of 33 percent of
Mexico's GDP (INEGI, 2008), and 32 percent in the model. To this
end, I set
![]() (the fixed cost of offshoring
for Northern firms),
(the fixed cost of offshoring
for Northern firms),
![]() and
and
![]() (the fixed costs of
exporting for the Northern and Southern firms, respectively), as
well as
(the fixed costs of
exporting for the Northern and Southern firms, respectively), as
well as ![]() (the Pareto distribution
coefficient).27 Without loss of generality, I set
the lower bound of the support interval for firm-specific
productivity in the North and the South at
(the Pareto distribution
coefficient).27 Without loss of generality, I set
the lower bound of the support interval for firm-specific
productivity in the North and the South at
![]() .
.
Table 2. Calibration parameters and steady-state targets - Panel A: Calibration Parameters
| Fixed Cost of Offshoring | |
|---|---|
| Fixed cost of exporting, North | |
| Fixed cost of exporting, South | |
| Pareto distribution coefficient |
Table 2. Calibration parameters and steady-state targets - Panel B: Steady-state targets
| Data | Model | |
|---|---|---|
| Maquila. VA in Mex. manufacturing | 20% | 25% |
| Maquila. share in Mexican exports | 50% | 60% |
| Maquila. share in manuf. employment | 25% | 22% |
| Mexico's imports as % of GDP | 33% | 32% |
Table 2 summarizes the calibration of key parameters of the model, and also compares the steady state values of key macroeconomic variables with their empirical counterparts.
In order to obtain a steady-state asymmetry in the cost of
effective labor across countries, I set the sunk entry cost - which
reflects headquarter activities sensitive to the regulation of
starting a business in the firms' country of origin - to be larger
in the South than in the North (
![]() and
and ![]() ). As a result, the steady state number of firms, the
labor demand and the real wage are relatively lower in the South.
The calibration reflects the considerable variation in the cost of
starting a business across countries: The corresponding monetary
cost is 3.3 times higher in Mexico than in the U.S. or Canada; it
is 6.2 times higher in Hungary than in the U.K. (World Bank, 2007).
The asymmetric sunk entry costs, along with the iceberg trade cost
). As a result, the steady state number of firms, the
labor demand and the real wage are relatively lower in the South.
The calibration reflects the considerable variation in the cost of
starting a business across countries: The corresponding monetary
cost is 3.3 times higher in Mexico than in the U.S. or Canada; it
is 6.2 times higher in Hungary than in the U.K. (World Bank, 2007).
The asymmetric sunk entry costs, along with the iceberg trade cost
![]() and the values for
and the values for ![]() ,
, ![]() and
and
![]() reported above, generate a
steady state value for the terms of labor that is less than one (
reported above, generate a
steady state value for the terms of labor that is less than one (
![]() ).28 In
other words, the steady state cost of effective labor in the South,
defined as real wage divided by aggregate productivity, is
76 percent of the corresponding level in the
North. The calibration provides an incentive for the Northern firms
to produce offshore in steady state.
).28 In
other words, the steady state cost of effective labor in the South,
defined as real wage divided by aggregate productivity, is
76 percent of the corresponding level in the
North. The calibration provides an incentive for the Northern firms
to produce offshore in steady state.
The resulting steady-state fraction of the Northern firms that
use foreign labor (![]() ) is 1.4 percent; the fraction of exporting firms (
) is 1.4 percent; the fraction of exporting firms (![]() ) is 10.1 percent. Since I model
offshoring in an asymmetric two-country framework that abstracts
from the exchanges of U.S. firms with the rest of the world (other
than Mexico), the steady state values reported above are less than
their empirical counterparts. In the data, approximately 14 percent
of the U.S. firms (other than domestic wholesalers) used imported
inputs from both Mexico and the rest of the world in 1997 (Bernard,
Jensen, Redding and Schott, 2007). Out of that, intra-firm imports
represented half of the total amount, while the rest was accounted
by arm's length transactions (Bardhan and Jafee, 2004).29Approximately 21 percent of the U.S.
manufacturing plants were exporters in 1992 (Bernard, Eaton, Jensen
and Kortum, 2003).
) is 10.1 percent. Since I model
offshoring in an asymmetric two-country framework that abstracts
from the exchanges of U.S. firms with the rest of the world (other
than Mexico), the steady state values reported above are less than
their empirical counterparts. In the data, approximately 14 percent
of the U.S. firms (other than domestic wholesalers) used imported
inputs from both Mexico and the rest of the world in 1997 (Bernard,
Jensen, Redding and Schott, 2007). Out of that, intra-firm imports
represented half of the total amount, while the rest was accounted
by arm's length transactions (Bardhan and Jafee, 2004).29Approximately 21 percent of the U.S.
manufacturing plants were exporters in 1992 (Bernard, Eaton, Jensen
and Kortum, 2003).
The calibration also implies that, in the North, the steady-state expenditure share of the varieties produced by Northern firms domestically (66.0 percent) - firms which are relatively less productive than the average - is less than their fraction in the total number of varieties available in the North (89.2 percent). In contrast, since the offshored varieties are produced by the relatively more productive Northern firms, their expenditure share (21.2 percent) is more than their fraction in the total number of varieties available in the North (1.2 percent). The pattern is consistent with the more productive firms having larger market shares than their less productive counterparts.30
5 Results
5.1 Offshoring to Mexico's Maquiladora Sector
In this section I describe the cyclicality of offshoring motivated by lower production costs using data from U.S. manufacturing and Mexico's maquiladora sector. In particular, I document the business cycle dynamics of the extensive margin of offshoring from the U.S. to Mexico, which will be useful to assess the implications of the model with offshoring that are described in the following sections.
Mexico's maquiladora sector The maquiladora sector represents an appropriate empirical setup to study the cyclicality of offshoring by U.S. manufacturing firms motivated by lower production costs, due to the absence of local consumption in Mexico and its direct links to U.S. manufacturing. The plants operating under Mexico's maquiladora program import inputs, process them, and ship the resulting goods back to the country of origin (Gruben, 2001).31 Although only a subset of the maquiladora plants are U.S.-owned, most of them accommodate the offshoring operations of U.S. firms: They import most of their inputs from the U.S. (82 percent), and export most of their output (90 percent) back to the U.S. (Hausman and Kaytko, 2003; Burstein, Kurz and Tesar, 2009). The value added of the maquiladora sector is part of Mexico's manufacturing output.
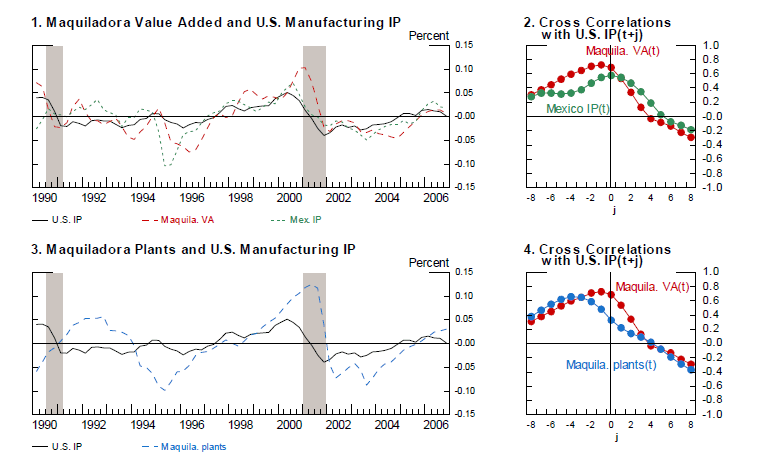
Empirical cross-correlations Mexico's total manufacturing output and, in particular, the maquiladora value added are strongly correlated with U.S. manufacturing. In Figure 3 (panel 1), I plot the detrended series for Mexico's maquiladora value added (the dashed line) and Mexico's total manufacturing output (the dotted line) against the manufacturing component of U.S. industrial production (henceforth U.S. IP, the solid line), for the interval between 1990:Q1 and 2006:Q4.32 The chart shows that the U.S. recessions in 1990 and 2001, as well as the expansion throughout the late 1990s, were associated with similar patterns in the maquiladora value added. During the 1994-95 financial crisis in Mexico, the decline in the maquiladora value added was less pronounced than the drop in Mexico's total manufacturing output, as the offshoring sector in Mexico benefited from the direct links with U.S. manufacturing. The cross-correlations in panel 2 show that Mexico's maquiladora value added moves closely together with the U.S. manufacturing output, and that its correlation with U.S. manufacturing is larger than that of Mexico's total manufacturing output.
In panel 3 (bottom left), I plot the detrended series for the number of maquiladora plants in Mexico (the dashed line) - which reflects the extensive margin of offshoring - against the U.S. IP for manufacturing (the solid line). The cross-correlations in panel 4 show that U.S. manufacturing leads the number of maquiladora plants by about four quarters. The result suggests that the extensive margin of offshoring adjusts gradually over time, whereas the maquiladora value added is contemporaneously correlated with the U.S. manufacturing output.
Figure 3: Business cycles dynamics of offshoring to Mexico
5.2 Impulse Responses of Offshoring
I log-linearize the baseline model of offshore production under
financial autarky around the steady state, and compute the impulse
responses to a transitory one-percent increase in aggregate
productivity in the North. I assume that aggregate productivity is
described by the autoregressive process
![]() , with the
persistence parameter
, with the
persistence parameter ![]() .
.
Figure 4 shows the impulse responses of the baseline model of offshoring (thick solid lines), and contrasts them to those from two alternative frameworks: (i) a model of offshoring in which the productivity cutoff is fixed, so that the fraction of offshoring firms is constant over the business cycle (thin solid lines)33; and (ii) the extreme case with no offshoring, a case in which I replicate the model with exports in Ghironi and Melitz (2005) (dashed lines). For each variable, the horizontal axis illustrates quarters after the initial shock, and the vertical axis shows the percent deviations from the original steady state in each quarter.
Figure 4: Impulse responses to one-percent shock to aggregate productivity in the North, baseline model of offshoring with adjustable productivity cutoff (thick solid line); alternative models with fixed productivity cutoff (thin solid line) and no offshoring (dashed line).
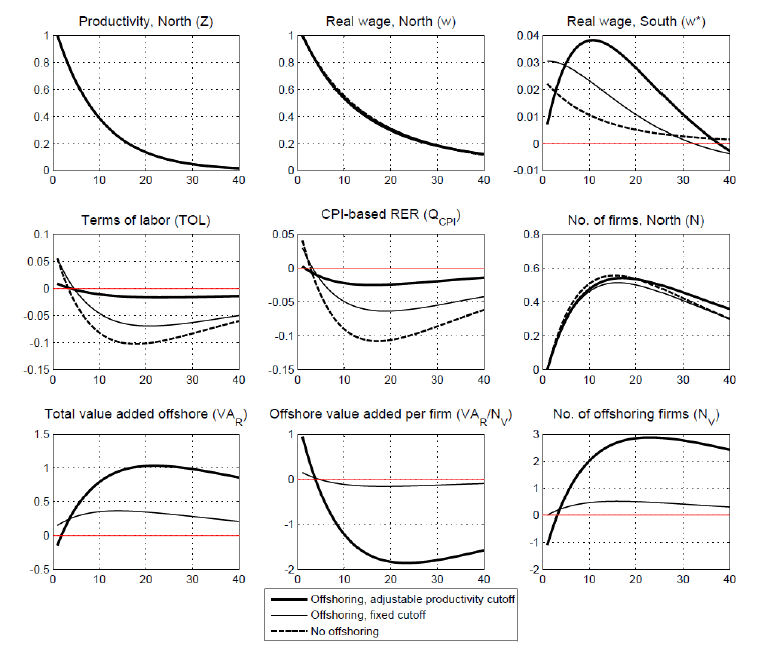
The intensive margin In the baseline model (thick solid lines), on impact, the
increase in aggregate labor productivity in the North generates a
proportional increase in the real wage ![]() . The
rising demand for varieties produced both domestically and offshore
causes an immediate increase in offshoring along its intensive
margin (i.e. offshore value added per firm). Since the increase in
aggregate productivity in the North is not replicated in the South,
the excess demand for Southern effective labor causes the real wage
in the South
. The
rising demand for varieties produced both domestically and offshore
causes an immediate increase in offshoring along its intensive
margin (i.e. offshore value added per firm). Since the increase in
aggregate productivity in the North is not replicated in the South,
the excess demand for Southern effective labor causes the real wage
in the South
![]() and the terms of
labor
and the terms of
labor
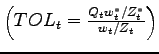 to jump. As a result, the number of Northern firms that produce
offshore (
to jump. As a result, the number of Northern firms that produce
offshore (![]() ) drops on impact due to: (i) the
increase in the cost of effective labor offshore, and (ii) the
increase in the fixed cost of offshoring, both of which are
sensitive to the effective wage in the South.
) drops on impact due to: (i) the
increase in the cost of effective labor offshore, and (ii) the
increase in the fixed cost of offshoring, both of which are
sensitive to the effective wage in the South.
The extensive margin As the aggregate labor productivity in the North persists above
its initial steady state, the larger market size encourages firm
entry, as shown by the gradual increase in the number of incumbent
firms (![]() ). In turn, firm entry leads to an
increase in the demand for Northern labor, which causes the cost of
effective labor to appreciate gradually in the North relative to
the South. In Figure 4, this appreciation is visible as the real
wage in the North declines more slowly after the initial shock than
aggregate productivity, and thus the terms of labor persist below
their initial steady state level. Following the appreciation of the
terms of labor, the number of offshoring firms (
). In turn, firm entry leads to an
increase in the demand for Northern labor, which causes the cost of
effective labor to appreciate gradually in the North relative to
the South. In Figure 4, this appreciation is visible as the real
wage in the North declines more slowly after the initial shock than
aggregate productivity, and thus the terms of labor persist below
their initial steady state level. Following the appreciation of the
terms of labor, the number of offshoring firms (![]() ) increases, as some of the more productive Northern
firms relocate production to the South. Notably, the increase in
the number of offshoring firms is gradual, as it mirrors the
gradual appreciation of the terms of labor.
) increases, as some of the more productive Northern
firms relocate production to the South. Notably, the increase in
the number of offshoring firms is gradual, as it mirrors the
gradual appreciation of the terms of labor.
The total value added offshore (![]() )
increases by more under the baseline model of offshoring (thick
solid line) than in the alternative model of offshoring in which
the productivity cutoff is fixed (thin solid line). Thus, 20
quarters after the shock, more than half of the increase in the
total value added offshore is due to the adjustment along the
extensive margin.
)
increases by more under the baseline model of offshoring (thick
solid line) than in the alternative model of offshoring in which
the productivity cutoff is fixed (thin solid line). Thus, 20
quarters after the shock, more than half of the increase in the
total value added offshore is due to the adjustment along the
extensive margin.
In the South, the initial jump in the real wage - caused by the
spike of the intensive margin of offshoring - is followed by an
additional increase which occurs gradually over time, as some of
the more productive Northern firms relocate production to the
South. Since the increase in offshoring along its extensive margin
transfers some of the upward pressure from the domestic to the
foreign wage, the terms of labor appreciate by less (![]() declines by less) in the baseline model of offshoring
(thick solid line) than in the alternative models with no extensive
margin adjustment (thin solid line) and no offshoring (dashed
line).
declines by less) in the baseline model of offshoring
(thick solid line) than in the alternative models with no extensive
margin adjustment (thin solid line) and no offshoring (dashed
line).
5.3 The Extensive and Intensive Margins of Offshoring
In this section I provide evidence in support of the model of offshoring with extensive margin adjustments over the business cycle. Thus, I analyze the empirical cross-correlations between lags and leads of the U.S. manufacturing output and two empirical indicators of offshore production in Mexico: (i) the number of maquiladora establishments, as an empirical proxy for the extensive margin; and (ii) the value added per establishment, as a proxy for the intensive margin. Then I compare the empirical correlations to their model counterparts.
In the model, the total value added offshore, VA
![$ _{t}=N_{V,t}\left[ \tau \frac{\theta}{\theta-1}\frac{w_{t}^{\ast}Q_{t}}{Z_{t}^{\ast}\widetilde {z}_{V,t}}\right] ^{1-\theta}C_{t}$](img273.gif) , is a function of the number of offshoring firms, their average
idiosyncratic productivity, the foreign cost of effective labor,
and the aggregate consumption in the North. The number of
offshoring firms (
, is a function of the number of offshoring firms, their average
idiosyncratic productivity, the foreign cost of effective labor,
and the aggregate consumption in the North. The number of
offshoring firms (![]() ) measures the
extensive margin of offshore production, and constitutes the
counterpart of the number of maquiladora plants in Mexico. The real
value added per offshoring firm (VA
) measures the
extensive margin of offshore production, and constitutes the
counterpart of the number of maquiladora plants in Mexico. The real
value added per offshoring firm (VA
![]() ) represents the intensive
margin of offshoring; it is the model counterpart of the value
added per maquiladora plant.34
) represents the intensive
margin of offshoring; it is the model counterpart of the value
added per maquiladora plant.34
Model vs. empirical cross-correlations Figure 5 (panels 1 and 2) shows the empirical correlations between U.S. manufacturing and the two margins of the maquiladora sector (black line), together with their 95 percent confidence intervals. It also shows the model correlations generated by the baseline model of offshoring under financial autarky (red solid line), as well as those generated by the baseline model augmented with elastic labor supply (green dotted line). Aggregate productivity follows the bivariate autoregressive process:
![$\displaystyle \left[ \begin{array}[c]{l} \log Z_{t}\\ \log Z_{t}^{\ast} \end{array} \right] =\left[ \begin{array}[c]{ll} \rho_{Z} & \rho_{ZZ^{\ast}}\\ \rho_{Z^{\ast}Z} & \rho_{Z^{\ast}} \end{array} \right] \left[ \begin{array}[c]{l} \log Z_{t-1}\\ \log Z_{t-1}^{\ast} \end{array} \right] +\left[ \begin{array}[c]{l} \xi_{t}\\ \xi_{t}^{\ast} \end{array} \right] ,$](img281.gif)
|
(24) |
where the persistence parameters are
![]() , and the
spillovers are
, and the
spillovers are
![]() , as
in Backus, Kehoe, and Kydland (1992). The variance of the shocks is
, as
in Backus, Kehoe, and Kydland (1992). The variance of the shocks is
![]() and the covariance is
and the covariance is
![]() , values which correspond
to a correlation of innovations of 0.258.
, values which correspond
to a correlation of innovations of 0.258.
Figure 5: Empirical vs. Theoretical cross-correlations: maquiladora variables at t and the U.S. manufacturing outpout at t + j
Regarding the extensive margin (panel 1), the data shows a strong and positive correlation between the number of maquiladora plants and the past U.S. manufacturing output. As discussed, expansions in U.S. manufacturing tend to lead the number of offshore plants by about four quarters. The model is successful in capturing this pattern; the correlation between the number of offshoring firms and the past output in the North is positive, and reaches a peak for the Northern output lagged by four quarters. The result is explained by the fact that, following a productivity improvement in the North, the increase in the number of offshoring firms is gradual, as it mirrors the gradual appreciation of the terms of labor caused by domestic firm entry. Although the contemporaneous correlation between the number of offshoring firms and Northern output is slightly negative35 (rather than positive as in the data), the model replicates the inter-temporal dynamics of the extensive margin.
Turning towards the intensive margin (panel 2), the empirical correlation between the maquiladora value added per plant and the past U.S. manufacturing output is negative and statistically significant. The model is successful in replicating this pattern as well. Following a positive technology shock in the North, the number of offshoring firms increases faster than the total value added offshore due to the appreciation of the terms of labor. As a result, the value added per offshoring firm declines below its initial level several quarters after the shock, and the correlation between the intensive margin of offshoring and past output in the North is negative.
5.4 The Co-Movement of Output and Offshore Production
In this section I illustrate the cross-country correlations of Northern output and the value added offshore generated by the baseline model of offshoring, and examine their sensitivity to the trade cost and the persistence of aggregate productivity.
The co-movement of output and the
value added offshore I assume that aggregate productivity follows the bivariate
autoregressive process described by equation (24). The
persistence parameters are asymmetric across the two economies (
![]() and
and
![]() ), there are no
spillovers (
), there are no
spillovers (
![]() ), and
the technology shocks are less volatile in the North than in the
South (i.e. variances
), and
the technology shocks are less volatile in the North than in the
South (i.e. variances
![]() vs.
vs.
![]() ), with the covariance
), with the covariance
![]() implying a correlation of
shocks of 0.27. These assumptions are based on the
estimates of the bivariate productivity process for the U.S. and
Mexico in Mandelman and Zlate (2008), that use data on total factor
productivity (TFP) for the two countries.
implying a correlation of
shocks of 0.27. These assumptions are based on the
estimates of the bivariate productivity process for the U.S. and
Mexico in Mandelman and Zlate (2008), that use data on total factor
productivity (TFP) for the two countries.
Table 3 shows the cross-country correlation of output
![]() , the correlation
of output in the country of origin with the value added offshore
, the correlation
of output in the country of origin with the value added offshore
![]() , and also the
cross-country correlation of consumption
, and also the
cross-country correlation of consumption
![]() generated by the
model of offshoring.36 It also reports the correlations
generated by the alternative framework in which I shut down
offshoring, and thus replicate the model with endogenous exports in
Ghironi and Melitz (2005).
generated by the
model of offshoring.36 It also reports the correlations
generated by the alternative framework in which I shut down
offshoring, and thus replicate the model with endogenous exports in
Ghironi and Melitz (2005).
Table 3. Cross-country contemporaneous correlations
| Model: | Financial autarky: Offshoring | Financial autarky: No offshoring | International Bond trading: Offshoring | International Bond trading: No offshoring |
|---|---|---|---|---|
| Corr(YR,Y*R) | 0.35 | 0.27 | 0.34 | 0.32 |
| Corr(YR,VAR) | 0.99 | n/a | 0.99 | n/a |
| Corr(CR,C*R) | 0.40 | 0.28 | 0.44 | 0.37 |
Table 3 summarizes the cross-country contemporaneous correlations of output, offshore value added and consumption generated by the models with and without offshoring, for the cases of financial autarky (left panel) and financial integration (right panel).
Two notable results emerge from Table 3. First, the correlation
of Northern output with the value added offshore is larger than the
cross-country correlation of total output,
![]() , a
result which is consistent with the empirical correlations
documented above (i.e. the maquiladora value added co-moves more
closely with the U.S. manufacturing output than does Mexico's total
manufacturing output.) In the model, the value added offshore is
closely related to aggregate productivity, net firm entry and the
appreciation of the cost of effective labor in the North, and thus
is strongly correlated with the Northern output. In contrast, the
total output in the South, on one hand, receives the positive
contribution of the offshoring sector, which enhances its
co-movement with the Northern output. On the other hand, the
relative productivity increase in the North dampens firm entry in
the South, and thus partially offsets the additional co-movement
generated by offshoring. In addition, offshoring reduces the
competitiveness of the Southern exporters, as the relocation of
production transfers some of the upward pressure from the Northern
wage to the Southern one, which further dampens output co-movement.
Nonetheless, under international bond trading, the cross-country
co-movement of total output is further reduced by the
resource-shifting effect that occurs as households lend across the
border to finance firm entry in the country receiving the favorable
productivity shock.
, a
result which is consistent with the empirical correlations
documented above (i.e. the maquiladora value added co-moves more
closely with the U.S. manufacturing output than does Mexico's total
manufacturing output.) In the model, the value added offshore is
closely related to aggregate productivity, net firm entry and the
appreciation of the cost of effective labor in the North, and thus
is strongly correlated with the Northern output. In contrast, the
total output in the South, on one hand, receives the positive
contribution of the offshoring sector, which enhances its
co-movement with the Northern output. On the other hand, the
relative productivity increase in the North dampens firm entry in
the South, and thus partially offsets the additional co-movement
generated by offshoring. In addition, offshoring reduces the
competitiveness of the Southern exporters, as the relocation of
production transfers some of the upward pressure from the Northern
wage to the Southern one, which further dampens output co-movement.
Nonetheless, under international bond trading, the cross-country
co-movement of total output is further reduced by the
resource-shifting effect that occurs as households lend across the
border to finance firm entry in the country receiving the favorable
productivity shock.
Second, the model with offshoring enhances the co-movement of output relative to the special case with no offshoring. Intuitively, in the model with no offshoring in Ghironi and Melitz (2005), the positive shock to aggregate productivity in the North generates an increase in the demand for all varieties - produced both in the North and in the South - as well as an immediate increase in the relative price of Southern varieties. The resulting substitution away from Southern varieties is offset by the increase in net firm entry and the gradual appreciation of the cost of effective labor in the North, which enhances the export competitiveness of the Southern firms. Therefore, the model with no offshoring still generates positive output co-movement across the two economies.
Offshoring introduces an additional transmission mechanism that enhances the co-movement of output. Following an increase in aggregate productivity in the North, firm entry causes a gradual appreciation of the terms of labor, which in turn provides an incentive for some of the more productive Northern firms to relocate production to the South. The increase of output in the North (generated by the positive shock to aggregate productivity) and also in the South (generated by the initial jump in Northern demand for offshored varieties and, subsequently, the gradual relocation of production by the Northern firms to the South), enhance the co-movement of total output across the two economies. The effect is dampened under international trade in bonds, as the Southern households lend to finance firm entry during expansions in the North.
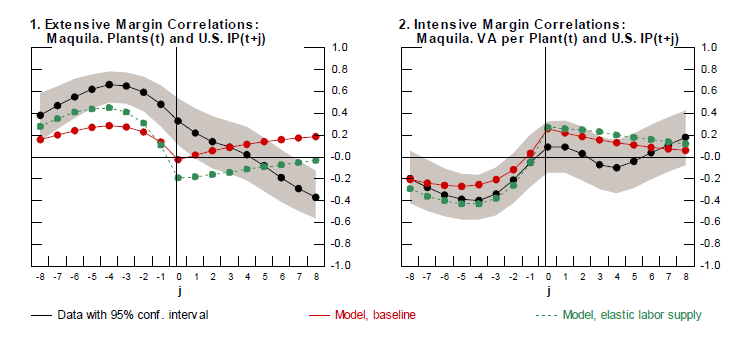
The remainder of this section examines the sensitivity of
cross-country correlations to: (a) variation in the iceberg trade
cost ![]() and (b) variation in the persistence of
the bivariate autoregressive productivity process
and (b) variation in the persistence of
the bivariate autoregressive productivity process ![]() . Figures 6 and 7 show that the model with offshoring
generates larger cross-country correlations for both output and
consumption relative to the special case with no offshoring,
results which hold for a wide range of possible values for the
trade cost
. Figures 6 and 7 show that the model with offshoring
generates larger cross-country correlations for both output and
consumption relative to the special case with no offshoring,
results which hold for a wide range of possible values for the
trade cost
![]()
![]() and
the persistence parameter
and
the persistence parameter
![]() .
.
Sensitivity to the trade cost
![]() The cross-country correlation of output is greater for lower
values of the trade cost (Figure 6). During expansions in the
North, a lower trade cost (that applies to both offshoring and non
offshoring-related trade) enhances the demand for varieties
produced in the South (either by Northern offshoring firms or by
Southern exporters). A lower trade cost also facilitates the
relocation of production offshore over the business cycle, and thus
enhances the cross-country co-movement of output.
The cross-country correlation of output is greater for lower
values of the trade cost (Figure 6). During expansions in the
North, a lower trade cost (that applies to both offshoring and non
offshoring-related trade) enhances the demand for varieties
produced in the South (either by Northern offshoring firms or by
Southern exporters). A lower trade cost also facilitates the
relocation of production offshore over the business cycle, and thus
enhances the cross-country co-movement of output.
Figure 6: Cross-country correlations of output and consumption, sensitivity to ![]()
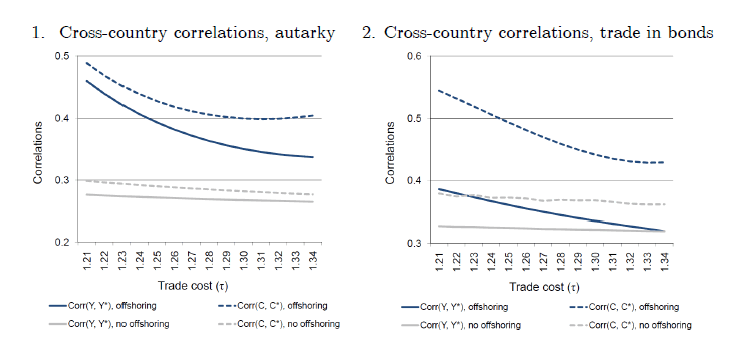
The result is consistent with the empirical regularity documented in Burstein, Kurz, and Tesar (BKT, 2009), namely that country pairs with (i) larger shares of offshoring-related trade in bilateral trade and (ii) larger bilateral trade flows relative to output also exhibit larger correlations of manufacturing output. In BKT (2009), the regression of output correlations between the U.S. and foreign economies on (i) the production-sharing intensity of foreign exports and (ii) the share of exports in foreign output generates OLS coefficients that are positive and statistically significant (0.746 and 0.140, respectively). In the model considered in this paper, a decline in the trade cost from its baseline calibration value to the lower extreme (i.e. from 1.3 to 1.21) is associated with an 11 percentage point increase in the correlation of output (Figure 6, panel 1 for financial autarky). The same reduction in the trade cost is linked to (i) an increase in the steady-state share of offshoring-related trade in the Southern exports (from 60 to 92 percent), and also (ii) an increase in the share of exports in the Southern output (from 40 to 86 percent). The resulting slope between the output correlation and the steady-state share of offshoring-related trade in Southern exports (0.344) is roughly half the corresponding OLS coefficient in BKT (2009). The slope between the output correlation and the steady-state share of exports in Southern output (0.240) is slightly larger than its empirical counterpart.
Sensitivity to the aggregate
productivity persistence ![]() The model with offshoring generates larger cross-country
correlations of output than the alternative model with no
offshoring for the entire range of values of the persistence
parameter
The model with offshoring generates larger cross-country
correlations of output than the alternative model with no
offshoring for the entire range of values of the persistence
parameter ![]() .37 More, the additional
co-movement generated by offshoring increases with the persistence
parameter. Under financial autarky (panel 1 in Figure 7), the
additional correlation brought by offshoring increases from
6 to 12 percentage points
as the persistence parameter rises from
.37 More, the additional
co-movement generated by offshoring increases with the persistence
parameter. Under financial autarky (panel 1 in Figure 7), the
additional correlation brought by offshoring increases from
6 to 12 percentage points
as the persistence parameter rises from
![]() to
to
![]() . Following a positive
technology shock in the North, the larger persistence of aggregate
productivity leads to a larger increase in domestic demand, and
thus to a larger increase in offshoring along its intensive margin
on impact. The larger persistence also enhances firm entry and
generates a larger appreciation of the terms of labor over the
business cycle, which in turn provides a greater incentive for
firms to relocate production offshore. Under financial integration
(panel 2), the result is dampened by the resource-shifting effect
that occurs when households lend to the country that receives a
positive technology shock.
. Following a positive
technology shock in the North, the larger persistence of aggregate
productivity leads to a larger increase in domestic demand, and
thus to a larger increase in offshoring along its intensive margin
on impact. The larger persistence also enhances firm entry and
generates a larger appreciation of the terms of labor over the
business cycle, which in turn provides a greater incentive for
firms to relocate production offshore. Under financial integration
(panel 2), the result is dampened by the resource-shifting effect
that occurs when households lend to the country that receives a
positive technology shock.
Figure 7: Cross-country correlations, sensitivity to ![]()
5.5 Real Exchange Rate Dynamics
Offshoring narrows the price dispersion across countries, as it dampens the appreciation of the real exchange rate that follows a domestic increase in aggregate productivity. In the absence of offshoring, the framework with firm entry and endogenously traded varieties in Ghironi and Melitz (2005) generates the Harrod-Balassa-Samuelson effect (i.e. more productive economies exhibit higher average prices), as the country that receives a favorable shock to aggregate productivity also experiences an appreciation of the terms of labor and a rise in import prices. However, offshoring dampens this effect though a number of channels, including the transfer of upward pressure from the domestic to the foreign wage, the reduced size of the domestic non-traded sector, and the decline in import prices as offshoring crowds out the less productive foreign exporters.
Average prices and product
variety I use the consumer price index (CPI)-based real exchange rate
![]() as the theoretical counterpart for the empirical real exchange
rate, since the average prices
as the theoretical counterpart for the empirical real exchange
rate, since the average prices
![]() and
and
![]() best represent the
corresponding empirical CPI levels in the presence of endogenous
product variety (Broda and Weinstein, 2003). To this end, I break
down the welfare-based price indexes
best represent the
corresponding empirical CPI levels in the presence of endogenous
product variety (Broda and Weinstein, 2003). To this end, I break
down the welfare-based price indexes ![]() and
and
![]() into components reflecting (a)
product variety and (b) average prices as
into components reflecting (a)
product variety and (b) average prices as
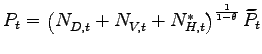 for the North and
for the North and
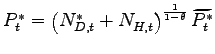 for the South. The resulting expression for the CPI-based real
exchange rate is:
for the South. The resulting expression for the CPI-based real
exchange rate is:
![$\displaystyle Q_{CPI,t}^{1-\theta}=\left( \frac{N_{D,t}^{{}}+N_{V,t}^{{}}+N_{H,t}^{\ast} }{N_{D,t}^{\ast}+N_{H,t}^{{}}}\right) \frac{N_{D,t}^{\ast}\left( \frac{TOL_{t}}{\widetilde{z}_{D,t}^{\ast}}\right) ^{1-\theta}+N_{H,t}\left( \frac{\tau_{t}^{\ast}}{\widetilde{z}_{H,t}}\right) ^{1-\theta}} {N_{D,t}\left( \frac{1}{\widetilde{z}_{D,t}}\right) ^{1-\theta} +N_{V,t}\left( \frac{\tau_{t}TOL_{t}}{\widetilde{z}_{V,t}}\right) ^{1-\theta}+N_{H,t}^{\ast}\left[ \frac{\tau_{t}TOL_{t}}{\widetilde{z} _{H,t}^{\ast}}\right] ^{1-\theta}},$](img335.gif)
|
(25) |
where the terms of labor
![]() measures the cost of effective labor in the South relative to the
North; the iceberg trade costs
measures the cost of effective labor in the South relative to the
North; the iceberg trade costs ![]() and
and
![]() affect the imports of the
North and the South, respectively.
affect the imports of the
North and the South, respectively.
Analytical results The log-linearized version of (25) is:
![$\displaystyle =\left[ s_{D}^{{}}-s_{V}^{{}}+s_{D}^{\ast}-1\right] \widehat{TOL}_{t}+$](img340.gif)
|
(C1) | |
| (C2) | ||
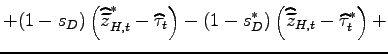
|
(C3) | |
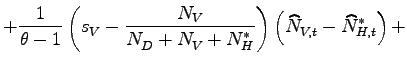
|
(C4) | |
![$\displaystyle +\frac{1}{\theta-1}\left[ \begin{array}[c]{c} \left( \frac{N_{D}^{\ast}}{N_{D}^{\ast}+N_{H}^{{}}}-s_{D}^{\ast}\right) \left( \widehat{N}_{D,t}^{\ast}-\widehat{N}_{H,t}^{{}}\right) -\\ -\left( \frac{N_{D}}{N_{D}^{{}}+N_{V}^{{}}+N_{H}^{\ast}}-\left( s_{D}^{{} }-s_{V}^{{}}\right) \right) \left( \widehat{N}_{D,t}^{{}}-\widehat{N} _{H,t}^{\ast}\right) \end{array} \right] ,$](img344.gif)
|
(C5) |
where the variables marked with a hat denote percent deviations
from their steady states. Parameter
![]() is the steady-state share of
spending in the North on varieties produced by Northern firms
both domestically and offshore;
is the steady-state share of
spending in the North on varieties produced by Northern firms
both domestically and offshore;
![]() is the steady-state share of
spending in the North only on varieties produced by Northern
firms offshore (I shut down offshoring when
is the steady-state share of
spending in the North only on varieties produced by Northern
firms offshore (I shut down offshoring when
![]() and
and
![]() );
);
![]() is the steady-state share of
spending in the South on varieties produced by Southern firms. The
calibration ensures that: (a)
is the steady-state share of
spending in the South on varieties produced by Southern firms. The
calibration ensures that: (a)
![]() ,
as the domestically-produced varieties represent more than 50
percent of consumption spending in each country; (b)
,
as the domestically-produced varieties represent more than 50
percent of consumption spending in each country; (b)
![]() and
and
![]() i.e. the market shares of varieties produced domestically by the
less productive firms are smaller than their fraction
in the total number of varieties; and (c)
i.e. the market shares of varieties produced domestically by the
less productive firms are smaller than their fraction
in the total number of varieties; and (c)
![]() , i.e. the market share of varieties produced offshore by
themore productive Northern firms is larger than
their fraction in the total number of varieties available in the
North. The model implies that the relatively more productive
offshoring firms have larger market shares than their less
productive domestic counterparts, which is in line with the
empirical evidence in Kurz (2006).
, i.e. the market share of varieties produced offshore by
themore productive Northern firms is larger than
their fraction in the total number of varieties available in the
North. The model implies that the relatively more productive
offshoring firms have larger market shares than their less
productive domestic counterparts, which is in line with the
empirical evidence in Kurz (2006).
The log-linearized form of (25) outlines five
channels (labeled C1-C5 in the
log-linearized equation above) through which the CPI-based real
exchange rate is affected by: (1) changes in the price of
non-traded varieties induced by fluctuations in the terms of labor
(
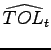 ); (2) changes in the price
of offshored varieties caused by fluctuations in the average
productivity of offshoring firms
); (2) changes in the price
of offshored varieties caused by fluctuations in the average
productivity of offshoring firms
 and in the magnitude of trade costs
and in the magnitude of trade costs
![]() ; (3)
changes in relative import prices triggered by fluctuations in the
average productivity of Southern exporters
; (3)
changes in relative import prices triggered by fluctuations in the
average productivity of Southern exporters
![]() relative to that of their Northern counterparts
relative to that of their Northern counterparts
![]() ; (4) changes
in the number of varieties produced by the Northern firms offshore
; (4) changes
in the number of varieties produced by the Northern firms offshore
![]() relative to the
number of imported varieties produced by Southern firms (
relative to the
number of imported varieties produced by Southern firms (
![]() ); and (5) changes
in the number of domestic varieties (
); and (5) changes
in the number of domestic varieties (
![]() ) relative to the
number of imported Southern varieties (
) relative to the
number of imported Southern varieties (
![]() ).
).
Impulse responses Offshoring dampens the appreciation of the real exchange rate
that follows an increase in aggregate productivity in the North.
The effect occurs through channels C1, C3 and C4 defined above.
Figure 8 describes the effect of each channel on the real exchange
rate in the baseline model of offshoring with financial autarky: It
shows the impulse responses of the real exchangte rate and related
variables to a transitory one-percent increase in aggregate
productivity in the North, when productivity follows the
autoregressive process
![]() with
persistence
with
persistence ![]() .
.
(C1) Changes in the price of non-traded varieties. In the
model with no offshoring (dashed lines), a productivity increase in
the North encourages firm entry and leads to the appreciation of
the terms of labor in the medium run (i.e. ![]() decreases). This causes the average price of non-traded varieties
in the North to increase relative to that in the South, and thus
leads to the appreciation of the CPI-based real exchange rate (i.e.
decreases). This causes the average price of non-traded varieties
in the North to increase relative to that in the South, and thus
leads to the appreciation of the CPI-based real exchange rate (i.e.
![]() decreases).
decreases).
Offshoring (thick solid line) dampens the appreciation of the
real exchange rate through this channel in two ways: (a) Offshoring
dampens the appreciation of the terms of labor (i.e. causes
![]() to decrease by less) relative to the
alternative models with no offshoring (dashed line) or to the model
with a fixed productivity cutoff (thin solid line), because the
relocation of production transfers upward pressure from the
domestic to the foreign wage. (b) Offshoring also reduces the
impact of the terms of labor on the real exchange rate, since it
reduces the share of non-traded varieties in total spending. The
effect is illustrated by the coefficient on
to decrease by less) relative to the
alternative models with no offshoring (dashed line) or to the model
with a fixed productivity cutoff (thin solid line), because the
relocation of production transfers upward pressure from the
domestic to the foreign wage. (b) Offshoring also reduces the
impact of the terms of labor on the real exchange rate, since it
reduces the share of non-traded varieties in total spending. The
effect is illustrated by the coefficient on
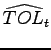 in channel C1 (
in channel C1 (
![]() ), which
decreases with the share of offshored varieties in total spending (
), which
decreases with the share of offshored varieties in total spending (
![]() ).
).
(C2) Changes in the price of offshored varieties. On
impact, the increase in the Southern wage causes the number of
offshoring firms to drop and their average productivity to
increase. However, offshoring becomes an increasingly profitable
option in the medium run due to the gradual appreciation of the
terms of labor. As a result, the number of offshoring firms rises,
their average productivity
![]() declines, and their
average price increases over time. Thus, offshoring contributes to
the appreciation of the real exchange rate in the medium run
through this channel.38
declines, and their
average price increases over time. Thus, offshoring contributes to
the appreciation of the real exchange rate in the medium run
through this channel.38
(C3) Changes in relative import prices. In the absence of
offshoring, the appreciation of the terms of labor reduces the
export profitability of the Northern firms relative to that of
their Southern counterparts. As a result, the average productivity
of the surviving Northern exporters
![]() increases relative to
that of Southern exporters
increases relative to
that of Southern exporters
![]() ,
and their average price declines. This causes an increase in the
average price of imports in the North relative to the South, which
leads to the appreciation of the real exchange rate.
,
and their average price declines. This causes an increase in the
average price of imports in the North relative to the South, which
leads to the appreciation of the real exchange rate.
Offshoring reverses this effect. As the relocation of production
places upward pressure on the Southern wage, offshoring harms the
export competitiveness of Southern firms, and causes the average
productivity of the surviving Southern exporters
![]() to
increase relative to that of their Northern counterparts
to
increase relative to that of their Northern counterparts
![]() . In contrast to the
model with exports only, offshoring causes a decline in the average
price of imports in the North relative to the South, and therefore
dampens the appreciation of the real exchange rate.
. In contrast to the
model with exports only, offshoring causes a decline in the average
price of imports in the North relative to the South, and therefore
dampens the appreciation of the real exchange rate.
(C4) Expenditure switching from imports towards offshored
varieties. As offshoring reduces the competitiveness of
Southern exports, consumers in the North switch their expenditure
away from the less competitive Southern varieties (
![]() decreases) and towards the
relatively cheaper varieties produced offshore (
decreases) and towards the
relatively cheaper varieties produced offshore (
![]() increases). The result dampens
the appreciation of the real exchange rate.
increases). The result dampens
the appreciation of the real exchange rate.
(C5) Expenditure switching from imports towards domestic
varieties. Firm entry in the North causes the number of
domestic varieties (
![]() ) to increase relative to that
of imported foreign varieties (
) to increase relative to that
of imported foreign varieties (
![]() ). Thus, consumers switch
their expenditure away from imported varieties and towards the
varieties produced domestically by the relatively less productive
firms, which are available at relatively higher prices. This
channel works towards the appreciation of the real exchange
rate.
). Thus, consumers switch
their expenditure away from imported varieties and towards the
varieties produced domestically by the relatively less productive
firms, which are available at relatively higher prices. This
channel works towards the appreciation of the real exchange
rate.
Figure 8: Impulse responses to one-percent shock to aggregate productivity in the North
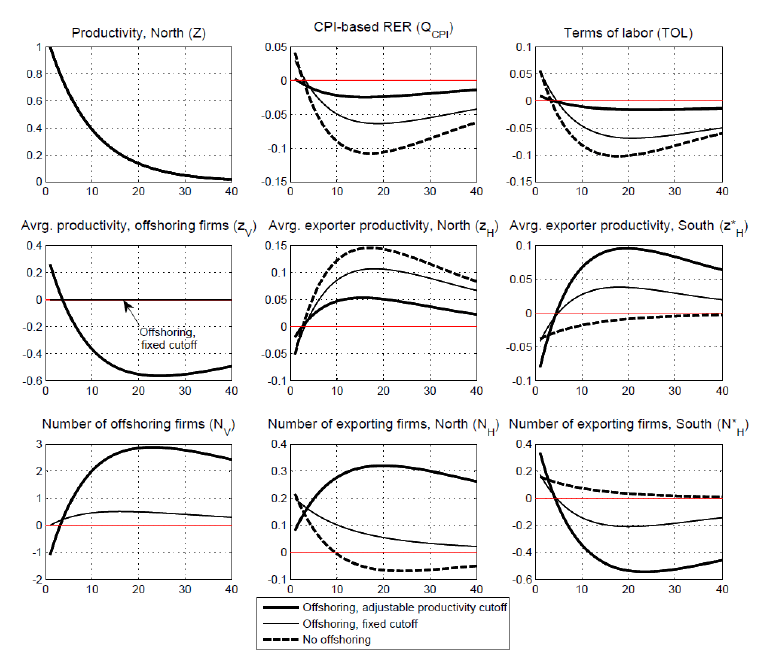
6 Conclusion
I study the effect of offshoring on the cross-country transmission of business cycles, while focusing on its extensive and intensive margins as separate transmission mechanisms. The paper considers a model of offshoring with heterogeneous firms that is consistent with the empirical patterns of offshoring from U.S. manufacturing to Mexico's maquiladora sector. First, following an aggregate productivity increase in the country of origin (North), the value added per offshoring firm jumps on impact and then returns to its initial steady state. However, domestic firm entry causes a gradual increase in the relative cost of effective labor (i.e. the wage adjusted by aggregate productivity), which in turn generates a gradual increase in the number of offshoring firms (the extensive margin), as in the data. Second, offshoring enhances the cross-country co-movement of output relative to the model with endogenous exports. The result is consistent with the empirical regularity documented in Burstein, Kurz, and Tesar (2009) that country pairs with larger shares of offshoring-related trade in bilateral trade also exhibit larger correlations of manufacturing output. Third, offshoring reduces the appreciation of the real exchange rate that follows an aggregate productivity improvement in the parent country, and thus dampens the Harrod-Balassa-Samuelson effect that occurs in the framework with firm entry and endogenously traded varieties.
There are a number of possible extensions to the model considered in this paper. First, the framework is useful to analyze the impact of offshore production on employment in the parent and the host countries. Second, a possible extension with rich policy implications would involve the study of interactions between offshore production and labor migration in a unified framework, in which both offshoring and labor mobility are driven by fluctuations in the relative wage across countries. Third, while this paper studies the fluctuations of offshoring over the business cycle, further research should address the long-run developments in offshore production and its implications for U.S. manufacturing.
References
Alessandria G. and Horag Choi. 2007. "Do Sunk Costs of Exporting Matter for Net Export Dynamics?" Quarterly Journal of Economics, 122(1): 289-336.
Anderson, James and Erik van Wincoop. 2004. "Trade Costs." Journal of Economic Literature, 42(3): 691-751.
Antras, Pol and E. Helpman. 2004. "Global Sourcing." Journal of Political Economy, 112 (3): 552-580.
Backus, D. K., P.J. Kehoe and F.E. Kydland. 1992. "International Real Business Cycles." Journal of Political Economy, University of Chicago Press, 100(4): 745-75 (August).
Bardhan, Ashok Deo and Dwight Jaffee. 2004. "On Intra-Firm Trade and Multinationals: Foreign Outsourcing and Offshoring in Manufacturing." University of California, Berkeley, mimeo, April 7, 2004.
Baldwin, Richard and James Harrigan. 2007. "Zeros, Quality and Space: Trade Theory and Trade Evidence." NBER Working Paper 13214.
BEA (Bureau of Economic Analysis). 2007. "International Economic Accounts, Operations of Multinational Companies."
Bergin, Paul R., Robert C. Feenstra, and Gordon H. Hanson. 2008. "Outsourcing and Volatility: Evidence from Mexico's Maquiladora Industry." American Economic Review, forthcoming.
Bergin, Paul R., Robert C. Feenstra, and Gordon H. Hanson. 2007. "Outsourcing and Volatility." NBER Working Paper No. W13144.
Bernard, Andrew B., Jonathan Eaton, J. Bradford Jensen, and Samuel Kortum. 2003. "Plants and Productivity in International Trade." American Economic Review, 93(4): 1268-1290.
Bernard, Andrew B., J. Bradford Jensen, Stephen Redding, and Peter K. Schott. 2007. "Firms in International Trade." Centre for Economic Performance Discussion Papers 0795.
Besedes, Tibor and Thomas J. Prusa. 2006. "Product Differentiation and Duration of US Import Trade." Journal of International Economics, 70(2): 339-358.
Broda, Christian and David E. Weinstein. 2006. "Globalization and the Gains from Variety." Quarterly Journal of Economics, 121(2): 541-585.
Burstein, A., C. Kurz and L. Tesar. 2009. "International Trade, Production Sharing and the Transmission of Business Cycles." Journal of Monetary Economics, 55(4): 775-795.
Contessi, Silvio. 2006. "What Happens When Wall-Mart Comes to Your Country? On the Dynamic Macroeconomic Effects of Multinational Firms' Entry." Johns Hopkins University, mimeo.
Corsetti, G., O. Martin, and P. Pesenti. 2007. "Productivity, Terms of Trade and the Home Market Effect." Journal of International Economics, 73(1): 99-127.
Ghironi F. and M.J. Melitz. 2005. "International Trade and Macroeconomic Dynamics with Heterogeneous Firms." Quarterly Journal of Economics, 120(3): 865-915.
Gruben, William C. 2001. "Was NAFTA behind Mexico's High Maquiladora Growth?" Economic and Financial Review, Third Quarter 2001, Federal Reserve Bank of Dallas.
Hanson, Gordon H., Raymond J. Mataloni and Matthew J. Slaughter. 2005. "Vertical Production Networks in Multinational Firms." Review of Economics and Statistics, 87(4): 664-678.
Hausman, Angela and Diana L. Haytko. 2003. "Cross-Border Supply Chain Relationships: Interpretive Research of Maquiladora Realized Strategies." Journal of Business and Industrial Marketing, 18(6/7): 545-563.
Helpman, E. 2006. "Trade, FDI, and the Organization of Firms." Journal of Economic Literature, 44(3): 589-630.
Helpman, E., M. Melitz, and S. Yeaple. 2004. "Export versus FDI with Heterogeneous Firms." American Economic Review, 94(1): 300-316.
Helpman, E. 1984. "A Simple Theory of International Trade with Multinational Corporations." Journal of Political Economy, 92(3): 451-471.
Hummels, David and Peter J. Klenow. 2005. "The Variety and Quality of a Nation's Exports," American Economic Review, 95(3): 704-723.
INEGI, (El Instituto Nacional de Estadística y Geografía, Mexico). 2008. Banco de Información Económica, http://dgcnesyp.inegi.org.mx/cgi-win/bdieintsi.exe
Kurz, Christopher J. 2006. "Outstanding Outsourcers: A Firm- and Plant-Level Analysis of Production Sharing." FEDs Working Paper No. 2006-04.
Mandelman, Federico S. and Andrei Zlate. 2008. "Immigration and the Macroeconomy." Working Paper 2008-25, Federal Reserve Bank of Atlanta.
Marin, D. 2006. "A New International Division of Labor in Europe: Outsourcing and Offshoring to Eastern Europe." Journal of the European Economic Association, 4(2-3): 612-622.
Mejean, Isabelle. 2006. "Can Firms' Location Decisions Counteract the Balassa-Samuelson Effect?" CEPII Working Paper No. 2006-12.
Meyer, Thomas. 2006. "Offshoring to New Shores: Nearshoring to Central and Eastern Europe." In Digital Economy and Structural Change, Antje Stobbe (editor), Deutsche Bank Research, August 14, 2006.
Melitz, Marc. 2003. "The Impact of Trade on Intra-Industry Reallocations and Aggregate Industry Productivity." Econometrica, 71(6): 1695-1725.
World Bank. 2007. "Doing Business" (The Cost of Starting a Business), Washington, DC.
Zlate, Andrei. 2009. "Offshore Production, Labor Migration, and the Macroeconomy." Doctoral Dissertation, Department of Economics, Boston College.
Appendix
A.1 Offshoring with Financial Autarky
Table A.1: Model Summary
| Euler equation, bonds |
|
|---|---|
| Euler equation, stocks |
|
| Free entry |
|
| Rule of motion, total number of firms |
|
| Aggregate accounting |
|
| Consumption price index |
|
| Total profits |
|
| Total number of firms (North) | |
| Offshoring profits link (North) | 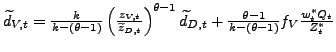 |
| Export profits link |
|
| Avrg. prod. of domestic producers (North) | ![$ \widetilde{z}_{D,t}=\nu z_{\min}z_{V,t}\left[ \frac{z_{V,t}^{k-(\theta -1)}-z_{\min}^{k-(\theta-1)}}{z_{V,t}^{k}-z_{\min}^{k}}\right] ^{\frac {1}{\theta-1}}$](img19a1.gif) |
| Avrg. prod. of offshore producers (North) | 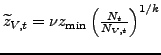 |
| Avrg. productivity of exports |
|
| Balanced Trade |
|
![]()
A.2 Offshoring with International Bond Trading
I introduce international bond trading in the model with offshoring. International asset markets are incomplete, as the representative household in each economy holds risk-free, country-specific bonds from both the North and the South. Each type of bonds provides a real return denominated in units of the issuing country's consumption basket. Quadratic costs of adjustment for bond holdings ensure stationarity for the net foreign assets in the presence of temporary shocks.
The representative household in the North maximizes inter-temporal utility subject to:
| (26) | ||
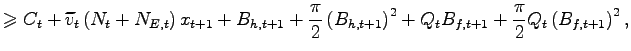
|
where ![]() and
and
![]() are the rates of return of the
North and South-specific bonds;
are the rates of return of the
North and South-specific bonds;
![]() and
and
![]() denote the
principal and interest income from each type of bonds;
denote the
principal and interest income from each type of bonds;
![]() and
and
![]() are the
adjustment costs for each type of bond holdings;
are the
adjustment costs for each type of bond holdings; ![]() is the fee rebate. Setting
is the fee rebate. Setting ![]() , I
add the two Euler equations for bonds to the baseline model:
, I
add the two Euler equations for bonds to the baseline model:
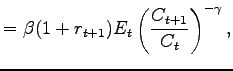
|
(27) | |
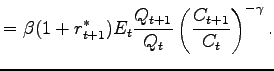
|
(28) |
For the Southern representative household, the Euler equations for bonds are:
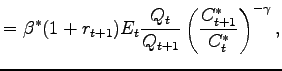
|
(29) | |
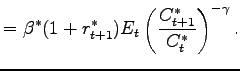
|
(30) |
The market clearing conditions for bonds are:
| (31) | ||
| (32) |
Thus, financial integration through trade in bonds adds four new
variables (
![]()
![]() ) and six new equations
(27, 28, 29, 30, 31 and 32) while removing
the original two Euler equations from the baseline model with
financial autarky. Also, the new expressions for aggregate
accounting in the North and the South are:
) and six new equations
(27, 28, 29, 30, 31 and 32) while removing
the original two Euler equations from the baseline model with
financial autarky. Also, the new expressions for aggregate
accounting in the North and the South are:
| (33) | ||
| (34) |
Finally, I replace the balanced current account condition from financial autarky with the expression for the balance of international payments:
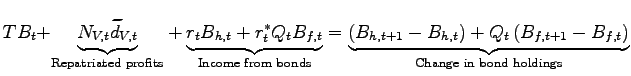
|
(35) |
which shows that the current account balance (trade balance plus repatriated profits plus investment income) must equal the negative of the financial account balance (the change in bond holdings).
Average Firm-Specific Productivity Levels
Firms producing offshore I obtain the average productivity of the Northern firms that produce offshore by integrating over the upper range of the support interval, above the offshoring productivity cutoff:
![$\displaystyle =\left[ \frac{1}{1-G(z_{V,t})}\overset{\infty }{\underset{z_{V,t}}{\int}}z^{\theta-1}g(z)dz\right] ^{\frac{1}{\theta-1} }=\left[ \left( \frac{z_{V,t}}{z_{\min}}\right) ^{k}\overset{\infty }{\underset{z_{V,t}}{\int}}z^{\theta-1}\frac{kz_{\min}^{k}}{z^{k+1}}dz\right] ^{\frac{1}{\theta-1}}=$](img414.gif)
|
||
![$\displaystyle =\left[ \left( \frac{z_{V,t}}{z_{\min}}\right) ^{k}\frac{kz_{\min}^{k} }{k-(\theta-1)}z_{V,t}^{\theta-1-k}\right] ^{\frac{1}{\theta-1}}=$](img415.gif)
|
(36) | |
| (37) |
where
![$ \nu\equiv\left[ \frac{k}{k-(\theta-1)}\right] ^{\frac{1}{\theta-1}}.$](img417.gif)
Firms producing domestically The average productivity of the Northern firms that produce domestically is:
![$\displaystyle =\left[ \frac{1}{G(z_{V,t})}\overset{z_{V,t} }{\underset{z_{\min}}{\int}}z^{\theta-1}g(z)dz\right] ^{\frac{1}{\theta-1} }=\left[ \frac{z_{V,t}^{k}}{z_{V,t}^{k}-z_{\min}^{k}}\overset{z_{V,t} }{\underset{z_{\min}}{\int}}z^{\theta-1}\frac{kz_{\min}^{k}}{z^{k+1} }dz\right] ^{\frac{1}{\theta-1}}=$](img419.gif)
|
||
![$\displaystyle =\left[ \frac{z_{V,t}^{k}}{z_{V,t}^{k}-z_{\min}^{k}}\frac{kz_{\min}^{k} }{\left( \theta-k-1\right) }\left( z_{V,t}^{\theta-1-k}-z_{\min} ^{\theta-1-k}\right) \right] ^{\frac{1}{\theta-1}}=$](img420.gif)
|
||
![$\displaystyle =\nu\left[ \frac{\left( z_{\min}z_{V,t}\right) ^{k}}{z_{\min} ^{k}-z_{V,t}^{k}}\left( \frac{1}{z_{V,t}^{k-\left( \theta-1\right) }} -\frac{1}{z_{\min}^{k-\left( \theta-1\right) }}\right) \right] ^{\frac {1}{\theta-1}}=$](img421.gif)
|
(38) | |
![$\displaystyle =\nu z_{\min}z_{V,t}\left[ \frac{z_{V,t}^{k-\left( \theta-1\right) }-z_{\min}^{k-\left( \theta-1\right) }}{z_{V,t}^{k}-z_{\min}^{k}}\right] ^{\frac{1}{\theta-1}}.$](img422.gif)
|
(39) |
A.4 Average Profits from Domestic and Offshore Production
The average profit of the Northern firms producing domestically is:
![$\displaystyle =d_{D,t}(\widetilde{z}_{D,t})=\frac{1}{\theta}\left[ \frac{\theta}{\theta-1}\frac{w_{t}}{Z_{t}\widetilde{z}_{D,t}}\right] ^{1-\theta}C_{t}=\frac{1}{\theta}\left[ \frac{\theta}{\theta-1}\frac{w_{t} }{Z_{t}}\right] ^{1-\theta}C_{t}\widetilde{z}_{D,t}^{\theta-1}=$](img424.gif)
|
||
![$\displaystyle =\frac{1}{\theta}\left[ \frac{\theta}{\theta-1}\frac{w_{t}}{Z_{t}}\right] ^{1-\theta}C_{t}\left( \nu z_{\min}z_{V,t}\right) ^{\theta-1}\left[ \frac{z_{V,t}^{k-\left( \theta-1\right) }-z_{\min}^{k-\left( \theta -1\right) }}{z_{V,t}^{k}-z_{\min}^{k}}\right] =$](img425.gif)
|
||
![$\displaystyle =\underset{d_{D,t}(z_{V,t})}{\underbrace{\frac{1}{\theta}\left[ \frac{\theta}{\theta-1}\frac{w_{t}}{Z_{t}z_{V,t}}\right] ^{1-\theta}C_{t}} }\left( \nu z_{\min}\right) ^{\theta-1}\left[ \frac{z_{V,t}^{k-\left( \theta-1\right) }-z_{\min}^{k-\left( \theta-1\right) }}{z_{V,t}^{k} -z_{\min}^{k}}\right] =$](img426.gif)
|
||
![$\displaystyle =d_{D,t}(z_{V,t})\left( \nu z_{\min}\right) ^{\theta-1}\left[ \frac{z_{V,t}^{k-\left( \theta-1\right) }-z_{\min}^{k-\left( \theta -1\right) }}{z_{V,t}^{k}-z_{\min}^{k}}\right] .$](img427.gif)
|
(40) |
The average profit of the Northern firms producing offshore is:
![$\displaystyle =d_{V,t}(\widetilde{z}_{V,t})=\frac{1}{\theta}\left[ \tau\frac{\theta}{\theta-1}\frac{w_{t}^{\ast}Q_{t}}{Z_{t}^{\ast}\widetilde {z}_{V,t}}\right] ^{1-\theta}C_{t}-f_{V}\frac{w_{t}^{\ast}Q_{t}}{Z_{t}^{\ast }}=$](img429.gif)
|
||
![$\displaystyle =\frac{1}{\theta}\left[ \tau\frac{\theta}{\theta-1}\frac{w_{t}^{\ast} Q_{t}}{Z_{t}^{\ast}}\right] ^{1-\theta}C_{t}\widetilde{z}_{V,t}^{\theta -1}-f_{V}\frac{w_{t}^{\ast}Q_{t}}{Z_{t}^{\ast}}=$](img430.gif)
|
||
![$\displaystyle =\underset{d_{V,t}(z_{V,t})}{\underbrace{\left\{ \frac{1}{\theta}\left[ \tau\frac{\theta}{\theta-1}\frac{w_{t}^{\ast}Q_{t}}{Z_{t}^{\ast}z_{V,t} }\right] ^{1-\theta}C_{t}-f_{V}\frac{w_{t}^{\ast}Q_{t}}{Z_{t}^{\ast} }\right\} }}\nu^{\theta-1}+$](img431.gif)
|
||
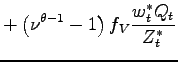
|
||
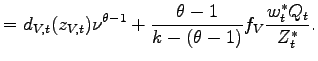
|
(41) |
The Northern firm with productivity equal to the cutoff
![]() is indifferent between producing
domestically or offshore. I use the equality of profits at the
productivity cutoff,
is indifferent between producing
domestically or offshore. I use the equality of profits at the
productivity cutoff,
![]() , and
equations (40) and
(41) to write the
link between the two average profits as:
, and
equations (40) and
(41) to write the
link between the two average profits as:
![$\displaystyle =\underset{=d_{D,t}(z_{V,t})}{\underbrace{\left( \frac{1}{\nu z_{\min}}\right) ^{\theta-1}\left[ \frac{z_{V,t}^{k-\left( \theta-1\right) }-z_{\min}^{k-\left( \theta-1\right) }}{z_{V,t}^{k} -z_{\min}^{k}}\right] ^{-1}\widetilde{d}_{D,t}}}\nu^{\theta-1}+\frac {\theta-1}{k-(\theta-1)}f_{V}\frac{w_{t}^{\ast}Q_{t}}{Z_{t}^{\ast} }=$](img437.gif)
|
||
![$\displaystyle =z_{\min}^{1-\theta}\left[ \frac{z_{V,t}^{k-\left( \theta-1\right) }-z_{\min}^{k-\left( \theta-1\right) }}{z_{V,t}^{k}-z_{\min}^{k}}\right] ^{-1}\widetilde{d}_{D,t}+\frac{\theta-1}{k-(\theta-1)}f_{V}\frac{w_{t}^{\ast }Q_{t}}{Z_{t}^{\ast}}=$](img438.gif)
|
||
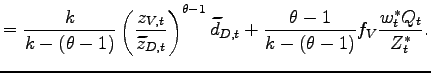
|
(42) |
A.5 The Real Exchange Rate
The CPI-based real exchange rate is
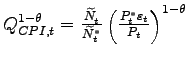 , in which
, in which
![]() and
and
![]() are the total number of varieties available to consumers in the
North and the South. For the price indexes
are the total number of varieties available to consumers in the
North and the South. For the price indexes ![]() and
and
![]() , I use the average price
formulas implied by the broader framework of offshoring described
in footnotes 11 and 16 to obtain:
, I use the average price
formulas implied by the broader framework of offshoring described
in footnotes 11 and 16 to obtain:
![$\displaystyle =\frac{\widetilde{N}_{t}^{{}}}{\widetilde{N} _{t}^{\ast}}\frac{N_{D,t}^{\ast}\left( \widetilde{\rho}_{D,t}^{\ast} P_{t}^{\ast}\varepsilon_{t}\right) ^{1-\theta}+N_{H,t}\left( \widetilde {\rho}_{H,t}P_{t}^{\ast}\varepsilon_{t}\right) ^{1-\theta}}{N_{D,t}\left( \widetilde{\rho}_{D,t}P_{t}\right) ^{1-\theta}+N_{V,t}\left( \widetilde {\rho}_{V,t}P_{t}\right) ^{1-\theta}+N_{H,t}^{\ast}\left[ \widetilde{\rho }_{H,t}^{\ast}P_{t}\right] ^{1-\theta}}=$](img446.gif)
|
||
![$\displaystyle =\frac{\widetilde{N}_{t}^{{}}}{\widetilde{N}_{t}^{\ast}}\frac{N_{D,t} ^{\ast}\left( \frac{w_{t}^{\ast}P_{t}^{\ast}\varepsilon_{t}}{Z_{t}^{\ast }\widetilde{z}_{D,t}^{\ast}}\right) ^{1-\theta}+N_{H,t}\left[ \left( \frac{\tau_{t}^{\ast}}{TOL_{t}}\right) ^{\eta}\frac{w_{t}^{\ast}P_{t}^{\ast }\varepsilon_{t}}{Z_{t}^{\ast}\widetilde{z}_{H,t}}\right] ^{1-\theta} }{N_{D,t}\left( \frac{w_{_{t}}P_{t}}{Z_{t}\widetilde{z}_{D,t}}\right) ^{1-\theta}+N_{V,t}\left[ \frac{\left( \tau_{t}TOL_{t}\right) ^{1-\alpha }w_{_{t}}P_{t}}{Z_{t}\widetilde{z}_{V,t}}\right] ^{1-\theta}+N_{H,t}^{\ast }\left[ \frac{\left( \tau_{t}TOL_{t}\right) ^{\eta^{\ast}}w_{_{t}}P_{t} }{Z_{t}\widetilde{z}_{H,t}^{\ast}}\right] ^{1-\theta}}=$](img447.gif)
|
||
![$\displaystyle =\frac{\frac{N_{D,t}^{\ast}}{\widetilde{N}_{t}^{\ast}}\left[ \frac {TOL_{t}}{\widetilde{z}_{D,t}^{\ast}}\right] ^{1-\theta}+\frac{N_{H,t} }{\widetilde{N}_{t}^{\ast}}\left[ \frac{\left( \tau_{t}^{\ast}\right) ^{\eta}TOL_{t}^{1-\eta}}{\widetilde{z}_{H,t}}\right] ^{1-\theta}} {\frac{N_{D,t}}{\widetilde{N}_{t}^{{}}}\left( \frac{1}{\widetilde{z}_{D,t} }\right) ^{1-\theta}+\frac{N_{V,t}}{\widetilde{N}_{t}^{{}}}\left[ \frac{\left( \tau_{t}TOL_{t}\right) ^{1-\alpha}}{\widetilde{z}_{V,t} }\right] ^{1-\theta}+\frac{N_{H,t}^{\ast}}{\widetilde{N}_{t}^{{}}}\left[ \frac{\left( \tau_{t}TOL_{t}\right) ^{\eta^{\ast}}}{\widetilde{z} _{H,t}^{\ast}}\right] ^{1-\theta}}.$](img448.gif)
|
(43) |
In what follows I use the notation
![$ s_{D}\equiv N_{D}\left( \frac {w}{Z\widetilde{z}_{D}}\right) ^{1-\theta}+N_{V}\left[ \frac{w} {Z\widetilde{z}_{V}}\left( \tau TOL\right) ^{1-\alpha}\right] ^{1-\theta}$](img449.gif) to denote the steady-state share of spending in the North on
varieties produced by the Northern firms both domestically and
offshore. Expression
to denote the steady-state share of spending in the North on
varieties produced by the Northern firms both domestically and
offshore. Expression
![$ s_{V}^{{}}\equiv N_{V}\left[ \frac{w}{Z\widetilde{z}_{V}}\left( \tau TOL\right) ^{1-\alpha}\right] ^{1-\theta}$](img450.gif) denotes the steady-state share of spending in the North on goods
produced by the Northern firms offshore only. (Note that
denotes the steady-state share of spending in the North on goods
produced by the Northern firms offshore only. (Note that
![]() .) Expression
.) Expression
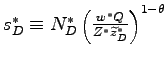 denotes the steady-state share of spending in the South on goods
produced by the Southern firms domestically. The average
productivity of the Southern firms producing domestically
denotes the steady-state share of spending in the South on goods
produced by the Southern firms domestically. The average
productivity of the Southern firms producing domestically
![]() is constant over
time. Using all of the above, I log-linearize the CPI-based real
exchange rate:
is constant over
time. Using all of the above, I log-linearize the CPI-based real
exchange rate:
![$\displaystyle =s_{D}^{\ast}\left[ \widehat{N}_{D,t} ^{\ast}-\widehat{\widetilde{N}}_{t}^{\ast}+\left( 1-\theta\right) \widehat{TOL}_{t}\right] +$](img455.gif)
|
||
![$\displaystyle +\left( 1-s_{D}^{\ast}\right) \left[ \widehat{N}_{H,t}^{{}} -\widehat{\widetilde{N}}_{t}^{\ast}+\left( 1-\theta\right) \left( \eta\widehat{\tau}_{t}^{\ast}+\left( 1-\eta\right) \widehat{TOL} _{t}-\widehat{\widetilde{z}}_{H,t}\right) \right] -$](img456.gif)
|
||
![$\displaystyle -\left( s_{D}^{{}}-s_{V}^{{}}\right) \left[ \widehat{N}_{D,t}^{{} }-\widehat{\widetilde{N}}_{t}-\left( 1-\theta\right) \widehat{\widetilde{z} }_{D,t}\right] -$](img457.gif)
|
||
![$\displaystyle -s_{V}^{{}}\left[ \widehat{N}_{V,t}^{{}}-\widehat{\widetilde{N}} _{t}+\left( 1-\theta\right) \left( \left( 1-\alpha\right) (\widehat{\tau }_{t}+\widehat{TOL}_{t})-\widehat{\widetilde{z}}_{V,t}\right) \right] -$](img458.gif)
|
||
![$\displaystyle -(1-s_{D}^{{}})\left[ \widehat{N}_{H,t}^{\ast}-\widehat{\widetilde{N}} _{t}+\left( 1-\theta\right) \left( \eta^{\ast}(\widehat{\tau}_{t} +\widehat{TOL}_{t})-\widehat{\widetilde{z}}_{H,t}^{\ast}\right) \right] .$](img459.gif)
|
(44) |
I set
![]() so that my model of
offshoring nests the framework with endogenous exports in Ghironi
and Melitz (2005): In addition to the firms that produce
domestically or offshore for their home market, a subset of firms
from each economy also serve the foreign markets through exports.
The log-linearized expression for the CPI-based real exchange rate
becomes:
so that my model of
offshoring nests the framework with endogenous exports in Ghironi
and Melitz (2005): In addition to the firms that produce
domestically or offshore for their home market, a subset of firms
from each economy also serve the foreign markets through exports.
The log-linearized expression for the CPI-based real exchange rate
becomes:
![$\displaystyle =\left[ s_{D}^{{}}-(1-\alpha)s_{V}^{{}}+s_{D}^{\ast }-1\right] \widehat{TOL}_{t}+$](img462.gif)
|
||
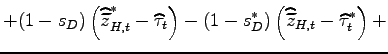
|
||
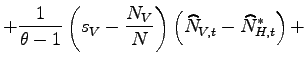
|
||
![$\displaystyle +\frac{1}{\theta-1}\left[ \left( \frac{N_{D}^{\ast}}{N^{\ast}} -s_{D}^{\ast}\right) \left( \widehat{N}_{D,t}^{\ast}-\widehat{N}_{H,t}^{{} }\right) -\left( \frac{N_{D}}{N}-\left( s_{D}^{{}}-s_{V}^{{}}\right) \right) \left( \widehat{N}_{D,t}^{{}}-\widehat{N}_{H,t}^{\ast}\right) \right] .$](img466.gif)
|
(45) |
A.6 Asymmetric Steady State
In this section I provide the steady state solution for the
model of offshoring in the presence of a cross-country asymmetry in
the cost of effective labor (i.e. the terms of labor ![]() ). To this end, I use the broad framework described
in footnotes 11 and 16 of the paper that nests both the baseline
model of offshoring (for
). To this end, I use the broad framework described
in footnotes 11 and 16 of the paper that nests both the baseline
model of offshoring (for
![]() ) and the model with exports
only in Ghironi and Melitz (2005) (for
) and the model with exports
only in Ghironi and Melitz (2005) (for
![]() ).
).
I obtain a numerical solution for the unique steady state using
a non-linear system of 12 equations in 12 unknowns. The equations
are described by 46-57 below. The
unknowns are the steady state values of ![]() (the
offshoring productivity cutoff in the North),
(the
offshoring productivity cutoff in the North), ![]() (the exporting productivity cutoff in the North),
(the exporting productivity cutoff in the North),
![]() (the terms of labor),
(the terms of labor),
![]() (the real consumption
ratio in units of the same consumption basket),
(the real consumption
ratio in units of the same consumption basket), ![]() (the real exchange rate),
(the real exchange rate),
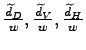 (the real profits from domestic and offshore production for the
domestic market, as well as the profit from production for the
export market, each divided by the real wage in the
North)
(the real profits from domestic and offshore production for the
domestic market, as well as the profit from production for the
export market, each divided by the real wage in the
North)![]()
![]() (the exporting productivity
cutoff in the South),
(the exporting productivity
cutoff in the South),
![]() (the average price of
Northern exports),
(the average price of
Northern exports),
![]() (the average
price of Southern exports), and
(the average
price of Southern exports), and
![]() (the ratio of the
number of firms in the North and the South). Subsequently, I use
the numerical solutions for these 12 variables to compute the
steady state values for the remaining variables.
(the ratio of the
number of firms in the North and the South). Subsequently, I use
the numerical solutions for these 12 variables to compute the
steady state values for the remaining variables.
The following price and profit formulas (in which the aggregate
productivity is
![]() ) are useful in computing the
steady state solution:
) are useful in computing the
steady state solution:
Table A.2. - Panel A: Average Prices
| 1. Domestic production, North | |
|---|---|
| 2. Domestic production, South | |
| 3. Offshore production ( |
|
| 4. Exports ( |
|
| 5. Exports ( |
Table A.2. - Panel B: Average Profits
| 1. Domestic production, North | |
|---|---|
| 2. Domestic production, South | |
| 3. Offshore production ( |
|
| 4. Exports ( |
|
| 5. Exports ( |
Introducing
![]() ,
,
![]() , and
, and
![]() in the expression for the total
profits in the North (see Table A.1), the first equation of the
system is:
in the expression for the total
profits in the North (see Table A.1), the first equation of the
system is:
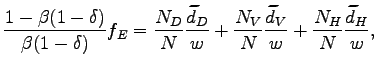
|
(46) |
where
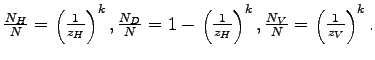
Next, the profit formulas for the Northern economy (see Table A.3) imply:
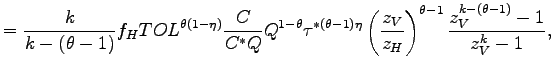
|
(47) | |
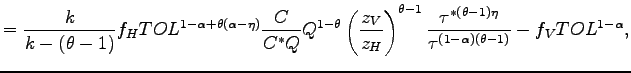
|
(48) | |
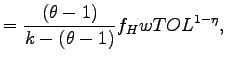
|
(49) | |
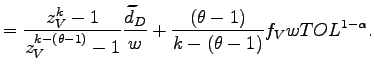
|
(50) |
Using the expression for the total profits in the South (see Table A.1), it follows that:
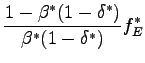
|
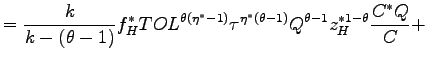
|
(51) |
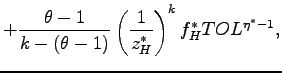
|
The consumption ratio in units of the same consumption basket is:
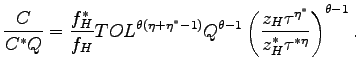
|
(52) |
From the balanced current account condition, I obtain:
![$\displaystyle \left( 1-\alpha\right) z_{V}^{-k}TOL^{-\alpha}\left[ \frac{\left( \theta-1\right) k}{k-(\theta-1)}f_{H}^{\ast}\left( \frac{z_{V}}{z_{H}^{\ast }}\right) ^{\theta-1}\frac{TOL^{\theta\left( \alpha+\eta^{\ast}-1\right) } }{\tau^{\left( \theta-1\right) \left( 1-\alpha-\eta^{\ast}\right) }} +f_{V}\right]$](img500.gif)
|
(53) | |
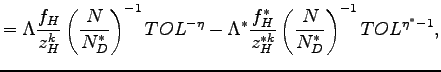
|
where
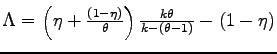 and
and
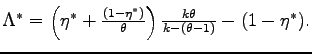
The expression for the real exchange rate in steady state is:
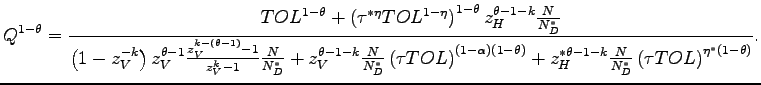 |
(54) |
The remaining equations are:
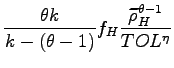
|
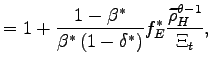
|
(55) |
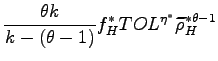
|
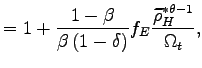
|
(56) |
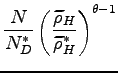
|
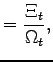 |
(57) |
with:
![$\displaystyle =\left[ \frac{1}{z_{H}}\left( \frac{\tau^{\ast}}{TOL}\right) ^{\eta}\right] ^{\theta-1}+z_{H}^{-k}\frac{N}{N_{D}^{\ast}},$](img512.gif)
|
||
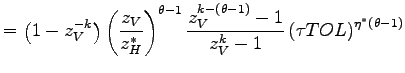
|
||
![$\displaystyle +z_{V}^{-k}\left[ \frac{z_{V}}{z_{H}^{\ast}}\left( \tau TOL\right) ^{\eta^{\ast}+\alpha-1}\right] ^{\theta-1}+z_{H}^{\ast-k}\left( \frac {N}{N_{D}^{\ast}}\right) ^{-1}.$](img515.gif)
|
A.7 Empirical Impulse Responses of Offshoring to Mexico
I estimate the empirical impulse responses of offshoring to Mexico's maquiladora sector (total value added, number of plants, and the value added per plant) to permanent technology shocks in U.S. manufacturing. To this end, I use a structural VAR model with five variables: (i) labor productivity in U.S. manufacturing, (ii) labor productivity in Mexico's maquiladora, (iii) value added per plant and (iv) the number of plants in Mexico's maquiladora, as well as (v) hours worked in U.S. manufacturing. The estimation details are discussed in Zlate (2009). With the exception of the intensive margin, all variables have a unit root and therefore enter the VAR model in first differences. My identification strategy assumes that long-run labor productivity in U.S. manufacturing responds exclusively to U.S. technology shocks. Conversely, long-run labor productivity in Mexico's maquiladora sector - which uses production machinery received on loan from U.S. firms - responds to both the U.S. and Mexico-specific permanent technology shocks.
In Figure A.1, I plot the estimated impulse responses of Mexico's maquiladora variables, together with the +/- 2 standard error confidence intervals. Following a positive, one standard deviation, permanent technology shock to U.S. manufacturing, the number of maquiladora plants (the extensive margin) does not react on impact, but increases gradually over time. The value added per maquiladora plant (the intensive margin) exhibits an immediate jump, followed by an additional increase until it reaches a peak two quarters after the shock. The intensive margin then declines below its initial level, but returns to it over time.
The predictions of the theoretical model of offshoring (illustrated in Figure 4) are consistent with the empirical impulse responses. In the model, following a positive transitory shock to aggregate productivity in the North, the extensive margin of offshoring increases gradually over time, despite the initial drop. The intensive margin jumps on impact, then declines below its initial steady state and returns to it in the medium run, as in the data.
Figure A.1: Empirical impulse responses of offshore production to a permanent U.S. technology shock.
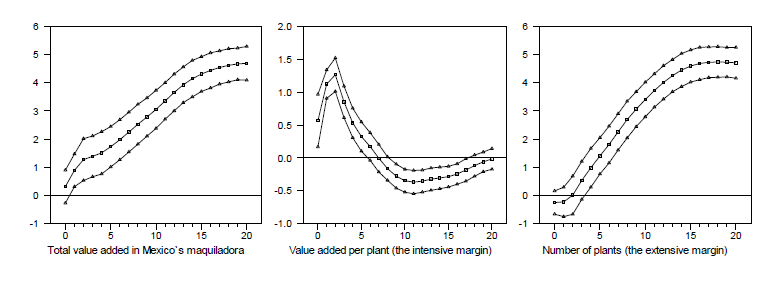
Footnotes
1. I am grateful to Fabio Ghironi, James Anderson and Susanto Basu for their help during my dissertation work at Boston College. Special thanks to George Alessandria, Richard Arnott, David Arseneau, Marianne Baxter, Paul Bergin, Michele Cavallo, Bora Durdu, Matteo Iacoviello, Peter Ireland, Federico Mandelman, Joel Rodrigue, Vitaliy Strohush, Linda Tesar and Christina Wang for insightful discussions on this paper. I would like to recognize participants at the 2010 Winter Meeting of the Econometric Society, the 2009 SCIEA Meeting of the Federal Reserve, the IEFS/ASSA 2009 Meeting, the 4th Dynare Conference at the Boston Fed, the Green Line Macro Workshop at Boston College/Boston University (Spring 2008), as well as the R@BC and Dissertation Workshops at Boston College for important suggestions. Dissertation fellowships at the FRB of Atlanta and the FRB of Boston were extremely useful for the development of this paper. Return to text
2. Contact: [email protected], (202) 452-3542. The author is a staff economist in the Division of International Finance, Board of Governors of the Federal Reserve System, Washington, D.C. 20551 U.S.A. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
3. "Offshoring" refers to the activity of firms that relocate certain stages of production to foreign countries; firms can either become integrated across borders through vertical or/and horizontal FDI, or purchase intermediate goods and services from unaffiliated foreign suppliers. In contrast, "outsourcing" applies to firms that purchase intermediates from unaffiliated suppliers - either at home or abroad - rather than producing them in house (see Helpman, 2006). Return to text
4. Helpman, Melitz and Yeaple (2004) model exports and horizontal FDI as alternative internationalization strategies for multinational firms. Contessi (2006) analyzes this tradeoff in a business cycle framework. Return to text
5. Bergin, Feenstra and Hanson (2008) show that the extensive margin of offshoring accounts for more than one third of the adjustment of industry-level employment, and for nearly half of the adjustment of total employment in Mexico's maquiladora sector. Return to text
6. The maquiladora sector consists of manufacturing plants that import intermediate goods, process them, and export the resulting output. Return to text
7. In Burstein, Kurtz and Tesar (2008), the low elasticity of substitution between the domestic and foreign goods enhances the cross-country co-movement of output. Return to text
8. I maintain a one-to-one correspondence between an offshoring firm, a variety, and an offshore plant. Return to text
9. In the traditional international real business cycle literature, in contrast, a domestic increase in aggregate productivity leads to increased production at home but not offshore, as in Backus, Kehoe and Kydland (1992). Return to text
10. Recent empirical literature highlights the role of the extensive margin in international trade in the presence of fixed exporting costs: Baldwin and Harrigan (2007) show that the number of traded goods (the extensive margin) decreases with distance and increases with the size of the importing country. Besedes and Prusa (2006) find that the survival rate of exports for differentiated good varieties increases with the initial transaction size and also with the length of the relationship. Hummels and Klenow (2005) show that larger economies have larger exports, and that the extensive margin accounts for as much as 60 percent of this difference. Return to text
11. "Exporter hysteresis" refers to the behavior of firms that continue to serve the foreign market even after a real exchange rate appreciation reduces their export competitiveness. Return to text
12. All Southern firms produce domestically because the higher cost of effective labor in the North offers them no incentive to produce offshore. Return to text
13. Strategies (1) and (2) are the special
cases of a more general framework of offshoring, in which the
offshoring firm with idiosyncratic labor productivity ![]() uses a combination of Northern and Southern labor,
uses a combination of Northern and Southern labor,
![]() and
and
![]() . The output of firm
. The output of firm ![]() is a Cobb-Douglas function of domestic and foreign inputs,
is a Cobb-Douglas function of domestic and foreign inputs,
![$ y_{V,t}(z)=\left[ \frac{Z_{t}zl_{t}^{{}}}{\alpha }\right] ^{\alpha}\left[ \frac{Z_{t}^{\ast}zl_{t}^{\ast}}{1-\alpha}\right] ^{1-\alpha}$](img15.gif) , as in Antras and Helpman (2004). In this paper, I explore two
special cases: At one extreme, I set
, as in Antras and Helpman (2004). In this paper, I explore two
special cases: At one extreme, I set ![]() to
shut down offshore production, a case which replicates Ghironi and
Melitz (2005). At the other extreme, I set
to
shut down offshore production, a case which replicates Ghironi and
Melitz (2005). At the other extreme, I set ![]() so that the firms choosing to produce offshore use exclusively
foreign inputs. The smaller
so that the firms choosing to produce offshore use exclusively
foreign inputs. The smaller ![]() , the larger
the range of operations that the offshoring firms relocate abroad.
I use the l'Hôpital rule and
, the larger
the range of operations that the offshoring firms relocate abroad.
I use the l'Hôpital rule and
![]() to obtain:
to obtain:
![]()
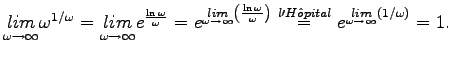 Return to text
Return to text
14. The cost of effective labor is the
ratio between the real wage and aggregate productivity in each
country. The real exchange rate
![]() is the ratio
between the price indexes in the South and the North expressed in
the same currency, where
is the ratio
between the price indexes in the South and the North expressed in
the same currency, where
![]() is the nominal exchange
rate. Return to text
is the nominal exchange
rate. Return to text
15. The cost of ![]() units of Southern effective labor is equivalent to
units of Southern effective labor is equivalent to
![]() units of the
Southern consumption basket. Return to
text
units of the
Southern consumption basket. Return to
text
16. A useful implication of model with
firm heterogeneity is that the more productive firms have larger
output and revenue. Given two firms with idiodsyncratic
productivity
![]() , the ratios of output and
profits are
, the ratios of output and
profits are
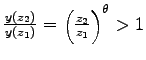 and
and
 (see Melitz, 2003). Empirical studies show that firms using
imported inputs in production are not only more productive, but
also have larger revenues and employ more workers (Kurz,
2006). Return to text
(see Melitz, 2003). Empirical studies show that firms using
imported inputs in production are not only more productive, but
also have larger revenues and employ more workers (Kurz,
2006). Return to text
17. A second condion necessary to avoid
the corner solution when all firms would produce offshore is that
![]() . It
ensures that
. It
ensures that
![]() in all
periods. Return to text
in all
periods. Return to text
18. I view exporting as a special case
within a more general framework, in which firms serve the foreign
market using a mix of domestic and foreign inputs in production:
![$ y_{H,t}(z)=\left[ \frac {Z_{t}zl_{H,t}}{\eta}\right] ^{\eta}\left[ \frac{Z_{t}^{\ast}zl_{H,t}^{\ast }}{1-\eta}\right] ^{1-\eta},$](img85.gif) where a larger
where a larger ![]() is equivalent to a smaller
content of Southern inputs used in the production of goods sold in
the South. In my model, I incorporate the special case with
endogenous exports as in Ghironi and Melitz (2005) by setting
is equivalent to a smaller
content of Southern inputs used in the production of goods sold in
the South. In my model, I incorporate the special case with
endogenous exports as in Ghironi and Melitz (2005) by setting
![]() . Alternatively, I would model the case
in which Northern firms serve the Southern market exclusively
through their foreign affiliates (as in Contessi, 2006) by setting
. Alternatively, I would model the case
in which Northern firms serve the Southern market exclusively
through their foreign affiliates (as in Contessi, 2006) by setting
![]() . Return to
text
. Return to
text
19. In the model with financial autarky
(in which mutual fund shares and bonds are not traded across
countries), the equilibrium conditions for stock and bond holdings
are
![]() and
and
![]() . Bond holdings play a role
in the extended model with incomplete financial markets, in which
the representative household buys risk-free, country-specific bonds
in the presence of quadratic adjustment costs for bond holdings
(Appendix A.2). Return to text
. Bond holdings play a role
in the extended model with incomplete financial markets, in which
the representative household buys risk-free, country-specific bonds
in the presence of quadratic adjustment costs for bond holdings
(Appendix A.2). Return to text
20. The sunk entry cost is equivalent to
![]() units of the Northern
consumption basket. Return to
text
units of the Northern
consumption basket. Return to
text
21. Note that
![]() is the average
productivity of offshoring firms, whereas
is the average
productivity of offshoring firms, whereas ![]() is the productivity cutoff above which firms produce
offshore. Return to text
is the productivity cutoff above which firms produce
offshore. Return to text
22. See Appendix A.3. Return to text
23. I use the Pareto c.d.f.
![]() and the
share of Northern firms producing offshore
and the
share of Northern firms producing offshore
![]() to
write the productivity cutoff as
to
write the productivity cutoff as
![]() . The
share of Northern firms producing domestically is
. The
share of Northern firms producing domestically is
![]() .
Parameter
.
Parameter ![]() reflects the dispersion of the
productivity draws: A relatively larger
reflects the dispersion of the
productivity draws: A relatively larger ![]() implies a
smaller dispersion and a higher concentration of productivities
implies a
smaller dispersion and a higher concentration of productivities
![]() towards the lower productivity bound
towards the lower productivity bound
![]() . Return
to text
. Return
to text
24. See Appendix A.4. Return to text
25. In the case with international trade in bonds, the current account balance equals the change in bond holdings, which is the negative of the financial account balance (Appendix A.2). Return to text
26. The model summary is in Appendix A.1. The steady-state solution is available in Appendix A.6. Return to text
27. In the alternative model with exports
only, I set
![]() and
and
![]() so that the fraction of
Northern exporting firms (10 percent) and that of Southern
exporting firms (63 percent) match the corresponding steady state
values from the model with offshoring. Return to text
so that the fraction of
Northern exporting firms (10 percent) and that of Southern
exporting firms (63 percent) match the corresponding steady state
values from the model with offshoring. Return to text
28. The terms of labor is the ratio
between the cost of effective labor in the South and the North
expressed in units of the same consumption basket. The calibration
ensures that the condition
![]() from Section 2.2 is satisfied
in steady state. Return to text
from Section 2.2 is satisfied
in steady state. Return to text
29. The value of 14 percent would understate the fraction of plants that use foreign inputs if the offshoring firms tend to operate multiple plants that produce different varieties. Return to text
30. In the South, the share of Southern varieties in total spending (61.7 percent) is less than their fraction in the total number of varieties (62.8 percent), since Northern exporters are more productive than the average Southern firm. Return to text
31. The maquiladora sector accounts for about 20 percent of Mexico's manufacturing value added (INEGI), for 50 percent of manufacturing exports, and for 25 percent of Mexico's employment (Bergin, Feenstra and Hanson, 2007, 2008). Return to text
32. The seasonally adjusted data in natural logs is expressed in deviations from a Hodrick-Prescott trend. The data for U.S. manufacturing IP is provided by the Federal Reserve Board. The data for Mexico's manufacturing IP and the maquiladora sector (real value added and the number of plants) is provided by INEGI (2008). I aggregate the maquiladora data into quarters (from the original monthly frequency), and seasonally adjust it using the X-12-ARIMA method of the U.S. Census Bureau. Return to text
33. In the alternative model with fixed productivity cutoff, the fraction of offshoring firms is constant, but the number of offshoring firms varies over time due to firm entry in the country of origin. During expansions in the North, the new entrants that draw idiosyncratic productivity factors above the cutoff start by producing directly offshore. However, none of the firms that initially produce at home can relocate offshore when the terms of labor appreciate. Return to text
34. I deflate the value added offshore by
the average price index of the varieties produced offshore, VA
![]() VA
VA
![]() . To this end, I
decompose the price index for the offshore varieties into
components reflecting (a) variety and (b) average price as
. To this end, I
decompose the price index for the offshore varieties into
components reflecting (a) variety and (b) average price as
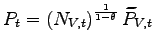 , to obtain VA
, to obtain VA
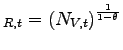 VA
VA![]() . Return to text
. Return to text
35. Following a positive shock to aggregate productivity in the North, the initial drop in the number of offshoring firms - caused by a spike in the Southern wage - is followed by a gradual increase above the initial steady state level, as the terms of labor appreciate over time. Return to text
36. In order to compute the cross-country
correlations, I deflate output and consumption by the average price
indexes in each country, since the empirical price deflators are
best represented by the average price index
![]() rather than the
welfare-based price index
rather than the
welfare-based price index ![]() . For instance,
I use
. For instance,
I use
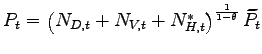 to deflate output in the North as
to deflate output in the North as
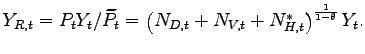 I deflate the value added offshore by the average price index of
the varieties produced offshore as VA
I deflate the value added offshore by the average price index of
the varieties produced offshore as VA
![]() VA
VA
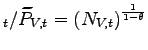 VA
VA![]() . Return to
text
. Return to
text
37. I assume that the persistence parameter is symmetric across the North and the South, that there are zero spillovers, but maintain the variance-covariance matrix of shocks from Mandelman and Zlate (2008). Return to text
38. Exogenous policy changes can also
affect the price of goods produced offshore. For instance, tariff
cuts for the varieties produced offshore, reflected by a decrease
in ![]() , would dampen the appreciation of
the CPI-based real exchange rate. Return
to text
, would dampen the appreciation of
the CPI-based real exchange rate. Return
to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text