skip to main navigation skip to secondary navigation skip to content
Board of Governors of the Federal Reserve System
skip to content

FEDS Notes

January 6, 2014

The Rise in Equity Valuation Ratios


Missaka Warusawitharana

Recent discussions by some market participants have noted that a number of equity valuation ratios are elevated. This FEDS Note argues that there has been a secular rise in equity valuation ratios and this rise could reflect changes in discount rates used by investors.

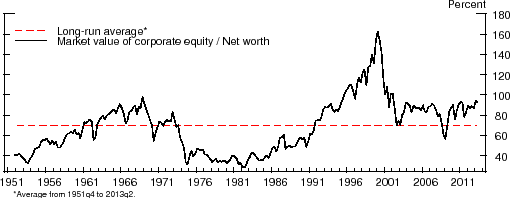
One such valuation ratio can be derived from the Financial Accounts of the United States (formerly known as the Flow of Funds Accounts). Line 39 of Table B.102 reports the ratio of the market value of equity to the net worth of the nonfinancial business sector. The market value of equity is based on stock market valuations, while the net worth of the sector is measured as the market value of the sector's assets minus the book value of its liabilities. Figure 1 plots this ratio from 1951:Q4 to 2013:Q2. Over the past 25 years, this ratio averages nearly 90%, 1.29 times its long-run historical average of about 70%.

Figure 1: Market value of corporate equity to net worth
This is a line graph showing two lines. The x axis shows the time span from 1951 to 2013. The y axis shows percent and ranges from 20 to 180. The first of the two lines is a black solid line that shows the market value of corporate equity divided by net worth. This has a lot of variability but generally slopes up to the late 1960s, peaking at around 100 percent. Then falls to the 30s until the late 80s when it starts to slope up until the late 90s where it peaks around 170. The rate then falls sharply back down to stay between 70 and 100. The second line is a red dashed horizontal line showing the long run average (from 1951q4 to 2013q2) at 70 percent.

Accessible Version

 

What may explain this secular rise in equity valuation ratios? The following (admittedly simplified) approach to gauging valuations shows how even modest changes in discount rates lead to sharp movements in the ratio of the market value of equity to net worth. Denote the net worth of the nonfinancial business sector as A . Assume that the income earned by shareholders each period equals a constant fraction, z , of net worth. Thus, the per-period income to shareholders is given by

\displaystyle z A. (1)

In addition, assume that the net worth of the business sector grows at a constant rate, \gamma . This growth reflects the overall long-run growth of the economy. Finally, assume that shareholders discount the income from the business sector at a constant discount rate r . Now, we can write the market value of the business sector, V , using the following present-value formula:
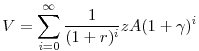\displaystyle V = \sum_{i=0}^{\infty} \frac{1}{(1+r)^{i}} zA(1+\gamma)^{i} (2)

The above sum can be simplified by applying the formula for telescoping sums to generate the following:

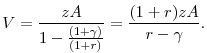
\displaystyle V = \frac{z A}{1 - \frac{(1+\gamma)}{(1+r)}} = \frac{(1+r) z A}{r - \gamma}.
Dividing through by net worth, A , one obtains the following formula for the ratio of the market value of equity to net worth of the business sector:
\displaystyle \frac{V}{A} = \frac{(1+r) z}{r - \gamma}. (3)

Now consider an unanticipated permanent change in the discount rate from r to \tilde{r} while keeping unchanged A , \gamma and z . The new valuation ratio will be given by

\displaystyle \frac{\tilde{V}}{A} = \frac{(1+\tilde{r}) z}{\tilde{r} - \gamma}. (4)

One could then combine equations (3) and (4) to write the new valuation ratio as a multiple of the old ratio:
\displaystyle \frac{\tilde{V}}{A} = \frac{(1+\tilde{r})}{\tilde{r} - \gamma}\frac{r - \gamma}{(1+r)} \frac{V}{A}. (5)

This simplified framework allows us to examine the effect of an unanticipated change in discount rates used by investors. This analysis is motivated by studies such as (Fama and French, 2002), who argue that returns to U.S. equities over the post-war period are greater than would be justified by fundamentals. (Lettau and Van Nieuwerburgh, 2008) present evidence in favor of a structural break in the dividend-price ratio of the aggregate stock market. A number of recent econometric studies such as (Warusawitharana, 2013), (Wachter and Warusawitharana, 2013), and (Avdis and Wachter, 2013) also argue that the expected return to equity or the closely-related equity premium is about 1 to 2 percentage points lower than the corresponding sample counterpart that is typically used to obtain a discount rate. Related, (Cogley and Sargent, 2008) and (Lettau, Ludvigson, and Wachter, 2008) present theoretical models supporting a decline in the equity premium.

To quantify the effect of a change in discount rates, we'll use a growth rate of \gamma = 0.02 , matching the long-run growth rate of real per-capita consumption. Set the initial discount rate r = 6.5\% , at about the long-run historical real return to US equities and the new, lower discount rate 1 percentage point lower at \tilde{r} = 5.5\% . Applying these calibrated values to equation (5), one obtains the following link between the valuation ratios:

\displaystyle \frac{\tilde{V}}{A} = 1.27 \times \frac{V}{A}.

Strikingly, this multiple is quite similar to that obtained by comparing the average value of the valuation ratio over the past 25 years to its long-run historical average, as noted above.

The above analysis indicates that even a fairly modest decline in discount rates of 1 percentage point can have a marked effect on valuation ratios such as the ratio of the market value of equity to the net worth of nonfinancial firms. Thus, the fact that this valuation ratio is elevated relative to its historical average may not necessarily be an indicator of an overvalued market, but instead a reflection of a change in discount rates.

Bibliography

Avdis, Efstathios, and Jessica A. Wachter, 2013. Maximum likelihood estimation of the equity premium, Working paper.

Cogley, Timothy, and Thomas J. Sargent, 2008. The market price of risk and the equity premium: A legacy of the Great Depression?, Journal of Monetary Economics 55, 454-476.

Fama, Eugene F., and Kenneth R. French, 2002. The equity premium, Journal of Finance 57, 637-659.

Lettau, Martin, Sydney C. Ludvigson, and Jessica A. Wachter, 2008. The declining equity premium: What role does macroeconomic risk play?, Review of Financial Studies 21, 1653-1687.

Lettau, Martin, and Stijn Van Nieuwerburgh, 2008. Reconciling the return predictability evidence, Review of Financial Studies 21, 1607-1652.

Wachter, Jessica A., and Missaka Warusawitharana, 2013. What is the chance that the equity premium varies over time? Evidence from regressions on the dividend-price ratio, NBER Working paper #17334.

Warusawitharana, Missaka, 2013. The expected real return to equity, Journal of Economic Dynamics & Control 37, 1929-46.

Please cite as:

Warusawitharana, Missaka (2014). "The Rise in Equity Valuation Ratios," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, January 06, 2014. https://doi.org/10.17016/2380-7172.0006

Disclaimer: FEDS Notes are articles in which Board economists offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers.

Search Working Papers




Skip stay connected section
Last update: January 6, 2014