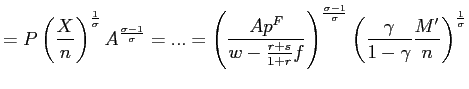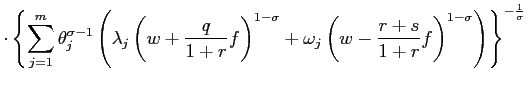Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 796, April 2004--Screen Reader Version*
Sand in the Wheels of the Labor Market: The Effect of Firing Costs on Employment
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper examines the effects of firing costs in a dynamic general equilibrium model where firms face stochastic demand. It derives analytically two simple closed-form equations, one for the supply of labor, the other for its demand. These equations determine the comparative static effects of changes in firing costs on the labor market. When negative shocks are more likely to occur than positive shocks, and when the frequency of these shocks is high, firing costs have a substantial negative impact on aggregate employment. In addition, product market integration, as it has occurred in the formation of the European Union, induces firms to be more wary of future possible downturns and therefore intensifies the negative consequences of firing costs.
Keywords: employment protection legislation, European labor markets.
JEL Classifications: E24, L16, J50
*Staff economist of the Division of International Finance of the Federal Reserve Board. E-mail: [email protected]. This paper is an updated version of chapter 1 of my dissertation. I am extremely grateful to George Akerlof and Chad Jones for guidance, encouragement and patience. I received useful comments and suggestions from seminar participants at UC Berkeley, the ECB, Tilburg University, IIES (Stockholm), Warwick Univerisity, the Federal Reserve Board, Baruch College, Southern Methodist University and Florida International University. Special thanks to Andrew Figura, Johnathan Leonard and David Romer. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1 Introduction
Employment in Europe has been stagnant for the last thirty years; unemployment has risen and participation in the workforce has fallen. These dramatic events have occurred against a backdrop of legislative efforts to make it more difficult for European firms to layoff workers. These high and rising firing costs are among the leading suspects as the reason for the poor performance of labor markets in several European countries.1There exists a large literature that analyzes the effects of job security regulations on the functioning of the labor market. Most available evidence indicates that firing costs have a negative impact on employment (Heckman and Pages, 2000). Yet, no consensus has emerged from the theoretical side of the debate. This disagreement is not surprising since the effect of firing costs on employment are deeply ambiguous. The first impact of job security provisions is to increase employment by discouraging layoffs when firms are hit by negative shocks. Conversely, the fear of high firing costs in the event of a future downturn acts as a hiring cost, effectively reducing the creation of new jobs when firms are hit by positive shocks. Which of the two channels dominates depends on the specification of the model and, in particular, on the nature of uncertainty.
This paper will develop a tractable general equilibrium model that delivers a clear and intuitive understanding of how the labor market is affected by job security regulations. Specifically, we will spell out precise conditions under which firing costs reduce aggregate employment and will illustrate these results with simple comparative statics.
We make three main assumptions. The first is that of monopolistic competition in the product market, which determines the size of the rent. The second is to represent uncertainty by letting demand for each product increase or decrease, according to a simple Markov process, in steps. The third is that of linear layoff costs, which yields partial but instantaneous adjustment.
This approach allows us to derive analytically simple expressions that characterize firms' hiring and firing policies. At each level of demand, there is an upper threshold of employment above which firms are firing workers; and a lower threshold, below which firms are hiring workers. We can then solve for the steady-state probability of employment at all levels, and aggregate to derive an expression for the expected value of total labor demand. Finally, since demand for the firms' products depend upon the prices, we compute the optimal prices that the firms will charge for their goods, as well as the equilibrium wage rate that equates the supply of labor to the demand for labor.
The model derives explicit expressions for the supply of and the demand for labor, and thus sheds light on the ambiguity of the effects of firing costs on aggregate employment. It shows that when the economy is ``depressed,'' these effects will be negative. Our notion of depressed economy refers to a situation in which the Markov process is such that the probability to move downward is greater than the probability to move upward, so firms are more likely to think that they will have to be firing workers than hiring them in the near future. On the other hand, firing costs will have a positive effect on employment when the economy is doing well, and firms are more likely to be hiring workers than firing them. Thus, the model yields the theory underlying the view that the poor performance of Europe's labor markets is the result of the interaction between ``bad'' labor market institutions and adverse shocks (Blanchard and Wolfers, 2000).
In addition, comparative static exercises indicate that these negative effects become stronger when the economy is more ``turbulent''. Our notion of turbulence pertains to the frequency of the demand shocks. Thus, the model also provides rigorous foundation for the long-standing argument that when demand is stable and growing, the hiring policy of firms is not affected by job security provisions; while, when demand turns flat and volatile, severance payments and rules become important obstacles to employment creation (Blanchard et al., 1986, Ljungqvist and Sargent, 2002).
The model provides the answer to another important question. Besides the increase in firing costs, another major change has been the creation of the European Union. This historical event, together with globalization and privatization of public companies, is changing the economic landscape from a collection of small national protected markets to a single large competitive market. We attribute to this ongoing process a general fall in the market power of existing firms. The model allows an assessment of how high firing costs interact with deregulation in the product market to determine aggregate employment.
The last part of the paper is devoted to the simulation of the model using plausible parameter values. As the aim of the paper is to explain the poor performance of Europe's labor market, we need to check how well the model can reproduce the experience of most European countries. Here, we need to keep in mind that employment and unemployment are not mirror images of each other. If workers' participation decisions are influenced by job protection policies (as shown by Lazear, 1990), a reduction in employment will be associated with a decline in participation rates. Thus, the unemployment rate is not the best indication of how institutional differences affect the functioning of the labor market. Figure 1 shows, instead, the ratio between employment and working age population for selected European countries and the US since 1973.2 One fact strongly comes out: a significant downward trend in most European countries, which is even more striking if compared with the experience for the US.
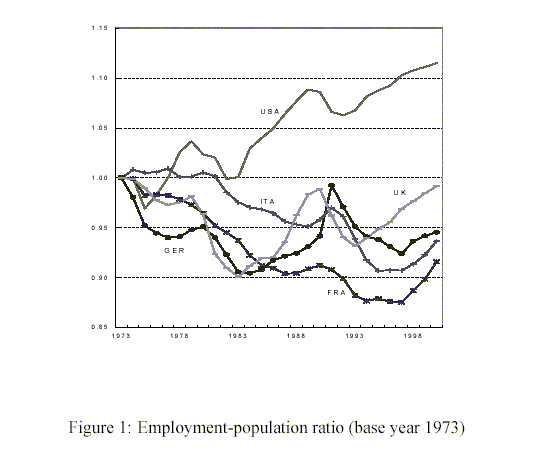
Our model will deliver this downward trend. High layoff costs have a sizeable negative impact on employment when the economy is depressed and turbulent. In addition, we will show that a fall in the market power of firms, while it stimulates production and employment, also causes firms to be more fearful of possible future downturns and therefore increases the prospective costs of hiring workers. In other words, product market deregulations generate better results for employment when associated with low layoff costs.
The remainder of this paper is organized as follows. Section 2 discusses the related literature. Section 3 sets up a simple model of an economy with both product and labor market regulations. Section 4 solves for the steady-state general equilibrium, in which both employment and the wage are endogenously determined. Section 5 presents numerical simulations to examine how the various dimensions of regulation affect the functioning of the labor market. Finally, section 6 discusses possible extensions of the basic model and summarizes the conclusions.
2 Literature Review
The goal of this section is to motivate our contribution by discussing the existing literature on employment protection regulations. Both theoretical and applied work have been carried out on this topic.
On the theoretical side, we can identify at least three different approaches to the question of whether layoff costs have a significant impact on employment. Bentolila and Bertola (1989) analyze the case of a firm that faces uncertainty in the returns to labor in a dynamic partial equilibrium model. Assuming linear and asymmetric adjustment costs, they show that dismissal costs have a negligible effect on hiring decisions and, surprisingly, slightly increase average employment. These results are quite sensitive to different assumptions about the persistence of the shocks, the magnitude of the discount rate, and the cyclicality of voluntary quits. Thus, less persistent shocks and lower discount rates cause layoff costs to have larger negative effects on employment, because both factors reduce hiring relative to firing (Bentolila and Saint-Paul, 1994). In addition, allowing for a procyclical - rather than constant - quit rate increases the fear of dismissal costs as fewer workers leave their jobs voluntarily during downturns. In De Michelis (2003), we show that layoff costs can depress labor demand when quits are procyclical.
Hopenhayn and Rogerson (1993) develop a general equilibrium model that incorporates the structure presented by Bertola and Bentolila. Calibrating the stochastic process driving labor productivity to match US evidence on job creation and destruction, they find that layoff costs reduce the turnover rate and the overall efficiency of the economy, and have a sizable negative impact on aggregate employment. These results (however) depend greatly on the assumption of decreasing returns to scal: higher firing costs increase firms' size, and thus result into lower productivity, lower demand and lower employment.
The search and matching framework by Mortensen and Pissarides has been adapted to study how job protection provisions affect the functioning of the labor market. Blanchard (2000) and various coauthors show that costly layoffs reduce workers' flows to and from employment. This causes longer unemployment spells, while the impact on unemployment is ambiguous. Ljungqvist and Sargent (2002), on the other hand, calibrate a search model to show that the combination of high severance payments with increasing economic turbulence can generate a significant fall in the rate of employment.
On the empirical side, most available evidence shows a consistent, although not always statistically significant, negative impact of job security provisions on employment. This is true not only in the Western world (Lazear, 1990, Addison and Grosso, 1996) but in Latin America as well (Heckman and Pages, 2000). In contrast, the evidence regarding the impact on unemployment is ambiguous, but we suspect that there are conceptual reasons for such findings. Specifically, Bertola (1990), Blanchard (2000), and Nickell (1997) find no effect of job security regulations on unemployment, while Lazear (1990) and Scarpetta (1996) find positive effects. Yet, it should not be a surprise that a negative impact on employment is not always mirrored in a positive effect on unemployment. Lazear (1990) shows that job security policies affect workers' participation decision: thus, a reduction in employment will cause a decline in participation rates.
One point on which the literature has converged is the
formalization of the adjustment cost function. A series of studies
indicate that convexity à la Tobin's ![]() is not the best way to proceed
(Hamermesh 1993, 1995, and Hamermesh and Pfann, 1996). The last
study, for example, concludes: ``Adjustment costs are definitely
not uniformly symmetric and convex.'' (p. 1281) Thus, we make the
choice to follow the new standard assumption (since Nickell, 1986)
of asymmetric linear adjustment costs. In particular, we formalize
employment protection as a state-mandated cost that a firm has to
pay if it wants to lay off an employee. We think of it as a cost to
the firm-worker pair, rather than a transfer from the firm to the
worker: the conventional wisdom is that, in most European
countries, the legal and administrative costs associated with
dismissals exceed the monetary value of severance payments
(Blanchard, 2000).
is not the best way to proceed
(Hamermesh 1993, 1995, and Hamermesh and Pfann, 1996). The last
study, for example, concludes: ``Adjustment costs are definitely
not uniformly symmetric and convex.'' (p. 1281) Thus, we make the
choice to follow the new standard assumption (since Nickell, 1986)
of asymmetric linear adjustment costs. In particular, we formalize
employment protection as a state-mandated cost that a firm has to
pay if it wants to lay off an employee. We think of it as a cost to
the firm-worker pair, rather than a transfer from the firm to the
worker: the conventional wisdom is that, in most European
countries, the legal and administrative costs associated with
dismissals exceed the monetary value of severance payments
(Blanchard, 2000).
Summarizing, the assertion that job security does not have a negative impact on employment is based on indirect evidence concerning unemployment, not employment. However, this finding is not supported by a rigorous theoretical argument. The ambition of this paper is to fill this gap. We will show that high layoff costs significantly reduce employment when the economy is in a phase of depression and high volatility, but not when it is booming and uncertainty is small. This result offers an explanation for why, in the early 1970s, European labor markets began to perform poorly. In addition, we will also explain how the interaction of layoff costs and the degree of competition among firms is important to assess the impact of job security regulations on aggregate employment.
It has been argued that product market constraints might significantly contribute to the poor performance of European labor markets. A recent and small literature attempts to formalize this idea in simple models3. In particular, Blanchard and Giavazzi (2001) develop a general equilibrium model to analyze how the interaction of product and labor market deregulations can give rise, in the short run, to lower real wages and higher unemployment and, in the long run, to a recovery of the labor share and a decrease of equilibrium unemployment.
We follow Blanchard and Giavazzi in modeling product market regulations as determining the degree of market power of firms. But, while they identify labor market regulations with the bargaining power of workers, we focus our attention on the impact of employment protection regulations. As high firing costs are likely to strengthen the hands of workers in bargaining, leading to higher wages, one might be tempted to argue that our paper has nothing new to add. However, costly layoffs also affect labor flows - layoffs directly, hirings indirectly - and not only the bargaining strength of workers. Thus, our contribution to this literature is to explain how the interaction of product market regulations and firing restrictions affect aggregate employment in a stochastic environment.
Unfortunately, there is little direct evidence on the size and importance of product market constraints. A rare exception is a paper by Goldberg and Verboven (2001) in which the authors examine the European car market from 1980 to 1993: while they document a significant price dispersion across country, their findings also suggest that price discrimination plays a minor and diminishing role. Since labor demand is derived from the behavior of firms, it seems reasonable that regulations in the product market might inhibit the redeployment of workers and hence affect firms' hiring and firing policies.
Before we start spelling out the details of the model, we want to clarify what we mean by the term firing, in case the reader still had some doubt. In this paper, a fired worker is a laid off worker, not a worker fired with cause. This distinction is important because job security provisions can affect labor markets through two different channels. First, such regulations raise the costs that firms must bear in order to adjust their stock of employees. And this is what this paper is about. However, they also change the relation between employer and employee as it becomes harder to fire those workers who are not sufficiently productive. On this issue, see, among others, Kugler and Saint-Paul (2000). Anyway, for the remainder of the paper, we will use the terms ``fire,'' ``layoff'' and ``dismiss'' interchangeably to indicate a decrease in the employment level of a given firm.
3 The Model
3.1 Setup
Demand side. This is a discrete-time model with infinite horizon. At time 0, the representative agent's preference are given by:
where
The second term gives the effect of real money balances. Nominal
money balances, ![]() , are
deflated by the nominal price index,
, are
deflated by the nominal price index, ![]() , associated with the composite good
, associated with the composite good ![]() . The parameter
. The parameter ![]() denotes the importance of
denotes the importance of
![]() relative to
relative to
![]() in utility;
in utility;
![]() . The reason why we
include money in the utility function is to avoid Say's law. It is
a well-known fact in economic theory that the supply of products by
the monopolistically competitive firms - as we choose to model the
supply side in this model - automatically generates its own demand
unless agents have the choice between these goods and something
else (Hart, 1982). If there were only this type of good, the
equilibrium in the labor market would be always indeterminate.
Here, we follow Blanchard and Kiyotaki (1987), and assume that the
choice is between buying goods and holding money. This is most
simply and crudely achieved by having real money balances in the
utility function.
. The reason why we
include money in the utility function is to avoid Say's law. It is
a well-known fact in economic theory that the supply of products by
the monopolistically competitive firms - as we choose to model the
supply side in this model - automatically generates its own demand
unless agents have the choice between these goods and something
else (Hart, 1982). If there were only this type of good, the
equilibrium in the labor market would be always indeterminate.
Here, we follow Blanchard and Kiyotaki (1987), and assume that the
choice is between buying goods and holding money. This is most
simply and crudely achieved by having real money balances in the
utility function.
The third term gives the disutility from work; ![]() is the amount of work supplied by
the household. The parameter
is the amount of work supplied by
the household. The parameter ![]() measures the importance of leisure in utility.
The term
measures the importance of leisure in utility.
The term ![]() is the
elasticity of marginal disutility of labor. We assume
is the
elasticity of marginal disutility of labor. We assume ![]() and
and ![]() . Since leisure enters
utility as an additively separable term, we rule out any income
effects on the supply of labor.
. Since leisure enters
utility as an additively separable term, we rule out any income
effects on the supply of labor.
The budget constraint is:
where ![]() and
and
![]() denote the
price and the demand for good
denote the
price and the demand for good ![]() in period
in period ![]() ,
, ![]() denotes net assets (besides money) at the end of period
denotes net assets (besides money) at the end of period
![]() ,
, ![]() denotes the wage rate in period
denotes the wage rate in period
![]() ,
, ![]() denotes lump transfers in period
denotes lump transfers in period
![]() (see below for
details). We assume that
(see below for
details). We assume that ![]() and
and ![]() are both positive and exogenously determined.
are both positive and exogenously determined.
All of the above is quite standard. Now, we introduce our first
new idea. We assume that there is a measure ![]() of differentiated goods and demand
varies across goods, that is consumers like different products
differently. Specifically, we divide the
of differentiated goods and demand
varies across goods, that is consumers like different products
differently. Specifically, we divide the ![]() 's goods into
's goods into ![]() taste groups and assume symmetric
demand within each group. The taste parameter
taste groups and assume symmetric
demand within each group. The taste parameter ![]() takes value in the set
takes value in the set
![]() ,
,
![]() , and
, and
![]() is
increasing in
is
increasing in ![]() : thus,
products located in higher taste groups (i.e. higher
: thus,
products located in higher taste groups (i.e. higher ![]() ) will be in higher demand. We use
) will be in higher demand. We use ![]() to denote the
taste for good
to denote the
taste for good ![]() . We
can therefore define a `` taste-adjusted'' composite good:
. We
can therefore define a `` taste-adjusted'' composite good:
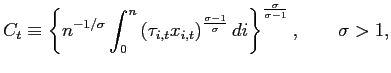
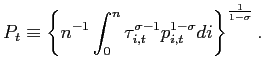
|
(3) |
Thus, the composite good ![]() is the usual index à
la Dixit and Stiglitz except for the presence of the taste
parameter,
is the usual index à
la Dixit and Stiglitz except for the presence of the taste
parameter, ![]() . The
interpretation is straightforward: goods in higher demand, i.e.
with higher
. The
interpretation is straightforward: goods in higher demand, i.e.
with higher ![]() , provide
more consumption-utility. The term
, provide
more consumption-utility. The term
![]() is added
to neutralize the variety effect, thus an increase in the number of
products does not increase utility directly. The parameter
is added
to neutralize the variety effect, thus an increase in the number of
products does not increase utility directly. The parameter
![]() denotes the
elasticity of substitution across all products. We make the usual
assumption that
denotes the
elasticity of substitution across all products. We make the usual
assumption that ![]() to guarantee the existence of an
equilibrium.
to guarantee the existence of an
equilibrium.
The price index is also standard but for ![]() . Again, the intuition is very
simple. Recall that the price index measures the least expenditure
that buys one unit of the composite good. Thus, equation (3) says
that the prices of goods in higher demand must be discounted more
as they provide more consumption-utility.
. Again, the intuition is very
simple. Recall that the price index measures the least expenditure
that buys one unit of the composite good. Thus, equation (3) says
that the prices of goods in higher demand must be discounted more
as they provide more consumption-utility.
Uncertainty. Demand for each good
![]() is uncertain.
Specifically, we assume that the taste parameter
is uncertain.
Specifically, we assume that the taste parameter ![]() is stochastic and follows an
is stochastic and follows an
![]() -step Markov process
where the upward transition probability is
-step Markov process
where the upward transition probability is ![]() and the downward transition
probability is
and the downward transition
probability is ![]() . Note
that
. Note
that ![]() and
and ![]() do not sum to
do not sum to ![]() so that there is a nonzero
probability that demand remains constant. If the demand shifter
hits one of the extreme states
so that there is a nonzero
probability that demand remains constant. If the demand shifter
hits one of the extreme states
![]() or
or
![]() , it stays
there until demand reverts towards the center. Thus, for example,
, it stays
there until demand reverts towards the center. Thus, for example,
![]() .
.
In section 4.2, we will show that this specification with taste shocks is perfectly equivalent to the standard assumption of productivity shocks. Thus, while our model attributes all uncertainty to shocks on the demand side, there is an alternative interpretation of the same structure in which the disturbances reflect supply shocks. Of course, the truth lies in the middle and both types of shock are important.
The justification for these idiosyncratic demand/productivity shocks is a series of studies by Leonard (1987) and Davis and Haltiwanger (1992). These authors provide evidence that gross rates of job creation and destruction are remarkably large. For the US manufacturing sector, they amount to roughly 10 in a typical year. In this paper, we suggest that idiosyncratic shocks of significant size are the source for this observed heterogeneity of employment changes across firms.
While these shocks occur at a micro-level, this setup provides a
simple framework to analyze the effects of macro shocks as well. If
![]() , firms are
uniformly distributed over the line of measure
, firms are
uniformly distributed over the line of measure ![]() : there is the same number of firms
in each taste group. Firms face an idiosyncratic risk but aggregate
demand is stable. Furthermore, the closer to
: there is the same number of firms
in each taste group. Firms face an idiosyncratic risk but aggregate
demand is stable. Furthermore, the closer to ![]() is the sum of
is the sum of ![]() and
and ![]() , the higher is the uncertainty that firms must face.
If
, the higher is the uncertainty that firms must face.
If ![]() , the
distribution of firms is no longer uniform. In particular, we can
model a ``depressed'' economy setting
, the
distribution of firms is no longer uniform. In particular, we can
model a ``depressed'' economy setting ![]() . As negative shocks are more
likely to occur than positive shocks, the economy converges to a
steady-state where the majority of firms are in states of low
demand. Thus, we can formalize a recession - a macro shock - by
raising
. As negative shocks are more
likely to occur than positive shocks, the economy converges to a
steady-state where the majority of firms are in states of low
demand. Thus, we can formalize a recession - a macro shock - by
raising ![]() relative to
relative to
![]() .
.
Regulations. As we discussed in the
introduction, we (partially) follow Blanchard and Giavazzi (2001)
in their modeling product market regulation and assume that
governments can affect the elasticity of substitution.
Specifically, we assume that the government sets ![]() .
.
We make the choice to identify labor market regulations with employment protection institutions which we formalize as state-mandated costs that a firm has to pay when it lays off an employee. We think of it as a cost to the firm-worker pair, rather than a transfer from the firm to the worker. This captures the fact that, in most European countries, firms consider legal and administrative costs associated with layoffs - due to notice periods, plant closing legislation, bureaucratic procedures - to vastly exceed the monetary value of the severance payments.4
In particular, we follow the recent literature and specify
asymmetric linear adjustment costs. The firm bears a layoff cost,
![]() , per dismissed worker
while, for simplicity, we set hiring costs to zero:
, per dismissed worker
while, for simplicity, we set hiring costs to zero:
![$\displaystyle F(Z_{i,t})=\left\{ \begin{array}[c]{c} fZ_{i,t}\text{, if }Z_{i,t}>0\\ 0\text{, otherwise,} \end{array} \right.$](img49.gif)
|
(4) |
where
While job security regulations impose a cost to the worker-firm
pair, we assume that they are not a deadweight loss to the economy
as a whole. We think that the related legal fees and administrative
duties are eventually spent to purchase goods ![]() 's. Thus, for simplicity, we
assume that they are rebated to the representative agent as a lump
sum transfer; the expression for
's. Thus, for simplicity, we
assume that they are rebated to the representative agent as a lump
sum transfer; the expression for ![]() in the budget constraint (2) is given by:
in the budget constraint (2) is given by:
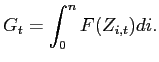
This is a technical assumption to simplify algebra. Since total adjustment costs also enter the budget constraint through the expression for assets (the agent owns the firms), these two terms cancel each other out. Nonetheless, note that this simplification goes against the argument that costly layoffs negatively affect aggregate employment since we are ruling out any direct effect of firing costs on total income.6
Firms and technology. There is a
continuum of firms of measure ![]() producing differentiated goods using homogeneous
labor,
producing differentiated goods using homogeneous
labor, ![]() . Each
product,
. Each
product, ![]() , is
produced by a single firm but all firms use the same linear
technology:
, is
produced by a single firm but all firms use the same linear
technology:
| (5) |
Thus, labor productivity is always
Firms are placed in a monopolistically competitive market. We make the standard assumption that firms take the behavior of other existing firms as given.
The firm chooses an employment and firing policy each period to maximize the present discounted value of expected net revenues over the infinite future:
![$\displaystyle v_{i,1}=\max_{\left\{ x_{i,t}\text{, }L_{i,t},\text{ }Z_{i,t}\rig... ..._{t}}\right) ^{t}\left[ p_{i,t}x_{i,t}-w_{t}L_{i,t}-F(Z_{i,t} )\right] \right\}$](img58.gif)
|
(6) | |
| subject to (1), (2), (4), (5), |
and
4 Solution of the Model
Definition of equilibrium. A
competitive equilibrium for this economy is a collection of
quantities
![]() and prices
and prices
![]() such that:
such that:
� taking
![]() as given, the representative agent chooses
as given, the representative agent chooses
![]() ,
,
![]() ,
, ![]() and
and ![]() to maximize (1) subject to the
budget constraint (2) and
to maximize (1) subject to the
budget constraint (2) and ![]() and
and ![]() given;
given;
� taking
![]() and
and ![]() as given, each
firm
as given, each
firm ![]() chooses
chooses ![]() ,
, ![]() and
and ![]() to solve (6);
to solve (6);
�
![]() are such that all markets clear:
are such that all markets clear:
![]() (market for good
(market for good ![]() )
)
![]() (money
market)
(money
market)
![]() (labor
market)
(labor
market)
![]() (asset
market).
(asset
market).
We solve only for the steady-state equilibrium in which all
prices and quantities are time invariant. Thus, in order to
simplify notation, we choose, whenever possible, to omit the time
index for the remainder of the paper.
We proceed by solving first for the partial equilibrium, in which prices are exogenous. Specifically, in section 4.1, we characterize the behavior of the representative agent, in section 4.2 the behavior of firms, and in sections 4.3 and 4.5, we aggregate the individual behavior in the steady-state. Finally, in section 4.5, we solve for the steady-state general equilibrium in which prices are endogenous and markets clear.
4.1 The representative agent's problem
As the economy is in a stationary state, the value of aggregate assets for the whole economy is not time dependent:
Since there are no intertemporal links, we can characterize the
behavior of the representative agent with a relation between real
money balances and aggregate demand, a demand function for each
product and a labor supply equation (see appendix A.1 for details).
Let
![]() be
an index for real aggregate consumption expenditures, which we call
`` aggregate demand'' for short. Then, in equilibrium, we find
that:
be
an index for real aggregate consumption expenditures, which we call
`` aggregate demand'' for short. Then, in equilibrium, we find
that:
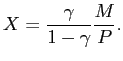 |
(7) |
In equilibrium, desired real money balances are proportional to consumption expenditures.
Demand for good ![]() s
given by:
s
given by:
As in a standard monopolistically competitive model, the demand
for each type of good relative to aggregate demand is a function of
the ratio of its price to the price index, with elasticity
![]() . Furthermore, a
higher demand shifter,
. Furthermore, a
higher demand shifter, ![]() , causes demand to be higher.
, causes demand to be higher.
Finally, aggregate labor supply is given by:
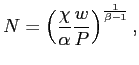
|
(9) |
where
4.2 The firm's problem
We characterize the behavior of firms using dynamic programming.
All firms solve the same problem, thus, to simplify notation, we
omit the goods' index, ![]() .
.
Let the state variable be ![]() and the control variable
and the control variable ![]() , where
, where ![]() and
and ![]() are yesterday's and today's levels
of employment, respectively. Combine equations (5) and (8) to
substitute for
are yesterday's and today's levels
of employment, respectively. Combine equations (5) and (8) to
substitute for ![]() and
and
![]() into the firm's
objective function. It is convenient to solve the firm's
maximization problem using dynamic programming. Let
into the firm's
objective function. It is convenient to solve the firm's
maximization problem using dynamic programming. Let
![]() be the value function where
be the value function where
![]() is the state
variable,
is the state
variable, ![]() and
and
![]() the values of the
demand shifter one period back and in the current period,
respectively7.
the values of the
demand shifter one period back and in the current period,
respectively7.
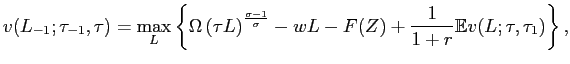
|
(10) |
where
![]() . Note that
. Note that
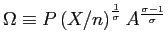 is constant with respect to the choice variable,
is constant with respect to the choice variable,
![]() . Furthermore, as
. Furthermore, as
![]() and
and ![]() have the same exponent, the above
expression makes clear that, while we model uncertainty coming from
taste shocks, the same structure would arise if firm-level supply
shocks were the source of risk. In other words, if
have the same exponent, the above
expression makes clear that, while we model uncertainty coming from
taste shocks, the same structure would arise if firm-level supply
shocks were the source of risk. In other words, if ![]() denoted idiosyncratic
productivity shocks and consumers had symmetric demands across all
goods, firms would solve the same maximization problem as in
equation (10).
denoted idiosyncratic
productivity shocks and consumers had symmetric demands across all
goods, firms would solve the same maximization problem as in
equation (10).
The optimization problem defined in (10) is non-standard because
the derivative of the objective function changes with the sign of
![]() . The first order
condition with respect to
. The first order
condition with respect to ![]() in fact yields:
in fact yields:
The above system is analogous to the deterministic expressions
derived by Nickell (1986). The difference between
![]() and
and ![]() gives the
net (of the wage) product the marginal worker while
gives the
net (of the wage) product the marginal worker while
![]() denotes
the expected present discounted value of the marginal worker in the
next period. Thus, the left hand side of the above equation can be
interpreted as the net shadow value of the current marginal worker.
If
denotes
the expected present discounted value of the marginal worker in the
next period. Thus, the left hand side of the above equation can be
interpreted as the net shadow value of the current marginal worker.
If ![]() , some workers
are being laid off and equation (11) states that, at the optimum,
the firm equates the expected discounted value of the future
savings due to dismissing the marginal employee to the layoff cost
today. Inaction, i.e.
, some workers
are being laid off and equation (11) states that, at the optimum,
the firm equates the expected discounted value of the future
savings due to dismissing the marginal employee to the layoff cost
today. Inaction, i.e. ![]() , is optimal when the net expected cost of the
marginal worker is smaller than the dismissal cost and greater than
the zero cost of hiring. If
, is optimal when the net expected cost of the
marginal worker is smaller than the dismissal cost and greater than
the zero cost of hiring. If ![]() , the firm is hiring and equation (11) states
that, at the optimum, the firm sets to zero the net shadow value of
the marginal worker.
, the firm is hiring and equation (11) states
that, at the optimum, the firm sets to zero the net shadow value of
the marginal worker.
Recall that ![]() takes value in the set
takes value in the set
![]() . Thus, the first
order condition in (11) implicitly defines the hiring and firing
policy for each firm in state
. Thus, the first
order condition in (11) implicitly defines the hiring and firing
policy for each firm in state ![]() . When a firm moves from a higher to a lower state,
it will lay off some workers but it will set employment above the
optimally desired level, at which the marginal product of labor is
equal to the wage. The intuition behind this result is
straightforward: as the firm faces adjustment costs, the adjustment
will be partial. Furthermore, the linear specification of the
adjustment cost implies that all the adjustment occurs immediately:
there is no advantage to smooth layoffs over time. This result is
in sharp contrast with the implication of convex adjustment costs
à la Tobin's
. When a firm moves from a higher to a lower state,
it will lay off some workers but it will set employment above the
optimally desired level, at which the marginal product of labor is
equal to the wage. The intuition behind this result is
straightforward: as the firm faces adjustment costs, the adjustment
will be partial. Furthermore, the linear specification of the
adjustment cost implies that all the adjustment occurs immediately:
there is no advantage to smooth layoffs over time. This result is
in sharp contrast with the implication of convex adjustment costs
à la Tobin's ![]() . Thus,
equation (11) identifies a firing threshold,
. Thus,
equation (11) identifies a firing threshold, ![]() , at which employment will
be set when a firm falls from state
, at which employment will
be set when a firm falls from state ![]() to state
to state ![]() . Similarly, when a firm moves from a higher to a
lower state, it will hire additional workers but it will set
employment level below the optimally desired level. The firm takes
into account that some workers may have to be fired in the future
if demand turns down, and this is costly. This prospective cost
acts as a hiring cost, deterring the creation of new jobs in good
states. Again, the linear specification of the adjustment cost
implies that all the adjustment occurs immediately. Thus, for each
. Similarly, when a firm moves from a higher to a
lower state, it will hire additional workers but it will set
employment level below the optimally desired level. The firm takes
into account that some workers may have to be fired in the future
if demand turns down, and this is costly. This prospective cost
acts as a hiring cost, deterring the creation of new jobs in good
states. Again, the linear specification of the adjustment cost
implies that all the adjustment occurs immediately. Thus, for each
![]() , equation (11)
identifies a hiring threshold,
, equation (11)
identifies a hiring threshold, ![]() , at which employment will be set when a firm
jumps from state
, at which employment will be set when a firm
jumps from state ![]() to
state
to
state ![]() .
.
We set the values of structural parameters and exogenous
variables to ensure that
![]() for all
for all ![]() 's so that
when a firm is hit by a negative shock it will lay off some workers
and when it is hit by a positive shock it will hire some workers.
In other words, we assume that the demand shocks, i.e. the
difference between
's so that
when a firm is hit by a negative shock it will lay off some workers
and when it is hit by a positive shock it will hire some workers.
In other words, we assume that the demand shocks, i.e. the
difference between
![]() and
and
![]() , are
large enough to induce the firm to change its employment level each
time it is hit by a shock.8
, are
large enough to induce the firm to change its employment level each
time it is hit by a shock.8
In appendix B, we report the details of the derivation of the
hiring and firing thresholds in the steady-state equilibrium, when
the probability mass over the employment is not time dependent.
Here, we just present and discuss the results. The firing threshold
in state ![]() is equal
to:
is equal
to:
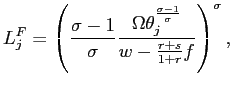
|
(12) |
for
The hiring threshold in state ![]() is equal to:
is equal to:
 ,
, |
(13) |
for
Note that we have not discussed how ![]() and
and ![]() vary with
vary with ![]() . This is because
. This is because ![]() depends on
depends on ![]() and both vary with
and both vary with ![]() . Thus, we postpone this
discussion for when we find an expression for
. Thus, we postpone this
discussion for when we find an expression for ![]() in equilibrium.
in equilibrium.
4.3 The steady-state distribution of firms
In order to derive aggregate labor demand, we have first to
determine the distribution of firms over the employment line; that
is, for example, how many firms are employing
![]() workers. In
the steady-state equilibrium, there is uncertainty at the
firm-level but the aggregate economy is in a stationary state, for
any given pair
workers. In
the steady-state equilibrium, there is uncertainty at the
firm-level but the aggregate economy is in a stationary state, for
any given pair ![]() and
and
![]() .11 A basic feature is that the number of
new hires will be equal to the number of layoffs.
.11 A basic feature is that the number of
new hires will be equal to the number of layoffs.
Recall that we set the values of structural parameters and
exogenous variables to ensure that
![]() for all
for all ![]() 's. Thus,
even if a firm initially employs more than
's. Thus,
even if a firm initially employs more than ![]() , over time, it will fall
over time at or below
, over time, it will fall
over time at or below
![]() .
Similarly, in steady-state, no firm will have
.
Similarly, in steady-state, no firm will have ![]() workers. In other words,
workers. In other words,
![]() and
and
![]() are the two
extremes of the distribution.
are the two
extremes of the distribution.
We are now ready to derive the probability distribution of firms
along the employment line. Let
![]() indicate
the percentage of firms that employ
indicate
the percentage of firms that employ ![]() workers, and
workers, and
![]() indicate
the percentage of firms that employ
indicate
the percentage of firms that employ ![]() . Thus, for example, the probability that a
firm is at
. Thus, for example, the probability that a
firm is at ![]() is
equal to the probability that a firm was in the same state in the
preceding period and did not move,
is
equal to the probability that a firm was in the same state in the
preceding period and did not move,
![]() ,
plus the probability that the firm was in state
,
plus the probability that the firm was in state ![]() and moved up to state
and moved up to state
![]() ,
,
![]() . Note that
if a firm was in state
. Note that
if a firm was in state ![]() and moved down, then it would set employment to
and moved down, then it would set employment to
![]() not to
not to
![]() :
:
![]() does not
depend directly on the percentage of firms in state
does not
depend directly on the percentage of firms in state ![]() . In steady state, these weights
are time invariant and sum up to one, so that we need to solve the
following system:
. In steady state, these weights
are time invariant and sum up to one, so that we need to solve the
following system:
![\begin{displaymath} \left\{ \begin{array}[c]{l} \lambda_{j}=(1-s-q)\lambda_{j}+s... ...\lambda_{j})=1\ \omega_{m}=\lambda_{1}=0. \end{array}\right. \end{displaymath}](img125.gif)
The first two equations form a system of two second order linear
difference equations in
![]() and
and
![]() . The other
four equations give the boundary conditions. The solution of the
above system yields:
. The other
four equations give the boundary conditions. The solution of the
above system yields:
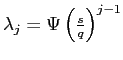 for
for
![]()
![]()
![]()
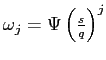 for
for
![]()
![]()
![]()

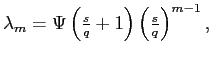
where
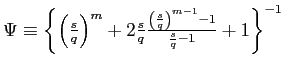 . Note that
. Note that ![]() is
decreasing in
is
decreasing in
![]() .
.
4.4 The partial equilibrium
As the measure of firm is ![]() , there are
, there are
![]() firms
employing
firms
employing ![]() workers and
workers and
![]() firms
employing
firms
employing ![]() workers. Thus, we can easily compute the steady-state aggregate
labor demand as a weighted sum of
workers. Thus, we can easily compute the steady-state aggregate
labor demand as a weighted sum of ![]() and
and ![]() :
:
where
Unfortunately, the expression in (14) is not convenient to
illustrate the qualitative effects of the key parameters,
![]() and
and ![]() , on labor demand. The
following approximation is extremely useful to understand the
economic intuition behind the analytical result. As
, on labor demand. The
following approximation is extremely useful to understand the
economic intuition behind the analytical result. As ![]() increases, the total number of
employees of firms in the extreme states
increases, the total number of
employees of firms in the extreme states ![]() and
and ![]() becomes very small since
becomes very small since ![]() and
and ![]() become a small fraction of
the total. Thus, for
become a small fraction of
the total. Thus, for ![]() large
enough, we can ignore the impact of these two extremes on the
aggregate labor demand. This methodology greatly simplifies algebra
and notation and we can focus on where the driving forces are at
work.12 Since
large
enough, we can ignore the impact of these two extremes on the
aggregate labor demand. This methodology greatly simplifies algebra
and notation and we can focus on where the driving forces are at
work.12 Since
![]() for
for ![]()
![]()
![]()
![]() , one can show that
, one can show that
![]() is
(approximately) proportional to:
is
(approximately) proportional to:
where
Finally, note that ![]() does not depend on the measure of firms,
does not depend on the measure of firms,
![]() . This can be easily
checked substituting
. This can be easily
checked substituting
 for
for ![]() in
equation (14). This result comes from the specification of the
utility function since aggregate demand turns out to be independent
of
in
equation (14). This result comes from the specification of the
utility function since aggregate demand turns out to be independent
of ![]() .
.
4.5 The general equilibrium
In partial equilibrium, each firm sets its price, ![]() , freely according to the first
order condition (11) and takes aggregate demand,
, freely according to the first
order condition (11) and takes aggregate demand, ![]() , as given. In general equilibrium,
instead, prices and aggregate demand are endogenously
determined.
, as given. In general equilibrium,
instead, prices and aggregate demand are endogenously
determined.
In appendix C, we show that all firms at any firing thresholds
charge the same price, ![]() :
:
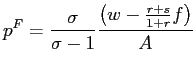
|
(16) |
Since
![]() is
the cost of the marginal worker in a firing threshold and
is
the cost of the marginal worker in a firing threshold and
![]() denotes labor
productivity,
denotes labor
productivity,
![]() represents the
cost of the marginal unit of output. Thus, equation (16) says that
equilibrium price is a simple markup over marginal cost.13 Similarly, all firms at any hiring
thresholds charge the same price,
represents the
cost of the marginal unit of output. Thus, equation (16) says that
equilibrium price is a simple markup over marginal cost.13 Similarly, all firms at any hiring
thresholds charge the same price, ![]() :
:
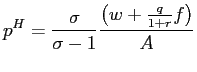
|
(17) |
Since
![]() is
the cost of the marginal worker in a hiring threshold, we find once
again the standard condition that equilibrium price is a markup
over marginal cost. Substituting (16) and (17) for
is
the cost of the marginal worker in a hiring threshold, we find once
again the standard condition that equilibrium price is a markup
over marginal cost. Substituting (16) and (17) for ![]() and
and ![]() into equation (3), we find an
expression for the price index as a function of the structural
parameters of the model:
into equation (3), we find an
expression for the price index as a function of the structural
parameters of the model:
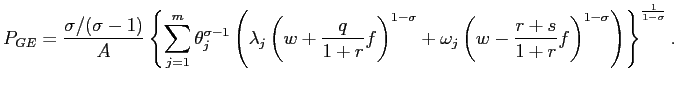
|
(18) |
Secondly, in general equilibrium, aggregate demand, ![]() , is endogenously determined: in
particular, it is proportional to real money balances. Hence, we
need to express
, is endogenously determined: in
particular, it is proportional to real money balances. Hence, we
need to express
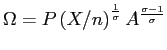 as a function of
as a function of ![]() and the structural parameters of the model, and then substitute
this expression for
and the structural parameters of the model, and then substitute
this expression for ![]() into equation (14). Simple algebra (again see appendix C for
details) yields the following equation for aggregate labor demand
in General Equilibrium:
into equation (14). Simple algebra (again see appendix C for
details) yields the following equation for aggregate labor demand
in General Equilibrium:
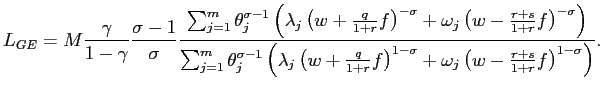
|
(19) |
In order to compare partial and general equilibrium, it is again convenient to carry the same approximation as in section 4.5 which yield:
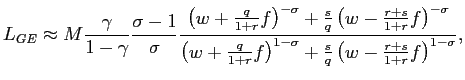
|
(20) |
and then put side by side expressions (15) and (20). If the economy is depressed and turbulent, that is if
Finally, equilibrium aggregate employment is given by the
intersection of equation (19) with the labor supply schedule. Using
the expression (18) to substitute in for ![]() equation (9), it is straightforward
to show that aggregate labor supply in general equilibrium is given
by:
equation (9), it is straightforward
to show that aggregate labor supply in general equilibrium is given
by:
![$\displaystyle N_{GE}=\left( \frac{\left( \sigma-1\right) A\chi w}{\sigma\alpha}... ...gma}\right) \right] ^{\frac{1}{\left( \beta-1\right) \left( \sigma-1\right) }},$](img174.gif)
|
(21) |
and, with the usual approximation, we find:
![$\displaystyle N_{GE}\approx\left( \frac{\left( \sigma-1\right) A\chi w}{\sigma\... ...ma}\right] \right\} ^{\frac{1}{\left( \beta-1\right) \left( \sigma-1\right) }}.$](img175.gif)
|
(22) |
The above expression makes clear that, for a depressed and
turbulent economy, aggregate labor supply is decreasing in
![]() . Intuitively, this
happens because the fall in production causes a rise in the price
index, and thus a fall in the real wage. Note how this price effect
counterbalances the price effect of labor demand, therefore
intensifying the negative impact of firing costs on aggregate
employment.
. Intuitively, this
happens because the fall in production causes a rise in the price
index, and thus a fall in the real wage. Note how this price effect
counterbalances the price effect of labor demand, therefore
intensifying the negative impact of firing costs on aggregate
employment.
The intersection of equations (19) and (21) gives the
equilibrium wage, ![]() ,
and the equilibrium level of employment,
,
and the equilibrium level of employment, ![]() . As for a depressed and
turbulent economy, firing costs shift to the left both labor demand
and labor supply schedules, we find that firing costs hurt
employment.
. As for a depressed and
turbulent economy, firing costs shift to the left both labor demand
and labor supply schedules, we find that firing costs hurt
employment.
5 Numerical Simulations
In this section, we examine the effects of product and market regulations on the functioning of the labor market. We run numerical simulations using the exact expressions for labor demand and supply, equations (19) and (21), and plausible parameter values. The goal is to assess the quantitative effects of firing costs and the markup rate, and to see if we can replicate, at least partially, the downward trend in the employment-population ratio depicted in Figure 1.
First, we present and discuss the several assumptions we need to make about the parameter values.
The first two concern the size and the probability of shocks.
The problem is that there are no estimates of ![]() ,
, ![]() , and the
, and the
![]() 's: we can
only try to infer their sizes from firms' reaction to shocks. Davis
and Haltiwanger (1992) measure establishment level employment
changes in the US manufacturing sector. Three of the main findings
of the paper are that: (i) ``most of annual job creation and
destruction reflects persistent establishment-level employment
changes,'' (ii) ``job destruction is highly concentrated,'' and
(iii) the ``rate of job reallocation is of impressive magnitude''
(p. 821). Therefore, we suppose that firms are hit by large and
infrequent shocks. In other words, the transition probabilities,
's: we can
only try to infer their sizes from firms' reaction to shocks. Davis
and Haltiwanger (1992) measure establishment level employment
changes in the US manufacturing sector. Three of the main findings
of the paper are that: (i) ``most of annual job creation and
destruction reflects persistent establishment-level employment
changes,'' (ii) ``job destruction is highly concentrated,'' and
(iii) the ``rate of job reallocation is of impressive magnitude''
(p. 821). Therefore, we suppose that firms are hit by large and
infrequent shocks. In other words, the transition probabilities,
![]() and
and ![]() , seem to be small, but when these
shocks occur the taste/productivity parameter,
, seem to be small, but when these
shocks occur the taste/productivity parameter,
![]() , seems to
vary considerably.
, seems to
vary considerably.
Furthermore, most European countries experienced substantially
higher productivity growth and substantially lower probability of
negative demand shocks in the 1950s and 1960s than subsequently. In
other words, the slowdown in the rate of productivity growth, the
increase in real oil prices, and the increase in real interest
rates and the fiscal cuts associated with the launch of the Euro
profoundly altered the macroeconomic environment where firms
operate. For this reason, we think we characterize as ``depressed''
most of the European economies in the last thirty years. In other
words, we will simulate an economy where firms are hit more often
by negative than by positive shocks, i.e. ![]() .
.
Another important assumption must be made about the elasticity
of labor supply with respect to the real wage. Equation (9) yields
an elasticity equal to
![]() .
Using
.
Using
![]() which
yields
which
yields
![]() , so we
can infer
, so we
can infer
![]() from
estimates of the elasticity of the labor supply with respect to the
real wage. Here, we set a value for the elasticity of
from
estimates of the elasticity of the labor supply with respect to the
real wage. Here, we set a value for the elasticity of ![]() , bigger than conventional micro
estimates but smaller than those often assumed in aggregate models.
Summarizing, we need
, bigger than conventional micro
estimates but smaller than those often assumed in aggregate models.
Summarizing, we need
![]() ,
which is consistent with
,
which is consistent with ![]() and
and ![]() .
.
Finally, our last key assumption pertains to the degree of
competition among firms. The literature indicates that the markup
rate varies considerably across industries (Roger, 1995).
Unfortunately, our model does not allow for firm's heterogeneity
besides the level of demand. Thus, with this caveat in mind, we set
the markup rate
![]() (or alternatively
(or alternatively
![]() .
We think this corresponds to a plausible situation where firms have
significant market power.
.
We think this corresponds to a plausible situation where firms have
significant market power.
The value of the other parameters are: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.
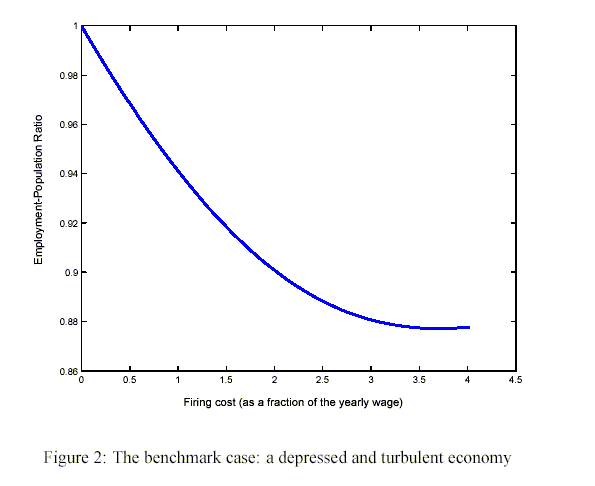
The benchmark case
![]()
For a given set of parameters, we first compute the employment and the wage when firing costs are zero. Then, we use this employment level as a measure of the population for our simulated economy, and this wage rate as a reference for the size of the firing cost.
Figure 2 shows the result of the simulation exercise. On the
horizontal axes, we report the firing cost as a fraction of the
reference wage level. On the vertical axis, we report the ratio
between equilibrium employment and the measure for population. The
message is clear: high layoff costs reduce employment. Even the
magnitude of this change is consistent with Europe's experience in
the past thirty years: an increase in the layoff costs from one to
two times the reference annual wage causes a fall in the
employment-population ratio of about ![]() .
.
We also need to comment on the convex shape of the line depicted
in Figure 2. Specifically, employment becomes slightly increasing
when firing costs are extremely high. Not surprisingly, if job
security provisions are very strict, firms stop firing workers: in
our model, ![]() moves very close to
moves very close to
![]() . The other
side of the coin is that adjustment costs paid by firms become very
high, causing a sharp fall in profits. It seems reasonable that
when profits are too low, some firms will leave the market, causing
a fall in employment. Thus, future work should extend the model by
allowing firms to exit (and enter) the market in order to account
for the impact of firing costs on the extensive margin.
. The other
side of the coin is that adjustment costs paid by firms become very
high, causing a sharp fall in profits. It seems reasonable that
when profits are too low, some firms will leave the market, causing
a fall in employment. Thus, future work should extend the model by
allowing firms to exit (and enter) the market in order to account
for the impact of firing costs on the extensive margin.
Higher frequency (![]() ,
,
![]() ,
, ![]() )
)
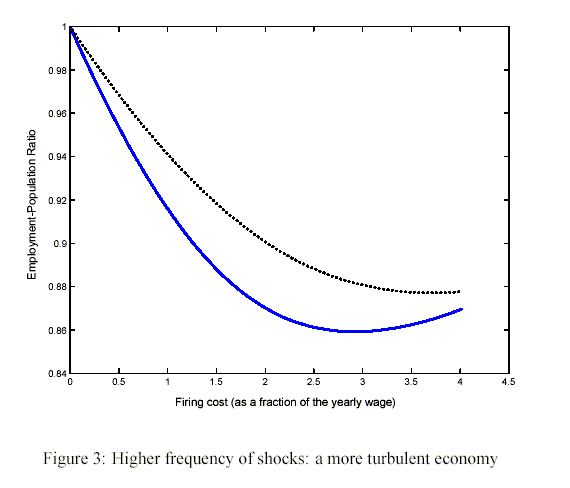
Ljungqvist and Sargent (2002) show how an increase in economic
turbulence - which they measure as workers' income variability - in
conjunction with high unemployment benefits and layoff costs can
contribute to persistently high unemployment. In this paper, by
contrast, we focus on the effect of job security provisions on the
labor demand side. Still, we reach a similar conclusion. An
increase in economic turbulence - here defined as the frequency of
shocks to products' demand - is associated with a more negative
impact of firing costs on employment. For example, in Figure 3, we
raise the transition probabilities (while keeping their ratio
constant), and we find that an increase in the layoff costs from
one to two times the reference annual wage now causes a fall in the
employment-population ratio of about ![]() . The comparison with the benchmark case (the
dotted line) makes evident that, in a depressed economy, an
increase in the frequency of shocks intensifies the negative
consequences of firing costs on employment.
. The comparison with the benchmark case (the
dotted line) makes evident that, in a depressed economy, an
increase in the frequency of shocks intensifies the negative
consequences of firing costs on employment.
Lower market power (![]() ,
, ![]() ,
,
![]() )
)
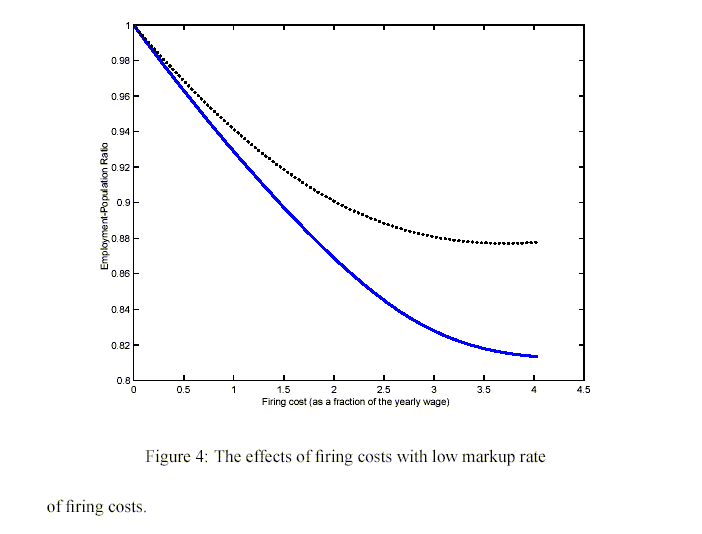
Martins et al. (1996) provide estimates of the markup rate over the period 1970-92, for 36 manufacturing industries in 14 OECD countries. Interestingly for us, they document a downward trend in all European countries they examine. Their results confirm the common belief that the ongoing product market deregulation - associated with the process of European integration - is reducing the market power of firms.
In Figure 4, we reduce the markup rate from ![]() to
to ![]() , and the simulation exercise
shows that lowering the market power intensifies the negative
consequences of layoff costs. For example, an increase in the
layoff costs from one to two times the reference annual wage causes
a fall in the employment-population ratio of about
, and the simulation exercise
shows that lowering the market power intensifies the negative
consequences of layoff costs. For example, an increase in the
layoff costs from one to two times the reference annual wage causes
a fall in the employment-population ratio of about ![]() . Intuitively, the decrease in
rents induces firms to be more worried about future possible
adverse shocks when they are hiring new workers. The comparison
with the benchmark case (the dotted line) clearly shows that, in a
depressed economy, a fall in the markup rate increases the negative
consequences of firing costs.
. Intuitively, the decrease in
rents induces firms to be more worried about future possible
adverse shocks when they are hiring new workers. The comparison
with the benchmark case (the dotted line) clearly shows that, in a
depressed economy, a fall in the markup rate increases the negative
consequences of firing costs.
6 Conclusions
While most empirical evidence links high firing costs to low levels of employment, no agreement has yet emerged about the proper way to model this effect. We have argued that a suitable model must solve five problems simultaneously. The first of these is that the modeling of firing costs involves establishing, for different firms, an upper threshold of employment. Above this threshold, firms fire workers. Second, such a model must establish a lower threshold of employment. Below this threshold, firms hire workers. Third, because the effects of firing costs involves the hires and fires that are made, demand must be represented as subject to shocks; otherwise there will be neither hires nor fires. Fourth, it is necessary to solve for the steady-state probabilities of employment at all levels, and aggregate to compute total steady-state employment. Finally, since aggregate demand depends upon the prices that firms will charge for their goods, it is necessary to solve for the optimal prices, as it is also necessary to compute the wage rate that will clear the labor market.
We were able to accomplish all five of these steps using
standard modeling techniques. We assumed that uncertainty is
governed by a simple ![]() -state
Markov chain, which enabled us to derive analytical solutions for
labor supply and labor demand. In contrast, a standard assumption
in the previous related literature was to characterize uncertainty
with a continuous-time stochastic process. This choice required
that the models had to be solved numerically, so that the forces
driving the results were hidden beneath the surface.
-state
Markov chain, which enabled us to derive analytical solutions for
labor supply and labor demand. In contrast, a standard assumption
in the previous related literature was to characterize uncertainty
with a continuous-time stochastic process. This choice required
that the models had to be solved numerically, so that the forces
driving the results were hidden beneath the surface.
Our analytic solutions, instead, clearly show when firing costs have positive or negative effect on employment. The reasons for such effects are also clear. Job security legislation reduces aggregate employment when (i) negative shocks are more likely to occur than positive shocks, and when (ii) the frequency of shocks is high. In addition, we find that product market deregulation, with an associated fall in market power, induces firms to be more concerned about future possible downturns, intensifying the negative consequences of firing costs.
7 References
Addison, J. and Grosso, J. (1996), `` Job Security Provisions and Employment: Revised Estimates,'' Industrial Relations, Vol. 35, N. 4.
Akerlof, G., Rose, A. and Yellen, J. (1988), `` Job Switching and Job Satisfaction in the US Labor Market,'' Brooking Paper of Economic Activity, Vol. 2, pp. 495-582.
Bentolila S. and Bertola, G. (1989), `` Firing Costs and Labour Demand: How Bad is Eurosclerosis?,'' Review of Economic Studies, Vol. 57, pp. 381-402.
Bentolila S. and Saint-Paul, G. (1994), `` A Model of Labour Demand with Linear Adjustment Costs,'' Labour Economics, Vol. 1, pp. 303-326.
Bertola, G. (1990), `` Job Security, Employment and Wages,'' European Economic Review, Vol. 34, pp. 851-886.
Blanchard, O. (1997), `` The Medium Run,'' mimeo, MIT.
Blanchard, O. (2000), `` Employment Protection, Sclerosis, and the Effect of Shocks on Unemployment,'' Lecture 3, Lionel Robbins Lectures, London School of Economics.
Blanchard, O., Dornbusch, R., Drèze, J., Giersch, H., Layard, R. and Monti, M. (1986), `` Employment and Growth in Europe: A Two Handed Approach,'' in Blanchard, O., Dornbusch, R. and Layard, R. (eds.), Restoring Europe's Prosperity; Macroeconomic Papers from the Centre for European Policy Studies, MIT Press, pp. 95-124.
Blanchard, O. and Giavazzi, F. (2001), `` Macroeconomic Effects of Regulation and Deregulation in Goods and Labor Markets,'' NBER Working Paper, N. 8120.
Blanchard, O. and Kiyotaki, N. (1987), `` Monopolist Competition and the Effects of Aggregate Demand,'' American Economic Review, Vol. 77, N. 4, pp. 647-666.
Blanchard, O. and Wolfers, J. (2000), `` Shocks and Institutions in the Rise of European Unemployment. The Aggregate Evidence,'' Economic Journal, Vol. 110, N. 1, pp. 1-33.
Burda, M. and Wyplosz, C. (1988), `` Gross Labor Market Flows in Europe: Some Stylized Facts,'' CEPR Discussion Paper, N. 439.
Capdeviellle, P. and Sherwood, K. (2002), `` Providing Comparable International Labor Statistics,'' Monthly Labor Review, Vol. 6, pp. 3-14.
Davis, S. and Haltiwanger, J. (1992), `` Gross Job Creation, Gross Job Destruction, and Employment Reallocation,'' Quarterly Journal of Economics, Vol. 107, N. 3, pp.819-863.
De Michelis, A. (2003), `` Costly Layoffs with Procyclical Quits,'' in Essays on the Macroeconomic Effects of Labor Market Rigidities, Chapter 2, Ph.D. Thesis, U.C. Berkeley, pp. 40-61.
Goldberg, P. and Verboven, F. (2001), `` The Evolution of Price Dispersion in the European Car Market,'' Review of Economic Studies, Vol. 68, pp. 811-848.
Grimmett, G. and Stirzaker, D. (1995), Probability and Random Processes, 2nd edition, Clarendon Press, Oxford.
Kugler, A, and Saint-Paul, G. (2000), `` Hiring and Firing Costs, Adverse Selection and Long-term Unemployment,'' mimeo, Universitat Pompeu Fabra.
Hart, O. (1982), `` A Model of Imperfect Competition with Keynesian Features,'' Quarterly Journal of Economics, Vol. 97, pp. 109-138.
Hamermesh, D. (1993), Labor Demand, Princeton University Press.
Hamermesh, D. (1995), `` Labour Demand and the Source of Adjustment Costs,'' The Economic Journal, Vol. 105, pp. 620-634.
Hamermesh, D. and Pfann, G. (1996), `` Adjustment Costs in Factor Demand,'' Journal of Economic Literature, Vol. 34, pp. 1264-1292.
Heckman, J. and Pages, C. (2000) `` The Cost of Job Security Regulation: Evidence from Latin American Labor Markets,'' NBER Working Paper, N. 7773.
Hopenhayn, H. and Rogerson, R. (1993), `` Job Turnover and Policy Evaluations: a General Equilibrium Analysis,'' Journal of Political Economy, Vol. 101, pp. 915-938.
Lazear, E. (1990), `` Job Security Provisions and Unemployment,'' Quarterly Journal of Economics, Vol. 102, pp. 699-726.
Leonard, J. (1987), `` In the Wrong Place at the Wrong Time: the Extent of Structural and Frictional Unemployment,'' in Lang, K. and Leonard, J. (eds.), Unemployment and the Structure of Labor Markets, Basil Blackwell, pp. 141-163.
Leonard, J. and Van Audenrode, M. (1993), `` Corporatism run amok: job stability and industrial policy in Belgium and the United States,'' in Lang, K. and Leonard, S. (eds.), Unemployment and the Structure of Labor Markets, Basil Blackwell, pp. 141-163.
Ljungqvist, L. and Sargent, T. (2002), `` The European Employment Experience,'' mimeo, Stanford University.
Martins, J., Scarpetta, S. and Pilat, D. (1996), `` Markup Ratios in Manufacturing Industries. Estimates from 14 OECD Countries,'' OECD Working Paper, N. 162.
Nickell, S. J. (1986),`` Dynamic Model of Labour Demand,'' in Ashenfelter, O. and R. Layard (eds.), Handbook of Labor Economics, Vol. 1, Elsevier Science Publishers, pp. 473-522.
Nickell, S. J. (1997), `` Unemployment and Labor Market Rigidities: Europe versus North America,'' Journal of Economic Perspectives, Vol. 1, N. 3, pp. 55-74.
OECD (1999), `` Employment Protection and Labour Market Performance,'' in Employment Outlook, Chapter 2, pp.48-132.
Roeger, W. (1995), `` Can Imperfect Competition Explain the Difference between Primal and Dual Productivity Measures? Estimates for US manufacturing,'' Journal of Political Economy, Vol. 103, N. 2, pp. 316-330.
Scarpetta, S. (1996), `` Assessing the Role of Labour Market Policies and Institutional Settings on Unemployment: A Cross Country Study,'' OECD Economic Studies, N. 26, pp. 43-98.
Shapiro, C. and Stiglitz, J. E. (1984), `` Equilibrium Unemployment as a Worker Discipline Device,'' American Economic Review, Vol. 74, N. 3., pp. 433-444.
A Appendix
A.1 The derivation of each individual demand functions and each individual labor supply
Let us begin with the definition of the price index,
![]() . Formally,
. Formally,
![]() is given by:
is given by:
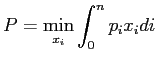 |
(23) |
subject to
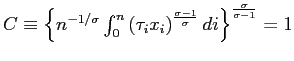 . Set up the Lagrangian:
. Set up the Lagrangian:
![$\displaystyle L=\int_{0}^{n}p_{i}x_{i}di+\lambda_{P}\left\{ 1-\left[ n^{-1/\sig... ...ight) ^{\frac{\sigma-1}{\sigma}}di\right] ^{\frac{\sigma}{\sigma-1}}\right\} . $](img210.gif)
Thus, the first order condition with respect to ![]() yields:
yields:
| (24) |
where
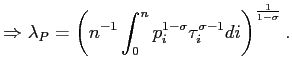
|
(25) |
Plugging (24) and (25) into (23), we get:
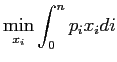 |
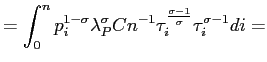
|
|
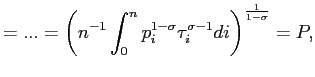
|
which is equation (3).
Recall that we solve the model for the stationary equilibrium.
Thus, consumption, money holding and labor supply is constant over
time. The Euler condition then yields that ![]() , and so no savings:
, and so no savings:
![]() . This
implies that the representative agent consumes the annuity value of
its wealth, which is equal to total firms' profits:
. This
implies that the representative agent consumes the annuity value of
its wealth, which is equal to total firms' profits:
![]() .
.
We are now ready to solve the representative agent's utility maximization problem within each period. We do this into steps. First, each worker chooses the optimal composition of consumption and money holding for a given level of income. Setup the Lagrangian:
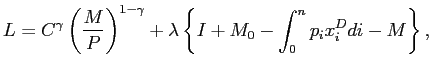
Since (27) holds for all goods
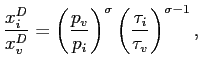
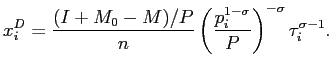
|
(28) |
Let
![]() be `` aggregate demand,'' so taking the ratio of (27) over (26)
yields:
be `` aggregate demand,'' so taking the ratio of (27) over (26)
yields:
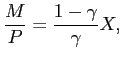
Plugging the above expression into (28) gives the demand
function for good ![]() ,
equation (8):
,
equation (8):
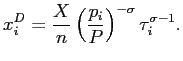
Hence, demand of the composite good for a given level of income is:
| (29) |
The second and final step is to determine labor supply, given the demand functions for money and the composite good:
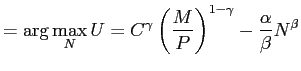
|
||
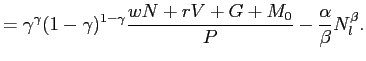
|
The first order condition with respect to ![]() gives:
gives:

B The derivation of the hiring and the firing thresholds
We set the values of structural parameters and exogenous
variables to ensure that
![]() for all
for all ![]() 's so that
when a firm is hit by a negative shock it will lay off some workers
and when it is hit by a positive shock it will hire some
workers.
's so that
when a firm is hit by a negative shock it will lay off some workers
and when it is hit by a positive shock it will hire some
workers.
Recall the Bellman equation (10) and the first order condition
(11). The main issue is to compute
![]() inside
the first order condition. The key to the solution of this problem
is to understand that since future employment decisions will be
taken optimally, the envelope theorem ensures us that they can be
taken as given (in probability distribution) when setting the
current policy. In other words, the marginal worker at period
inside
the first order condition. The key to the solution of this problem
is to understand that since future employment decisions will be
taken optimally, the envelope theorem ensures us that they can be
taken as given (in probability distribution) when setting the
current policy. In other words, the marginal worker at period
![]() is perceived as
marginal for the infinite future.
is perceived as
marginal for the infinite future.
Let ![]() be
the optimal value of the employment level in the current period as
defined by equation (11) and
be
the optimal value of the employment level in the current period as
defined by equation (11) and ![]() is next period's value of the demand shifter.
Taking the derivative of next period value function with respect to
today's control variable yields:
is next period's value of the demand shifter.
Taking the derivative of next period value function with respect to
today's control variable yields:
where
![]() .
Note that
.
Note that ![]() denotes the value of the demand shifter two period ahead and
denotes the value of the demand shifter two period ahead and
![]() the
expectation operator conditional to the information available in
the next period. Since the function
the
expectation operator conditional to the information available in
the next period. Since the function ![]() is not continuously differentiable at zero, we
have to be careful when we expand the expression in (30). Let
consider first the case when the firm will lay off some workers in
the next period, i.e.
is not continuously differentiable at zero, we
have to be careful when we expand the expression in (30). Let
consider first the case when the firm will lay off some workers in
the next period, i.e. ![]() . Then, next period's adjustment costs are
equal to:
. Then, next period's adjustment costs are
equal to:
Using this result in equation (30), we find that the one period ahead shadow value of the current marginal employee is equal to:
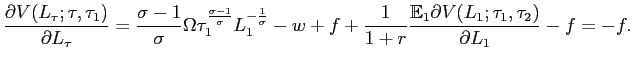
|
(31) |
We used equation (11) to substitute in 0 for
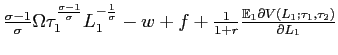 . Intuitively, if the firm will be laying off workers in
period
. Intuitively, if the firm will be laying off workers in
period ![]() , the
shadow value of the marginal employee in period
, the
shadow value of the marginal employee in period ![]() will be equal to the dismissal cost,
will be equal to the dismissal cost,
![]() . Let now consider the
case when the firm will not lay off any worker in the next period,
. Let now consider the
case when the firm will not lay off any worker in the next period,
![]() . Then:
. Then:
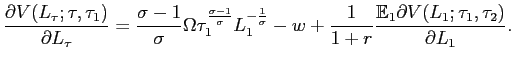
|
(32) |
Using equations (31) and (32) to expand the first order condition, we find:
![$\displaystyle \frac{\partial F(Z)}{\partial L}=\frac{\sigma-1}{\sigma}\Omega\th... ...ft[ 0+(1-s-q)\frac{\partial V(L;\theta_{j},\theta_{j})}{\partial L}-qf\right] ,$](img260.gif)
|
(33) |
for
We are now ready to find the hiring and the firing thresholds.
Suppose that, in the last period, the firm ![]() was in state
was in state ![]() and this period is in state
and this period is in state
![]() . Combing equations
(33) and (34), we find an expression for the firing threshold in
state
. Combing equations
(33) and (34), we find an expression for the firing threshold in
state ![]() :
:
![$\displaystyle \frac{\sigma-1}{\sigma}\Omega\theta_{j}^{\frac{\sigma-1}{\sigma}}... ...{F}\right) ^{-\frac{1}{\sigma}}-w+\frac{1}{1+r}\left[ 0-(1-s-q)f-qf\right] =-f $](img262.gif)
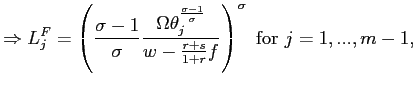
![$\displaystyle \frac{\sigma-1}{\sigma}\Omega\theta_{j}^{\frac{\sigma-1}{\sigma}}... ...( L_{j}^{H}\right) ^{-\frac{1}{\sigma}}-w+\frac{1}{1+r}\left[ 0+0-qf\right] =0 $](img267.gif)
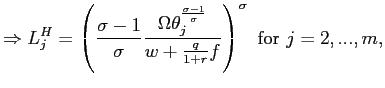
C The characterization of the general equilibrium
We start by finding the equilibrium prices. Recall from the first order condition of the consumer maximization problem:
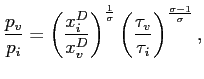
|
(35) |
where
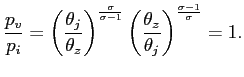
Thus,
![]() Similarly, one can check that
Similarly, one can check that
![]() . Finally, equation (35) implies
that the ratio between
. Finally, equation (35) implies
that the ratio between ![]() and
and ![]() is:
is:
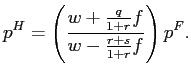
Using these results into the expression for the price index
![]() , we get:
, we get:
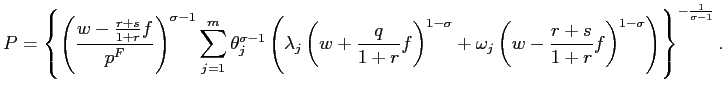
|
(36) |
Using the above expression and recalling that aggregate demand
is proportional to real money balances, we can express ![]() as a function of
as a function of ![]() :
:
Therefore, in general equilibrium, the aggregate supply of goods
![]() 's is:
's is:
 |
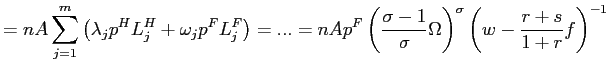
|
|
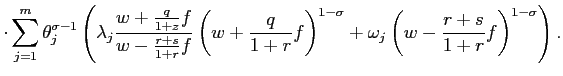
|
Using equation (37) to substitute in for ![]() in the above expression
yields:
in the above expression
yields:
![$\displaystyle \int_{0}^{n}p_{i}x_{i}di=...=\left[ \frac{Ap^{F}}{\frac{\sigma}{\... ...}\left( w-\frac{r+s}{1+r}f\right) }\right] ^{\sigma}\frac{\gamma }{1-\gamma}M. $](img283.gif)
Recall
![]() and
and
![]() , thus, the equilibrium
price charged by all firms at any firing threshold is given by:
, thus, the equilibrium
price charged by all firms at any firing threshold is given by:
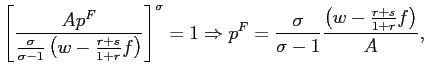
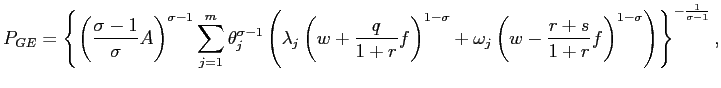
We now have all the elements to write down an expression for
aggregate labor demand in general equilibrium, ![]() :
:
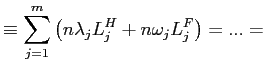
|
||
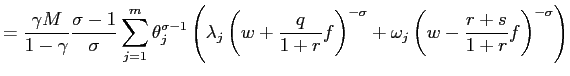
|
||
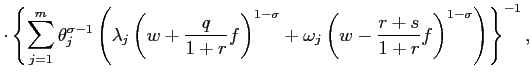
|
which the same as equation (19).
The final step is to solve for labor supply in general equilibrium, equation (21):

|
||
![$\displaystyle =\left\{ Aw\frac{\chi}{\alpha}\frac{\sigma-1}{\sigma}\left[ \sum ... ...^{1-\sigma}\right) \right] ^{\frac{1}{\sigma-1}}\right\} ^{\frac{1} {\beta-1}}.$](img295.gif)
|
D The benchmark case of no adjustment costs
When layoff costs are equal to zero, the firm ![]() sets marginal the product of labor
is equal to the wage in all periods. Therefore, we have:
sets marginal the product of labor
is equal to the wage in all periods. Therefore, we have:
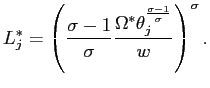
|
(38) |
It is easy to check that the case of zero layoff costs is yields
the same steady-state distribution of firms along the employment
line. Define with ![]() the steady-state probability that a firm is
in state
the steady-state probability that a firm is
in state ![]() , then
, then
![]() . In fact, it is
straightforward to show that the solution of
. In fact, it is
straightforward to show that the solution of
![]() with
boundary conditions
with
boundary conditions
![]() and
and
![]() is given by
is given by
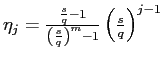 for
for ![]()
![]()
![]() .
.
Given this, it is immediate to find an expression for
equilibrium aggregate employment without layoff costs. Let us begin
with deriving aggregate labor demand in partial equilibrium,
![]() . Recall that
equation (38) defines the employment level,
. Recall that
equation (38) defines the employment level,
![]() , at which
the marginal product of labor is equal to the wage. Thus, we find:
, at which
the marginal product of labor is equal to the wage. Thus, we find:
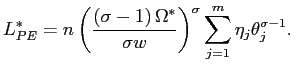
In general equilibrium, we need to consider that all firms set
the same price
![]() so
that:
so
that:
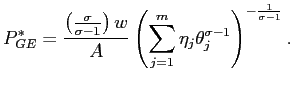
Similarly, we need to adjust the labor supply equation. Thus, aggregate labor demand and aggregate labor supply without layoff costs are given by:
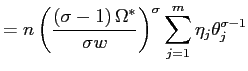
|
||
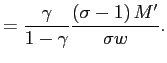
|
For the numerical simulations, it is also useful to compute
![]() in
general equilibrium:
in
general equilibrium:
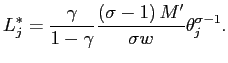
Finally, aggregate labor supply in general equilibrium is given by:
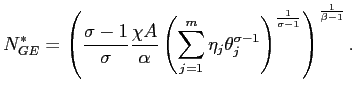
Summarizing, both
![]() and
and
![]() are
decreasing in
are
decreasing in ![]() , thus
both schedules shift out following a fall in
, thus
both schedules shift out following a fall in ![]() resulting into higher employment
and higher wage.
resulting into higher employment
and higher wage.
Footnotes
1. Much of the current job security regulations were introduced between the 1950s and the 1970s. The recession following the 1973 oil shock gave an additional impetus to goverments to adopt various protective measures. Since then, the broad evolution has been towards deregulation, but at an extremly slow pace (OECD, 1999). Return to text
2. All employment figures in the paper are based on BLS data which put foreign countries on a similar basis as the US. See Capdeviellle and Sherwood (2002) for a detailed presentation of the BLS international data.
In Figure 1, we normalized the employment-population ratios across country using 1973 as a base year. This is because social norms have a substantial impact on labor partecipation, especially for women and young individuals. By indexing our data with a base year, we want to direct the reader's attention to the change in the employment-population ratio that occured over time. Return to text
3. To the best of our knowledge, Leonard and Van Audenrode (1993) were the first to argue this conjecture. Return to text
4. Furthermore, the potential impact of severance payments could be undone by designing a wage contract that cancels out the effect of a transfer from firms to laid off workers. For example, as in the efficiency wage model of Shapiro and Stiglitz (1984), we could have workers post a bond of the value of the transfer which they would forfeit in case they are dismissed. Alternatively and more realistically, think of an employment package which pays rising wages over time. This is in fact equivalent to a constant wage, except that the firm keeps part of the early payments as a bond and returns it to the worker later if she is still employed. Return to text
5. The assumption of zero hiring cost does not affect the qualitative conclusions of the paper. It could be easily relaxed at the cost of longer and more cumbersome notation.
Furthermore, note that as labor is homogenoeus, net and gross labor flows coincide. Return to text
6. In fact, this is the argument exploited by Hopenhayn and Rogerson (1993): firing costs are equivalent to a less productive technology, and so reduce employment and welfare. Here, we want to show that firing costs can have a negative effect on employment through a different channel. Return to text
7. The value function depends on the lagged value of the demand shifter because today's adjustment costs depend on how a firm got to the current state, by firing or hiring workers. Return to text
8. Alternatively, we could think that it takes two or more consecutive positive (or negative) shocks to make the firm want to hire (layoff). However, this alternative assumption would just complicate notation without adding any new insight. Return to text
9. Recall that we have defined
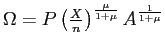 and
and
![]() Return to text
Return to text
10. See the Appendix D for a complete analysis of the benchmark case of zero layoff costs. Return to text
11. Irrespective of the initial
conditions, the stochastic process converges towards a steady-state
where the probability mass at any level of employment is not time
dependen. Formally, this result comes from the assumption that we
are considering a discrete time finite-state Markov chain which is
ergodic, i.e. irreducible with aperiodic, recurrent states. An
ergodic Markov chain converges to a distribution where the
probability of being in state ![]() is independent of the initial state. For a proof of
this result and a thorough analysis of the stationarity, the limit
theorem and the ergodic theorem for Markov chains, see Grimmett and
Stirzaker (1995), section 6.4, pp. 207-218, and section 9.5, pp.
367-380. Return to text
is independent of the initial state. For a proof of
this result and a thorough analysis of the stationarity, the limit
theorem and the ergodic theorem for Markov chains, see Grimmett and
Stirzaker (1995), section 6.4, pp. 207-218, and section 9.5, pp.
367-380. Return to text
12. We check the accuracy of these approximation by carrying out simulations for both the exact case and for the approximate case. Return to text
13. As usual, the markup rate,
![]() , is given demand's
elasticty according to:
, is given demand's
elasticty according to:
![]() . Return to text
. Return to text
14. Note that
![]() as
as ![]() and that we still have
and that we still have
![]() . Thus, the dominating term is
. Thus, the dominating term is
![]() which is
decreasing in
which is
decreasing in ![]() .
.
15. Note that in state ![]() , firms will remain in the same state
next period with probability
, firms will remain in the same state
next period with probability ![]() and will move to state
and will move to state ![]() with probablity
with probablity ![]() . Thus, the first order condition
is:
. Thus, the first order condition
is:
![$ \frac{\sigma-1}{\sigma}\Omega\theta_{1}^{\frac{\sigma-1}{\sigma}}\left( L_{1}^{F}\right) ^{-\frac{1}{\sigma}}-w+\frac{1}{1+r}\left[ s0-(1-s)f\right] =0.$](img266.gif) This expression still implies equation (12). Return to text
This expression still implies equation (12). Return to text
16. Note that in state ![]() , firms will remain in the same state
next period with probability
, firms will remain in the same state
next period with probability ![]() and will move to state
and will move to state ![]() with probablity
with probablity ![]() . Thus, the first order condition
is:
. Thus, the first order condition
is:
![$ \frac{\sigma-1}{\sigma}\Omega\theta_{m}^{\frac{\sigma-1}{\sigma}}\left( L_{m}^{H}\right) ^{-\frac{1}{\sigma}}-w+\frac{1}{1+r}\left[ q0-(1-q)f\right] =0.$](img270.gif) This expression still implies equation (13). Return to text
This expression still implies equation (13). Return to text
This version is optimized for use by screen readers. A printable pdf version is available.
![$\displaystyle U_{0}=\mathbb{E}_{0}\sum_{t=0}^{\infty}\left( \frac{1}{1+\delta}\... ...ac{M_{t}}{P_{t}}\right) ^{1-\gamma }-\frac{\alpha}{\beta}N_{t}^{\beta}\right] ,$](img2.gif)
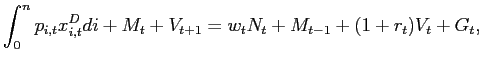
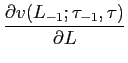
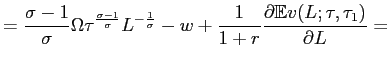
![$\displaystyle =\frac{\partial F(Z)}{\partial L}=\left\{ \begin{array}[c]{l} -f\... ...\left[ -f,\text{ }0\right] \text{, if }Z=0\\ 0,\text{ }Z<0. \end{array} \right.$](img93.gif)
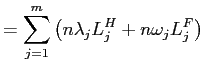
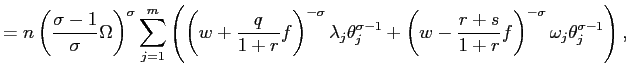
![$\displaystyle L_{PE}\approx\Lambda\left[ \left( w+\frac{q}{1+r}f\right) ^{-\sigma} +\frac{s}{q}\left( w-\frac{r+s}{1+r}f\right) ^{-\sigma}\right] ,$](img148.gif)
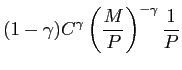
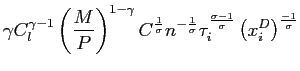
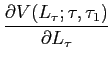
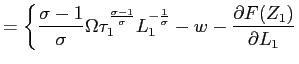
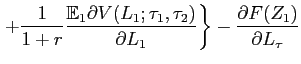
![$\displaystyle \frac{\partial V(L;\theta_{j},\theta_{j})}{\partial L}=\left\{ \b... ...c]{c} -f,\text{ if }L=L_{j}^{F}\\ 0,\text{ if }L=L_{j}^{H}. \end{array} \right.$](img261.gif)