A Quantitative Credit Risk Model and Single-Counterparty Credit Limits

Data and Calibration

Before describing the credit risk model in detail it is useful to discuss the key model parameter that will inform the calibration of the inter-SIFI credit concentration limit. The correlation between two SIFIs plays an important role in determining an appropriate credit limit in the model.

Correlation is a key risk management concept that has been instrumental in modeling and understanding risk since Markowitz's Nobel Prize winning model of portfolio selection.⁵ A key insight of modern risk management theory is that assets that display a large and positive correlation with each other present more risk when paired in a portfolio than assets with a relatively low degree of correlation, even if each asset's risk level is the same when considered in isolation. A SIFI that makes a credit extension to another company that is highly correlated with the performance of the rest of the SIFI's assets results in greater risk than a credit extension to a company that exhibits a lower correlation with the rest of the SIFI's asset portfolio.

Given the importance of the correlation parameter to the results of the model, it is important to have an empirically based and theoretically sound estimate of the correlation between a SIFI and another SIFI and the correlation between a SIFI and a non-SIFI. There are a number of approaches that could be used to estimate these correlations. Data on the market value of assets among SIFIs and non-SIFIs could be analyzed. The correlation in equity values could also be analyzed as equity represents a claim on a firm's underlying assets. Data on underlying credit or CDS spreads could be also used.

This analysis considers CDS spreads, as they are directly informative about probability of default. Default probabilities are of direct relevance to the issue of credit concentration limits and the credit risk model that will be used to calibrate the inter-SIFI credit limit.

Weekly data on CDS spreads of 13 GSIBs and SIFIs that have been identified by the FSOC over the 2006-15 period are considered in this analysis.⁶ The firms used in the analysis were chosen as a representative sample of SIFIs with high-quality and continuous CDS data over the entire sample period. In the analysis that follows, the weekly changes in these CDS spreads are used to form an estimate of the correlation between two SIFIs. Finally, note that among 13 SIFIs, there are 78 ((13x12)/2) distinct SIFI-to-SIFI pairings that can be considered in the analysis.

For non-SIFIs, weekly data on CDS spreads from 256 companies that are cleared by Intercontinental Exchange (ICE) Clear Credit and for which a continuous record of weekly CDS data over the entire 2006-15 sample period is available are used in this analysis. Attention is restricted to companies for which CDS are cleared by ICE Clear Credit to ensure that the underlying companies have relatively liquid CDS markets for which high-quality and reliable CDS data can be obtained. The companies used in this analysis are drawn from a range of industries including consumer goods, financials, industrials, and technology and represent a broad sample of the types of non-SIFI companies to which a SIFI may have a credit exposure. The data on non-SIFI CDS spreads is combined with the data on SIFI CDS spreads to estimate the correlation between a SIFI and non-SIFI. Finally, note that since there are 256 non-SIFI companies and 13 SIFIs considered in the analysis, there are 3,328 (13x256) distinct SIFI to non-SIFI pairings that can be considered in the analysis.

Figure 1 shows the average rolling two-year (100 week) correlation in the weekly change in CDS spreads between each of the 78 SIFI-to- SIFI pairings (solid line) and the average rolling two-year (100 week) correlation in the weekly change in CDS spreads between each of the 3,328 SIFI to non-SIFI pairings (dashed line) over the sample period.

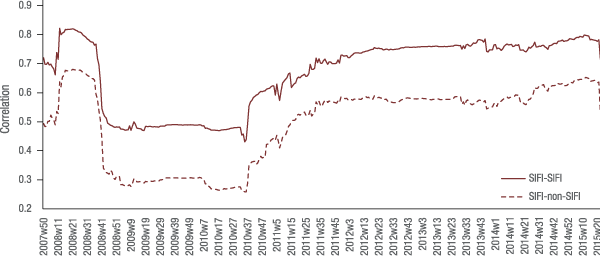
Figure 1 shows that throughout the sample period the average correlation between two SIFIs (solid line) was uniformly above that of the average correlation between a SIFI and non-SIFI (dashed line).⁷ Moreover, while the absolute level of correlation does change over time, which is consistent with broad empirical evidence that correlations are time-varying, the relative ordering of the two correlation measures is stable. The average correlation among SIFIs is always larger than the average correlation among a SIFI and non-SIFI. The time-series average of the SIFI to SIFI correlation (solid line) is 0.67 while the time series average of the SIFI to non-SIFI correlation is 0.50.

The results in figure 1 also accord with theoretical considerations that would suggest that two SIFIs would exhibit a higher correlation with each other than would a SIFI with a non-SIFI. As discussed earlier, SIFIs generally are engaged in a similar mix of business lines, share many counterparties in common, and rely on similar sources of funding. As a result, it is natural to expect that two SIFIs would exhibit a greater degree of correlation with each other than would be exhibited between a SIFI and non-SIFI company. More generally, it is quite common in empirical economic models to assume that companies within the same sector exhibit a higher degree of correlation than companies across sectors.

In the context of the credit risk model that will be used to calibrate the level of the inter-SIFI credit limit, what matters is the correlation between SIFIs during a period when the credit-granting SIFI's counterparty is either approaching or is in default. Empirical data analysis is limited in its ability to measure such correlations since SIFI defaults did not occur over the sample period. Also, even though the data sample covers the period of the financial crisis, the extraordinary government support that was provided over this period makes it difficult to rely on correlation estimates alone. Moreover, all of the economic forces that tend to result in a larger correlation between SIFIs in the weekly CDS data would likely be magnified in a period of stress if a SIFI defaulted, as the effects of the SIFI default spread throughout the capital markets and influenced counterparty relationships, funding costs, and overall financial conditions. Accordingly, there are sound economic considerations that would suggest that the increase in the SIFI to SIFI correlation relative to the SIFI to non-SIFI correlation may be even larger in a period of stress than that suggested by these data.

The correlation estimates presented in figure 1 represent, at each point in time, the average correlation between two SIFIs and the average correlation between a SIFI and non-SIFI. In practice, there are a range of correlations that exist between SIFIs and between a SIFI and non-SIFI. From a risk-management perspective, it is important to consider more than just the average correlation, since correlations that are above the average present more risk than that suggested by the average. Figure 2 shows a time series plot that is constructed in exactly the same manner as figure 1, except that instead of taking the average correlation at each point in time, the 90th percentile correlation among all possible company pairings is plotted. This figure provides a sense of the magnitude of the correlations that exist between companies that are more tightly connected than that depicted by the average correlation.

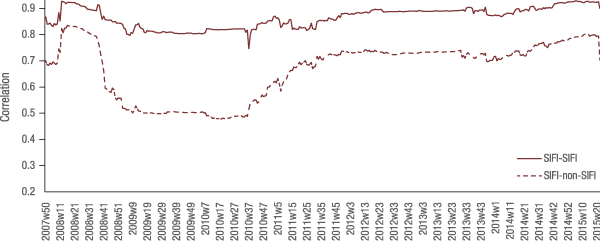
Figure 2 shows that the estimated correlation increases when considering companies that are more tightly connected than the average. This is true when considering both the SIFI to SIFI correlation and the SIFI to non-SIFI correlation. The time-series average of the SIFI to SIFI correlation depicted in figure 2 (solid line) is 0.87 while the corresponding time-series average for the SIFI to non-SIFI correlation (dashed line) is 0.67. Moreover, the difference in the correlation estimates shown in figure 2, which is roughly 0.2, is similar to the difference depicted in figure 1, which suggests that it is reasonable to assume that the SIFI to SIFI correlation exceeds the correlation between a SIFI and non-SIFI by roughly 0.2.

The correlation estimates and related discussion presented above indicate that there is a strong rationale for more stringent single-counterparty credit limits on inter-SIFI credit extensions. The financial performance of a SIFI is more tightly connected to other SIFIs than to non-SIFIs and so the total amount of risk that is incurred from SIFI to SIFI credit extensions is greater than that incurred by SIFI to non-SIFI credit extensions. In order to ensure that SIFI to SIFI credit extensions do not pose significantly greater risk to SIFI lenders, and ultimately financial stability, the single-counterparty credit limit on inter-SIFI credit exposures must be more stringent than that on SIFI to non-SIFI credit exposures.

In order to quantify an appropriate inter-SIFI credit limit, a quantitative model is required. The next section discusses the quantitative model employed and provides a range of inter-SIFI credit limits consistent with observed data and the model.

Back to section top

Quantitative Credit Risk Model Description

The model described below considers a situation in which a SIFI with a pre-existing portfolio of assets extends a single loan to a counterparty. The case of extending a loan to a non-SIFI is described and then the case of extending a loan to a SIFI is described.

Consider a SIFI with a portfolio of assets that decides to extend a loan to a non-SIFI in an amount that is equal to the credit exposure limit of 25 percent of capital. Further normalize the assets of the bank to $1 and assume that the bank's capital ratio is 10 percent. Accordingly, the size of the loan extended to the non-SIFI is given by:

$$ a=0.25\times0.10=0.025$$

and the size of the SIFI's remaining assets are given by:

$$ A=1-a=0.975$$

so that total assets of the SIFI are given by $$ A+a=1$$.

Further assume that the rate of return on all assets are log-normally distributed and have the same mean rate of return of 1 percent. The volatility of log assets is assumed to be 3 percent in the case of the SIFI's overall asset portfolio net of the loan, $$ A$$, and 9 percent in the case of the individual loan, $$ a$$. The increased risk of the individual loan relative to the remainder of the SIFI's assets is motivated on the grounds that a single loan carries significant idiosyncratic risk while the entirety of the SIFI's balance sheet benefits from substantial offsets and diversification across multiple borrowers and business lines such as trading, real estate loans, corporate loans, and consumer loans.

Under these assumptions, the value of each component of the SIFI's assets one period ahead in the future is given by,

$$ \tilde{A}=A\exp(0.01+0.03\varepsilon)$$

$$ \tilde{a}=a\exp(0.01+0.09\upsilon)$$

and the correlation between the future value of the non-SIFI loan and the rest of the SIFI's assets is determined by the correlation between the shocks - $$ \varepsilon$$ and $$ \upsilon$$. These shocks should be interpreted as factors that either increase or decrease the value of the SIFI's assets and the loan over time. As an example, a negative shock to the borrower's product market that results in greatly diminished revenues and makes loan default more likely would be represented by a negative value of $$ \upsilon$$. For the purposes of this exercise, it is assumed that the correlation between the value of the loan and the value of the remainder of the SIFI's assets, $$ \rho(\tilde{A},\tilde{a})$$, is 65 percent, which is consistent with the empirical correlation analysis that was previously discussed. Specifically, a correlation value of 0.65 is consistent with the time-series average correlation depicted in figure 2 (dashed line), which presents the 90th percentile correlation between a SIFI and non-SIFI. A correlation value of 0.65 is also within the range of the time series of the average correlations presented in figure 1 (dashed line).

The probability that the SIFI enters default depends on the assumption that is made about the level of capital that is required to remain viable as a going concern. One assumption is that a SIFI can remain viable until all of its capital is exhausted. The financial crisis demonstrated, however, that SIFIs can become non-viable long before their entire capital stock is depleted. Once a SIFI's capital reaches a threshold value, their counterparties and funding providers begin to run, which can result in a downward spiral that, absent outside intervention, results in non-viability as a going concern and ultimately default. For the purposes of this exercise it is assumed that a SIFI is deemed to be non-viable and effectively in default whenever its capital level reaches 4.5 percent, which is consistent with existing minimum regulatory capital requirements. Accordingly, the probability of default is simply the probability that the total value of the SIFI's assets falls below a level that results in less than a 4.5 percent capital ratio. The SIFI's level of equity at the end of the period, $$ \tilde{E}$$, is given by,

$$ \tilde{E}=0.10-\left(1-(\tilde{A}+\tilde{a})\right)$$

and the SIFI's capital ratio is given by,

$$ \frac{\tilde{E}}{\tilde{A}+\tilde{a}}$$

so that the probability that the SIFI enters default is given by,

$$ Pr\left(\frac{\tilde{E}}{\tilde{A}+\tilde{a}}<0.045\right)$$

Now consider the same SIFI deciding instead to allocate the marginal loan to a SIFI counterparty rather than to a non-SIFI counterparty. The entire preceding analysis is unaffected except that the assumed correlation between the SIFI extending the credit and the SIFI that is receiving the credit is higher than the previously assumed correlation between the SIFI lender and the non-SIFI borrower.

As discussed previously, given the similarity in broad risk exposures and business lines among SIFIs, it is reasonable to expect that the correlation between the value of the loan made to a SIFI and the rest of the SIFI's assets is significantly higher than is the case when a loan is made to a non-SIFI. Specifically, drawing on the previous empirical correlation analysis it is assumed that the correlation $$ \rho(\tilde{A},\tilde{a})$$ is 85 percent. This heightened SIFI to SIFI correlation is consistent with the correlation analysis discussed above. Specifically, a correlation value of 85 percent is consistent with the time-series average correlation depicted in figure 2 (solid line) which presents the 90th percentile correlation between two SIFIs. A correlation value of 85 percent is also broadly consistent with the range of the time series of the average correlations that is presented in figure 1 (solid line). In particular, note that the relative increase in the inter-SIFI correlation is 0.2 (0.85 versus 0.65), which is consistent with the data presented in both figures 1 and 2. In what follows, the model will also be analyzed using a lower correlation assumption of 70 percent and a higher correlation assumption of 99 percent to gauge its sensitivity to this key input, but the value of 85 percent will serve as the baseline. Finally, before describing the model results, the model's key initial conditions and assumptions are summarized in table 1 for ease of reference.

Table 1. Model initial conditions and assumptions

Model initial conditions
Initial value of assets	1.0
Initial value of loan	0.025
Initial capital ratio	0.10
Model assumptions
Statistical distribution	Log-normal
Rate of return on assets	0.01
Volatility of value of (log) bank assets ex-loan (A)	0.03
Volatility of (log) loan asset (a)	0.09
Correlation between SIFI and non-SIFI borrower	0.65
Correlation between SIFI and SIFI borrower-- lower than baseline	0.70
Correlation between SIFI and SIFI borrower-- baseline	0.85
Correlation between SIFI and SIFI borrower-- higher than baseline	0.99

Back to section top

Model Results and Calibrated Inter-SIFI Credit Limits

The model described above is simulated and figure 3 below depicts the resulting probability of the bank's default as a function of the stringency of the inter-SIFI limit. The horizontal green line depicts the default probability that results in the case of a SIFI to non-SIFI loan when the single-counterparty credit limit is 25 percent. This line is not sensitive to the inter-SIFI limit since the loan to a non-SIFI counterparty is not bound by the inter-SIFI limit.⁸ The solid red upward sloping line represents the probability of default that arises in the context of a SIFI to SIFI loan as the inter-SIFI credit limit rises from 0 to 25 percent when the inter-SIFI correlation is set to the baseline level of 85 percent.

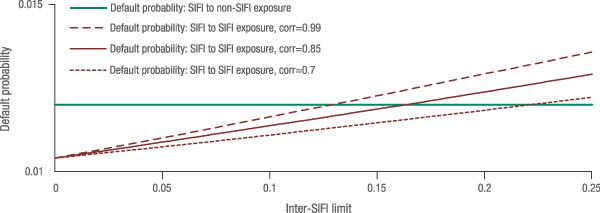
As shown in figure 3, setting the inter-SIFI limit at the original 25 percent limit results in a larger default probability than the SIFI to non-SIFI case, because the correlation between the assets of the credit-granting SIFI and the SIFI borrower are highly correlated relative to the non-SIFI borrower. As the inter-SIFI limit is tightened, the probability of default declines. The decline in default probability occurs because, as the size of the loan to the SIFI declines, the bank is investing more of its assets in a less risky and more diversified pool of assets. Accordingly, an implicit assumption of this analysis is that assets that are not lent out to the borrower SIFI are re-invested back into the lender SIFI's asset mix in a proportional manner without creating another large exposure to a risky counterparty.

According to figure 3, the particular constellation of model parameters that are reported in table 1 under the baseline case indicates that reducing the inter-SIFI limit to a level of roughly 17 percent would equalize the total credit risk across loans made to a SIFI and a non-SIFI counterparty. Graphically, this is the point where the red and green lines intersect.

Of course, these results are generated from a model that has been calibrated in a particular way. In practice there is likely a range of parameters that could be used to calibrate the model and so a single calibration of the model should not be exclusively relied upon. Figure 3 also depicts the results from two additional calibrations of the model in which the correlation between the SIFI lender and SIFI borrower, a key model parameter, has been set to values above and below the baseline value of 85 percent. More specifically, figure 3 shows two additional dashed lines that depict how the default probability reacts to the inter-SIFI credit limit when the assumed correlation is 70 percent (dotted line below the solid red line) and 99 percent (dashed line above the solid red line). These correlation levels are roughly equidistant from the baseline level of 85 percent and are broadly within the range of observed inter-SIFI correlations that are presented in figures 1 and 2. The point of intersection between each dashed line and the solid green line identifies the inter-SIFI credit limit that would be consistent with the higher and lower assumed correlation value.

As shown in figure 3, a higher assumed correlation between SIFIs results in an even more stringent inter-SIFI credit limit as the dashed line above the solid red line intersects the solid red line at roughly 13 percent. Correspondingly, a lower assumed correlation between SIFIs results in a less stringent inter-SIFI credit limit as the dotted line below the solid red line intersects the solid red line at roughly 23 percent. Accordingly, this model combined with a data-based calibration indicates that an appropriate level for the inter-SIFI credit limit could range between 13 and 23 percent. The specific magnitudes are useful for providing a quantitative sense of the reasonable range over which such inter-SIFI credit limits may be set.

Finally, and importantly, it should also be noted that the preceding analysis does not explicitly make any adjustments to reflect the greater social costs associated with multiple SIFI defaults relative to a situation in which a SIFI enters default as the result of a default of a non-SIFI. The adverse effects on the financial system and economy are likely many times greater than the adverse effects of a SIFI default paired with the default of a non-SIFI. In addition, this analysis also excludes from consideration the additional knock on effects that could reverberate through the financial system following a multiple SIFI default event. All of these considerations suggest that an appropriate inter-SIFI credit limit could reasonably be set meaningfully more stringently than the levels that are indicated in figure 3.

Back to section top

References

• Other Formats

• Full report (PDF)

• Stay Connected

• Twitter
• YouTube
• Flickr
• RSS Feeds
• Subscribe