FEDS Notes
May 7, 2014
Forecasting Stock Market Crashes is Hard--Especially Future Ones: Can Option Prices Help?
Eric Engstrom 1
Yogi Berra's admonition, "It's tough to make predictions, especially about the future," applies to many types of prognostication, but it is especially appropriate for forecasting the stock market. Stock market gyrations are notoriously hard to predict, and not for lack of effort by legions of investors, market commentators and academics. In this article, we investigate whether efforts to forecast stock market crashes, in particular, can be aided by using information embedded in options prices.
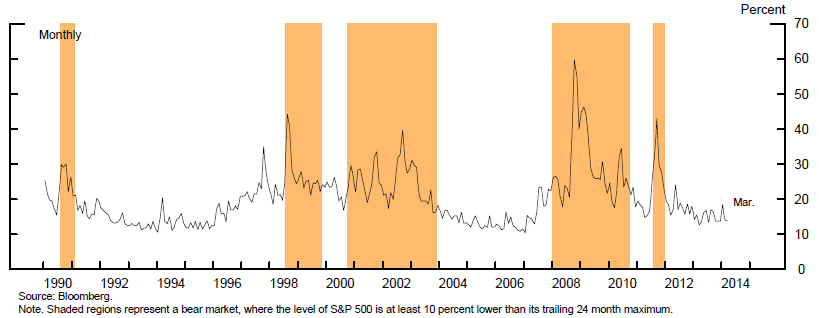
It is natural to suppose that the prices of options might be useful for forecasting crashes, given the long history of using options prices as indicators of investor sentiment and uncertainty regarding the outlook for the prices of financial assets. Perhaps the most commonly cited index of option prices is the VIX, a weighted average of prices of options on the S&P 500 index that is calculated by the Chicago Board Options Exchange. The VIX is often referred to as the "market fear gauge" because of its tendency to shoot up during periods of market stress. As depicted in Figure 1, the VIX is substantially higher, on average, during bear markets, the shaded regions. Of course, this is not to say that high levels of the VIX index forecast bear markets. Alas, increases in the VIX tend mostly to just coincide with declines in equity prices. However, it turns out that the VIX is somewhat useful as a statistical forecaster of future market volatility, the magnitude of fluctuations in equity prices, both up and down.2
Of course, beyond volatility, information regarding the likelihood of large stock declines is naturally of great interest to market participants and observers. It is perhaps not surprising then that other indexes, also based on the prices of options, have been developed specifically to focus on expectations for stock market crashes. In particular, some analysts calculate the so-called "option-implied probabilities," or OIPs, of large stock market declines.
| Figure 2: Calculating Option-Implied Probability (OIP), Hypothetical Example |
|---|
|
Note: In this example, the rate of return on a risk-free bond is assumed to be zero. |
Figure 2 describes how, in principle, option prices could be used to calculate the OIP of a stock market crash. Consider a "binary" option that pays $1.00 should the S&P 500 drop by 10 percent or more over the coming month and pays nothing otherwise, offering a kind of insurance against losses. If the market price of this option were 2 cents, then the "option-implied" probability, or OIP, of a 10 percent crash or worse is defined as 2 percent (the two cent price divided by the $1 payoff in the event a crash occurs). In practice, we do not directly observe many of these binary options, but we can still impute OIPs from prices of standard call and put options that trade on the S&P 500 index.
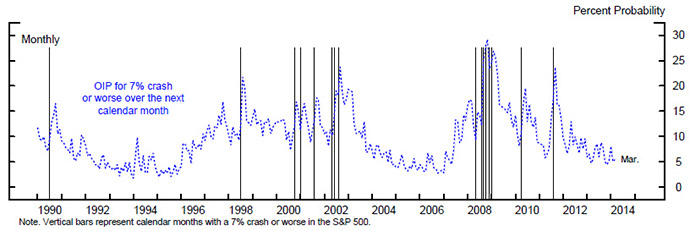
For concreteness, the dotted blue line in Figure 3 shows a historical monthly time series of the OIP for a 7 percent or worse decline in the S&P 500 index over the coming month. The vertical lines indicate months in which the S&P 500 fell by 7 percent or more, on net, which occurred in about 5 percent of months in this sample. It can be seen that the OIP does tend to be elevated in periods during which crashes were more frequent, such as in the early 2000s and during the recent financial crisis. This tendency provides hope that the OIP might be useful for forecasting crashes. That said, there are also relatively long periods--such as from 1996 through 1997--during which the OIP was elevated and yet no crashes occurred.
The remainder of this article is aimed at testing more formally whether these OIPs have been helpful in forecasting U.S. stock market crashes over the past 25 years.3 To preview our conclusions, we find, first, that OIPs are upwardly biased predictors, in that they tend to predict more crashes than actually occur (reminding us of the joke about economists forecasting eight of the last two recessions). Second, we find that OIPs can help forecast crashes, on the margin, but they are best used in conjunction with other forecasting variables. Lastly, but perhaps least surprising, we find that stock market crashes remain very difficult to forecast even using the best models, at least among those that we considered.
| Figure 5: Why do Option-Implied Probabilities Overstate Real-World Probabilities? |
|---|
|
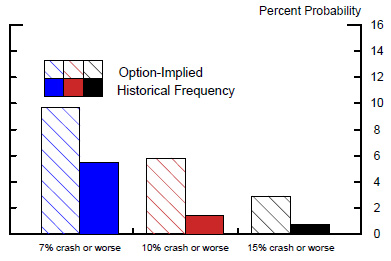
We begin with some simple descriptive statistics. In Figure 4, the long-run average level of the OIP for a 7 percent crash is shown by the blue hashed bar to be about 10 percent. This is almost twice the frequency with which crashes actually occurred since 1990, shown by the solid blue bar to be about 5-1/2 percent. This divergence indicates that the OIP is an upwardly biased predictor of crashes, on average. The OIPs for larger stock market crashes--the other hatched bars--are also, on average, substantially higher than the corresponding historical frequencies (the other solid bars).
Figure 5 lists two explanations for why OIPs tend to overstate real world probabilities. First, market participants may be risk averse and therefore bid the price of options that offer protection against declines in their stock market wealth above their actuarially fair value. Second, some research suggests that, in some circumstances, people exhibit a subjective bias such that they tend to over-estimate the probabilities for rare events, especially those for dramatic rare events, such as extreme stock market returns. Nonetheless, even though the average level of OIPs appears to be upwardly biased, the time variation in OIPs might still turn out to be useful for forecasting crashes. For instance, a higher-than-average level of OIPs may signal a higher-than-average actual probability of a crash in the coming month.
| Figure 6: Can OIPs be Used to Forecast Crashes? |
|---|
|
|
Note: Financial market indiciators include the earnings-price ratio for the S&P 500 and recent positive and negative semivariances of returns. Business Cycle indicators include the unemployment rate and inflation. |
Figure 6 outlines our strategy for answering the question: Can the time-variation in the levels of OIPs be used to help forecast crashes? We tested this hypothesis in the context of two recently developed statistical models.4, 5 Both models allow us to estimate, for each month in the sample, the likelihoods of all possible stock market returns over the next month, including the probability of crashes, as functions of forecasting variables.
To test the relative value of OIPs for forecasting crashes, we estimate three alternative specifications of the model using different sets of forecasting variables. The first specification, "OIP only," forecasts crashes using the OIPs alone as forecasting variables. The second specification, labeled "macro," does not use OIPs; instead, its forecasts rely on other macroeconomic variables, including financial market and business cycle indicators. Finally, the "full" specification produces forecasts using the OIPs and all of the macroeconomic variables.
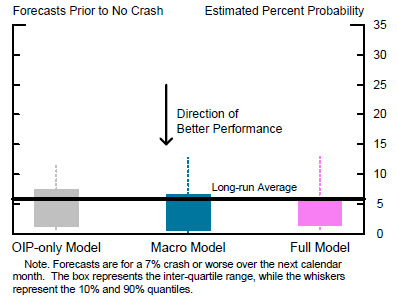
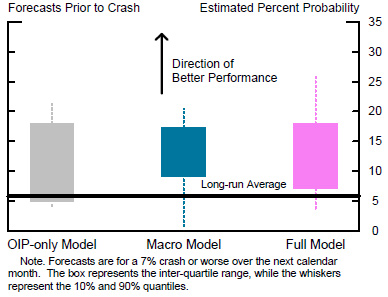
After estimating all three specifications, we proceeded to test which one works best. We begin, in Figure 7, by considering each model's propensity for "false positives," by which we mean cases when the forecasted probability is relatively high, but no crash actually follows. We therefore look at the model forecasts in months prior to no crash. For this test, the direction of better performance is to have a lower forecast. Each solid bar represents the interquartile range of probabilities indicated by the three specifications, and the whiskers represent 80 percent confidence intervals. For comparison, the horizontal line shows the long-run historical average frequency of these crashes. All three specifications generally produce lower-than-average probabilities. The differences across the forecasts are not large, but the "macro" model, represented in blue, and the "full" version, in pink, perform a bit better than the "OIP-only" model, in gray.
Moving to the right, in Figure 8, we report on the degree to which the three models tend to produce "true positives," by which we mean cases when the forecasted probability is relatively high ahead of months in which crashes actually occurred. Plotted are the ranges of probabilities indicated by each model in months just preceding a crash. In this case, the direction of better performance is positive. Not surprisingly, all three specifications show only a modest ability to correctly warn of an impending crash. Still, all three specifications do usually show some elevated risk. On the margin, the "full" specification, in pink, performs the best, with the highest range of forecasts.
More generally, formal statistical tests, not presented here, which take into account the three models' performance in all periods, also suggest that the "full" model forecast is the best of the three.6 Based on these results, we use the estimates of the "full" specification below as our preferred "model-estimated crash probabilities." We now compare these model-estimates of crash probabilities to the raw OIP data. The purpose of this exercise is to gain insight into how movements in the OIP compare to those of the model-estimated probability of a crash.
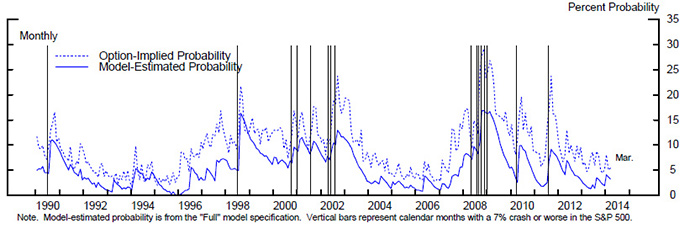
Figure 9 plots, in solid blue, the historical model-estimated probability of a crash from the "full model," and re-plots the option-implied probabilities and actual crash occurrences. The two series are highly correlated, suggesting that OIPs do carry information about the real world probability of a crash. However, as expected, the OIPs are reliably higher than the model estimates. Moreover, OIP exaggerates the model-implied estimates by the largest margins in months following actual crashes. For instance, in the first month following a crash, the average level of the gap between the OIP and the model-estimated probability of a crash is nearly twice its long run average.
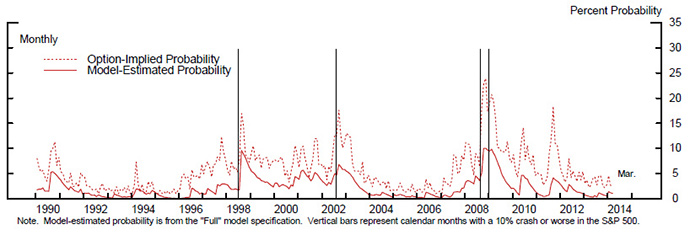
Figure 10 shows analogous results for a more severe crash level, a 10 percent or worse crash. As illustrated by the vertical lines, larger crashes are more likely to be "strikes from the blue" – that is, very difficult to forecast. Moreover, the model-estimated probabilities of large crashes generally remain elevated for only brief periods, except during periods of extreme turmoil. In contrast the OIPs are again higher on average and are slower to adjust down, again possibly reflecting that investor risk aversion is slow to subside.
To sum up, OIPs do appear to be somewhat useful for increasing the accuracy of some models designed to forecast crashes, but using them for this purpose requires controlling for the time-varying upward bias of OIPs and incorporating other macroeconomic and financial market indicators in constructing the forecasts, at least in the context of the models that we considered. However, an important takeaway from this research, and that from many other studies, is that a high degree of humility is in order for those who would endeavor to forecast stock market crashes.
1. The views expressed in this document do not represent those of the Federal Reserve System, its Board of Governors, or staff. This article benefitted greatly from the assistance of Alex Zentefis and Mihir Ghandi. Return to text
2. See, for instance, Ser-Huang Poon and Clive W. J. Granger (2005), "Practical Issues in Forecasting Volatility," Financial Analysts Journal, vol. 61, pp. 45-56. Return to text
3. A substantial body of academic literature has also considered the predictive content of options prices for various financial and macroeconomic phenomena. For a summary, see, for instance, Peter Christoffersen, , Kris Jacobs, and Bo Young Chang (2013), "Forecasting with Option Implied Information," in Graham Elliott and Allen Timmerman, eds., Handbook of Economic Forecasting, vol.2, pp. 581-656, and references therein. Return to text
4. Halbert White , Tae-Hwan Kim, and Simone Manganelli (2010), "Modeling Autoregressive Conditional Skewness and Kurtosis with Multi-Quantile CAViaR," in TimBollerslev,Jeffrey R. Russell, and Mark Watson, eds., Volatility and Time Series Econometrics: Essays in Honour of Robert F. Engle. Return to text
5. Geert Bekaert, Eric Engstrom, and Andrey Ermolov (2014), "Bad Environments, Good Environments: A Non-Gaussian Asymmetric Volatility Model." Available at SSRN: http://ssrn.com/abstract=2296898 or http://dx.doi.org/10.2139/ssrn.2296898 Return to text
6. Additionally, in an out-of-sample exercise, we re-estimated the parameters of the "full" model using data only through 2006. We then tested the performance of the model under this restricted estimation later on data from 2007 to present. There was no significant deterioration of performance in the out-of-sample period in terms of either "false positives" or "true positives" relative to the model using parameters estimated over the full sample period. Return to text
Please cite as:
Engstrom, Eric (2014). "Forecasting Stock Market Crashes is Hard--Especially Future Ones: Can Option Prices Help?," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, May 07, 2014. https://doi.org/10.17016/2380-7172.0017
Disclaimer: FEDS Notes are articles in which Board economists offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers.