FEDS Notes
November 18, 2016
Front-End Term Premiums in Federal Funds Futures Rates and Implied Probabilities of Future Rate Hikes
Don H. Kim and Hiroatsu Tanaka 1
A few recent market commentaries have proposed simple rules of thumb that describe term premiums in money market futures and forward rates in the current interest rate environment as a linear function of horizon with a slope of about minus 1 to minus 2 basis points per month.2 Such term premiums can have significant effect on inferences regarding the market-implied probability of future monetary policy actions at the next few FOMC meetings, but solid empirical evidence on term premiums at such horizons has been lacking. In this note, we examine empirical evidence on term premiums at the very front end, utilizing federal funds futures data as well as responses to the Desk's sell-side survey (Survey of Primary Dealers, or PD survey) and buy-side survey (Survey of Market Participants), and discuss plausible front-end term premium assumptions that one can use to extract probabilities of a rate hike at upcoming meetings from market quotes.3
We find that, for horizons over the next two to three FOMC meetings, a simple assumption that term premiums are zero produces a good agreement between federal funds futures data and the Desk survey data on the distribution of the timing of the next rate hike, while an assumption of significantly negative term premiums suggested by some market commentaries produces futures-implied probabilities of near-term rate hikes that appear generally much higher compared with those from the surveys. In addition, Desk survey responses on the distribution of the federal funds rate at year-ends are also consistent with the assessment that term premiums are small in magnitude at two-to-three-meeting horizons while more sizable (negative) further out; however, even at somewhat longer horizons of about six months, estimated term premiums are generally smaller in magnitude than some of the numbers proposed in recent commentaries. Overall, it appears that term premiums are nonlinear with respect to horizons at the front end.
The Fed Funds Rate Step Path and Term Premiums
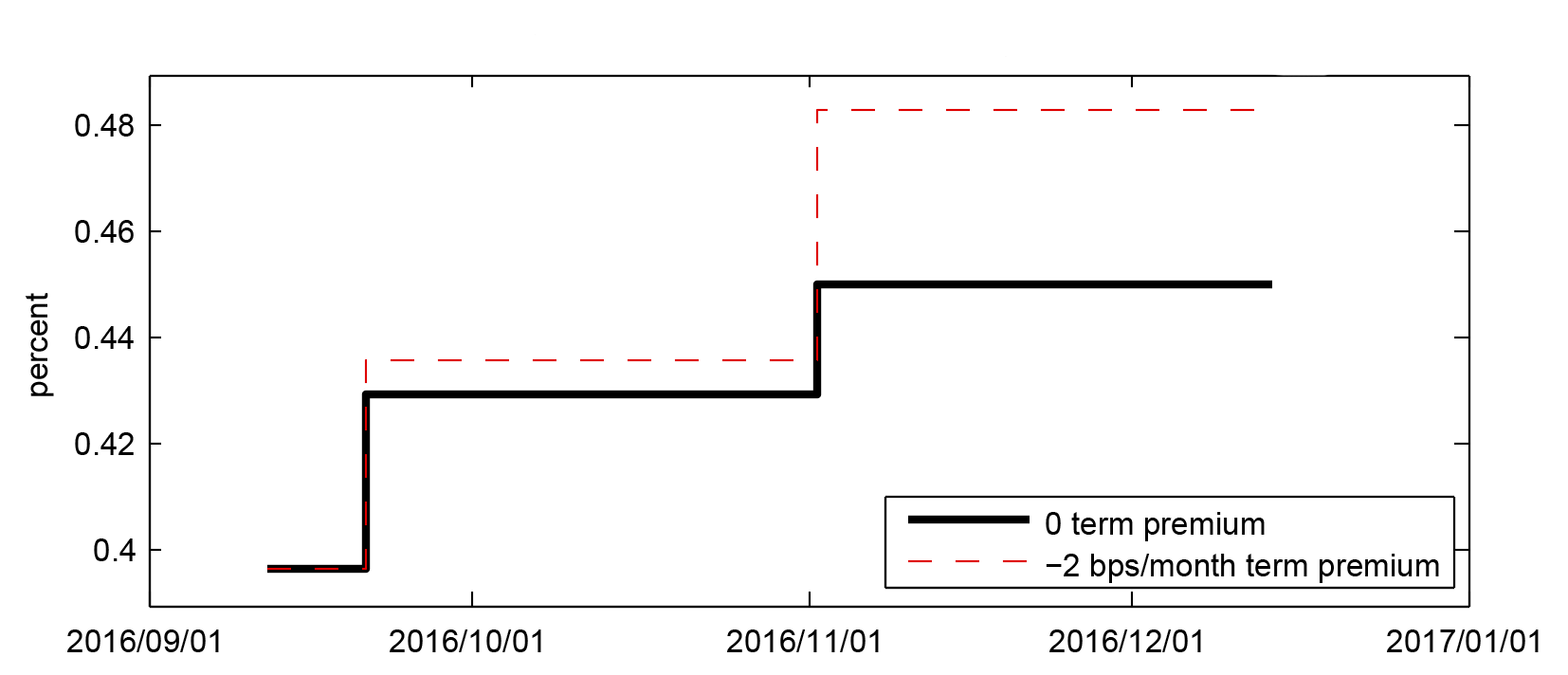
In order to measure very near-term policy expectations precisely from financial market data, we need to consider the fact that the federal funds target rate/range changes are discrete and occur only on FOMC meeting dates, which means that the expected path of the fed funds rate is well described as a "step" path.4 One example of such a path, implied by fed funds futures data on September 12, 2016 (turn-in deadline for September Desk surveys), is shown in figure 1.5 The black solid line is the step path assuming zero term premiums. As an illustrative example, we also plot the step path adjusted for term premiums of minus 2 basis points per month (see the red dashed lines).6
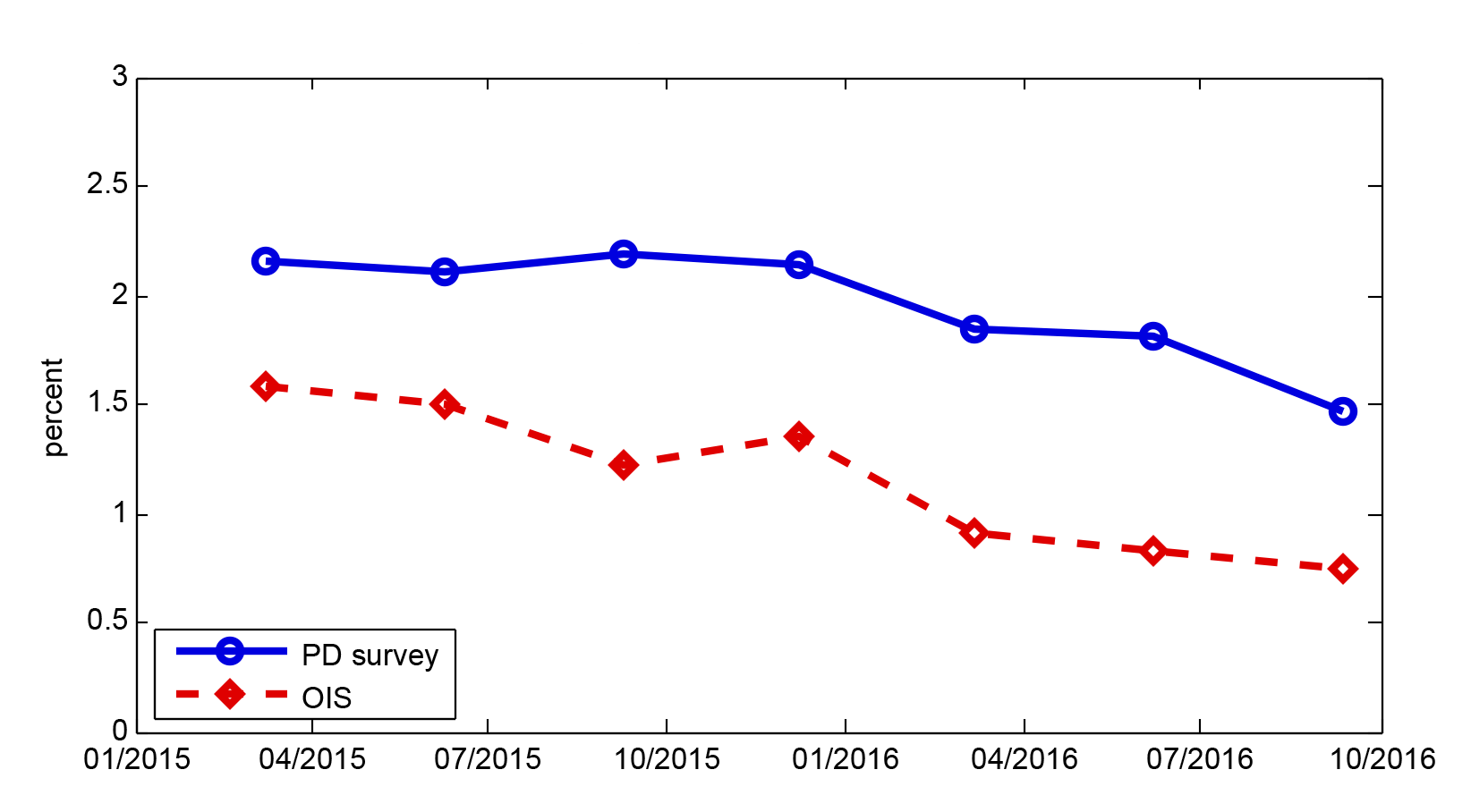
We examine term premiums for the very near-term using fed funds futures data (step paths) and survey data from 2015 and 2016. For most of 2015, the fed funds target rate remained at the 0 to 25 basis point range, but, similar to now, the market-implied path (for example, OIS path) was substantially lower than the survey-based modal path beyond the very front end of the term structure. Indeed, as can be seen from figure 2, the gap between the OIS-implied fed funds rate expectations two years ahead (red line) and the PD survey's modal forecast two years ahead (blue line) has remained fairly large and negative.7 In other words, term premiums appear to have been negative over this period.8 Term premium calculations along the lines of "x bps/month" suggested by recent market commentaries typically aim to match significantly negative term premiums in these intermediate horizons, and compute term premiums for horizons in between through a simple linear interpolation all the way to zero. Applying such rules at very near horizons, such as the next two to three meetings, can imply a substantial adjustment to the futures-implied probability of rate hikes at those horizons.
 |
|
Note: "OIS" is the two-years-ahead forward rate based on OIS quotes, and "PD survey" is the average of the modal forecasts from the Survey of Primary Dealers, linearly interpolated for the two-year horizon. Source: Bloomberg, FRBNY, Authors' calculation.
Implied Probabilities of Future Rate Hikes Adjusted for Term Premiums
We can deduce the odds of future monetary policy actions from the step path discussed above, but those odds would obviously depend on assumptions regarding term premiums. Fortunately, the Desk surveys include a question on the distribution of the timing of the next rate hike, the responses with which we can compare the step-path-based results to evaluate various term premium assumptions; that is, we can examine which term premium assumption, applied to futures-based step paths, gives results that are consistent with survey-based information.9 To this end, with the 2016 surveys, we compare the survey-based probability that the next rate hike occurs within the next two meetings with futures-based counterparts; with the 2015 surveys, taking advantage of the availability of timing probabilities for additional horizons, we compare the probability that the next rate hike occurs within the next three meetings.10
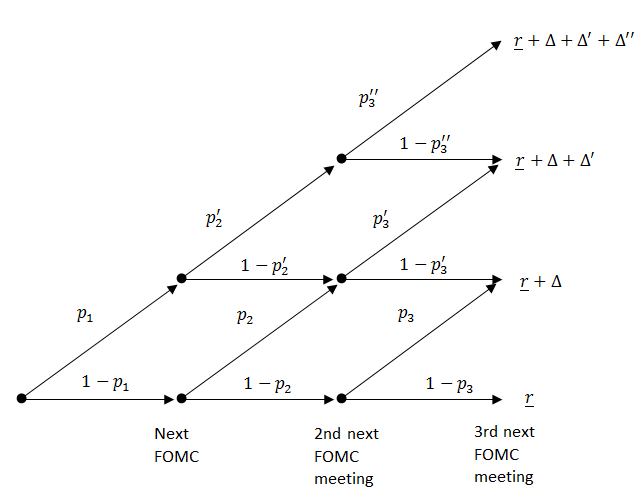
To convert futures-based step paths into futures-based probabilities of the next rate hike, we must entertain some model that describes the dynamics of the fed funds rate. For this purpose, we construct a simple binomial tree model. A schematic illustration of the model is provided in figure 3.11
The estimates of the probability of the next rate hike based on the model may depend somewhat on auxiliary assumptions. In particular, we must take a stand on the level of the fed funds rate at the initial node $$(\underline{r})$$, which could either be the midpoint of the target range, or a recent average of the effective fed funds rate. Additionally, in 2015, there was some ambiguity about where in the next range the effective fed funds rate would settle after liftoff $$(\underline{r}+\Delta)$$, with both sell-side and buy-side survey respondents generally predicting the fed funds rate to settle at around 35 basis points, a bit below the midpoint of the next range (37.5 basis points). Table 1 summarizes the futures-implied probability of the next rate hike (liftoff) occurring within the next three meetings on four survey dates in 2015 for different modeling assumptions: [Ave, 35], [Mid, 35] and [Mid, 37.5], where "Ave" and "Mid" refer to using either a recent average of the effective fed funds rate or the midpoint of the target range for the initial node, and "35" and "37.5" refer to the expected value of the fed funds rate after the first rate hike, respectively.12 Under these assumptions, we compute futures-implied probabilities under the term premium assumption of 0 or minus 2 basis points per month and examine how they compare with the sell-side and buy-side surveys. Similarly, for 2016 (post-liftoff), table 2 shows the futures-implied probability of the next rate hike occurring within the next two meetings on three survey dates, March, June, and September, using different model assumptions: [Ave] and [Mid], again with 0 or minus 2 basis points per month term premium.13
As can be seen in tables 1 and 2, in all survey dates examined, the zero term premium assumption provided fairly good agreement with sell-side and buy-side results for different combinations of auxiliary conditions (35 versus 37.5, Ave versus Mid). For example, in March 2015, probabilities were in the 36 to 41% range, compared with the sell-side and buy-side survey probabilities in the 33 to 36% range.14 The probabilities implied by assuming zero term premium were somewhat larger than the survey values in March 2016 and somewhat smaller than survey values in September 2015, which, at face value, would imply that the front-end term premium was positive in March 2016 and negative in September 2015. Meanwhile, applying the minus 2 basis points per month term premium assumption led to futures-implied probabilities that had a worse match with survey data, with the exception of September 2015.15 For example, in March and June 2015, the probabilities were about 15 to 25 percentage points higher than the surveys, and about 10 to 25 percentage points higher in the 2016 surveys.16
| Date | Model | Survey | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 term premium | -2 bps/mo term premium | |||||||
| Ave, 35 | Mid, 35 | Mid, 37.5 | Ave, 35 | Mid, 35 | Mid, 37.5 | Sell-side | Buy-side | |
| 2015/3 | 41% | 40% | 36% | 59% | 59% | 55% | 33% | 36% |
| 2015/6 | 56% | 56% | 52% | 72% | 72% | 68% | 51% | 53% |
| 2015/9 | 62% | 63% | 60% | 75% | 76% | 73% | 69% | 74% |
| 2015/12 | 96% | 96% | 92% | 98% | 98% | 96% | 95% | 98% |
Note: The three meetings for each date are the first three meetings including the FOMC meeting on the designated date. For example, for 2015/12, the three meetings include the December 2015, January 2016, and the March 2016 FOMC meetings. The probabilities reported for the surveys are averages of each individual respondent's probability.
| Date | Model | Survey | ||||
|---|---|---|---|---|---|---|
| 0 term premium | -2 bps/mo term premium | |||||
| Ave | Mid | Ave | Mid | Sell-side | Buy-side | |
| 2016/3 | 30% | 24% | 42% | 36% | 17% | 13% |
| 2016/6 | 24% | 22% | 36% | 34% | 26% | 25% |
| 2016/9 | 20% | 28% | 32% | 39% | 20% | 21% |
Note: The two meetings for each date are the first two meetings including the FOMC meeting on the designated date. For example, for 2016/9, the two meetings include the September 2016 and the November 2016 FOMC meetings. The probabilities reported for the surveys are averages of each individual respondentís probability.
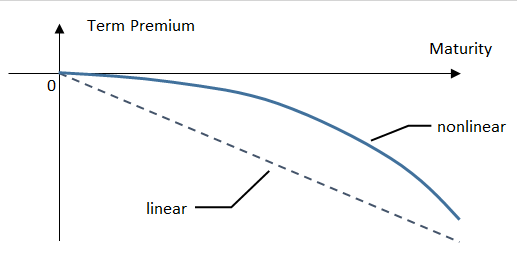
Overall, based on 2015 and 2016 data, the assumption of a zero term premium appears to provide good agreement between survey data and futures data for very near-term horizons, such as the next two to three meetings. As we have seen, the futures-based results depend somewhat on modeling assumptions, but a significantly negative term premium such as minus 2 basis points per month usually appears too large in magnitude to justify under any "reasonable" assumption. Nevertheless, we stress that a zero term premium is likely a good assumption only for the very near-term; in order to reconcile it with the presence of a significant negative term premium at intermediate horizons, the term premium as a function of horizon has to be nonlinear, as schematically illustrated in figure 4.17 Therefore, the probability of the next rate hike occurring at horizons beyond the next few meetings, computed from a "straight read" of funds futures data, may be indeed distorted by term premium effects.
Front-End Term Premium from Year-End Distributions of the Fed Funds Rate
We augment our analysis by providing term premium estimates using the responses to Desk survey question on the probability distribution of the fed funds rate at the end of the year.18 The futures-based step-path value at year-end minus the mean of the survey-based year-end distribution averaged over each respondent can provide a measure of term premium.19 Since the question does not allow us to compute a time series of constant maturity term premium estimates, we use only a limited number of surveys: the September surveys in 2015 and 2016 to compute about-three-months-ahead term premiums, and the June surveys in 2015 and 2016 to compute about-six-months-ahead term premiums, with both the sell-side and buy-side surveys. Except for the September 2016 survey, the size of the crucial bins in the survey questions were rather wide, leading to some uncertainty as to what rate we should assign to a particular bin; therefore, tables 3 and 4 report point estimates of term premiums along with their plausible lower and upper bounds in brackets.20 We see that the about-three-months-ahead term premium is indeed close to zero from the fairly recent (September 2016) survey. The term premium estimate for the same horizon was negative in September 2015, at around minus 4.6 to minus 3.3 basis points, which was the occasion where the survey data on the distribution of the timing of a rate hike (discussed earlier) also implied some negative front-end term premium. If we move to the about-six-months-ahead horizon, term premiums become more negative, as one may guess from our discussion of intermediate-horizon term premiums. However, it is worth noting that the magnitude of negativity is significantly smaller than one would expect from the information of large negative term premiums in the intermediate horizon and the assumption of a linear relation between term premiums and the maturity. Even accounting for the possible range of estimates, an assumption such as minus 2 basis points per month for the front-end maturities seems to be close to the lower bound. All told, evidence presented in this note suggests that term premiums are nonlinear with respect to maturity.
| Date | Sell-side | Buy-side |
|---|---|---|
| 2015/9 | -3.3 | -4.6 |
| [-5.8, -3.3] | [-7.4, -4.6 ] | |
| 2016/9 | 0 | -1.9 |
| Date | Sell-side | Buy-side |
|---|---|---|
| 2015/6 | -5.3 | -5 |
| [-10.3, -5.3] | [-10.3, -5.0] | |
| 2016/6 | -2.3 | -3 |
| [-9.2, 4.5] | [ -9.4, 3.4] |
References
Golay, Ellen Correia, Steven Friedman, and Michael McMorrow (2013). "Understanding the New York Fed's Survey of Primary Dealers," Current Issues in Economics and Finance, vol. 19, pp. 1-8.
Gurkaynak, Refet (2005), "Using Federal Funds Futures Contracts for Monetary Policy Analysis", FEDS Working Paper, 2005-29.
LH Meyer (2016), "Market-Implied Expectations and the OIS Curve," LH Meyer Fixed Income Focus, September 15.
Perli, Roberto (2016). "Quick Take: The Odds of a September Hike have Gone up, but not Drastically," Cornerstone Macro Policy Research, July 27.
Wright, Jonathan (2016). "Term Premiums in Overnight Indexed Swaps," LH Meyer Fixed Income Focus, September 8.
1. We thank Eric LeSueur and Min Wei for useful comments, and Mary Bean for editorial assistance. Return to text
2. Wright (2016) and LH Meyer (2016), for example, have suggested a slope of minus 2 basis points per month and minus 1 basis point per month, respectively. On a related note, Perli (2016), in a market commentary in late July, argued that due to negative term premiums the relatively low probability of a September rate hike implied by a straight read of market quotes at the time (about 20%) was not inconsistent with his view that market participants actually placed about even odds on the September rate hike. In order to obtain 50% odds on a September rate hike, there had to be about a minus 6 to minus 8 basis point term premium in October fed funds futures contracts as of late July. If the term premium is linear, this amounts to minus 3 to minus 4 basis points per month of term premiums. Return to text
3. The PD survey is conducted by the New York Fed's Market Group (the Desk) one to two weeks before each FOMC meeting. See Correia Golay, Friedman, and McMorrow (2013) for details on this survey. The Survey of Market Participants is similar to the PD survey and conducted simultaneously with a subset of questions taken directly from the PD survey. Return to text
4. An intermeeting move in the target rate is in principle possible, but at least in the current environment it is extremely unlikely, and it seems quite reasonable to assume that the market is not pricing in such a possibility. Return to text
5. We assume that the effective fed funds rate is depressed by 5 basis points at month-ends. For a general discussion of deducing step paths from fed funds futures data, see, for example, Gurkaynak (2005). Return to text
6. We assume the term premium also has a step structure. In order to apply x bps/month term premium, we assume that the term premium immediately following an FOMC meeting is x times the time between now and that FOMC meeting (measured in months). Return to text
7. Though in recent years fed funds futures contracts have been available for maturities up to about two years, we use OIS data instead to compute market-implied policy expectations here, out of concern about the liquidity of fed funds futures at such a horizon. Return to text
8. Note that although a substantial part of this gap likely reflects negative term premiums, a portion of this gap can also be attributed to the difference between mean (futures) and modal (PD survey) forecasts: An increase in the downside skew of the fed funds rate distribution will make the mode larger than the mean. Indeed, the gap appears to be a bit wider now compared with the first half of 2015, which is consistent with a somewhat greater mode-mean differential since mid-2015 when concerns about global downside risks became more pronounced following the Chinese equity market declines and the People's Bank of China's yuan devaluation. For example, based on average responses to the September 2016 Desk survey questions on the 2018 year-end fed funds rate distributions and modal forecasts, the difference between the mean and mode for approximately the two-year horizon was about minus 25 basis points (sell-side) and minus 40 basis points (buy-side) at the time. Return to text
9. Though obviously uncontaminated by term premium effects, survey-based results have drawbacks of their own, including their infrequent availability and potential inaccuracy due to sampling uncertainty. Return to text
10. In the 2015 surveys, respondents provided probabilities they attach to the next rate hike (liftoff) occurring at the next six to seven FOMC meetings. After the liftoff in December 2015, that survey question was modified, and the subsequent surveys have provided information on the respondent's probabilities of the next rate hike occurring at the next two FOMC meetings. Return to text
11. In this model, there are two outcomes at the next FOMC meeting: stay at the current range or move up to the next range. At each subsequent FOMC meeting, the number of "states" increases by one, corresponding to each node having two possible outcomes of either no-move or an up-move. Hence, this binomial tree assumes that the market is ruling out the possibility of a decrease in the policy rate. While this assumption may be reasonable for most of the 2015-16 period, there were brief periods in which the market appeared to perceive small odds of a decrease in the policy rate in the near term such as the period immediately following Brexit (late June and early July 2016), for which the assumption would be less reasonable. At a given FOMC meeting, we set the probability of an up-move to be the same for all nodes for simplicity, as we cannot separately identify the up-move probabilities at different nodes. This amounts to setting $$p_2=p_2'$$ and $$p_3=p_3'=p_3''$$, where $$p$$ denotes up-move probabilities for different nodes. Note that the probability of the next rate hike occurring at the next FOMC meeting is $$p_1$$, the probability of the next rate hike occurring at the second next FOMC meeting is $$(1-p_1 ) p_2$$, and so on. The probability of the next rate hike occurring within the next two meetings is therefore $$p_1+(1-p_1 ) p_2$$.
We acknowledge that there would be cases when this assumption may seem less plausible. On the one hand, for instance, if there is a small probability of the next rate hike occurring in the next meeting and a large probability of a next rate hike occurring in the second next meeting, our assumption will imply that in the rare occasion that the rate hike occurs in the next meeting, there will be a large probability that there will be another rate hike in the following meeting, which is counter to the notion of a gradual pace of tightening. On the other hand, in such a scenario, since the probability of a rate hike next meeting is small in the first place, assumptions about the probabilities assigned to subsequent nodes may be quantitatively irrelevant.
To address concerns of robustness across different model assumptions, we also computed probabilities from an alternative specification where we assume there is zero probability of more than one future rate hike within the horizons--that is, $$p_2'=p_3'=p_3''=0$$. While we think the exercise is informative, this assumption is relatively strong because it completely rules out the possibility of any additional rate hikes in all states of the world. In fact, this assumption is inconsistent with survey data (for example, the 2016-end rate distribution) as well as futures options data which typically point to positive odds on scenarios of multiple rate hikes at two-to-three-meeting horizons. In any case, we find that the model based on this assumption has a worse fit with survey data than our benchmark model (with a term premium in the range of zero to minus 2 basis points per month), generally producing numbers that are larger than survey results. This is because the alternative model must assign somewhat larger initial up-move probabilities than the benchmark model in order to match the same futures data. In some cases, for example, in December 2015, the alternative model produced clearly unreasonable results of rate hike probabilities exceeding 1, since the futures-implied step path was rising with the horizon at a fast enough pace at the time so that the assumption of no additional rate hikes was clearly inappropriate. Return to text
12. For the recent average of the effective fed funds rate, we use the moving average of the past 30 calendar days. Return to text
13. We assume the fed funds rate increases by 25 basis point increments after the first rate hike from the effective lower bound. In other words, we assume $$\Delta'=\Delta''=25$$ basis points for observations in 2015, and $$\Delta=\Delta'=25$$ basis points for observations in 2016 (we require no assumptions for $$\Delta''$$ since we compute only up to two meetings ahead). Return to text
14. In both tables 1 and 2, we use fed funds futures data on survey-turn-in days. Using the futures data from the Friday before the survey-turn-in days gave similar results except for September 2016, when federal funds futures rates were somewhat volatile around the turn-in date. Return to text
15. In December 2015, there was not much difference between the probability numbers based on the zero term premium and the minus 2 basis points per month term premium because market participants placed very high odds on a rate hike occurring at the upcoming (December) meeting, for which the term premium adjustment was quite small due to the relatively short time until that meeting. Return to text
16. To save space, we do not report the model-implied probabilities for the minus 1 basis point per month term premium assumption, but they are at about the midpoint of the numbers for the zero term premium and the minus 2 basis point per month term premium. It can therefore be seen that a minus 1 basis point per month term premium also provides a worse fit to the survey numbers than the zero term premium, albeit to a lesser degree, typically producing numbers that exceed the survey counterparts. Return to text
17. Term premiums at horizons further out are also likely to be more variable over time, given their likely larger magnitudes. Return to text
18. For example, the September 2016 Desk surveys asked respondents to provide their distributions of the fed funds rate at the end of 2016, 2017, 2018 and 2019. Return to text
19. The Desk surveys also provide respondents' modal expectations for the fed funds rate after each of the next six to seven FOMC meetings. However, related to our discussion above, using modal expectations may produce a biased estimate of term premiums. For example, suppose all survey respondents have the modal expectation that there will be no rate hike at the upcoming meeting, though they still assign a non-zero probability to the event of a rate hike. Then the survey-based "modal" expectation for the fed funds rate after the meeting would be about the same as the current fed funds rate. However, the mean expected fed funds rate after the meeting would be somewhat larger than that, reflecting the non-zero probability of a rate hike (Note that futures rates are mean-expectations in the so-called risk-neutral measure). Therefore, in order to measure the front-end term premiums accurately, we need survey-respondent's views on not only the modal expectation but also the probabilities they assign to non-modal outcomes. Note this positive bias of individual modal forecasts cannot be eliminated by averaging over them. In other words, the mean of the modal forecasts is different from mean expectations, and we need the latter to compute term premiums. Return to text
20. For example, in the June 2016 survey, the bin spanning the range of 0.51 to 1.00% contains two possible scenarios, the rate being near 0.625% (one rate hike) or 0.875 (two rate hikes), and it is not obvious what rate should be assigned to the bin. However, we can still obtain a reasonable point estimate of term premiums along with a lower and upper bound. Note that the bounds are not statistical confidence intervals, and the point estimate and bounds differ by the assumption on what rate (center of mass) to assign for the 0.51% to 1% bin. For June and September 2015, we set the center of mass of the fed funds rate to 0.6%, 0.725%, and 0.6%, for calculating the point estimate, lower bound, and upper bound of term premiums, respectively (here we assume the fed funds rate settles at 35 basis points after the first hike and increases by 25 basis points afterward). This assumption seems reasonable, as no respondent reported a modal forecast of two additional rate hikes for 2015 year-end. For June 2016, we use 0.75%, 0.875%, and 0.625% as the center of mass of the fed funds rate for calculating the point estimate, lower bound, and upper bound of term premiums, respectively, with adjustments for the recent average of the fed funds rate, given that about half of the respondents' modal forecasts for 2016 year-end was 0.875%. The bins in the September 2016 survey is granular enough so that we do not need this assumption. We use the recent average of the fed funds rate at the survey turn-in date as the expected value of the federal funds rate for survey bins that include that value. Return to text
Please cite as: Kim, Don and Hiroatsu Tanaka (2016). "Front-end Term Premiums in Federal Funds Futures Rates and Implied Probabilities of Future Rate Hikes," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, November 18, 2016, https://doi.org/10.17016/2380-7172.1884.
Disclaimer: FEDS Notes are articles in which Board economists offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers.