FEDS Notes
August 30, 2024
Monetary Policy in Uncertain Times
Simon C. Smith, Allan Timmermann, Jonathan H. Wright*
Introduction
"... gradualism is a well-established principle for central banks in times of uncertainty. When faced with uncertainty about the resilience of the economy, it pays to move carefully. In keeping with this, we have adjusted our forward guidance on interest rates to temper expectations of any abrupt or automatic moves." (Christine Lagarde, 2022.)1
As the opening quote suggests, it may be optimal for monetary policymakers to act more cautiously when uncertainty is high. Uncertainty comes in many forms. One crucial source of uncertainty surrounds the slope of the Phillips curve. The Phillips curve is a key element of the New-Keynesian macroeconomic model and is critical in how central banks think of the macroeconomy. Misjudging the slope of the Phillips curve will hinder the central bank's ability to meet its inflation target. This is particularly concerning given the mounting evidence that the Phillips curve is unstable. For example, previous studies have identified that the Phillips curve may have flattened towards the end of last century (Hazell et al. 2022; Smith et al. 2023) and steepened during the pandemic (Cerrato and Gitti 2022; Benigno and Eggertsson 2023).
In this note, we investigate the impact of breaks in the Phillips curve on optimal monetary policy for both the United States (US) and the European Union (EU). Since different regions and countries experience different business cycles, disaggregate data provide richer information than aggregate data, enabling more precise identification of breaks. Also, since the central bank does not target inflation in any particular region, disaggregate data with time fixed effects circumvents the endogeneity bias (towards zero) in the Phillips curve that arises from successful inflation targeting when using aggregate data (Hooper et al. 2020; Fitzgerald et al. forthcoming; McLeay and Tenreyro 2020). Empirically, we find evidence of a break in the Phillips curve for both the US and the EU around the turn of the century, after which the Phillips curve flattens.
Next, we investigate the implications of these breaks for optimal monetary policy. For both the US and the EU, we find that breaks induce additional parameter uncertainty, causing the central bank to respond more cautiously to deviations in the unemployment rate gap from zero. This caution stems from the policymaker's increased uncertainty about the link between economic slack and inflation, in line with Brainard (1967)'s "conservatism principle" that is encapsulated in the opening quote. However, the policy-maker compensates for this increased caution by responding more aggressively to deviations in inflation from target. These results are relevant for the recent global monetary policy actions.
Data
We source the monthly total Consumer Price Index (CPI) and corresponding unemployment rate for 22 MSAs in the US from the Bureau of Labor Statistics (BLS) for the sample period from 1980 through 2022. We compute annual inflation rates from annual levels that are constructed as the average of all monthly observations in the corresponding year. We source the quarterly US national unemployment rate from the BLS and the corresponding estimates of the natural rate of unemployment from the Congressional Budget Office. At the quarterly frequency, we source the nominal federal funds rate from the Federal Reserve Economic Database (FRED) and the national total CPI from the BLS.
From 1986 to 2021, we source headline annual inflation rates for 28 EU countries (the 27 current members and the United Kingdom) from the European Central Bank (ECB) statistical warehouse and the corresponding annual country-level unemployment rate and natural rate of unemployment estimates from the DG ECFIN/AMECO—the European Commission's macroeconomic database.
Breaks in the Phillips Curve
For the US, our model allows for an unknown number of $$K$$ breaks occurring at unknown times $$ \iota = (\iota_{1}, \ldots, \iota_{K})$$.2
$$$$ \pi_{it} = \alpha_{i} + \gamma_{t} + \rho_{k} \pi_{it-1} + \lambda_{k} {URATE}_{it-1} + e_{it} \textit{,}\ \ \ k=1,\ldots , K+1 \ (1)$$$$
in which $$\pi_{it}$$ denotes the inflation rate for the $$i$$th MSA at year $$t$$, $$ \alpha_{i} $$ and $$ \gamma_{t} $$ denote two-way fixed effects, $$ URATE_{it-1} $$ denotes the unemployment rate for the $$i$$th MSA at year $$t$$, $$ \rho_{k} $$ denotes the autoregressive parameter, $$ \lambda_{k} $$ denotes the Phillips curve slope, and $$ e_{it} $$ is the residual for the $$i$$th series at year $$t$$. The parameters $$ \rho_{k} $$ and $$ \lambda _{k} $$ can shift across regimes.
Since there are no MSA-level estimates of the natural rate, we use the unemployment rate as the slack measure, relying on the fixed effects to absorb variation in the natural rate across time and cities. Common time variation in inflation expectations is also absorbed by the time fixed effects. The same model is applied to the EU, substituting the unemployment rate gap for the unemployment rate as we have access to country-level estimates of the natural rate of unemployment.3
Empirically, we find evidence of a break around the turn of the century, after which there is a modest flattening of the Phillips curve slope from -0.29 in the first regime (1980-2000) to -0.25 in the second regime, in which the slope remains significant (Table 1a).4 Broadly similar patterns are found for the EU (Table 1b), albeit the break occurs a few years later and the degree of flattening is larger.5
Table 1a: Breaks in the Phillips Curve
US (1980-2022)
| 1980-2000 | 2001-2022 | 1980-2022 | |
|---|---|---|---|
| PC slope | -0.29∗∗∗ | -0.25∗∗∗ | -0.23∗∗∗ |
Note: Table 1a displays estimates of the Phillips curve slope coefficient on the 22 MSA-level unemployment rates from the baseline model displayed in Equation (1). Significance at the 5, and 1 percent levels are denoted by ∗∗ and ∗∗∗. We display results for the two regimes identified by the model, and for the full sample (by estimating the model but precluding breaks).
Table 1b: Breaks in the Phillips Curve
EU (1986-2021)
| 1986-2003 | 2004-2021 | 1986-2021 | |
|---|---|---|---|
| PC slope | -0.72∗∗ | -0.09∗∗∗ | -0.15∗∗ |
Note: Table 1b displays estimates of the Phillips curve slope coefficient from the baseline model displayed in Equation (1) with the unemployment rate gap (not the unemployment rate) as the measure of economic slack for the 28 EU countries (including the United Kingdom). Significance at the 5, and 1 percent levels are denoted by ∗∗ and ∗∗∗. We display results for the two regimes identified by the model, and for the full sample.
Implications for Optimal Monetary Policy
Next, we examine the implication of breaks in the Phillips curve for optimal monetary policy. We consider a standard model consisting of a Phillips curve and an Investment-Saving (IS) curve:
$$$$ u_{t} = \beta_{u} u_{t-1} + \beta_{i} i_{t-1} + e_{t,u}\textit{,}\\ \pi = \gamma_{u} u_{t-1} + \gamma_{\pi} \pi_{t-1} + e_{t,\pi} \textit{,} \ (2)$$$$
where $$ u_{t} $$ is the unemployment rate gap, $$ \pi_{t} $$ is the deviation of inflation from steady state (all constants are dropped), and $$ i_{t} $$ is the central bank's policy rate at time $$t$$. Following common assumptions, the objective of the central bank is to minimize $$ E (u^{2} + \pi^{2} ) $$ using a rule of the
form $$ i_{t} = \rho_{u} u_{t-1} + \rho_{\pi} \pi_{t-1} $$. By substituting these formulae and plugging in the parameter estimates, we can find the choice of $$\rho_{u} $$ and $$ \rho_{\pi} $$ that minimizes this loss.
We obtain the IS curve by estimating a Bayesian time series regression (with no breaks) of the quarterly percent US national unemployment rate gap on an intercept, its own one quarter lag, and the real federal funds rate lagged one quarter, again using conventional Normal-Inverse Gamma priors that are relatively uninformative.6 We combine these estimates with our Phillips curve estimates for the US and the EU to gauge how the break in the Phillips curve affects optimal monetary policy.7 To evaluate the policy impact of allowing for breaks, we compare results based on the Phillips curve estimates from our breakpoint model and the full-sample model that precludes breaks.
Table 2a shows that in the US, allowing for breaks induces more parameter uncertainty, causing the policymaker to respond more cautiously to deviations in the unemployment rate gap from zero (-0.65 versus -0.88) because they are less certain about the relation between the unemployment rate gap and inflation. The policymaker compensates for this additional caution by responding more aggressively to inflation deviations.8 Indeed, this has been the action taken by many central banks during the re-opening of the economy after the pandemic.
Table 2a: Optimal monetary policy
US
| Model specification | Optimal coefficient | |
|---|---|---|
| Unemployment | Inflation | |
| No break | -0.88 | 0.68 |
| Break | -0.65 | 1.1 |
| Break in PC mean holding distribution fixed | -0.82 | 0.71 |
Note: Table 2a displays the optimal monetary policy rule coefficients on the unemployment rate gap and inflation simulated for the US using the Phillips curve estimates from our panel break model, scaled by the non-tradeables share to back out the implied national Phillips curve slope (Hazell et al. 2022). We display estimates for specifications that preclude breaks, allow for breaks in all parameters, and allow for breaks in the mean of the Phillips curve coefficient holding the distribution fixed.
Table 2b: Optimal monetary policy
EU
| Model specification | Optimal coefficient | |
|---|---|---|
| Unemployment | Inflation | |
| No break | -1.01 | 1.16 |
| Break | -0.65 | 1.29 |
| Break in PC mean holding distribution fixed | -0.99 | 1.16 |
Note: Table 2b displays the optimal monetary policy rule coefficients on the unemployment rate gap and inflation simulated using the (scaled) EU Phillips curve estimates from our panel break model. We display estimates for specifications that preclude breaks, allow for breaks in all parameters, and allow for breaks in the mean of the Phillips curve coefficient holding the distribution fixed.
Breaks cause both the point estimate of the Phillips curve and the precision of this estimate to differ across regimes. The effect on optimal monetary policy that we just described is the combined effect from both these channels. To disentangle the impact on optimal monetary policy coming from each of these two channels, we next allow the point estimate of the Phillips curve to be flatter in the second regime than in the first, but we keep the precision of the estimate in the second regime equal to its value in the first regime. The final row of the Table shows that in this case we see no difference in optimal policy relative to the no-break case. This finding suggests that it is not the flattening of the Phillips curve slope itself that affects optimal policy, but the additional uncertainty surrounding the slope that is induced by the break.
The top panel of Figure 1 illustrates the increased uncertainty surrounding the Phillips curve induced by breaks. The posterior distribution of the Phillips curve is more dispersed under the break model (black line) than under the no break model (red line).9
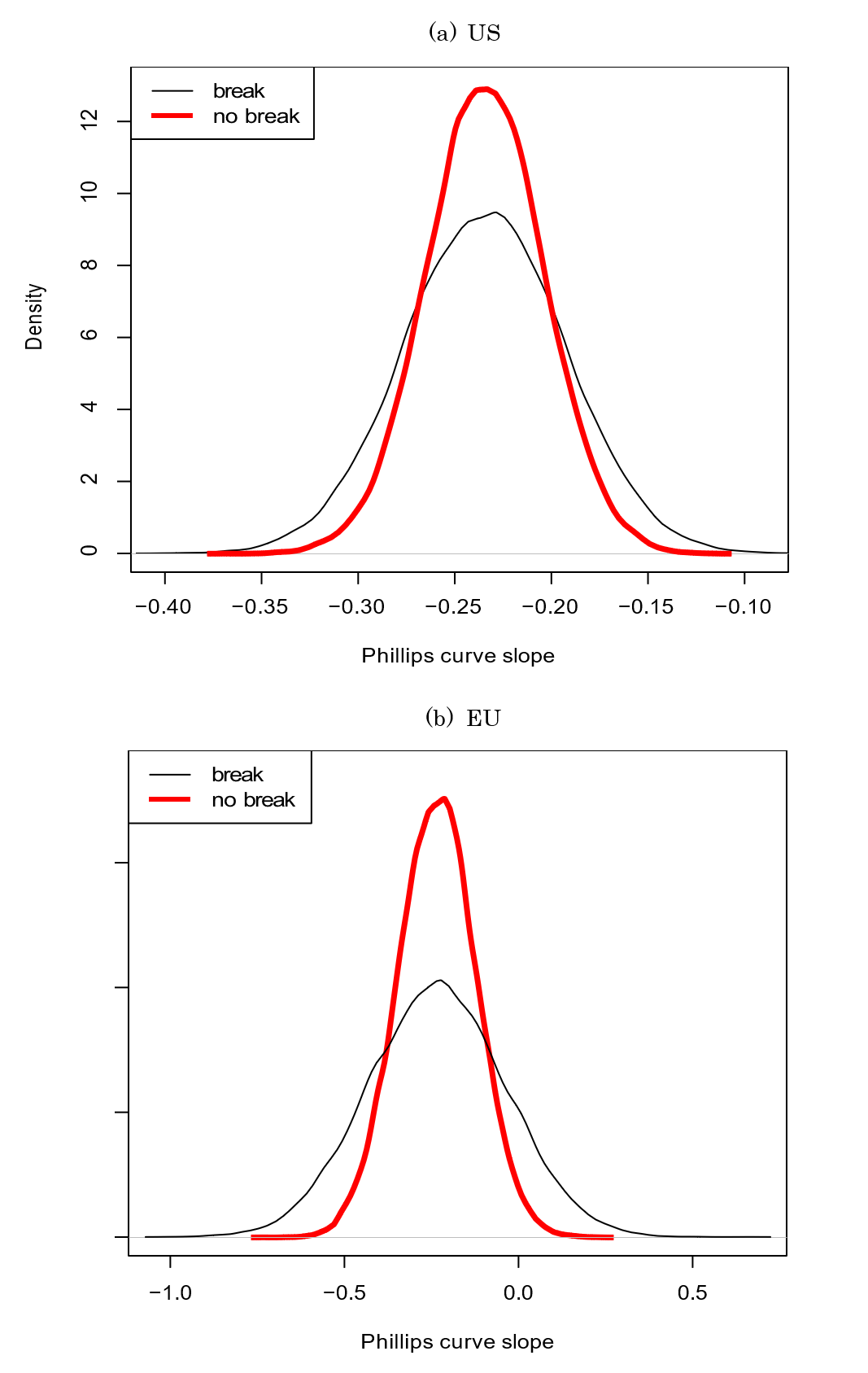
Note: The top panel of this figure displays the density plot of the Phillips curve slope in the US from the model that precludes breaks (red line). To isolate the increased dispersion of the Phillips curve induced by breaks, the break density plot (black line) is assigned the same mean as the no break plot and its standard error is computed as the weighted average of the standard errors of the Phillips curve estimates in the two regimes. The lower panel displays the same information estimated using the EU data.
We see a similar pattern for the EU (Table 2b). Allowing for breaks causes optimal monetary policy to respond less aggressively to deviations in the unemployment rate gap from zero and to compensate for this increased caution by responding more aggressively to deviations in inflation from target. Once again, Table 2b shows that a shift in the Phillips curve slope alone (holding the precision of the estimate fixed) has no impact and so the change in optimal monetary policy responsiveness is driven by the additional parameter uncertainty around the slope of the Phillips curve that the break induces (lower panel of Figure 1).
Finally, the magnitude of our estimated effects of breaks in the Phillips curve on optimal monetary policy should be viewed as a lower bound because they are estimated ex-post using the full data sample. In practice, policymakers face additional uncertainty as they must determine in real time whether a break has occurred and, if so, estimate the slope of the Phillips curve in the new regime.
References
Benigno, P. and Eggertsson, G. B. (2023). It's baaack: The surge in inflation in the 2020s and the return of the non-linear Phillips curve, NBER Working Paper.
Brainard, W. C. (1967). Uncertainty and the effectiveness of policy. American Economic Review, 57 (2), 411–425.
Cerrato, A. and Gitti, G. (2022). Inflation Since COVID: Demand or Supply, Available at SSRN 4193594.
Fitzgerald, T. J., Jones, C., Kulish, M., Nicolini, J. P. et al. (forthcoming). Is there a stable relationship between unemployment and future inflation? AEJ: Macro.
Hazell, J., Herreno, J., Nakamura, E. and Steinsson, J. (2022). The slope of the Phillips Curve: Evidence from U.S. states. Quarterly Journal of Economics, 137 (3), 1299–1344.
Hooper, P., Mishkin, F. S. and Sufi, A. (2020). Prospects for inflation in a high pressure economy: Is the Phillips curve dead or is it just hibernating? Research in Economics, 74 (1), 26–62.
McLeay, M. and Tenreyro, S. (2020). Optimal inflation and the identification of the Phillips curve. NBER Macroeconomics Annual, 34, 199–255.
Rudebusch, G. D. (2001). Is the Fed too timid? Monetary policy in an uncertain world. Review of Economics and Statistics, 83 (2), 203–217.
Sack, B. (2000). Does the Fed act gradually? A VAR analysis. Journal of Monetary Economics, 46 (1), 229–256.
Smith, S., Timmermann, A. and Wright, J. H. (2023). Breaks in the Phillips Curve: Evidence from Panel Data. Tech. rep., National Bureau of Economic Research.
Smith, S. C. and Timmermann, A. (2021). Break risk. Review of Financial Studies, 34 (4), 2045–2100.
Söderström, U. (2002). Monetary policy with uncertain parameters. Scandinavian Journal of Economics, 104 (1), 125–145.
* Email addresses: [email protected] (Simon C. Smith, Federal Reserve Board), [email protected] (Allan Timmermann, University of California, San Diego), [email protected] (Jonathan H. Wright, Johns Hopkins University)
The views expressed in this paper are those of the authors and do not necessarily reflect the views and policies of the Board of Governors or the Federal Reserve System. The authors have no conflict of interest to declare. Return to text
1. This quote is taken from the speech "Monetary policy in an uncertain world" by Christine Lagarde, President of the European Central Bank (ECB), at "The ECB and Its Watchers XXII conference, 17 March 2022." Return to text
2. Breaks are assumed to hit all $$ i = 1, \ldots, N $$ series in the cross-section at the same time. Return to text
3. We use conventional priors. Regime durations, $$ l_{k} = \iota_{k} - \iota_{k-1} $$, have a Poisson prior whose intensity parameter has a Gamma prior, calibrated such that breaks occur on average every twenty years. Relatively uninformative Normal-Inverse Gamma priors are specified over the regression coefficients and residual variances. Our model is estimated using the Markov chain Monte Carlo algorithm developed by Smith and Timmermann (2021). Return to text
4. The national Phillips curve can be recovered by dividing this regional Phillips curve by the non-tradeables share, which is about 0.7 (Hazell et al. 2022). Return to text
5. Our results are robust to using the contemporaneous measure of slack instead of the lagged measure. Return to text
6. The real federal funds rate is measured as the nominal four-quarter average federal funds rate minus the four-quarter headline CPI inflation rate in percent. Return to text
7. To isolate the impact of the break in the Phillips curve, we preclude breaks in the IS curve and hold the IS curve estimates fixed across our US and EU calculations. Return to text
8. As noted by Söderström (2002), once one accounts for uncertainty surrounding the persistence parameter the policymaker may respond more aggressively to additional uncertainty. Sack (2000) and Rudebusch (2001) also consider the effect of uncertainty on the aggressiveness of optimal monetary policy responses. Return to text
9. To isolate the increased dispersion of the Phillips curve induced by breaks, the break density plot is assigned the same mean as the no break plot and its standard error is computed as the weighted average of the standard errors of the Phillips curve estimates in the two regimes. Return to text
Smith, Simon C., Allan Timmermann, and Jonathan H. Wright (2024). "Monetary Policy in Uncertain Times," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, August 30, 2024, https://doi.org/10.17016/2380-7172.3603.
Disclaimer: FEDS Notes are articles in which Board staff offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers and IFDP papers.