FEDS Notes
September 04, 2024
Nonlinear Phillips Curves
Simon C. Smith, Allan Timmermann, Jonathan H. Wright*
Introduction
"What happened to the Phillips curve that it is acting so differently now than in the pre-pandemic period?" (Chris Waller, 2023.)1
The Phillips curve is a key element of the New-Keynesian macroeconomic model and is critical in how central banks think of the macroeconomy. As the opening quote suggests, there has been much debate about potential nonlinearities in the Phillips curve which could, in turn, hinder central banks' ability to monitor, forecast, and control inflation, having major policy implications. This note combines regional data with a novel estimation methodology to jointly identify nonlinearities and structural breaks in the Phillips curve. A break is a time point separating two regimes, each of which has a significantly different Phillips curve slope from the other that applies in all states of the labor market; a nonlinearity is a threshold value of unemployment separating a hot labor market from a more normal one in a given regime. Importantly, we will show how breaks and nonlinearities interact.2
Disaggregate data, whether categorized by region or country, offer notable advantages over aggregate data. Since different regions and countries experience different business cycles, there is extra information in disaggregate data that enables us to identify nonlinearities more precisely than using aggregate data alone. In addition, several recent papers (e.g. Hooper et al. (2020), Fitzgerald et al. (forthcoming) and McLeay and Tenreyro (2020)) have pointed out that if the central bank is successfully targeting inflation, this creates an endogeneity bias in the slope of the Phillips curve, biasing the coefficient towards zero. The use of disaggregate data in conjunction with the inclusion of time fixed effects avoids this problem because the central bank does not specifically target inflation in any one particular region. Identifying the Phillips curve slope through regional variation in the data also helps control for global supply chain disruptions, which were important in the pandemic but likely affected different regions similarly.
As noted by Hooper et al. (2020), identifying nonlinearities in the Phillips curve is easier with disaggregate data since the national labor market has not reached its recent extremely tight levels since the late 1960s, whereas many individual Metropolitan Statistical Areas (MSAs) have had tight labor markets in this time period. The black squares in the top panel of Figure 1 plot the annual aggregate headline Consumer Price Index (CPI) inflation rate against the lagged annual unemployment rate from 1980 through 2022. There are few observations corresponding to very tight labor markets, which we will later explain is defined as an unemployment rate below five percent. On the other hand, the green circles in the same panel plot the corresponding MSA-level data and there are many observations with tight labor markets. The bottom panel of the Figure displays the same information for countries within the EU, although here we use the unemployment rate gap. Again, many countries experience tight labor markets quite frequently – defined as an unemployment rate gap below minus 1.5 percent – but the EU as a whole does not.
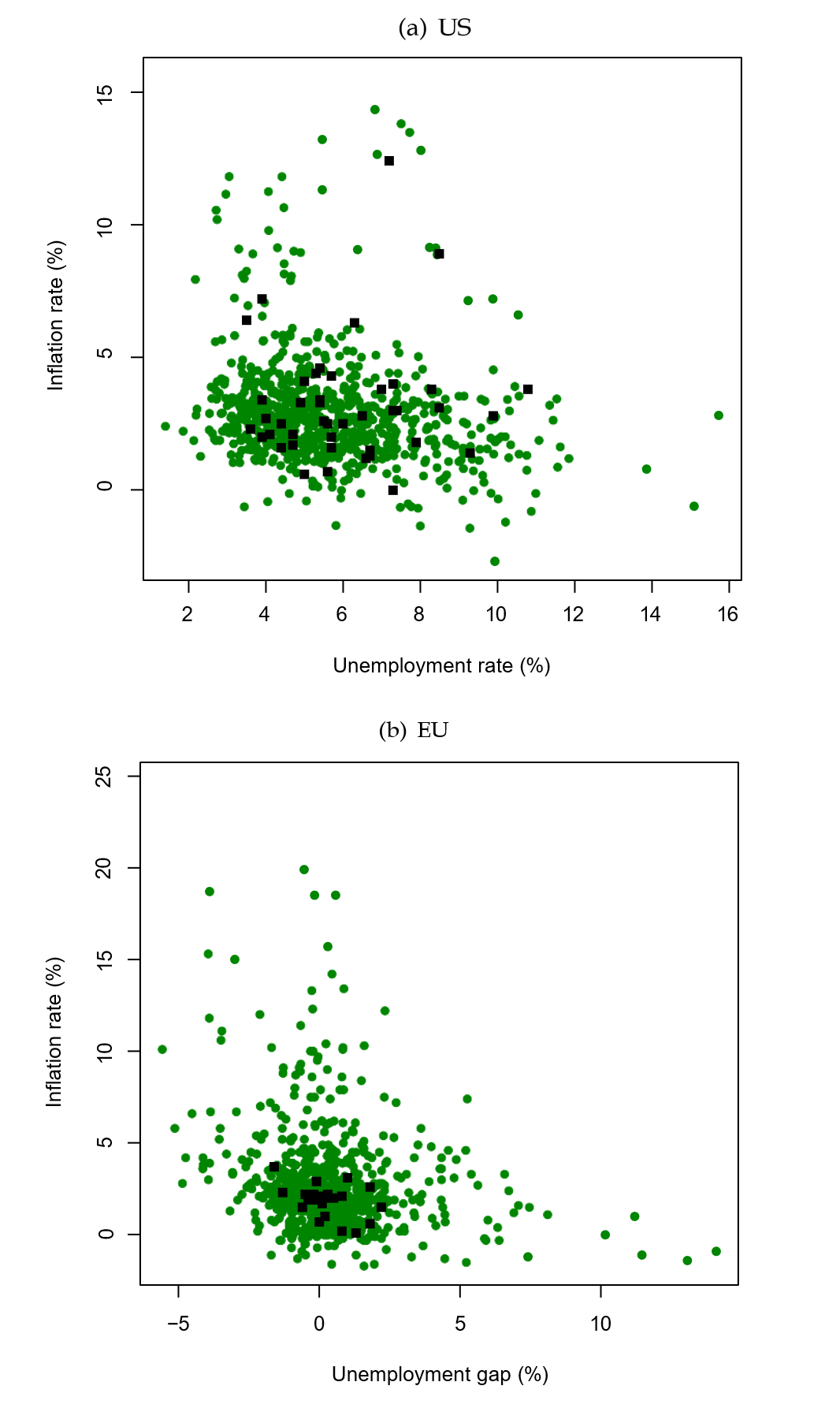
Figure 1a (Top Chart): United States inflation-unemployment rate tradeoff
Note: The green circles (black squares) in this figure plot the annual headline CPI inflation rate against the annual unemployment rate for the 22 MSAs (national aggregate) during our sample period from 1980 through 2022.
Figure 1b (Bottom Chart): European Union inflation-unemployment rate gap tradeoff
Note: The green circles (black squares) in the bottom panel plot the annual inflation rate against the annual unemployment gap for each of the EU countries (the EU aggregate) in our sample from 1986 through 2021. Due to extreme outliers, Romania is excluded from the plot.
We consider US price Phillips curves using disaggregation at the MSA level and wage Phillips curves at the state level. We also examine Phillips curves at the country level within the European Union.
Data
We source monthly total CPIs and corresponding unemployment rates for 22 MSAs in the US from the Bureau of Labor Statistics (BLS). We compute annual inflation rates from annual levels that are constructed as the average of all monthly observations in the corresponding year.
Following Hooper et al. (2020), we compute average hourly earnings (AHE) for each of the 50 states and the District of Columbia using the latest (2019) CEPR uniform extract from the Current Population Survey (CPS). Aggregating from monthly data, we construct quarterly data from 1980:Q1 through 2019:Q4, from which we construct quarterly annualized wage inflation. From the BLS, we use the end of quarter monthly unemployment rate for all 51 states.
From 1986 to 2021, we source headline annual inflation rates for 28 European Union countries (the 27 current members and the United Kingdom) from the European Central Bank (ECB) statistical warehouse and the corresponding annual country-level unemployment rate and natural rate of unemployment estimates from the DG ECFIN/AMECO—the European Commission's macroeconomic database.
Methodology
Our analysis applies the pooled panel multiple breakpoint model developed by Smith and Timmermann (2021) to exploit information in the cross-section and obtain increased power to estimate an unknown number of $$K$$ breaks occurring at unknown times $$ \iota = (\iota_{1}\textit{,}\ldots , \iota_{K}) $$. Breaks are assumed to be common to all $$ i = 1, \ldots, N $$ series in the cross-section. For the annual MSA-level data, the model for the $$k$$th regime (for $$ k = 1, \ldots, K +1 $$) is:
$$$$ \pi_{it} = \alpha_{i} + \gamma_{t} + \rho_{k} \pi_{it-1} + \lambda_{k} URATE_{it} +\omega_{k}(URATE_{it} - \theta) 1_{URATE_{it} < \theta} + e_{it} \ (1) $$$$
in which $$ \pi_{it} $$ denotes the inflation rate for the $$i$$th MSA at year $$t$$, $$\alpha_{i}$$ and $$\gamma_{t} $$ denote two-way fixed effects, $$ \pi_{it-1} $$ is the lagged inflation rate for MSA $$i$$, $$ URATE_{it} $$ denotes the unemployment rate for the $$i$$th MSA at year $$t$$, and $$ e_{it} $$ is the residual for the $$i$$th series at year $$t$$. The parameters $$ \rho \textit{,}\ \lambda\ $$ and $$ \omega $$ are allowed to shift across regimes.
Our framework allows the unemployment-inflation trade-off to have a kink at a pre- specified threshold, $$\theta $$, with a Phillips curve slope of $$ \lambda $$ whenever $$ URATE_{it} \geq \theta $$ and a slope of $$ \lambda + \omega $$ otherwise. Note that there is no discontinuity at the threshold point ($$ \theta $$) but the magnitude of the kink in the Phillips curve ($$ \omega_{k} $$) is regime-specific. We use a threshold of five percent, also used by Babb and Detmeister (2017). We identify this value by performing a grid search across all unemployment rate values, using 0.1 percent increments and estimating the R-squared of each model without breaks on the full sample of data. Using this approach, the R-squared is maximized when the unemployment rate is five percent. We condition on this threshold value when estimating the breakpoint model in Equation (1).
The specification in Equation (1) uses the unemployment rate as the slack measure since there are no estimates of the natural rate of unemployment at the MSA-level so we rely on the two-way fixed effects to absorb variation in the natural rate across time and cities. Common time variation in inflation expectations in Equation (1) is also absorbed by the time fixed effects. The same model with the same threshold is applied to the state wage level data. And it is also applied to the EU-level data, except that here the unemployment rate gap replaces the unemployment rate. We use the same grid search approach to identify a threshold of -1.5 percent for the unemployment rate gap which has been used in earlier studies (Stock and Watson 2009).3
Empirical Results
First, Table 1 shows that there is a break in the US price Phillips curve in 2000, with a modest flattening in normal labor markets from a significant -0.26 to a still significant -0.18.4 Second, in the post-2000 regime, the size of the kink (i.e. the difference between the slope of the Phillips curve in normal labor markets and the slope when the unemployment rate is below five percent) is notably bigger than it is for the full sample (-0.28 versus -0.19).5 Since the turn of the century, the Phillips curve has therefore (i) flattened in normal labor markets but (ii) remained equally steep in a tight labor market as it was pre-2000 due to the magnitude of the kink having increased. Ignoring breaks would therefore underestimate the steepness of the Phillips curve in tight labor markets currently.
Table 1: Annual 22 CPI MSA-level inflation rates (1980-2022)
| 1980-2000 | 2001-2022 | 1980-2022 | |
|---|---|---|---|
| PC | -0.26∗∗∗ | -0.18∗∗∗ | -0.19∗∗∗ |
| Extra PC (U. rate <5%) | -0.22∗∗∗ | -0.28∗∗∗ | -0.19∗∗∗ |
We identify a similar break date in the US wage Phillips curve (Table 2), after which the slope in normal labor markets falls modestly from -0.41 to -0.32. We find even stronger evidence of a much steeper wage Phillips curve in tight labor markets. For example, the slope of the wage Phillips curve after 2000 is -0.32 when the unemployment rate exceeds five percent but, at -0.8, is nearly three times steeper when unemployment falls below this level. This suggests that very tight labor markets benefit workers who are able to extract larger real wage gains during these periods, as has been observed during the pandemic.
Table 2: Wage Phillips curve: 51 state-level quarterly wage inflation rates (1980-2019)
| 1980:1-2000:1 | 2000:2-2019:4 | 1980:1-2019:4 | |
|---|---|---|---|
| PC | -0.41∗∗∗ | -0.32∗∗∗ | -0.35∗∗∗ |
| Extra PC (U < 5%) | -0.54∗∗∗ | -0.48∗∗∗ | -0.52∗∗∗ |
Broadly similar patterns are found in the EU, albeit the break occurs a few years later (Table 3). Again, we see evidence of a significant flattening of the Phillips curve in normal labor markets and indeed the magnitude of the flattening is greater than found in US data, but the Phillips curve remains steep in the most recent regime when in a tight labor market. Ignoring breaks causes the magnitude of this kink to be underestimated, underscoring the insights from considering nonlinearity and structural stability jointly.
Table 3: Annual 28 EU countries inflation (1986-2021)
| 1986-2003 | 2004-2021 | 1986-2021 | |
|---|---|---|---|
| PC | -1.15∗∗∗ | -0.07∗∗ | -0.21∗ |
| Extra PC (UGAP < -1.5%) | 3.28 | -0.56∗∗∗ | -0.17 |
In sum, our findings suggest that the Phillips curve has flattened since 2000 in normal labor markets but remains steep in tight labor markets. These results hold for both the US and the EU. This finding is clearly relevant to policy debates about the costs and benefits of a hot labor market. It also suggests that monetary policy-makers face a fundamentally different inflation-unemployment tradeoff in tight labor markets compared with in loose labor markets and should account for this when setting policy.
References
Babb, N. and Detmeister, A. K. (2017). Nonlinearities in the Phillips curve for the United States: Evidence using metropolitan data, FEDS Working Paper 2017-70.
Fitzgerald, T. J., Jones, C., Kulish, M., Nicolini, J. P. et al. (forthcoming). Is there a stable relationship between unemployment and future inflation? AEJ: Macro.
Hazell, J., Herreno, J., Nakamura, E. and Steinsson, J. (2022). The slope of the Phillips Curve: Evidence from U.S. states. Quarterly Journal of Economics, 137 (3), 1299–1344.
Hooper, P., Mishkin, F. S. and Sufi, A. (2020). Prospects for inflation in a high pressure economy: Is the Phillips curve dead or is it just hibernating? Research in Economics, 74 (1), 26–62.
McLeay, M. and Tenreyro, S. (2020). Optimal inflation and the identification of the Phillips curve. NBER Macroeconomics Annual, 34, 199–255.
Smith, S., Timmermann, A. and Wright, J. H. (2023). Breaks in the Phillips Curve: Evidence from Panel Data. Tech. rep., National Bureau of Economic Research.
Smith, S. C. and Timmermann, A. (2021). Break risk. Review of Financial Studies, 34 (4), 2045–2100.
Stock, J. H. and Watson, M. W. (2009). Phillips curve inflation forecasts. In Understanding Inflation and the Implications for Monetary Policy: A Phillips Curve Retrospective, MIT Press.
* Email addresses: [email protected] (Simon C. Smith, Federal Reserve Board), [email protected] (Allan Timmermann, University of California, San Diego), [email protected] (Jonathan H. Wright, Johns Hopkins University). Return to text
1. This quote is from Federal Reserve Governor Chris Waller's speech entitled "The Unstable Phillips Curve" on March 31, 2023; https://www.federalreserve.gov/newsevents/speech/waller20230331a.htm. Return to text
2. This note is based on a more detailed analysis in Smith et al. (2023). Return to text
3. We use conventional priors. Regime durations, $$ l_{k} = \iota_{k} - \iota_{k-1} $$, have a Poisson prior whose intensity parameter has a Gamma prior, calibrated such that breaks occur on average every twenty years. Relatively uninformative Normal-Inverse Gamma priors are specified over the regression coefficients and residual variances. Our model is estimated using the Markov chain Monte Carlo algorithm developed by Smith and Timmermann (2021). Return to text
4. Our results are robust to using either the contemporaneous or lagged measure of slack. Hazell et al. (2022) show that the national Phillips curve can be recovered by dividing the regional Phillips curve by the nontradeables share, which is about 0.7. This implies a flattening of the aggregate Phillips curve from -0.37 to -0.26. Return to text
5. Our finding that the Phillips curve has not flattened much since the turn of the century when we are in a tight labor market also holds for the sacrifice ratio: the sacrifice ratio when the unemployment rate is below five percent is little changed after the break (Smith et al. 2023). Return to text
Smith, Simon C., Allan Timmermann, and Jonathan Wright (2024). "Nonlinear Phillips Curves," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, September 04, 2024, https://doi.org/10.17016/2380-7172.3596 .
Disclaimer: FEDS Notes are articles in which Board staff offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers and IFDP papers.