FEDS Notes
January 08, 2019
A Simple Macro-Finance Measure of Risk Premia in Fed Funds Futures
Anthony Diercks and Uri Carl
Term premia can contaminate the policy expectations that we derive from Fed Funds Futures while assuming risk neutrality. Existing estimates of term premia used in the literature are computed from term structure models that depend on mean reversion (based on historical data) and survey expectations.1 Term structure models that depend on mean reversion can imply terminal or long-run rates that may not correspond to the current economic environment. For instance, the OIS-ZLB model of Priebsch (2017)2 estimates (based on historical data going back 25 years) a terminal rate close to 4 percent and a steeper path of policy when compared to current surveys. The end result is potentially larger negative term premia than would otherwise be the case if the terminal rate were estimated to be lower. In addition, term structure models tend to shed little light on why term premia have changed signs and size over time.
To address some of these issues, we offer an alternative macro-finance reduced-form measure of term premia in Fed Funds Futures that is parsimonious and motivated by economic theory. In a nutshell, we will use rolling covariances between real and nominal activity in a regression framework, combined with a model averaging approach, to uncover intuitive dynamics in the term premium. To preview some of our findings,
- Compared to the OIS-ZLB model of Priebsch (2017), our measure implies a smaller level of negative term premia (roughly 3x smaller) since exiting the zero lower bound, and is currently closer to -1 basis point per month across maturities of 3 to 9 months. This implies a 12 % (at 3 months) to 36 % (at 9 months) upward adjustment to calculations for the probability of a rate hike, depending on the maturity.
- Consistent with other models in the literature, our measure of term premia has recently become less negative.
- Our monthly measure improves upon existing measures in the literature with respect to out-of-sample forecast errors of the federal funds rate.
Two snapshots in time show pertinent implications for policy expectations:
(1) Looking back to April 2018, the probability that was priced into the market for a fourth rate hike by the end of the year 2018 was:
- Fed Funds Futures (Zero Term Premium): 0 %
- Fed Funds Futures (Term-Premium Adjusted based on OIS-ZLB): 100 %
- Fed Funds Futures (Term-Premium Adjusted based on Diercks and Carl): 35 %
(2) As of December 20, 2018, the number of hikes priced in by the end of June 2019:
- Fed Funds Futures (Zero Term Premium):
- 45% of 1 hike
- Fed Funds Futures (Term-Premium Adjusted based on OIS-ZLB):
- 100 % of 1 hike and 35 % of a second hike
- Fed Funds Futures (Term-Premium Adjusted based on Diercks and Carl):
- 70% of 1 hike
Review of Existing Measures of Short Horizon Term Premia
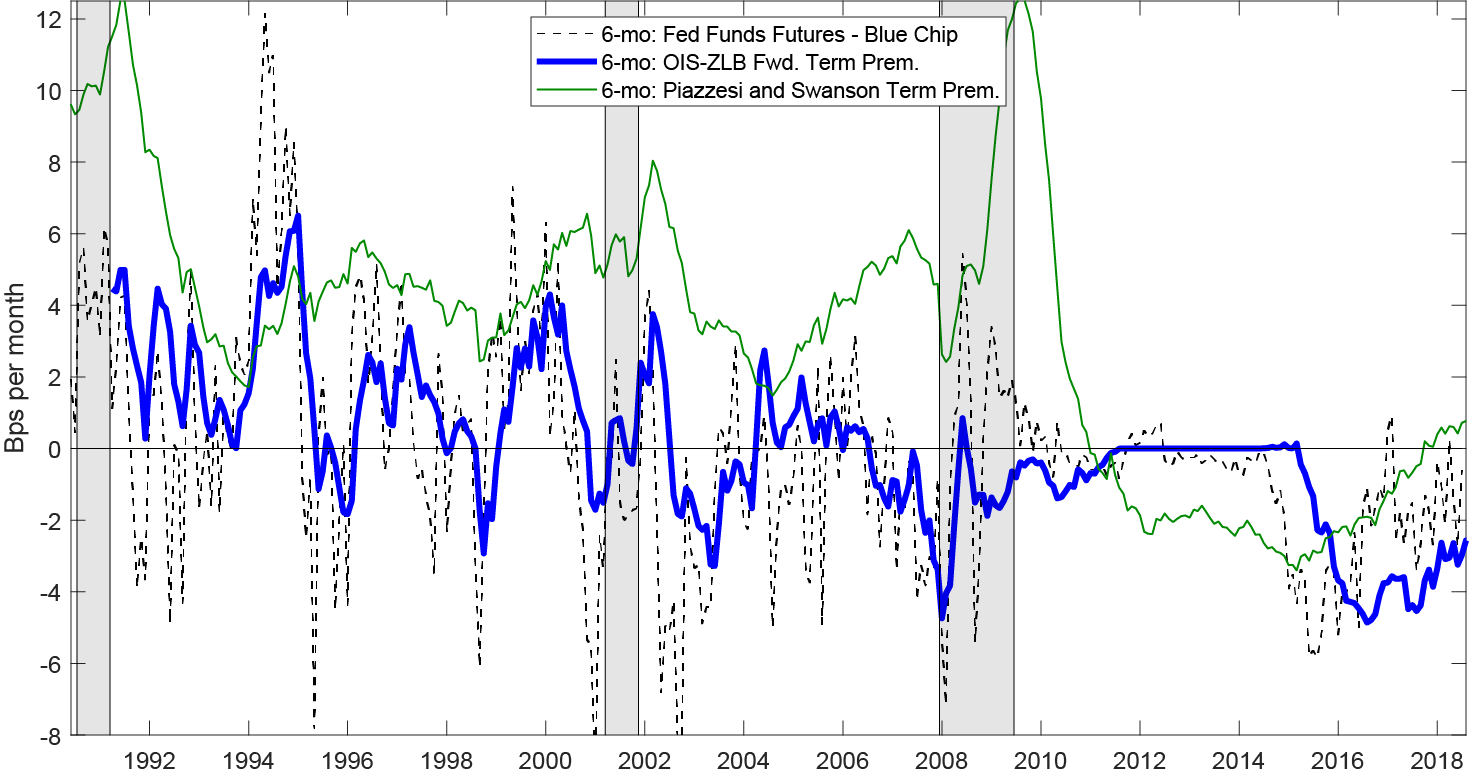
Before introducing our proposed estimate of term premia, in this section we briefly describe three existing measures of short horizon term premia, as proposed in the literature.
- As Figure 1 shows, this measure of term premia (dashed gray line) is volatile, exhibiting sizable spikes that appear to be unrelated to macro-fundamentals.
- This volatility may be related to the necessary interpolation (conversion from quarterly to monthly, which we describe in detail in the Appendix) or idiosyncrasies associated with surveys (such as infrequent availability and potential inaccuracy due to sampling uncertainty).
- OIS-ZLB Term Premia
- Based on Priebsch (2017),5 computes real-time daily term premia (solid blue line) estimates using a term structure model in which the short rate follows a Gaussian process censored at 0.
- Gap between Fed Funds Futures and realized Federal Funds Rate n-months ahead
- Piazzesi and Swanson (2008)6 focus on the excess return between Federal Funds Futures and the ex-post realized value of the federal funds rate for the contracted month.
- Uses basic regressions to extract the predictable component to capture the term premium (solid green line), but tends to generate extreme values for term premia that could be a function of forecast error rather than risk compensation.
Figure 1 shows the time series at the 6-month horizon for the measures described above. While our analysis will focus only on horizons of 3- to 9-months (due to liquidity issues at longer horizons and interpolation issues at shorter horizons7), the dynamics across these horizons are roughly consistent with the 6-month horizon that is shown in Figure 1.
A few more items for consideration:
- The Piazzesi and Swanson (2008) measure (solid green) reaches extreme levels of term premia that could imply up to a 72 basis point (12 bps per mo. x 6-mo.) difference with the zero premium measure (the equivalent of about 3 rate hikes/cuts).
- The OIS-ZLB term premium (solid blue) has a different sign than the survey based term premia (dashed gray line) 121 out of the 327 months in the sample (37% of the time). During the months in which the sign is not the same, the mean absolute difference is 15 total basis points, or 60% of a rate cut / hike.
- Each of the measures imply a term premium that has become less negative since the end of 2015.
Economic factors of term premia:
Our goal in this note is to glean estimates of and movements in term premia that are grounded in observable macroeconomic quantities and economic theory. To identify candidate variables to explain the dynamics of term premiums, we start with standard no-arbitrage conditions in general equilibrium models. In that context, the following equation holds (as is derived in the Appendix):
$$$$ f_t^{(1)} - E_t [r_{t+1}] = -Cov_t(Y_{t+1}, r_{t+1}) $$$$
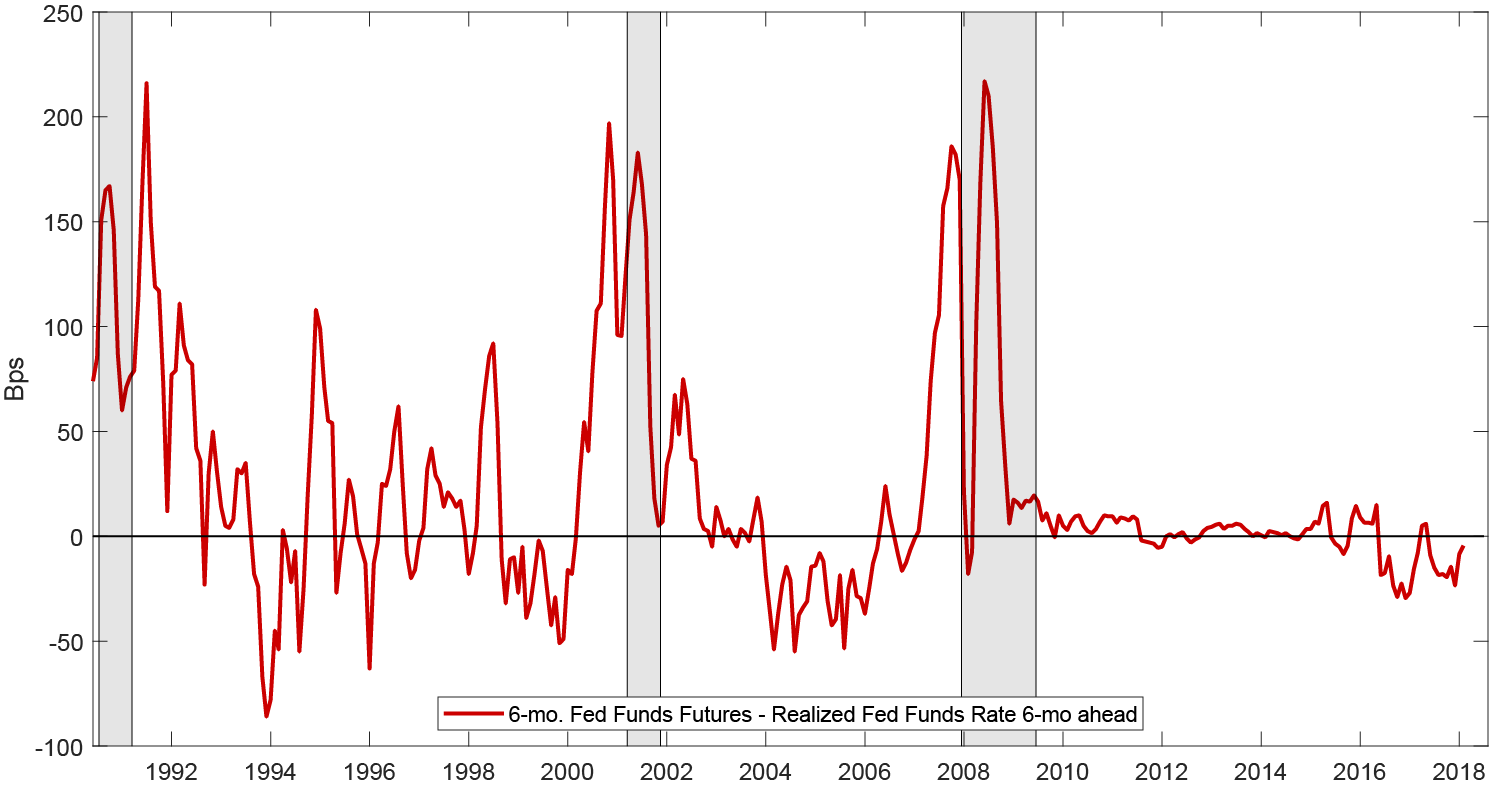
where $$f_t^{(1)}$$ is the expected federal funds rate based on Fed Funds Futures at time t, 1 month ahead, $$E_t [r_{t+1}]$$ is the expected federal funds rate based on Blue Chip forecasts, 1 month ahead at time t, and $$Y_{t+1}$$ can reflect a measure of real activity.8 In simple terms, it states that if rate declines are associated with adverse macroeconomic conditions (positive covariance between output and interest rates), the term premium should be negative. In this case, a Fed Funds Futures contract would provide insurance, as its realized return $$(f_t^{(1)} - r_{t+1})$$ is highest in bad states of the world. This is clearly evident in Figure 2, which plots the realized returns (red line) and shows that the realized returns significantly rise during recessions (denoted in gray).
Data and Methodology
For the left hand side variable in our regression framework, we use the gap between the Fed Funds Futures and the Blue Chip Median Forecast. We will attempt to explain variation in this survey-based measure using economic factors and a model averaging approach at the monthly frequency (monthly is the highest frequency available given our reliance on macroeconomic data). The predicted value from this exercise will represent our measure of term premia and we believe that it
- Represents an improvement over Piazzesi and Swanson (2008) as it is less subject to forecast error (since forecast errors are in both the Fed Funds Futures and the survey9)
- Allows us to filter out movements in the survey based measure that are unrelated to the theory described above.
- Not subject to issues related to historical mean reversion, in which the terminal or long-run rates may not correspond adequately to the current economic environment. Our framework allows us to avoid taking an explicit stand on the level of long-run rates, which could otherwise impact the slope of the expected path of policy.
The right hand side in our regressions will have a constant and a covariance:
$$$$ f_t^{(n)} - E_t [r_{t+n}] = \alpha + \beta_{i,k,m} Cov_{i,k,m}(Y_t^i, R_t^k), $$$$
i = 1:2 (2 real activity measures)
k = 1:3 (3 nominal measures)
m = 1:20 (20 window sizes ranging from 1 to 20 years)
$$Y_t^i$$ represents one of the two real activity measures that we include separately in the regression: the 12-month percentage change in industrial production and the 12-month percentage change in nonfarm payrolls. In $$R_t^k$$, we include the federal funds rate, as well as two measures of inflation: CPI-U (Consumer Price Index for All Urban Consumers) and PCE-All (Personal Consumption Expenditures price Index), which we conjecture to provide predictive power for forward dynamics of the federal funds rate. Including these additional measures is a parsimonious way of bringing us closer to the forward-looking conditional covariance derived from theory.10
For our model averaging approach (which we will explain more in detail in the following section), we try to be agnostic and not take a stance on the length of the memory for the covariance, so we include memories as short as one year up to as long as twenty years, in one year increments. Hence, $$Cov_{m=1:20}$$ represents an unconditional covariance of real activity and the federal funds rate along with other nominal measures, with m representing the 20 window sizes ranging from 1 to 20 years in length. Combining all the possible configurations of m, i, and k leads to 120 possible regressions, all of which we incorporate in our model averaging approach.
Figure 3 shows the 120 covariances (between real activity and the federal funds rate and inflation) used in the regressions, and for expositional purposes, we flip the sign to show the negative covariance so that it coincides with the theory. The solid black (dotted black) line reflects the average (median) at each point in time across the 120 different negative covariances. As can be seen in Figure 3, the average negative covariance was most positive prior to 1990 (indicative of positive term premia), and then changes signs near 2000, moving from positive to negative. This figure helps provide one explanation for why the term premium is currently negative, why it has changed sign over time, and why it is becoming smaller or less negative more recently (also consistent with the OIS-ZLB model and surveys).
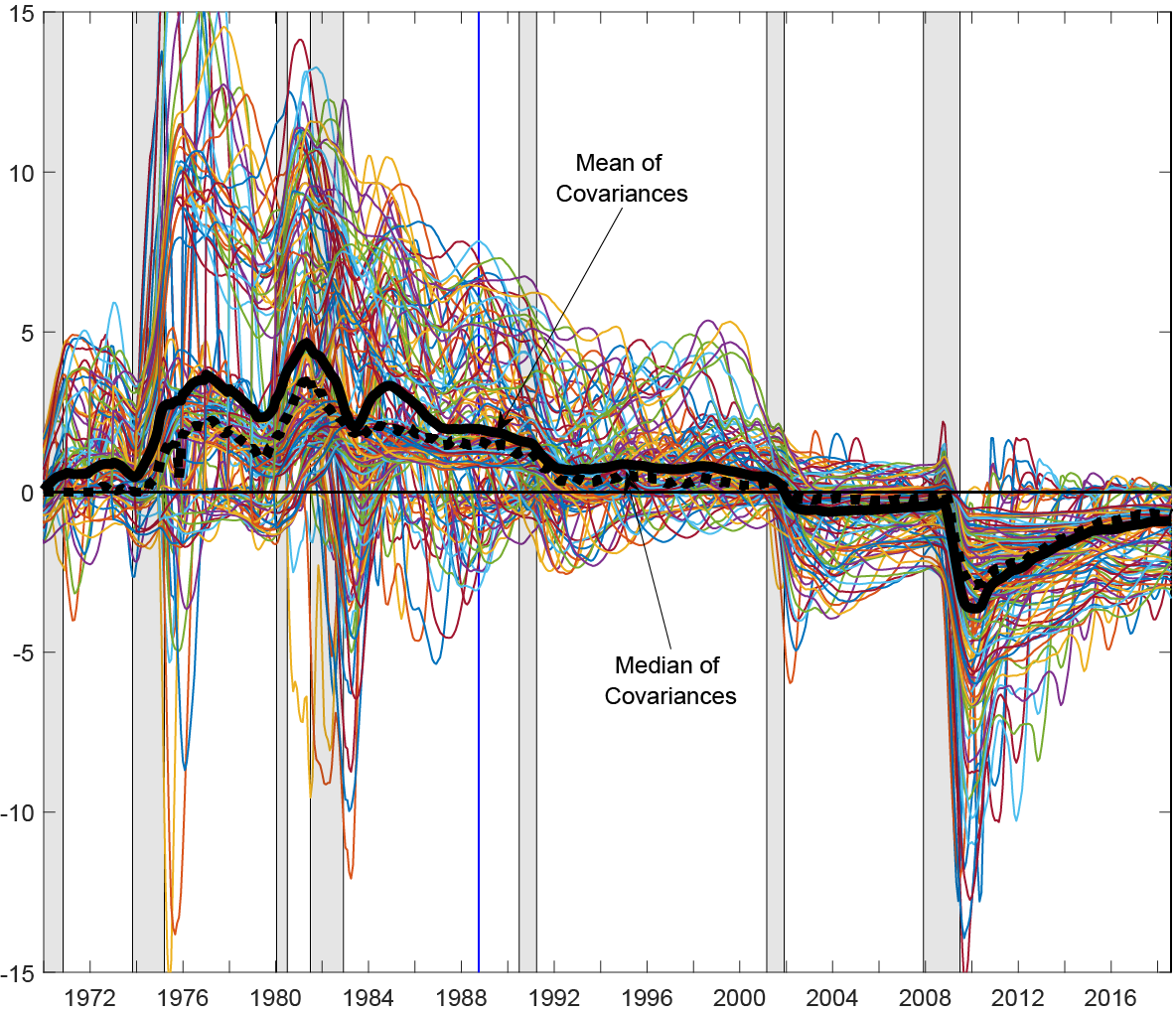
Note: 120 lines are plotted reflecting all of the negative covariances used in the regressions for the model averaging. The 120 lines (20 x 2 x 3) reflect 20 different window lengths ranging from 1 to 20 years, with two possible real activity measures (industrial production 12-mo percent change and non-farm payrolls 12-month percent change) and three nominal measures (the federal funds rate, CPI-U, PCE-all inflation). The solid vertical blue line reflects the beginning of the full in-sample period of 1988:10 to 2018:08. The thick solid black (thick dotted black) line reflects the average (median) of the 120 covariances at each time period.
Model Averaging
Model averaging or forecast combinations is a statistical technique, where multiple regressions—made up of various permutations or sets of regressors—are averaged together, and has been shown to have better performance than individual forecasts based on a single regression.11 These benefits are greatest when
(1) individual forecasts are misspecified,
(2) there is an unstable forecasting environment and past track records are unreliable,
(3) the time sample is relatively short.
Each of these three characteristics roughly applies to our current goal of estimating the term premia in the rates on Federal Funds Futures contracts. Furthermore, economic theory does not offer guidance on which inflation or real activity measure we should be including. For our exercise, we use an equal weighting scheme in which each individual forecast receives the same weight in the construction of the weighted averaged combined forecast. Such a scheme has been shown to provide robust performance in small samples and may better handle structural breaks.12
Results: Full In-Sample Predicted Term Premia
We look at specific maturities of 3- to 9-months for Federal Funds Futures rates (horizons beyond these maturities have lower liquidity and horizons at 1 to 2 months have interpolation issues13). The in-sample period is 1988:10 to 2018:08. Note that to better capture the effects of forward guidance, we add a dummy variable to the regression for the period 2008:12-2014:12.14 Shown in Figure 4 is the predicted term premium (in basis points per month) at the 6-month horizon based on model averaging using equal weights (the other maturities provide similar results, see Figure 5 in the Appendix).
Figure 4 shows that the previously-used rule-of-thumb (the so-called "Kohn Rule") of 1 basis point per month for term premia is consistent with our estimated macro-finance reduced form measure (red line) during the early to mid-1990s. However, starting in 2000, the average term premium flipped signs to negative one basis point per month. It was zero during the forward guidance period, and then moved back into more negative territory than before. Although it continues to be negative after lift-off from the zero lower bound, the magnitude is declining and becoming less negative. Lastly, Figure 4 shows that the OIS-ZLB term premium has been about three times larger than our estimate since exiting the zero lower bound.
Robustness: Average In-Sample Coefficients and Out- of-Sample Predictions
We find that across the 120 in-sample regressions, the average covariance term has a negative sign close to one, with the sign being consistent with economic theory.15 The coefficients range from -1.2 to -1.6 across horizons and are provided in Table 1 of the Appendix.
Moving to out-of-sample analysis, a natural way to compare the different models is to investigate their ability to predict future short-term interest rates. We follow Adrian, Crump, and Moench (2013)16 and generate monthly forecasts, with a training window from 1988:10 through 1991:03. We choose this training window to match up with the available estimates of the OIS-ZLB model, which starts in 1991:04. We take the OIS-ZLB model's in-sample estimates of term premia as given, while we re-estimate the other models at monthly intervals with an expanding estimation window and compare the federal funds rate predictions from 3 to 9 months ahead against realized values of the federal funds rate.
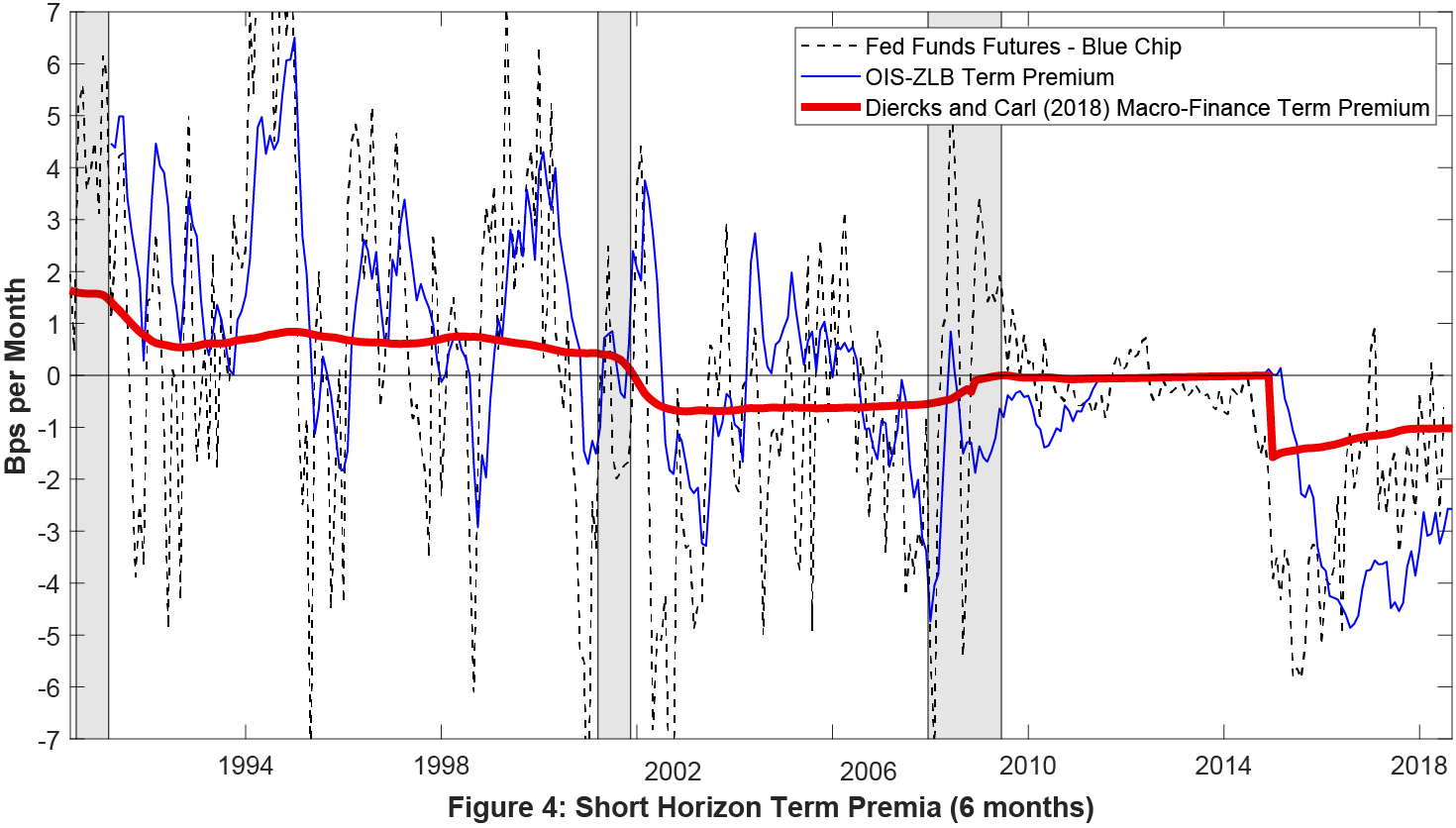
Note: Plotted are the 6-month predicted in-sample term premia (solid red) based on model averaging using equal weights. The dark-gray dashed line represents the difference at the 6-month horizon between the Fed funds futures and the Blue Chip median forecast, in basis points per month. The in-sample estimation period extends from 1988:10 to 2018:08. Predicted term premia for other maturities are roughly consistent and shown in the Appendix.
Table 2: RMSE Out-of-Sample Performance
| 3-mo | 4-mo | 5-mo | 6-mo | 7-mo | 8-mo | 9-mo | |
|---|---|---|---|---|---|---|---|
| Diercks & Carl (2018) | 28.27 | 37.24 | 46.67 | 56.24 | 66.72 | 73.47 | 80.67 |
| Federal Funds Futures | 28.51 | 37.79 | 47.73 | 57.89 | 68.54 | 74.62 | 82.54 |
| Blue Chip Median | 30.7 | 40.7 | 51.04 | 61.64 | 72.41 | 83.11 | 93.79 |
| OIS-ZLB In Sample | 28.52 | 37.8 | 47.72 | 57.87 | 68.51 | 74.59 | 82.5 |
| Piazzesi & Swanson (2008) | 31.61 | 43.48 | 54.77 | 63.3 | 68.93 | 79.71 | 84.17 |
Note: This table compares out of-sample performance based on root mean squared errors (RMSE) through 2018:08. The training window is from 1988:10 through 1991:03. The OIS-ZLB model’s term premia are based on in-sample estimates.
According to this exercise, we find that the Piazzesi & Swanson (2008) and Blue Chip Median Forecasts generate the largest RMSE. The OIS-ZLB framework provides similar performance to the Federal Funds Futures and provides lower RMSE beyond the 5-mo horizon. The Diercks & Carl framework yields the lowest RMSE among the models tested across the 3- to 9-mo horizons.
Implications for the Current Path for the Federal Funds Rate
As of December 20, 2018, the number of hikes priced in by the end of June 2019:
- Fed Funds Futures (Zero Term Premium):
- 45% of 1 hike
- Fed Funds Futures (Term-Premium Adjusted based on OIS-ZLB):
- 100 % of 1 hike and 35 % of a second hike
- Fed Funds Futures (Term-Premium Adjusted based on Diercks and Carl):
- 70% of 1 hike
Looking further ahead, Figure 3 and Figure 4 show that our estimates of the term premium have quite a bit of persistence. Absent any fundamental shifts in the economy such as a recession, this implies that -1 basis point per month could be an appropriate adjustment going forward for an extended period of time.
Conclusion
Our goal in this note is to develop an alternative measure of term premia in Federal Funds Futures that remains parsimonious while providing intuition. Our macro-finance reduced-form measure moves beyond historical mean reversion and surveys and allows us to address questions about why term premia are negative and why they are changing sign and magnitude over time. Our analysis suggests term premia switched signs in the early 2000s and became even more negative following the financial crisis as a result of the changing covariances between real activity and nominal measures. Consistent with other measures of term premia, our measure is becoming less negative more recently and suggests a term premium that is currently closer to -1 basis point per month across horizons of 3 to 9 months. This is in contrast to the OIS-ZLB framework, which is suggesting negative term premia that are up to three times larger at similar maturities. Overall, model diversity can be beneficial in attempting to quantify the dynamics and magnitudes of unobservable term premia in Federal Funds Futures, and we consider our measure to be a worthwhile supplement to existing frameworks in the literature.
Appendix
Note the following zero-cost no arbitrage condition
$$ 0 = E_t [M_{t+1} (f_t^{(1)} - r_{t+1})] $$
where $$M_{t+1}$$ is the stochastic discount factor (SDF)17.
Any expectation of a product can be decomposed into the following:
$$ 0 = E_t [M_{t+1}] E_t [(f_t^{(1)} - r_{t+1})] + Cov_t (M_{t+1}, (f_t^{(1)}-r_{t+1})) $$
Dividing both sides by $$E_t [M_{t+1}]$$ and subtracting the covariance from both sides (for simplicity and to save space, we do not put $$E_t [M_{t+1}]$$ in the denominator of the covariance term)
$$ -Cov_t (M_{t+1}, (f_t^{(1)} - r_{t+1})) = E_t [(f_t^{(1)} - r_{t+1})] $$
Note that $$f_t^{(1)}$$ is known at time t:
$$ -Cov_t (M_{t+1}, -r_{t+1}) = f_t^{(1)} - E_t [r_{t+1}] $$
Distributing the covariance
$$ f_t^{(1)} - E_t [r_{t+1}] = Cov_t (M_{t+1}, r_{t+1}) $$
The stochastic discount factor captures the marginal utility of investors, and this variable is typically found to be high during recessions and low during expansions. Based on this logic, we make the following assertion, $$M_{t+1} \approx -Y_{t+1}$$, where $$Y_{t+1}$$ can reflect a measure of real activity.
$$ f_t^{(1)} - E_t [r_{t+1}] = -Cov_t (Y_{t+1}, r_{t+1}) $$
Rewriting the covariance based on its definition
$$ f_t^{(1)} - E_t [r_{t+1}] = -\rho_{\sigma_m,\sigma_r} \sigma_{Y_{t+1}} \sigma_{r_{t+1}} $$
This equation suggests that the risk premium will be of greater magnitude if there is greater uncertainty about the economy and/or federal funds rate. More importantly, it suggests that the correlation, $$\rho_{\sigma_Y, \sigma_r}$$, between economic activity and the federal funds rate will determine the sign of the risk premia.
Interpolation of Blue Chip Financial Forecasts
The Blue Chip Financial Forecasts provide survey-based estimates of the federal funds rate 0 to 5 quarters ahead. Note, these quarters are tied to the calendar and do not roll forward with the passage of each month. In other words, the start of one quarter ahead can range from 3 months to 1 month away, depending on if we are in the first or last month of the current quarter (the zero quarter).
In order to construct our monthly series, we note that the surveys are typically completed in the last week of the prior month. For instance, the results of the March survey will actually be based on responses from the last week of February.
To go from quarterly to monthly, we assume quarterly values correspond to the second month of each quarter and linearly interpolate. Once we have converted to monthly, we then take the forecast horizon and subtract by one month and store in the previous month. For instance, the results of the March survey projected 5 months ahead are stored in the February month as the 6 month horizon. This allows us to compare directly to the federal funds futures, which are stored based on the last day of each month (using the average of the last week gives nearly identical results).
For horizons of 1 to 2 months, we find that estimates are significantly different from the estimates spanning 3 to 9 months. We conjecture this is due to the timing of the survey release, which as stated in the previous paragraph, forces us to subtract the horizon by one month and store the results under the previous month. For instance, the forecast for the 2 month horizon from February is taken as the one month horizon from the March release. Such close proximity seems to distort the basis points per month calculations, and this does not appear to be an issue for later maturities that do not depend as much on the zero quarter values.
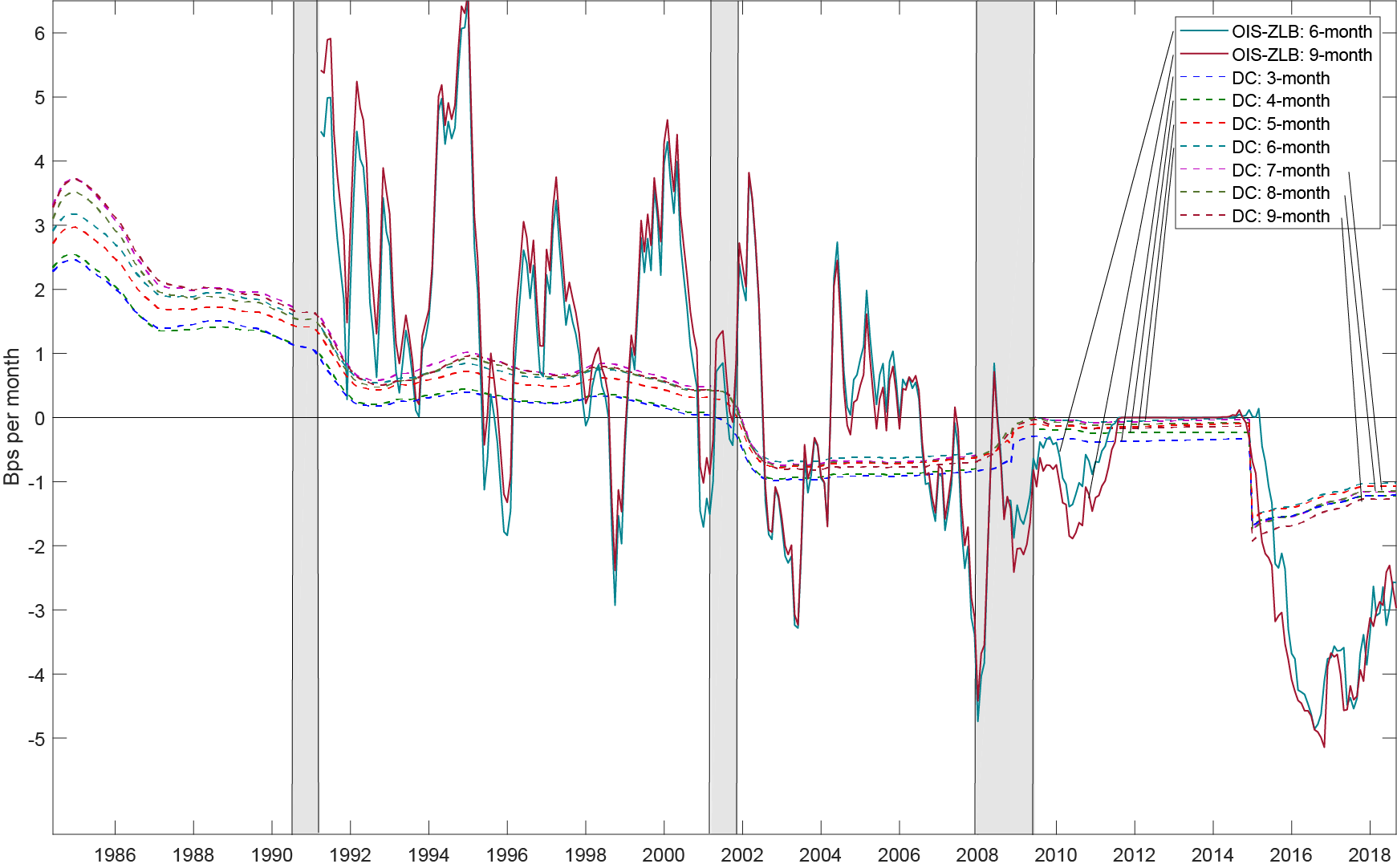
Note: Plotted are the 3- to 9-month predicted term premia based on model averaging using equal weights. The OIS-ZLB forward term premia are labeled in the legend by month of maturity. The in-sample estimation period extends from 1988:10 to 2018:08.
Table 1: Average Coefficients Across Regressions
| α | Cov | Cov*Dummy | |
|---|---|---|---|
| 3-mo | -0.56** | -1.39*** | 1.54*** |
| 4-mo | -0.51** | -1.28*** | 1.47*** |
| 5-mo | -0.39** | -1.27*** | 1.44*** |
| 6-mo | -0.26 | -1.32*** | 1.47*** |
| 7-mo | -0.51 | -1.45*** | 1.58*** |
| 8-mo | -0.39* | -1.43*** | 1.58*** |
| 9-mo | -0.26 | -1.58*** | 1.67*** |
Note: This table shows the average coefficients across the 120 regressions, with the average significance denoted by *** (99 percent), **(95 percent) and * (90 percent). The 120 regressions are made up of 120 possible covariances (20 window lengths of 1 to 20 years, 2 real activity measures, and 3 nominal measures including the federal funds rate, CPI-U, and PCE-All).
1. It is pointed out in Piazzesi and Swanson (2008) that at one point in time, Board staff estimates of policy expectations tended to use the so-called "Kohn rule," which stipulated subtracting 1 basis point per month from forward rates to account for term premia and therefore assumed that term premia were positive and linearly increasing in maturity. Return to text
2. Based on Priebsch, Marcel A. (2017). "A Shadow Rate Model of Intermediate-Term Policy Rate Expectations," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, October 4, 2017, https://doi.org/10.17016/2380-7172.2056. Return to text
3. Wolters Kluwer Legal and Regulatory Solutions U.S., Blue Chip Financial Forecasts. Return to text
4. See Kim, Don and Hiroatsu Tanaka (2016). "Front-end Term Premiums in Federal Funds Futures Rates and Implied Probabilities of Future Rate Hikes," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, November 18, 2016, https://doi.org/10.17016/2380-7172.1884. Return to text
5. Priebsch, Marcel A. (2017). "A Shadow Rate Model of Intermediate-Term Policy Rate Expectations," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, October 4, 2017, https://doi.org/10.17016/2380-7172.2056. Return to text
6. Piazzesi, Monika, and Eric T. Swanson. "Futures prices as risk-adjusted forecasts of monetary policy." Journal of Monetary Economics 55.4 (2008): 677-691. Return to text
7. See the Appendix for our description of the interpolation process. Return to text
8. We could allow a scaling factor for Y because this is just an approximation, which is what we essentially do later in the regressions. Return to text
9. Forecast errors in fed funds futures and the surveys are not identical but have similar magnitudes and dynamics. Return to text
10. Technically, the covariance as derived in the theory is a conditional covariance. It should be noted that we do not view our analysis as a direct test of the theory, but more as a guide in determining our reduced-form framework, especially in the context of model averaging that takes into account various specifications. Return to text
11. For an extensive overview of model averaging and forecast combinations, see Elliott and Timmermann (2013). “Handbook of Economic Forecasting.” Return to text
12. See Elliott and Timmermann (2013). “Handbook of Economic Forecasting.” It is possible that the errors introduced by more sophisticated combination schemes offset the gains when compared to equal weighting. We have tried other weighting schemes and found that using equal weights provided superior out-of-sample performance. Return to text
13. See the Appendix for our description of the interpolation process. Return to text
14. Based on real measures and inflation measures alone, the regressions are not able to determine that forward guidance is in effect, which therefore necessitates the framework to have this dummy in place. Results for the post-ZLB time period are similar, with or without the dummy. Return to text
15. Median values for the coefficients are quantitatively similar. Return to text
16. Adrian, Tobias, Richard K. Crump, and Emanuel Moench. "Pricing the term structure with linear regressions." Journal of Financial Economics 110.1 (2013): 110-138. Return to text
17. In macro models, the SDF is the marginal rate of intertemporal substitution, $$\beta \frac{u'(c_{t+1})}{u'(c_t)}$$. Note that this quantity is low in good times and high in bad times. In theory, the term $$\beta \frac{u'(c_{t+1})}{u'(c_t)}$$ is the price of the riskless one period bond and therefore financial data can be used to discipline its properties. Furthermore, if one assumes simple power utility, the $$M_{t+1} = (\frac{c_t}{c_{t+1}})^\gamma$$ where $$\gamma$$ is the risk aversion parameter. Return to text
Diercks, Anthony M., and Uri Carl (2019). "A Simple Macro-Finance Measure of Risk Premia in Fed Funds Futures," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, January 8, 2019, https://doi.org/10.17016/2380-7172.2305.
Disclaimer: FEDS Notes are articles in which Board staff offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers and IFDP papers.