Board of Governors of the Federal Reserve System

An example calling the MATLAB Implementation of AIM

This example uses a simple two-equation model to demonstrate how to use the MATLAB implementation of the Anderson-Moore Algorithm.

The Firm Value Model

We investigate the solution of a simple linear model which describes the value of a firm. We investigate the solution of a simple linear model which describes the value of a firm.

The model consists of two equations:

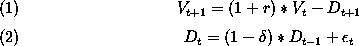
where V is the value of the firm, D is the dividend, r is the interest rate, is the growth rate of the dividend (here, negative). E is the error term for stochastic shocks.

Using the Anderson Moore Algorithm

The AIM routine requires three input files:

1. A model file in syntax called MODELEZ
2. A parameter file.
3. The setup script to execute AIM.

Model Representation in MDLEZ

 

Here is what the MODELEZ  file for our example looks like.

Below we will explain each line of the file. 

MODEL> FIRMVALUE

ENDOG>                                    
                    V     
                    DIV   
                    e_    
                    one   


EQUATION> VALUE
EQ>     LEAD(V,1) = (1+R)*V - LEAD(DIV,1)

EQUATION> DIVIDEND
EQ>     DIV = (1-DELTA)*LAG(DIV,1)

EQUATION>  e_
EQ>        e_ = 0 * one

EQUATION>   ONE
EQ>         one = LAG(one,1)

END

MODEL>
The name of the model.

ENDOG>
The names of the endogenous variables. In the AIM formulation, models must completely describe the long-run behavior of the system. Thus all variables are endogenous. "Exogenous variables must have, at least, a trivial forecasting equation.

EQUATION>
The name of the equation.

EQ>
The model equation definition.

The parameter file for our example is called firmparms.m: 

 
R = 0.10;
DELTA = 0.60;

The following script, which we call runfirm.m, executes AIM for the firmvalue model: 

 
dirnam='./'; % directory of this example 
parnam='firmparms';
modnam='firmvalue';
[cof, scof, cofb, param_, eqname_,...
 endog_, eqtype_, vtype_, neq, nlag, nlead, rts, lgrts,aimcode]=...
SPSolve(dirnam, modnam, parnam);

Sample run of the firmvalue model on Unix: 
 

Change the directory to the directory where the script resides:
The script to run aim is: runfirm.m
The model file name is: firmvalue
The parameter file name is: firmparms.m
 

 
 
mqmx3(174)% cd ~/yourPathTo/examples/firm

Call matlab and execute the run script
 

 
msulx1(124)% matlab -nodesktop

                              < M A T L A B >
                  Copyright 1984-2005 The MathWorks, Inc.
                   Version 7.0.4.352 (R14) Service Pack 2
                              January 29, 2005

 
  To get started, type one of these: helpwin, helpdesk, or demo.
  For product information, visit www.mathworks.com.
 
>> addpath('~/sp_solve')
addpath('~/sp_solve')
>> runfirm
runfirm
SPSolve version:($Name:  $,$Revision: 1.4 $)

ans =

found Aim on system classpath

initializing parsers
Aim Java Parser Version 1.03: Reading from file ./firmvalue...
Aim Java Parser Version 1.03: No syntactic errors found.
Checking for errors......
No semantic errors found.
chose modelez parser
>>

Displaying the results:

In the output below:
"cof" is the structural coefficients matrix (neqs by neqs*(nlag+nlead+1))
"cofb" is the reduced form coefficients matrix (neqs by neqs * nlag)
"scof" is the observable structure matrix (neqs by neqs*(nlag+1))
"rts" returns the eigenvector
"aimerr(aimcode)" returns a diagnostic message about the model
 

where: "neq" = number of equations
        "nlag" =number of lags
        "nlead" =number of leads

 

 
> cof
cof

cof =

  Columns 1 through 7 

         0         0         0         0   -1.1000         0         0
         0   -0.4000         0         0         0    1.0000   -1.0000
         0         0         0         0         0         0    1.0000
         0         0         0   -1.0000         0         0         0

  Columns 8 through 12 

         0    1.0000    1.0000         0         0
         0         0         0         0         0
         0         0         0         0         0
    1.0000         0         0         0         0

> cofb
cofb

cofb =

         0    0.2286         0         0
         0    0.4000         0         0
         0         0         0         0
         0         0         0    1.0000

> scof
scof

scof =

  Columns 1 through 7 

         0         0         0         0   -1.1000    0.6286         0
         0   -0.4000         0         0         0    1.0000   -1.0000
         0         0         0         0         0         0    1.0000
         0         0         0   -1.0000         0         0         0

  Column 8 

         0
         0
         0
    1.0000

> rts
rts

rts =

    1.1000
    1.0000
    0.4000

> aimerr(aimcode)
aimerr(aimcode)

ans =

Aim: unique solution.

References