FEDS Notes
July 29, 2022
What does the Beveridge curve tell us about the likelihood of a soft landing?
Andrew Figura and Chris Waller*
Any assessment of the likelihood and characteristics of a soft landing should take into account the situation in the labor market currently and the likely dynamics in the labor market going forward. Modern labor market models centered around the Beveridge curve are a useful tool in this assessment. In a recent policy brief, Blanchard, Domash, and Summers (2022), henceforth BDS, put forward a Beveridge curve framework and an analysis of past episodes where vacancies have fallen significantly to argue that the unemployment rate must increase significantly going forward and that the prospects of a soft landing are essentially zero. In this note, we use a framework that is in tune with modern theoretical analysis of the Beveridge curve to investigate what conditions would be necessary for a soft landing in the labor market to occur and whether the likelihood of these conditions really are essentially zero, as BDS suggest. We find that a soft landing is a plausible outcome for the labor market going forward.
Deriving the Beveridge curve
We first present our Beveridge curve framework, which is quite standard but differs somewhat from the framework in BDS. It is standard in the literature to account for the dynamics in the labor market by accounting for the flows of individuals in and out of unemployment. Consequently, the change in unemployment, $$\Delta U$$, is given by
$$ \Delta U = E \ast s - U \ast f $$
Flows into unemployment equal the separation rate, $$s$$, times the level of employment. Since for simplicity we normalize the labor force to equal 1, employment equals 1 minus unemployment, $$U$$. Flows out of unemployment equal the rate of job finding, $$f$$, times the number of unemployed. In steady state, flows into unemployment must equal flows out of unemployment, the right side. Thus, we can derive the Beveridge curve from a steady-state equation for unemployment, shown in equation (1).1
(1) $$(1-U) \ast s = U \ast f$$
Rearranging this equation yields an expression for the steady-state unemployment rate, equation (2).2
(2) $$U = \frac{s}{s+f}$$
Because flows into and out of unemployment are quite high, the actual unemployment rate converges to the steady-state unemployment rate quickly, and the steady-state unemployment rate typically tracks the actual rate closely.3
So, our construct of the Beveridge curve starts by accounting for dynamic flows of individuals across states of employment and unemployment. This is the standard approach for deriving the Beveridge curve in all modern labor search models. We stress this because BDS do not account for these flows in their analysis, which is why we refer to their analysis as non-standard.
The job finding rate can be related through a matching function to the V-U ratio. A matching function, shown in equation (3), posits that the number of hires is an increasing function of both the number of job vacancies and the number of unemployed individuals searching for jobs: The more firms there are looking for workers and the more workers there are looking for jobs, the more matches, or hires, there will be.
(3) $$H = M(V,U) = \mu V^{\sigma}U^{1-\sigma}$$
For convenience, we assume the matching function takes a Cobb-Douglas form. There are two key parameters in the matching function: $$\mu$$ and $$\sigma$$. The parameter $$\mu$$ measures matching efficiency. Matching efficiency represents factors that can increase (or decrease) hires without a change in labor market tightness. If the workers searching for jobs are well suited for the jobs that are available, matching efficiency will be high; on the other hand, if many searching workers are not well suited for the available jobs, matching efficiency will be low. The parameter $$\sigma$$ captures the relative importance of vacancies for creating hires. If $$\sigma$$ is low, vacancies are less productive at creating matches than unemployed workers.
With regards to the matching function, we use the same expression as BDS. The key differences are (1) how we use the matching function to solve the model and (2) the numerical values used for $$\mu$$ and $$\sigma$$ in our respective analyses.4
Turning to point 1, we use the matching function to derive the job finding rate. If we divide both sides of equation (3) by unemployment, we get equation (4), which expresses the job finding rate as a function of the ratio of vacancies to unemployment, or labor market tightness.
(4) $$f = \frac{H}{U} = \mu \left(\frac{V}{U}\right)^{\sigma}$$
Because we have data for the both the left and right sides of equation (4), we can estimate it and obtain parameter values for the elasticity of job finding with respect to labor market tightness, $$\sigma$$, and matching efficiency, $$\mu$$. Specifically, we regress $$log(f)$$ on $$log\left(\frac{V}{U}\right)$$ using JOLTS data on job openings and BLS data on unemployment and transitions from unemployment to employment from 2009 to 2019. This results in estimates of $$\mu=.27$$, and $$\sigma=.3$$.
Plugging the expression for job finding into equation (2), the steady-state unemployment rate, yields equation (5).
(5) $$U = \frac{s}{s+\mu\left(\frac{V}{U}\right)^{\sigma}}$$
Equation (5) shows how vacancies affect the unemployment rate. To illustrate this relationship, we solve equation (5) for different values of $$V$$ and $$s$$, holding the matching efficiency parameter constant. The result is shown in Figure 1, which plots four curves showing the effect of vacancies on unemployment for four different separation rates. Each curve is convex; as the number of vacancies increases relative to the number of individuals looking for work, it becomes harder for firms to fill jobs with suitable workers, and more jobs remain vacant. This is exactly the situation many employers are now experiencing. Because more vacancies generate fewer and fewer hires, they result in smaller and smaller reductions in unemployment. But additional vacancies continue to strongly boost wage growth.
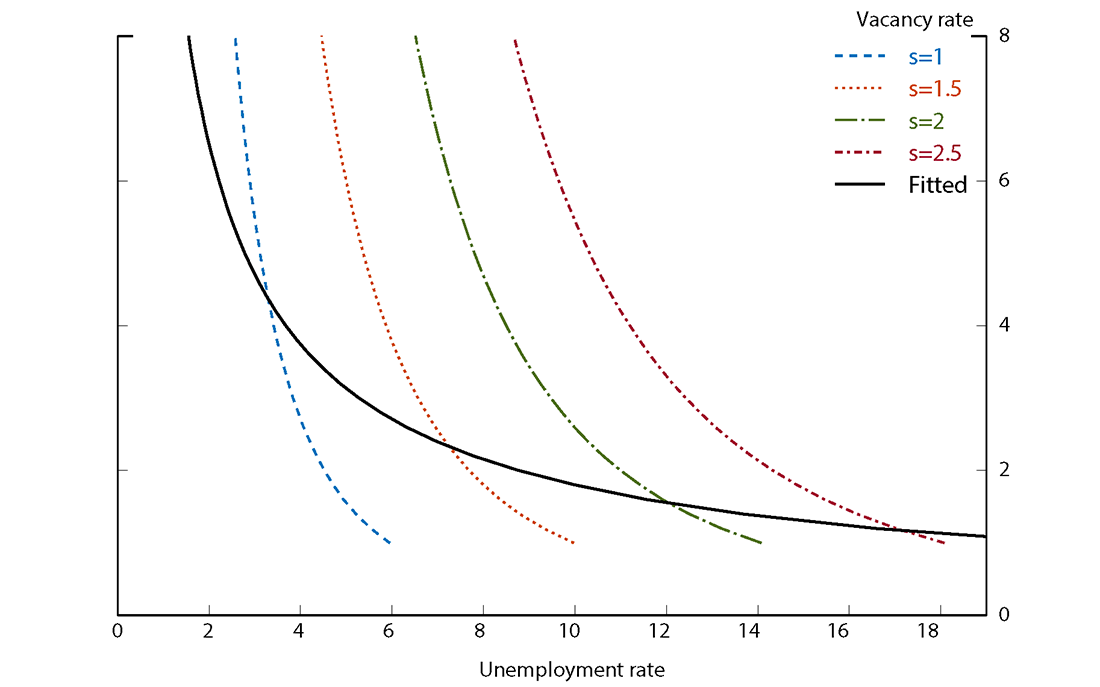
Source: Author's calculations.
The combination of movements in separations and vacancies is shown by the black curve, which is fit to actual values of $$V$$ and $$U$$. Decreases in the separations rate reduce the unemployment rate without changing vacancies, imparting a flatness to the fitted curve, relative to the steeper curves that only reflect the effect of vacancies. If we want to just focus on the effect of vacancies, then we should be looking at the steep curves, especially when the labor market is tight, as it is now.
Comparing our framework to that of BDS
As noted earlier, our framework is somewhat different than that of BDS. They simply rewrite the matching function as
(6) $$U = \frac{H}{\mu\left(\frac{V}{U}\right)^{\sigma}}$$
and then call this the Beveridge curve. We prefer our approach for deriving the Beveridge curve from the flow equation (1) for a few reasons. First, there are no separations in the BDS decomposition of the unemployment rate. Separations increase importantly in business cycle downturns, and most research attributes to separations a key role in driving cyclical movements in unemployment.5 As a result, a model that excludes separations will have a hard time explaining movements in unemployment. Relatedly, it is difficult to think about the role of reallocation in driving movements in unemployment without separations. Changes in relative demand and technology across products often result in a need to reallocate labor across firms and industries. If reallocating workers move first into unemployment before finding another job, as is often the case, then reallocation increases unemployment. The key event driving reallocation's effect on unemployment is the movement of a worker from employment to unemployment, or a separation.
BDS use the hiring rate to account for the effects of reallocation on unemployment, but this can be problematic because BDS also use hires to estimate matching efficiency (as we do). But using hires to estimate matching efficiency implies that it cannot also provide independent information about the level of reallocation. A simple example helps to illustrate this. Suppose that matching efficiency increases from time $$t_0$$ to time $$t_1$$, resulting in more hires for given levels of vacancies and unemployment. Suppose further that at time $$t_1$$, the levels of vacancies and unemployment are similar to the levels at $$t_0$$. Then, from $$\mu = \frac{H}{V^{\sigma}U^{1-\sigma}}$$, the percent change in the hiring rate from $$t_0$$ to $$t_1$$ will be the same as the percent change in matching efficiency. But BDS will interpret the change in hires as an increase in reallocation, when it is only matching efficiency (not reallocation) that has changed. Finally, BDS also assume that hires are fixed along the Beveridge curve. As a result, what they call the Beveridge curve is just an isoquant from the matching function that shows the combinations of $$V$$ and $$U$$ that produce the same level of hires for a given matching efficiency. This is non-standard and we find this assumption overly restrictive and unnecessary.
A model of the Beveridge curve based on the steady-state unemployment rate and including separations does not have these problems, and we think it is the most useful tool to assess prospects for the labor market. Nevertheless, we would agree with the two following broad points in BDS: (1) changes in labor demand or activity increase the V-U ratio and move the economy up along a convex Beveridge curve and (2) increases in reallocation and decreases in matching efficiency both push out the Beveridge curve and increase unemployment.
What will a significant decline in vacancies imply for the unemployment rate?
Next, we argue that whether the economy can experience a soft landing if the vacancy rate declines significantly from current levels depends on two important factors: (1) the slope of the Beveridge curve, which depends importantly on the current position of the labor market along the Beveridge curve, and (2) whether layoffs increase significantly.
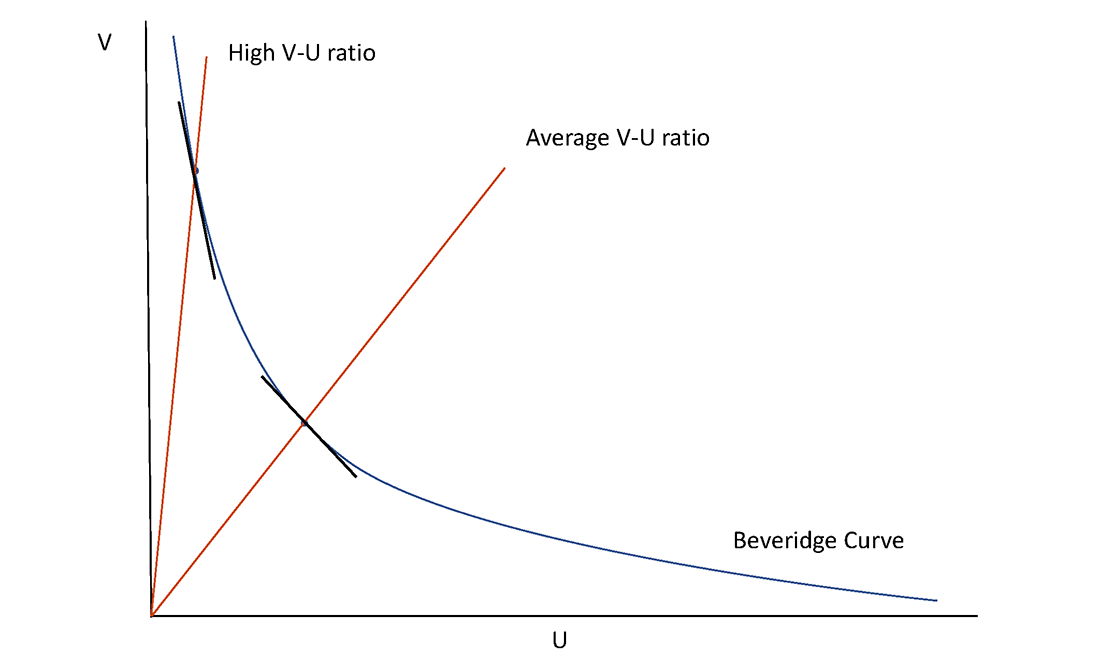
Regarding the slope of the Beveridge curve, currently, the V-U ratio is historically high, implying that the labor market is on a very steep portion of the Beveridge curve. The stylized Beveridge curve in Figure 2 illustrates this point. When the V-U ratio is equal to the ray from the origin labeled "High V-U ratio", the slope of the convex Beveridge curve is much steeper than when the V-U ratio is equal to the ray labeled "Average V-U ratio". A steeper curve implies that the unemployment rate will change less for a given reduction in vacancies (holding separations constant).
Of course, we don't know precisely what the slope of the Beveridge curve is. In our model (and in BDS), the slope depends on the parameter $$\sigma$$. BDS read the literature as suggesting that $$\sigma$$ should lie between .3 and .5. We prefer .3 because that's what a matching function equation estimated with aggregate U.S. data suggests, but it's possible $$\sigma$$ could be larger. Figure 3 shows Beveridge curves with values of .3, .4, and .45 for $$\sigma$$. As $$\sigma$$ increases, the Beveridge curve becomes flatter.
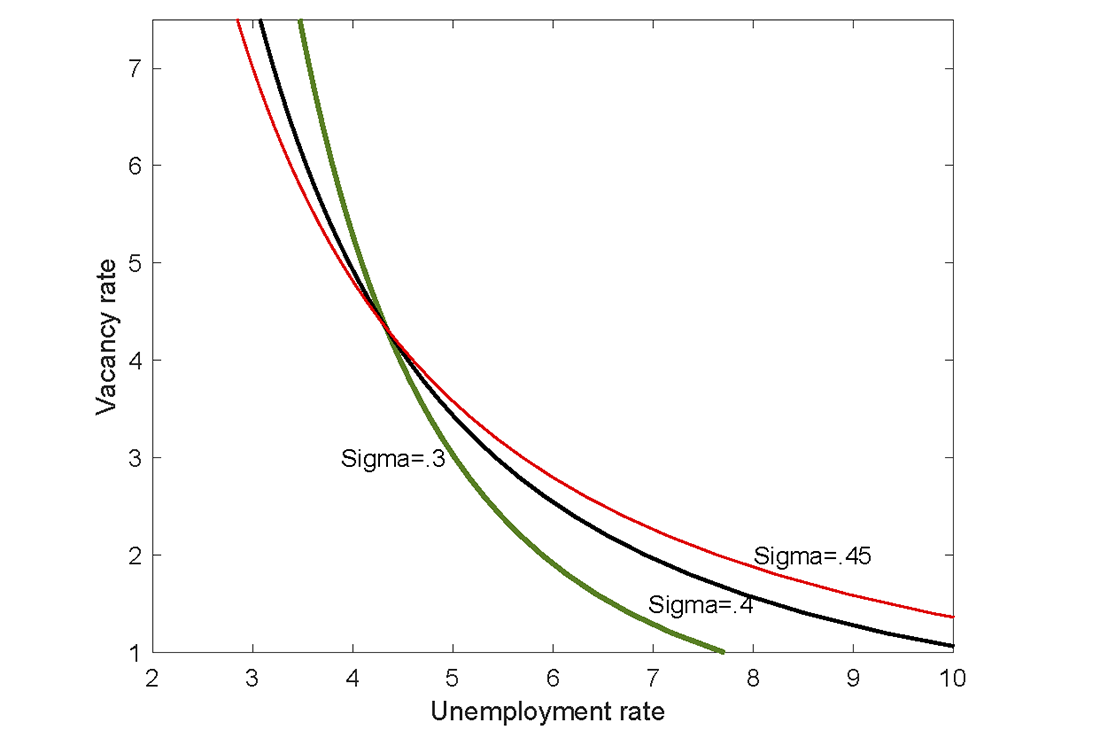
Note: Matching efficiency is assumed to be 90 percent of pre-Covid level, and the separations rate is assumed to be 1.1 percent.
We can use our simple model to estimate how much the unemployment rate will increase if the vacancy rate declines from its current level of around 7 percent to the level that prevailed prior to Covid, 4.6 percent. The first row of Table 1 shows these increases for three levels of $$\sigma$$: 0.3, 0.4, and 0.45. As would be expected, as $$σ$$ increases and the Beveridge curve flattens, the implied increase in the unemployment rate is larger.
Table 1. Change in unemployment rate resulting from a decline in the vacancy rate from 7 percent to 4.6 percent
| $$\mu$$ | $$\sigma$$ | ||
|---|---|---|---|
| .3 | .4 | .45 | |
| Pre-Covid | 0.58 | 0.83 | 0.96 |
| 90 percent of pre-Covid | 0.66 | 0.97 | 1.14 |
| 80 percent of pre-Covid | 0.77 | 1.15 | 1.37 |
BDS find that matching efficiency has decreased during the pandemic. Decreases in matching efficiency will shift out the Beveridge curve but also change its slope. The second and third rows of the table examine how a decrease in matching efficiency during the pandemic can affect the implied change in the unemployment rate. We consider both a 20 percent decline in matching efficiency, estimated by BDS, and a 10 percent change, which we find to be more consistent with our estimated matching function. The table shows that the change in unemployment will increase somewhat as the assumed deterioration in matching efficiency increases.
Table 2 compares these estimates to what the change in the unemployment rate would be if the 2.4 percentage point decline in the vacancy rate occurred when the vacancy rate starts at 4.6 percent, a level much more typical of previous strong labor markets. The estimated increase is significantly larger, 2 to 3 times as large as when the vacancy rate starts at 7 percent, illustrating the importance of taking into account the labor market's current position. In a very tight labor market, such as we are in now, vacancies are so high relative to available workers, that the marginal vacancy results in a much lower probability of a hire over a given period of time than in a more balanced labor market. As a result, a given decline in vacancies has a smaller effect on hires and, thus, a smaller effect on unemployment than in a more typical labor market. In short, we would expect the unemployment rate to increase if vacancies fall (absent a change in matching efficiency or reallocation), but the increase should be significantly smaller than would be the case if the labor market were currently on a flatter portion of the curve.
Table 2. Change in unemployment rate resulting from a decline in the vacancy rate from 4.6 percent to 2.2 percent
| $$\mu$$ | $$\sigma$$ | ||
|---|---|---|---|
| .3 | .4 | .45 | |
| Pre-Covid | 1.27 | 2.04 | 2.56 |
| 90 percent of pre-Covid | 1.45 | 2.37 | 3 |
| 80 percent of pre-Covid | 1.67 | 2.78 | 3.56 |
The second key question when assessing the chances of a soft landing is whether the separations rate increases significantly. As we noted earlier, increases in the separations rate shift out the Beveridge curve and lead to large increases in unemployment. Tables 3a, 3b, and 3c illustrate this fact by showing how the changes in unemployment in Table 1 are affected if the separations rate increases at the same time as the assumed decline in vacancies. We consider increases in separations of 10, 25, and 50 percent. For context, the separations rate increased 50 percent from 2007 to 2009, during the Great Recession, and by about 20 percent from 2000 to 2002, during the early 2000s recession.
Table 3a. Change in unemployment rate resulting from a decline in the vacancy rate from 7 percent to 4.6 percent and a 10 percent increase in the separations rate (to 1.21 percent)
| $$\mu$$ | $$\sigma$$ | ||
|---|---|---|---|
| .3 | .4 | .45 | |
| Pre-Covid | 1.08 | 1.39 | 1.57 |
| 90 percent of pre-Covid | 1.24 | 1.63 | 1.86 |
| 80 percent of pre-Covid | 1.43 | 1.93 | 2.23 |
Table 3b. Change in unemployment rate resulting from a decline in the vacancy rate from 7 percent to 4.6 percent and a 25 percent increase in the separations rate (to 1.38 percent)
| $$\mu$$ | $$\sigma$$ | ||
|---|---|---|---|
| .3 | .4 | .45 | |
| Pre-Covid | 1.86 | 2.29 | 2.54 |
| 90 percent of pre-Covid | 2.12 | 2.67 | 2.99 |
| 80 percent of pre-Covid | 2.45 | 3.15 | 3.58 |
Table 3c. Change in unemployment rate resulting from a decline in the vacancy rate from 7 percent to 4.6 percent and a 50 percent increase in the separations rate (to 1.65 percent)
| $$\mu$$ | $$\sigma$$ | ||
|---|---|---|---|
| .3 | .4 | .45 | |
| Pre-Covid | 3.2 | 3.88 | 4.29 |
| 90 percent of pre-Covid | 3.64 | 4.5 | 5.02 |
| 80 percent of pre-Covid | 4.2 | 5.27 | 5.96 |
Table 3a shows that if separations increase by 10 percent, the increase in the unemployment rate will be about 60-80 percent larger than if the separations rate remains constant. If separations increase 50 percent, the increase in the unemployment rate will be around 5 times larger than if separations are unchanged. The numbers in the tables clearly indicate that a soft landing depends critically on avoiding a significant increase in layoffs.
Can a significant decline in vacancies correspond to a soft landing?
We interpret our calculations above as suggesting that there can be a soft landing in the labor market going forward. Under most assumptions about current levels of matching efficiency and the curvature of the Beveridge curve, a decline in the vacancy rate from 7 percent to 4.6 percent would lead to an increase in the unemployment rate of about 1 percentage point or less. This increase would put the unemployment rate at a level below 5 percent, which in historical terms is quite low and, in our view, consistent with a soft landing. (However, we are cognizant that any increase in unemployment is not simply a number and reflects substantial change for any household.)
A soft landing also depends on the economy not experiencing a significant increase in layoffs. Table 3a suggests that the unemployment rate would remain under 5 percent for a 10 percent increase in separations given our preferred parameters, but it would not if the Beveridge curve is significantly flatter than we assume. Increases in the separations rate of 25 percent or greater, consistent with the unemployment rate rising to at least 5-1/2 percent and in some cases well above that, would clearly not be consistent with a soft landing.
We recognize that it would be unprecedented for vacancies to decline by a large amount without the economy falling into recession. As a result, we are, in effect, saying that something unprecedented can occur because the labor market is in an unprecedented situation. Because the V-U ratio is so high currently, it is possible to reduce vacancies with a much smaller effect on hiring than is typical. In addition, because such a decline in vacancies would still leave labor demand strong (a 4.6 vacancy rate is historically still quite high), it seems plausible that layoffs, which historically are only elevated (above their longer-run trend) when labor demand is weak, would not rise significantly.
Of course, there are other possible outcomes. As the economy slows, households and firms could become extremely risk averse, pull back on spending and investment, and start to layoff workers. This is typically what happens in recessions. And if that happens going forward, we will not achieve a soft landing. In addition, if supply shocks continue, inflation continues to be elevated, and inflation expectations drift higher, it will be extremely challenging to bring inflation lower and still have a soft landing. Though these are important risks, most professional forecasters continue to project a soft landing with the unemployment rate rising only modestly and the inflation rate moving down toward the FOMC's 2 percent target. Clearly, they also believe that a soft landing in the labor market is possible.
References
Ahn, Hie Joo, and Leland Crane (2020). "Dynamic Beveridge Curve Accounting," Finance and Economics Discussion Series 2020-027. Washington: Board of Governors of the Federal Reserve System, March, https://doi.org/10.17016/FEDS.2020.027.
Ahn, Hie Joo, and James Hamilton (2020). "Heterogeneity and Unemployment Dynamics," Journal of Business & Economic Statistics, vol. 38 (July), pp. 554–69.
Barnichon, Regis, and Andrew Figura (2015). "Labor Market Heterogeneity and the Aggregate Matching Function," American Economic Journal: Macroeconomics, vol. 7 (October), pp. 222–49.
Blanchard, Olivier, Alex Domash, and Lawrence H. Summers (2022). "Bad News for the Fed from the Beveridge Space," Peterson Institute for International Economics, Policy Brief 22-7.
Elsby, Michael, Bart Hobijn, and Aysegul Sahin (2015). "On the Importance of the Participation Margin for Labor Market Fluctuations," Journal of Monetary Economics, vol. 72 (May), pp. 64–82.
Elsby, Michael, Ryan Michaels, and David Ratner (2015). "The Beveridge Curve: A Survey," Journal of Economic Literature, vol. 53 (September), pp. 571–630.
Elsby, Michael, Ryan Michaels, and Gary Solon (2009). "The Ins and Outs of Cyclical Unemployment," American Economic Journal: Macroeconomics, vol. 1 (January), pp. 84–110.
Fujita, Shigeru, and Garey Ramey (2009). "The Cyclicality of Separation and Job Finding Rates," International Economic Review, vol. 50 (May), pp. 415–30.
Pissarides, Christopher (2000). Unemployment, MIT Press.
Shimer, Robert (2012). "Reassessing the Ins and Outs of Unemployment," Review of Economic Dynamics, vol. 15 (April), pp. 127–48.
* We thank Charles Fleischman, Jane Ihrig, and Dave Ratner for helpful comments. The views expressed in this note are our own and do not necessarily represent the views of the Board of Governors or the Federal Reserve System. Return to text
1. See, for example, Pissarides (2000). Return to text
2. If the labor force is allowed to vary, then the expression is similar but somewhat more complicated. Return to text
3. For more on decomposing unemployment rate movements, see Shimer (2012), Elsby, Michaels and Solon (2009), Fujita and Ramey (2012), and Ahn and Crane (2020). Return to text
4. Our parameter $$\mu$$ is the same as the BDS parameter a, and our parameter $$\sigma$$ is the same as BDS parameter $$\alpha$$. Return to text
5. See, for example, Fujita and Ramey (2009) or Elsby, Michaels, and Solon (2009). Return to text
Figura, Andrew, and Chris Waller (2022). "What does the Beveridge curve tell us about the likelihood of a soft landing?," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, July 29, 2022, https://doi.org/10.17016/2380-7172.3190.
Disclaimer: FEDS Notes are articles in which Board staff offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers and IFDP papers.