International Finance Discussion Papers (IFDP)
December 1989
A Substitute for the Capital Stock Variable in Investment Functions
Guy V.G. Stevens
Abstract:
Capital stock variables appearing in investment and other equations are almost always constructed by the "perpetual inventory method." Successive values are related by the well-known equation:
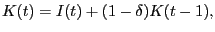
where K(t) is the measure of the real capital stock at time t, I(t) is the real rate of investment, and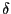 
the rate of depreciation. By successive backward substitutions for K(t-l), K(t) can be expressed equivalently as a weighted sum of past levels of investment plus the depreciated value of an initial real capital stock:
![$ K(t)= {\textstyle\sum\limits_{i=0}^{t-1}} [I(t-i)(1-\delta)^{i}]+K(0)(1-\delta)^{t}.$](/pubs/ifdp/1989/368/img3.gif)
The initial real capital stock, K(O), that is implicitly a component of every measure of the capital stock calculated by this method can rarely be measured, however, with any degree of accuracy. As demonstrated in this paper, the measurement error can frequently lead to severe bias in the estimated coefficients of investment functions.
This paper proposes a method to bypass this source of measurement error. In important cases it is then possible to estimate unbiased and consistent coefficients.
PDF: Full Paper
Disclaimer: The economic research that is linked from this page represents the views of the authors and does not indicate concurrence either by other members of the Board's staff or by the Board of Governors. The economic research and their conclusions are often preliminary and are circulated to stimulate discussion and critical comment. The Board values having a staff that conducts research on a wide range of economic topics and that explores a diverse array of perspectives on those topics. The resulting conversations in academia, the economic policy community, and the broader public are important to sharpening our collective thinking.