FEDS Notes
August 05, 2019
The Mysterious Cross-Country Dispersion in Mobile Phone Price Trends
Introduction
The construction of prices for information and communications technology (ICT) is a longstanding priority of the economic measurement community.2 ICT price trends are a key indicator of technical progress in the global economy, and despite the moderate nominal share of ICT equipment and services in consumption and investment spending, they contribute importantly to aggregate economic growth (in volume) and to productivity because of the uncommonly rapid pace of price declines they typically display.3 In recent years, the emergence of a new stage of the ICT revolution, distinguished by a radical increase in mobility, has led to renewed attention to ICT measurement, fueled by the perceived disconnect between its impact on business and household activity and the small imprint this wave of ICT seems to have left on measured economic growth.4
Aizcorbe et al. (2019) established that constant-quality prices for mobile phones, the key consumer platform for the new wave of ICT innovations, have fallen 15 to 20 percent per year in the United States since 2010, a comparable rate to inflation for personal computers during the previous wave of ICT innovation in the late 1990s. Byrne and Corrado (2019) fold this result into an assessment of the surrounding consumer ICT ecosystem and estimate there have been substantial welfare gains from this wave of innovation. Similar assessments of other markets require suitable price indices, but international research on mobile phone prices has been limited and official price indices display curious properties.
This note examines mobile phone consumer price indices (CPIs) reported by national statistical agencies (NSIs) for 12 countries--the members of the G7 plus Australia, China, Finland, Korea, and New Zealand. Their CPIs vary wildly, ranging from no change (for Japan) to over 20 percent declines per annum (for New Zealand and the United Kingdom (UK)), on average, over a ten-year period from 2008 to 2018 (figure 1, table 1).5 Although there is evidence that fundamental factors are at play, this massive spread in growth rates over an extended period--implying a nine-fold difference in quality-adjusted price levels between Japan and the UK, for example--raises concern that CPIs may be constructed inconsistently across NSIs. In this note, these CPIs are placed in the context of other public data on these markets and consultancy data from IDC Research, Inc. (IDC) with a view toward focusing attention on the need for international harmonization.
Fundamental Factors
The markets for mobile phones in the economies considered here have distinct characteristics and these features appear to be related to the pace of recorded price change. Mobile phones, like most electronic equipment produced in high volume, are manufactured by a globally integrated supply chain, so there is little room for differences in production costs to explain the cross-country variation in inflation. However, markups may differ across countries for a variety of reasons. On the supply side, country markets differ appreciably in the level of competition. Concentration, as measured by the Herfindal-Hirschman index (HHI), ranges from values indicating a highly competitive market, such as China with an average HHI over this period of 0.1, to values indicating a highly concentrated market, with an average HHI of 0.4 for Korea. Consequently, prices may be expected to include noticeably different markups. More importantly, for several markets, concentration has evolved over the time period studied, suggesting that the growth rate of the mobile phone index may embody rising or falling markups. As shown in figure 2, price index growth is indeed correlated with changes in the HHI in this period. (The correlation coefficient is 0.47.) While this correlation is not dispositive--the relationship between concentration and aggregate price trends is a complicated one--it is consistent with the idea that rising markups may be tempering price declines in some markets.
On the demand side, cross-country differences in preferences and household income may play a role as well. As shown in figure 3, countries with rapidly rising mobile phone adoption tended to report slower rates of price decline, suggesting that a shift in market demand may have played a role in moderating price declines. (The correlation coefficient is 0.51). For example, The World Bank has reported for China, where prices declined 3 percent per year, that mobile cellular subscriptions per 100 people rose from 48 in 2008 to 105 in 2017. In contrast, for the United Kingdom, where prices have fallen at the fastest rate, subscriptions per 100 people changed very little over this period. This was also a period of rapid migration toward smartphones from their simpler "feature phone" predecessors, according to IDC data. The average smartphone share of (unit) sales across these countries rose from 20 percent to 95 percent over this time period, with extremely rapid shifts in China and Korea, where price declines have been subdued. Again, these observations are not conclusive, but suggest consumers were more eager to acquire new technology in some markets than others, and this may have played a role in the dispersion of price changes for phones of comparable quality across countries.
Measurement Factors
Absent evidence to the contrary, one assumes that NSI-calculated price indices are accurate. But, when a statistic is consequential for our understanding of the economy, it should be subject to careful scrutiny. In this case, spending on mobile phones constitutes nearly 1 percent of personal consumption expenditure (PCE) for these 12 countries, on average, and a positive measurement error of, say, 20 percentage points for mobile phone inflation would imply that overall PCE inflation is overstated by 0.2 percentage point--a magnitude clearly significant for economic policy. We consider three broad aspects of the methodology employed by NSIs: the scope of the published index shown, the treatment of quality change when new items are added to the index, and the index number formulas employed.6
Scope
The indices shown are narrowly defined to be solely for mobile phones in all but 4 cases. The exceptions are the CPIs for Australia, Canada, New Zealand, and the United States, which include other devices as well as mobile phones. The index for Australia is the most broadly defined, covering "telecommunications equipment and services."7 The Australian index is among the slowest-falling indices and is likely to overstate mobile phone inflation in light of the inclusion of services, for which official inflation tends to be higher than for ICT equipment in countries that publish a separate CPI for telecommunications services. In contrast, the New Zealand index, which covers "telecommunications equipment," is among the fastest-falling indices and is likely to be a fairly good indicator for mobile phone inflation, as mobile phones constitute a very large share of the index. In the case of Canada, the index is for "multifunction devices," including tablet personal computers as well as smartphones; for the United States, the narrowest published index is for "telephone hardware, calculators, and other consumer information items." The Canadian and U.S. indices each fall at an average annual rate of 7 percent, which is the median rate of change across the country indices, and mobile phones constitute a large but not dominant share of the index. One would not expect a priori for the other items in the index--similar consumer electronics--to have markedly different price trends from mobile phones.8 In any event, the coefficient of variation for the average rate of mobile phone inflation does not change appreciably when these four countries are excluded, so it does not appear the broad scope of these indices is a major contributor to the dispersion among country price trends.
Quality Adjustment
NSIs use a variety of methods to account for quality when new items are added to the basket employed in calculating a CPI.9 Each approach implicitly or explicitly apportions to quality and inflation the premium (or discount) paid for the new item relative to incumbent items. For example, the "direct compare" method treats the incoming item as of equal quality to the item it is replacing and any price difference is attributed to inflation. In contrast, the "overlap method" treats the entire price difference as a measure of quality.
Judgmental adjustment informed by expert knowledge of the market is an intermediate approach. This may entail the use of the option costs for the distinguishing characteristics of the new item if such pricing is available. In the case of a motor vehicles CPI, for example, the additional cost for adding leather upholstery may be subtracted from the price of a model newly added to the item basket if it is replacing a model without such seating. Alternatively, the judgmental adjustment may employ hedonic analysis, or regression of item prices on characteristics. Hedonic analysis is particularly appropriate when quality-relevant product characteristics can be identified and measures of those characteristics are readily available.10 This is arguably the case for ICT products, where variation in easily quantified engineering features often explains a substantial share of price variation. Hedonic studies of prices for ICT products have typically found that that constant-quality price indices fall quite rapidly, often in excess of 10 percent per year. Research studies most commonly use a time-dummy approach to construct a price index, wherein the index level is formed by multiplying together the anti-log of coefficients on successive time period indicator variables that have been estimated while controlling for variation in price-determining characteristics. In contrast, NSIs most commonly use cross-sectional regressions. In this approach, one treats coefficients on characteristics as "implicit prices" for characteristics and adjusts the price of an incoming product by removing the estimated valuation of any distinctive features of the item. These approaches are nearly isomorphic and one should expect to get similar results under typical circumstances (Triplett, 2006).
At first glance, the use of hedonics does appear to be a contributor to the cross-country dispersion in mobile phone price trends: The two countries with the fastest falling price indices, New Zealand and the United Kingdom, employ hedonics, and the countries with the slowest falling prices, such as Japan, Australia, and Korea, do not. However, the price index for Germany employs hedonic adjustment but falls at only the median rate for these countries. Furthermore, when countries have adopted a hedonic approach mid-way through the period of this study, their price indices have not always fallen noticeably faster afterward. Germany, New Zealand, and the United States switched to hedonic quality adjustment in 2015, 2014, and 2018, respectively, with varied results. The German mobile phone CPI has fallen at an average annual rate of 6.4 percent since a hedonic approach was adopted, and fell 5.0 percent on average in the three years prior. The U.S. mobile phone CPI has fallen at an average annual rate of 12.3 percent since adopting hedonics and fell 8.9 percent on average in the three years prior. The New Zealand mobile phone CPI has fallen at an average annual rate of 20.0 percent since it was first calculated using hedonics, but fell faster--at a 27.9 percent annual rate--in the three years prior.
NSIs apply hedonics, direct comparison, overlap, and other methods of quality adjustment as deemed appropriate on a case-by-case basis, making it difficult to ascertain whether any NSI policy or predisposition toward excessive or inadequate quality adjustment introduces bias to a particular index. As discussed in Triplett (2006), if an NSI were to take the extreme approach of consistently using the direct compare method or exclusively using the overlap method, one could draw conclusions the potential for the introduction of bias. That is not the case for the countries studied here. Consequently, without examining the price observations used in constructing the index, one cannot assess if the indices are mis-measured due to the quality adjustment approach employed.
Elementary Index Formulas
For the CPIs of most of the countries in this study, elementary price indices--the indices at the lowest level of the system of aggregation--are constructed using one of two elementary index formulas, namely Dutot or Jevons. (These formulas are provided in the appendix.) Finland, France, Italy, the United Kingdom, and the United States use the Jevons formula, which is the ratio of current to previous period unweighted geometric means of individual items. Japan uses the Dutot formula, which is the ratio of current period to previous period unweighted arithmetic means of item prices. Canada, Germany and Korea use either the Dutot or the Jevons formula, depending on the product, and do not specify which is employed for mobile phones.11
Under some circumstances, the choice among these elementary index formulas can make a material difference. Silver and Heravi (2007) demonstrate that when the dispersion of the item prices used to calculate the index changes appreciably over time, a Dutot index and a Jevons index calculated with the same data can diverge significantly. As it happens, the dispersion of model-level prices for mobile phones does change noticeably over time for most of the countries examined here. The coefficient of variation for quarterly-frequency price data for smartphone models from IDC changes by 1 percentage point or more per year, on average, in the case of every country except Canada.12 The magnitude of these changes suggests that the choice of elementary index may play a role in the divergence of indices across countries, though it is not possible to quantify the effect without additional information on the formula employed for all the countries in this study.
Alternatives to Official CPIs
In some cases, alternative indices are available for comparison to official CPIs. Statistics Canada, for example, has recently developed a price index for smartphones employed in the producer price index system beginning in 2015. This index has the appeal for the present study of being closer to mobile phones in scope than the CPI--as of 2015, smartphones dominated the Canadian mobile phone market according to IDC--and is calculated with retail prices from IDC. It has fallen at an average annual rate of 12 percent since being introduced, or 7 percentage points faster than the multifunction device index. For the U.S. market, as mentioned above, a recently developed hedonic index for mobile phones falls at an average annual rate of 17 percent (Aizcorbe et al., 2019). Relative to the CPI, which represents a broader basket of goods, the research index falls 10 percentage points faster. And, the Japanese corporate goods price index (CGPI) for mobile phones is a hedonic index which falls at an average annual rate of 8.4 percent from 2008 to 2018, a period when the CPI showed no change, on average. If one adjusted the official CPIs by these estimates of bias for Canada, Japan, and the United States, the average across the country-specific mean rates of decline would be 2 percentage points lower. As it happens, though, dispersion is unaffected: The standard deviation of these 12 country-specific average rates would be essentially unchanged.
Evidence from the European Union System of Harmonized Price Indices
Quantifying the contributions to mobile phone CPI dispersion from fundamental factors and from mis-measurement is beyond the scope of this paper, but the statistical system employed by the European Central Bank (ECB) does provide suggestive evidence from their effort to harmonize price methods across the member countries of the European Union (EU). Under the directive of the ECB, countries in the EU are required to provide price statistics that conform to the standards of the Harmonized Index of Consumer Prices (HICP) (Eurostat, 2018). EU NSI price indices for mobile phones, shown in figure 4, nonetheless display appreciable variation. In all, 29 countries published an HICP for mobile phones in 2018 and growth rates for that year ranged from a decline of 11 percent to an increase of 1 percent. Focusing on the 9 countries which have at least five years of history for their mobile phone HICP, the range of average annual price declines for the 2014-2018 period is 9 percentage points and the average annual standard deviation is 3 percentage points, substantially smaller than the 25 percentage point range and 8 percentage point standard deviation for the 12 countries in this study.
While it is tempting to treat the HICP variation as a measure purely of the effect of fundamental factors on mobile phone prices, one cannot draw that conclusion. Substantial variation in methods is permitted within the HICP system. The HICP methodological manual contains legal directives, such as proscribing the use of the Carli formula for elementary indices but allowing the use of both the Dutot and the Jevons formula, and the manual expresses principles of good price index construction, such as guidance for the choice among quality adjustment methods, but leaves far too much freedom of choice among methods for variation in HICPs across EU countries to be considered solely the effect of fundamental factors. Nevertheless, relative to the 12-country group used for this paper, the much smaller variation observed among HICPs does encourage the view that an effort to harmonize practices may reduce spurious cross-country variation even if the resulting alignment of methods is incomplete.
Conclusion
Getting prices right for ICT goods and services is essential to understanding the macroeconomy. The ICT sector is a locus of rapid technical change that has been a harbinger of broad productivity growth in the past as ICT was deployed across the economy. After a blizzard of activity coincident with the "ICT Revolution" in the late 1990s and early 2000s, research on ICT measurement seemed to go dormant. Subsequently, the quality of ICT price measures degraded and they began to give confusing signals (Byrne and Pinto, 2015). A flurry of recent work has buttressed the stable of U.S. prices (Byrne and Corrado, 2017a, 2017b; Aizcorbe et al., 2019). And, indeed, efforts in other countries have accelerated as well, e.g. the surge in measurement research in the United Kingdom heralded by the "Bean Report" (Bean, 2016).
However, Ahmad et al. (2019) have noted that broad price indices for ICT categories--for ICT equipment, for computer software and databases, and for communication services--seem to be implausibly dissonant across countries. Taking a more narrow focus, this paper notes that for mobile phones, the marquee product of the newest wave of the ICT revolution, prices are wildly different across countries. The magnitude of this variation is highly implausible, though differences in market concentration and consumer tastes may rationalize some of the difference.
The exploratory analysis presented here points to the value to be expected from more rigorous work on the potential impact on ICT price variation of disparate choices across NSIs for methods of quality adjustment, index formulas, and other aspects of price index construction. Close examination of NSI documentation and correspondence with analysts has shed some light on the sources of cross-country variation in mobile phone inflation but did not resolve the mystery. Exploring the analysis of alternative data sources such as the consultancy data employed in this paper and carefully varying all aspects of index construction is a natural next step.
Table 1: Mobile Phone Prices by Country - Average Annual Growth, 2008-2018
| Country | Consumer Price Index | Average Price |
|---|---|---|
| Australia | -1.9 | 9.4 |
| Canada | -7.0 | 10.1 |
| China | -3.2 | 9.4 |
| Finland | -16.4 | ND |
| France | -15.6 | 9.1 |
| Germany | -6.9 | 10.5 |
| Italy | -12.1 | 9.1 |
| Japan | 0.4 | 4.9 |
| Korea | -3.0 | 6.1 |
| New Zealand | -21.1 | 5.1 |
| United Kingdom | -24.3 | 12.2 |
| United States | -7.0 | 6.0 |
Note: Canada CPI begins in 2012; Italy and UK CPIs begin in 2011. CPIs for Australia, Canada, New Zealand, and United States are for broader categories.
Source: National statistical institutes (CPIs); IDC Research, Inc. (average price)
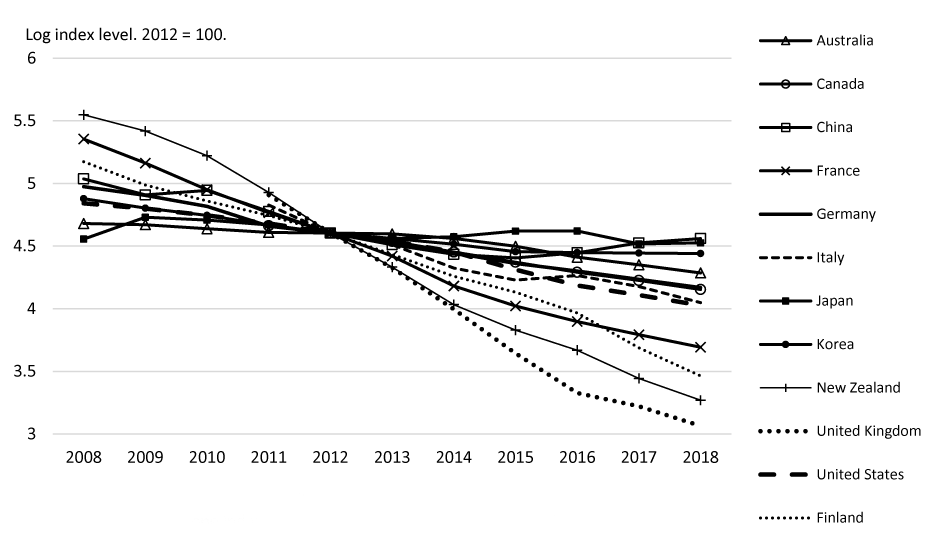
Note: Mobile phone index divided by country overall consumer price index.
Source: National statistical institutes.
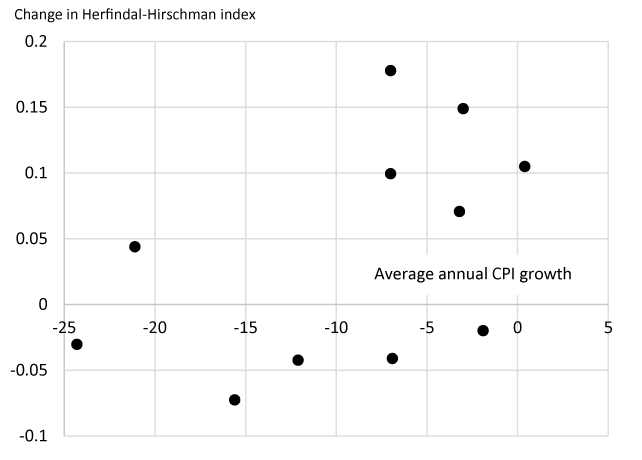
Note: HHI is sum of squared market share by company. Finland is omitted.
Source: National statistical institutes; author's calculations using IDC Research, Inc. data.
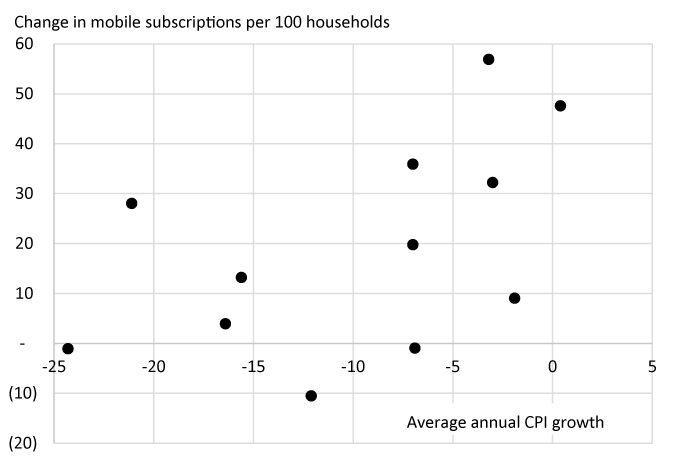
Note: Subscription data through 2017.
Source: National statistical institutes; World Bank World Development Indicators.
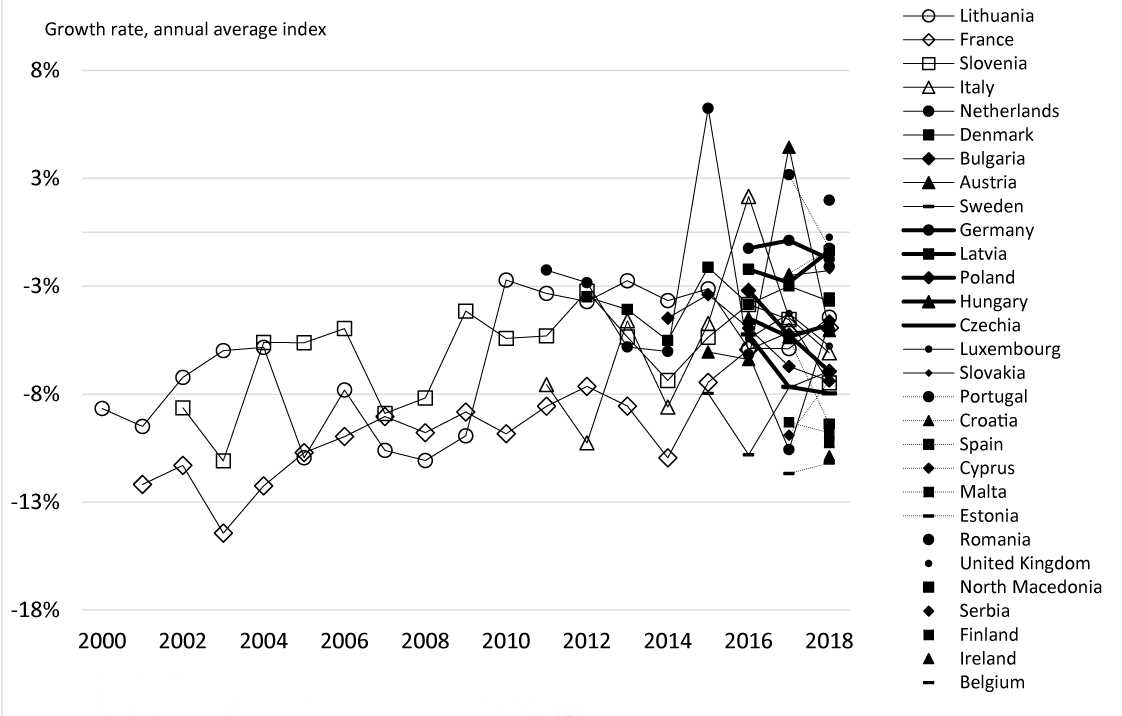
Note: Mobile phone index divided by country HICP for all items.
Source: Eurostat.
Appendix
The elementary price index formulas referenced in the text are included here. The price index relative to the prior period, $$P_t$$ , are shown as a function of item prices, $$p_{i,t}$$ , for those items in the basket in period $$t$$, $$\Omega_t$$. Price index levels are constructed by setting the base period equal to 100 and multiplying by the relative prices in a cumulative fashion. For simplicity, the issue of unbalanced price series are ignored. That is, these formulas assume prices are available for all items in current and prior periods or suitable imputations are available in the cases of entering and exiting products.
Carli
$$$$ P_t= \frac{1}{n_t} \sum_{i \in \Omega_t} \frac{p_{i,t}}{p_{i,t-1}} $$$$
Dutot
$$$$ P_t = \frac{ \frac{1}{n_t} \sum_{i \in \Omega_t} p_{i,t} }{ \frac{1}{n_{t-1}} \sum_{i \in \Omega_{t-1}} p_{i,t-1} } $$$$
Jevons
$$$$ P_t= \frac{ (\Pi_{i \in \Omega_t} p_{i,t} )^{\frac{1}{n_t}} }{ (\Pi_{i \in \Omega_{t-1}} p_{i,t-1})^{\frac{1}{n_{t-1}}} } $$$$
References
Ahmad, N., Ribarsky, J. and Reinsdorf, M. (2017), "Can potential mismeasurement of the digital economy explain the post-crisis slowdown in GDP and productivity growth?".
Aizcorbe, A., Byrne, D. and Sichel, D. (2019) Getting Smart About Phones: New Price Indexes and the Allocation of Spending Between Devices and Services Plans in Personal Consumption Expenditures .
Aizcorbe, A. (2014), A Practical Guide to Price Index and Hedonic Techniques, New York, NY: Oxford University Press.
Bean, C. (2016), "Independent review of UK economic statistics," Chancellor of the Exchequer, London.
Brynjolfsson, E., Collis, A. and Eggers, F. (2019), "Using massive online choice experiments to measure changes in well-being," Proceedings of the National Academy of Sciences of the United States of America , 116, 7250-7255.
Byrne, D. and Corrado, C. (2019), "Accounting for Innovations in Consumer Digital Services: IT still matters," Finance and Economics Discussion Series .
Byrne, D. M. and Corrado, C. A. (2017a), "ICT Services and Their Prices: What Do They Tell Us about Productivity and Technology?," International Productivity Monitor, vol. 33, pp. 150-181.
Byrne, D. and Corrado, C. (2017b), "ICT Asset prices: marshaling evidence into new measures," Finance and Economics Discussion Series , 2017-016.
Byrne, D., Corrado, C. and Sichel, D. (2017), "The Rise of Cloud Computing: Minding your Ps, Qs and Ks," in Measuring and Accounting for Innovation in the 21st Century. University of Chicago Press.
Byrne, D. and Pinto, E. (2015), "The Recent Slowdown in High-Tech Equipment Price Declines and some Implications for Business Investment and Labor Productivity," FEDS Notes.
Eurostat. (2018), Harmonized Index of Consumer Prices (HICP) Methodological Manual, Luxembourg: Eurostat.
Jorgenson, D. (2001), "Information Technology and the U.S. Economy," American Economic Review , 91, 1-32.
Jorgenson, D., Ho, M. and Stiroh, K. (2008), "A Retrospective Look at the U.S. Productivity Growth Resurgence," Journal of Economic Perspectives , 22, 3-24.
Oliner, S. and Sichel, D., 2000. "The resurgence of growth in the late 1990s: is information technology the story?". Journal of Economic Perspectives, 14(4), pp.3-22.
Silver, M. and Heravi, S. (2007), "Why elementary price index number formulas differ: Evidence on price dispersion," Journal of Econometrics , 140, 874-883.
Triplett, J. (2006), Handbook on Hedonic Indexes and Quality Adjustments in Price Indexes: Special Application to Information Technology Products. Paris and Washington, D.C.: Organisation for Economic Co-operation and Development.
1. Author affiliation: Federal Reserve Board of Governors. ([email protected]) This paper is not an expression of the views of the Board of Governors. The author thanks Ana Aizcorbe, Marshall Reinsdorf, Dan Sichel, and Rob Vigfusson for helpful comments and the staffs of the national statistical institutes of the countries covered in this study. Return to text
2. See references to this literature in Triplett (2006) and Aizcorbe (2014). Return to text
3. See Jorgenson (2001) on the importance of ICT. Oliner and Sichel (2002); Jorgenson, Ho, and Stiroh (2008); and Byrne and Corrado (2017a) explore the contribution of ICT to productivity growth. Return to text
4. An incomplete list: Byrne, Corrado, and Sichel (2018) consider the importance of the shift in the business sector to cloud computing; Byrne and Corrado (2019) examine the consumer ICT ecosystem since the emergence of radical mobility and free services; Brynjolfsson, Collis and Eggers (2019) break new measurement ground to assess the value of the new wave of consumer ICT. Return to text
5. Mobile phone CPIs are shown in figure 1 relative to the overall consumer price index. This is an imperfect adjustment for cross-country comparability. The domestically-purchased value added--shipping, insurance, wholesale and retail costs--are presumably affected by the aggregate economic forces behind the general rate of inflation, but the cost of the assembled phone may not be. In any event, the adjustment only changes the standard deviation of country mobile phone CPI growth rates differs by 0.1 percentage point. Exchange rate movements appear to be a second-order issue as well. If one assumes mobile phones are shipped from China and removes the appreciation of the domestic currency versus the Chinese Yuan, the standard deviation of the average annual rate of change for mobile phone CPIs is reduced from 8.3 to 7.6. Return to text
6. Other issues that may contribute to measurement challenges include (1) pricing schemes for mobile phones, such as the bundling of equipment and services, (2) the frequency with which the basket of items priced is refreshed, and (3) the omission of weights at the elementary index level. Return to text
7. The average growth rate for an unpublished index for mobile phones available from the Australian Bureau of Statistics differs only slightly from the index employed in this note from 2014 to 2018. Return to text
8. The approximate mobile phone shares of the index baskets was conveyed to the author in communication with the NSIs of Canada, New Zealand, and the United States. Return to text
9. This section discusses what is known about NSI practices for CPIs in general. The methods employed for mobile phones in particular are not specified in NSI documentation in most cases. Return to text
10. Importantly, one need not employ hedonics to successfully account for quality change; any of the methods in the standard NSI toolkit, when used appropriately, can do so. Return to text
11. The New Zealand mobile phone price index uses a Törnqvist formula, which is distinguished from the other formulas by the use of weights. In particular, a Törnqvist index weights relative prices using the simple average of item expenditure weights in the current and previous observation periods. Information was not found on the formula employed by China. Return to text
12. Silver and Heravi derive a formula under the assumption that prices are log-normally distributed where the Jevons relative price equals the Dutot relative price times a function of the change in the variance of log-prices between periods. The coefficient of variation is used here instead to simply illustrate the presence of rising dispersion. Return to text
Byrne, David (2019). "The Mysterious Cross-Country Dispersion in Mobile Phone Price Trends," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, August 5, 2019, https://doi.org/10.17016/2380-7172.2413.
Disclaimer: FEDS Notes are articles in which Board staff offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers and IFDP papers.