FEDS Notes
September 21, 2020
Avoiding Sovereign Default Contagion: A Normative Analysis
Sergio de Ferra1 and Enrico Mallucci2
1. Introduction
Sovereign debt crises happen in waves, spreading from one country to the other. The euro-area debt crisis of 2011-12 is a good example of that. Stress in the sovereign debt market quickly spread from Greece and Ireland to Portugal, Spain, and Italy. Following this crisis, an interesting debate has emerged on the desirability of cross-country arrangements aimed at reducing contagion in the sovereign market. On the one side, some have argued that such arrangements are needed to reduce cross-country spillovers. On the other side, some have expressed concerns that cross-country arrangements may lead to moral hazard, with countries issuing excessive debt and defaulting more frequently.
Most recently, the debate has gained renewed attention in the euro area in light of the fiscal stress imposed on some countries by the COVID-19 crisis. This note highlights how the work of de Ferra and Mallucci (2020) speaks to this debate. Through the lens of a two-country sovereign default model, we quantitatively evaluate how a set of cross-country policies affects governments' borrowing decisions, default risk, and households' welfare. We find that ex-post policies, such as bailouts, are counterproductive as they induce moral hazard and lead to a decline in welfare. On the contrary, ex-ante policies, such as a closer coordination of governments' borrowing policies, are effective as they mitigate contagion and improve welfare.
2. Methodology
We develop a two-country endogenous sovereign default model that builds on the work of Arellano (2008) and Arellano et al. (2017). The model economy is composed of two countries--Periphery and Outskirt—that reproduce the behavior of two euro-area peripheral economies and a continuum of common lenders. A key feature of the model is that the lenders are risk averse as in Lizarzo (2013) and Pouzo and Presno (2016). Hence, the price of government bonds not only depends on credit risk, but also on investors' wealth.3 This feature introduces the possibility of cross-country contagion. The borrowing and default decisions in one country affect investors' wealth and, thereby, government bond prices and the borrowing and default policies of the other country.
The model economy is calibrated to the euro-area periphery. In particular, we calibrate Outskirt so that it replicates the annual evolution of Italy, while Periphery is calibrated so that it replicates the rest of the euro-area periphery: Greece, Portugal, and Spain.
3. Contagion
When either of the two countries defaults, investors suffer a wealth loss. This loss, in turn, affects investors' propensity to lend to the other country. Panel A in Figure 1 plots the price function for Outskirt's debt when Periphery enjoys market access and when it does not. When Periphery cannot issue debt, Outskirt's borrowing terms worsen.
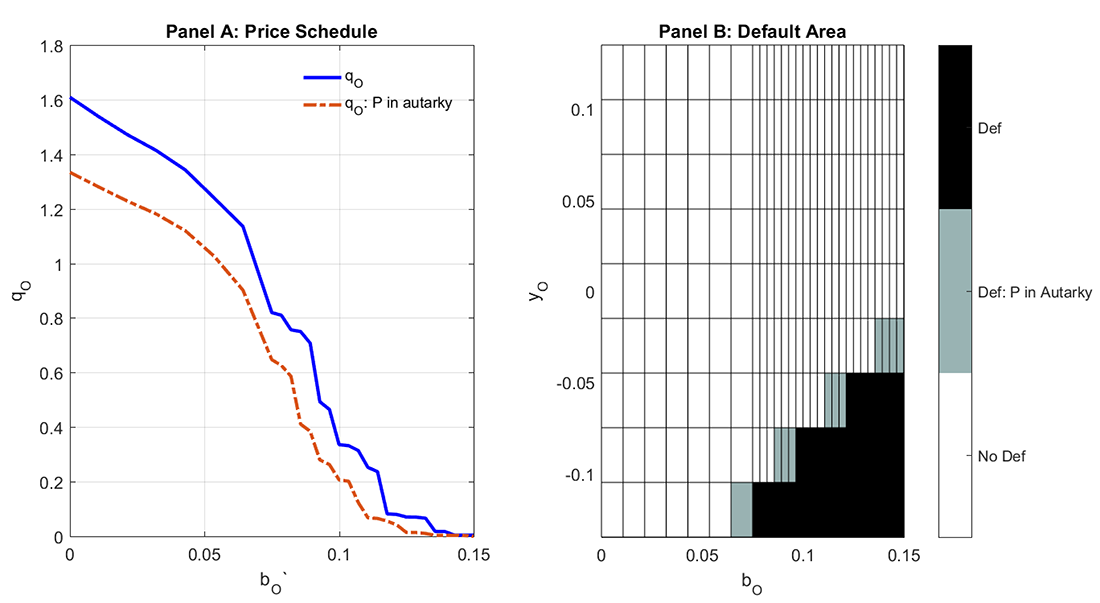
Panel A reports the price function for Outskirt's debt (y-axis) as a function of Outskirt's debt supply (x-axis). The blue line corresponds to the case in which Periphery enjoys market access, while the orange line corresponds to the case in which Periphery is in autarky--that is Periphery has no access to international financial markets--. Panel B, plots Outskirt's default set as a function of Outskirt's debt (x-axis) and endowment (y-axis) and for a given productivity and debt level in the Periphery.
Cross-country spillovers may even lead to "sovereign default contagion". That is, defaults in one country may trigger defaults in the other country. As shown in Panel B of Figure 1, Outskirt's default area expands when the Periphery has no access to financial markets implying that defaults in Periphery increase the likelihood of a default in Outskirt.
To quantify the importance of cross-country spillovers, we compare borrowing terms in our benchmark model with borrowing terms in an alternative scenario that eliminates cross-country contagion. Results are reported in Table 1. We find that spreads in Outskirt and Periphery are roughly 25% lower after we eliminate spillovers and that the incidence of defaults declines. Our results are consistent with those of Beirne and Fratzscher (2013), who find that spreads in the euro-area periphery are, on average, 27% percent lower when spillovers from other euro-area economies are filtered out.
Table 1. Cross-Country Spillovers
| Moments | Data | Model | Model without Spillovers |
|---|---|---|---|
| Mean Spread O | 99 | 103 | 66 |
| Mean Spread P | 204 | 231 | 173 |
| Mean Def Rate O | − | 0.70% | 0.50% |
| Mean Def Rate P | 2.10% | 1.70% | 1.40% |
Table 1 compares key moment from the data, from the benchmark model and from the modified model without spillovers.
4. Normative Analysis
We evaluate whether cross-country arrangements can reduce the risk of contagion and improve welfare. In particular, in light of the ongoing debate around the euro area, we examine ex-post policies, such as bailouts, that are implemented after defaults are announced as well as ex-ante policies, such as borrowing rules, which are implemented before defaults are announced.
4.1. Ex-post Bailouts
We begin our analysis by looking at the case of bailouts. When either of the two countries announces a plan to default, the other country can come to rescue with one-off transfers.4 We focus the attention on bailouts that benefit both countries: The receiving country is better off receiving the transfer rather than defaulting; and the supplying country is better off paying the transfer rather than letting the other country default.
Table 2 compares key moments in the data (column 1) with those obtained from our benchmark model (column 2) and those obtained from the modified model that allows for bailouts (columns 3). We find that bailouts induce moral hazard. Following the introduction of bailouts, debt-to-GDP ratios increase and so do spreads suggesting that government relax their borrowing policies, anticipating that they will be bailed out in the event of the crisis. 5 Furthermore, bailouts happen fairly frequently as once every 25 years either of the two countries receives a bailout with an average size close to 0.6% of GDP.
Table 2. Economic Dynamics
| Moments | Data | Model | Bailouts | Central Borrower |
|---|---|---|---|---|
| Mean Debt/GDP O | 7% | 7% | 9% | 6% |
| Mean Debt/GDP P | 6% | 6% | 8% | 5% |
| Mean Spread O | 99 | 103 | 285 | 52 |
| Mean Spread P | 204 | 231 | 300 | 136 |
| Bailout Rate O | - | - | 1.30% | - |
| Bailout Rate P | - | - | 2.70% | - |
| Mean Transfer/GDP O | - | - | 0.72% | - |
| Mean Transfer/GDP P | - | - | 0.55% | - |
Table 2 reports average moments obtained from model simulation. The model is simulated 200 times for 10,000 periods. The first column reports moments from the data. The second column reports moments obtained from our benchmark economy. The third column reports moments obtained when bailouts are introduced. Finally, the last column reports moments obtained when the borrowing decision is taken by the central borrower.
4.2. Ex-ante Borrowing rules
Given the undesirable implications of bailouts, we proceed by studying ex-ante rules that aim to mitigate cross-country contagion and prevent defaults before they occur. In particular, we characterize the optimal borrowing decision of a central planner that takes the borrowing decisions on behalf of the two governments maximizing the joint welfare of Outskirt and Periphery. This scenario captures the existence of supranational fiscal rules that limit governments' ability to borrow.6
Column (4) in Table 2 shows that the central planner borrows less and defaults less frequently than individual governments. Thus, spreads also decline. These results suggest that, in a multi-country setting with cross-country contagion, the socially optimal debt level is lower than the individually optimal one.
Admittedly, the institution of a central borrower may be extremely complicated to implement, as countries need to give up their fiscal sovereignty. However, we show that the central-planner equilibrium can be achieved in a decentralized setting with the introduction of Pigouvian taxes on government debt. Table 3 characterizes the optimal taxes that replicate central borrower's allocation. Such taxes should be higher when output is low, when debt is high, and when spreads are high.
Table 3. Pigouvian Taxation
| Moments | $$\bar{\tau}_i$$ | $$\rho(\tau_i, y_i)|b_i = \bar{b}_i $$ | $$\rho(\tau_i, b_i)|y_i = \bar{y}_i $$ | $$\rho(\tau_i, {spread}_i)$$ |
|---|---|---|---|---|
| i = Outskirt | 2.60% | −0.37 | 0.29 | 0.08 |
| i = Periphery | 6.70% | −0.50 | 0.31 | 0.25 |
Table 3 reports moments for the Pigouvian tax rate $$\tau$$ that replicates the borrowing policies of the central borrower. Moments are computed simulating the model 200 times over 10,000 periods. The first column reports average tax rates in Outskirt and Periphery. The second column reports the correlation between that optimal tax rate and output, conditional on the debt level being equal to its long-run average. The third column reports the correlation between the optimal tax rate and the debt level, conditional on the output being equal to its mean level. Finally, the last column reports the unconditional correlation between the optimal tax rate and spreads.
4.3. Welfare Analysis
Do policies that reduce cross-country contagion improve welfare? To answer this question, we compute consumption-equivalent welfare changes that make agents indifferent between an economy in which such policies are implemented and the benchmark economy.7
Results are reported in Table 4. Bailouts reduce the welfare of borrowing countries as higher debt levels reduce consumption. Investors, instead, gain from bailouts as higher debt levels translate into higher investors' wealth. The institution of a central borrower, instead, improves the welfare of borrowers as debt levels decline and government devote less resources to servicing the debt. Investors' welfare declines as lower government debt translates into lower investors' wealth.
Table 4. Welfare Gains
| Bailouts | Central Borrower | |
|---|---|---|
| $$\Delta^W_O$$ | -0.15% | 0.06% |
| $$\Delta^W_P$$ | -0.11% | 0.12% |
| $$\Delta^W_I$$ | 0.42% | -0.07% |
Table 4 reports consumption equivalent welfare changes computed simulating our model 200 times over 10,000 periods. $$\Delta^W_O$$ is the consumption equivalent welfare change that makes Outskirt indifferent between the two scenarios. $$\Delta^W_P$$ is the consumption equivalent welfare change for Periphery. $$\Delta^W_I$$is the consumption equivalent welfare change for investors. The first column reports welfare gains associated with anticipated bailouts. The second column reports welfare gains associated with the central borrower.
References
Arellano, Cristina, "Default Risk and Income Fluctuations in Emerging Economies," American Economic Review, 2008, 98 (3), 690–712.
Yan Bai, and Sandra Lizarazo, "Sovereign Risk Contagion," NBER Working Papers 24031, National Bureau of Economic Research, Inc. November 2017.
Beirne, John and Marcel Fratzscher, "The pricing of sovereign risk and contagion during the European sovereign debt crisis," Journal of International Money and Finance, 2013, 34 (C), 60–82.
de Ferra, Sergio and Enrico Mallucci, "Avoiding Sovereign Default Contagion: A Normative Analysis," International Finance Discussion Papers 1275, Board of Governors of the Federal Reserve System (U.S.) February 2020.
Lizarazo, Sandra Valentina, "Default risk and risk averse international investors," Journal of International Economics, 2013, 89 (2), 317–330.
Pouzo, Demian and Ignacio Presno, "Sovereign Default Risk and Uncertainty Premia," American Economic Journal: Macroeconomics, July 2016, 8 (3), 230–266.
1. Stockholm University. E-mail: [email protected]. Return to text
2. Board of Governors of the Federal Reserve System, Washington, D.C. 20551 U.S.A.. E-mail: [email protected]. Return to text
3. Risk-averse investors dislike fluctuations in their consumption path and are less willing to buy risky debt when their wealth is low. Risk-neutral investors, instead, are only concerned about the expected payoff of assets and wealth fluctuations do not affect their behavior. Return to text
4. It is assumed that both Outskirt and Periphery have perfect information about the state of the economy in the other country. Thus, governments cannot announce defaults strategically. Return to text
5. The model is calibrated to reproduce the average ratio of the short-term external government debt and GDP, which is 7% and 6% respectively in the two country blocks. Return to text
6. In this case, such rules are so stringent that the central borrower fully controls borrowing decisions. Return to text
7. Formally, let $$c^*_i$$ be agent's $$i$$ equilibrium consumption in the benchmark economy and let $$c^{**}_i$$ be agent's $$i$$ equilibrium when policies that mitigate contagion are implemented. The consumption welfare change $$\Delta w$$ that makes agent $$i$$ indifferent between the two scenarios solves: $$W (c^*_i (1 + \Delta w)) = W (c^{**})$$
de Ferra, Sergio, and Enrico Mallucci (2020). "Avoiding Sovereign Default Contagion: A Normative Analysis," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, September 21, 2020, https://doi.org/10.17016/2380-7172.2600.
Disclaimer: FEDS Notes are articles in which Board staff offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers and IFDP papers.