IFDP Notes
October 23, 2018
BAT Signals from Asset Markets: Estimating the U.S. Dollar Response to a Destination-Based Cash-Flow Tax1
Tessa Morrison and Robert Vigfusson
Introduction
In early 2017, there was substantial discussion about changing the U.S. corporate tax system to a destination-based cash-flow tax (DBCFT). The DBCFT proposal, also often referred to as a border-adjusted tax (BAT), would exclude exports from taxable revenues and exclude imports from allowable deductions.
The discussion highlighted that the economic implications of switching to a BAT depended crucially on how the exchange rate would respond. The BAT proposal, by introducing an effective export subsidy and an effective import tax relative to the existing system, could potentially encourage exports and discourage imports. Given that the proposed rate of the BAT is 20 percent, the effect could be dramatic. But the effects depend on how much the exchange value of the dollar responds. Proponents of the BAT, such as Auerbach (2017), argued that the dollar would appreciate sufficiently to offset the direct effects on export and imports of the tax and would therefore not distort international trade. However, Erceg, Prestipino and Raffo (2018) cast doubt on those claims. Their structural macroeconomic models would imply that the response to such a tax change would be only half as large as would be needed to isolate the economy from the effects of a BAT tax change. In contrast, the model in Barbiero, Farhi, Gopinath and Itskhoki (2018) implies that the dollar appreciates by almost as much as the tax adjustment. Finally, Linde and Pescatori (2017) finds that the amount of exchange rate appreciation is conditional on a number of modeling assumptions. Given the differences in model-derived results, empirical evidence regarding the responsiveness of the dollar would be helpful. But the challenge in assessing the effects of a BAT is that there are very few historical episodes that can guide us in how much the exchange rate might respond.
In order to provide some empirical evidence, we use daily asset price movements in late 2016 and early 2017 to assess the likelihood that market participants attached to the passage of the BAT and, conditional on passage, how much they expected the dollar to appreciate.
Although the actual tax bill that was passed in late 2017 is a territorial-based tax system rather than a destination-based system, our estimates may still be useful in quantifying the expected effects of a destination-based system should such a system be considered in the future either in the United States or elsewhere.
Our methodology, based on movements in oil prices, stock prices, and the exchange value of the dollar, suggest that market participants' estimates of the probability of passage of BAT peaked on March 7, 2017, with an estimated probability almost 20 percentage points higher relative to its value before the November 2016 U.S. election. Subsequently, the estimated probability declined and continued to decline through late April, when the White House first announced a tax plan that excluded a border tax. In addition, according to our estimates, market participants expected that the dollar would increase less than half as much as the proposed magnitude of the border tax, suggesting that market participants were not expecting dollar appreciation to fully offset the direct effects of the BAT on international trade.
Data and Model
We consider three asset prices that are likely to be affected by passage of the BAT.
The first is oil prices. We look at the difference between oil prices for Brent and WTI, which is referred to as the spread. The price of Brent is the benchmark price for international crude, whereas the price of WTI (West Texas Intermediate) is the benchmark price for crude produced in the United States. Rather than looking at the current price of oil, we consider the futures quotes for oil to be delivered 12 months in the future.
Because oil imports would no longer be deductible and oil exports would not be taxed, passage of the BAT would discourage U.S. imports of foreign crude and encourage U.S. exports of domestic crude. Passage of the BAT should therefore cause the spread to narrow from its current positive value.
Our analysis is based on the following derivation. Define the spread one year from today as
$$Z_{t+k}=P^{Brent}_{t+k} – P^{WTI}_{t+k},$$
where $$t+k$$ denotes the value one year from now. The expected value of the spread $$EZ_{t+k}$$ today is related to its expected value conditional on the BAT becoming law $$E(Z_{t+k}\vert BAT),$$ its expected value conditional on the BAT not being passed $$E(Z_{t+k}\vert No BAT),$$ and the probability that the BAT becomes law $$Prob(BAT)$$ in the following way:
$$EZ_{t+k} = Prob(BAT) * (E(Z_{t+k}\vert BAT))+(1-Prob(BAT))*(E(Z_{t+k}\vert NoBAT)),$$
or equivalently
$$E(Z_{t+k})=Prob(BAT)*(E(Z_{t+k}\vert BAT)-E(Z_{t+k}\vert No BAT))+E(Z_{t+k}\vert No BAT).$$
Futures quotes that are reported today for Brent and WTI to be delivered 12 months in the future are equal to the expected values of the respective oil price plus a risk premium.
$$F^{WTI}_{t,k}=EP^{WTI}_{t+k}+\phi^{WTI}_{t}$$
and
$$F^{Brent}_{t,k}=EP^{Brent}_{t+k}+\phi^{Brent}_{t}$$
(Note that the time subscript for daily data somewhat obscures that future quotes are expressed as delivery for a specific month rather than for a specific day. However, this distinction is not important for our analysis.)
Therefore the spread based on futures quotes can be defined as
$$X_{t}=F^{Brent}_{t,k}-F^{WTI}_{t,k}$$
which can be rewritten as
$$X_{t}=EZ_{t+k}+\phi^{Brent}_{t}-\phi^{WTI}_{t}.$$
Therefore we have that the spread based on futures quotes can be written as:
$$X_{t}=E(Z_{t+k}\vert No BAT)+Prob(BAT)_{t}*(E*Z_{t+k}\vert BAT)-E(Z_{t+k}\vert No BAT))+\phi^{Brent}_{t}-\phi^{WTI}_{t}.$$
Now we must make some strong identifying assumptions. First, we assume that daily changes in the differential of the risk premium are not correlated with changes in the probability of BAT passage. Second we assume that $$E(Z_{t+k}\vert BAT)$$ and $$E(Z_{t+k}\vert No BAT)$$ are constant during our estimation period. In other words, we assume that, during late 2016 and early 2017, no major disruptions changed the expected spread except for changing probabilities of BAT passage. Taking the first difference of this equation where
$$\Delta X_{t}=X_{t}-X_{t-1}$$,
we have that
$$\Delta X_{t}=\Delta Prob(BAT)_{t}*(E(Z_{t+k}\vert BAT)-E(Z_{t+k}\vert No BAT))+\Delta\phi^{Brent}_{t}-\Delta\phi^{WTI}_{t}$$
Therefore, the resulting equation can be written as
$$\Delta X_{t}=\Delta Prob(BAT)_{t}*\lambda_{x}+\upsilon^{x}_{t}$$
where
$$\lambda_{x}=E(Z_{t+k}\vert BAT)-E(Z_{t+k}\vert NoBAT)$$
The additional variable $$\upsilon^{x}_{t}$$ represents both changes to the risk premium plus any other shocks to the system that are not correlated with changes in the probability that the BAT becomes law.
Knowing the value of $$\lambda_{x}$$ is needed to identify the value of $$\Delta Prob(BAT)$$. Therefore, our working assumption is that BAT passage will cause next year's spread to equal 0, whereas, a lack of passage implies that the spread will be its historical value over the past year. This assumption for $$\lambda_{x}$$ is likely a reasonable upper bound on its true value. If the true value of $$\lambda_{x}$$ would be half its assumed value, then the estimated value of $$\Delta Prob(BAT)_{t}$$ would be twice its actual value.
In isolation, changes in oil price spreads could not determine what are movements in $$\Delta Prob(BAT)_{t}$$ versus movements in $$\upsilon^{x}_{t}$$. However, by studying simultaneous movements in two other variables that are also affected by $$\Delta Prob(BAT)_{t}$$, the exchange value of the dollar and the relative return on stock prices of U.S. retailers, we can estimate $$\Delta Prob(DBCFT)$$.
The other two variables in our analysis will be
-
Changes in the exchange rate, $$\Delta S$$ – Increased probability of BAT passage should cause the dollar to appreciate. The exchange rate is measured using a weighted average of the foreign exchange value of the dollar against the currencies of major advanced U.S. trading partners. As is discussed in Auerbach et al. (2017), in theory, the BAT should result in enough dollar appreciation to offset the differential tax treatment under BAT of imports and exports. However, in our analysis, we do not assume that effect, but rather estimate the assumed rate of appreciation.
Our estimating equation is based on uncovered interest parity,
$$S_{t}=ES_{t+k}+i_{t}+\phi^{S}_{t}+u^{S}_{t},$$
according to which the current exchange rate equals the expected exchange rate plus the differential between domestic and foreign interest rates, a risk premium, and an error term.
With a similar derivation as above, the estimation equation becomes
$$\Delta S_{t} = \Delta Prob(BAT)_{t} * \lambda_{S} + \upsilon^{S}_{t}$$
where $$\upsilon^{S}_{t}$$ includes both any interest rate differential changes as well as any currency risk premium. The estimated value of $$\lambda_{s}$$ will be the expected rate of appreciation conditional on passage $$(S_{BAT} – S_{no BAT})$$.
- Changes in the daily return on U.S retail stocks minus the daily return on all U.S. stocks (excluding the oil sector), $$\Delta R$$. In early 2017, many newspapers articles reported that retailers were those most concerned about BAT passage, reflecting the retail sector's relatively greater reliance on imported goods. An increased probability of BAT passage should cause retail stocks to perform worse than the overall stock market. However, if the dollar were to increase completely to offset the effect of the BAT, then there should be no effect of the BAT on retail stocks performance over all U.S. stocks. Therefore, the resulting equation is
$$\Delta R_{t} = \Delta Prob(BAT)_{t} * \lambda_{R} + \upsilon^{R}_{t}.$$
Stacking these equations results in the following system of equations.
$$\left(\begin{align}&\Delta S_{t} \\ &\Delta R_{t}\\ &\Delta X_{t}\end{align}\right)=$$ $$\left(\begin{align}&\lambda_{S} \\ &\lambda_{R} \\ &\lambda_{X}\end{align}\right)$$ $$\Delta Prob(BAT)_{t}+\left(\begin{align}&\upsilon^{s}_{t} \\ &\upsilon^{R}_{t}\\ &\upsilon^{X}_{t}\end{align}\right).$$
We estimate this system of equations along with the following additional equation, the state equation.
$$\Delta Prob(BAT)_{t}=\phi\Delta Prob(BAT)_{t}+\epsilon_{t}.$$
The error term $$(\upsilon_{S}\quad\upsilon_{R}\quad\upsilon_{X})\prime$$ is assumed to be mean zero with a diagonal variance covariance matrix with variances $$(\sigma^{2}_{s}\quad\sigma^{2}_{R}\quad\sigma^{2}_{X})$$ and uncorreleated with $$\epsilon_{t}$$.
Our working assumption is that all of these asset prices will respond to changes in $$\Delta Prob(BAT)_{t}$$, but that the response of the exchange rate is not large enough to generate complete pass-through, which would leave the other asset prices unaffected. In addition, our exercise requires that no other common shock to all three variables exists. For example, although the literature on commodity currencies suggests that oil prices and exchange rates might be correlated, the price spread between Brent and WTI oil should not be correlated with the exchange rate.
The model is estimated on daily data from November 1, 2016 to April 27, 2017. Our estimation sample begins a week before the November 2016 U.S. election to capture any effects from the election and the end of the sample is when the White House released its tax proposal, which did not include a BAT. Being such a short period limits the ability of other events to influence the regression.
Results
Table 1 shows the model estimates. As mentioned above, the value of $$\lambda_{S}$$, is the expected rate of appreciation conditional on passage. Therefore, the expected appreciation of the dollar in response to BAT becoming law would be about 8.6 percent. Such an estimate seems reasonable and is about half of the full response to a 20 percent BAT tax. The 90 percent confidence interval for $$\lambda_{S}$$ is from negative 5 to 22 percent. This confidence interval does include full appreciation; so we cannot reject the null hypothesis that the exchange rate response would be complete. However, given the point estimate, a partial response seems a better estimate of market participants' views.
In addition, as mentioned before, the estimated value of $$\lambda_{S}$$ is conditional on the assumed value for $$\lambda_{x}$$, the effect of the BAT on oil price spread. We have assumed a value of $$\lambda_{x}$$ that could be on the high side. If the true value of $$\lambda_{x}$$ is smaller than we have assumed, then the true value of $$\lambda_{S}$$ will be smaller than we have estimated.
Table 1: Coefficient Estimates
| Coefficient | Estimate | Standard Error |
|---|---|---|
| $$\phi$$ | 0.116 | 0.484 |
| $$\lambda_{S}$$ | 0.086 | 0.071 |
| $$\lambda_{x}$$ (Constrained) | -0.042 | |
| $$\lambda_{R}$$ | -0.324 | 1.854 |
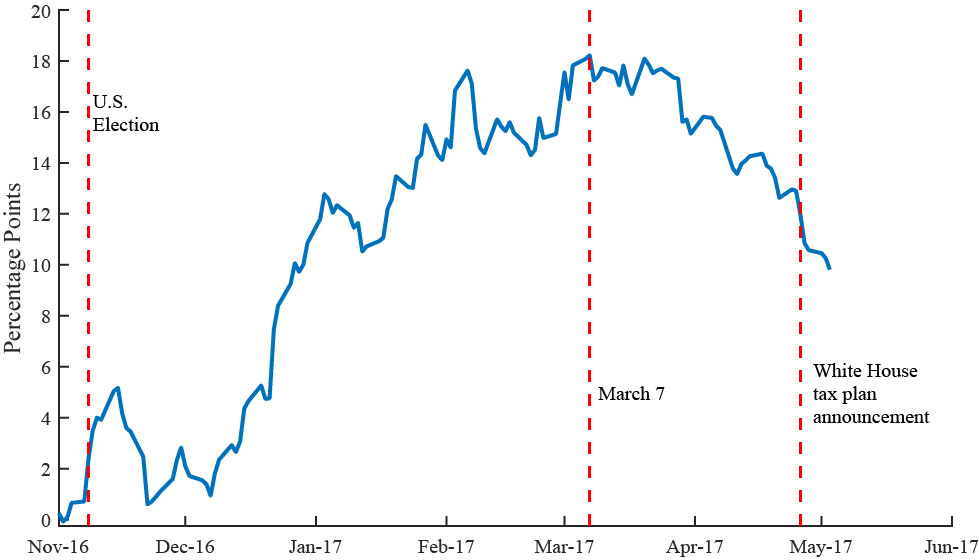
Figure 1 shows the estimated cumulative change in the probability of BAT passage since November 1, 2016. The probability of BAT passage peaked on March 7, 2017. Given our assumption of how much a BAT would affect the oil spread, the maximum increase in probability is 18 percentage points more likely than on November 1, 2016. The probability of BAT passage then steadily declines throughout the period leading up to the White House tax proposal announcement on April 26, 2017, thought it still remains 10 percentage points more likely than it was before the election.
Conclusion
Taken as a whole, the evidence suggests that the financial markets expected the dollar to appreciate only 8.6 percent in response to the proposed 20 percent BAT, and thus only partially insulate the economy from the effects of the BAT. It bears repeating that both the probability of BAT passage and the exchange rate response are estimated with some uncertainty. Moreover, at best we are only estimating what the markets think will happen. What actually happens could be different.
References
Auerbach, Alan J., Michael P. Devereux, Michael Keen, and John Vella, 2017 "Destination-Based Cash Flow Taxation" Oxford University Centre for Business Taxation WP 17/01; Oxford Legal Studies Research Paper No. 14/2017. http://dx.doi.org/10.2139/ssrn.2908158
Barbiero Omar, Emmanuel Farhi, Gita Gopinath and Oleg Itskhoki 2018, "The Macroeconomics of Border Taxes", NBER manuscript. http://papers.nber.org/conf_papers/f101756/f101756.pdf
Erceg, Christopher, Andrea Prestipino, and Andrea Raffo, 2018. "The Macroeconomic Effects of Trade Policy" Federal Reserve Board manuscript.
Linde, Jesper, and Andrea Pescatori 2017: "The Macroeconomic Effects of Trade Tariffs: Revisiting the Lerner Symmetry Result," CEPR Discussion Paper No. DP12534
1. When this note was being completed, Tessa Morrison was an Eranda Rothschild Foundation Junior Fellow at the Peterson Institute for International Economics (PIIE). Robert Vigfusson is an Assistant Director and Section Chief in the International Finance Division, Board of Governors of the Federal Reserve System, Washington DC 20551 U.S.A and can be reached at [email protected]. The views expressed are solely the responsibility of the authors. These views are not a product of a PIIE project nor were they subject to PIIE review. These views should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
Morrison, Tessa and Robert Vigfusson (2018). "BAT Signals from Asset Markets: Estimating the U.S. Dollar Response to a Destination-Based Cash Flow Tax," IFDP Notes. Washington: Board of Governors of the Federal Reserve System, October 2018., https://doi.org/10.17016/2573-2129.47.
Disclaimer: IFDP Notes are articles in which Board economists offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than IFDP Working Papers.